Understanding Future Climate in the Upper Awash Basin (UASB) with Selected Climate Model Outputs under CMIP6
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Used
2.2. Methodology
2.2.1. Climate Model Selection
2.2.2. Downscaling, Bias Adjustment, and Future Scenarios
3. Results
3.1. Selection of Climate Model
3.1.1. Identification of Distribution
3.1.2. Trend Analysis
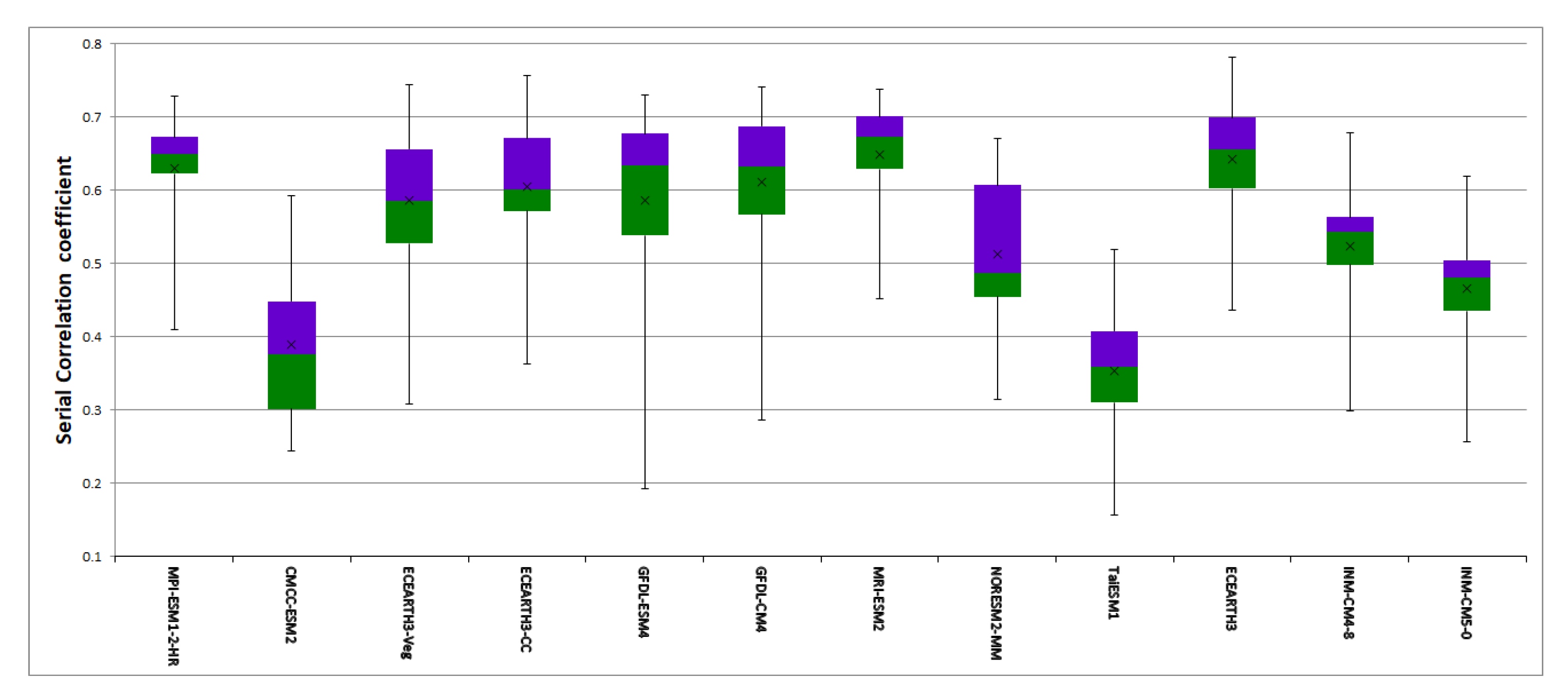
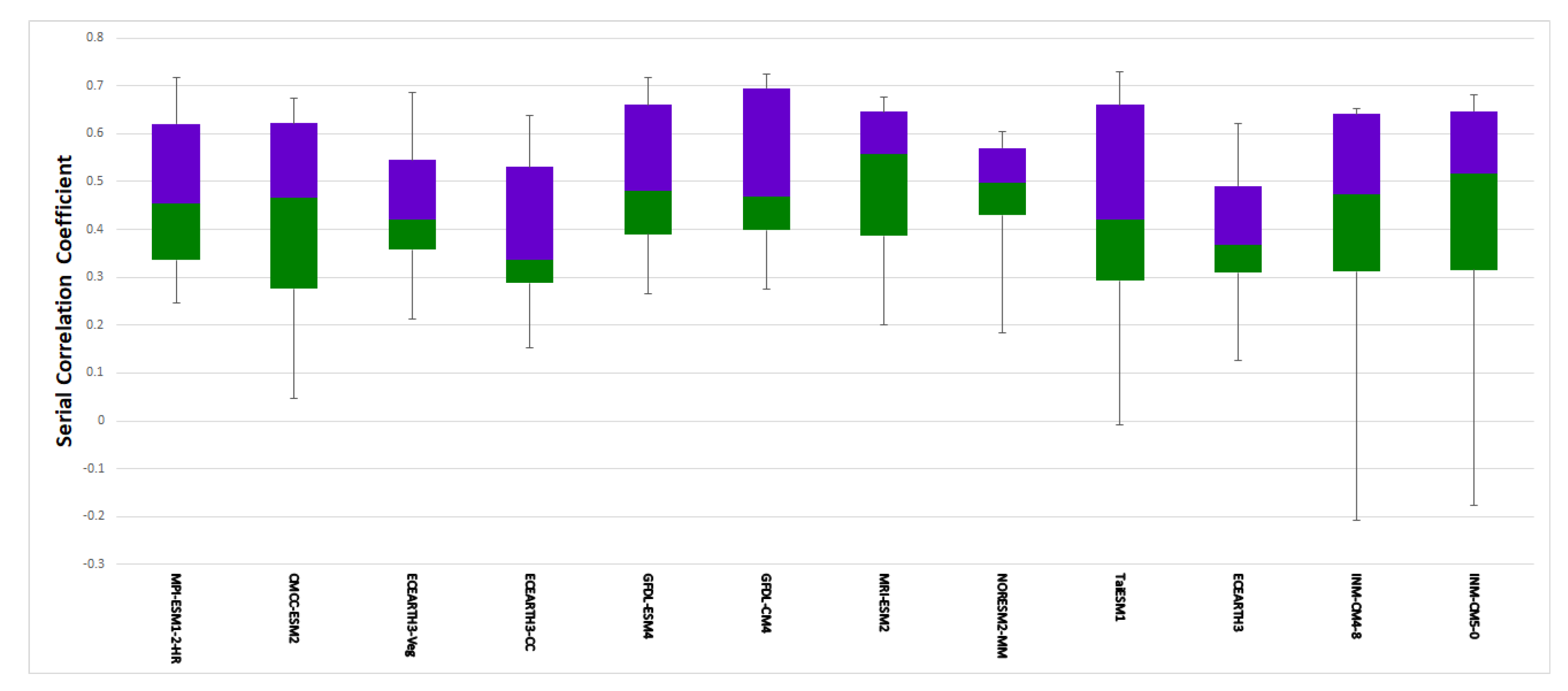
3.1.3. Performance Metrics
3.1.4. Time Series Clustering
3.1.5. Principal Component Analysis (PCA)
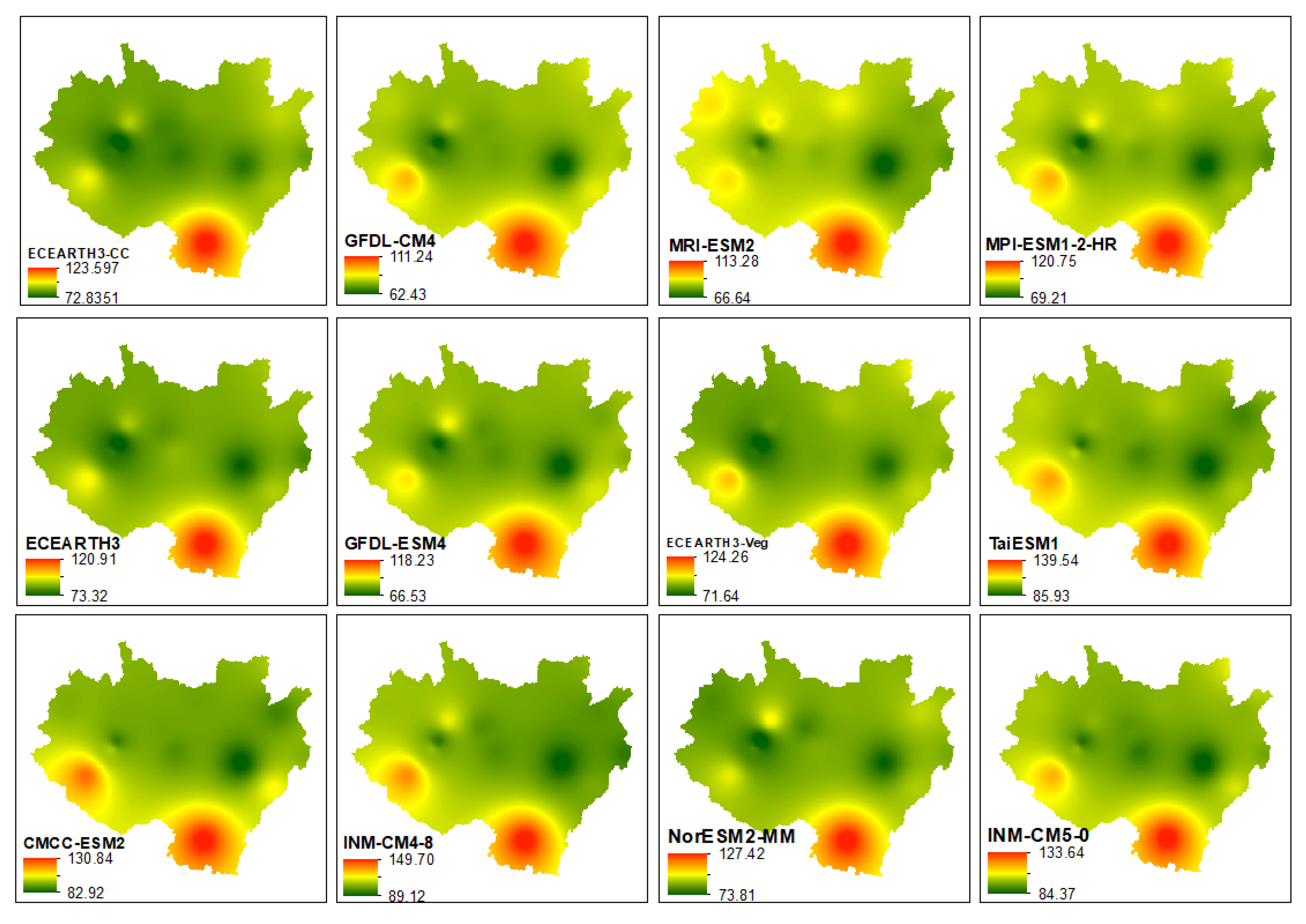
3.1.6. Spatial Performances of the Models
3.2. Model Ranking and Interpretation
3.3. Future Climate Projections
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Water, C. Leaving No One Behind. In The United Nations World Water Development Report Paris; UNESCO: Paris, France, 2019. [Google Scholar]
- Gleick, P.H. Water in Crisis; Oxford University Press: New York, NY, USA, 1993; Volume 100. [Google Scholar]
- Thakural, L.; Kumar, S.; Jain, S.K.; Ahmad, T. The impact of climate change on rainfall variability: A study in central himalayas. In Climate Change Impacts; Springer: Singapore, 2018; pp. 181–192. [Google Scholar]
- Shaaban, F.; Othman, A.; Habeebullah, T.M.; El-Saoud, W.A. An integrated GPR and geoinformatics approach for assessing potential risks of flash floods on high-voltage towers, Makkah, Saudi Arabia. Environ. Earth Sci. 2021, 80, 1–15. [Google Scholar] [CrossRef]
- Claire, S.; Denise, G. DroughtScape. 2019, pp. 3–6. Available online: https://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1052&context=droughtscape (accessed on 14 November 2022).
- NMA. Climate Change National Adaptation Programme of Action (NAPA) of Ethiopia; National Meteorological Services Agency (NMA), Ministry of Water Resources, Federal Democratic Republic of Ethiopia: Addis Ababa, Ethiopia, 2007. [Google Scholar]
- Shawul, A.A.; Chakma, S. Spatiotemporal detection of land use/land cover change in the large basin using integrated approaches of remote sensing and GIS in the Upper Awash basin, Ethiopia. Environ. Earth Sci. 2019, 78, 1–13. [Google Scholar] [CrossRef]
- Nanesa, K. Awash River’s the Ongoing Irrigation Practices, Future Projects and its Impacts on the Environment of Awash River Basin. Irrig. Drain. Syst. Eng. 2021, 10. [Google Scholar] [CrossRef]
- Aregahegn, Z.; Zerihun, M. Study on Irrigation Water Quality in the Rift Valley Areas of Awash River Basin, Ethiopia. Appl. Environ. Soil Sci. 2021, 2021, 8844745. [Google Scholar] [CrossRef]
- Mersha, A.N.; de Fraiture, C.; Masih, I.; Alamirew, T. Dilemmas of integrated water resources management implementation in the Awash River Basin, Ethiopia: Irrigation development versus environmental flows. Water Environ. J. 2021, 35, 402–416. [Google Scholar] [CrossRef]
- Edossa, D.C.; Babel, M.S.; Gupta, A.D. Drought analysis in the Awash river basin, Ethiopia. Water Resour. Manag. 2010, 24, 1441–1460. [Google Scholar] [CrossRef]
- Shenduli, P.R.; Van Andel, S.J.; Mamo, S.; Masih, I. Improving hydrological prediction with global datasets: Experiences with Brahmaputra, Upper Awash and Kaap catchments. In Proceedings of the E-Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]
- Edwards, P.N. History of climate modeling. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 128–139. [Google Scholar] [CrossRef]
- Bhuvandas, N.; Timbadiya, P.V.; Patel, P.L.; Porey, P.D. Review of downscaling methods in climate change and their role in hydrological studies. Int. J. Environ. Ecol. Geol. Mar. Eng. 2014, 8, 713–718. [Google Scholar]
- Soriano, E.; Mediero, L.; Garijo, C. Selection of bias correction methods to assess the impact of climate change on flood frequency curves. Water 2019, 11, 2266. [Google Scholar] [CrossRef]
- Lutz, A.F.; ter Maat, H.W.; Biemans, H.; Shrestha, A.B.; Wester, P.; Immerzeel, W.W. Selecting representative climate models for climate change impact studies: An advanced envelope-based selection approach. Int. J. Climatol. 2016, 36, 3988–4005. [Google Scholar] [CrossRef]
- Brief, C. How Do Climate Models Work? 2018. Available online: https://www.carbonbrief.org/qa-how-do-climate-models-work/ (accessed on 17 August 2021).
- Ayugi, B.; Zhihong, J.; Zhu, H.; Ngoma, H.; Babaousmail, H.; Rizwan, K.; Dike, V. Comparison of CMIP6 and CMIP5 models in simulating mean and extreme precipitation over East Africa. Int. J. Climatol. 2021, 41, 6474–6496. [Google Scholar] [CrossRef]
- Wilby, R. Evaluating climate model outputs for hydrological applications. Hydrol. Sci. J. J. Des. Sci. Hydrol. 2010, 55, 1090–1093. [Google Scholar] [CrossRef]
- Khayyun, T.S.; Alwan, I.A.; Hayder, A.M. Selection of suitable precipitation CMIP-5 sets of GCMs for Iraq using a symmetrical uncertainty filter. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 671, p. 012013. [Google Scholar]
- Homsi, R.; Shiru, M.S.; Shahid, S.; Ismail, T.; Harun, S.B.; Al-Ansari, N.; Chau, K.W.; Yaseen, Z.M. Precipitation projection using a CMIP5 GCM ensemble model: A regional investigation of Syria. Eng. Appl. Comput. Fluid Mech. 2020, 14, 90–106. [Google Scholar] [CrossRef]
- Samadi, S.Z.; Sagareswar, G.; Tajiki, M. Comparison of general circulation models: Methodology for selecting the best GCM in Kermanshah Synoptic Station, Iran. Int. J. Glob. Warm. 2010, 2, 347–365. [Google Scholar] [CrossRef]
- Pitman, A.; Perkins, S. Reducing uncertainty in selecting climate models for hydrological impact assessments. IAHS Publ. 2007, 313, 3. [Google Scholar]
- Alemseged, T.H.; Tom, R. Evaluation of regional climate model simulations of rainfall over the Upper Blue Nile basin. Atmos. Res. 2015, 161, 57–64. [Google Scholar] [CrossRef]
- Ongoma, V.; Chen, H.; Gao, C. Evaluation of CMIP5 twentieth century rainfall simulation over the equatorial East Africa. Theor. Appl. Climatol. 2019, 135, 893–910. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Symmetrical uncertainty and random forest for the evaluation of gridded precipitation and temperature data. Atmos. Res. 2019, 230, 104632. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Rana, A.; Moradkhani, H.; Sharma, A. Multi-criteria evaluation of CMIP5 GCMs for climate change impact analysis. Theor. Appl. Climatol. 2017, 128, 71–87. [Google Scholar] [CrossRef]
- Rana, A.; Madan, S.; Bengtsson, L. Performance evaluation of regional climate models (RCMs) in determining precipitation characteristics for Gothenburg, Sweden. Hydrol. Res. 2014, 45, 703–714. [Google Scholar] [CrossRef]
- Wilcke, R.A.; Bärring, L. Selecting regional climate scenarios for impact modelling studies. Environ. Model. Softw. 2016, 78, 191–201. [Google Scholar] [CrossRef]
- Friedman, J.H. Data Mining and Statistics: What’s the connection? Comput. Sci. Stat. 1998, 29, 3–9. [Google Scholar]
- Srinivasa Raju, K.; Nagesh Kumar, D. Ranking general circulation models for India using TOPSIS. J. Water Clim. Chang. 2015, 6, 288–299. [Google Scholar] [CrossRef]
- Hailemariam, K. Impact of climate change on the water resources of Awash River Basin, Ethiopia. Clim. Res. 1999, 12, 91–96. [Google Scholar] [CrossRef]
- Taye, M.T.; Dyer, E.; Hirpa, F.A.; Charles, K. Climate change impact on water resources in the Awash basin, Ethiopia. Water 2018, 10, 1560. [Google Scholar] [CrossRef]
- Tadese, M.T.; Kumar, L.; Koech, R. Climate change projections in the Awash River Basin of Ethiopia using Global and Regional climate models. Int. J. Climatol. 2020, 40, 3649–3666. [Google Scholar] [CrossRef]
- Daba, M.H.; You, S. Assessment of climate change impacts on river flow regimes in the upstream of Awash Basin, Ethiopia: Based on IPCC fifth assessment report (AR5) climate change scenarios. Hydrology 2020, 7, 98. [Google Scholar] [CrossRef]
- Bussi, G.; Whitehead, P.G.; Jin, L.; Taye, M.T.; Dyer, E.; Hirpa, F.A.; Yimer, Y.A.; Charles, K.J. Impacts of Climate Change and Population Growth on River Nutrient Loads in a Data Scarce Region: The Upper Awash River (Ethiopia). Sustainability 2021, 13, 1254. [Google Scholar] [CrossRef]
- Emiru, N.C.; Recha, J.W.; Thompson, J.R.; Belay, A.; Aynekulu, E.; Manyevere, A.; Demissie, T.D.; Osano, P.M.; Hussein, J.; Molla, M.B.; et al. Impact of Climate Change on the Hydrology of the Upper Awash River Basin, Ethiopia. Hydrology 2022, 9, 3. [Google Scholar] [CrossRef]
- Gebresellase, S.H.; Wu, Z.; Xu, H.; Muhammad, W.I. Evaluation and selection of CMIP6 climate models in Upper Awash Basin (UBA), Ethiopia. Theor. Appl. Climatol. 2022, 149, 1521–1547. [Google Scholar] [CrossRef]
- Schulzweida, U. CDO User Guide. 2021. Available online: https://zenodo.org/record/5614769#.Y3wxceRBxPY (accessed on 14 November 2022). [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape,(with discussion). Appl. Stat. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- De Lucas, D.C. Classification Techniques for Time Series and Functional Data. Ph.D. Thesis, Universidad Carlos III de Madrid, Madrid, Spain, 2010. [Google Scholar]
- Montero, P.; Vilar, J.A. TSclust: An R Package for Time Series Clustering. J. Stat. Softw. 2014, 62, 1–43. [Google Scholar] [CrossRef]
- Kabacoff, R.I. R in Action: Data Analysis and Graphics with R; Manning Publishings Co.: New York, NY, USA, 2015. [Google Scholar]
- Hartmann, K.; Krois, J.; Waske, B. E-Learning Project SOGA: Statistics and Geospatial Data Analysis; Department of Earth Sciences, Freie Universitaet Berlin: Berlin, Germany, 2018; Volume 33. [Google Scholar]
- Sarvina, Y.; Pluntke, T.; Bernhofer, C. Comparing bias correction methods to improve modelled precipitation extremes. J. Meteorol. Dan Geofis. 2019, 19, 103–110. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Tabari, H.; Paz, S.M.; Buekenhout, D.; Willems, P. Comparison of statistical downscaling methods for climate change impact analysis on precipitation-driven drought. Hydrol. Earth Syst. Sci. 2021, 25, 3493–3517. [Google Scholar] [CrossRef]
- Maraun, D. Bias correcting climate change simulations-a critical review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Iturbide, M.; Bedia, J.; Herrera, S.; Baño-Medina, J.; Fernández, J.; Frías, M.; Manzanas, R.; San-Martín, D.; Cimadevilla, E.; Cofiño, A.; et al. climate4r: An r-based open framework for reproducible climate data access and post-processing. Environ. Modell. Softw. 2018. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and dynamical downscaling of the Seine basin climate for hydro-meteorological studies. Int. J. Climatol. J. R. Meteorol. Soc. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Planton, Y.Y.; Guilyardi, E.; Wittenberg, A.T.; Lee, J.; Gleckler, P.J.; Bayr, T.; McGregor, S.; McPhaden, M.J.; Power, S.; Roehrig, R.; et al. Evaluating climate models with the CLIVAR 2020 ENSO metrics package. Bull. Am. Meteorol. Soc. 2021, 102, E193–E217. [Google Scholar] [CrossRef]
- Alhamshry, A.; Fenta, A.A.; Yasuda, H.; Kimura, R.; Shimizu, K. Seasonal rainfall variability in Ethiopia and its long-term link to global sea surface temperatures. Water 2020, 12, 55. [Google Scholar] [CrossRef]
- Taye, M.T.; Dyer, E.; Charles, K.J.; Hirons, L.C. Potential predictability of the Ethiopian summer rains: Understanding local variations and their implications for water management decisions. Sci. Total Environ. 2021, 755, 142604. [Google Scholar] [CrossRef]
- Jungclaus, J.; Fischer, N.; Haak, H.; Lohmann, K.; Marotzke, J.; Matei, D.; Mikolajewicz, U.; Notz, D.; Von Storch, J. Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI-Earth system model. J. Adv. Model. Earth Syst. 2013, 5, 422–446. [Google Scholar] [CrossRef]
- Gutjahr, O.; Putrasahan, D.; Lohmann, K.; Jungclaus, J.H.; von Storch, J.S.; Brüggemann, N.; Haak, H.; Stössel, A. Max planck institute earth system model (MPI-ESM1. 2) for the high-resolution model intercomparison project (HighResMIP). Geosci. Model Dev. 2019, 12, 3241–3281. [Google Scholar] [CrossRef]
- Cherchi, A.; Fogli, P.G.; Lovato, T.; Peano, D.; Iovino, D.; Gualdi, S.; Masina, S.; Scoccimarro, E.; Materia, S.; Bellucci, A.; et al. Global mean climate and main patterns of variability in the CMCC-CM2 coupled model. J. Adv. Model. Earth Syst. 2019, 11, 185–209. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, B.; Midgley, B. IPCC 2013: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.; et al. IPCC 2021: The Physical Science Basis, Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; p. 2391. [Google Scholar] [CrossRef]
- Stasinopoulos, M.; Rigby, B.; Akantziliotou, C. Instructions on How to Use the Gamlss Package in R, 2nd ed.; Gamlss: London, UK, 2008. [Google Scholar]
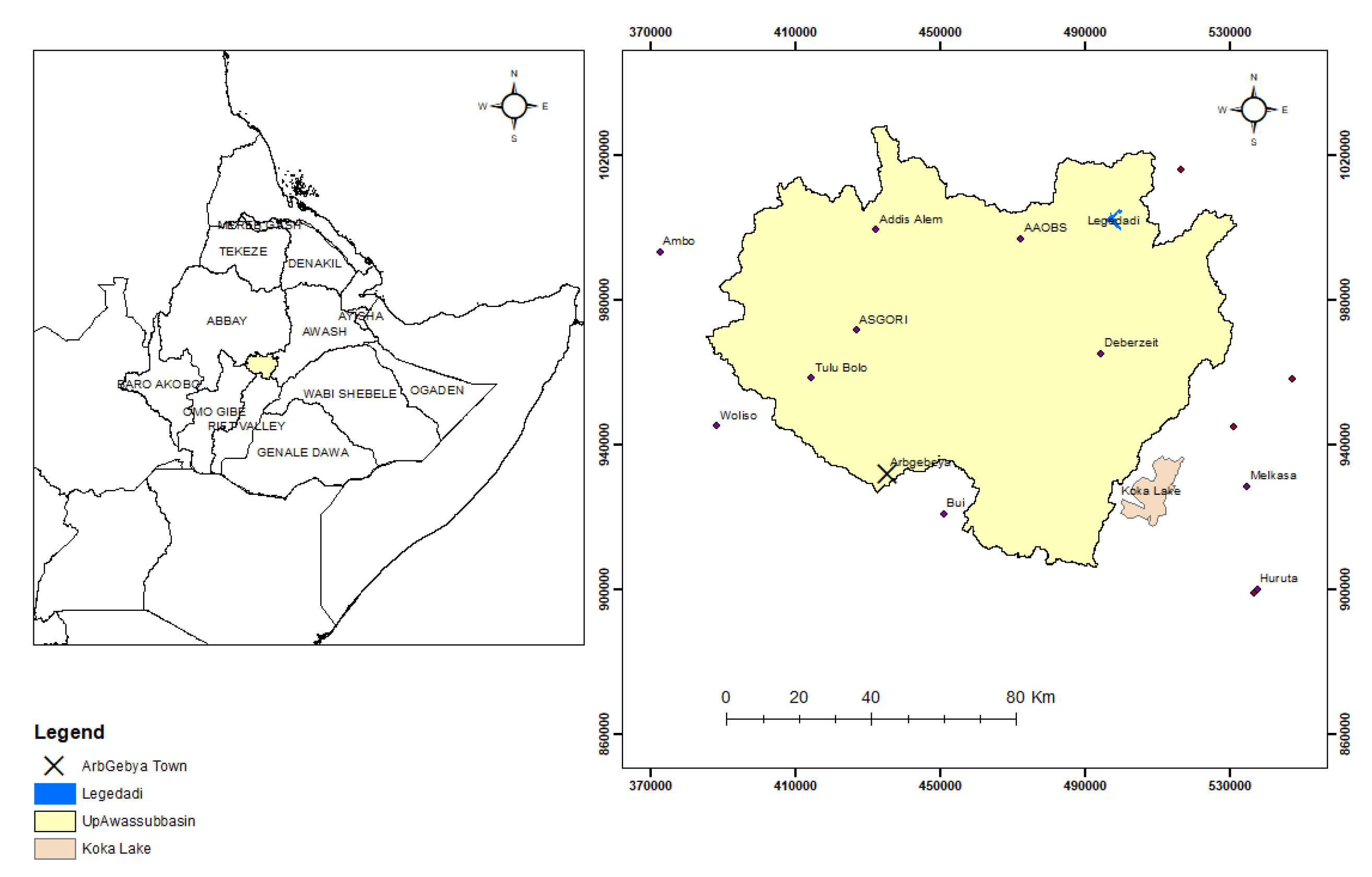

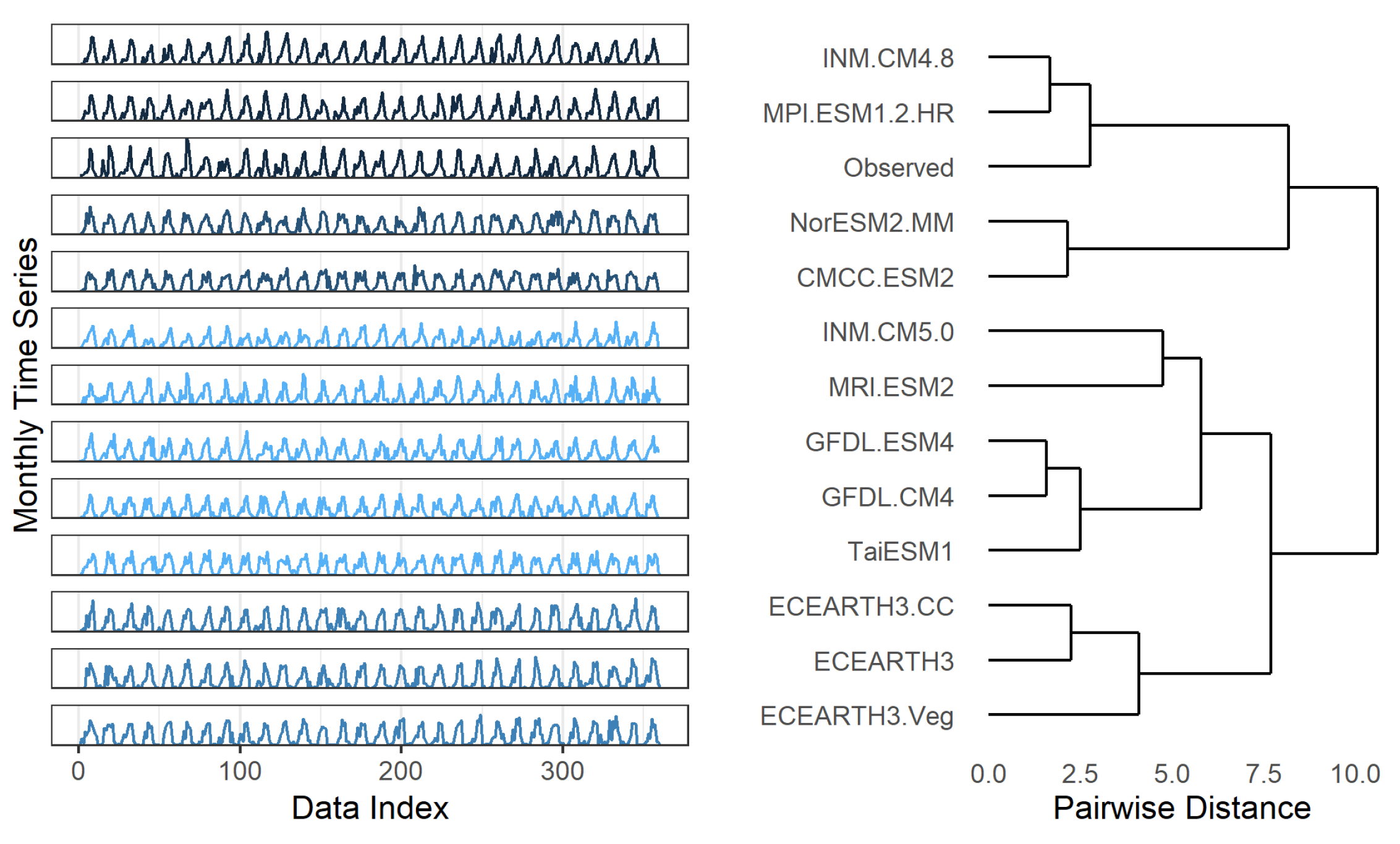



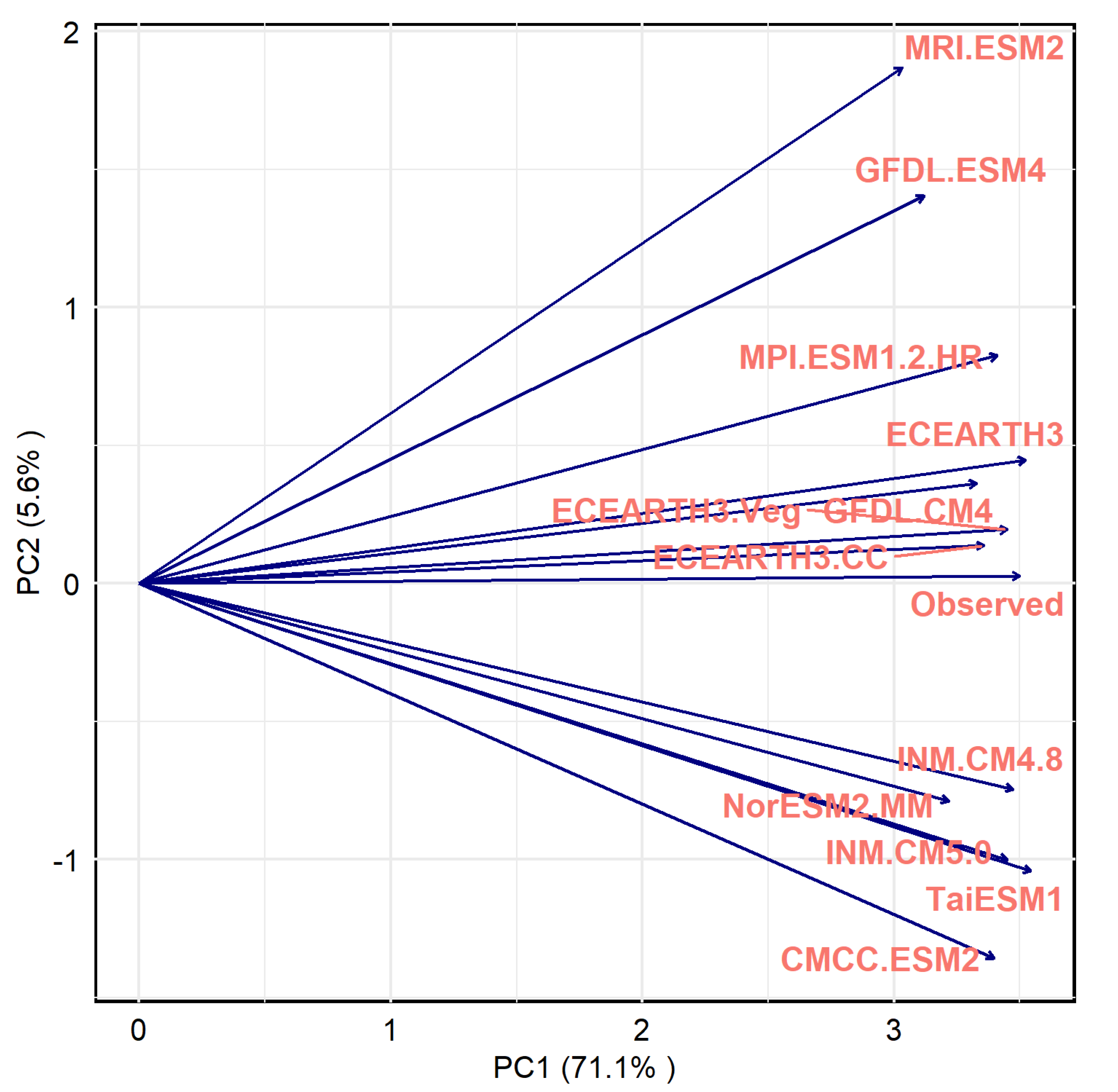
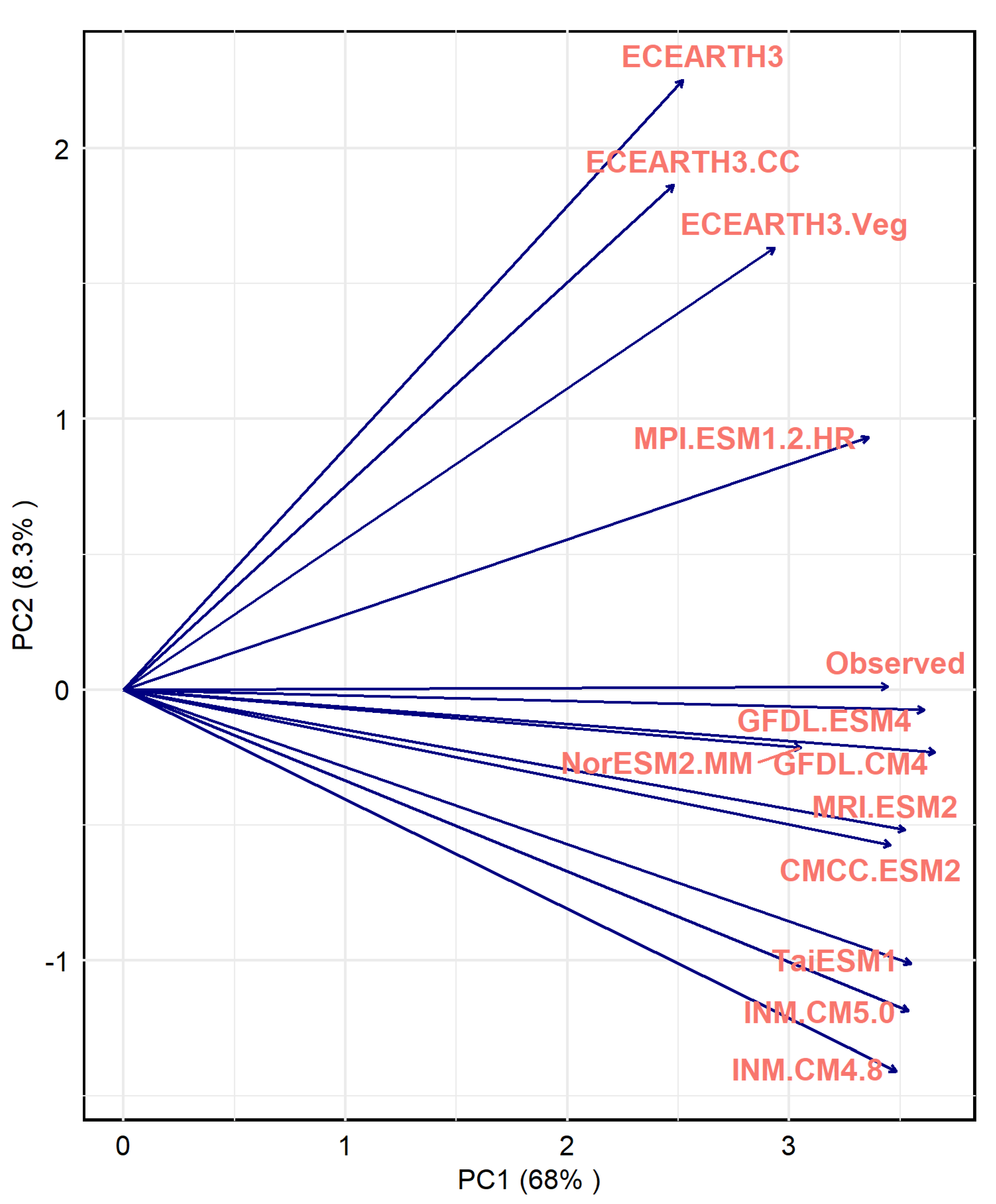

| No. | Station Name | Location (y) | Location (x) | Altitude |
|---|---|---|---|---|
| 1 | Addis Ababa Obs * | 472,248.08 | 996,952.4 | 2386 |
| 2 | Addis Alem ** | 432,225.93 | 999,552.91 | 2372 |
| 3 | Aleltu | 516,771.63 | 1,016,119.33 | 2648 |
| 4 | Ambo ** | 372,449.79 | 993,358.73 | 2068 |
| 5 | Asgori * | 426,775.97 | 971,700.31 | 2072 |
| 6 | Boneya | 460,591.24 | 971,046.06 | 2251 |
| 7 | Bui ** | 450,940.01 | 920,899.89 | 2054 |
| 8 | ChefeDonsa | 513,542.53 | 991,537.73 | 2392 |
| 9 | Debrezeit * | 494,500.33 | 965,370.79 | 1900 |
| 10 | Ejere | 528,246.66 | 969,798.67 | 2254 |
| 11 | Enselale | 435,870.79 | 987,532.37 | 2000 |
| 12 | Ginchi | 404,738.43 | 996,808.09 | 2132 |
| 13 | Hombole | 475,209.16 | 925,006.74 | 1743 |
| 14 | Huruta * | 537,697.21 | 900,012.17 | 2044 |
| 15 | Melkasa * | 534,861.76 | 928,532.98 | 1540 |
| 16 | Mojo | 511,901.68 | 951,220.7 | 1763 |
| 17 | Nazret | 531,179.91 | 945,113.49 | 1622 |
| 18 | Sebeta | 459,322.66 | 986,027.98 | 2220 |
| 19 | Teji | 430,354.91 | 976,481.48 | 2091 |
| 20 | Tulu Bolo * | 414,188.26 | 958,456.67 | 2100 |
| 21 | Welenchiti | 547,305.49 | 958,395.38 | 1458 |
| 22 | Woliso ** | 388,113.76 | 945,249.62 | 2058 |
| Model | Institute | Country |
|---|---|---|
| MRI-ESM2-0 | Meteorological Research Institute | Japan |
| ECEARTH3-CC | EC-Earth consortium | Sweden |
| NorESM2-MM | Norwegian Climate Center | Norway |
| TaiESM1 | Academia Sinica | Taiwan |
| ECEARTH3.Veg | EC-Earth consortium | Sweden |
| MPI-ESM1.2.HR | Max Planck Institute for Meteorology | Germany |
| ECEARTH3 | EC-Earth consortium | Sweden |
| CMCC-ESM2 | Centro Euro-Mediterraneo sui Cambiamenti Climatici | Italy |
| GFDL-CM4 | NOAA | USA |
| GFDL-ESM4 | NOAA | USA |
| INM-CM4-8 | Institute for Numerical Mathematics | Russia |
| INM-CM5-0 | Institute for Numerical Mathematics | Russia |
| Monthly Average | JJAS | MAM | Annual | |||||
|---|---|---|---|---|---|---|---|---|
| Data Type | AIC | DT | AIC | DT | AIC | DT | AIC | DT |
| Precipitation | ||||||||
| Observed | 221.62 | NO | 359.84 | LO | 348.147 | GA | 370.72 | NO |
| CMCC-ESM2 | 210.09 | SN2 | 229.72 | SN2 | 272.3 | SEP1 | 359.19 | SN2 |
| ECEARTH3 | 213.9 | SN2 | 268.16 | WEI | 277.63 | WEI3 | 362.99 | SN2 |
| ECEARTH3-CC | 229.69 | RG | 257.03 | GA | 285.2 | GA | 378.79 | RG |
| ECEARTH3-Veg | 228.64 | SEP1 | 249.17 | SEP3 | 274.55 | RG | 381.82 | IGAMMA |
| GFDL-CM4 | 196.06 | WEI3 | 254.98 | WEI | 266.21 | NO | 345.16 | WEI |
| GFDL-ESM4 | 214.78 | SEP3 | 233.74 | SEP2 | 259.64 | NO | 364.56 | IGAMMA |
| MPI-ESM1-2-HR | 217.1 | SEP1 | 263.67 | WEI3 | 275.74 | SEP1 | 366.19 | SEP1 |
| MRI-ESM2 | 232.6 | NO | 261.15 | LO | 271.72 | GA | 381.7 | NO |
| NorESM2-MM | 229.68 | LO | 277.26 | LO | 295.01 | GA | 378.77 | LO |
| TaiESM1 | 209.12 | NO | 237.44 | IGAMMA | 272.38 | LO | 358.22 | NO |
| INM-CM4-8 | 233.88 | WEI | 281.42 | SEP2 | 238.5 | WEI3 | 382.97 | WEI3 |
| INM-CM5-0 | 226.62 | SN2 | 280.22 | NO | 261.28 | WEI2 | 377.17 | SN2 |
| Maximum Temperature | ||||||||
| Observed | 45.97 | SN2 | 28.93 | RG | 51.31 | WEI | 13.19 | PE2 |
| CMCC-ESM2 | 32.12 | WEI3 | 52.57 | SN2 | 37.6 | LO | 32.12 | WEI3 |
| ECEARTH3 | 30.55 | NO | 44.69 | WEI3 | 53.16 | GT | 30.55 | NO |
| ECEARTH3-CC | 30.06 | SN2 | 39.55 | GG | 42.85 | SN2 | 30.06 | SN2 |
| ECEARTH3-Veg | 26.53 | NO | 42.93 | SN2 | 45.23 | NO | 26.53 | NO |
| GFDL-CM4 | 8.59 | SN2 | 37.81 | RG | 45.1 | IGAMMA | 8.59 | SN2 |
| GFDL-ESM4 | 27.57 | SN2 | 42.36 | WEI3 | 49.34 | LO | 27.57 | SN2 |
| MPI-ESM1-2-HR | 14.35 | NO | 34.3 | SN2 | 57.13 | NO | 14.35 | NO |
| MRI-ESM2 | 10.66 | NO | 42.33 | WEI | 42.31 | PE2 | 10.66 | NO |
| NorESM2-MM | 37.52 | SHASH | 58.02 | SN2 | 55.42 | WEI3 | 37.52 | SHASH |
| TaiESM1 | 2.78 | WEI3 | 31.94 | WEI | 25.06 | NET | 2.78 | WEI3 |
| INM-CM4-8 | 14.07 | WEI3 | 14.57 | IGAMMA | 31.78 | PE | 14.07 | WEI3 |
| INM-CM5-0 | 11.02 | WEI | 27.42 | LO | 35.8 | NET | 11.02 | WEI |
| Minimum Temperature | ||||||||
| Observed | 42.35 | SEP1 | 30.9 | NO | 34.09 | NO | 16.98 | IGAMMA |
| CMCC-ESM2 | 33.67 | SEP1 | 24.05 | SN2 | 45.87 | GA | 33.67 | SEP1 |
| ECEARTH3 | 44.68 | WEI3 | 47.64 | WEI | 23.2 | NET | 44.68 | WEI3 |
| ECEARTH3-CC | 40.14 | SN2 | 52.83 | WEI | 31.7 | GU | 40.14 | SN2 |
| ECEARTH3-Veg | 45.88 | WEI3 | 16.64 | BCPEo | 28.47 | PE | 45.88 | WEI3 |
| GFDL-CM4 | 3.73 | IGAMMA | -6.15 | RG | 28.03 | IGAMMA | 3.73 | IGAMMA |
| GFDL-ESM4 | 31 | WEI | 15.08 | WEI3 | 38.77 | NO | 31 | WEI |
| MPI-ESM1-2-HR | 21.35 | IGAMMA | 10.89 | SEP3 | 3.36 | NO | 21.35 | IGAMMA |
| MRI-ESM2 | 29.13 | RG | 9.45 | GT | 30.08 | RG | 29.13 | RG |
| NorESM2-MM | 50 | SHASH | 37.67 | SEP1 | 45.7 | WEI | 50 | SHASH |
| TaiESM1 | 16.68 | NET | 12.72 | LO | 34.01 | LO | 16.68 | NET |
| INM-CM4-8 | 16.43 | WEI | -6.83 | WEI | 33.46 | SN2 | 16.43 | WEI |
| INM-CM5-0 | 12.78 | SEP3 | -7.68 | SN2 | 40 | IG | 12.78 | SEP3 |
| Data Type | Annual | Monthly Ave. | JJAS | MAM | ||||
|---|---|---|---|---|---|---|---|---|
| Z-val | Sen S. | Z-val | Sen S. | Z-val | Sen S. | Z-val | Sen S. | |
| Precipitation | ||||||||
| Observed | −0.43 | −0.91 | −0.43 | −0.08 | −0.07 | −0.06 | 0.07 | 0.05 |
| CMCC-ESM2 | 0.04 | 0.09 | 0.04 | 0.01 | −1.39 | −0.32 | 1.82 | 0.89 |
| ECEARTH3 | 1.39 | 3.62 | 1.39 | 0.30 | 2.64 | 1.06 | −0.21 | −0.05 |
| ECEARTH3-CC | 1.78 | 5.61 | 1.78 | 0.47 | 3.14 | 1.00 | −0.39 | −0.29 |
| ECEARTH3-Veg | 0.39 | 1.51 | 0.39 | 0.13 | 0.64 | 0.21 | −0.36 | −0.27 |
| GFDL-CM4 | 1.68 | 3.14 | 1.68 | 0.26 | 1.04 | 0.33 | −0.18 | −0.05 |
| GFDL-ESM4 | −0.25 | −1.02 | −0.25 | −0.09 | −1.43 | −0.25 | −0.86 | −0.45 |
| MPI-ESM1-2-HR | 0.21 | 0.55 | 0.21 | 0.05 | −0.25 | −0.08 | 0.61 | 0.17 |
| MRI-ESM2 | 1.57 | 4.52 | 1.57 | 0.38 | 0.5 | 0.25 | 0.46 | 0.31 |
| NorESM2-MM | 1.21 | 3.29 | 1.21 | 0.27 | 0.14 | 0.1 | 0.14 | 0.08 |
| TaiESM1 | −0.86 | −1.94 | −0.86 | −0.16 | −1.61 | −0.5 | 0.64 | 0.24 |
| INM-CM4-8 | 2.87 | 4.25 | 2.87 | 0.35 | 1.32 | 1.04 | 1.04 | 0.29 |
| INM-CM5-0 | 0.71 | 2.71 | 0.71 | 0.23 | 0.00 | −0.01 | 1.14 | 0.52 |
| Maximum Temperature | ||||||||
| Observed | 7.36 | 0.03 | 7.36 | 0.03 | 1.27 | 0.02 | 2.38 | 0.05 |
| CMCC-ESM2 | 2.13 | 0.02 | 2.13 | 0.02 | 1.00 | 0.03 | 0.34 | 0.01 |
| ECEARTH3 | 4.32 | 0.04 | 4.32 | 0.04 | 2.54 | 0.05 | 1.8 | 0.05 |
| ECEARTH3-CC | 1.29 | 0.01 | 1.29 | 0.01 | 3.23 | 0.03 | 1.00 | 0.02 |
| ECEARTH3-Veg | 3.4 | 0.03 | 3.4 | 0.03 | 2.97 | 0.04 | 0.37 | 0.01 |
| GFDL-CM4 | 1.32 | 0.02 | 1.32 | 0.02 | 0.4 | 0.01 | 0.79 | 0.02 |
| GFDL-ESM4 | 2.48 | 0.02 | 2.48 | 0.02 | 0.32 | 0.01 | 2.38 | 0.05 |
| MPI-ESM1-2-HR | 0.08 | 0.00 | 0.08 | 0.00 | 0.26 | 0.01 | 0.00 | 0.00 |
| MRI-ESM2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.69 | 0.02 | −1.47 | −0.01 |
| NorESM2-MM | 1.99 | 0.02 | 1.99 | 0.02 | 0.26 | 0.01 | 0.63 | 0.01 |
| TaiESM1 | 6.63 | 0.02 | 6.63 | 0.02 | 1.95 | 0.03 | 1.69 | 0.02 |
| INM-CM4-8 | 2.48 | 0.03 | 2.48 | 0.03 | 2.85 | 0.04 | 1.74 | 0.02 |
| INM-CM5-0 | 2.99 | 0.02 | 2.99 | 0.02 | 1.56 | 0.02 | 1.48 | 0.02 |
| Minimum Temperature | ||||||||
| Observed | 1.8 | 0.02 | 1.8 | 0.02 | 2.32 | 0.03 | 1.11 | 0.02 |
| CMCC-ESM2 | 1.57 | 0.02 | 1.57 | 0.02 | 2.37 | 0.02 | 0.64 | 0.01 |
| ECEARTH3 | 2.8 | 0.06 | 2.8 | 0.06 | 3.38 | 0.07 | 3.01 | 0.03 |
| ECEARTH3-CC | 1.41 | 0.03 | 1.41 | 0.03 | 4.02 | 0.05 | 1.69 | 0.03 |
| ECEARTH3-Veg | 4.02 | 0.04 | 4.02 | 0.04 | 2.64 | 0.05 | 1.89 | 0.01 |
| GFDL-CM4 | 1.22 | 0.01 | 1.22 | 0.01 | 2.48 | 0.02 | −0.79 | −0.01 |
| GFDL-ESM4 | 4.76 | 0.04 | 4.76 | 0.04 | 4.13 | 0.02 | 2.46 | 0.04 |
| MPI-ESM1-2-HR | 1.00 | 0.01 | 1.00 | 0.01 | 0.79 | 0.01 | −0.87 | −0.01 |
| MRI-ESM2 | 5.9 | 0.04 | 5.9 | 0.04 | 5.58 | 0.04 | 2.09 | 0.03 |
| NorESM2-MM | 0.87 | 0.01 | 0.87 | 0.01 | 1.76 | 0.02 | 0.48 | 0.02 |
| TaiESM1 | 0.79 | 0.01 | 0.79 | 0.01 | 6.24 | 0.02 | 1.69 | 0.02 |
| INM-CM4-8 | 8.95 | 0.02 | 8.95 | 0.02 | 6.83 | 0.02 | 1.06 | 0.01 |
| INM-CM5-0 | 2.38 | 0.02 | 2.38 | 0.02 | 3.73 | 0.01 | 2.01 | 0.03 |
| Ranks | |||||
|---|---|---|---|---|---|
| Data Type | RMSE | MAE | BIAS | Sum of Rank | |
| Precipitation | |||||
| ECEARTH3 | 6 | 2 | 2 | 4 | 14 |
| ECEARTH3-Veg | 2 | 6 | 1 | 10 | 19 |
| GFDL-ESM4 | 3 | 1 | 8 | 12 | 24 |
| CMCC-ESM2 | 10 | 5 | 9 | 1 | 25 |
| INM-CM4-8 | 1 | 10 | 7 | 8 | 26 |
| NorESM2-MM | 5 | 11 | 6 | 5 | 27 |
| MPI-ESM1-2-HR | 4 | 8 | 5 | 11 | 28 |
| MRI-ESM2 | 9 | 9 | 3 | 7 | 28 |
| TaiESM1 | 7 | 3 | 10 | 9 | 29 |
| GFDL-CM4 | 8 | 4 | 12 | 6 | 30 |
| INM-CM5.0 | 12 | 12 | 4 | 2 | 30 |
| ECEARTH3-CC | 11 | 7 | 11 | 3 | 32 |
| Maximum Temperature | |||||
| TaiESM1 | 6 | 1 | 1 | 3 | 11 |
| INM-CM5-0 | 4 | 2 | 2 | 6 | 14 |
| ECEARTH3 | 1 | 4 | 9 | 1 | 15 |
| INM-CM4-8 | 7 | 3 | 3 | 4 | 17 |
| ECEARTH3-CC | 2 | 7 | 4 | 10 | 23 |
| MPI-ESM1-2-HR | 8 | 6 | 5 | 5 | 24 |
| GFDL-ESM4 | 3 | 5 | 6 | 12 | 26 |
| ECEARTH3-Veg | 9 | 8 | 8 | 2 | 27 |
| GFDL-CM4 | 10 | 9 | 7 | 7 | 33 |
| MRI-ESM2 | 5 | 12 | 11 | 11 | 39 |
| CMCC-ESM2 | 12 | 10 | 10 | 8 | 40 |
| NorESM2-MM | 11 | 11 | 12 | 9 | 43 |
| Minimum Temperature | |||||
| GFDL-CM4 | 4 | 1 | 1 | 1 | 7 |
| MPI-ESM1-2-HR | 1 | 2 | 3 | 11 | 17 |
| TaiESM1 | 3 | 4 | 4 | 6 | 17 |
| INM-CM4-8 | 5 | 3 | 2 | 12 | 22 |
| ECEARTH3-Veg | 2 | 8 | 8 | 7 | 25 |
| INM-CM5-0 | 10 | 6 | 7 | 4 | 27 |
| MRI-ESM2 | 12 | 7 | 5 | 3 | 27 |
| GFDL-ESM4 | 9 | 5 | 6 | 10 | 30 |
| CMCC-ESM2 | 6 | 9 | 9 | 8 | 32 |
| NorESM2-MM | 8 | 12 | 12 | 2 | 34 |
| ECEARTH3 | 7 | 11 | 10 | 9 | 37 |
| ECEARTH3-CC | 11 | 10 | 11 | 5 | 37 |
| Model | PDF Rank | Trend Rank | PM Rank | Cluster Rank | PCA Rank | SpatCorr | SpaRMSE | Sum of Rank | Final Rank |
|---|---|---|---|---|---|---|---|---|---|
| Precipitation | |||||||||
| MRI-ESM2 | 1 | 1 | 8 | 6 | 1 | 1 | 3 | 21 | 1 |
| GFDL-ESM4 | 5 | 1 | 3 | 4 | 3 | 5 | 2 | 23 | 2 |
| MPI-ESM1-2-HR | 5 | 1 | 7 | 1 | 5 | 4 | 4 | 27 | 3 |
| GFDL-CM4 | 5 | 1 | 10 | 8 | 2 | 3 | 1 | 30 | 4 |
| ECEARTH3 | 5 | 10 | 1 | 9 | 4 | 2 | 5 | 36 | 5 |
| NorESM2-MM | 2 | 1 | 6 | 5 | 8 | 8 | 8 | 38 | 6 |
| ECEARTH3-Veg | 5 | 1 | 2 | 12 | 7 | 7 | 7 | 41 | 7 |
| INM-CM5-0 | 5 | 1 | 11 | 3 | 10 | 10 | 10 | 50 | 8 |
| CMCC-ESM2 | 5 | 1 | 4 | 10 | 11 | 11 | 9 | 51 | 9 |
| ECEARTH3-CC | 4 | 10 | 12 | 7 | 6 | 6 | 6 | 51 | 9 |
| INM-CM4-8 | 5 | 12 | 5 | 2 | 9 | 9 | 12 | 54 | 11 |
| TaiESM1 | 2 | 1 | 9 | 11 | 12 | 12 | 11 | 58 | 12 |
| Maximum Temperature | |||||||||
| ECEARTH3 | 4 | 6 | 3 | 3 | 4 | 3 | 1 | 24 | 1 |
| INM-CM5-0 | 4 | 2 | 2 | 5 | 8 | 4 | 3 | 28 | 2 |
| INM-CM4-8 | 4 | 6 | 4 | 4 | 5 | 2 | 4 | 29 | 3 |
| MPI-ESM1-2-HR | 4 | 9 | 6 | 1 | 6 | 1 | 2 | 29 | 3 |
| TaiESM1 | 4 | 2 | 1 | 2 | 9 | 7 | 8 | 33 | 5 |
| ECEARTH3-CC | 2 | 12 | 5 | 8 | 1 | 5 | 5 | 38 | 6 |
| ECEARTH3-Veg | 4 | 6 | 8 | 6 | 2 | 6 | 6 | 38 | 6 |
| CMCC-ESM2 | 4 | 2 | 11 | 7 | 10 | 8 | 7 | 49 | 8 |
| GFDL-CM4 | 1 | 9 | 9 | 11 | 3 | 9 | 9 | 51 | 9 |
| GFDL-ESM4 | 2 | 1 | 7 | 10 | 11 | 10 | 10 | 51 | 9 |
| NorESM2-MM | 4 | 2 | 12 | 9 | 7 | 11 | 12 | 57 | 11 |
| MRI-ESM2 | 4 | 9 | 10 | 12 | 12 | 12 | 11 | 70 | 12 |
| Minimum Temperature | |||||||||
| GFDL-CM4 | 2 | 1 | 1 | 4 | 2 | 1 | 1 | 12 | 1 |
| MPI-ESM1-2-HR | 1 | 5 | 2 | 1 | 6 | 6 | 7 | 28 | 2 |
| TaiESM1 | 5 | 1 | 3 | 7 | 7 | 4 | 3 | 30 | 3 |
| GFDL-ESM4 | 2 | 9 | 8 | 3 | 1 | 3 | 5 | 31 | 4 |
| MRI-ESM2 | 5 | 9 | 7 | 2 | 4 | 2 | 2 | 31 | 4 |
| CMCC-ESM2 | 2 | 1 | 9 | 5 | 5 | 8 | 8 | 38 | 6 |
| INM-CM5-0 | 5 | 9 | 6 | 6 | 8 | 5 | 4 | 43 | 7 |
| INM-CM4-8 | 5 | 7 | 4 | 8 | 9 | 7 | 9 | 49 | 8 |
| NorESM2-MM | 5 | 5 | 10 | 11 | 3 | 9 | 6 | 49 | 8 |
| ECEARTH3-Veg | 5 | 7 | 5 | 9 | 10 | 10 | 10 | 56 | 10 |
| ECEARTH3-CC | 5 | 1 | 12 | 10 | 11 | 11 | 11 | 61 | 11 |
| ECEARTH3 | 5 | 9 | 11 | 12 | 12 | 12 | 12 | 73 | 12 |
| Data Type | Precip Rank | Tmax Rank | Tmin Rank | Sum of Rank | Final Rank |
|---|---|---|---|---|---|
| MPI-ESM1-2-HR | 3 | 3 | 2 | 8 | 1 |
| GFDL-CM4 | 4 | 9 | 1 | 14 | 2 |
| GFDL-ESM4 | 2 | 9 | 4 | 15 | 3 |
| INM-CM5-0 | 8 | 2 | 7 | 17 | 4 |
| MRI-ESM2 | 1 | 12 | 4 | 17 | 4 |
| ECEARTH3 | 5 | 1 | 12 | 18 | 6 |
| TaiESM1 | 12 | 5 | 3 | 20 | 7 |
| INM-CN4-8 | 11 | 3 | 8 | 22 | 8 |
| CMCC-ESM2 | 9 | 8 | 6 | 23 | 9 |
| ECEARTH3-Veg | 7 | 6 | 10 | 23 | 9 |
| NorESM2-MM | 6 | 11 | 8 | 25 | 11 |
| ECEARTH3-CC | 9 | 6 | 11 | 26 | 12 |
| Scenarios | Near | Mid | End | |
|---|---|---|---|---|
| Precipitation (%) | SSP5-8.5 | (−2.1–5.3) 1.3 | (6.1–16.1) 10.6 | (11.8–29.4) 19.7 |
| SSP2-4.5 | (−0.7–6.8) 2.7 | (2.0–11.9) 6.4 | (2.2–15.0) 7.9 | |
| SSP1-2.6 | (−1.2–9.0) 3.4 | (1.4–16.6) 8.2 | (−0.3–14.2) 6.2 | |
| Tmax (°C) | SSP5-8.5 | (0.8–1.5) 1.2 | (1.7–2.3) 2.0 | (2.8–3.2) 3.0 |
| SSP2-4.5 | (0.7–1.5) 1.1 | (1.3–2.0) 1.6 | (1.7–2.3) 2.0 | |
| SSP1-2.6 | (0.7–1.4) 1.1 | (0.9–1.7) 1.3 | (0.9–1.8) 1.3 | |
| Tmin (°C) | SSP5-8.5 | (1.0–1.9) 1.4 | (2.2–2.9) 2.5 | (3.7–4.2) 4.0 |
| SSP2-4.5 | (1.0–1.7) 1.3 | (1.6–2.3) 2.0 | (2.1–2.7) 2.4 | |
| SSP1-2.6 | (0.9–1.7) 1.3 | (1.2–2.0) 1.6 | (1.1–2.0) 1.6 |
| MAM | JJAS | |||||
|---|---|---|---|---|---|---|
| Near | Mid | End | Near | Mid | End | |
| SSP5-8.5 | (−0.15–0.46) 0.03 | (−0.10–0.47) 0.08 | (−0.04–0.58) 0.15 | (−0.12–0.02) −0.06 | (−0.06–0.11) 0.01 | (0.02–0.16) 0.08 |
| SSP2-4.5 | (−0.13 −0.6) 0.08 | (−0.08–0.45) 0.09 | (−0.11–0.48) 0.08 | (−0.11–0.04) −0.04 | (−0.10–0.07) −0.02 | (−0.06–0.08) 0.00 |
| SSP1-2.6 | (−0.14–0.6) 0.07 | (−0.06–0.56) 0.14 | (−0.07–0.43) 0.09 | (−0.11–0.06) −0.04 | (−0.09–0.09) −0.01 | (−0.08–0.07) −0.02 |
| Stations | Scenarios | Near | Mid | End |
|---|---|---|---|---|
| Precip (%) | ||||
| AA | SSP5-8.5 | (4.3–9.7) 7.4 | (6.0–25.9) 17.5 | (28.6–33.2) 31.3 |
| SSP2-4.5 | (24.6–26.3) 25.3 | (10.5–13.3) 11.7 | (10.0–10.0) 10.0 | |
| Ejere | SSP5-8.5 | (−1.6–13.2) 3.8 | (21.1–23.9) 22.8 | (29.7–46.9) 36.2 |
| SSP2-4.5 | (11.1–37.9) 20.9 | (5.2–28.7) 14.0 | (6.9–24.1) 13.4 | |
| Hombole | SSP5-8.5 | (−23.4–63.7) −2.6 | (3.4–77.7) 22.0 | (7.5–123.3) 36.6 |
| SSP2-4.5 | (−14.5–93.9) 11.4 | (−12.5–93.7) 14.1 | (−12.0–86.1) 12.6 | |
| Ginchi | SSP5-8.5 | (−3.3–5.1) −0.1 | (14.2–15.1) 14.6 | (18.0–34.6) 24.5 |
| SSP2-4.5 | (6.3–26.5) 14.1 | (2.3–17.8) 8.4 | (0.2–21.3) 8.5 | |
| Tmax (°C) | ||||
| AA | SSP5-8.5 | (1.0–1.3) 1.2 | (2.4–2.4) 2.4 | (3.3–3.6) 3.5 |
| SSP2-4.5 | (0.8–0.9) 0.8 | (2.1–2.3) 2.2 | (2.6–2.8) 2.7 | |
| Bui | SSP5-8.5 | (0.6–2.1) 1.3 | (2.4–3.4) 2.9 | (3.8–4.6) 4.2 |
| SSP2-4.5 | (0.5–1.6) 1.1 | (2.1–3.3) 2.7 | (2.7–4.0) 3.3 | |
| Debrezeit | SSP5-8.5 | (1.3–1.5) 1.4 | (2.9–3.2) 3.0 | (4.0–4.6) 4.3 |
| SSP2-4.5 | (1.0 -1.1) 1.1 | (2.7–2.8) 2.7 | (3.5–3.5) 3.5 | |
| Tulubolo | SSP5-8.5 | (−0.1–2.8) 1.4 | (1.3–3.8) 2.6 | (2.5–4.9) 3.7 |
| SSP2-4.5 | (−0.3–2.5) 1.1 | (1.0–3.8) 2.4 | (1.5–4.4) 3.0 | |
| Tmin (°C) | ||||
| AA | SSP5-8.5 | (1.5–1.7) 1.6 | (2.6–2.7) 2.7 | (3.8–4.4) 4.1 |
| SSP2-4.5 | (1.1–1.2) 1.2 | (2.2–2.3) 2.2 | (2.6–3.0) 2.8 | |
| Bui | SSP5-8.5 | (1.3–3.8) 2.5 | (3.5–5.4) 4.5 | (5.4–7.0) 6.2 |
| SSP2-4.5 | (1.0–3.0) 2.0 | (2.9–5.1) 4.0 | (3.3–5.8) 4.6 | |
| Debrezeit | SSP5-8.5 | (1.5–1.9) 1.7 | (3.2–3.3) 3.2 | (4.4–4.9) 4.7 |
| SSP2-4.5 | (1.2–1.3) 1.2 | (2.7–2.8) 2.8 | (3.1–3.6) 3.3 | |
| Tulubolo | SSP5-8.5 | (0.9–1.8) 1.4 | (1.9–4.1) 3.0 | (3.2–5.2) 4.2 |
| SSP2-4.5 | (0.8–1.4) 1.1 | (1.4–3.9) 2.7 | (1.8–4.5) 3.1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balcha, Y.A.; Malcherek, A.; Alamirew, T. Understanding Future Climate in the Upper Awash Basin (UASB) with Selected Climate Model Outputs under CMIP6. Climate 2022, 10, 185. https://doi.org/10.3390/cli10120185
Balcha YA, Malcherek A, Alamirew T. Understanding Future Climate in the Upper Awash Basin (UASB) with Selected Climate Model Outputs under CMIP6. Climate. 2022; 10(12):185. https://doi.org/10.3390/cli10120185
Chicago/Turabian StyleBalcha, Yonas Abebe, Andreas Malcherek, and Tena Alamirew. 2022. "Understanding Future Climate in the Upper Awash Basin (UASB) with Selected Climate Model Outputs under CMIP6" Climate 10, no. 12: 185. https://doi.org/10.3390/cli10120185
APA StyleBalcha, Y. A., Malcherek, A., & Alamirew, T. (2022). Understanding Future Climate in the Upper Awash Basin (UASB) with Selected Climate Model Outputs under CMIP6. Climate, 10(12), 185. https://doi.org/10.3390/cli10120185








