Air Pollution and Mobility, What Carries COVID-19?
Abstract
:1. Introduction
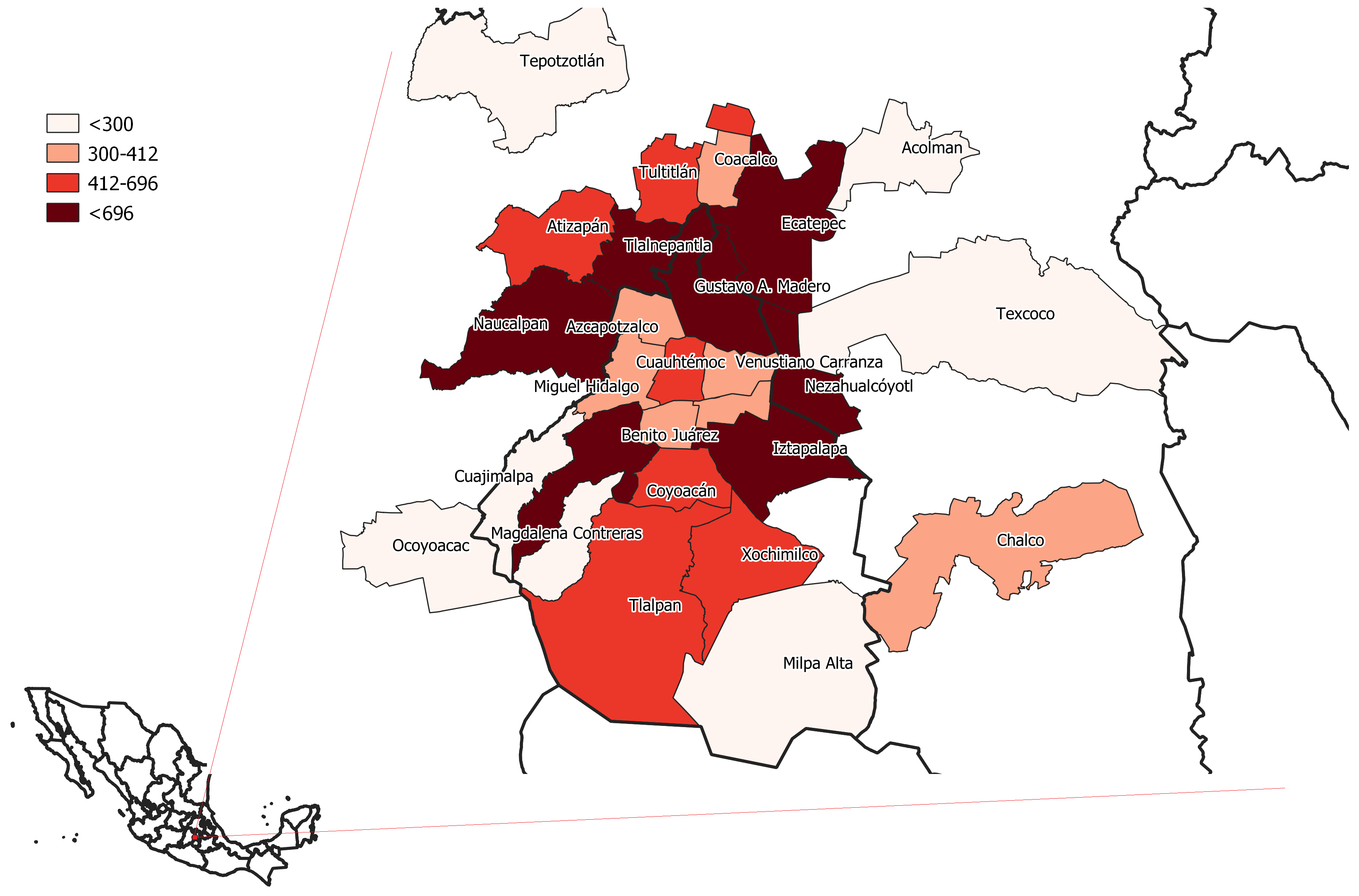
2. The Mexico City Metropolitan Area
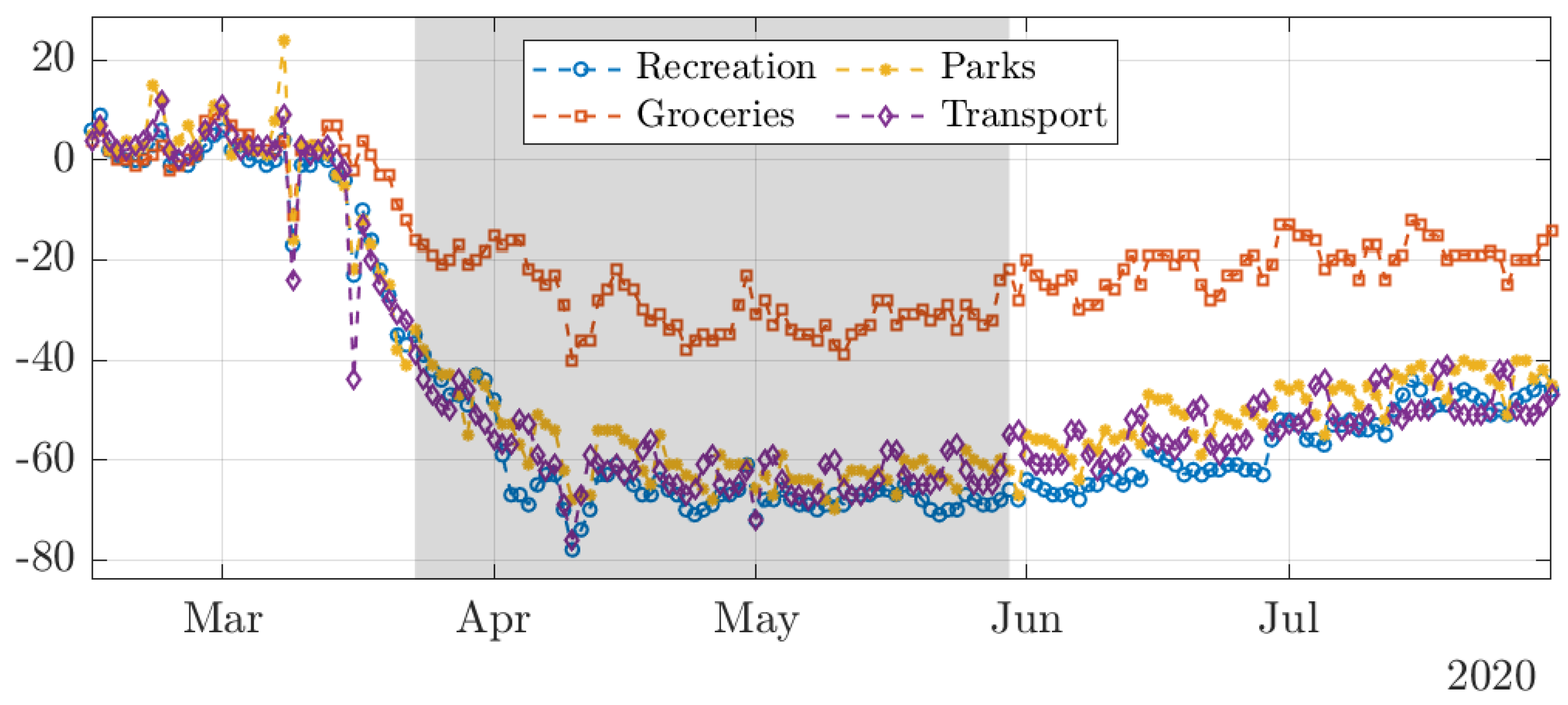
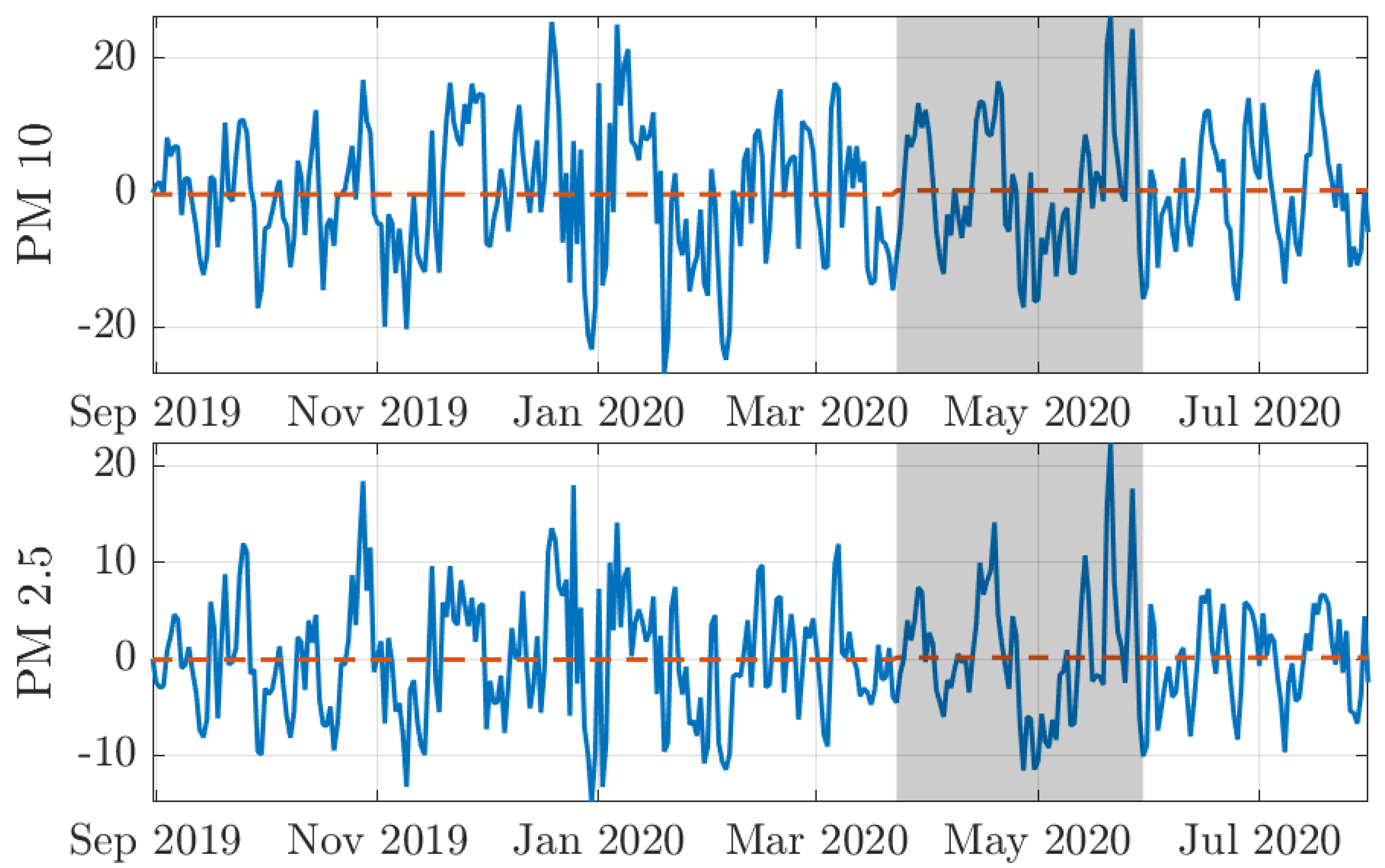
2.1. Data
2.2. Restrictions Due to COVID-19
3. Econometric Methodology
4. Testing for Stationarity and Cross-Sectional Dependence
5. Main Estimation Results
6. Future Extensions and Limitations
6.1. Future Extensions
6.2. Limitations
- Our data only include the first wave of the pandemic in the MCMA. However, a year after the first wave, as many other countries in the world, Mexico has faced second and third waves. Unfortunately, the public RAMA database has been moved to another repository, and it could not be consulted by the time this paper was written.
- Models (1) and (2) do not cover the case where the panel includes a lagged dependent variable limiting a deeper dynamic analysis. In this respect, possible improvements can be considering models proposed by Chudik and Pesaran (2015), and Moon and Weidner (2017).
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| 1 | The link is tomtom.com/engb/traffic-index/ranking/ (accessed on 1 November 2020). |
| 2 | Available online at datos.cdmx.gob.mx (accessed on 20 September 2020). |
| 3 | Mulcollinearity might easily occur in a model in which cross-sectional dependence is approximated by cross-sectional averages such as in the Pesaran’s approach. Some software codes check automatically for collinearity in data and chose an efficient algorithm to invert the data matrices. An usual method is by the generalized inverse as in Pesaran (2006). |
| 4 | Another difference between both approaches is the assumption regarding slope parameters. The MGE method assumes heterogeneous parameters, while IFE works with homogeneous slopes, i.e., , , , and for all i. |
| 5 | The analysis reports that all variables involved are stationary. Results are not reported here for the sake of brevity, but available upon request. |
| 6 | Pesaran’s CIPS test performances well in small-sample in the presence of a single unobserved common factor, however, if the number of common factors is higher, the test exhibits size distortions. In this respect, Pesaran et al. (2013) propose an extension to cover a multi-factor error structure. We employ the CIPS and CSB tests proposed for number of factors and we find the same conclusions. Tables are available upon request. |
| 7 | |
| 8 | |
| 9 | The plots for actual and fitted series, as well as that of the residual are available upon request |
References
- Adams, Matthew D. 2020. Air pollution in Ontario, Canada during the COVID-19 State of Emergency. Science of The Total Environment 742: 140516. [Google Scholar] [CrossRef]
- Bai, Jushan, and Serena Ng. 2008. Large Dimensional Factor Analysis. Norwell: Now Publishers Inc. [Google Scholar]
- Bai, Jushan. 2009. Panel data models with interactive fixed effects. Econometrica 77: 1229–79. [Google Scholar]
- Bailey, Natalia, George Kapetanios, and M. Hashem Pesaran. 2016. Exponent of cross-sectional dependence: Estimation and inference. Journal of Applied Econometrics 31: 929–60. [Google Scholar] [CrossRef] [Green Version]
- Baldasano, José M. 2020. COVID-19 lockdown effects on air quality by NO2 in the cities of Barcelona and Madrid (Spain). Science of The Total Environment 741: 140353. [Google Scholar] [CrossRef] [PubMed]
- Berman, Jesse D., and Keita Ebisu. 2020. Changes in U.S. air pollution during the COVID-19 pandemic. Science of The Total Environment 739: 139864. [Google Scholar] [CrossRef]
- Bianconi, Vanessa, Paola Bronzo, Maciej Banach, Amirhossein Sahebkar, Massimo Mannarino, and Matteo Pirro. 2020. Particulate matter pollution and the COVID-19 outbreak: Results from Italian regions and provinces. Archives of Medical Science 16: 985–92. [Google Scholar] [CrossRef] [PubMed]
- Borisova, Tatiana, and Serhiy Komisarenko. 2020. Air pollution particulate matter as a potential carrier of SARS-CoV-2 to the nervous system and/or neurological symptom enhancer: Arguments in favor. Environmental Science and Pollution Research. [Google Scholar] [CrossRef]
- Cataño, Duván Humberto, C. Vladimir Rodríguez-Caballero, Daniel Peña, and Chang Chiann. 2021. Wavelet estimation for factor models with time-varying loadings. International Journal of Wavelets, Multiresolution and Information Processing. [Google Scholar] [CrossRef]
- Chudasama, Yogini V., Clare L. Gillies, Karen Appiah, Francesco Zaccardi, Cameron Razieh, Melanie J. Davies, Thomas Yates, and Kamlesh Khunti. 2020. Multimorbidity and SARS-CoV-2 infection in UK Biobank. Diabetes & Metabolic Syndrome 14: 775–76. [Google Scholar]
- Chudik, Alexander, and M. Hashem Pesaran. 2015. Common correlated effects estimation of heterogeneous dynamic panel data models with weakly exogenous regressors. Journal of Econometrics 188: 393–420. [Google Scholar] [CrossRef] [Green Version]
- Coccia, Mario. 2021. The effects of atmospheric stability with low wind speed and of air pollution on the accelerated transmission dynamics of COVID-19. International Journal of Environmental Studies 78: 1–27. [Google Scholar] [CrossRef]
- Comunian, Silvia, Dario Dongo, Chiara Milani, and Paola Palestini. 2020. Air pollution and covid-19: The role of particulate matter in the spread and increase of covid-19’s morbidity and mortality. International Journal of Environmental Research and Public Health 17: 4487. [Google Scholar] [CrossRef] [PubMed]
- Conticini, Edoardo, Bruno Frediani, and Dario Caro. 2020. Can atmospheric pollution be considered a co-factor in extremely high level of SARS-CoV-2 lethality in Northern Italy? Environmental Pollution 261: 114465. [Google Scholar] [CrossRef] [PubMed]
- Ditzen, Jan. 2021. Xtcse2: Stata Module to Estimate the Exponent of Cross-Sectional Dependence in Large Panels. Available online: https://EconPapers.repec.org/RePEc:boc:bocode:s458670 (accessed on 20 September 2020).
- Ergemen, Yunus, Velasco, and Carlos. 2017. Estimation of fractionally integrated panels with fixed effects and cross-section dependence. Journal of Econometrics 196: 248–58. [Google Scholar] [CrossRef] [Green Version]
- Farias Costa, Fernanda, Wilian Reis Rosário, Ana Cláudia Ribeiro Farias, Ramon Guimaraes de Souza, and Roberta Sabrine Duarte Gondim. 2020. Metabolic syndrome and COVID-19: An update on the associated comorbidities and proposed therapies. Diabetes & Metabolic Syndrome: Clinical Research & Reviews 14: 809–14. [Google Scholar] [CrossRef]
- Frontera, Antonio, Lorenzo Cianfanelli, Konstantinos Vlachos, Giovanni Landoni, and George Cremona. 2020. Severe air pollution links to higher mortality in COVID-19 patients: The “double-hit” hypothesis. Journal of Infection 81: 255–59. [Google Scholar] [CrossRef] [PubMed]
- Google. 2020. COVID-19 Community Mobility Reports. Available online: https://www.google.com/covid19/mobility/ (accessed on 16 January 2021).
- Groulx, Nicolas, Bruce Urch, Caroline Duchaine, Samira Mubareka, and James A. Scott. 2018. The Pollution Particulate Concentrator (PoPCon): A platform to investigate the effects of particulate air pollutants on viral infectivity. Science of the Total Environment 628–629: 1101–7. [Google Scholar] [CrossRef]
- Guerra, Erick. 2015. The geography of car ownership in mexico city: A joint model of households’ residential location and car ownership decisions. Journal of Transport Geography 43: 171–80. [Google Scholar] [CrossRef] [Green Version]
- Gupta, Ankit, Hemant Bherwani, Sneha Gautam, Saima Anjum, Kavya Musugu, Narendra Kumar, Avneesh Anshul, and Rakesh Kumar. 2020. Air pollution aggravating COVID-19 lethality? Exploration in Asian cities using statistical models. Environment, Development and Sustainability. [Google Scholar] [CrossRef] [PubMed]
- Instituto Federal de Telecomunicaciones. 2020. Evolución de la Adopción y el uso de las TIC en México 2015–2019. Available online: http://www.ift.org.mx/sites/default/files/contenidogeneral/estadisticas/evoluciondelastic2015-2019_0.pdf (accessed on 16 January 2021).
- Kapetanios, George, M. Hashem Pesaran, and Takashi Yamagata. 2011. Panels with non-stationary multifactor error structures. Journal of Econometrics 160: 326–48. [Google Scholar] [CrossRef] [Green Version]
- Kneip, Alois, Robin C. Sickles, and Wonho Song. 2012. A new panel data treatment for heterogeneity in time trends. Econometric Theory 28: 590–628. [Google Scholar] [CrossRef] [Green Version]
- Kraemer, Moritz U. G., Chia-Hung Yang, Bernardo Gutierrez, Chieh-Hsi Wu, Brennan Klein, David M. Pigott, Louis du Plessis, Nuno R. Faria, Ruoran Li, William P. Hanage, and et al. 2020. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 368: 493–97. [Google Scholar] [CrossRef] [Green Version]
- López-Feldman, Alejandro, David Heres, and Fernanda Marquez-Padilla. 2021. Air pollution exposure and COVID-19: A look at mortality in Mexico City using individual-level data. Science of the Total Environment 756: 143929. [Google Scholar] [CrossRef] [PubMed]
- Maddala, Gangadharrao S., and Shaowen Wu. 1999. A comparative study of unit root tests with panel data and a new simple test. Oxford Bulletin of Economics and Statistics 61: 631–52. [Google Scholar] [CrossRef]
- Marquès, Montse, Joaquim Rovira, Martí Nadal, and José L. Domingo. 2021. Effects of air pollution on the potential transmission and mortality of COVID-19: A preliminary case-study in Tarragona Province (Catalonia, Spain). Environmental Research 192: 110315. [Google Scholar] [CrossRef] [PubMed]
- Moffet, Ryan C., Yury Desyaterik, Rebecca J. Hopkins, Alexei V. Tivanski, Mary K. Gilles, Yu Wang, Vaithiyalingam Shutthanandan, Luisa T. Molina, Rodrigo Gonzalez Abraham, Kirsten S. Johnson, and et al. 2008. Characterization of aerosols containing zn, pb, and cl from an industrial region of mexico city. Environmental Science & Technology 42: 7091–97. [Google Scholar]
- Molina, Luisa, and Mario J. Molina. 2002. Air Quality in the Mexico Megacity: An Integrated Assessment. Berlin: Springer Science & Business Media, vol. 2. [Google Scholar]
- Moon, Hyungsik Roger, and Martin Weidner. 2017. Dynamic linear panel regression models with interactive fixed effects. Econometric Theory 33: 158–95. [Google Scholar] [CrossRef] [Green Version]
- Nakada, Liane Yuri Kondo, and Rodrigo Custodio Urban. 2020. COVID-19 pandemic: Impacts on the air quality during the partial lockdown in São Paulo state, Brazil. Science of The Total Environment 730: 139087. [Google Scholar] [CrossRef] [PubMed]
- Nouvellet, Pierre, Sangeeta Bhatia, Anne Cori, Kylie E. C. Ainslie, Kylie Baguelin, Samir Bhatt, Adhiratha Boonyasiri, Nicholas F. Brazeau, Lorenzo Cattarino, Laura V. Cooper, and et al. 2021. Reduction in mobility and COVID-19 transmission. Nature Communications, 1–9. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Ron Smith. 1995. Estimating long-run relationships from dynamic heterogeneous panels. Journal of Econometrics 68: 79–113. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, L. Vanessa Smith, and Takashi Yamagata. 2013. Panel unit root tests in the presence of a multifactor error structure. Journal of Econometrics 175: 94–115. [Google Scholar] [CrossRef] [Green Version]
- Pesaran, M. Hashem. 2006. Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica 74: 967–1012. [Google Scholar] [CrossRef] [Green Version]
- Pesaran, M. Hashem. 2007. A simple panel unit root test in the presence of cross-section dependence. Journal of Applied Econometrics 22: 265–312. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Caballero, C. Vladimir, and J. Eduardo Vera-Valdés. 2020. Long-lasting economic effects of pandemics: Evidence on growth and unemployment. Econometrics 8: 37. [Google Scholar] [CrossRef]
- Rodríguez-Caballero, C. Vladimir. 2021. Energy consumption and GDP: A panel data analysis with multi-level cross-sectional dependence. Econometrics and Statistics. [Google Scholar] [CrossRef]
- Rodriguez-Villamizar, Laura A., Luis Carlos Belalcázar-Ceron, Julián Alfredo Fernández-Niño, Diana Marcela Marín-Pineda, Oscar Alberto Rojas-Sánchez, Lizbeth Alexandra Acuña-Merchán, Nathaly Ramírez-García, Sonia Cecilia Mangones-Matos, Jorge Mario Vargas-González, Julián Herrera-Torres, and et al. 2020. Air pollution, sociodemographic and health conditions effects on COVID-19 mortality in Colombia: An ecological study. Science of the Total Environment. [Google Scholar] [CrossRef]
- Secretaría de Salud. 2020. Jornada Nacional de Sana Distancia. Available online: https://www.gob.mx/cms/uploads/attachment/file/541687/Jornada_Nacional_de_Sana_Distancia.pdf (accessed on 20 September 2020).
- Setti, Leonardo, Fabrizio Passarini, Gianluigi De Gennaro, Pierluigi Barbieri, Maria Grazia Perrone, Massimo Borelli, Jolanda Palmisani, Alessia Di Gilio, Prisco Piscitelli, and Alessandro Miani. 2020. Airborne transmission route of covid-19: Why 2 meters/6 feet of inter-personal distance could not be enough. International Journal of Environmental Research and Public Health 17: 2932. [Google Scholar] [CrossRef] [Green Version]
- Shehzad, Khurram, Muddassar Sarfraz, and Syed Ghulam Meran Shah. 2020. The impact of COVID-19 as a necessary evil on air pollution in India during the lockdown. Environmental Pollution 266: 115080. [Google Scholar] [CrossRef]
- Son, Ji-Young, Kelvin C. Fong, Seulkee Heo, Honghyok Kim, Chris C. Lim, and Michelle L. Bell. 2020. Reductions in mortality resulting from reduced air pollution levels due to COVID-19 mitigation measures. Science of the Total Environment 744: 141012. [Google Scholar] [CrossRef] [PubMed]
- Travaglio, Marco, Yizhou Yu, Rebeka Popovic, Liza Selley, Nuno Santos Leal, and Luis Miguel Martins. 2021. Links between air pollution and covid-19 in england. Environmental Pollution 268: 115859. [Google Scholar] [CrossRef]
- Vera-Valdés, J. Eduardo, odríguez-Caballero, and C. Vladimir. 2021. Air Pollution and Mobility in the Mexico City Metropolitan Area in Times of COVID-19. Atmósfera. Available online: https://www.revistascca.unam.mx/atm/index.php/atm/article/view/53052 (accessed on 20 September 2020).
- Vera-Valdés, J. Eduardo. 2021. The political risk factors of COVID-19. International Review of Applied Economics 35: 269–287. [Google Scholar] [CrossRef]
- Westerlund, Joakim, and Jean-Pierre Urbain. 2015. Cross-sectional averages versus principal components. Journal of Econometrics 185: 372–77. [Google Scholar] [CrossRef]
- Yang, Jing, Ya Zheng, Xi Gou, Ke Pu, Zhaofeng Chen, Qinghong Guo, Rui Ji, Haojia Wang, Yuping Wang, and Yongning Zhou. 2020. Prevalence of comorbidities and its effects in patients infected with SARS-CoV-2: A systematic review and meta-analysis. International Journal of Infectious Diseases 94: 91–95. [Google Scholar] [CrossRef] [PubMed]
- Yao, Ye, Jinhua Pan, Weidong Wang, Zhixi Liu, Haidong Kan, Yang Qiu, Xia Meng, and Weibing Wang. 2020. Association of particulate matter pollution and case fatality rate of COVID-19 in 49 Chinese cities. Science of The Total Environment 741: 140396. [Google Scholar] [CrossRef] [PubMed]




| MW. Maddala and Wu (1999) | CIPS. Pesaran (2007) | |||||||
|---|---|---|---|---|---|---|---|---|
| Incubation Period | ||||||||
| 15D | 7D | 15D | 7D | 15D | 7D | 15D | 7D | |
| Without Trend | With Trend | Without Trend | With Trend | |||||
| Death toll | 50.778 *** | 46.362 *** | 41.466 *** | 40.858 *** | −5.027 *** | −5.461 *** | −5.597 *** | −5.979 *** |
| Cases | 64.173 *** | 48.814 *** | 130.05 *** | 127.100 *** | −3.533 *** | −3.744 *** | −4.511 *** | −4.681 *** |
| PM10 | 44.345 *** | 47.272 *** | 57.327 *** | 69.405 *** | −6.164 *** | −6.929 *** | −5.173 *** | −5.918 *** |
| PM2.5 | 41.298 *** | 44.364 *** | 36.233 *** | 41.658 *** | −6.295 *** | −6.878 *** | −5.503 *** | −6.100 *** |
| Std. Err. | [95% Conf. Interval] | |||
|---|---|---|---|---|
| Inc. Period. 15 D | ||||
| Death toll | 0.999 | 0.067 | 0.867 | 1.131 |
| Cases | 1.001 | 0.038 | 0.925 | 1.078 |
| PM10 | 1.001 | 0.041 | 0.919 | 1.083 |
| PM2.5 | 1.001 | 0.049 | 0.904 | 1.098 |
| Inc. Period. 7 D | ||||
| Death toll | 1.001 | 0.071 | 0.860 | 1.140 |
| Cases | 1.001 | 0.046 | 0.910 | 1.093 |
| PM10 | 1.002 | 0.047 | 0.909 | 1.094 |
| PM2.5 | 1.002 | 0.076 | 0.851 | 1.151 |
| Dep. Variable | Daily Death Toll | |||||
|---|---|---|---|---|---|---|
| Incubation | 14 Days | 7 Days | ||||
| Model | MG | CCEMG | IFE | MG | CCEMG | IFE |
| PM10 | −0.149 *** | 0.017 | −0.044 | −0.190 *** | −0.001 | −0.021 |
| (0.031) | (0.030) | (0.024) | (0.045) | (0.035) | (0.022) | |
| PM2.5 | 0.240 *** | −0.016 | 0.063 | 0.0261 *** | 0.054 | 0.031 |
| (0.051) | (0.029) | (0.039) | (0.071) | (0.034) | (0.024) | |
| constant | 4.916 *** | −0.090 | 4.840 *** | 5.745 *** | 0.152 | 3.600 *** |
| (1.316) | (0.811) | (0.070) | (1.493) | (0.555) | (0.051) | |
| 0.547 | 0.803 | 0.847 | 0.538 | 0.800 | 0.925 | |
| 0.239 | 0.083 | 0.064 | 0.636 | 0.079 | −0.061 | |
| CIPS | −4.802 *** | −5.341 *** | −5.451 *** | −3.503 *** | −4.154 *** | −4.554 *** |
| 55.36 *** | 62.29 *** | |||||
| Dep. Variable | Daily number of cases | |||||
| Incubation | 14 days | 7 days | ||||
| Model | MG | CCEMG | IFE | MG | CCEMG | IFE |
| PM10 | −1.139 *** | −0.034 | −0.019 | −1.287 *** | 0.027 | −0.034 |
| (0.216) | (0.198) | (0.107) | (0.295) | (0.101) | (0.103) | |
| PM2.5 | 1.318 *** | 0.042 | −0.103 | 1.350 *** | 0.082 | −0.045 |
| (0.231) | (0.242) | (0.169) | (2.212) | (0.216) | (0.163) | |
| constant | 51.359 *** | −0.041 | 40.100 *** | 53.137 *** | 1.402 | 37.300 *** |
| (11.604) | (1.330) | (0.309) | (11.767) | (1.539) | (0.291) | |
| 0.583 | 0.931 | 0.940 | 0.554 | 0.933 | 0.943 | |
| 0.250 | 0.066 | 0.066 | 0.649 | 0.061 | 0.060 | |
| CIPS | −4.829 *** | −5.492 *** | −5.674 *** | −3.664 *** | −3.859 *** | −4.149 *** |
| 114.11 *** | 139.81 *** | |||||
| Mobility Index | Daily Death Toll | Daily Number of Cases | ||
|---|---|---|---|---|
| Incubation Period | 14 Days | 7 Days | 14 Days | 7 Days |
| Recreation | 0.730 | 0.658 | 0.447 | 0.408 |
| Groceries | 0.691 | 0.662 | 0.488 | 0.355 |
| Parks | 0.751 | 0.663 | 0.426 | 0.296 |
| Transport | 0.675 | 0.588 | 0.490 | 0.558 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Caballero, C.V.; Vera-Valdés, J.E. Air Pollution and Mobility, What Carries COVID-19? Econometrics 2021, 9, 37. https://doi.org/10.3390/econometrics9040037
Rodríguez-Caballero CV, Vera-Valdés JE. Air Pollution and Mobility, What Carries COVID-19? Econometrics. 2021; 9(4):37. https://doi.org/10.3390/econometrics9040037
Chicago/Turabian StyleRodríguez-Caballero, C. Vladimir, and J. Eduardo Vera-Valdés. 2021. "Air Pollution and Mobility, What Carries COVID-19?" Econometrics 9, no. 4: 37. https://doi.org/10.3390/econometrics9040037
APA StyleRodríguez-Caballero, C. V., & Vera-Valdés, J. E. (2021). Air Pollution and Mobility, What Carries COVID-19? Econometrics, 9(4), 37. https://doi.org/10.3390/econometrics9040037







