On Spurious Causality, CO2, and Global Temperature
Abstract
1. Introduction
2. Information Flows, Non-Innocuous Assumptions and VARs
Since the dynamics are unknown, we first need to choose a model. As always, a linear model is the natural choice, at least at the initial stage of development.
2.1. Acknowledging the Identification Problem: Vector Autoregressions
2.2. An Adequate Measure of IF Based on the VAR
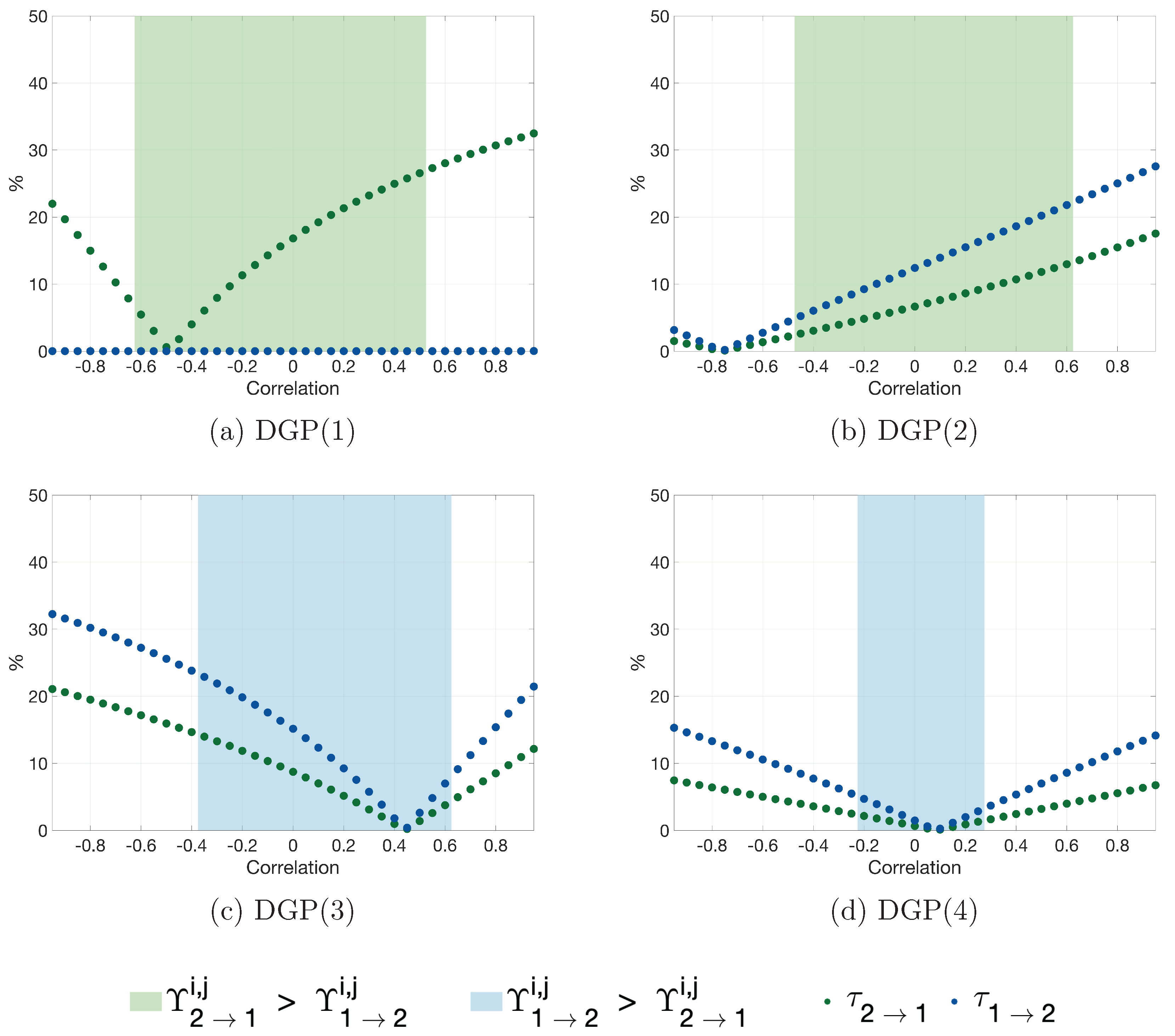
3. Simulations
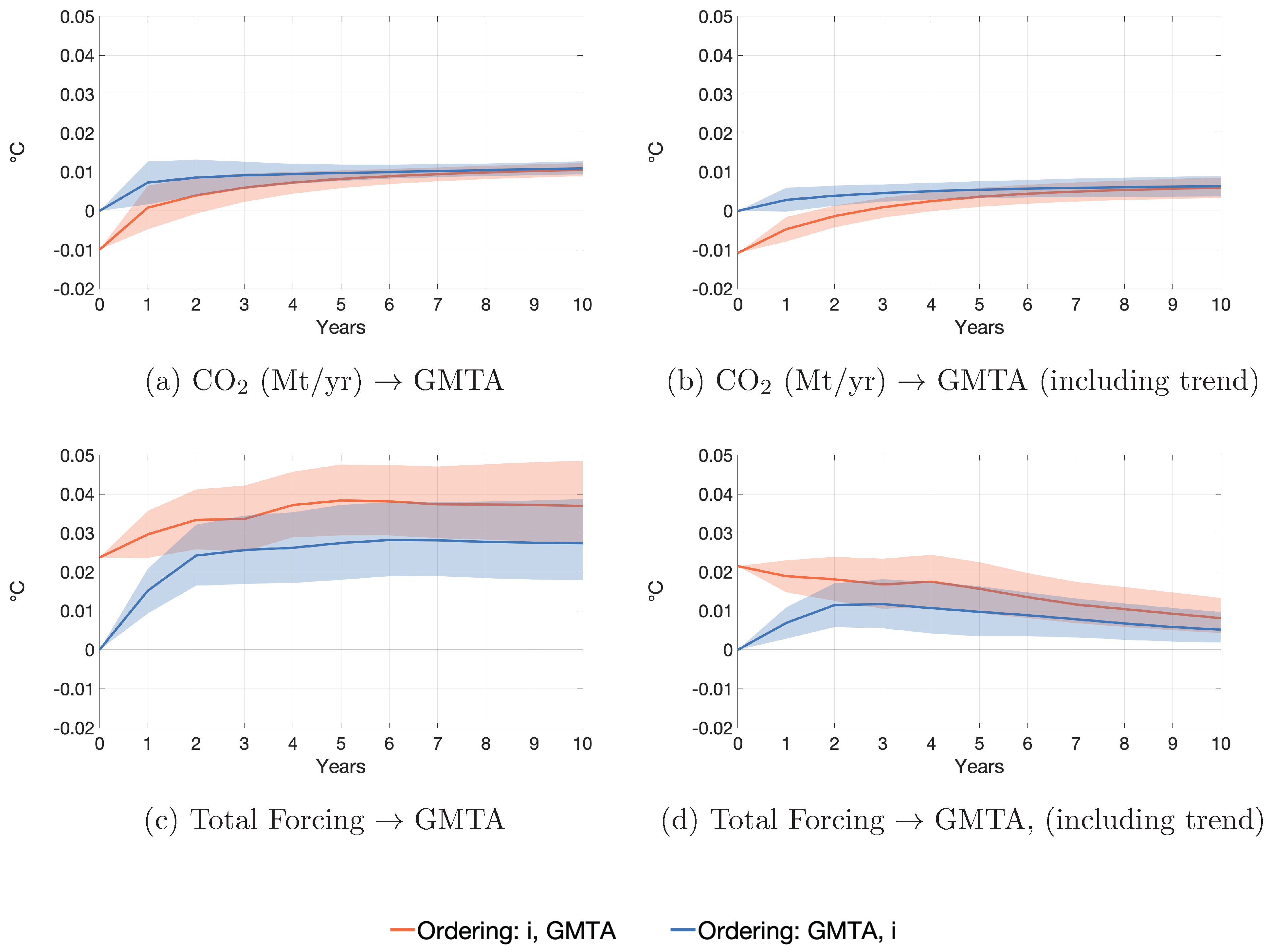
4. GMTA and Radiative Forcing Revisited
4.1. What’s Up with CO?
4.2. Impulse Response Functions
4.3. Are VAR Estimates Quantitatively Reasonable?
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources
| Abbreviation | Description | Data Source |
|---|---|---|
| Total Forcing | annual; 1850–2005 | KNMI Climate Explorer |
| Anthropogenic | annual; 1850–2005 | KNMI Climate Explorer |
| CO-ERF (W/m) | annual; 1850–2005 | KNMI Climate Explorer |
| Aerosol | annual; 1850–2005 | KNMI Climate Explorer |
| Solar | annual; 1850–2005 | KNMI Climate Explorer |
| Volcanic | annual; 1850–2005 | KNMI Climate Explorer |
| PDO | annual averages of monthly observations; 1900–2005 | KNMI Climate Explorer |
| GMTA | annual; global; 1900–2005 | HadCRUT4 |
| CO (Million Tonnes/Year) | annual; global production-based emissions; 1850–2005 | Our World in Data—not in use |
| CO (ppm) | annual; global 1850–2014 (Meinshausen et al. 2017): 2015–2017 (NOAA-ESRL): | IAC ETH Zürich NOAA-ESRL |
Appendix B. Additional Simulation Results
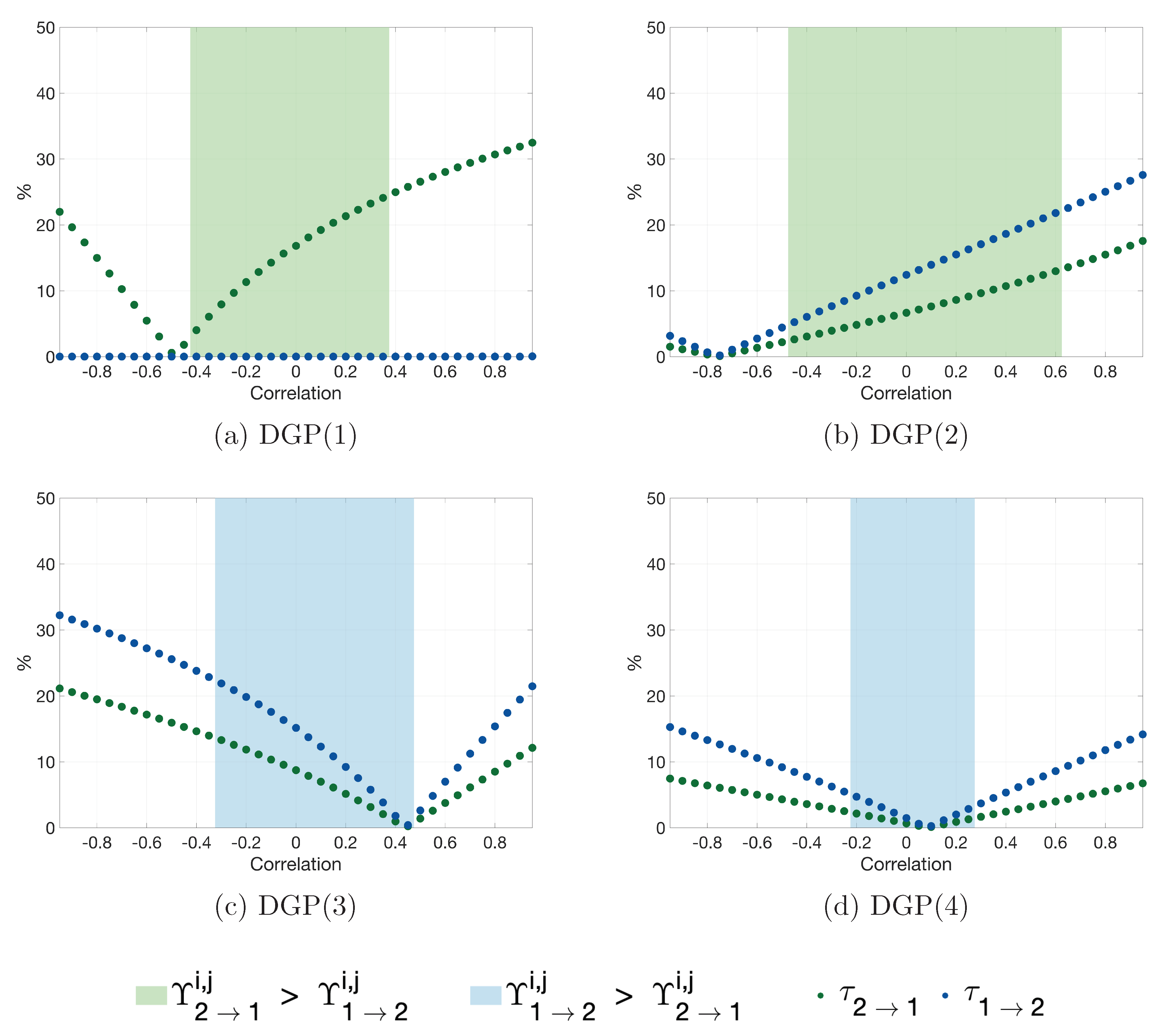
Appendix C. Additional Empirical Results
| Correlation | Normalized IF (IF × 100) | FEVD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Lags (P) | Correlation of Residuals () | Ordering: i, GMTA | Ordering: GMTA, i | ||||||
| i→ GMTA | GMTA → i | ||||||||
| Total Forcing | 0.82 | 36.8 | 29.5 | 4 | 0.23 *** | 48.0 | 15.6 | 28.3 | 29.3 |
| (17.2) | (15.3) | 1 | 0.29 *** | 55.7 | 14.4 | 30.0 | 36.6 | ||
| Anthropogenic | 0.91 | 43.7 | −18.9 | 4 | −0.16 ** | 6.5 | 5.0 | 4.9 | 13.5 |
| (39.9) | (−0.6) | 1 | −0.15 ** | 4.2 | 5.1 | 2.4 | 13.7 | ||
| CO—ERF (W/m) SMCGL | 0.91 | 43.5 | −13.0 | 4 | −0.10 | 5.75 | 9.2 | 5.3 | 15.4 |
| (39.0) | (−0.3) | 1 | −0.11 | 2.1 | 3.1 | 1.2 | 8.0 | ||
| Aerosol | −0.84 | 37.9 | −45.7 | 4 | −0.17 ** | 3.9 | 2.9 | 6.1 | 0.0 |
| (19.4) | (−1.3) | 1 | −0.00 | 2.0 | 33.3 | 2.0 | 33.1 | ||
| Solar | 31.4 | 7.0 | 2.1 | 8 | 0.05 | 4.6 | 0.9 | 3.1 | 1.4 |
| (1.1) | (0.6) | 1 | 0.06 | 6.7 | 1.0 | 4.4 | 2.0 | ||
| Volcanic | 0.11 | 1.3 | −0.3 | 4 | 0.18 ** | 10.1 | 0.5 | 2.7 | 2.4 |
| (0.2) | (−0.2) | 1 | 0.20 *** | 7.1 | 0.3 | 0.6 | 3.7 | ||
| PDO | 0.15 | −2.3 | −0.4 | 4 | 0.4 *** | 31.0 | 0.8 | 3.9 | 13.7 |
| (−0.3) | (−0.3) | 1 | 0.38 *** | 9.5 | 0.3 | 0.7 | 13.5 | ||
| CO (Mt/yr) | 0.89 | 42.0 | 1.0 | 2 | −0.12 | 7.9 | 1.9 | 8.8 | 0.3 |
| (31.0) | (0.00) | 1 | −0.10 | 5.4 | 0.0 | 5.4 | 0.7 | ||
| CO (W/m) | 0.91 | 43.4 | −13.4 | 2 | 0.18 ** | 5.0 | 16.1 | 6.1 | 6.2 |
| (38.3) | (−0.3) | 1 | 0.06 | 1.5 | 3.4 | 1.0 | 1.6 | ||
| Ordering | Without Trend | With Trend | ||||
|---|---|---|---|---|---|---|
| TCR | TCR | TCR | TCR | |||
| CO, GMTA | 1.46 C | 1.94 C | 1.76 C | 2.35 C | ||
| GMTA, CO | 0.58 C | 1.79 C | 0.97 C | 2.22 C | ||
| 1 | In Tawia Hagan et al. (2019), IFs are used on daily data, which can alleviate the problem if there are no intra-day relationships. This last condition is something that should be verified, not assumed. |
| 2 | Of course, there are identification schemes outside of the family of “orderings” obtained by Choleski decomposition, but those are beyond the scope of this paper and unnecessary to make our main point. |
| 3 | For a discussion on how to think about “shocks” in a physical system, see Goulet Coulombe and Göbel (2021). |
| 4 | Variances of and are one. |
| 5 | It is important to note that while we consider cases where either or , there is a continuum of possibilities between those. We do so for simplicity of exposition (it makes the problem dichotomous). Moreover, setting either or to zero corresponds to a causal ordering that is by far the most common identification scheme used in practice, which happens to be what we will be using in Section 4. |
| 6 | Resolving this puzzle has led to re-evaluating the role of oceans in the interplay of radiative forcing and the climatic response (Marotzke and Forster 2015; Tollefson 2014). |
| 7 | Data on the Pacific Decadal Oscillation (PDO) range from 1900 to 2005. |
| 8 | The sample was restricted to 1850–2005 to match that of SMCGL. Table A2 reports results extending the sample to 2017. |
| 9 | There are other identification schemes that cannot be cast as “orderings”. That is, there are rotations of (even when ) giving different structural shocks. Hence, while the two orderings span a lot of possibilities (and those traditionally considered first in practice), they do represent the universe of rotations of into . |
| 10 | Hansen et al. (2006) states that global warming did not start to accelerate prior to the 1970s. Only after 1975 did the global temperature increase by approximately 0.2 C per decade. |
| 11 | See: Available online: https://drive.google.com/file/d/1yhaJi92dvY_Lax0H5BFIzJeNc517Gn44/view?usp=sharing (accessed on 31 August 2021). |
| 12 | Especially NO is found to be well-correlated with CO emissions (Forster et al. 2020). |
| 13 | An annual increase of 1% in atmospheric CO concentration results in a doubling of CO after approximately 70 years, which is described more formally as: for (Montamat and Stock 2020). |
| 14 | With the proliferation of new methods to extract information flows between time series (e.g., fractal regressions (Kristoufek and Ferreira 2018) or multiscale transfer entropy (Zhao et al. 2018)), there is much research to be done on dealing with the simultaneity problem within those heterogeneous frameworks. |
References
- Andrews, T., P. M. Forster, O. Boucher, N. Bellouin, and A. Jones. 2010. Precipitation, Radiative Forcing and Global Temperature Change. Geophysical Research Letters 37. [Google Scholar] [CrossRef]
- Bindoff, N. L., P. A. Stott, P. A. AchutaRao, M. R. Allen, N. Gillett, D. Gutzler, K. Hansingo, G. Hegerl, Y. Hu, S. Jain, and et al. 2013. Chapter 10—Detection and Attribution of Climate Change: From Global to Regional. In Climate Change 2013: The Physical Science Basis. IPCC Working Group I Contribution to AR5. Cambridge: Cambridge University Press. [Google Scholar]
- Bruns, S. B., Z. Csereklyei, and D. I. Stern. 2020. A Multicointegration Model of Global Climate Change. Journal of Econometrics 214: 175–97, Annals Issue: Econometric Models of Climate Change. [Google Scholar] [CrossRef]
- Chen, Gang, Daniel R. Glen, Ziad S. Saad, J. Paul Hamilton, Moriah E. Thomason, Ian H. Gotlib, and Robert W. Cox. 2011. Vector autoregression, structural equation modeling, and their synthesis in neuroimaging data analysis. Computers in Biology and Medicine 41: 1142–55. [Google Scholar] [CrossRef]
- Estrada, Francisco, Pierre Perron, and Benjamín Martínez-López. 2013. Statistically derived contributions of diverse human influences to twentieth-century temperature changes. Nature Geoscience 6: 1050–5. [Google Scholar] [CrossRef]
- Etminan, M., G. Myhre, E. J. Highwood, and K. P. Shine. 2016. Radiative Forcing of Carbon Dioxide, Methane, and Nitrous Oxide: A significant Revision of the Methane Radiative Forcing. Geophysical Research Letters 43: 12614–23. [Google Scholar] [CrossRef]
- Forster, P. M., H. I. Forster, M. J. Evans, M. J. Gidden, C. D. Jones, C. A. Keller, R. D. Lamboll, C. L. Quéré, J. Rogelj, D. Rosen, and et al. 2020. Current and Future Global Climate Impacts Resulting from COVID-19. Nature Climate Change 10: 913–19. [Google Scholar] [CrossRef]
- Forster, P., T. Storelvmo, K. Armour, W. Collins, J. L. Dufresne, D. Frame, D. J. Lunt, T. Mauritsen, M. D. Palmer, M. Watanabe, and et al. 2021. The Earth’s Energy Budget, Climate Feedbacks, and Climate Sensitivity. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. Edited by V. Masson-Delmotte, P. Zhai, A. Pirani, S. Connors, C. Péan, S. Berger, Y. Caud, N. Chen, L. Goldfarb, M. Gomis and et al. Cambridge: Cambridge University Press. [Google Scholar]
- Goulet Coulombe, Philippe. 2020. The Macroeconomy as a Random Forest. Available online: https://ssrn.com/abstract=3633110 (accessed on 31 August 2021).
- Goulet Coulombe, Philippe, and Maximilian Göbel. 2021. Arctic amplification of anthropogenic forcing: A vector autoregressive analysis. Journal of Climate. Forthcoming. [Google Scholar]
- Granger, Clive W. J. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society 37: 424–38. [Google Scholar] [CrossRef]
- Granville Tunnicliffe, Wilson. 2015. Atmospheric co2 and global temperatures: The strength and nature of their dependence. In Working Paper. Lancaster: Lancaster University. [Google Scholar]
- Hansen, J., M. Sato, R. Ruedy, K. Lo, D. W. Lea, and M. Medina-Elizade. 2006. Global Temperature Change. Proceedings of the National Academy of Sciences 103: 14288–93. [Google Scholar] [CrossRef]
- Kilian, Lutz, and Helmut Lütkepohl. 2017. Structural Vector Autoregressive Analysis. Cambridge: Cambridge University Press. [Google Scholar]
- Koutsoyiannis, Demetris, and Zbigniew W Kundzewicz. 2020. Atmospheric temperature and co2: Hen-or-egg causality? Sci 2: 83. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav, and Paulo Ferreira. 2018. Capital asset pricing model in portugal: Evidence from fractal regressions. Portuguese Economic Journal 17: 173–83. [Google Scholar] [CrossRef]
- Li, C., D. Notz, S. Tietsche, and J. Marotzke. 2013. The Transient versus the Equilibrium Response of Sea Ice to Global Warming. Journal of Climate 26: 5624–36. [Google Scholar] [CrossRef][Green Version]
- Liang, X. S. 2008. Information Flow within Stochastic Dynamical System. Phys. Rev. E 78: 031113. [Google Scholar] [CrossRef] [PubMed]
- Liang, X. S. 2014. Unraveling the Cause-Effect Relation between Time Series. Physical Review E 90: 052150. [Google Scholar] [CrossRef] [PubMed]
- Liang, X. S. 2015. Normalizing the Causality between Time Series. Physical Review E 92: 022126. [Google Scholar] [CrossRef]
- Liang, X. S. 2016. Information Flow and Causality as rigorous Notions ab initio. Physical Review E 94: 052201. [Google Scholar] [CrossRef]
- Marotzke, J., and P. M. Forster. 2015. Forcing, Feedback and Internal Variability in Global Temperature Trends. Nature 517: 565–70. [Google Scholar] [CrossRef]
- Masson-Delmotte, V., P. Zhai, H.-O. Pörtner, D. Roberts, J. Skea, P. R. Shukla, A. Pirani, W. Moufouma-Okia, C. Péan, R. Pidcock, and et al. 2018. IPCC, 2018: Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change. Sustainable Development, and Efforts to Eradicate Poverty. Available online: https://www.ipcc.ch/2018/10/08/summary-for-policymakers-of-ipcc-special-report-on-global-warming-of-1-5c-approved-by-governments/ (accessed on 31 August 2021).
- Meinshausen, M., E. Vogel, A. Nauels, K. Lorbacher, N. Meinshausen, D. M. Etheridge, P. J. Fraser, S. A. Montzka, P. J. Rayner, C. M. Trudinger, and et al. 2017. Historical greenhouse gas concentrations for climate modelling (cmip6). Geoscientific Model Development 10: 2057–116. [Google Scholar] [CrossRef]
- Montamat, G., and J. H. Stock. 2020. Quasi-experimental estimates of the transient climate response using observational data. Climatic Change 160: 361–71. [Google Scholar] [CrossRef]
- Myhre, G., D. Shindell, F.-M. Bréon, W. Collins, J. Fuglestvedt, J. Huang, D. Koch, J.-F. Lamarque, D. Lee, B. Mendoza, and et al. 2013. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Edited by T. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Doschung, A. Nauels, Y. Xia, V. Bex and P. Midgley. Cambridge: Cambridge University Press, pp. 659–740. [Google Scholar] [CrossRef]
- Nordhaus, W. 2014. Estimates of the social cost of carbon: Concepts and results from the dice-2013r model and alternative approaches. Journal of the Association of Environmental and Resource Economists 1: 273–312. [Google Scholar] [CrossRef]
- Notz, D., and J. Stroeve. 2016. Observed arctic sea-ice loss directly follows anthropogenic co2 emission. Science 354: 747–50. [Google Scholar] [CrossRef] [PubMed]
- Otto, A., F. E. L. Otto, O. Boucher, J. Church, G. Hegerl, P. M. Forster, N. P. Gillett, J. Gregory, G. C. Johnson, R. Knutti, and et al. 2013. Energy Budget Constraints on Climate Response. Nature Geoscience 6: 415–6. [Google Scholar] [CrossRef]
- Phillips, P. C. B., T. Leirvik, and T. Storelvmo. 2020. Econometric Estimates of Earth’s Transient Climate Sensitivity. Journal of Econometrics 214: 6–32. [Google Scholar] [CrossRef]
- Pretis, Felix. 2020. Econometric Modelling of Climate Systems: The Equivalence of Energy Balance Models and Cointegrated Vector Autoregressions. Journal of Econometrics 214: 256–73. [Google Scholar] [CrossRef]
- Richardson, M., K. Cowtan, E. Hawkins, and M. B. Stolpe. 2016. Reconciled climate response estimates from climate models and the energy budget of earth. Nature Climate Change 6: 931–5. [Google Scholar] [CrossRef]
- Schurer, A., G. Hegerl, A. Ribes, D. Polson, C. Morice, and S. Tett. 2018. Estimating the Transient Climate Response from Observed Warming. Journal of Climate 31: 8645–63. [Google Scholar] [CrossRef]
- Shukla, P. R., J. Skea, E. Calvo Buendia, V. Masson-Delmotte, H.-O. Pörtner, D. C. Roberts, P. Zhai, R. Slade, S. Connors, R. van Diemen, and et al. 2019. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems. Available online: https://spiral.imperial.ac.uk/bitstream/10044/1/76618/2/SRCCL-Full-Report-Compiled-191128.pdf (accessed on 6 September 2021).
- Sims, Christopher A. 1980. Macroeconomics and reality. Econometrica: Journal of the Econometric Society 48: 1–48. [Google Scholar] [CrossRef]
- Stips, A., D. Macias, C. Coughlan, E. Garcia-Gorriz, and X. S. Liang. 2016. On the Causal Structure between CO2 and Global Temperature. Scientific Reports 6: 21691. [Google Scholar] [CrossRef] [PubMed]
- Tawia Hagan, Daniel Fiifi, Guojie Wang, X San Liang, and Han AJ Dolman. 2019. A time-varying causality formalism based on the liang–kleeman information flow for analyzing directed interactions in nonstationary climate systems. Journal of Climate 32: 7521–37. [Google Scholar] [CrossRef]
- Tollefson, J. 2014. Climate Change: The Case of the Missing Heat. Nature 505: 276–8. [Google Scholar] [CrossRef] [PubMed]
- Uhlig, H. 2005. What are the effects of monetary policy on output? results from an agnostic identification procedure. Journal of Monetary Economics 52: 381–419. [Google Scholar] [CrossRef]
- Zhao, Xiaojun, Yupeng Sun, Xuemei Li, and Pengjian Shang. 2018. Multiscale transfer entropy: Measuring information transfer on multiple time scales. Communications in Nonlinear Science and Numerical Simulation 62: 202–12. [Google Scholar] [CrossRef]
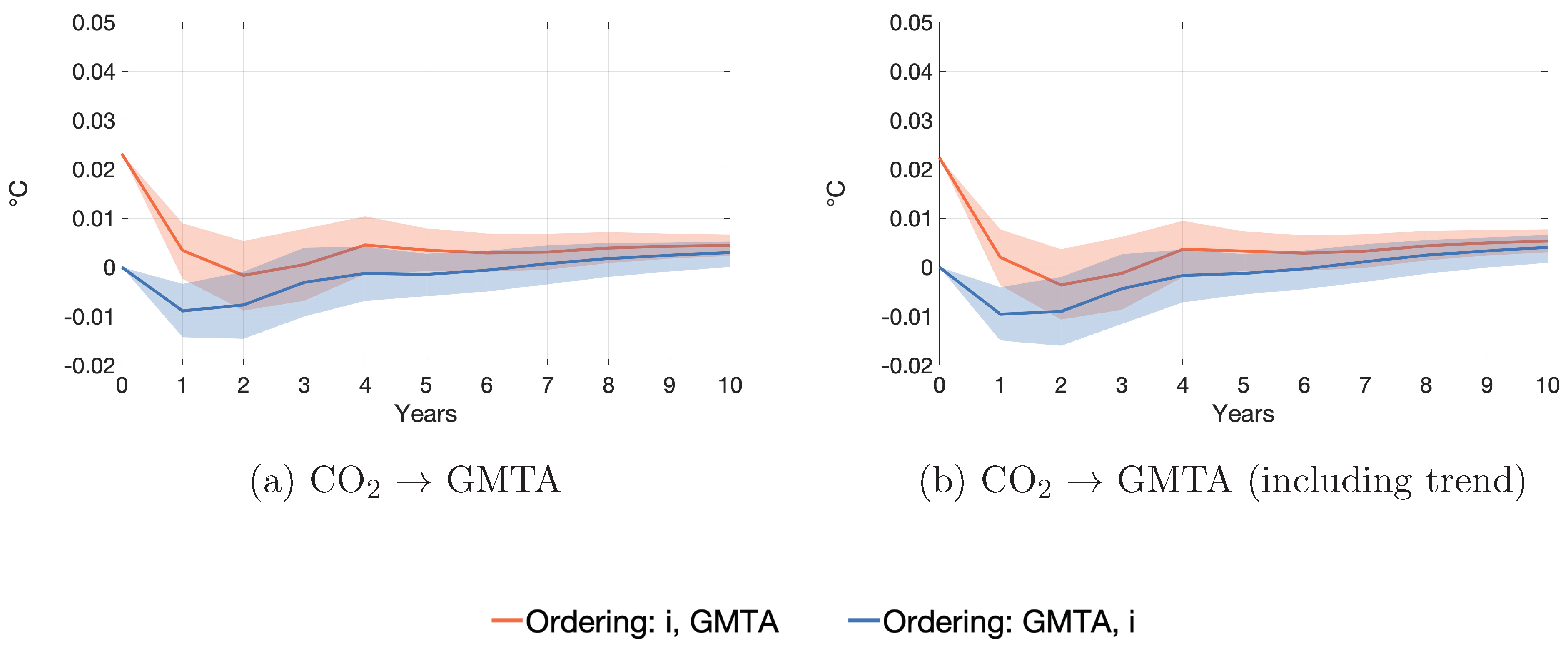
| Correlation | Normalized IF (IF × 100) | FEVD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Lags | Correlation of | Ordering: i, GMTA | Ordering: GMTA, i | ||||||
| i→ GMTA | GMTA → i | (P) | Residuals () | ||||||
| Total Forcing | 0.73 | 30.6 | 20.8 | 4 | 0.23 *** | 47.4 | 13.0 | 28.0 | 25.4 |
| (15.3) | (11.1) | 1 | 0.29 *** | 51.4 | 9.6 | 27.6 | 28.7 | ||
| Anthropogenic | 0.86 | 39.8 | −20.0 | 4 | −0.19 ** | 6.5 | 3.7 | 3.8 | 13.4 |
| (35.7) | (−0.6) | 1 | −0.19 ** | 5.0 | 5.8 | 2.2 | 17.1 | ||
| CO-ERF (W/m) SMCGL | 0.86 | 39.6 | −15.2 | 4 | −0.14 * | 6.5 | 8.4 | 5.6 | 17.4 |
| (35.1) | (−0.4) | 1 | −0.15 * | 2.8 | 4.7 | 1.1 | 12.8 | ||
| Aerosol | −0.82 | 35.9 | −24.5 | 4 | −0.19 ** | 2.9 | 0.6 | 2.1 | 1.6 |
| (24.3) | (−0.4) | 1 | −0.10 | 3.5 | 4.0 | 1.8 | 1.2 | ||
| Solar | 0.49 | 13.5 | 6.7 | 8 | 0.05 | 8.5 | 1.6 | 6.6 | 2.5 |
| (3.8) | (2.3) | 1 | 0.08 | 16.6 | 4.2 | 12.3 | 6.8 | ||
| Volcanic | 0.09 | 0.9 | −0.5 | 4 | 0.18 ** | 10.9 | 0.8 | 3.1 | 3.6 |
| (0.2) | (−0.4) | 1 | 0.20 ** | 7.1 | 1.4 | 0.6 | 3.7 | ||
| PDO | 0.17 | −1.2 | −0.6 | 4 | 0.35 *** | 31.1 | 0.9 | 6.3 | 10.3 |
| (−0.2) | (−0.5) | 1 | 0.34 *** | 9.1 | 0.5 | 0.2 | 10.7 | ||
| CO (Mt/yr) | 0.82 | 37.1 | −4.3 | 2 | −0.10 | 8.9 | 2.1 | 10.7 | 0.6 |
| (27.0) | (−0.0) | 1 | −0.05 | 4.2 | 0.0 | 4.4 | 0.4 | ||
| CO (W/m) | 0.86 | 39.5 | −14.0 | 4 | 0.23 *** | 5.2 | 16.8 | 2.9 | 4.7 |
| (34.5) | (−0.3) | 1 | 0.07 | 1.6 | 4.1 | 0.9 | 1.8 | ||
| Ordering | Without Trend | With Trend | ||||
|---|---|---|---|---|---|---|
| TCR | TCR | TCR | TCR | |||
| CO, GMTA | 1.99 C | 2.06 C | 2.17 C | 2.58 C | ||
| GMTA, CO | 0.57 C | 1.82 C | 0.85 C | 2.39 C | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goulet Coulombe, P.; Göbel, M. On Spurious Causality, CO2, and Global Temperature. Econometrics 2021, 9, 33. https://doi.org/10.3390/econometrics9030033
Goulet Coulombe P, Göbel M. On Spurious Causality, CO2, and Global Temperature. Econometrics. 2021; 9(3):33. https://doi.org/10.3390/econometrics9030033
Chicago/Turabian StyleGoulet Coulombe, Philippe, and Maximilian Göbel. 2021. "On Spurious Causality, CO2, and Global Temperature" Econometrics 9, no. 3: 33. https://doi.org/10.3390/econometrics9030033
APA StyleGoulet Coulombe, P., & Göbel, M. (2021). On Spurious Causality, CO2, and Global Temperature. Econometrics, 9(3), 33. https://doi.org/10.3390/econometrics9030033





