1. Introduction
Many time series indicate non-Gaussian characteristics, such as outliers, flat stretches, bursts of activity, and change points (
Le et al. 1996). Several methods have been proposed to deal with the presence of bursts and outliers such as applying robust or resistant estimation procedures (
Martin and Yohai 1986) or omitting the outliers based on the use of diagnostics (
Bruce and Martin 1989).
Le et al. (
1996) introduced a Mixture Transition Distribution (MTD) model to capture non-Gaussian and nonlinear patterns, using the Expectation–Maximization (EM) algorithm as its estimation method. The model was applied to two real datasets, i.e., the daily International Business Machines (IBM) common stock closing price from 17 May 1961 to 2 November 1962 and the series of consecutive hourly viscosity readings from a chemical process. The MTD model appears to capture the features of the data better than the Autoregressive Integrated Moving Average (ARIMA) models.
The Gaussian Mixture Transition Distribution (GMTD), which is a special form of MTD, was generalized to a Gaussian Mixture Autoregressive (GMAR) model by
Wong and Li (
2000). The model consists of a mixture of
K Gaussian autoregressive components and is able to model time series with both heteroscedasticity and multimodal conditional distribution. It was applied to both the daily IBM common stock closing price from 17 May 1961 to 2 November 1962 and the Canadian lynx data for the period 1821–1934. The results indicated that the GMAR model was better than the GMTD, ARIMA, and Self-Exciting Threshold Autoregressive (SETAR) models.
The use of the Gaussian distribution in the GMAR model still leaves problems, because it is able to capture only short-tailed data patterns. Some methods developed to overcome this problem include the use of distributions other than Gaussian, e.g., the Logistic Mixture Autoregressive with Exogenous Variables (LMARX) model (
Wong and Li 2001), Student
t-Mixture Autoregressive (TMAR) model (
Wong et al. 2009), Laplace MAR model (
Nguyen et al. 2016), and a mixture of autoregressive models based on the scale mixture of skew-normal distributions (SMSN-MAR) model (
Maleki et al. 2020).
Maleki et al. (
2020) proposed the finite mixtures of autoregressive processes assuming that the distribution of innovations belongs to the class of Scale Mixture of Skew-Normal (SMSN) distributions. This distribution innovation can be employed in data modeling that has outliers, asymmetry, and fat tails in the distribution simultaneously. However, the SMSN distribution’s mode was not stable in its location parameters (
Azzalini 2014). In this paper, we propose a new MAR model called the Fisher’s
z Mixture Autoregressive (ZMAR) model which assumes that the distribution of innovations belongs to the Fisher’s
z distributions (
Solikhah et al. 2021). The ZMAR model consists of a mixture of
K-component Fisher’s
z autoregressive models, where the numbers of components are based on the number of modes in the marginal density. The Fisher’s
z distribution’s mode is stable in its location parameters, whether it is symmetrical or skewed. Therefore, Fisher’s
z uses the errors in each component of the MAR model to capture the ‘most likely’ mode value—(not the mean, median, or quantile) of the conditional distribution
Yt given the past information. The conditional mode may be a more useful summary than the conditional mean when the conditional distribution of
Yt given the past information is asymmetric. Other distributions that also have a stable mode in its location parameter are the MSNBurr distribution (
Iriawan 2000;
Choir et al. 2019;
Pravitasari et al. 2020), the skewed Studen
t distribution (
Fernández and Steel 1998), and the log
F-distribution (
Brown et al. 2002).
The Bayesian technique using Markov Chain Monte Carlo (MCMC) is proposed to estimate the model parameters. Among the algorithms in the MCMC, the Gibbs sampling (
Geman and Geman 1984) and the Metropolis (
Metropolis et al. 1953) algorithms are widely applied and well-known algorithms. However, these algorithms have slow convergence due to inefficiencies in the MCMC processes, especially in the case of models with many correlated parameters (
Gelman et al. 2014, p. 269). Furthermore,
Neal (
2011) has shown that the Hamiltonian Monte Carlo (HMC) algorithm is a more efficient and robust sampler than Metropolis or Gibbs sampling for models with complex posteriors. However, the HMC suffers from a computational burden and the tuning process. The HMC can be tuned in three places (
Gelman et al. 2014, p. 303), i.e., the probability distribution for the momentum variables
φ, the step size of the leapfrog
ε, and the number of leapfrog steps
L per iteration. To overcome the challenges related to computation and tuning, the Stan program (
Gelman et al. 2014, p. 307;
Carpenter et al. 2015,
2017) was developed to automatically apply the HMC. Stan runs HMC using the no-U-turn sampler (NUTS) (
Hoffman and Gelman 2014).
Al Hakmani and Sheng (
2017) used NUTS for the two-parameter mixture IRT (Mix2PL) model and discussed in more detail its performance in estimating model parameters under eight conditions, i.e., two sample sizes per class (250 and 500), two test lengths (20 and 30), and two levels of latent classes (2-class and 3-class). The results indicated that overall, NUTS performs well in retrieving model parameters. Therefore, this research applies the Bayesian method to estimate the parameters of the ZMAR model, using MCMC with the NUTS algorithm, as well as simulation studies to examine different scenarios in order to evaluate whether the proposed mixture model outperforms its counterparts. The models are applied to both the daily IBM common stock closing price from 17 May 1961 to 2 November 1962 (
Box et al. 2015, p. 627) and the Brent crude oil price (
World Bank 2020). For model selection, we used cross-validation Leave-One-Out (LOO) coupled with the Pareto-smoothed important sampling (PSIS), namely PSIS-LOO. This approach has very efficient computation and was stronger than the Widely Applicable Information Criterion (WAIC) (
Vehtari et al. 2017).
The rest of this study is organized as follows.
Section 2 describes the definition and properties of Fisher’s
z distribution in detail. In
Section 3, we introduce the ZMAR model.
Section 4 demonstrates the flexibility of the ZMAR model compared with the TMAR and GMAR models using simulated datasets.
Section 5 contains the application and comparison of the models using the daily IBM stock prices and the monthly Brent crude oil prices. The conclusion and discussion are given in
Section 6.
2. Four-Parameter Fisher’s z Distribution
Let
be a random variable distributed as an
F distribution with
and
degrees of freedom. The density of
can be defined as
and the cumulative distribution function (CDF) of
is expressed as
where
is the exponential constant;
is the incomplete beta function ratio; and
is the beta function,
. Equations (1) and (2) are defined as a probability density function (p.d.f) and a CDF of standardized Fisher’s
z distribution, respectively. Let
be a random variable distributed as a standardized Fisher’s
z distribution. Let
be a location parameter, and let
be a scale parameter. The density of
is (
Solikhah et al. 2021)
where
and
Equation (3) is defined as a p.d.f of Fisher’s
z distribution. It is denoted as
. The CDF of the Fisher’s
z distribution is expressed as
where
The quantile function (QF) of the Fisher’s
z distribution is defined as
where
is the QF of the
F-distribution and
is the inversion of the incomplete beta function ratio. Let
be the inversion of the incomplete gamma function ratio. The QF of the Fisher’s
z distribution can be expressed as
where
and
are the QF of the chi-square distribution with
and
degrees of freedom, respectively. The proofs of Equation (1) up to Equation (6) are postponed to
Appendix A. The parameters
and
, known as the shape parameters, are defined for both skewness (symmetrical if
, asymmetrical if
) and fatness of the tails (large
and
imply thin tails). The Fisher’s
z distribution is also always unimodal and has the mode at
Furthermore, a change in the value of the parameter
only affects the mean of the distribution. It does not affect the variance, skewness, and kurtosis of the distribution. The detailed properties of the Fisher’s
z distribution are shown in
Appendix B.
A useful tutorial on adding custom function to Stan is provided by
Stan Development Team (
2018) and
Annis et al. (
2017). To add a user-defined function, it is first necessary to define a block of function code. The function block must precede all other blocks of Stan code. The code for the random numbers generator function (fisher_z_rng) is shown in
Appendix C.1, and the log probability function (fisher_z_lpdf) is shown in
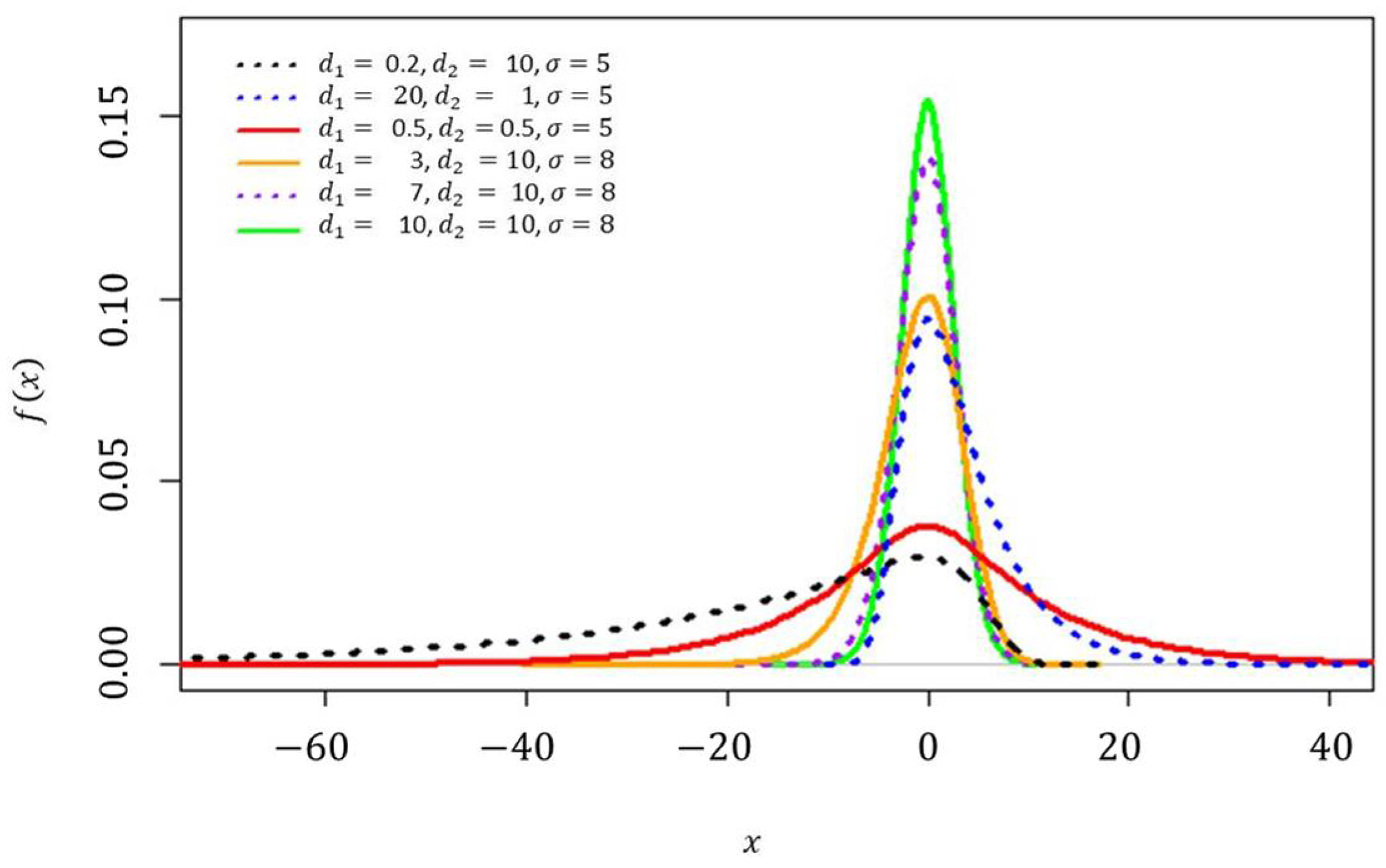
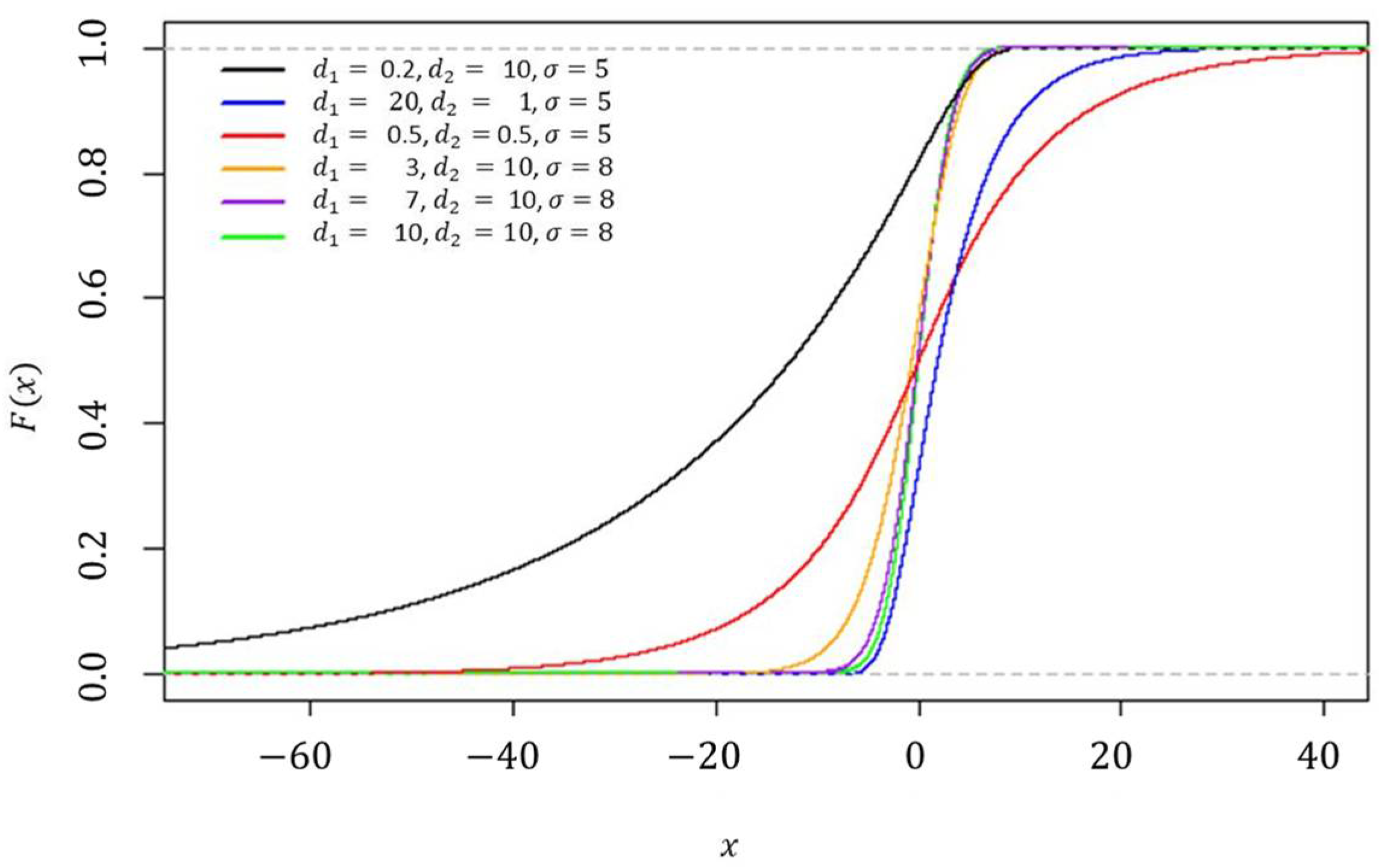
Appendix C.2. As an illustration, the p.d.f and CDF of the Fisher’s
z distribution with various parameter settings can be seen in
Figure 1 and
Figure 2, respectively.
4. Simulation Studies
A simulation study was carried out to evaluate the performance of the ZMAR model compared to the TMAR and GMAR models. We consider the simulations to accommodate eight scenarios for the conditional density in the first component of the ZMAR model. Furthermore, the conditional densities in the second and third components are specified as the symmetric-fat-tail of the Fisher’s z distributions.
We conducted a Bayesian analysis on the eight simulated datasets, whose datasets were generated by the following steps:
Step 1: Specify the ZMAR model with three components as where with 3 are the innovations in the first, second, and third components. The scenarios for the simulation are as follows:
- ○
Scenario 1: represent a mixture of a highly skewed (
Bulmer 1967, p. 63) to the left and two symmetrical distributions, where
, excess unconditional kurtosis is 5.73,
and
- ○
Scenario 2: represent a mixture of a highly skewed to the right and two symmetrical distributions, where excess unconditional kurtosis is 2.23, and
- ○
Scenario 3: represent a mixture of three symmetrical distributions, where excess unconditional kurtosis is 1.67, , and ;
- ○
Scenario 4: represent a mixture of moderately skewed (
Bulmer 1967, p. 63) distributions, where
excess unconditional kurtosis is 2.12,
and
- ○
Scenario 5: represent a mixture of three fairly symmetrical distributions (
Bulmer 1967, p. 63), where
excess unconditional kurtosis is 4.25,
and
- ○
Scenario 6: represent a mixture of three symmetrical distributions, where , excess unconditional kurtosis is 4.47, , and ;
- ○
Scenario 7: represent a mixture of three symmetrical distributions, where excess unconditional kurtosis is 1.63, , and ;
- ○
Scenario 8: represent a mixture of three symmetrical distributions, where , excess unconditional kurtosis is 0.67, , and ;
The innovations of Scenario 7 and Scenario 8 are the same as those of Scenario 3. The comparison of graph visualizations for the innovations in the first component in Scenario 1 to Scenario 6 represented specifically for the Fisher’s
z distribution can be seen in
Figure 1 and
Figure 2;
Step 2: Generate and ;
Step 3: Generate ; where ;
Step 4: Compute ; 3;
Step 5: Compute .
Furthermore, we generated 600 datasets and fit all of the models for each simulated dataset, respectively, to find the best performance in terms of model comparisons.
Figure 3 shows the simulated datasets for Scenario 1 to Scenario 8. We implemented the models using the rstan package (
Stan Development Team 2020), the R interface to Stan developed by the Stan Development Team in the R software. Suppose
Here is an example of the Stan code to fit the ZMAR model in Scenario 1:
fitMAR1 = "
functions{
real fisher_z_lpdf(real x,real d1,real d2,real mu,real sigma){
return (log(2)+0.5*d2*(log(d2)-log(d1))-d2*(x-mu)/sigma-log(sigma)-lbeta(0.5*d1,0.5*d2)-
(d1+d2)/2*log1p_exp((-2*(x-mu)/sigma)+log(d2)-log(d1)));
}
}
data {
int<lower=0> p1;
int<lower=0> p2;
int<lower=0> p3;
int T;
vector[T] y;
vector[3] con_eta;
}
parameters {
simplex[3] eta; //mixing proportions
vector<lower = 0>[3] sigma;
vector<lower = 0>[3] d1;
vector<lower = 0>[3] d2;
real phi1[p1];
real phi2[p2];
real phi3[p3];
}
model {
matrix[T,3] tau;
real lf[T];
eta ~ dirichlet(con_eta);
//priors
sigma[1] ~ student_t(3,5,0.1);
sigma[2] ~ student_t(3,8,0.1);
sigma[3] ~ student_t(3,10,0.1);
d1[1] ~ student_t(3,0.2,0.1);
d1[2] ~ student_t(3,1,0.1);
d1[3] ~ student_t(3,30,0.1);
d2[1] ~ student_t(3,10,0.1);
d2[2] ~ student_t(3,1,0.1);
d2[3] ~ student_t(3,30,0.1);
phi1[1] ~ normal(-0.6,0.1);
phi2[1] ~ normal(0.2,0.1);
phi3[1] ~ normal(0.7,0.1);
//ZMAR model
for(t in 1:T) {
if(t==1) {
tau[t,1] = log(eta[1])+fisher_z_lpdf(y[t]/sigma[1]|d1[1], d2[1],0,1)-log(sigma[1]);
tau[t,2] = log(eta[2])+fisher_z_lpdf(y[t]/sigma[2]|d1[2], d2[2],0,1)-log(sigma[2]);
tau[t,3] = log(eta[3])+fisher_z_lpdf(y[t]/sigma[3]|d1[3], d2[3],0,1)-log(sigma[3]);
} else {
real mu1 = 0;
real mu2 = 0;
real mu3 = 0;
for (i in 1:p1)
mu1 += phi1[i] * y[t-i];
for (i in 1:p2)
mu2 += phi2[i] * y[t-i];
for (i in 1:p3)
mu3 += phi3[i] * y[t-i];
tau[t,1] = log(eta[1])+fisher_z_lpdf((y[t]-mu1)/sigma[1]|d1[1],d2[1],0,1)-log(sigma[1]);
tau[t,2] = log(eta[2])+fisher_z_lpdf((y[t]-mu2)/sigma[2]|d1[2],d2[2],0,1)-log(sigma[2]);
tau[t,3] = log(eta[3])+fisher_z_lpdf((y[t]-mu3)/sigma[3]|d1[3],d2[3],0,1)-log(sigma[3]);
}
lf[t] = log_sum_exp(tau[t,]);
}
target += sum(lf);
} "
The warm-up stage in these simulation studies was set to 1500 iterations, 3 chains with 5000 sampling iterations, and 1 thin. The adapt_delta parameter was set to 0.99, and the max_treedepth was set to 15. For all scenarios, the parameter priors of the ZMAR, TMAR, and GMAR models are shown in
Appendix D, and their posterior inferences are presented in
Appendix E. There are a variety of convergence diagnoses, such as the potential scale reduction factor
(
Gelman and Rubin 1992;
Susanto et al. 2018;
Gelman et al. 2014, p. 285;
Vehtari et al. 2020) and the effective sample size
neff (
Gelman et al. 2014, p. 266;
Vehtari et al. 2020). If the MCMC chain has reached convergence, the
statistic is less than 1.01, and the
neff statistic is greater than 400 (
Vehtari et al. 2020). To compare the performance of the models, we use the PSIS-LOO.
Table 1 shows the summary simulation result for all scenarios, which indicates that the ZMAR model performs the best when the datasets are generated from the ZMAR model, in which one of the components is asymmetric. When all the components are symmetric, the ZMAR model also performs better than TMAR and GMAR, as long as the excess unconditional kurtosis is large enough or the intercept distances between the components are far apart. However, when all of the mixture components are symmetric, the excess unconditional kurtosis is small and the intercept distances between the components are close enough or the intercepts are the same, then the GMAR model plays the best. Let us now focus on the results of Scenario 3 and Scenario 6.
In the third and sixth scenarios, the datasets are generated from three symmetrical distributions. The two scenarios have the same intercepts and are generated with different unconditional kurtosis. Scenario 3 has a smaller unconditional kurtosis than Scenario 6. The best ZMAR, TMAR, and GMAR models for the two scenarios are ZMAR(3;1,1,1), TMAR(3;1,1,1), and GMAR(3;1,1,1), where the values of PSIS-LOO are 4483.30, 4483.10, and 4481.10, for the third scenario and 3490.10, 3496.20, and 3494.60, for the sixth scenario. Clearly, the PSIS-LOO value for the GMAR model is smaller than for the ZMAR and TMAR models in the third scenario, and the ZMAR model has the smallest PSIS-LOO value in the sixth scenario. When the intercepts in Scenario 3 are varied and determined as in Scenario 7, the GMAR model is also the best. However, when the intercepts in Scenario 3 are varied and determined as in Scenario 8, the ZMAR model is the best. For other scenarios, in datasets generated from asymmetric components (the first, second, fourth, and fifth scenarios), the ZMAR model is the best.
6. Conclusions
We have discussed the definition and properties of the four-parameter Fisher’s z distribution. The four-parameters of the Fisher’s z distribution are and The is a location parameter, the is a scale parameter, and the , are known as the shape parameters, defined for both skewness (symmetric if , asymmetric if ) and fatness of the tails (large and imply thin tails). The Fisher’s z distribution is always unimodal and has the mode at The value of only affects the mean of the distribution. It does not affect the variance, skewness, and kurtosis of the distribution. Furthermore, if , then the mean is equal to ; if , then the mean is less than ; and if , then the mean is greater than . The excess kurtosis value for this distribution is always positive.
We also discussed a new class of nonlinearity in the level (or mode) model for capturing time series with heteroskedasticity and with multimodal conditional distribution, using Fisher’s z distribution as an innovation in the MAR model. The model offers great flexibility that other models, such as the TMAR and GMAR models, do not. The MCMC algorithm, using NUTS, allows for the easy estimation of the parameters in the model. The paper provides a simulation study using eight scenarios to indicate the flexibility and superiority of the ZMAR model compared with the TMAR and GMAR models. The simulation result shows that the ZMAR model is the best for representing the datasets generated from asymmetric components. When all the components are symmetrical, the ZMAR model also performs the best, as long as the excess unconditional kurtosis is large enough or the intercept distances between the components are far apart. However, when the datasets are generated from symmetrical components with small excess unconditional kurtosis and close intercept distances between the components, the GMAR model is the best. Furthermore, we compared the proposed model with the GMAR and TMAR models using two real data, namely the daily IBM stock prices and the monthly Brent crude oil prices. The results show that the proposed model outperforms the existing ones.
Fong et al. (
2007) extended univariate the GMAR models to a Gaussian Mixture Vector Autoregressive (GMVAR) model. The ZMAR model can also be extended to a multivariate time-series context.
Jones (
2002) extended the standard multivariate
F distribution to the multivariate skew
t distribution and the multivariate Beta distribution. Likewise, the
F distributed can also be extended to multivariate Fisher’s
z distribution.