Selecting a Model for Forecasting
Abstract
:1. Introduction
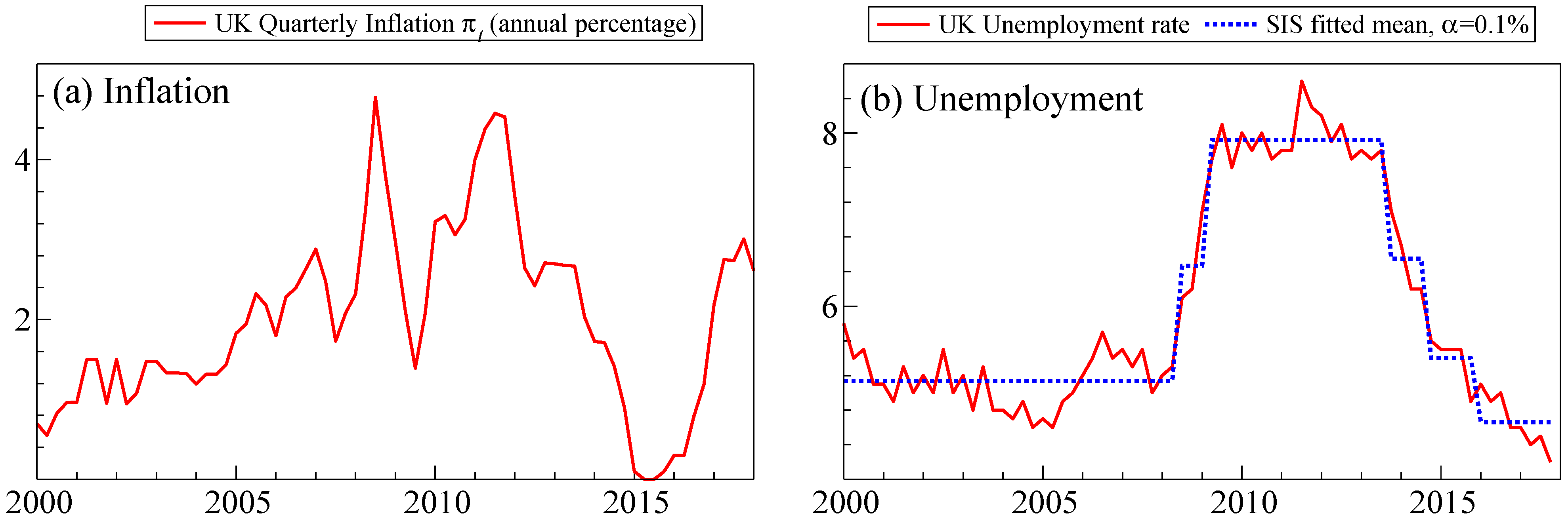
2. Empirical Motivation
3. The Analytic Design
4. Selection in a Stationary DGP
4.1. Known Future Values of Regressors
4.2. Selecting Regressors
4.3. The Choice of Significance Level
5. An Out-of-Sample Shift in the Regressors
5.1. Specification of the Out-of-Sample Shift
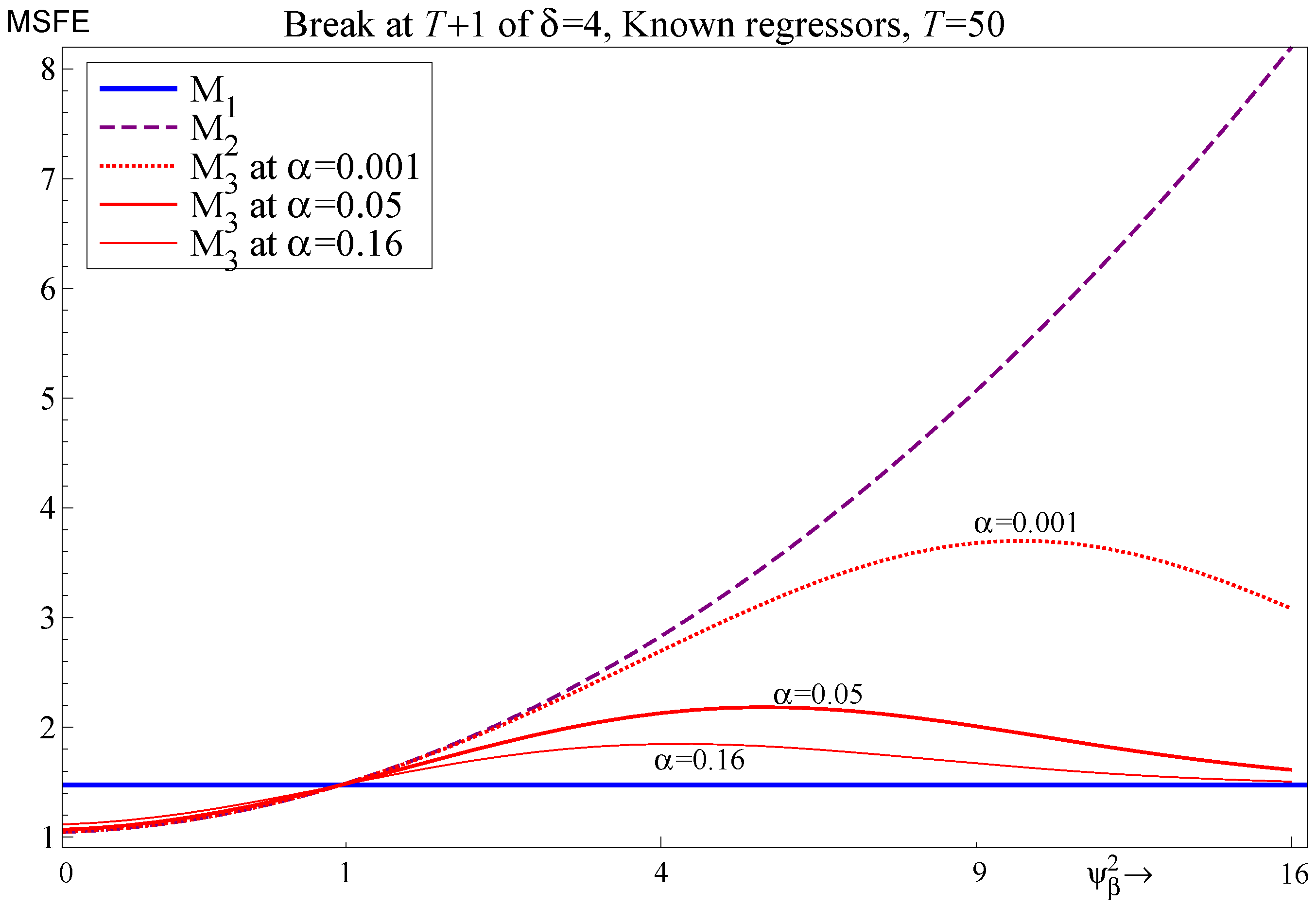
5.2. Known Future Values of Regressors
5.3. Selecting Regressors
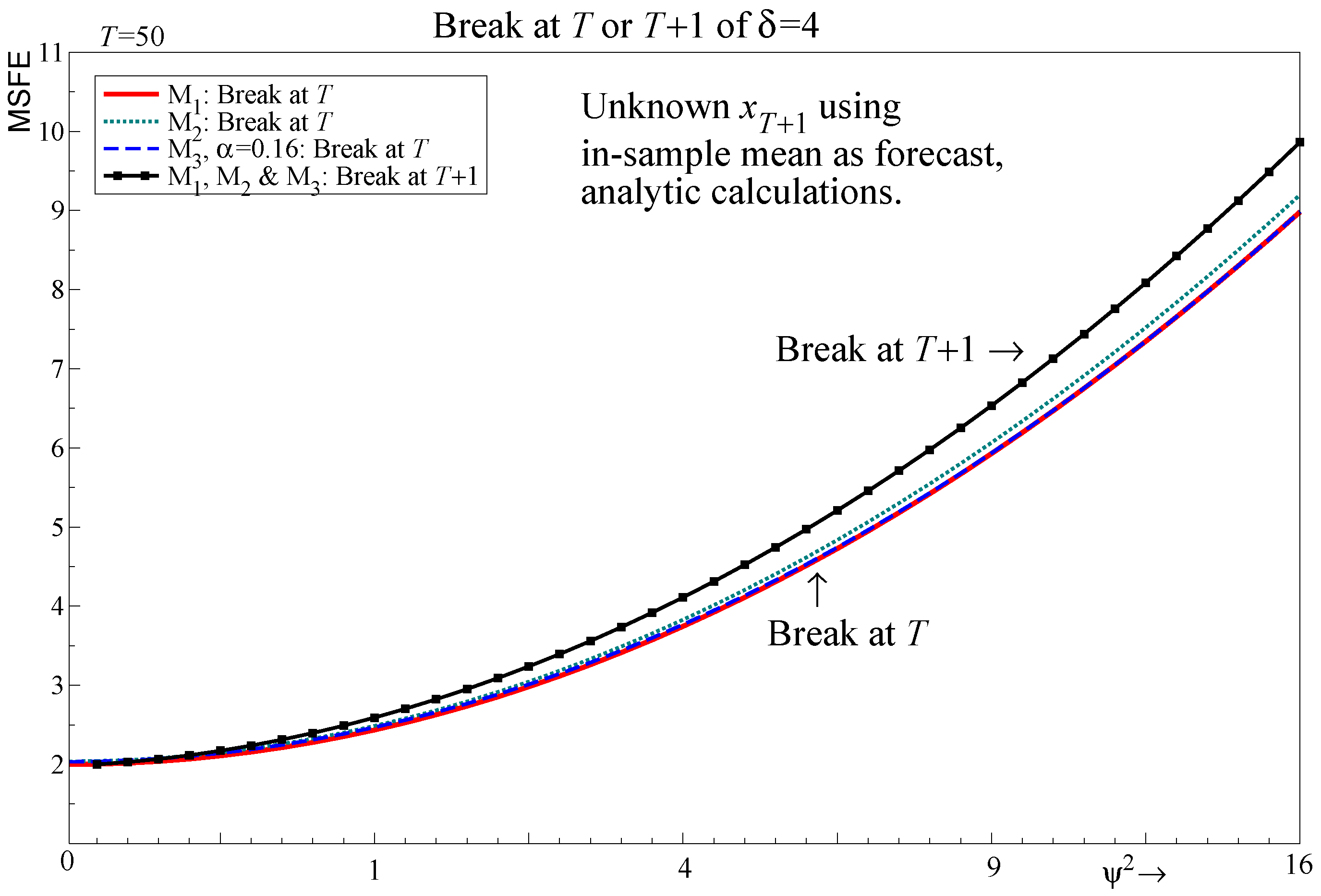
5.4. Unknown Future Values of Regressors
5.5. Forecasting Regressors with a Random Walk
5.6. Selecting Forecasted Regressors
6. An In-Sample Shift in the Regressors
6.1. Specification of the In-Sample Shift
6.2. Forecasting Regressors Using In-Sample Means
6.3. Selecting Regressors
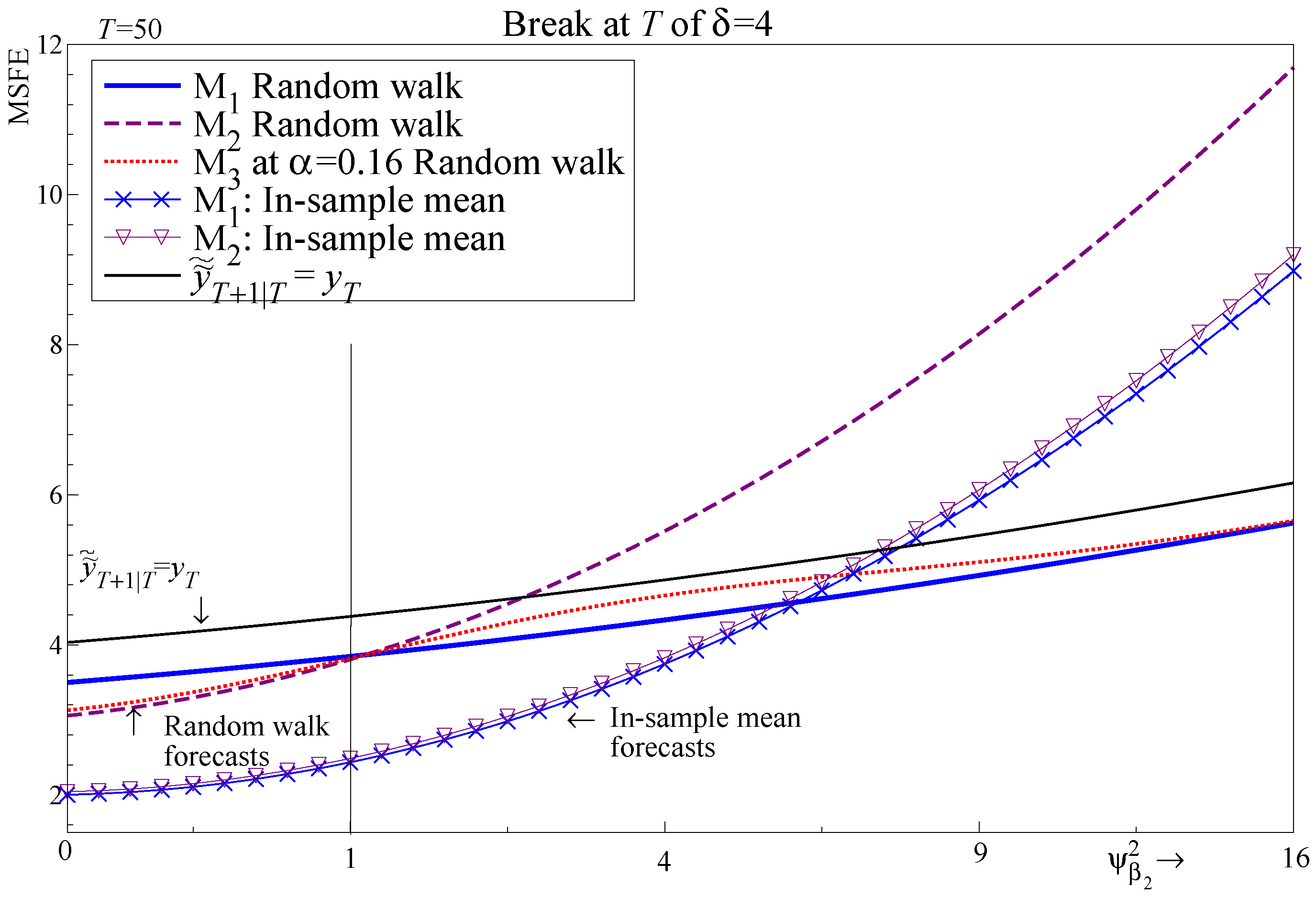
6.4. Forecasting Regressors Using a Random Walk
6.5. Selecting Forecasted Regressors
6.6. Forecasting the Dependent Variable Using a Random Walk
7. Summary of Analytic Results and the Impact of Selection
- Regressors should be retained if . This is established for DGPs that are stationary or with a break out of sample for known regressors and a break in sample for random walk forecasts.
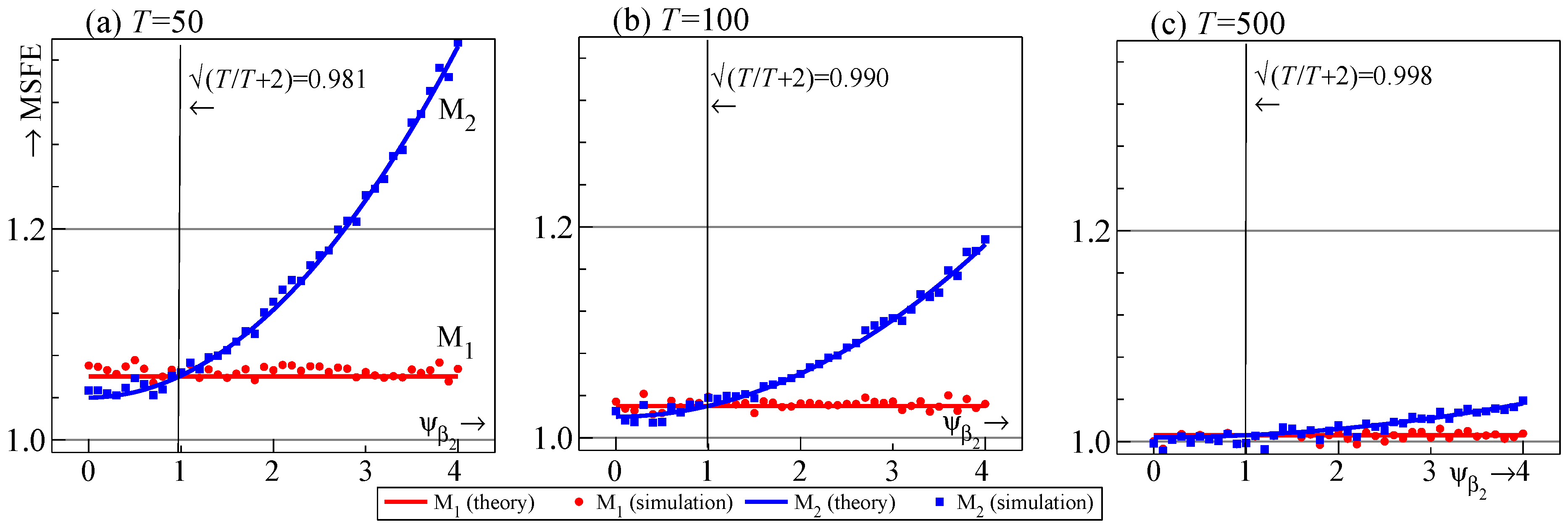
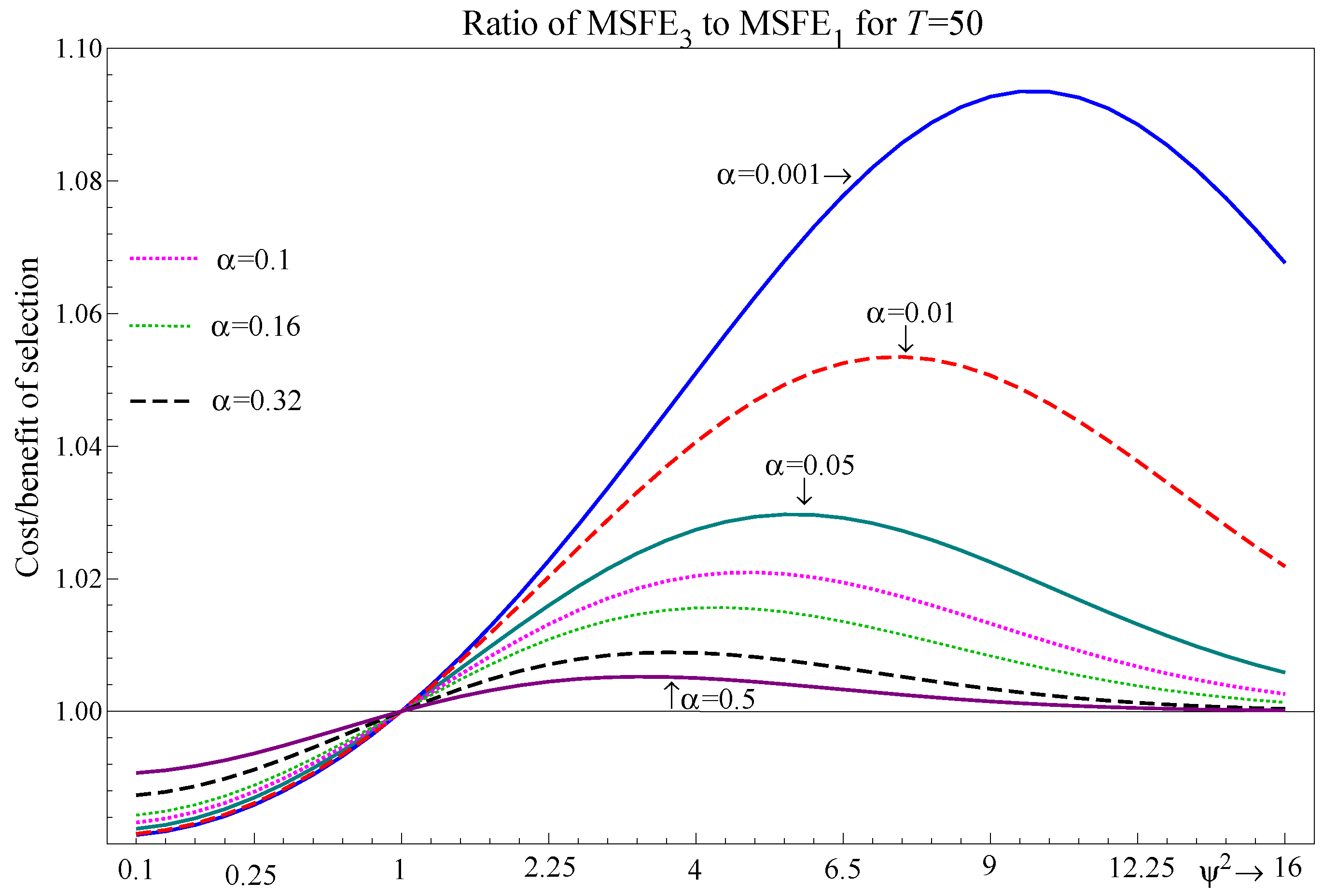
- For the two-regressor case, maps to . Selection delivers improvements to the one-step-ahead MSFE for and can be close to the correct model specification for , with the largest deviations occurring at intermediate values of .
- If there are breaks out of sample and contemporaneous regressors need to be forecast, the break dominates the MSFE and selection plays almost no role. Similar results are found even if the break occurs at the end of the sample, but the in-sample mean is used to forecast the regressors.
- Random walk forecasts are costly if there are no breaks (forecasting ) or if the breaks are unpredictable (a break at and forecasting ). However, they improve MSFE when the break is predictable (break at T and forecasting ).
8. Simulation Design
8.1. Data Generation Process
8.2. Models and Forecast Devices
- inf:
- future outcomes: ;
- avg:
- the in-sample average: ;
- arx:
- an AR(1) for each regressor: , estimated by OLS for each horizon from:
- rwx:
- the random walk forecast: ;
- rdx:
- cax:
- Cardt forecast of .
- rwy:
- a random walk forecast: ;
- ary:
- an AR(1) forecast: , estimated by OLS for each horizon;
- cay:
- Cardt forecasts of .
8.3. Selecting Regressors
9. Simulation Evidence
9.1. Forecasting before the Break
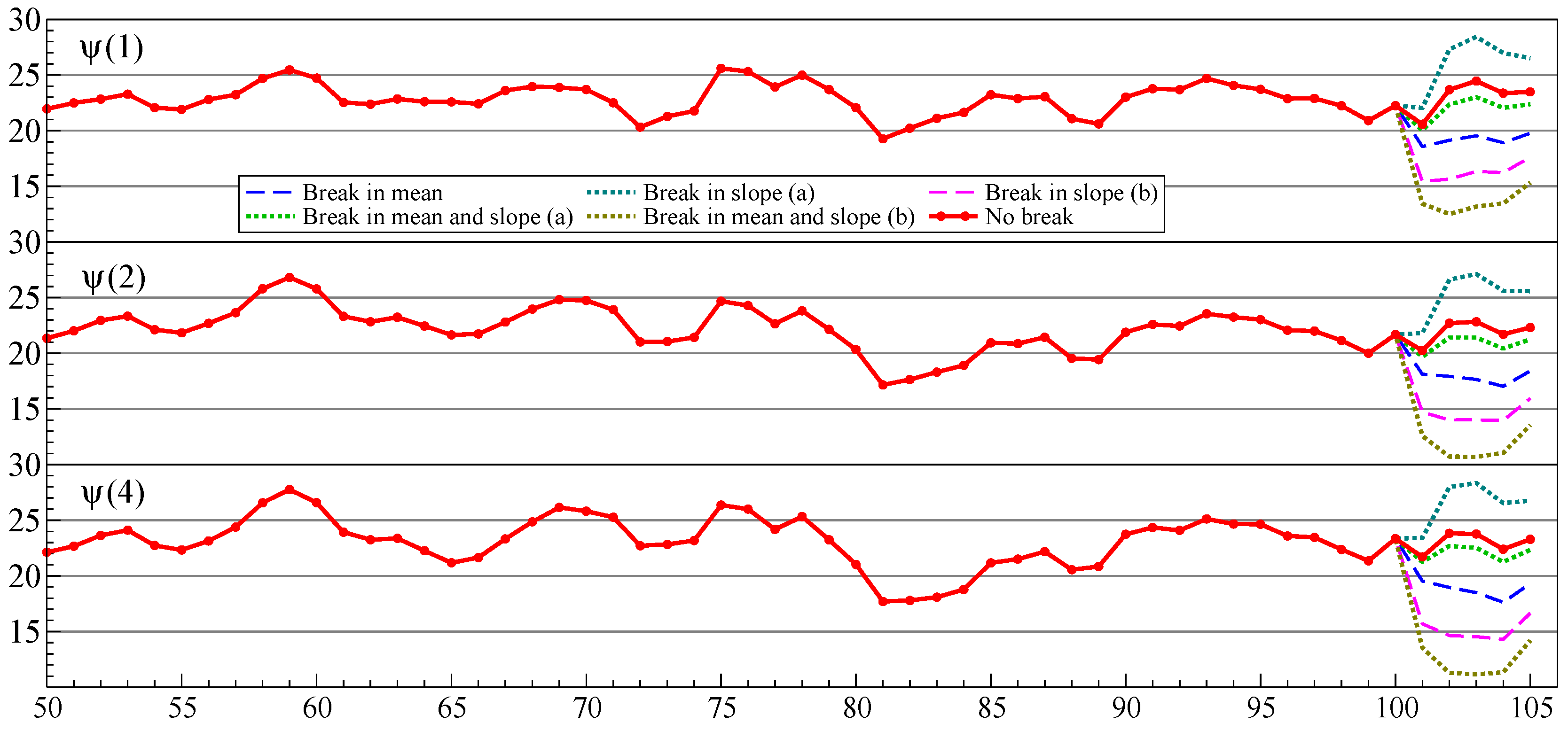
9.2. Selection and Location of the Break
- Break in relevant regressors
- ()The break shows up in y through the relevant variables. Inclusion of irrelevant variables in the forecasting model is not costly relative to the impact of the break. Loose selection is preferred, because it includes more relevant variables. For selection has no impact because the break is not observed (except for known regressors). Including regressors in arx and rwx gives a substantial improvement over ary.
- Break in irrelevant regressors
- ()There is no break in y, so any inclusion of irrelevant variables is costly, as their break offsets the small estimated coefficients. The more irrelevant variables included, the stronger this effect. The autoregression in y is almost always preferred.
- Break in all regressors
- ()The y variable is identical to that of a break in relevant variables only. Selection is now a trade-off between including variables that matter and help with forecasting, and irrelevant variables that make forecasts worse. Including regressors in arx and rwx gives a substantial improvement over ary.
9.3. Forecasting after theBreak
9.4. Is Selection Costly When Forecasting?
9.5. Forecast Combinations
- apool
- (arx + rwy)/2;
- cpool
- (arx + cay)/2.
9.6. Summary of the Simulation Results
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Analytic Calculations
Appendix A.1.
Appendix A.2.
Appendix A.3.
Appendix A.4.
Appendix A.5.
Appendix A.6.
Appendix A.7.
Appendix B
| MSFE Relative to | |||||
|---|---|---|---|---|---|
| Model | |||||
| Section 4.1 and Section 4.2 No shift with known future regressors | |||||
| 0.990 | 1.000 | 1.030 | 1.079 | 1.149 | |
| 0.990 | 1.000 | 1.026 | 1.048 | 1.035 | |
| 0.991 | 1.000 | 1.014 | 1.012 | 1.003 | |
| 0.992 | 1.000 | 1.008 | 1.004 | 1.001 | |
| Section 5.2 and Section 5.3 Out-of-sample shift with known future regressors | |||||
| 0.827 | 1.008 | 1.551 | 2.457 | 3.724 | |
| 0.827 | 1.008 | 1.497 | 1.895 | 1.651 | |
| 0.836 | 1.007 | 1.267 | 1.217 | 1.056 | |
| 0.855 | 1.005 | 1.152 | 1.081 | 1.013 | |
| Section 5.4 Out-of-sample shift with mean forecast of future regressors | |||||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| Section 5.5 Out-of-sample shift with random walk forecast of future regressors | |||||
| 0.997 | 1.002 | 1.013 | 1.024 | 1.033 | |
| 0.997 | 1.002 | 1.012 | 1.015 | 1.008 | |
| 0.997 | 1.002 | 1.006 | 1.004 | 1.001 | |
| 0.997 | 1.001 | 1.004 | 1.001 | 1.000 | |
| Section 6.2 and Section 6.3 In-sample shift with mean forecast of future regressors | |||||
| 1.010 | 1.009 | 1.008 | 1.007 | 1.007 | |
| 1.010 | 1.009 | 1.008 | 1.005 | 1.002 | |
| 1.010 | 1.008 | 1.004 | 1.001 | 1.000 | |
| 1.008 | 1.006 | 1.002 | 1.000 | 1.000 | |
| Section 6.4 and Section 6.5 In-sample shift with random walk forecast of future regressors | |||||
| 0.931 | 0.994 | 1.155 | 1.386 | 1.661 | |
| 0.931 | 0.994 | 1.140 | 1.237 | 1.158 | |
| 0.934 | 0.995 | 1.075 | 1.058 | 1.014 | |
| 0.942 | 0.996 | 1.043 | 1.021 | 1.003 | |
| 1 | Clements and Hendry (1993) argue that the generalized forecast error second moment should be used to evaluate forecast performance instead of MSFE. In this case the results would be equivalent, because we focus on one-step-ahead forecasts. |
| 2 | UK quarterly consumer price index (CPI) is given by ONS series D7BT, which is the quarterly average of the monthly index. Annual inflation percentage is defined as . UK Unemployment is the quarterly average of ONS series MGUK, LFS ILO unemployment rate (UK, All, Aged 16 and over, %, NSA). |
| 3 | Intermediate alternatives such as sub-sample estimation, recursive or rolling estimation could also be used. |
| 4 | Castle et al. (2012) demonstrate the ability of IIS to detect breaks in the form of location shifts at any point in the sample. |
References
- Akaike, Hirotogu. 1973. Information theory and an extension of the maximum likelihood principle. In Second International Symposium of Information Theory. Edited by Boris N. Petrov and Frigyes Csaki. Budapest: Akademiai Kiado, pp. 267–81. [Google Scholar]
- Bontemps, Christophe, and Grayham E. Mizon. 2003. Congruence and encompassing. In Econometrics and the Philosophy of Economics. Edited by Bernt P. Stigum. Princeton: Princeton University Press, pp. 354–78. [Google Scholar]
- Campos, Julia, David F. Hendry, and Hans-Martin Krolzig. 2003. Consistent model selection by an automatic Gets approach. Oxford Bulletin of Economics and Statistics 65: 803–19. [Google Scholar] [CrossRef]
- Castle, Jennifer L., Jurgen A. Doornik, and David F. Hendry. 2012. Model selection when there are multiple breaks. Journal of Econometrics 169: 239–46. [Google Scholar] [CrossRef] [Green Version]
- Castle, Jennifer L., Jurgen A. Doornik, and David F. Hendry. 2021. Forecasting principles from experience with forecasting competitions. Forecasting 3: 138–65. [Google Scholar] [CrossRef]
- Castle, Jennifer L., Jurgen A. Doornik, David F. Hendry, and Felix Pretis. 2015. Detecting location shifts during model selection by step-indicator saturation. Econometrics 3: 240–64. [Google Scholar] [CrossRef] [Green Version]
- Castle, Jennifer L., Michael P. Clements, and David F. Hendry. 2015. Robust approaches to forecasting. International Journal of Forecasting 31: 99–112. [Google Scholar] [CrossRef] [Green Version]
- Chu, Chia-Shang, Maxwell Stinchcombe, and Halbert White. 1996. Monitoring structural change. Econometrica 64: 1045–65. [Google Scholar] [CrossRef] [Green Version]
- Clements, Michael P., and David F. Hendry. 1993. On the limitations of comparing mean squared forecast errors (with discussion). In Journal of Forecasting. vol. 12, pp. 617–37, Reprinted in Mills, Terence C., ed. 1999. Economic Forecasting. Cheltenham: Edward Elgar Publishing. [Google Scholar]
- Clements, Michael P., and David F. Hendry. 1998. Forecasting Economic Time Series. Cambridge: Cambridge University Press. [Google Scholar]
- Clements, Michael P., and David F. Hendry. 2001. Explaining the results of the M3 forecasting competition. International Journal of Forecasting 17: 550–54. [Google Scholar]
- Doornik, Jurgen A. 2009. Autometrics. In The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry. Edited by Jennifer L. Castle and Neil Shephard. Oxford: Oxford University Press, pp. 88–121. [Google Scholar]
- Doornik, Jurgen A. 2018. Object-Oriented Matrix Programming Using Ox, 8th ed. London: Timberlake Consultants Press. [Google Scholar]
- Doornik, Jurgen A., Jennifer L. Castle, and David F. Hendry. 2020a. Card forecasts for M4. International Journal of Forecasting 36: 129–34. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., Jennifer L. Castle, and David F. Hendry. 2020b. Short-term forecasting of the coronavirus pandemic. International Journal of Forecasting. in press. [Google Scholar] [CrossRef] [PubMed]
- Fildes, Robert, and Keith Ord. 2002. Forecasting competitions—Their role in improving forecasting practice and research. In A Companion to Economic Forecasting. Edited by Michael P. Clements and David F. Hendry. Oxford: Blackwells, pp. 322–53. [Google Scholar]
- Hendry, David F. 2006. Robustifying forecasts from equilibrium-correction models. Journal of Econometrics 135: 399–426. [Google Scholar] [CrossRef]
- Hendry, David F., and Grayham E. Mizon. 2012. Open-model forecast-error taxonomies. In Recent Advances and Future Directions in Causality, Prediction, and Specification Analysis. Edited by Xiaohong Chen and Norman R. Swanson. New York: Springer, pp. 219–40. [Google Scholar]
- Hendry, David F., and Jurgen A. Doornik. 2018. Empirical Econometric Modelling—PcGive 15 Volume I. London: Timberlake Consultants Press. [Google Scholar]
- Ing, Ching-Kang, and Ching-Zong Wei. 2003. On same-realization prediction in an infinite-order autoregressive process. Journal of Multivariate Analysis 85: 130–55. [Google Scholar] [CrossRef] [Green Version]
- Leeb, Hannes, and Benedikt M. Pötscher. 2009. Model selection. In Handbook of Financial Time Series. Edited by Torben Andersen, Richard A. Davis, Jens-Peter Kreiss and Thomas Mikosch. Berlin: Springer, pp. 889–926. [Google Scholar]
- Makridakis, Spyros, and Michele Hibon. 2000. The M3-competition: Results, conclusions and implications. International Journal of Forecasting 16: 451–76. [Google Scholar] [CrossRef]
- Makridakis, Spyros, Evangelos Spiliotis, and Vassilios Assimakopoulos. 2020. The M4 competition: 100,000 time series and 61 forecasting methods. International Journal of Forecasting 36: 54–74. [Google Scholar] [CrossRef]
- Pötscher, Benedikt M. 1991. Effects of model selection on inference. Econometric Theory 7: 163–85. [Google Scholar] [CrossRef]
- Shibata, Ritei. 1980. Asymptotically efficient selection of the order of the model for estimating parameters of a linear process. Annals of Statistics 8: 147–64. [Google Scholar] [CrossRef]
- Stock, James, and Mark W. Watson. 2009. Phillips curve inflation forecasts. In Understanding Inflation and the Implications for Monetary Policy. Edited by Jeff Fuhrer, Yolanda Kodrzycki, Jane Sneddon Little and Giovanni Olivei. Cambridge: MIT Press, pp. 99–202. [Google Scholar]

| Conditioning on | M1 | M2 | M3 |
|---|---|---|---|
| Known | 0.535 | 0.530 | 0.515 |
| Mean forecast for | 0.519 | 0.530 | 0.542 |
| Random walk forecast for | 0.549 | 0.530 | 0.515 |
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 0.34 | 0.72 | 0.94 | 0.995 | |
| 0.16 | 0.51 | 0.85 | 0.98 |
| MSFE Relative to | ||||||
|---|---|---|---|---|---|---|
| Model | ||||||
| Section 4.1 and Section 4.2 No shift with known future regressors | ||||||
| 0.981 | 1.001 | 1.060 | 1.158 | 1.295 | ||
| 0.981 | 1.000 | 1.051 | 1.093 | 1.068 | ||
| 0.982 | 1.000 | 1.027 | 1.023 | 1.006 | ||
| 0.984 | 1.000 | 1.016 | 1.008 | 1.001 | ||
| Section 5.2 and Section 5.3 Out-of-sample shift with known future regressors | ||||||
| 0.709 | 1.014 | 1.927 | 3.450 | 5.582 | ||
| 0.709 | 1.013 | 1.836 | 2.505 | 2.095 | ||
| 0.724 | 1.011 | 1.449 | 1.366 | 1.095 | ||
| 0.756 | 1.009 | 1.256 | 1.136 | 1.022 | ||
| Section 5.4 Out-of-sample shift with mean forecast of future regressors | ||||||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | ||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | ||
| Section 5.5 Out-of-sample shift with random walk forecast of future regressors | ||||||
| 0.993 | 1.004 | 1.020 | 1.034 | 1.043 | ||
| 0.993 | 1.004 | 1.018 | 1.021 | 1.010 | ||
| 0.994 | 1.003 | 1.010 | 1.005 | 1.001 | ||
| 0.994 | 1.002 | 1.006 | 1.002 | 1.000 | ||
| Section 6.2 and Section 6.3 In-sample shift with mean forecast of future regressors | ||||||
| 1.020 | 1.021 | 1.022 | 1.023 | 1.024 | ||
| 1.020 | 1.021 | 1.020 | 1.014 | 1.006 | ||
| 1.019 | 1.017 | 1.011 | 1.004 | 1.000 | ||
| 1.017 | 1.014 | 1.006 | 1.001 | 1.000 | ||
| Section 6.4 and Section 6.5 In-sample shift with random walk forecast of future regressors | ||||||
| 0.871 | 0.990 | 1.273 | 1.653 | 2.078 | ||
| 0.871 | 0.990 | 1.246 | 1.401 | 1.258 | ||
| 0.878 | 0.991 | 1.132 | 1.097 | 1.022 | ||
| 0.892 | 0.993 | 1.075 | 1.036 | 1.005 | ||
| (2, 0.75) | (−0.3, 0.75) | (−0.3, 0.95) | (−0.3, 0.05) | (2, 0.05) | (2, 0.95) | |
|---|---|---|---|---|---|---|
| 8 | 5.7 | 7.3 | 0.1 | 2.4 | 9.6 | |
| 8 | 4.0 | 6.6 | −0.3 | 2.1 | 11.1 | |
| 8 | 5.0 | 7.0 | 1.8 | 3.6 | 10.3 |
| No break | 2 | 0.75 |
| Break in mean | −0.3 | 0.75 |
| Break in slope (a) | 2 | 0.95 |
| Break in slope (b) | 2 | 0.05 |
| Break in mean and slope (a) | −0.3 | 0.95 |
| Break in mean and slope (b) | −0.3 | 0.05 |
| Joint | Average | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.001 | 0.015 | 0.000 | 0.002 | 0.009 | 0.030 | 0.081 | 0.341 | 0.721 | 0.000 | 0.197 | 0.721 | 0.375 |
| 0.01 | 0.077 | 0.000 | 0.018 | 0.053 | 0.130 | 0.263 | 0.641 | 0.912 | 0.000 | 0.336 | 0.912 | 0.758 |
| 0.05 | 0.216 | 0.000 | 0.070 | 0.163 | 0.313 | 0.504 | 0.843 | 0.976 | 0.001 | 0.478 | 0.976 | 0.930 |
| 0.1 | 0.322 | 0.000 | 0.124 | 0.254 | 0.435 | 0.631 | 0.907 | 0.989 | 0.008 | 0.557 | 0.989 | 0.968 |
| 0.16 | 0.414 | 0.000 | 0.181 | 0.339 | 0.533 | 0.719 | 0.941 | 0.994 | 0.022 | 0.618 | 0.994 | 0.983 |
| 0.32 | 0.579 | 0.004 | 0.309 | 0.500 | 0.691 | 0.840 | 0.976 | 0.998 | 0.087 | 0.719 | 0.998 | 0.995 |
| Gauge | Potency | |||||
|---|---|---|---|---|---|---|
| 0.001 | 0.005 | 0.006 | 0.006 | 0.034 | 0.205 | 0.712 |
| 0.01 | 0.025 | 0.024 | 0.020 | 0.113 | 0.345 | 0.884 |
| 0.05 | 0.079 | 0.075 | 0.069 | 0.231 | 0.458 | 0.919 |
| 0.1 | 0.126 | 0.124 | 0.121 | 0.297 | 0.507 | 0.919 |
| 0.16 | 0.181 | 0.180 | 0.178 | 0.355 | 0.545 | 0.923 |
| 0.32 | 0.328 | 0.328 | 0.327 | 0.479 | 0.634 | 0.941 |
| inf | avg | arx | rwx | inf | avg | arx | rwx | inf | avg | arx | rwx | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | No break | |||||||||||
| 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1.03 | 1.01 | 1.02 | 1.03 | 0.95 | 1.06 | 0.99 | 1.02 | 0.83 | 1.13 | 0.94 | 0.99 | |
| 1.08 | 1.06 | 1.05 | 1.08 | 0.93 | 1.11 | 0.98 | 1.02 | 0.79 | 1.17 | 0.93 | 0.97 | |
| 1.13 | 1.13 | 1.08 | 1.12 | 0.95 | 1.19 | 0.99 | 1.03 | 0.83 | 1.23 | 0.95 | 0.99 | |
| 1.16 | 1.18 | 1.09 | 1.13 | 0.99 | 1.23 | 1.01 | 1.06 | 0.87 | 1.27 | 0.97 | 1.02 | |
| 1.19 | 1.23 | 1.11 | 1.15 | 1.01 | 1.28 | 1.04 | 1.08 | 0.91 | 1.31 | 1.00 | 1.04 | |
| 1.25 | 1.36 | 1.15 | 1.19 | 1.09 | 1.38 | 1.09 | 1.13 | 0.99 | 1.41 | 1.05 | 1.09 | |
| GUM | 1.34 | 1.51 | 1.20 | 1.23 | 1.18 | 1.50 | 1.13 | 1.17 | 1.08 | 1.52 | 1.10 | 1.14 |
| MSFEary | 1.15 | 1.31 | 1.43 | |||||||||
| Ratio | Average over five break types in relevant regressors | |||||||||||
| 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.90 | 1.00 | 1.00 | 1.01 | 0.58 | 1.02 | 0.99 | 1.00 | 0.37 | 1.05 | 0.97 | 0.98 | |
| 0.74 | 1.01 | 1.01 | 1.02 | 0.42 | 1.04 | 0.99 | 0.99 | 0.28 | 1.06 | 0.97 | 0.97 | |
| 0.57 | 1.03 | 1.01 | 1.02 | 0.37 | 1.06 | 0.99 | 0.99 | 0.28 | 1.08 | 0.97 | 0.98 | |
| 0.52 | 1.05 | 1.02 | 1.03 | 0.37 | 1.07 | 0.99 | 1.00 | 0.29 | 1.09 | 0.98 | 0.98 | |
| 0.50 | 1.06 | 1.02 | 1.03 | 0.37 | 1.08 | 1.00 | 1.01 | 0.30 | 1.10 | 0.99 | 0.99 | |
| 0.48 | 1.10 | 1.03 | 1.04 | 0.38 | 1.11 | 1.01 | 1.02 | 0.32 | 1.13 | 1.00 | 1.01 | |
| GUM | 0.49 | 1.13 | 1.05 | 1.05 | 0.41 | 1.14 | 1.03 | 1.03 | 0.35 | 1.16 | 1.01 | 1.02 |
| MSFEary | 18.58 | 18.80 | 18.98 | |||||||||
| Where | inf | avg | arx | rwx | inf | avg | arx | rwx | inf | avg | arx | rwx | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ary | Relevant | 54.42 | 50.41 | 6.75 | ||||||||||
| Relevant | 16.44 | 54.49 | 54.50 | 54.60 | 10.67 | 60.24 | 18.33 | 11.24 | 3.51 | 33.30 | 3.03 | 3.48 | ||
| GUM | Relevant | 11.43 | 54.78 | 54.63 | 54.77 | 10.15 | 60.60 | 13.56 | 9.76 | 2.89 | 41.42 | 2.43 | 4.15 | |
| ary | All | 54.42 | 50.41 | 6.75 | ||||||||||
| All | 18.32 | 54.49 | 54.50 | 54.60 | 11.19 | 61.32 | 18.71 | 11.70 | 3.32 | 33.28 | 2.89 | 3.61 | ||
| GUM | All | 16.42 | 54.78 | 54.63 | 54.77 | 14.12 | 64.35 | 17.41 | 13.64 | 3.05 | 42.12 | 2.55 | 4.21 | |
| ary | Irrel. | 1.15 | 1.19 | 1.18 | ||||||||||
| Irrel. | 3.19 | 1.36 | 1.26 | 1.31 | 2.86 | 2.59 | 2.55 | 2.80 | 1.82 | 2.04 | 1.80 | 1.89 | ||
| GUM | Irrel. | 6.71 | 1.75 | 1.39 | 1.42 | 5.74 | 6.16 | 5.38 | 5.52 | 2.18 | 3.39 | 2.02 | 2.00 | |
| ary | Relevant | 54.71 | 43.20 | 6.02 | ||||||||||
| Relevant | 7.90 | 54.86 | 54.82 | 54.98 | 4.84 | 61.25 | 12.40 | 5.43 | 2.64 | 37.40 | 2.51 | 3.87 | ||
| GUM | Relevant | 7.60 | 55.05 | 54.94 | 55.17 | 6.73 | 58.20 | 10.67 | 6.58 | 2.68 | 40.60 | 2.47 | 4.31 | |
| ary | All | 54.71 | 43.20 | 6.02 | ||||||||||
| All | 11.05 | 54.86 | 54.82 | 54.98 | 6.76 | 62.80 | 13.90 | 7.23 | 2.65 | 37.15 | 2.59 | 4.27 | ||
| GUM | All | 16.45 | 55.05 | 54.94 | 55.17 | 13.99 | 64.88 | 17.65 | 13.72 | 3.02 | 42.09 | 2.71 | 4.41 | |
| ary | Irrel. | 1.31 | 1.39 | 1.35 | ||||||||||
| Irrel. | 4.44 | 1.61 | 1.33 | 1.38 | 3.71 | 3.70 | 3.43 | 3.72 | 1.93 | 2.66 | 2.04 | 2.14 | ||
| GUM | Irrel. | 10.46 | 1.97 | 1.48 | 1.53 | 8.90 | 9.47 | 8.59 | 8.78 | 2.36 | 4.11 | 2.28 | 2.26 | |
| ary | Relevant | 54.98 | 39.74 | 5.66 | ||||||||||
| Relevant | 4.38 | 54.98 | 55.03 | 55.31 | 2.64 | 61.84 | 9.54 | 3.19 | 2.00 | 38.64 | 2.21 | 4.54 | ||
| GUM | Relevant | 4.56 | 55.27 | 55.21 | 55.51 | 4.20 | 56.23 | 8.50 | 4.27 | 2.42 | 39.53 | 2.45 | 4.47 | |
| ary | All | 54.98 | 39.74 | 5.66 | ||||||||||
| All | 8.45 | 54.98 | 55.03 | 55.31 | 5.27 | 63.59 | 11.82 | 5.71 | 2.31 | 38.55 | 2.55 | 5.00 | ||
| GUM | All | 16.47 | 55.27 | 55.21 | 55.51 | 13.89 | 65.37 | 17.89 | 13.79 | 3.00 | 42.11 | 2.85 | 4.59 | |
| ary | Irrel. | 1.43 | 1.52 | 1.49 | ||||||||||
| Irrel. | 5.20 | 1.82 | 1.39 | 1.45 | 4.09 | 4.37 | 3.92 | 4.23 | 1.92 | 3.09 | 2.16 | 2.25 | ||
| GUM | Irrel. | 13.46 | 2.17 | 1.57 | 1.63 | 11.33 | 12.03 | 11.05 | 11.29 | 2.47 | 4.62 | 2.44 | 2.43 | |
| arx | rwx | rdx | cax | rwy | cay | arx | rwx | rdx | cax | rwy | cay | arx | rwx | rdx | cax | rwy | cay | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No break | ||||||||||||||||||
| 1.10 | 1.15 | 1.31 | 1.15 | 1.21 | 1.29 | 1.11 | 1.16 | 1.31 | 1.16 | 1.21 | 1.29 | 1.10 | 1.14 | 1.30 | 1.15 | 1.21 | 1.28 | |
| 1.00 | 1.04 | 1.24 | 1.05 | 1.14 | 1.19 | 1.02 | 1.07 | 1.29 | 1.08 | 1.15 | 1.22 | 1.01 | 1.06 | 1.25 | 1.06 | 1.15 | 1.21 | |
| 0.96 | 1.00 | 1.23 | 1.01 | 1.12 | 1.16 | 0.97 | 1.02 | 1.26 | 1.03 | 1.12 | 1.17 | 0.96 | 1.00 | 1.23 | 1.00 | 1.12 | 1.17 | |
| Break in mean and slope (b) of irrelevant regressors | ||||||||||||||||||
| 2.14 | 2.35 | 3.30 | 2.33 | 1.21 | 1.29 | 1.53 | 1.61 | 1.75 | 1.64 | 1.21 | 1.29 | 1.20 | 1.25 | 1.35 | 1.25 | 1.21 | 1.28 | |
| 2.47 | 2.68 | 3.80 | 2.66 | 1.14 | 1.19 | 1.51 | 1.59 | 1.78 | 1.62 | 1.15 | 1.22 | 1.13 | 1.17 | 1.31 | 1.17 | 1.15 | 1.21 | |
| 2.58 | 2.79 | 3.90 | 2.76 | 1.12 | 1.16 | 1.45 | 1.51 | 1.73 | 1.53 | 1.12 | 1.17 | 1.07 | 1.11 | 1.29 | 1.11 | 1.12 | 1.17 | |
| Break in mean of all regressors | ||||||||||||||||||
| 0.62 | 0.50 | 0.34 | 0.50 | 0.63 | 0.57 | 0.48 | 0.47 | 0.75 | 0.48 | 0.28 | 0.26 | 0.72 | 0.69 | 0.82 | 0.69 | 0.67 | 0.67 | |
| 0.57 | 0.42 | 0.25 | 0.42 | 0.69 | 0.62 | 0.50 | 0.58 | 1.19 | 0.60 | 0.37 | 0.34 | 0.79 | 0.84 | 0.92 | 0.85 | 0.85 | 0.85 | |
| 0.54 | 0.37 | 0.22 | 0.37 | 0.72 | 0.65 | 0.51 | 0.69 | 1.61 | 0.72 | 0.43 | 0.40 | 0.81 | 0.96 | 0.98 | 0.96 | 0.94 | 0.94 | |
| Break in slope (a) of all regressors | ||||||||||||||||||
| 0.69 | 0.59 | 0.43 | 0.58 | 0.69 | 0.58 | 0.57 | 0.57 | 0.85 | 0.57 | 0.37 | 0.36 | 0.77 | 0.75 | 0.87 | 0.75 | 0.71 | 0.76 | |
| 0.64 | 0.51 | 0.34 | 0.50 | 0.73 | 0.63 | 0.58 | 0.66 | 1.29 | 0.68 | 0.48 | 0.46 | 0.82 | 0.87 | 0.98 | 0.86 | 0.87 | 0.92 | |
| 0.61 | 0.46 | 0.30 | 0.46 | 0.76 | 0.65 | 0.60 | 0.77 | 1.69 | 0.80 | 0.55 | 0.53 | 0.83 | 0.95 | 1.03 | 0.94 | 0.95 | 1.00 | |
| Break in slope (b) of all regressors | ||||||||||||||||||
| 0.41 | 0.28 | 0.42 | 0.29 | 0.38 | 0.33 | 0.42 | 0.41 | 0.49 | 0.42 | 0.21 | 0.21 | 0.85 | 0.86 | 0.99 | 0.84 | 1.16 | 1.03 | |
| 0.36 | 0.21 | 0.59 | 0.22 | 0.44 | 0.38 | 0.43 | 0.54 | 0.70 | 0.57 | 0.28 | 0.28 | 0.87 | 1.03 | 1.04 | 0.98 | 1.29 | 1.17 | |
| 0.32 | 0.19 | 0.78 | 0.19 | 0.49 | 0.41 | 0.45 | 0.69 | 0.91 | 0.74 | 0.33 | 0.34 | 0.87 | 1.18 | 1.05 | 1.11 | 1.35 | 1.24 | |
| Break in mean and slope (a) of all regressors | ||||||||||||||||||
| 0.83 | 0.78 | 0.75 | 0.78 | 0.86 | 0.87 | 0.88 | 0.91 | 1.11 | 0.92 | 0.79 | 0.82 | 0.99 | 1.01 | 1.14 | 1.01 | 1.00 | 1.05 | |
| 0.76 | 0.69 | 0.67 | 0.69 | 0.86 | 0.87 | 0.87 | 0.94 | 1.31 | 0.95 | 0.86 | 0.88 | 0.97 | 1.01 | 1.17 | 1.01 | 1.06 | 1.10 | |
| 0.73 | 0.65 | 0.63 | 0.64 | 0.87 | 0.87 | 0.85 | 0.95 | 1.42 | 0.96 | 0.88 | 0.91 | 0.93 | 1.00 | 1.18 | 1.00 | 1.08 | 1.10 | |
| Break in mean and slope (b) of all regressors | ||||||||||||||||||
| 0.37 | 0.23 | 0.39 | 0.25 | 0.35 | 0.32 | 0.43 | 0.53 | 0.67 | 0.60 | 0.21 | 0.22 | 0.86 | 1.09 | 1.07 | 1.03 | 1.64 | 1.44 | |
| 0.32 | 0.17 | 0.55 | 0.18 | 0.42 | 0.37 | 0.43 | 0.71 | 0.94 | 0.82 | 0.26 | 0.27 | 0.83 | 1.25 | 1.04 | 1.17 | 1.66 | 1.51 | |
| 0.30 | 0.14 | 0.71 | 0.16 | 0.46 | 0.40 | 0.45 | 0.88 | 1.19 | 1.04 | 0.30 | 0.31 | 0.82 | 1.41 | 1.02 | 1.30 | 1.67 | 1.55 | |
| Average over all breaks in all regressors | ||||||||||||||||||
| 0.58 | 0.48 | 0.47 | 0.48 | 0.58 | 0.54 | 0.56 | 0.58 | 0.77 | 0.60 | 0.37 | 0.37 | 0.84 | 0.88 | 0.98 | 0.87 | 1.04 | 0.99 | |
| 0.53 | 0.40 | 0.48 | 0.40 | 0.63 | 0.58 | 0.56 | 0.69 | 1.08 | 0.72 | 0.45 | 0.45 | 0.86 | 1.00 | 1.03 | 0.97 | 1.15 | 1.11 | |
| 0.50 | 0.36 | 0.53 | 0.36 | 0.66 | 0.60 | 0.57 | 0.80 | 1.37 | 0.85 | 0.50 | 0.50 | 0.85 | 1.10 | 1.05 | 1.06 | 1.20 | 1.17 | |
| inf | arx | rwx | rdx | cax | inf | arx | rwx | rdx | cax | inf | arx | rwx | rdx | cax | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No break in y: no break and break in irrelevant variables | |||||||||||||||
| 1.13 | 1.15 | 1.22 | 1.55 | 1.22 | 0.99 | 1.07 | 1.13 | 1.26 | 1.13 | 0.93 | 1.01 | 1.04 | 1.16 | 1.04 | |
| 1.52 | 1.47 | 1.59 | 2.14 | 1.57 | 1.14 | 1.21 | 1.27 | 1.45 | 1.28 | 0.99 | 1.05 | 1.10 | 1.25 | 1.10 | |
| 1.78 | 1.71 | 1.84 | 2.46 | 1.81 | 1.21 | 1.26 | 1.33 | 1.52 | 1.33 | 1.03 | 1.08 | 1.12 | 1.29 | 1.12 | |
| GUM | 3.69 | 3.55 | 3.64 | 4.17 | 3.61 | 1.46 | 1.41 | 1.42 | 1.60 | 1.41 | 1.21 | 1.17 | 1.19 | 1.41 | 1.19 |
| DGP | 0.82 | 0.92 | 0.96 | 1.12 | 0.96 | 0.83 | 0.93 | 0.97 | 1.14 | 0.97 | 0.82 | 0.93 | 0.96 | 1.13 | 0.96 |
| Break in y: break in all variables | |||||||||||||||
| 0.40 | 0.63 | 0.52 | 0.52 | 0.52 | 0.59 | 0.62 | 0.68 | 0.94 | 0.70 | 0.82 | 0.87 | 0.99 | 1.00 | 0.97 | |
| 0.31 | 0.56 | 0.43 | 0.48 | 0.44 | 0.54 | 0.56 | 0.67 | 1.02 | 0.70 | 0.82 | 0.85 | 0.99 | 1.01 | 0.96 | |
| 0.30 | 0.54 | 0.41 | 0.49 | 0.42 | 0.55 | 0.56 | 0.69 | 1.07 | 0.72 | 0.83 | 0.85 | 0.99 | 1.02 | 0.97 | |
| GUM | 0.38 | 0.54 | 0.44 | 0.64 | 0.43 | 0.67 | 0.65 | 0.79 | 1.26 | 0.83 | 0.96 | 0.91 | 1.00 | 1.09 | 0.98 |
| DGP | 0.17 | 0.44 | 0.29 | 0.41 | 0.30 | 0.36 | 0.40 | 0.61 | 1.11 | 0.66 | 0.64 | 0.72 | 1.02 | 0.86 | 0.97 |
| inf | avg | arx | rwx | rdx | cax | rwy | cay | apool | cpool | ary | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| No break | 0.99 | 1.22 | 1.03 | 1.07 | 1.27 | 1.07 | 1.16 | 1.22 | 0.96 | 1.00 | 1.00 |
| Break irrelevant | 1.69 | 1.99 | 1.68 | 1.78 | 2.25 | 1.77 | 1.16 | 1.22 | 1.13 | 1.20 | 1.00 |
| All breaks | 0.56 | 2.93 | 0.65 | 0.70 | 0.86 | 0.70 | 0.73 | 0.70 | 0.73 | 0.58 | 1.00 |
| Sum | 3.24 | 6.14 | 3.36 | 3.55 | 4.38 | 3.54 | 3.05 | 3.14 | 2.82 | 2.78 | 3.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castle, J.L.; Doornik, J.A.; Hendry, D.F. Selecting a Model for Forecasting. Econometrics 2021, 9, 26. https://doi.org/10.3390/econometrics9030026
Castle JL, Doornik JA, Hendry DF. Selecting a Model for Forecasting. Econometrics. 2021; 9(3):26. https://doi.org/10.3390/econometrics9030026
Chicago/Turabian StyleCastle, Jennifer L., Jurgen A. Doornik, and David F. Hendry. 2021. "Selecting a Model for Forecasting" Econometrics 9, no. 3: 26. https://doi.org/10.3390/econometrics9030026
APA StyleCastle, J. L., Doornik, J. A., & Hendry, D. F. (2021). Selecting a Model for Forecasting. Econometrics, 9(3), 26. https://doi.org/10.3390/econometrics9030026








