Temperature Anomalies, Long Memory, and Aggregation
Abstract
1. Introduction
2. Temperature Anomalies
3. Methods
3.1. Long Memory
- (i).
- In the spectral sense if as with a constant;
- (ii).
- In the self-similar sense if as where , with , , and is a constant;
- (iii).
- In the covariance sense if as with a constant.
3.2. Cross-Sectional Aggregation
3.3. Semiparametric Estimators of Long Memory
4. Results
4.1. Monthly Data with 1200 km Smoothing Radius and Optimal Bandwidth
4.2. Monthly Data with 250 km Smoothing Radius and Optimal Bandwidth
4.3. Robustness Exercises
5. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GISTEMP | NASA Goddard Institute for Space Studies Surface Temperature Analysis |
| North Hem. | Northern Hemisphere |
| South Hem. | Southern Hemisphere |
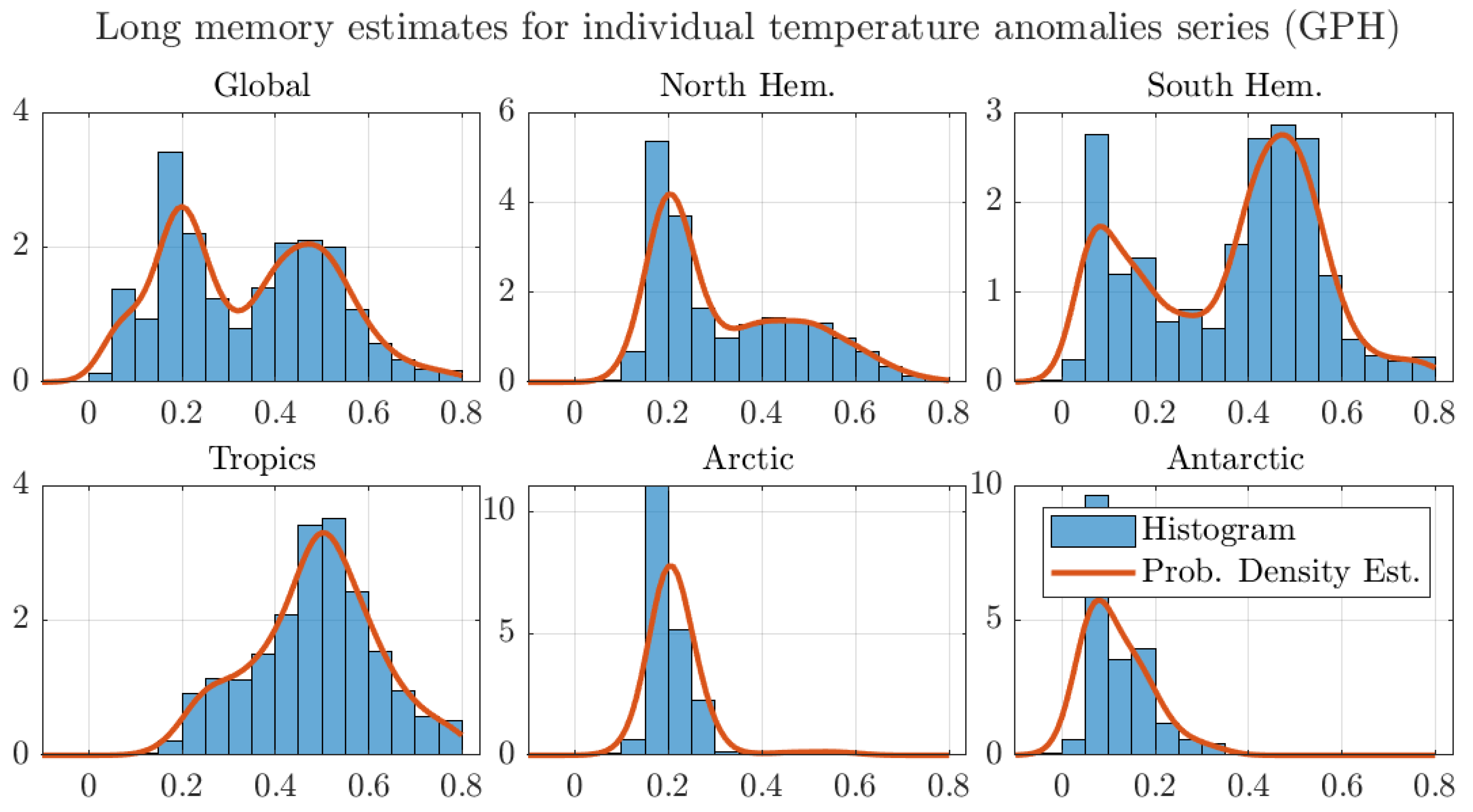
| GPH | Geweke and Porter-Hudak log-periodogram regression |
| AG | Andrews and Guggenberger bias reduced log-periodogram estimator |
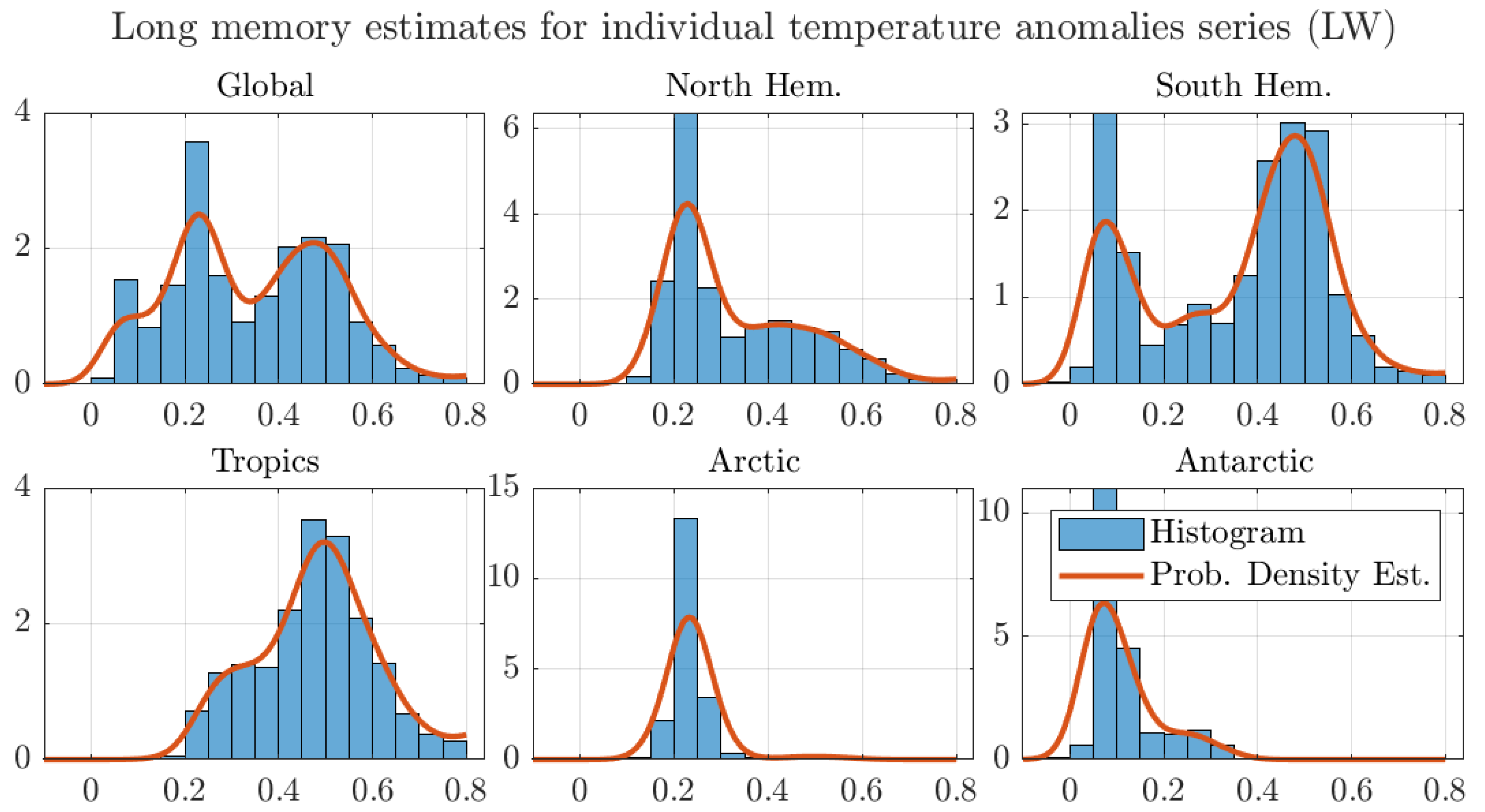
| LW | Local Whittle estimator |
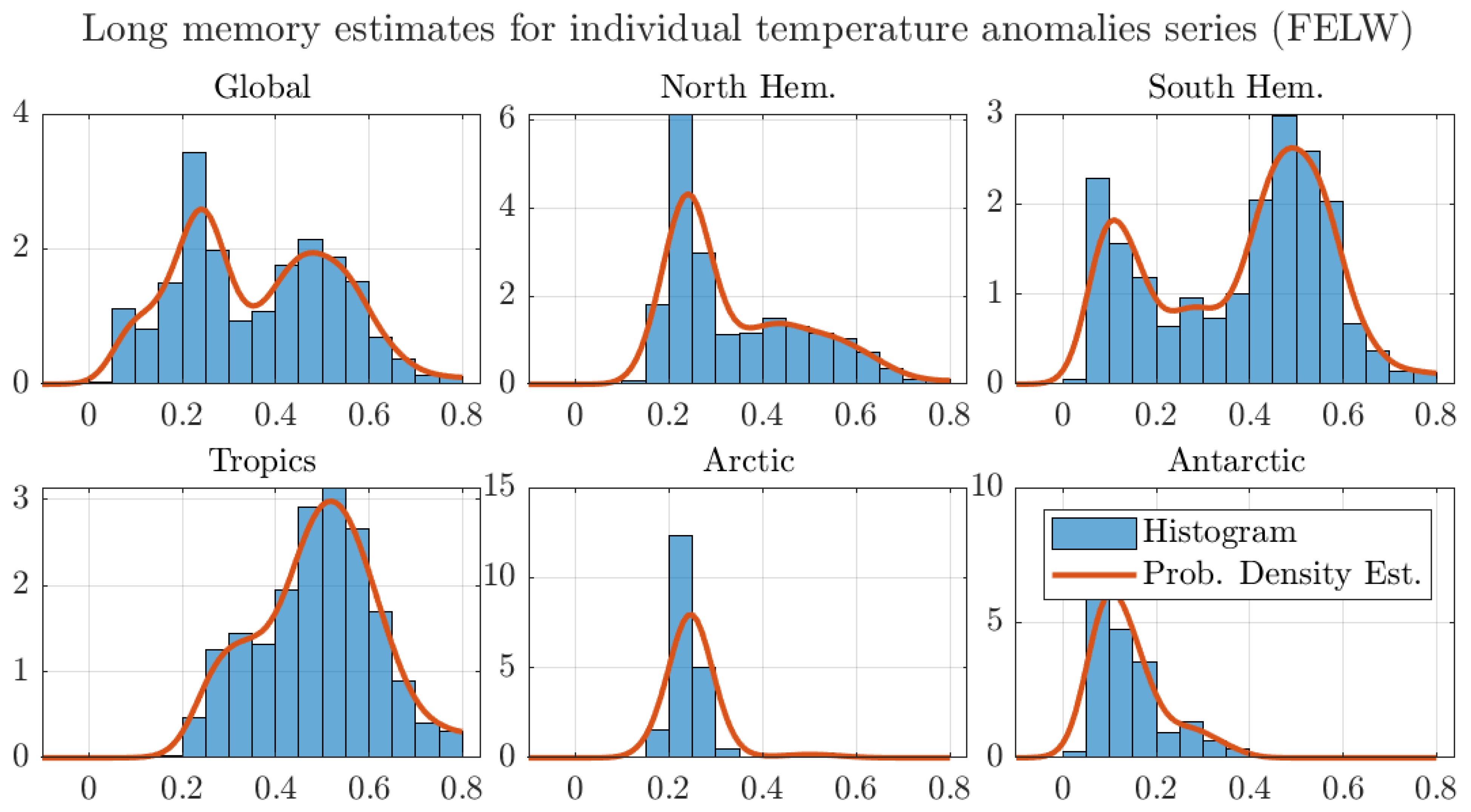
| FELW | Feasible Exact Local Whittle estimator |
| Std. Dev. | Standard deviation |
| Prob. Density Est. | Probability density estimate |
| No. of Grids | Number of grids |
Appendix A





References
- Altissimo, Filippo, Benoit Mojon, and Paolo Zaffaroni. 2009. Can Aggregation Explain the Persistence of Inflation? Journal of Monetary Economics 5: 231–41. [Google Scholar] [CrossRef]
- Andrews, Donald W. K., and Patrik Guggenberger. 2003. A Bias-Reduced Log-Periodogram Regression Estimator For The Long-Memory Parameter. Econometrica 71: 675–712. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Sang Kuck Chung. 2002. Modeling and forecasting from trend-stationary long memory models with applications to climatology. International Journal of Forecasting 18: 215–26. [Google Scholar] [CrossRef]
- Balcilar, Mehmet. 2004. Persistence in Inflation: Does Aggregation Cause Long Memory? Emerging Markets Finance and Trade 40: 25–56. [Google Scholar] [CrossRef]
- Bloomfield, Peter. 1992. Trends in global temperature. Climatic Change 21: 1–16. [Google Scholar] [CrossRef]
- Bloomfield, Peter, and Douglas Nychka. 1992. Climate spectra and detecting climate change. Climatic Change 21: 275–87. [Google Scholar] [CrossRef]
- Calel, Raphael, Sandra C. Chapman, David A. Stainforth, and Nicholas W. Watkins. 2020. Temperature variability implies greater economic damages from climate change. Nature Communications 11: 1–5. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Glenn D Rudebusch. 1989. Long Memory and Persistence in Agregate Output. Journal of Monetary Economics 24: 189–209. [Google Scholar] [CrossRef]
- Geweke, John, and Susan Porter-Hudak. 1983. The Estimation and Application of Long Memory Time Series Models. Journal of Time Series Analysis 4: 221–38. [Google Scholar] [CrossRef]
- Gil-Alana, Luis A. 2005. Statistical modeling of the temperatures in the Northern Hemisphere using fractional integration techniques. Journal of Climate 18: 5357–69. [Google Scholar] [CrossRef]
- GISTEMP Team. 2020. GISS Surface Temperature Analysis (GISTEMP), Version 4. NASA Goddard Institute for Space Studies. Available online: https://data.giss.nasa.gov/gistemp/ (accessed on 10 October 2020).
- Granger, Clive W. J. 1966. The Typical Spectral Shape of an Economic Variable. Econometrica 34: 150–61. [Google Scholar] [CrossRef]
- Granger, Clive W. J. 1980. Long Memory Relationships and the Aggregation of Dynamic Models. Journal of Econometrics 14: 227–38. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Roselyne Joyeux. 1980. An Introduction to Long Memory Time Series Models and Fractional Differencing. Journal of Time Series Analysis 1: 15–29. [Google Scholar] [CrossRef]
- Haldrup, Niels, and J. Eduardo Vera-Valdés. 2017. Long Memory, Fractional Integration, and Cross-Sectional Aggregation. Journal of Econometrics 199: 1–11. [Google Scholar] [CrossRef]
- Hansen, James, Reto Ruedy, Mki Sato, and Ken Lo. 2010. Global surface temperature change. Reviews of Geophysics 48: 29. [Google Scholar] [CrossRef]
- Hosking, Jonathan R. M. 1981. Fractional Differencing. Biometrika 68: 165–76. [Google Scholar] [CrossRef]
- Hurst, Harold E. 1956. The Problem of Long-Term Storage in Reservoirs. Hydrological Sciences Journal 1: 13–27. [Google Scholar] [CrossRef]
- Hurvich, Clifford M., Rohit Deo, and Julia Brodsky. 1998. The Mean Squared Error of Geweke and Porter-Hudak’s Estimator of the Memory Parameter of a Long-Memory Time Series. Journal of Time Series Analysis 19: 19–46. [Google Scholar] [CrossRef]
- Künsch, Hans. 1987. Statistical Aspects of Self-Similar Processes. Bernouli 1: 67–74. [Google Scholar]
- Lenssen, Nathan J. L., Gavin A. Schmidt, James E. Hansen, Matthew J. Menne, Avraham Persin, Reto Ruedy, and Daniel Zyss. 2019. Improvements in the GISTEMP Uncertainty Model. Journal of Geophysical Research: Atmospheres 124: 6307–26. [Google Scholar] [CrossRef]
- Linden, Mikael. 1999. Time Series Properties of Aggregated AR(1) Processes with Uniformly Distributed Coefficients. Economics Letters 64: 31–36. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B. 1967. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 156: 636–38. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, Benoit B., and John W. Van Ness. 1968. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Review 10: 422–37. [Google Scholar] [CrossRef]
- Mangat, Manveer Kaur, and Erhard Reschenhofer. 2020. Frequency-Domain Evidence for Climate Change. Econometrics 8: 28. [Google Scholar] [CrossRef]
- Marmol, Francesc. 1995. Spurious regressions between I (d) processes. Journal of Time Series Analysis 16: 313–21. [Google Scholar] [CrossRef]
- Mills, Terence C. 2007. Time series modelling of two millennia of northern hemisphere temperatures: Long memory or shifting trends? Journal of the Royal Statistical Society. Series A: Statistics in Society 170: 83–94. [Google Scholar] [CrossRef]
- Oppenheim, Georges, and Marie Claude Viano. 2004. Aggregation of Random Parameters Ornstein-Uhlenbeck or AR Processes: Some Convergence Results. Journal of Time Series Analysis 25: 335–50. [Google Scholar] [CrossRef]
- Osterrieder, Daniela, Daniel Ventosa-Santaulària, and J. Eduardo Vera-Valdés. 2019. The VIX, the Variance Premium, and Expected Returns. Journal of Financial Econometrics 17: 517–58. [Google Scholar] [CrossRef]
- Peterson, Thomas C., and Russell S. Vose. 1997. An overview of the global historical climatology network temperature database. Bulletin of the American Meteorological Society 78: 2837–50. [Google Scholar] [CrossRef]
- Phillips, Peter C.B., and Katsumi Shimotsu. 2004. Local whittle estimation in nonstationary and unit root cases. Annals of Statistics 32: 656–92. [Google Scholar] [CrossRef]
- Reschenhofer, Erhard, and Manveer Kaur Mangat. 2020. Detecting long-range dependence with truncated ratios of periodogram ordinates. Communications in Statistics—Theory and Methods 17: 1–16. [Google Scholar] [CrossRef]
- Robinson, Peter M. 1995a. Gaussian Semiparametric Estimation of Long Range Dependence. The Annals of Statistics 23: 1630–61. [Google Scholar] [CrossRef]
- Robinson, Peter M. 1995b. Log-Periodogram Regression of Time Series with Long Range Dependence. The Annals of Statistics 23: 1048–72. [Google Scholar] [CrossRef]
- Shimotsu, Katsumi, and Peter C.B. Phillips. 2005. Exact Local Whittle Estimation of Fractional Integration. The Annals of Statistics 33: 1890–933. [Google Scholar] [CrossRef]
- Shimotsu, Katsumi. 2010. Exact local Whittle estimation of fractional integration with unknown mean and time trend. Econometric Theory 26: 501–40. [Google Scholar] [CrossRef]
- Sutton, Rowan T., Buwen Dong, and Jonathan M. Gregory. 2007. Land/sea warming ratio in response to climate change: IPCC AR4 model results and comparison with observations. Geophysical Research Letters 34: 1–5. [Google Scholar] [CrossRef]
- Tsay, Wen-Jen, and Ching-Fan Chung. 2000. The spurious regression of fractionally integrated processes. Journal of Econometrics 96: 155–82. [Google Scholar] [CrossRef]
- Velasco, Carlos. 1999a. Gaussian semiparametric estimation of non-stationary time series. Journal of Time Series Analysis 20: 87–127. [Google Scholar] [CrossRef]
- Velasco, Carlos. 1999b. Non-stationary log-periodogram regression. Journal of Econometrics 91: 325–71. [Google Scholar] [CrossRef]
- Velasco, Carlos. 2000. Non-Gaussian Log-Periodogram Regression. Econometric Theory 16: 44–79. [Google Scholar] [CrossRef]
- Ventosa-Santaulària, Daniel, J. Eduardo Vera-Valdés, Katarzyna Łasak, and Ricardo Ramírez-Vargas. 2020. Spurious multivariate regressions under fractionally integrated processes. Communications in Statistics—Theory and Methods 6: 1–23. [Google Scholar] [CrossRef]
- Vera-Valdés, J. Eduardo. 2020. On long memory origins and forecast horizons. Journal of Forecasting 39: 811–26. [Google Scholar] [CrossRef]
- Zaffaroni, Paolo. 2004. Contemporaneous Aggregation of Linear Dynamic Models in Large Economies. Journal of Econometrics 120: 75–102. [Google Scholar] [CrossRef]







| Series | GPH | AG | LW | FELW | Sample Size |
|---|---|---|---|---|---|
| Global | 0.6332 | 0.7475 | 0.6682 | 0.6304 | 1688 |
| North Hem. | 0.5429 | 0.6247 | 0.5765 | 0.5584 | 1688 |
| South Hem. | 0.6407 | 0.6904 | 0.6430 | 0.6159 | 1688 |
| London (,) | 0.2346 | 0.2388 | 0.2288 | 0.2354 | 1688 |
| Std. Dev. * | (0.0328) | (0.0492) | (0.0256) | (0.0256) |
| Series | GPH | AG | LW | FELW | No. of Grids | |
|---|---|---|---|---|---|---|
| 0.3427 | 0.2951 | 0.3540 | 0.3738 | 1463 | 15,981 | |
| (0.0347) | (0.0521) | (0.0271) | (0.0271) | |||
| 0.3236 | 0.3082 | 0.3389 | 0.3539 | 1560 | 8100 | |
| (0.0338) | (0.0508) | (0.0264) | (0.0264) | |||
| 0.3624 | 0.2817 | 0.3695 | 0.3942 | 1364 | 7881 | |
| (0.0357) | (0.0536) | (0.0279) | (0.0279) | |||
| 0.4855 | 0.4103 | 0.5019 | 0.5216 | 1642 | 5397 | |
| (0.0332) | (0.0497) | (0.0259) | (0.0259) | |||
| 0.2164 | 0.2588 | 0.2404 | 0.2525 | 1286 | 2160 | |
| (0.0366) | (0.0549) | (0.0285) | (0.0285) | |||
| 0.1174 | 0.0874 | 0.1084 | 0.1401 | 681 | 2090 | |
| (0.0471) | (0.0707) | (0.0368) | (0.0368) |
| Series | GPH | AG | LW | FELW | No. of Grids | |
|---|---|---|---|---|---|---|
| 0.2279 | 0.2406 | 0.2277 | 0.2626 | 895 | 6185 | |
| (0.0423) | (0.0634) | (0.0330) | (0.0330) | |||
| 0.2179 | 0.2286 | 0.2315 | 0.2596 | 1106 | 3927 | |
| (0.0389) | (0.0583) | (0.0303) | (0.0303) | |||
| 0.2452 | 0.2615 | 0.2209 | 0.2678 | 528 | 2258 | |
| (0.0522) | (0.0783) | (0.0407) | (0.0407) | |||
| 0.3308 | 0.3406 | 0.3315 | 0.3786 | 732 | 1685 | |
| (0.0458) | (0.0687) | (0.0357) | (0.0357) | |||
| 0.2009 | 0.2259 | 0.2248 | 0.2678 | 845 | 797 | |
| (0.0432) | (0.0649) | (0.0337) | (0.0337) | |||
| 0.1680 | 0.2005 | 0.1205 | 0.1633 | 284 | 1070 | |
| (0.0669) | (0.1003) | (0.0521) | (0.0521) |
| Series | GPH | AG | LW | FELW | No. of Grids | |
|---|---|---|---|---|---|---|
| 0.4051 | 0.4278 | 0.3458 | 0.5573 | 78 | 6006 | |
| (0.1116) | (0.1674) | (0.0870) | (0.0870) | |||
| 0.3784 | 0.5079 | 0.3621 | 0.5218 | 94 | 3982 | |
| (0.1040) | (0.1560) | (0.0811) | (0.0811) | |||
| 0.4542 | 0.2802 | 0.3159 | 0.6225 | 47 | 2114 | |
| (0.1367) | (0.2051) | (0.1066) | (0.1066) | |||
| 0.4621 | 0.5088 | 0.4074 | 0.6608 | 66 | 1563 | |
| (0.1191) | (0.1786) | (0.0928) | (0.0928) | |||
| 0.3166 | 0.4880 | 0.3083 | 0.4939 | 77 | 761 | |
| (0.1134) | (0.1700) | (0.0884) | (0.0884) | |||
| 0.4682 | 0.1177 | 0.2578 | 0.6449 | 24 | 1059 | |
| (0.1779) | (0.2668) | (0.1387) | (0.1387) |
| Series | GPH | AG | LW | FELW | No. of Grids | |
|---|---|---|---|---|---|---|
| 0.5947 | 0.8443 | 0.5343 | 0.6429 | 78 | 6006 | |
| (0.2138) | (0.3206) | (0.1667) | (0.1667) | |||
| 0.6276 | 1.0159 | 0.5650 | 0.6364 | 94 | 3982 | |
| (0.2028) | (0.3042) | (0.1581) | (0.1581) | |||
| 0.5342 | 0.5284 | 0.4777 | 0.6549 | 47 | 2114 | |
| (0.2424) | (0.3636) | (0.1890) | (0.1890) | |||
| 0.6718 | 0.8727 | 0.6115 | 0.6725 | 66 | 1563 | |
| (0.2267) | (0.3401) | (0.1768) | (0.1768) | |||
| 0.5528 | 1.2723 | 0.4883 | 0.5924 | 77 | 761 | |
| (0.2138) | (0.3206) | (0.1667) | (0.1667) | |||
| 0.4133 | 0.4156 | 0.3766 | 0.6872 | 24 | 1059 | |
| (0.2868) | (0.4302) | (0.2236) | (0.2236) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vera-Valdés, J.E. Temperature Anomalies, Long Memory, and Aggregation. Econometrics 2021, 9, 9. https://doi.org/10.3390/econometrics9010009
Vera-Valdés JE. Temperature Anomalies, Long Memory, and Aggregation. Econometrics. 2021; 9(1):9. https://doi.org/10.3390/econometrics9010009
Chicago/Turabian StyleVera-Valdés, J. Eduardo. 2021. "Temperature Anomalies, Long Memory, and Aggregation" Econometrics 9, no. 1: 9. https://doi.org/10.3390/econometrics9010009
APA StyleVera-Valdés, J. E. (2021). Temperature Anomalies, Long Memory, and Aggregation. Econometrics, 9(1), 9. https://doi.org/10.3390/econometrics9010009






