Reducing the Bias of the Smoothed Log Periodogram Regression for Financial High-Frequency Data
Abstract
1. Introduction
2. Methods
2.1. Log Periodogram Regression
2.2. Smoothing the Periodogram
2.3. Using Subsamples
3. Simulations
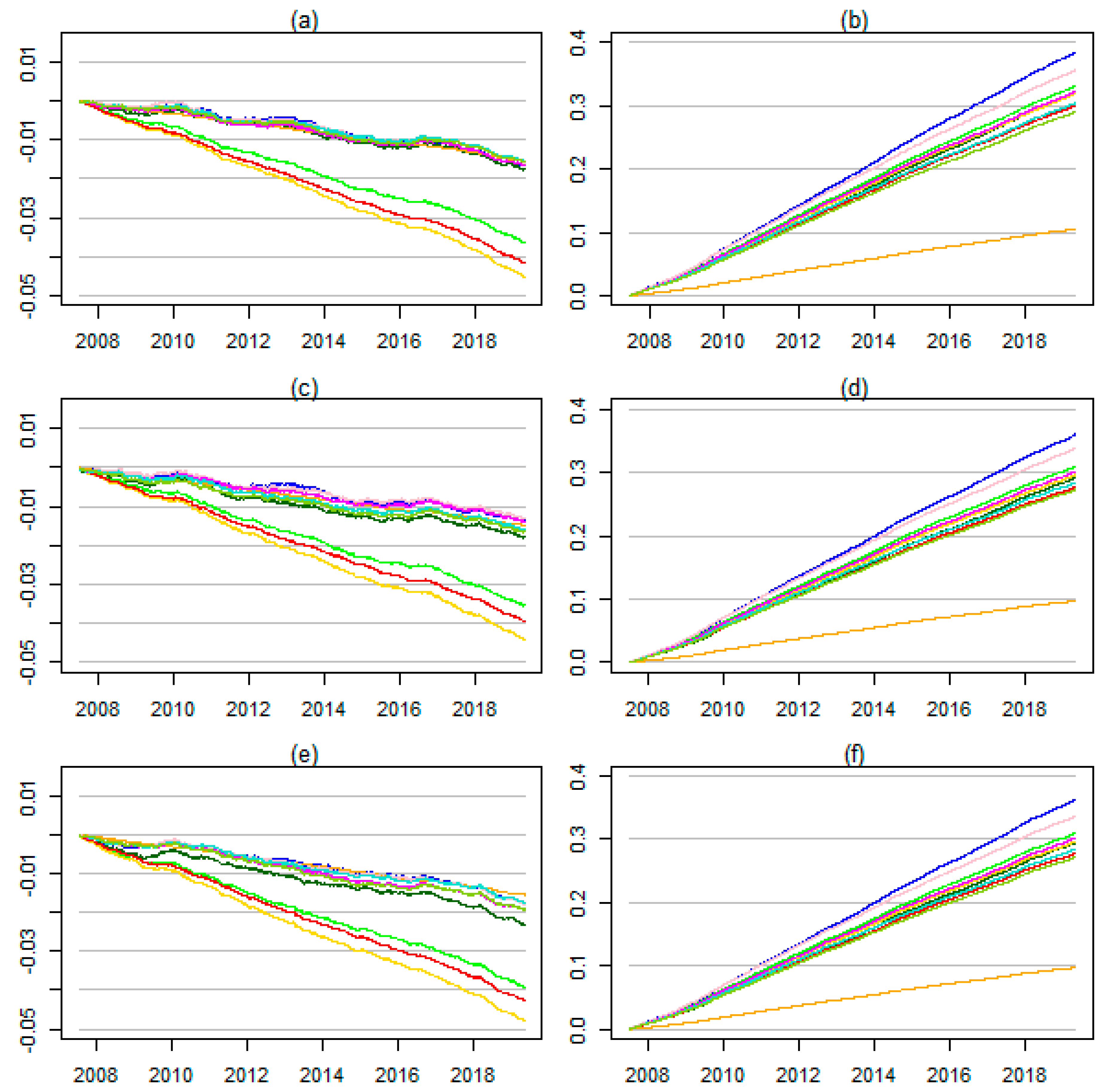
4. Empirical Results
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adenstedt, Rolf K. 1974. On Large-Sample Estimation for the Mean of Stationary Random Sequence. The Annals of Statistics 2: 1095–107. [Google Scholar] [CrossRef]
- Andrews, Donald W. K. 1991. Heteroskedasticity and autocorrelation consistent covariance matrix estimation. Econometrica 59: 817–58. [Google Scholar] [CrossRef]
- Auer, Benjamin R. 2016a. On the performance of simple trading rules derived from the fractal dynamics of gold and silver price fluctuations. Finance Research Letters 16: 255–67. [Google Scholar] [CrossRef]
- Auer, Benjamin R. 2016b. On time-varying predictability of emerging stock market returns. Emerging Markets Review 27: 1–13. [Google Scholar] [CrossRef]
- Barkoulas, John T., and Christopher F. Baum. 1996. Long-term dependence in stock returns. Economic Letters 53: 253–59. [Google Scholar] [CrossRef]
- Barkoulas, John T., Christopher F. Baum, and Nickolas Travlos. 2000. Long memory in the Greek stock market. Applied Financial Economics 10: 177–84. [Google Scholar] [CrossRef]
- Batten, Jonathan A., and Peter G. Szilagyi. 2007. Covered interest parity arbitrage and long-term dependence between the US dollar and the Yen. Physica A 376: 409–21. [Google Scholar] [CrossRef]
- Batten, Jonathan A., Craig A. Ellis, and Thomas A. Fethertson. 2008. Sample period selection and long-term dependence: New evidence from the Dow Jones Index. Chaos, Solitons Fractals 36: 1126–40. [Google Scholar] [CrossRef]
- Batten, Jonathan, Cetin Ciner, Brian M. Lucey, and Peter G. Szilagyi. 2013. The structure of gold and silver spread returns. Quantitative Finance 13: 561–70. [Google Scholar] [CrossRef]
- Cajueiro, Daniel O., and Benjamin M. Tabak. 2004. The Hurst exponent over time: Testing the assertion that emerging markets are becoming more efficient. Physica A 336: 521–37. [Google Scholar] [CrossRef]
- Carbone, Anna, Giuliano Castelli, and H. Eugene Stanley. 2004. Time-dependent Hurst exponent in financial time series. Physica A 344: 267–71. [Google Scholar] [CrossRef]
- Chen, Gemai, Bovas Abraham, and Shelton Peiris. 1994. Lag window estimation of the degree of differencing in fractionally integrated time series models. Journal of Time Series Analysis 15: 473–87. [Google Scholar] [CrossRef]
- Cheung, Yin-Wong, and Kon S. Lai. 1995. A search for long memory in international stock market returns. Journal of International Money and Finance 14: 597–615. [Google Scholar] [CrossRef]
- Crato, Nuno. 1994. Some international evidence regarding the stochastic behaviour of stock returns. Applied Financial Economics 4: 33–39. [Google Scholar] [CrossRef]
- Crato, Nuno, and Pedro J. F. de Lima. 1994. Long-range dependence in the conditional variance of stock returns. Economics Letters 45: 281–85. [Google Scholar] [CrossRef]
- Davis, Robert, and David Harte. 1987. Tests of the Hurst effect. Biometrika 74: 95–101. [Google Scholar] [CrossRef]
- Geweke, John, and Susan Porter-Hudak. 1983. The estimation and application of long memory time series models. Journal of Time Series Analysis 4: 221–38. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Roselyne Joyeux. 1980. An introduction to long-memory time series models and fractional differencing. Journal of Time Series Analysis 1: 15–29. [Google Scholar] [CrossRef]
- Grau-Carles, Pilar. 2000. Empirical evidence of long-range correlations in stock returns. Physica A 287: 396–404. [Google Scholar] [CrossRef]
- Greene, Myron T., and Bruce D. Fielitz. 1977. Long term dependence in common stock eturns. Journal of Financial Economics 4: 339–49. [Google Scholar] [CrossRef]
- Hassler, Uwe. 1993. Regression of spectral estimators with fractionally integrated time series. Journal of Time Series Analysis 14: 369–80. [Google Scholar] [CrossRef]
- Hauser, Michael A., and Erhard Reschenhofer. 1995. Estimation of the fractionally differencing parameter with the R/S method. Computational Statistics & Data Analysis 20: 569–79. [Google Scholar]
- Henry, Ólan T. 2002. Long memory in stock returns: Some international evidence. Applied Financial Economics 12: 725–29. [Google Scholar] [CrossRef]
- Hosking, Jonathan R. M. 1981. Fractional differencing. Biometrika 68: 165–76. [Google Scholar] [CrossRef]
- Hunt, R. L., M. Shelton Peiris, and N. C. Weber. 2003. The bias of lag window estimators of the fractional difference parameter. Journal of Applied Mathematics and Computing 12: 67–79. [Google Scholar] [CrossRef]
- Hurst, Harold E. 1951. Long term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers 116: 770–99. [Google Scholar]
- Hurvich, Clifford M., and Kaizo I. Beltrao. 1993. Asymptotics for the low-freqeuncy ordinates of the periodogram of a long-memory time series. Journal of Time Series Analysis 14: 455–72. [Google Scholar] [CrossRef]
- Hurvich, Clifford M., Rohit Deo, and Julia Brodsky. 1998. ‘The mean square error of Geweke and Porter-Hudak’s estimator of the memory parameter of a long-memory time series. Journal of Time Series Analysis 19: 19–46. [Google Scholar] [CrossRef]
- Künsch, Hans-Rudolf. 1986. Discrimination between monotonic trends and long-range dependence. Journal of Applied Probability 23: 1025–30. [Google Scholar] [CrossRef]
- Lo, Andrew. 1991. Long-term memory in stock market prices. Econometrica 59: 1279–313. [Google Scholar] [CrossRef]
- Lobato, Ignacio N., and N. E. Savin. 1998. Real and spurious long-memory properties of stock-market data. Journal of Business & Economic Statistics 16: 261–68. [Google Scholar]
- Mandelbrot, Benoît. 1971. When can price be arbitraged efficiently? A limit to the validity of the random walk and martingale models. The Review of Economics and Statistics 53: 225–36. [Google Scholar] [CrossRef]
- Mandelbrot, Benoît. 1972. Statistical methodology for non-periodic cycles: From the covariance to R/S analysis. Annals of Economic and Social Measurement 1: 259–90. [Google Scholar]
- Mandelbrot, Benoît. 1975. Limit theorems on the delf.-normalized range for weakly and strongly dependent processes. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 31: 271–85. [Google Scholar] [CrossRef]
- Mandelbrot, Benoît, and James Wallis. 1969. Computer experiments with fractional Gaussian noises. Parts 1, 2, 3. Water Resources Research 4: 909–18. [Google Scholar] [CrossRef]
- Mangat, Manveer K., and Erhard Reschenhofer. 2019. Testing for long-range dependence in financial time series. Central European Journal of Economic Modelling and Econometrics 11: 93–106. [Google Scholar]
- Newey, Whitney K., and Kenneth D. West. 1987. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55: 703–8. [Google Scholar] [CrossRef]
- Peiris, M. Shelton, and J. R. Court. 1993. A note on the estimation of degree of differencing in long memory time series analysis. Probability and Mathematical Statistics 14: 223–29. [Google Scholar]
- Pötscher, Benedikt M. 2002. Lower risk bounds and properties of confidence sets for ill-posed estimation problems with applications to spectral density and persistence estimation, unit roots, and estimation of long memory parameters. Econometrica 70: 1035–65. [Google Scholar] [CrossRef]
- R Core Team. 2018. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Reisen, Valderio A. 1994. Estimation of the fractional difference parameter in the ARIMA(p,d,q) model using the smoothed periodogram. Journal of Time Series Analysis 15: 335–50. [Google Scholar] [CrossRef]
- Reisen, Valderio A., Bovas Abraham, and Silvia Lopes. 2001. Estimation of parameters in ARFIMA processes: A simulation study. Communications in Statistics: Simulation and Computation 30: 787–803. [Google Scholar] [CrossRef]
- Reschenhofer, Erhard, and Manveer K. Mangat. 2020. Detecting long-range dependence with truncated ratios of periodogram ordinates. Communications in Statistics—Theory and Methods. [Google Scholar] [CrossRef]
- Reschenhofer, Erhard, Manveer K. Mangat, and Thomas Stark. 2020. Improved estimation of the memory parameter. Theoretical Economics Letters 10: 47–68. [Google Scholar] [CrossRef]
- Robinson, Peter M. 1995. Log-periodogram regression of time series with long range dependence. Annals of Statistics 23: 1048–72. [Google Scholar] [CrossRef]
- Souza, Sergio, Benjamin M. Tabak, and Daniel O. Cajueiro. 2008. Long-range dependence in exchange rates: The case of the European monetary system. International Journal of Theoretical and Applied Finance 11: 199–223. [Google Scholar] [CrossRef]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0.1475 | 0.0186 | 0.0072 | 0.0044 | 0.0027 | 0.0014 | 0.0013 | 0.001 | 0.0008 | 0.0005 |
| 2 | 0.3541 | 0.0002 | −0.0001 | −0.0004 | 0 | 0.0003 | −0.0003 | 0.0002 | 0.0002 | 0.0005 |
| 3 | 0.1364 | 0.133 | 0.0154 | 0.006 | 0.0032 | 0.0025 | 0.0009 | 0.001 | 0.0007 | 0.0003 |
| 4 | −0.0001 | 0.3541 | −0.0001 | −0.0002 | 0.0002 | 0.0008 | −0.0005 | −0.0002 | −0.0004 | −0.0003 |
| 5 | 0.0164 | 0.1316 | 0.1307 | 0.0144 | 0.005 | 0.0027 | 0.0019 | 0.0016 | 0.0008 | 0.0008 |
| 6 | −0.0001 | −0.0003 | 0.354 | 0.0002 | 0.0002 | −0.0004 | 0.0004 | 0.0001 | −0.0005 | 0.0005 |
| 7 | 0.007 | 0.0147 | 0.1311 | 0.1308 | 0.014 | 0.0043 | 0.0025 | 0.0021 | 0.0013 | 0.0011 |
| 8 | 0 | 0.0001 | 0.0004 | 0.3541 | 0.0004 | 0.0001 | −0.0001 | −0.0002 | −0.0001 | −0.0002 |
| 9 | 0.0035 | 0.0054 | 0.0143 | 0.1302 | 0.1302 | 0.0139 | 0.0051 | 0.003 | 0.0016 | 0.0009 |
| 10 | −0.0003 | 0 | −0.0001 | 0.0004 | 0.3539 | −0.0003 | 0.0003 | 0.0001 | −0.0005 | 0.0003 |
| 11 | 0.0023 | 0.0033 | 0.0047 | 0.0138 | 0.1301 | 0.13 | 0.0133 | 0.0054 | 0.0025 | 0.0014 |
| 12 | −0.0004 | −0.0001 | −0.0004 | −0.0001 | 0.0003 | 0.3542 | 0.0001 | −0.0001 | 0.0002 | 0 |
| 13 | 0.0013 | 0.002 | 0.0032 | 0.0053 | 0.0137 | 0.1305 | 0.1309 | 0.0147 | 0.004 | 0.003 |
| 14 | −0.0004 | 0.0001 | 0.0003 | 0.0004 | 0.0008 | 0.0002 | 0.3544 | −0.0002 | 0.0005 | −0.0002 |
| 15 | 0.0011 | 0.0016 | 0.002 | 0.0025 | 0.0059 | 0.014 | 0.1304 | 0.1297 | 0.0141 | 0.0055 |
| 16 | −0.0006 | 0.0001 | −0.0004 | 0 | 0.0002 | −0.0001 | −0.0001 | 0.354 | 0.0002 | 0.0002 |
| 17 | 0.0011 | 0.0009 | 0.0009 | 0.0021 | 0.0025 | 0.0049 | 0.0138 | 0.1305 | 0.1304 | 0.0137 |
| 18 | 0.0003 | −0.0002 | 0 | −0.0001 | −0.0006 | −0.0004 | −0.0002 | −0.0004 | 0.3541 | −0.0001 |
| 19 | 0.0008 | 0.0005 | 0.0011 | 0.0015 | 0.0019 | 0.0026 | 0.0046 | 0.0138 | 0.1306 | 0.1302 |
| 20 | −0.0001 | 0.0005 | 0.0001 | 0.0002 | 0.0008 | 0.0001 | 0.0007 | −0.0003 | −0.0005 | 0.3541 |
| −0.25 | −0.25 | 0.0074 | −0.0001 | −0.0073 | −0.0099 | 0.0345 | 0.1609 | 0.0087 | 0.0084 | 0.0098 | 0.0107 |
| −0.1 | 0.0050 | 0.0002 | −0.0083 | −0.0107 | 0.0345 | 0.1625 | 0.0080 | 0.0084 | 0.0087 | 0.0092 | |
| 0 | 0.0042 | −0.0031 | −0.0098 | −0.0124 | 0.0337 | 0.1641 | 0.0065 | 0.0065 | 0.0076 | 0.0086 | |
| 0.1 | 0.0097 | 0.0036 | −0.0049 | −0.0073 | 0.0380 | 0.1664 | 0.0126 | 0.0120 | 0.0128 | 0.0140 | |
| 0.25 | 0.0151 | 0.0110 | 0.0006 | −0.002 | 0.0436 | 0.1717 | 0.0165 | 0.0179 | 0.0201 | 0.0216 | |
| −0.1 | −0.25 | 0.0002 | −0.0029 | −0.0211 | −0.0280 | −0.008 | 0.0570 | 0.0008 | 0.0016 | 0.0006 | 0.0002 |
| −0.1 | 0.0015 | −0.0028 | −0.0212 | −0.0286 | −0.0085 | 0.0578 | −0.0001 | 0.0005 | 0.0001 | −0.0001 | |
| 0 | 0.0039 | 0.0017 | −0.0184 | −0.0251 | −0.0053 | 0.0601 | 0.0038 | 0.0052 | 0.0060 | 0.0057 | |
| 0.1 | 0.0014 | 0.0007 | −0.0197 | −0.0263 | −0.0056 | 0.0612 | 0.0024 | 0.0028 | 0.0039 | 0.0037 | |
| 0.25 | 0.0055 | 0.0059 | −0.0148 | −0.0215 | −0.0003 | 0.0666 | 0.0086 | 0.0099 | 0.0093 | 0.0101 | |
| 0 | −0.25 | −0.0043 | −0.0035 | −0.0282 | −0.0376 | −0.0321 | −0.0107 | −0.0038 | −0.0039 | −0.0048 | −0.0049 |
| −0.1 | −0.0011 | 0.0006 | −0.0258 | −0.0353 | −0.0299 | −0.0096 | −0.0004 | −0.0007 | −0.0004 | −0.0010 | |
| 0 | −0.0011 | −0.0001 | −0.0265 | −0.0361 | −0.0305 | −0.0087 | −0.0016 | −0.0004 | −0.0006 | −0.0006 | |
| 0.1 | −0.0001 | 0.0009 | −0.0235 | −0.0333 | −0.0278 | −0.0063 | 0.0016 | 0.0025 | 0.0019 | 0.0025 | |
| 0.25 | 0.0040 | 0.0064 | −0.0214 | −0.0309 | −0.0250 | −0.0022 | 0.0033 | 0.0060 | 0.0053 | 0.0073 | |
| 0.1 | −0.25 | 0.0009 | 0.0057 | −0.0274 | −0.039 | −0.0475 | −0.0762 | 0.0009 | −0.0003 | 0.0008 | −0.0001 |
| −0.1 | 0.0016 | 0.0056 | −0.0277 | −0.0396 | −0.0478 | −0.0754 | −0.0003 | 0.0002 | −0.0007 | −0.0006 | |
| 0 | −0.0005 | 0.0043 | −0.0277 | −0.0396 | −0.0479 | −0.0745 | −0.0012 | −0.0012 | −0.0012 | −0.0010 | |
| 0.1 | 0.0029 | 0.0059 | −0.0250 | −0.0374 | −0.0458 | −0.0727 | 0.0020 | 0.0028 | 0.0038 | 0.0034 | |
| 0.25 | 0.0097 | 0.0149 | −0.0186 | −0.0305 | −0.0392 | −0.0685 | 0.0088 | 0.0096 | 0.0114 | 0.0115 | |
| 0.25 | −0.25 | 0.0006 | 0.0102 | −0.0314 | −0.0451 | −0.0690 | −0.1748 | 0.0021 | 0.0018 | 0.0009 | 0.0006 |
| −0.1 | 0.0016 | 0.0112 | −0.0314 | −0.0453 | −0.0689 | −0.1744 | 0.0006 | 0.0011 | 0.0014 | 0.0010 | |
| 0 | 0.0044 | 0.0140 | −0.0281 | −0.0420 | −0.0656 | −0.1730 | 0.0032 | 0.0037 | 0.0040 | 0.0039 | |
| 0.1 | 0.0049 | 0.0162 | −0.0269 | −0.0408 | −0.0649 | −0.1718 | 0.0049 | 0.0065 | 0.0061 | 0.0060 | |
| 0.25 | 0.0079 | 0.0229 | −0.0228 | −0.0364 | −0.0600 | −0.1682 | 0.0105 | 0.0120 | 0.0130 | 0.0137 |
| −0.25 | −0.25 | 0.0330 | 0.0328 | 0.0201 | 0.018 | 0.0106 | 0.0011 | 0.0287 | 0.0259 | 0.0254 | 0.0238 |
| −0.1 | 0.0334 | 0.0339 | 0.0207 | 0.0185 | 0.0110 | 0.0012 | 0.0297 | 0.0266 | 0.0261 | 0.0245 | |
| 0 | 0.0342 | 0.0337 | 0.0209 | 0.0185 | 0.0108 | 0.0011 | 0.0296 | 0.0267 | 0.0262 | 0.0248 | |
| 0.1 | 0.0327 | 0.0330 | 0.0202 | 0.0180 | 0.0107 | 0.0011 | 0.0287 | 0.0262 | 0.0257 | 0.0240 | |
| 0.25 | 0.0323 | 0.0325 | 0.0199 | 0.0178 | 0.0106 | 0.0011 | 0.0287 | 0.0260 | 0.0258 | 0.0242 | |
| −0.1 | −0.25 | 0.0333 | 0.0327 | 0.0211 | 0.0187 | 0.0114 | 0.0011 | 0.0295 | 0.0268 | 0.0264 | 0.0250 |
| −0.1 | 0.0332 | 0.0317 | 0.0209 | 0.0186 | 0.0114 | 0.0011 | 0.0291 | 0.0264 | 0.0260 | 0.0250 | |
| 0 | 0.0334 | 0.0330 | 0.0212 | 0.0189 | 0.0115 | 0.0012 | 0.0298 | 0.0271 | 0.0267 | 0.0251 | |
| 0.1 | 0.0330 | 0.0315 | 0.0208 | 0.0185 | 0.0112 | 0.0011 | 0.0289 | 0.0262 | 0.0258 | 0.0246 | |
| 0.25 | 0.0328 | 0.0320 | 0.0209 | 0.0185 | 0.0112 | 0.0011 | 0.0291 | 0.0266 | 0.0263 | 0.0248 | |
| 0 | −0.25 | 0.0333 | 0.0322 | 0.0212 | 0.0191 | 0.0120 | 0.0012 | 0.0296 | 0.0268 | 0.0263 | 0.0250 |
| −0.1 | 0.0328 | 0.0320 | 0.0212 | 0.0191 | 0.0120 | 0.0012 | 0.0293 | 0.0268 | 0.0261 | 0.0252 | |
| 0 | 0.0335 | 0.0319 | 0.0214 | 0.0192 | 0.0119 | 0.0012 | 0.0297 | 0.0271 | 0.0266 | 0.0254 | |
| 0.1 | 0.0338 | 0.0323 | 0.0217 | 0.0195 | 0.0122 | 0.0012 | 0.0299 | 0.0271 | 0.0270 | 0.0260 | |
| 0.25 | 0.0332 | 0.0324 | 0.0213 | 0.0192 | 0.0120 | 0.0012 | 0.0300 | 0.0273 | 0.0269 | 0.0255 | |
| 0.1 | −0.25 | 0.0332 | 0.0327 | 0.0218 | 0.0198 | 0.0130 | 0.0012 | 0.0299 | 0.0274 | 0.0271 | 0.0260 |
| −0.1 | 0.0327 | 0.0321 | 0.0218 | 0.0199 | 0.0130 | 0.0012 | 0.0294 | 0.0269 | 0.0262 | 0.0252 | |
| 0 | 0.0328 | 0.0317 | 0.0214 | 0.0194 | 0.0127 | 0.0012 | 0.0293 | 0.0264 | 0.0263 | 0.0250 | |
| 0.1 | 0.0331 | 0.0321 | 0.0215 | 0.0195 | 0.0129 | 0.0012 | 0.0295 | 0.0269 | 0.0267 | 0.0256 | |
| 0.25 | 0.0326 | 0.0321 | 0.0217 | 0.0197 | 0.0130 | 0.0012 | 0.0293 | 0.0268 | 0.0263 | 0.0254 | |
| 0.25 | −0.25 | 0.0333 | 0.0315 | 0.0220 | 0.0202 | 0.0145 | 0.0013 | 0.0300 | 0.0271 | 0.0271 | 0.0260 |
| −0.1 | 0.0327 | 0.0323 | 0.0222 | 0.0205 | 0.0148 | 0.0013 | 0.0302 | 0.0278 | 0.0275 | 0.0265 | |
| 0 | 0.0328 | 0.0312 | 0.0219 | 0.0202 | 0.0146 | 0.0012 | 0.0297 | 0.0268 | 0.0264 | 0.0255 | |
| 0.1 | 0.0333 | 0.0325 | 0.0226 | 0.0207 | 0.0147 | 0.0013 | 0.0301 | 0.0274 | 0.0274 | 0.0262 | |
| 0.25 | 0.0339 | 0.0319 | 0.0226 | 0.0208 | 0.0150 | 0.0012 | 0.0302 | 0.0275 | 0.0272 | 0.0261 |
| −0.25 | −0.25 | 0.1818 | 0.1811 | 0.1421 | 0.1344 | 0.1084 | 0.1643 | 0.1697 | 0.1612 | 0.1595 | 0.1545 |
| −0.1 | 0.1827 | 0.1840 | 0.1442 | 0.1365 | 0.1104 | 0.1661 | 0.1724 | 0.1634 | 0.1618 | 0.1567 | |
| 0 | 0.1851 | 0.1837 | 0.1449 | 0.1368 | 0.1092 | 0.1674 | 0.1721 | 0.1635 | 0.1621 | 0.1578 | |
| 0.1 | 0.1812 | 0.1816 | 0.1423 | 0.1343 | 0.1103 | 0.1698 | 0.1700 | 0.1623 | 0.1607 | 0.1555 | |
| 0.25 | 0.1803 | 0.1807 | 0.1412 | 0.1335 | 0.1119 | 0.1751 | 0.1701 | 0.1621 | 0.1619 | 0.1571 | |
| −0.1 | −0.25 | 0.1825 | 0.1808 | 0.1466 | 0.1396 | 0.1070 | 0.0663 | 0.1717 | 0.1636 | 0.1624 | 0.1581 |
| −0.1 | 0.1823 | 0.1782 | 0.1460 | 0.1394 | 0.1072 | 0.0669 | 0.1705 | 0.1625 | 0.1611 | 0.1580 | |
| 0 | 0.1829 | 0.1816 | 0.1467 | 0.1398 | 0.1072 | 0.0691 | 0.1727 | 0.1647 | 0.1636 | 0.1585 | |
| 0.1 | 0.1817 | 0.1775 | 0.1454 | 0.1386 | 0.1061 | 0.0698 | 0.1699 | 0.1618 | 0.1607 | 0.1569 | |
| 0.25 | 0.1811 | 0.1789 | 0.1451 | 0.1378 | 0.1059 | 0.0745 | 0.1707 | 0.1634 | 0.1625 | 0.1578 | |
| 0 | −0.25 | 0.1826 | 0.1796 | 0.1481 | 0.1431 | 0.1142 | 0.0360 | 0.1721 | 0.1639 | 0.1624 | 0.1583 |
| −0.1 | 0.1812 | 0.1790 | 0.1479 | 0.1426 | 0.1137 | 0.0359 | 0.1713 | 0.1638 | 0.1615 | 0.1588 | |
| 0 | 0.1831 | 0.1785 | 0.1486 | 0.1433 | 0.1132 | 0.0351 | 0.1723 | 0.1646 | 0.1630 | 0.1593 | |
| 0.1 | 0.1837 | 0.1796 | 0.1491 | 0.1435 | 0.1139 | 0.0351 | 0.1729 | 0.1647 | 0.1645 | 0.1611 | |
| 0.25 | 0.1824 | 0.1801 | 0.1475 | 0.1418 | 0.1123 | 0.0345 | 0.1731 | 0.1653 | 0.1640 | 0.1599 | |
| 0.1 | −0.25 | 0.1822 | 0.1810 | 0.1502 | 0.146 | 0.1237 | 0.0837 | 0.1728 | 0.1657 | 0.1646 | 0.1612 |
| −0.1 | 0.181 | 0.1793 | 0.1502 | 0.1464 | 0.1237 | 0.0831 | 0.1715 | 0.1639 | 0.1617 | 0.1588 | |
| 0 | 0.181 | 0.1781 | 0.1490 | 0.1448 | 0.1226 | 0.0820 | 0.1711 | 0.1624 | 0.1622 | 0.1582 | |
| 0.1 | 0.1819 | 0.1792 | 0.1489 | 0.1446 | 0.1223 | 0.0805 | 0.1717 | 0.1641 | 0.1633 | 0.1599 | |
| 0.25 | 0.1808 | 0.1799 | 0.1485 | 0.1437 | 0.1206 | 0.0768 | 0.1713 | 0.1640 | 0.1626 | 0.1596 | |
| 0.25 | −0.25 | 0.1824 | 0.1778 | 0.1517 | 0.1493 | 0.1390 | 0.1784 | 0.1733 | 0.1648 | 0.1647 | 0.1612 |
| −0.1 | 0.1809 | 0.1800 | 0.1522 | 0.1502 | 0.1398 | 0.1780 | 0.1738 | 0.1666 | 0.1657 | 0.1629 | |
| 0 | 0.1810 | 0.1772 | 0.1505 | 0.1483 | 0.1375 | 0.1765 | 0.1723 | 0.1636 | 0.1626 | 0.1598 | |
| 0.1 | 0.1824 | 0.1809 | 0.1526 | 0.1495 | 0.1377 | 0.1754 | 0.1737 | 0.1657 | 0.1657 | 0.1621 | |
| 0.25 | 0.1842 | 0.1799 | 0.1522 | 0.1487 | 0.1363 | 0.1718 | 0.1740 | 0.1663 | 0.1654 | 0.1623 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reschenhofer, E.; Mangat, M.K. Reducing the Bias of the Smoothed Log Periodogram Regression for Financial High-Frequency Data. Econometrics 2020, 8, 40. https://doi.org/10.3390/econometrics8040040
Reschenhofer E, Mangat MK. Reducing the Bias of the Smoothed Log Periodogram Regression for Financial High-Frequency Data. Econometrics. 2020; 8(4):40. https://doi.org/10.3390/econometrics8040040
Chicago/Turabian StyleReschenhofer, Erhard, and Manveer K. Mangat. 2020. "Reducing the Bias of the Smoothed Log Periodogram Regression for Financial High-Frequency Data" Econometrics 8, no. 4: 40. https://doi.org/10.3390/econometrics8040040
APA StyleReschenhofer, E., & Mangat, M. K. (2020). Reducing the Bias of the Smoothed Log Periodogram Regression for Financial High-Frequency Data. Econometrics, 8(4), 40. https://doi.org/10.3390/econometrics8040040




