This section presents the data used to assess the long-lasting effects of periods that have covered pandemics on the economy, particularly in growth and unemployment. We use data from the United Kingdom given the availability of large datasets spanning several centuries.
3.2. Real GDP Per Capita in the UK
Here we focus on the longer time series, real GDP per capita, to analyze the persistence of different regimes, whose periods cover some relevant outbreaks and pandemics in history.
We consider a linear trend in Equation (
1) as follows:
for
, where
indicates the period, and
t is the time index. In Equation (
5),
is the real GDP per capita for the UK;
, and
are the intercept and the slope of each linear regression fitted in period
j; and
is a potentially fractionally differenced, random process. Then, the underlying idea to define a period is that either of the parameters (
, and
) vary in two consecutive periods calibrated by a trimming parameter.
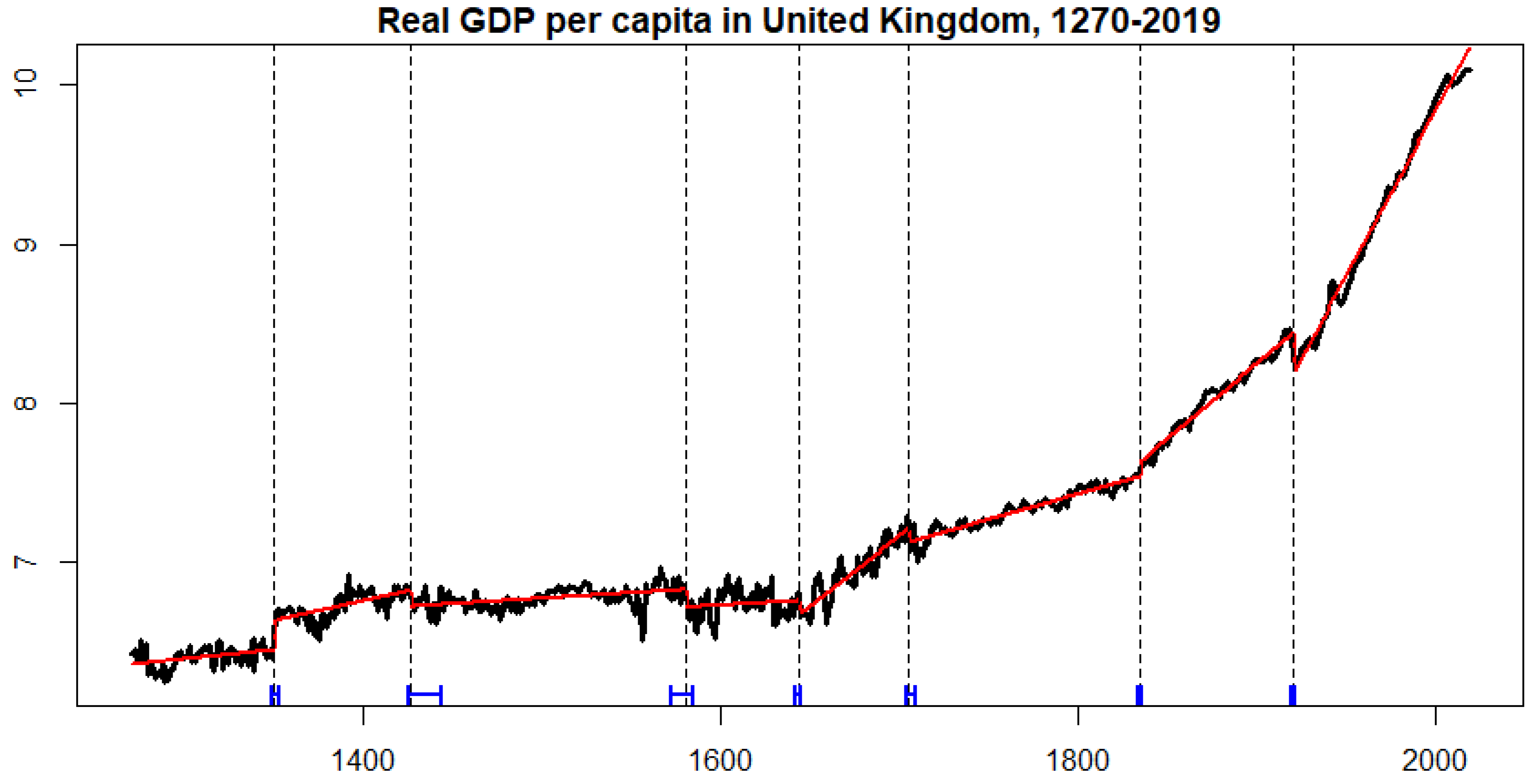
We work with the annual series of the real GDP per capita from 1270 to 2019.
Figure 1 displays the respective time series, the break estimated by the BP methodology, and their confidence intervals at 95% (also presented in
Table 3).
As we can see in
Figure 1, the BP methodology identifies eight periods over the last seven centuries in which GDP per capita of the United Kingdom undergoes structural changes in the aforementioned linear trend. To analyze the possible impact of COVID-19 within the current regime of the GDP per capita, firstly, it is relevant to identify the main outbreaks and pandemics along these centuries.
As seen in
Table 1, we can locate outbreaks and pandemics in some of the periods defined. We consider the regimes defined by the breaks estimated in
Table 3, and we estimate the respective persistence level of the random component for each period by the GPH and ELW methods explained before. The analysis is also accompanied by the MR test results to assess if there is a significant change in persistence between consecutive periods.
Table 4 presents the results and reveals some interesting findings.
First, there seems to be an increasing trend in the level of persistence through the regimes considered. However, we note a slight increase in persistence from the period finalizing with the Black Death pandemic to the next period that is not maintained to the subsequent period (where no major outbreak or pandemic is reported)—that is, the period after the Black Death pandemic seems to be more persistent than contiguous periods, pointing to the possible long-lasting effects of the pandemic on growth. Nonetheless, this increase in persistence does not appear to be statistically significant. The test for change in persistence does not reject the null of no change in persistence through the periods around the Black Death pandemic. One reason behind this result may be the short and imprecise data available before the pandemic.
Second, any shock before the 19th century has a non-permanent effect on the series, indicating that shocks originated from these outbreaks and epidemics were transitory even though potentially long-lasting. Moreover, we find that the small increases in persistence across the first five regimes are not statistically significant.
Third, shocks after the 19th century seem to have a permanent effect on the series, indicating that the most current outbreaks and epidemics have a longer-lasting effect on the GDP per capita. This could point to the fact that the world has become much more socially and economically connected in the last couple of centuries. Commerce and travel between countries are much more widespread, and thus the effects of global pandemics on growth are compounded. It is interesting to remark that persistence has statistically changed at 5% (at least) in the last three regimes. This gives us an idea that COVID-19 may present a change in the persistence of growth, which needs to be controlled by the policymakers.
These results highlight the relevance that the 21st century epidemics may have in the economy. It is too early to determine the persistence level of the COVID-19 pandemic on growth. Nonetheless, if the upward trend on the level of persistence of the effects of pandemics in growth is maintained, we would expect the effects of the COVID-19 pandemic to be long-lasting.
Assessing the impact of extreme events as pandemics from time series data is a big issue today. A classical perspective is conducted by a before-and-after comparison using a difference-in-difference approach. In a series of influential papers,
Abadie et al. (
2010), and
Abadie et al. (
2015) have introduced data-driven synthetic control groups by fitting multivariate time series models. On the other hand,
Harvey and Thiele (
2017) propose an auxiliary approach to assess the effect of an intervention or external shock from a time series perspective. However, given data limitations, it is not possible to follow these routes. In particular, by construction, there is only one real GDP per capita for the UK; and to the best of our knowledge, there is no yearly time series of confirmed cases and deaths from previous pandemics. Nevertheless, we design a pure time series analysis below to shed light on the impact of a pandemic in the economy. Once more data from the current pandemic is collected, a more conscientious analysis could be executed to deepen in this issue, but it remains out of the scope of the present paper.
To get a better understanding of the distinct behavior of real GDP between periods with pandemics and those without them,
Figure 2 presents an experiment using real GDP per capita in the UK between 1640 and 1800. The figure shows real GDP in the UK in the period associated with the Great Plague of London and the subsequent period. Moreover, we estimate the linear trend model with fractionally differenced disturbances, Equation (
5), in the period associated with the pandemic, and we use it to construct the counterfactual for the subsequent period. The periods were selected given that the Great Plague of London was a more localized event (see
Section 4), and that the pandemic occurred before the industrial revolution. Given our data, these two conditions allow us to study the change in trend and persistence when the international feedback loops were less pronounced. Moreover, the use of the fractional difference operator to forecast long memory processes is supported by the results of
Vera-Valdés (
2020). The author showed that fractionally differenced models are good at forecasting long memory processes regardless of the long memory generating mechanism.
Figure 2 allows us to compare the counterfactual behavior of real GDP in the UK under the no-break scenario against the actual values. The figure shows that the loss in real GDP was quite significant and lasted for almost a century. The average annual loss in GDP from the counterfactual to the actual values is 6%, with a maximum estimated decrease of 11%.
It is worth pointing out that we cannot directly extrapolate the results from the thought experiment in
Figure 2 to the current pandemic. The world is much more connected now, which allows the virus to spread fast instead of slowly developing waves, and both the economic and medical sciences have significantly advanced in the last two centuries, which allows for a more competent response. As a prime example, large randomized control trials for a vaccine are already in motion in record time, less than a year since the virus was discovered. In this sense, these results can only be considered as a lower bound. Nonetheless, the results are instructive in the sense that they point to a long post-pandemic recovery period in the absence of economic policies designed to soften the shock of the pandemic, as was the case in the 18th century.
Furthermore, as a robustness exercise, we analyze the yearly real GDP per capita for England from the
Thomas and Dimsdale (
2017) dataset. Results, available upon request, corroborate the upward increasing trend in persistence across the centuries and the slightly larger persistence after the Black Death pandemic. Moreover, we used other bandwidths for the long memory estimators obtaining qualitatively similar results.
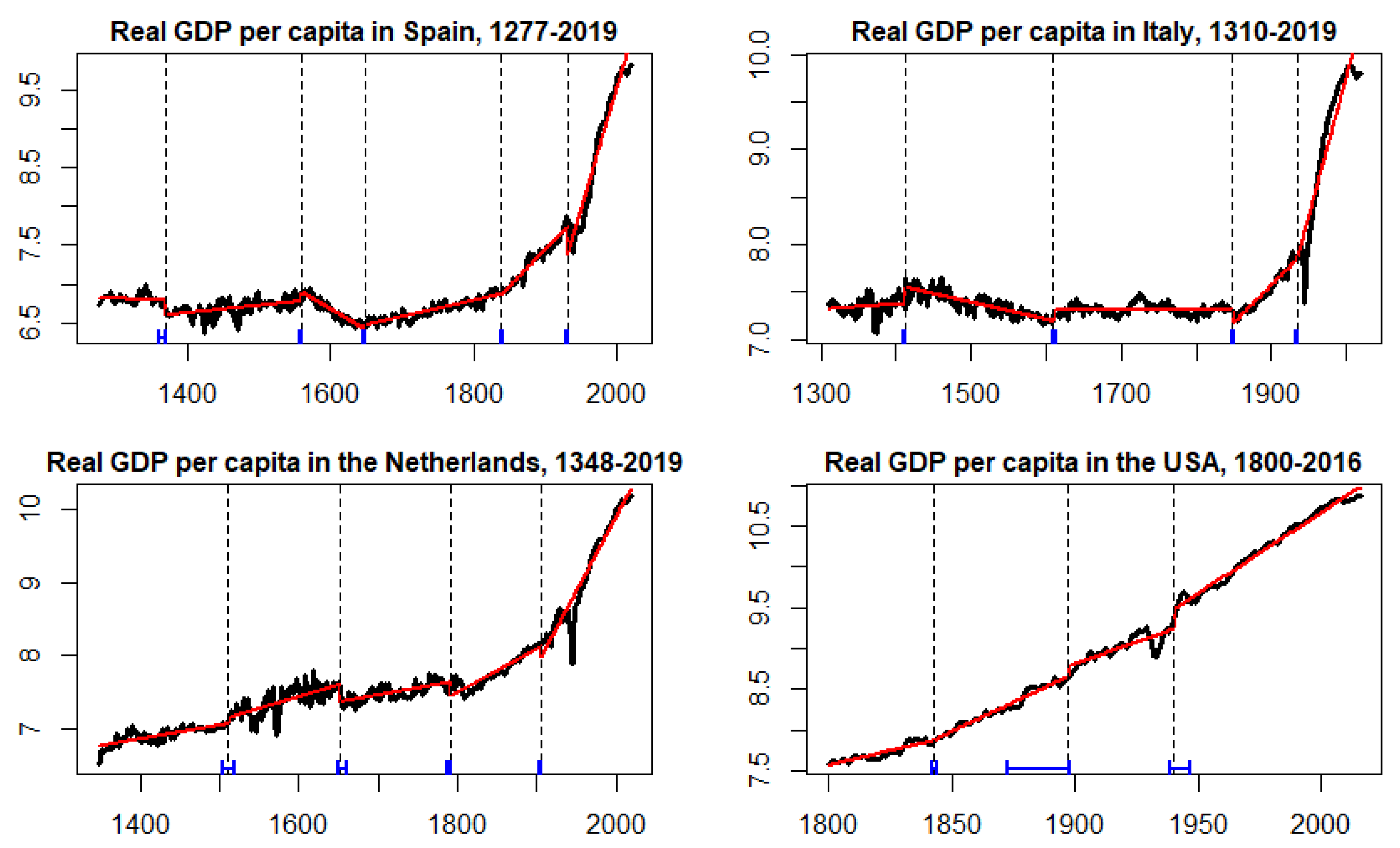
Finally,
Section 4 considers growth data in Spain, Italy, the Netherlands, and the USA to show that the findings for the UK case can be extended to other countries. Thus, our results confirm that the long-lasting effects on growth are international and not restricted to a particular country.
One caveat of the above analysis is that the low sampling of the data makes it difficult to properly disentangle the impact of, for example, the Spanish flu pandemic in the economy of the United Kingdom. Periods with major pandemics are sometimes accompanied by episodes of turmoil as the First and Second World Wars, or the Great Depression. In this respect, in the next section we use a series sampled more frequently to explore further the role that epidemics may play in the economy.
3.3. Unemployment in the UK
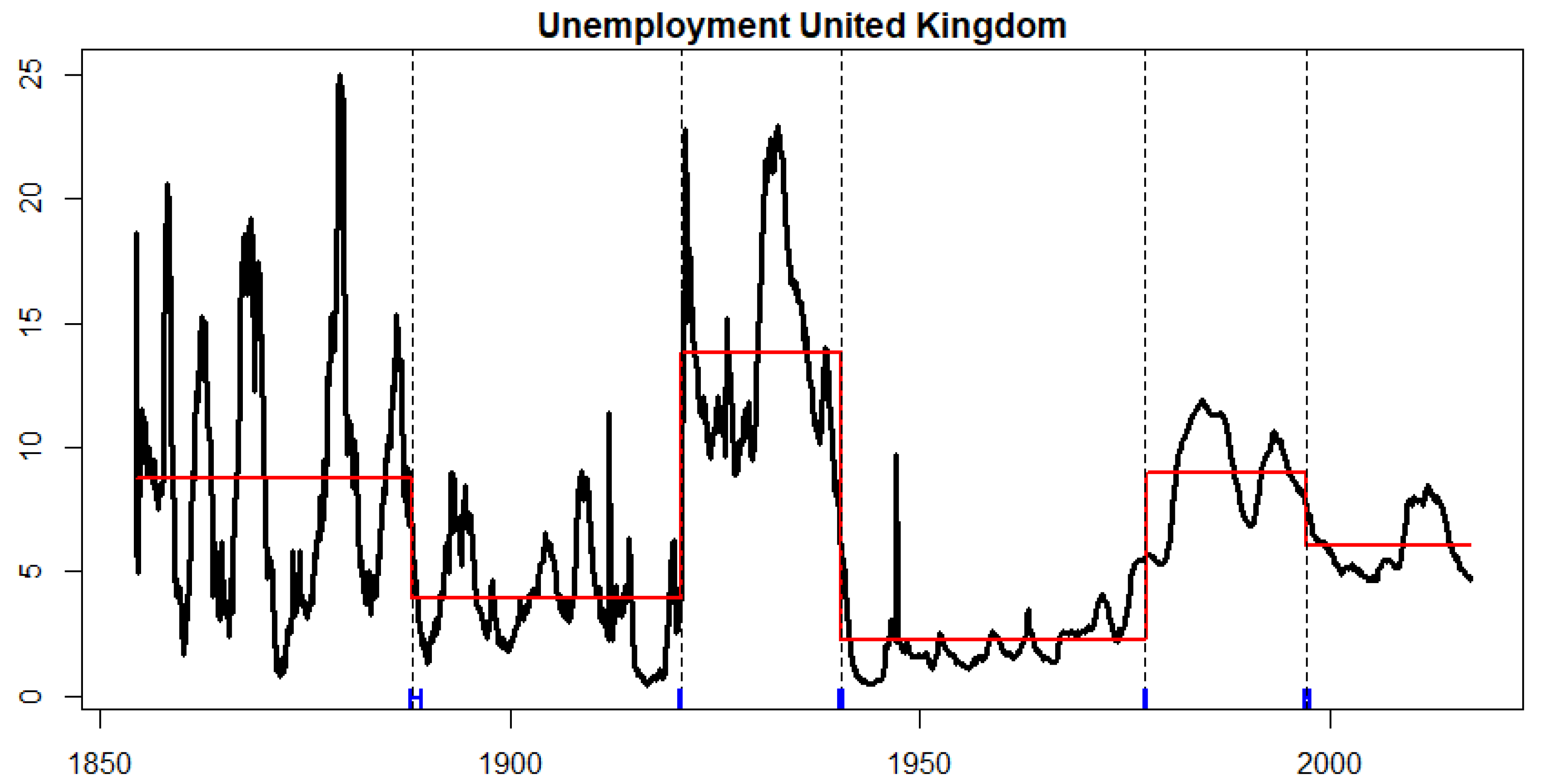
In this section, we focus on the monthly UK unemployment rate from July 1854 to December 2016. The more frequent sampling period allows us to disentangle better the economic effects that previous pandemics had in the economy.
To model structural change in unemployment, given that a linear trend is not observed, we consider a mean-shifting specification in Equation (
1) as follows:
for
, where
indicates the period, and
t is time index. In Equation (
6),
is the unemployment rate for the UK;
are the intercept of each linear regression fitted in period
j; and
is a, potentially fractionally differenced, random process.
Figure 3 shows the monthly UK unemployment rate from July 1854 to December 2016. Furthermore, the figure shows the structural changes detected by the BP methodology and the mean for each regime. The dates for the structural changes are shown in
Table 5.
The detected dates relate to major historical events, some of them already discussed for the real GDP per capita series (see
Table 1). In particular, we are interested in the long memory properties of the period associated with the Great Pandemic of 1870–1875 and the Russian flu, and the period after the Spanish flu pandemic. The figure shows the higher level of unemployment during the period associated with the Great Pandemic of 1870–1875 and the Russian flu. Moreover, it shows a decrease in unemployment in the following period where no major pandemics are recorded, followed by a rapid increase in unemployment after the Spanish flu pandemic. In this regard, the effects of the Spanish flu pandemic on unemployment are much in line with preliminary estimates for the effects of COVID-19 on unemployment. To better understand the long-run effects of pandemics on unemployment, we first remove the mean for each regime and estimate the persistence of the random component. Results from the long memory estimation are presented in
Table 6.
Table 6 presents the long memory estimates for each regime by the GPH and ELW methods as before. Moreover, it presents the critical values for the MR test for the 90%, 95%, and 99% confidence levels. The last column presents the associated MR statistic for the test for change in persistence on either direction from the regime in the row above to the current row.
Note that unemployment has gone through several changes in the level of persistence across the regimes. Given the shorter span of the unemployment series, we can only analyze the effects of the periods associated with the Great Pandemic of 1870–1875 and Russian flu, and the Spanish flu.
The Great Pandemic of 1870–1875 and the Russian flu are contained in the first period detected. Note that the persistence level estimated in this period is quite high. The confidence intervals for the level of persistence for both estimators contain the value that implies permanent effects on the economy. This contrasts with the persistence level for the subsequent period, where a persistence parameter of is estimated. Furthermore, the MR test for change in persistence rejects the null of no change in persistence. This points to the catastrophic long-lasting effect of the pandemic in unemployment during the Great Pandemic of 1870–1875 and the Russian flu.
Moreover, the long-lasting effects of the Spanish flu pandemic can be seen in the increase in persistence from the 1888:02–1920:09 regime to the 1920:09–1940:12 one. Both GPH and ELW estimates point to an increase in persistence from a value associated with a process that reverts to the mean, , to a value associated with everlasting effects, —that is, the period associated with the Spanish flu pandemic seems to have the double effect of increasing the level of unemployment while making it much more persistent. Furthermore, the MR test rejects the null of no change in persistence in either direction at the 99% confidence level. These results may point to the fact that it was much more difficult for survivors to return to work after the pandemic.
In the above discussion, we have associated the increase in unemployment level and persistence to the Spanish flu pandemic. Nonetheless, it could be argued that the First World War is the major historical event behind the results. To shed light on whether major wars may be the main driver behind the increase in unemployment, it is enlightening to see the results from the 1940:12–1976:06 regime, which can be associated with the Second World War. The table shows a decrease in persistence from the regime associated with the Spanish Flu pandemic or First World War to the regime associated with the Second World War. Furthermore, the test for change of persistence strongly rejects the null of no change in persistence. Thus, there seems to be evidence that the period after the Second World War was one of lower, less persistent, unemployment. Contrasting this result with the one associated with the Spanish flu pandemic or First World War suggests that the pandemic plays a significant role in the increased level and persistence of unemployment.
The results on unemployment are of particular interest in light of the current COVID-19 pandemic. As previously noted, governments across the globe decided to implement lockdowns to slow the speed of contagion. The restrictions have substantially impacted several sectors of the economy, like tourism, that no longer needs their staff. The historical evidence found from previous pandemics suggests that, without policies specifically designed to avoid an increase in job losses, we should expect a higher level of unemployment that lasts for an extended period.
As a robustness exercise, first, even though no significant lag at the monthly frequency is found in the autocorrelation function, we deseasonalize the quarterly unemployment rate to explore whether a seasonal component can be interfering in our analysis. Second, we analyze the yearly unemployment rate considering different bandwidths and trimming parameters. The robustness exercises, available upon request, are qualitatively similar to the main exercise presented. Unfortunately, the monthly unemployment series for other countries are not long enough to capture previous pandemics.