A Parametric Factor Model of the Term Structure of Mortality
Abstract
:1. Introduction
2. The Lee–Carter Model
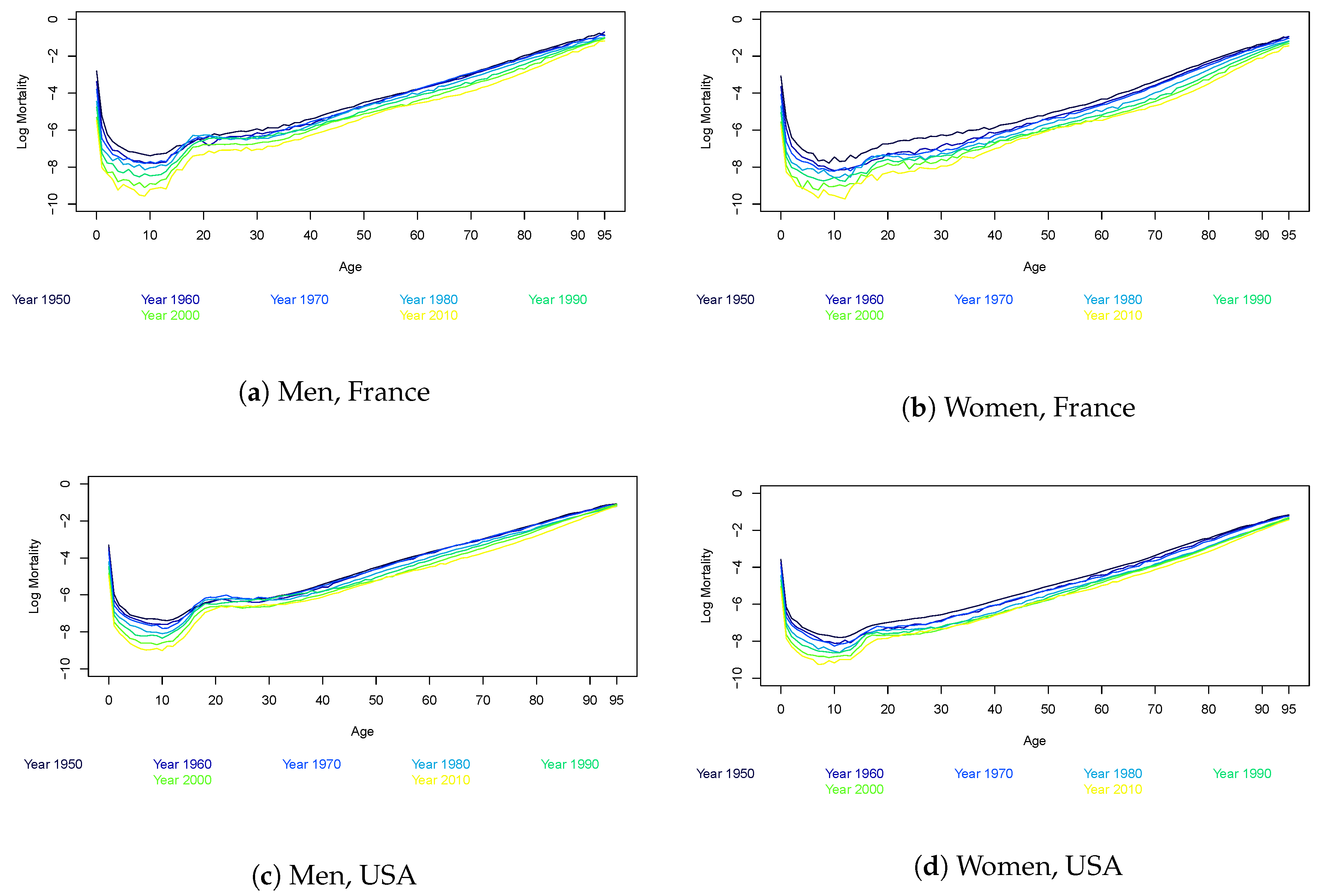
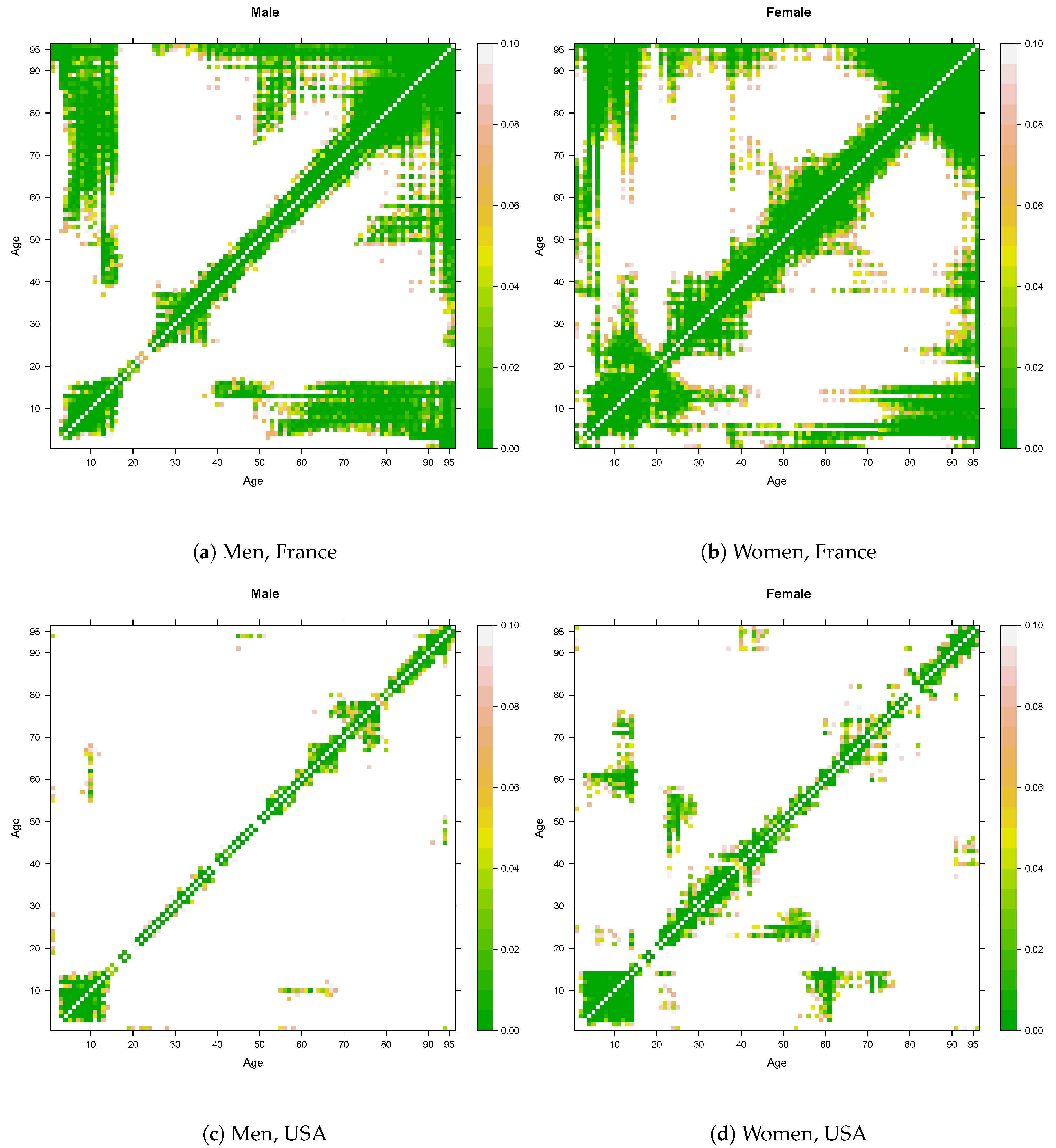
3. Stylized Facts of the Mortality Curve
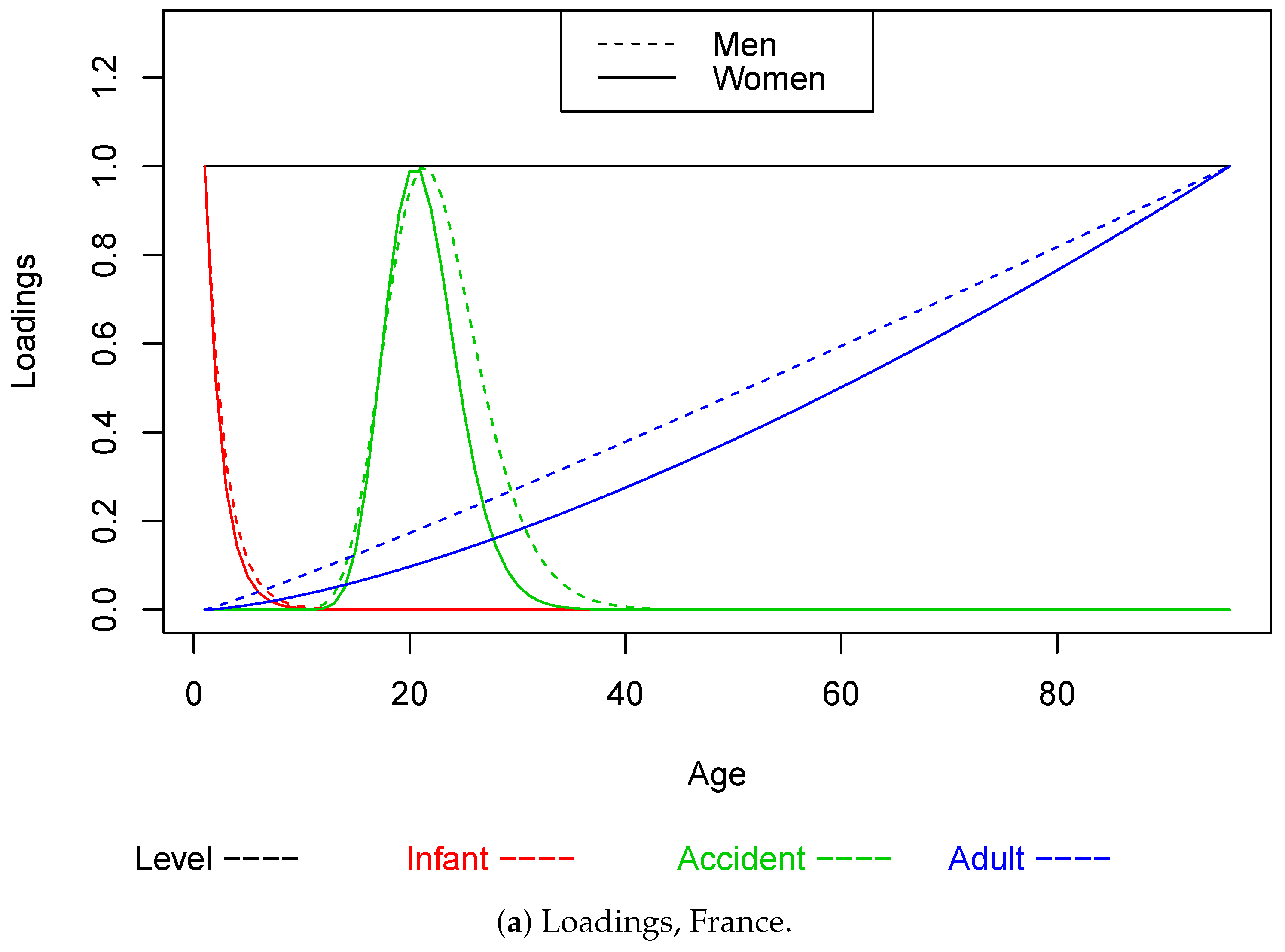
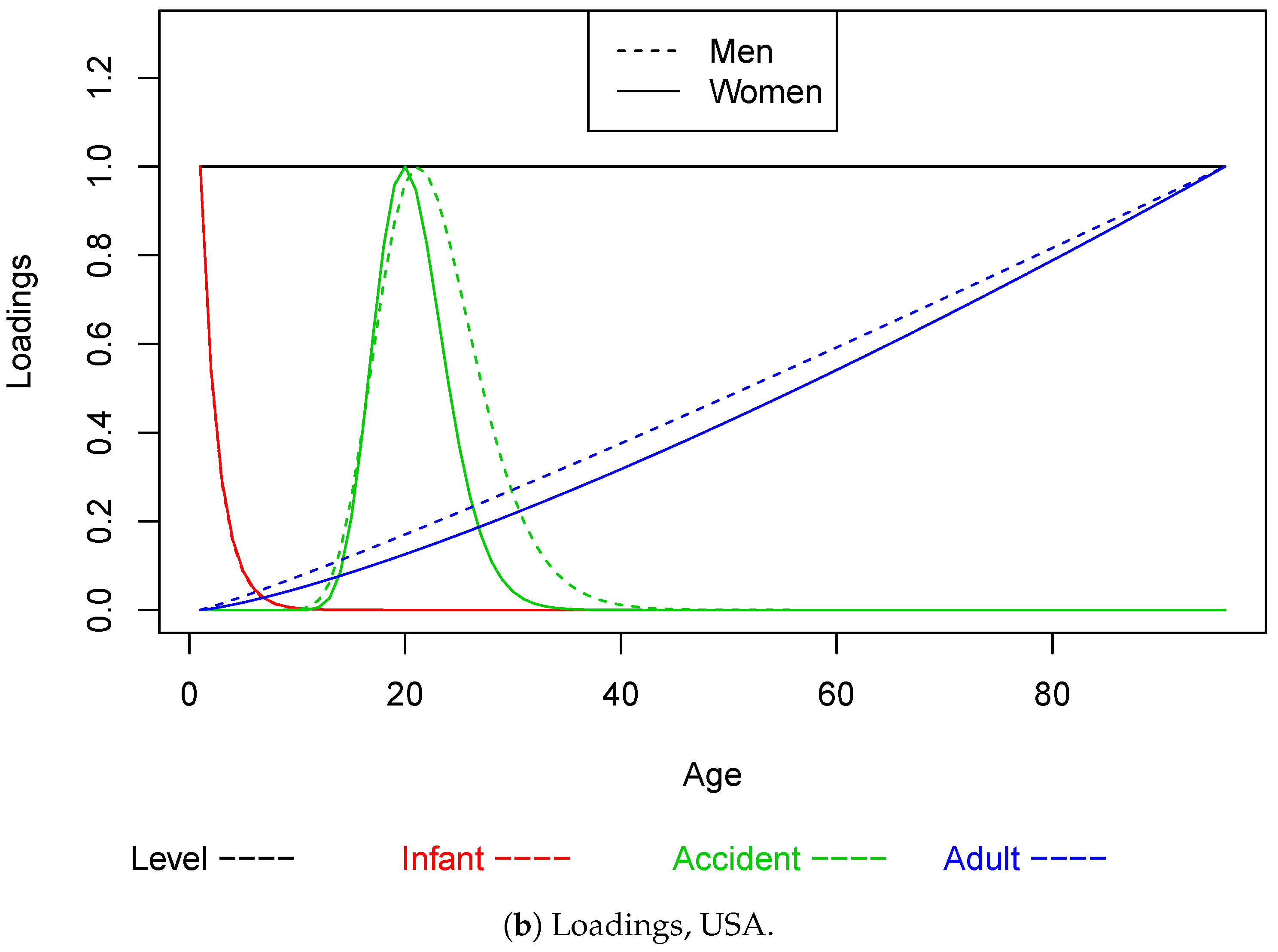
4. The Parametric Factor Model for the Term Structure of Mortality
5. Estimation Procedure for the Parametric Factor Model
5.1. The Two-Step Estimation Procedure
5.2. One-Step Estimation
6. Empirical Analysis
6.1. Estimates Using the Two-Step Procedure
6.2. Cointegrating Analysis of the Factors
6.3. Estimates Using the One-Step Procedure
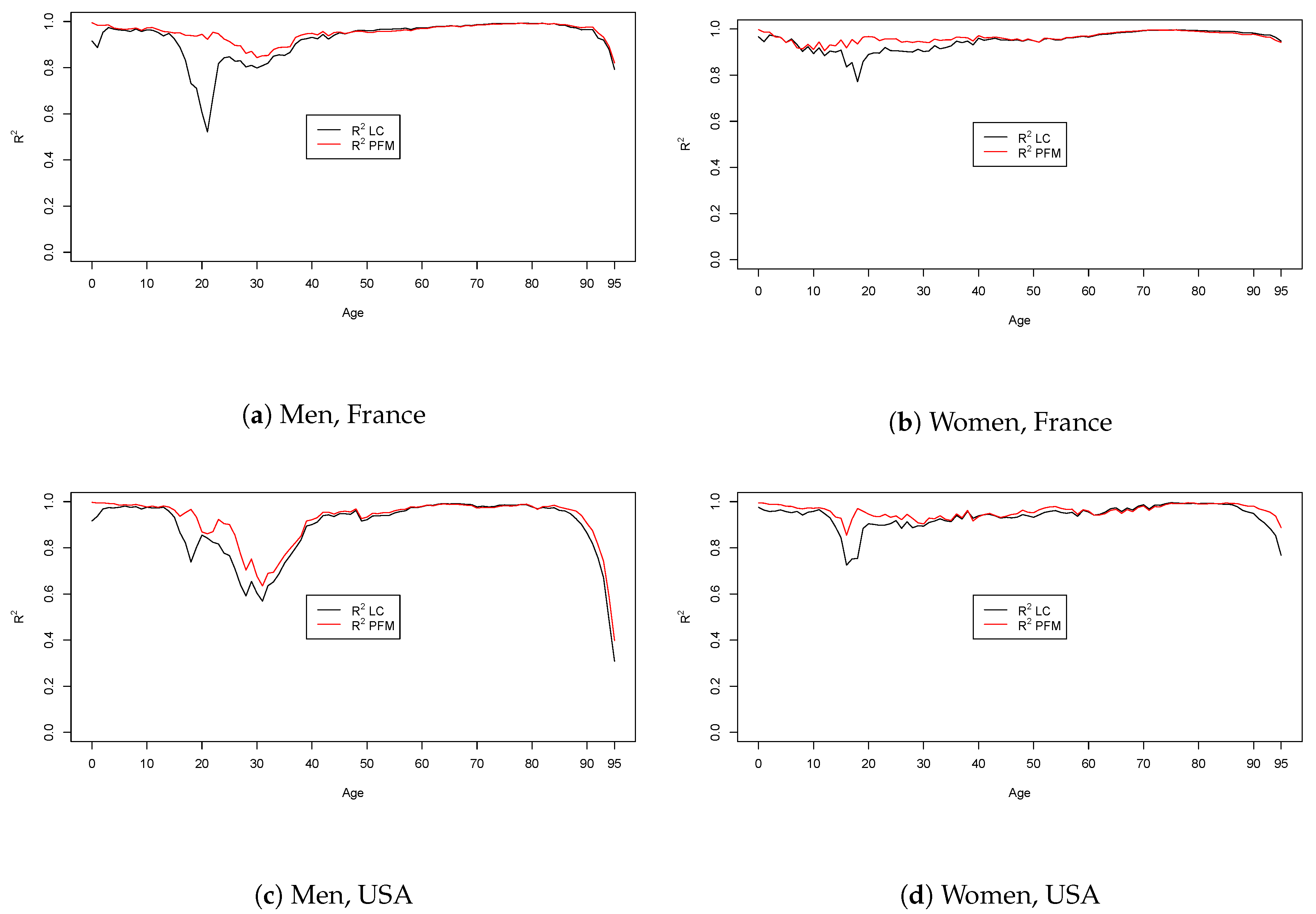
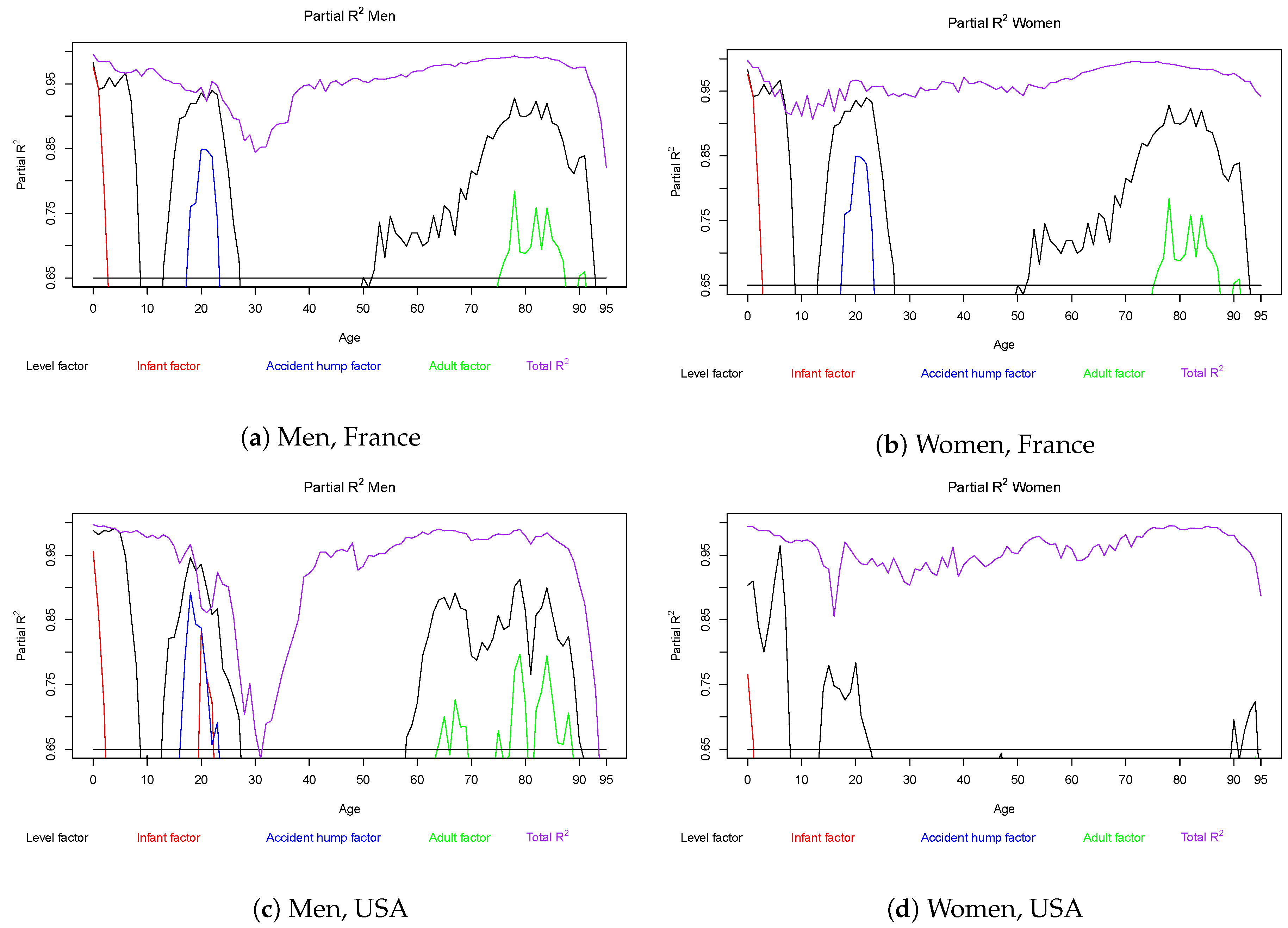
6.4. Model Fit
7. Forecast Evaluation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Booth, Heather, John Maindonald, and Len Smith. 2002. Applying Lee–Carter under conditions of variable mortality decline. Population Studies 56: 325–36. [Google Scholar] [CrossRef] [PubMed]
- Booth, Heather, and Leonie Tickle. 2008. Mortality modelling and forecasting: A review of methods. Annals of Actuarial Science 3: 3–43. [Google Scholar] [CrossRef]
- Box, G. E., and D. R. Cox. 1964. An analysis of transformations. Journal of the Royal Statistical Society. Series B (Methodological) 26: 211–52. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A poisson log-bilinear regression approach to the construction of projected lifetables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar] [CrossRef]
- Byrd, Richard H., Peihuang Lu, Jorge Nocedal, and Ciyou Zhu. 1995. A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing 16: 1190–208. [Google Scholar] [CrossRef]
- Cairns, Andrew J., David Blake, and Kevin Dowd. 2006. Pricing death: Frameworks for the valuation and securitization of mortality risk. Astin Bulletin: The Journal of the International Actuarial Association 36: 79–120. [Google Scholar] [CrossRef]
- Callot, Laurent, Niels Haldrup, and Malene Kallestrup-Lamb. 2016. Deterministic and stochastic trends in the Lee–Carter mortality model. Applied Economics Letters 23: 486–93. [Google Scholar] [CrossRef]
- De Jong, Piet, and Leonie Tickle. 2006. Extending Lee–Carter mortality forecasting. Mathematical Population Studies 13: 1–18. [Google Scholar] [CrossRef]
- Diebold, Francis, and Robert Mariano. 1995. Comparing predictive accuracy. Journal of Business and Economic Statistics 13: 253–63. [Google Scholar]
- Diebold, Francis X., and Canlin Li. 2006. Forecasting the term structure of government bond yields. Journal of Econometrics 130: 337–64. [Google Scholar] [CrossRef]
- Diebold, Francis X., Glenn D. Rudebusch, and S. B. Aruoba. 2006. The macroeconomy and the yield curve: A dynamic latent factor approach. Journal of Econometrics 131: 309–38. [Google Scholar] [CrossRef]
- Doornik, Jurgen A. 1998. Approximations to the asymptotic distributions of cointegration tests. Journal of Economic Surveys 12: 573–593. [Google Scholar] [CrossRef]
- Doornik, Jurgen A. 1999. Erratum [approximations to the asymptotic distribution of cointegration tests]. Journal of Economic Surveys 13. [Google Scholar]
- Doornik, Jurgen A. 2013. An Object-Oriented Matrix Programming Language Ox 6. Available online: https://ora.ox.ac.uk/objects/uuid:242f0a19-0665-4d9a-b863-774a35ce98c7 (accessed on 10 March 2019).
- Doz, Catherine, Domenico Giannone, and Lucrezia Reichlin. 2011. A two-step estimator for large approximate dynamic factor models based on kalman filtering. Journal of Econometrics 164: 188–205. [Google Scholar] [CrossRef]
- Durbin, James, and Siem Jan Koopman. 2012. Time Series Analysis by State Space Methods. Oxford: Oxford University Press, vol. 38. [Google Scholar]
- Gavrilov, L. A., and N. S. Gavrilova. 1979. Determination of species length of life. Doklady Akademii nauk SSSR: Biological Sciences 246: 905–8. [Google Scholar]
- Gavrilov, L. A., and N. S. Gavrilova. 1991. The Biology of Life Span: A Quantitative Approach. New York and Chur: Harwood Academic Publisher. [Google Scholar]
- Gompertz, B. 1825. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London 115: 513–83. [Google Scholar] [CrossRef]
- Hansen, Peter, and Asger Lunde. 2014. Mulcom 3.00. Econometric Toolkit for Multiple Comparisons. [Google Scholar]
- Hansen, Peter R., Asger Lunde, and James M. Nason. 2011. The model confidence set. Econometrica 79: 453–97. [Google Scholar] [CrossRef]
- Heligman, L., and J. H. Pollard. 1980. The age pattern of mortality. Journal of the Institute of Actuaries 107: 49–80. [Google Scholar] [CrossRef]
- Human Mortality Database. 2016. Human Mortality Database. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available online: www.mortality.org or www.humanmortality.de (accessed on 29 June 2016).
- Hyndman, Rob J. 2015. ‘forecast’: Forecasting Functions for Time Series And Linear Models. R package version 6.2. Available online: http://github.com/robjhyndman/forecast (accessed on 13 November 2016).
- Hyndman, Rob J., Heather Booth, Leonie Tickle, and John Maindonald. 2014. Demography: Forecasting Mortality, Fertility, Migration and Population Data. R package version 1.18. Available online: http://CRAN.R-project.org/package=demography (accessed on 13 November 2016).
- Hyndman, Rob J., and Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics & Data Analysis 51: 4942–56. [Google Scholar]
- Johansen, Soren. 1988. Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control 12: 231–54. [Google Scholar] [CrossRef]
- Johansen, Soren. 1991. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica: Journal of the Econometric Society 59: 1551–80. [Google Scholar] [CrossRef]
- Koopman, Siem Jan, Max I. Mallee, and Michel Van der Wel. 2010. Analyzing the term structure of interest rates using the dynamic nelson-siegel model with time-varying parameters. Journal of Business & Economic Statistics 28: 329–43. [Google Scholar]
- Lazar, Dorina, and Michel M. Denuit. 2009. A multivariate time series approach to projected life tables. Applied Stochastic Models in Business and Industry 25: 806–23. [Google Scholar] [CrossRef]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Lee, Ronald D., and Timothy Miller. 2001. Evaluating the performance of the Lee–Carter method for forecasting mortality. Demography 38: 537–49. [Google Scholar] [CrossRef] [PubMed]
- Makeham, William Matthew. 1860. On the law of mortality and the construction of annuity tables. The Assurance Magazine, and Journal of the Institute of Actuaries 8: 301–10. [Google Scholar] [CrossRef]
- McNown, Robert, and Andrei Rogers. 1989. Forecasting mortality: A parameterized time series approach. Demography 26: 645–60. [Google Scholar] [CrossRef] [PubMed]
- McNown, Robert, and Andrei Rogers. 1992. Forecasting cause-specific mortality using time series methods. International Journal of Forecasting 8: 413–32. [Google Scholar] [CrossRef]
- Nielsen, Bent, and Jens P. Nielsen. 2014. Identification and forecasting in mortality models. The Scientific World Journal 2014: 1–24. [Google Scholar] [CrossRef] [PubMed]
- Pfaff, Bernhard. 2008. VAR, SVAR and SVEC models: Implementation within R package vars. Journal of Statistical Software 27: 1–32. Available online: http://www.jstatsoft.org/v27/i04/ (accessed on 30 January 2017). [CrossRef]
- R Core Team. 2015. R: A Language and Environment for Statistical Computing; Vienna: R Foundation for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 13 November 2016).
- Renshaw, Arthur E., and Steven Haberman. 2003. Lee–Carter mortality forecasting with age-specific enhancement. Insurance: Mathematics and Economics 33: 255–72. [Google Scholar] [CrossRef]
- Rogers, Andrei, and Jani S. Little. 1994. Parameterizing age patterns of demographic rates with the multiexponential model schedule. Mathematical Population Studies 4: 175–95. [Google Scholar] [CrossRef] [PubMed]
- Siler, William. 1979. A competing-risk model for animal mortality. Ecology 60: 750–57. [Google Scholar] [CrossRef]
- Stigler, Matthieu. 2010. Threshold Cointegration: Overview and Implementation in R. R package version 0.7-2. Available online: http://stat.ethz.ch/CRAN/web/packages/tsDyn/vignettes/ThCointOverview.pdf (accessed on 30 January 2017).
- Strehler, Bernard L., and Albert S. Mildvan. 1960. General theory of mortality and aging. Science 132: 14–21. [Google Scholar] [CrossRef] [PubMed]
- Tabeau, Ewa, Anneke van den Berg Jeths, and Christopher Heathcote. 2001. Forecasting Mortality in Developed Countries: Insights From a Statistical, Demographic and Epidemiological Perspective. Dordrecht: Kluwer Academic Publishers. [Google Scholar]
- Wong-Fupuy, Carlos, and Steven Haberman. 2004. Projecting mortality trends: Recent developments in the United Kingdom and the United States. North American Actuarial Journal 8: 56–83. [Google Scholar] [CrossRef]
| 1 | Following Nielsen and Nielsen (2014), the choice of restrictions is of no importance for the resulting forecasts. Other normalizations could be considered; however, this gives an intuitive interpretation of . |
| 2 | We restrict the data to 1950 and onwards as this removes outliers, and we avoid structural changes in the exposure; see Lee and Miller (2001) and Booth et al. (2002). To avoid uncertainty about the death rates, due to a few observations, we further restrict the ages to cover the ages 0 to 95 as is standard in the mortality forecasting literature. |
| 3 | This is also called the Strehler-Mildvan correlation due to Strehler and Mildvan (1960). |
| 4 | This is similar to Lee and Carter (1992) who assumed a homoskedastic error term for the LC model. The i.i.d. homoscedasticity assumption is necessary for the analysis of the present paper, but the assumption may be critical in certain cases—see, e.g., Doz et al. (2011). |
| 5 | This corresponds to the partial correlation squared between the fitted and observed values. |
| 6 | The MCS approach is implemented via the Ox-package Mulcom 3.0 by Hansen and Lunde (2014) in Oxmetrics 7, see Doornik (2013). |
| 7 | For the case with only two models the forecast performance could be tested via the Diebold and Mariano (1995) test, which only allows for pairwise comparisons, whereas the MCS procedure allows for joint multiple model evaluation. |
| 8 | Note that we here use the period life expectancy (within year t), whereas the formula in Brouhns et al. (2002) computes the cohort life expectancy. |
| 9 | These specifications have often been used in studies applying graduation laws of mortality—see Booth and Tickle (2008); McNown and Rogers (1989, 1992). |
| 10 | In preliminary experiments, we also found this specification to give a better forecast performance compared with using other ARIMA models. |
| 11 | The factors are estimated using weighted principal components in the R package Demography—see Hyndman and Ullah (2007) and Hyndman et al. (2014) for further details. All other models are estimated using own codes and the packages ‘tsDyn’, ‘VARS’, and ‘Forecast’ in R (R Core Team 2015) by Pfaff (2008); Stigler (2010) and Hyndman (2015). |

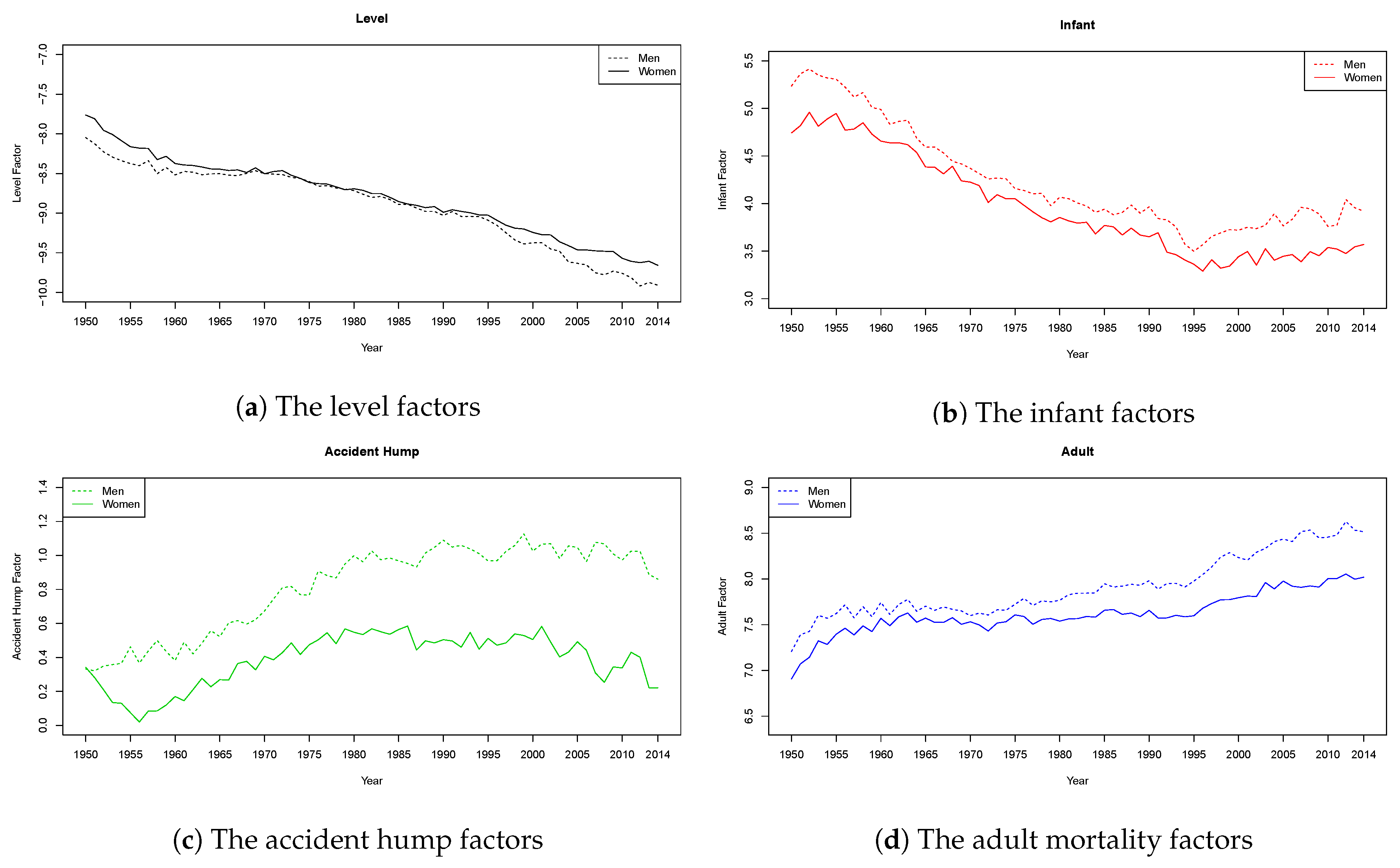


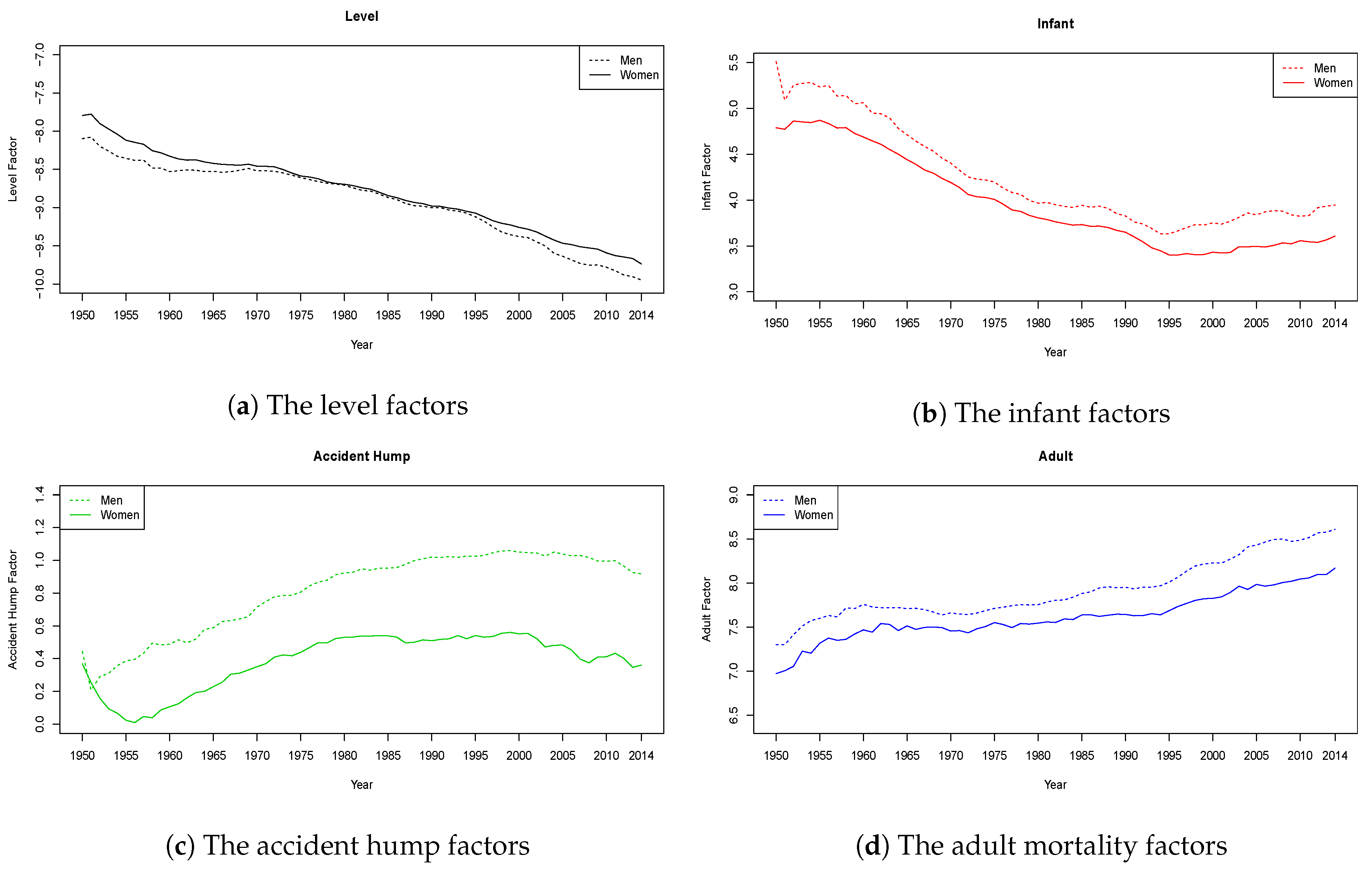

| Men | ||||||
|---|---|---|---|---|---|---|
| k | ||||||
| Fr | Estimate | 0.553 | 11.981 | 1.093 | 20.308 | 0.020 |
| Std. Err | 0.013 | 0.024 | 0.004 | 0.002 | 0.018 | |
| US | Estimate | 0.624 | 10.813 | 1.103 | 20.016 | 0.017 |
| Std. Err | 0.013 | 0.020 | 0.003 | 0.002 | 0.018 | |
| Women | ||||||
| Fr | Estimate | 0.649 | 18.092 | 1.453 | 19.492 | 0.023 |
| Std. Err | 0.013 | 0.060 | 0.003 | 0.005 | 0.018 | |
| US | Estimate | 0.607 | 19.029 | 1.295 | 18.675 | 0.013 |
| Std. Err | 0.010 | 0.042 | 0.003 | 0.004 | 0.018 | |
| USA | ||||
|---|---|---|---|---|
| Men | Women | |||
| Rank | Trace-Test | p-Value | Trace-Test | p-Value |
| 0 | 52.240 | [0.323] | 47.939 | [0.512] |
| 1 | 27.748 | [0.641] | 30.689 | [0.468] |
| 2 | 13.926 | [0.668] | 15.243 | [0.562] |
| 3 | 1.1522 | [0.992] | 3.0677 | [0.858] |
| France | ||||
| 0 | 106.790 | [0.000] ** | 108.730 | [0.000] ** |
| 1 | 56.044 | [0.001] ** | 47.599 | [0.014] * |
| 2 | 28.089 | [0.024] * | 24.893 | [0.064] |
| 3 | 3.642 | [[0.788] | 9.2236 | [0.171] |
| USA | France | |||
|---|---|---|---|---|
| Men and Women | Men and Women | |||
| Rank | Trace-Test | p-Value | Trace-Test | p-Value |
| 0 | 286.700 | [0.000] ** | 287.730 | [0.000] ** |
| 1 | 194.530 | [0.000] ** | 215.400 | [0.000] ** |
| 2 | 139.460 | [0.001] ** | 158.870 | [0.000] ** |
| 3 | 89.751 | [0.041] * | 116.050 | [0.000] ** |
| 4 | 52.267 | [0.321] | 76.354 | [0.002] ** |
| 5 | 34.795 | [0.257] | 47.410 | [0.015] * |
| 6 | 19.806 | [0.240] | 24.016 | [0.082] |
| 7 | 7.897 | [0.268] | 8.524 | [0.218] |
| Men | Women | |||
|---|---|---|---|---|
| USA and France | USA and France | |||
| Rank | Trace-Test | p-Value | Trace-Test | p-Value |
| 0 | 225.130 | [0.000] ** | 221.980 | [0.000] ** |
| 1 | 158.190 | [0.016] * | 152.790 | [0.036] * |
| 2 | 111.620 | [0.113] | 107.810 | [0.178] |
| 3 | 75.429 | [0.311] | 70.517 | [0.490] |
| 4 | 47.924 | [0.513] | 44.325 | [0.679] |
| 5 | 27.275 | [0.668] | 27.285 | [0.667] |
| 6 | 11.364 | [0.850] | 13.676 | [0.688] |
| 7 | 3.867 | [0.759] | 3.686 | [0.783] |
| Men | ||||||
|---|---|---|---|---|---|---|
| k | ||||||
| Fr | Estimate | 0.556 | 12.151 | 1.094 | 20.324 | 0.021 |
| Std. Err | 0.013 | 0.020 | 0.004 | 0.002 | 0.010 | |
| US | Estimate | 0.624 | 10.809 | 1.103 | 20.014 | 0.018 |
| Std. Err | 0.013 | 0.020 | 0.003 | 0.002 | 0.019 | |
| Women | ||||||
| Fr | Estimate | 0.648 | 18.711 | 1.453 | 19.450 | 0.024 |
| Std. Err | 0.013 | 0.048 | 0.003 | 0.004 | 0.018 | |
| US | Estimate | 0.608 | 18.930 | 1.295 | 18.703 | 0.013 |
| Std. Err | 0.010 | 0.043 | 0.003 | 0.004 | 0.005 | |
| France | Men | Women | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Year | 10 Year | 20 Year | 1 Year | 10 Year | 20 Year | ||||||||
| MSE | Pval | MSE | Pval | MSE | Pval | MSE | Pval | MSE | Pval | MSE | Pval | ||
| PFM | VAR1 | 0.098 | 0.000 | 2.493 | 0.022 | 13.480 | 0.000 | 0.164 | 0.000 | 1.719 | 0.000 | 7.529 | 0.000 |
| Arima | 0.103 | 0.001 | 0.967 | 1.000 | 4.147 | 1.000 | 0.071 | 0.002 | 0.144 | 0.233 | 0.370 | 0.920 | |
| VAR1 | 0.095 | 0.006 | 0.985 | 0.931 | 4.611 | 0.146 | 0.086 | 0.001 | 0.157 | 0.013 | 0.444 | 0.415 | |
| VECM2 | 0.095 | 0.002 | 0.986 | 0.931 | 4.511 | 0.087 | 0.082 | 0.000 | 0.138 | 0.233 | 0.439 | 0.484 | |
| VECM2SS | 0.234 | 0.000 | 1.331 | 0.284 | 4.393 | 0.712 | 0.359 | 0.000 | 0.741 | 0.005 | 1.041 | 0.036 | |
| RWD | 0.032 | 0.611 | 1.135 | 0.284 | 5.439 | 0.000 | 0.032 | 1.000 | 0.103 | 1.000 | 0.367 | 1.000 | |
| LC | 0.099 | 0.000 | 1.479 | 0.001 | 6.367 | 0.000 | 0.119 | 0.001 | 0.229 | 0.050 | 0.460 | 0.329 | |
| FDA | 0.030 | 1.000 | 1.085 | 0.875 | 5.436 | 0.002 | 0.037 | 0.301 | 0.410 | 0.134 | 1.581 | 0.329 | |
| USA | Men | Women | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Year | 10 Year | 20 Year | 1 Year | 10 Year | 20 Year | ||||||||
| MSE | Pval | MSE | Pval | MSE | Pval | MSE | Pval | MSE | Pval | MSE | Pval | ||
| PFM | VAR1 | 0.113 | 0.011 | 1.607 | 0.018 | 5.915 | 0.004 | 0.069 | 0.004 | 1.514 | 0.157 | 11.630 | 0.024 |
| Arima | 0.112 | 0.013 | 0.787 | 1.000 | 2.493 | 1.000 | 0.054 | 0.011 | 0.519 | 0.225 | 1.378 | 0.017 | |
| VAR1 | 0.110 | 0.010 | 0.897 | 0.140 | 3.094 | 0.038 | 0.057 | 0.011 | 0.562 | 0.005 | 1.369 | 0.002 | |
| VECM2 | 0.127 | 0.013 | 1.081 | 0.104 | 2.765 | 0.455 | 0.052 | 0.011 | 0.329 | 1.000 | 0.593 | 1.000 | |
| VAR1SS | 0.117 | 0.013 | 1.244 | 0.024 | 3.662 | 0.006 | 0.084 | 0.001 | 0.575 | 0.124 | 1.316 | 0.024 | |
| RWD | 0.035 | 1.000 | 1.240 | 0.104 | 4.016 | 0.000 | 0.023 | 1.000 | 0.435 | 0.225 | 1.243 | 0.011 | |
| LC | 0.138 | 0.013 | 1.771 | 0.018 | 5.375 | 0.001 | 0.080 | 0.006 | 0.682 | 0.069 | 1.790 | 0.003 | |
| FDA | 0.044 | 0.154 | 1.577 | 0.104 | 4.824 | 0.006 | 0.026 | 0.032 | 0.495 | 0.225 | 1.441 | 0.024 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haldrup, N.; Rosenskjold, C.P.T. A Parametric Factor Model of the Term Structure of Mortality. Econometrics 2019, 7, 9. https://doi.org/10.3390/econometrics7010009
Haldrup N, Rosenskjold CPT. A Parametric Factor Model of the Term Structure of Mortality. Econometrics. 2019; 7(1):9. https://doi.org/10.3390/econometrics7010009
Chicago/Turabian StyleHaldrup, Niels, and Carsten P. T. Rosenskjold. 2019. "A Parametric Factor Model of the Term Structure of Mortality" Econometrics 7, no. 1: 9. https://doi.org/10.3390/econometrics7010009
APA StyleHaldrup, N., & Rosenskjold, C. P. T. (2019). A Parametric Factor Model of the Term Structure of Mortality. Econometrics, 7(1), 9. https://doi.org/10.3390/econometrics7010009





