Structural Panel Bayesian VAR Model to Deal with Model Misspecification and Unobserved Heterogeneity Problems
Abstract
1. Introduction
2. Econometric Model and Specifications
2.1. Model Estimation
2.2. Model Features
3. Dynamic Analysis
3.1. Hierarchical Structure for Time-Varying Coefficient Vectors
3.2. Prior Assumptions
3.3. Posterior Distributions and MCMC Implementation
4. Empirical Application
4.1. The Data and the Empirical Model
4.2. Structural Spillovers and Shock Transmission
4.3. Heterogeneity and Interactions during the Crisis Period and Post-Crisis Consolidation
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Agudze, Komla Mawulom, Monica Billio, Roberto Casarin, and Francesco Ravazzolo. 2018. Markov Switching Panel with Network Interaction Effects. CAMP Working Paper Series No 1/2018. Oslo, Norway: Norwegian Business School. [Google Scholar]
- Albert, James H., and Siddhartha Chib. 1993. Bayes inference via gibbs sampling of autoregressive time series subject to markov mean and variance shifts. Journal of Business and Economic Statistics 11: 1–15. [Google Scholar]
- Beetsma, Roel, and Massimo Giuliodori. 2011. The effects of government purchase shocks: Review and estimates for the eu. Economic Journal 121: F4–F32. [Google Scholar] [CrossRef]
- Billio, Monica, Roberto Casarin, Francesco Ravazzolo, and Herman K. Van Dijk. 2016. Interconnections between eurozone and us booms and busts: A bayesian panel markov-switching var model. Journal of Applied Econometrics 31: 1352–70. [Google Scholar] [CrossRef]
- Buti, Marco, Daniele Franco, and Hedwig Ongena. 1998. Fiscal discipline and flexibility in emu: The implementation of the stability and growth pact. Oxford Review of Economic Policy 14: 81–97. [Google Scholar] [CrossRef]
- Canova, Fabio, and Matteo Ciccarelli. 2004. Forecasting and turning point predictions in a bayesian panel var model. Journal of Econometrics 120: 327–59. [Google Scholar] [CrossRef]
- Canova, Fabio, and Matteo Ciccarelli. 2009. Estimating multicountry var models. International Economic Review 50: 929–59. [Google Scholar] [CrossRef]
- Canova, Fabio, Matteo Ciccarelli, and Eva Ortega. 2007. Similarities and convergence in g7 cycles. Journal of Monetary Economics 54: 850–78. [Google Scholar] [CrossRef]
- Canova, Fabio, Matteo Ciccarelli, and Eva Ortega. 2012. Do institutional changes affect business cycles? Journal of Economic Dynamics and Control 36: 1520–33. [Google Scholar] [CrossRef]
- Canova, Fabio, and Jane Marrinan. 1997. Sources and propagation of international output cycles: Common shocks or transmission? Journal of International Economics 46: 133–66. [Google Scholar] [CrossRef]
- Carter, Chris K., and Robert Kohn. 1994. On gibbs sampling for state space models. Biometrika 81: 541–53. [Google Scholar] [CrossRef]
- Chib, Siddhartha. 1995. Marginal likelihood from the gibbs output. Journal of the American Statistical Association 90: 1313–21. [Google Scholar] [CrossRef]
- Chib, Siddhartha. 1996. Calculating posterior distributions and model estimates in markov mixture models. Journal of Econometrics 75: 79–97. [Google Scholar] [CrossRef]
- Chib, Siddhartha, and Edward Greenberg. 1995a. Hierarchical analysis of sur models with extensions to correlated serial errors and time-varying parameter models. Journal of Econometrics 68: 409–31. [Google Scholar] [CrossRef]
- Chib, Siddhartha, and Edward Greenberg. 1995b. Understanding the metropolis-hastings algorithm. The American Statistician 49: 327–35. [Google Scholar]
- Chib, Siddhartha, and Ivan Jeliazkov. 2001. Marginal likelihood from the metropolis–hastings output. Journal of the American Statistical Association 96: 270–81. [Google Scholar] [CrossRef]
- Ciccarelli, Matteo, Eva Ortega, and Maria T. Valderrama. 2018. Commonalities and cross-country spillovers in macroeconomic-financial linkages. Journal of Macroeconomics 16: 231–75. [Google Scholar] [CrossRef]
- Ciccarelli, Matteo, and Alessandro Rebucci. 2007. Measuring contagion using a bayesian time-varying coefficient model. Journal of Financial Econometrics 5: 285–320. [Google Scholar] [CrossRef]
- Cogley, Timothy, and Thomas J. Sargent. 2005. Drifts and volatilities: Monetary policy and outcomes in the post wwii u.s. Review of Economic Dynamics 8: 262–302. [Google Scholar] [CrossRef]
- Crespo-Cuaresma, Jesus, and Octavio Fernandez-Amadorb. 2013. Business cycle convergence in emu: A first look at the second moment. Journal of Macroeconomics 37: 265–84. [Google Scholar] [CrossRef]
- De Mol, Christine, Domenico Giannone, and Lucrezia Reichlin. 2008. Forecasting using a large number of predictors: Is bayesian regression a valid alternative to principal components? Journal of Econometrics 146: 318–28. [Google Scholar] [CrossRef]
- Dees, Stephane, Filippo di Mauro, M. Hashem Pesaran, and L. Vanessa Smith. 2007. Exploring the international linkages of the euro area: A global var analysis. Journal of Applied Econometrics 22: 1–38. [Google Scholar] [CrossRef]
- Degiannakis, Stavros, David Duffy, George Filis, and Alexandra Livada. 2016. Business cycle synchronisation in emu: Can fiscal policy bring member-countries closer? Economic Modelling 52: 551–63. [Google Scholar] [CrossRef]
- Doan, Thomas, Robert Litterman, and Christopher Sims. 1984. Forecasting and conditional projection using realistic prior distributions. Econometric Review 3: 1–100. [Google Scholar] [CrossRef]
- Eichengreen, Barry, and Charles Wyplosz. 1998. The stability pact: More than a minor nuisance? Economic Policy 13: 65–113. [Google Scholar] [CrossRef]
- Facchini, François, Mickael Melki, and Andrew Pickering. 2017. Labour costs and the size of government. Oxford Bulletin of Economics and Statistics 79: 251–75. [Google Scholar] [CrossRef]
- Forni, Mario, Marc Hallin, Marco Lippi, and Lucrezia Reichlin. 2000. The generalized dynami factor model: Identification and estimation. The Review of Economics and Statistics 82: 540–54. [Google Scholar] [CrossRef]
- Giannone, Domenico, Marta Banbura, and Lucrezia Reichlin. 2009. Large bayesian vector auto regressions. Journal of Applied Econometrics 25: 71–92. [Google Scholar]
- Gordon, Roger H., and A. Bovenberg. 1996. Why is capital so immobile internationally? possible explanations and implications for capital income taxation. The American Economic Review 86: 1057–75. [Google Scholar]
- Kadiyala, K. Rao, and Sune Karlsson. 1997. Numerical methods for estimation and inference in bayesian var models. Journal of Applied Econometrics 12: 99–132. [Google Scholar] [CrossRef]
- Kaufmann, Sylvia. 2010. Dating and forecasting turning points by bayesian clustering with dynamic structure: A suggestion with an application to austrian data. Journal of Applied Econometrics 25: 309–44. [Google Scholar] [CrossRef]
- Kaufmann, Sylvia. 2015. K-state switching models with time-varying transition distributions. does loan growth signal stronger effects of variables on inflation? Journal of Econometrics 187: 82–94. [Google Scholar] [CrossRef]
- Koop, Gary. 1996. Parameter uncertainty and impulse response analysis. Journal of Econometrics 72: 135–49. [Google Scholar] [CrossRef]
- Krolzig, Hans-Martin. 1997. Markov Switching Vector Autoregressions: Modelling, Statistical Inference and Application to Business Cycle Analysis. Berlin, Germany: Springer. [Google Scholar]
- Krolzig, Hans-Martin. 2000. Predicting Markov-Switching Vector Autoregressive Processes. Nuffield College Economics Working Papers 2000-WP31. Oxford, UK: Nuffield College Oxford University. [Google Scholar]
- Lane, Philip R., and Gian Maria Milesi-Ferretti. 2007. The external wealth of nations mark ii: Revised and extended estimates of foreign assets and liabilities, 1970–2004. Journal of International Economics 73: 223–50. [Google Scholar] [CrossRef]
- Litterman, Robert B. 1985. Ljung, l. and soderstrom, t. Automatica 21: 25–38. [Google Scholar]
- Litterman, Robert B. 1986. Forecasting with bayesian vector autoregressions five years of experience. Journal of Business and Economic Statistics 4: 25–38. [Google Scholar]
- Mastrogiacomo, Mauro, Nicole M. Bosch, Miriam D. Gielen, and Egbert L. Jongen. 2017. Heterogeneity in labour supply responses: Evidence from a major tax reform. Oxford Bulletin of Economics and Statistics 79: 769–96. [Google Scholar] [CrossRef]
- Pesaran, Hashem M., and Yongcheol Shinb. 1998. Generalized impulse response analysis in linear multivariate models. Economics Letters 58: 17–29. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Til Schuermann, and Scott M. Weiner. 2004. Modelling regional interdependencies using a global error correcting macroeconometric model. Journal of Business and Economic Statistics 22: 129–62. [Google Scholar] [CrossRef]
- Reinhart, Carmen M., and Kenneth S. Rogoff. 2009. The aftermath of financial crises. American Economic Review 99: 466–72. [Google Scholar] [CrossRef]
- Sims, Christopher A., and Tao Zha. 1998. Bayesian methods for dynamic multivariate models. International Economic Review 39: 949–68. [Google Scholar] [CrossRef]
- Sims, Christopher A., and Tao Zha. 2006. Were there regime switches in U.S. monetary policy? American Economic Review 96: 54–81. [Google Scholar] [CrossRef]
- Sorensen, Bent E., and Oved Yosha. 1998. International risk sharing and european monetary unification. Journal of International Economics 45: 211–38. [Google Scholar] [CrossRef]
| 1 | Hidden or Latent factors are variables that are not directly observed but are rather inferred from other variables that are observed and, hence, directly measured. |
| 2 | To be more precise, if the elements of , , and are stacked over i, it is possible to obtain matrices that are not block-diagonal for at least some l. |
| 3 | The vec operator transforms a matrix into a vector by stacking the columns of the matrix, one underneath the other. |
| 4 | A proxy variable is an easily measurable variable that is used in place of a variable that cannot be (directly) measured or is difficult to measure. |
| 5 | The Wishart distribution is a multivariate extension of distribution and, in Bayesian statistics, corresponds to the conjugate prior of the inverse-covariance matrix of a multivariate normal random vector. |
| 6 | The Gamma Distribution is a two-parameter family of continuous probability distributions that provides the probabilities of occurrence of different possible outcomes in an experiment. |
| 7 | For instance, the Minnesota priors are based on an approximation that involves replacing with an estimate, . See, e.g., Doan et al. (1984) and Litterman (1986). |
| 8 | These implementations do not allow for the use of the Minnesota prior since its covariance matrix is written in terms of blocks that vary across equations. |
| 9 | See, e.g., Chib and Greenberg (1995b). |
| 10 | The component corresponds to the sum of and . |
| 11 | Own computations. |
| 12 | The conditional projection for output growth is the one that the model would have obtained over the same period conditionally on the actual path of unexpected shock for that period. |
| 13 | The unconditional projection is the one that the model would obtain for output growth for that period only on the basis of historical information, and it is consistent with a model-based forecast path for the other variables. |
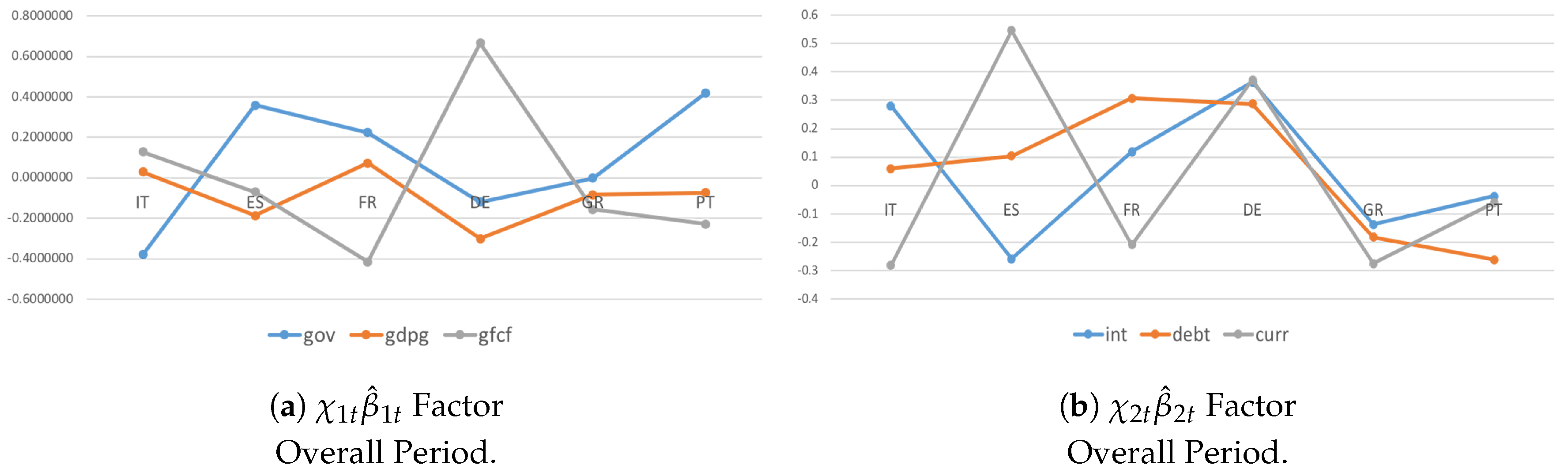
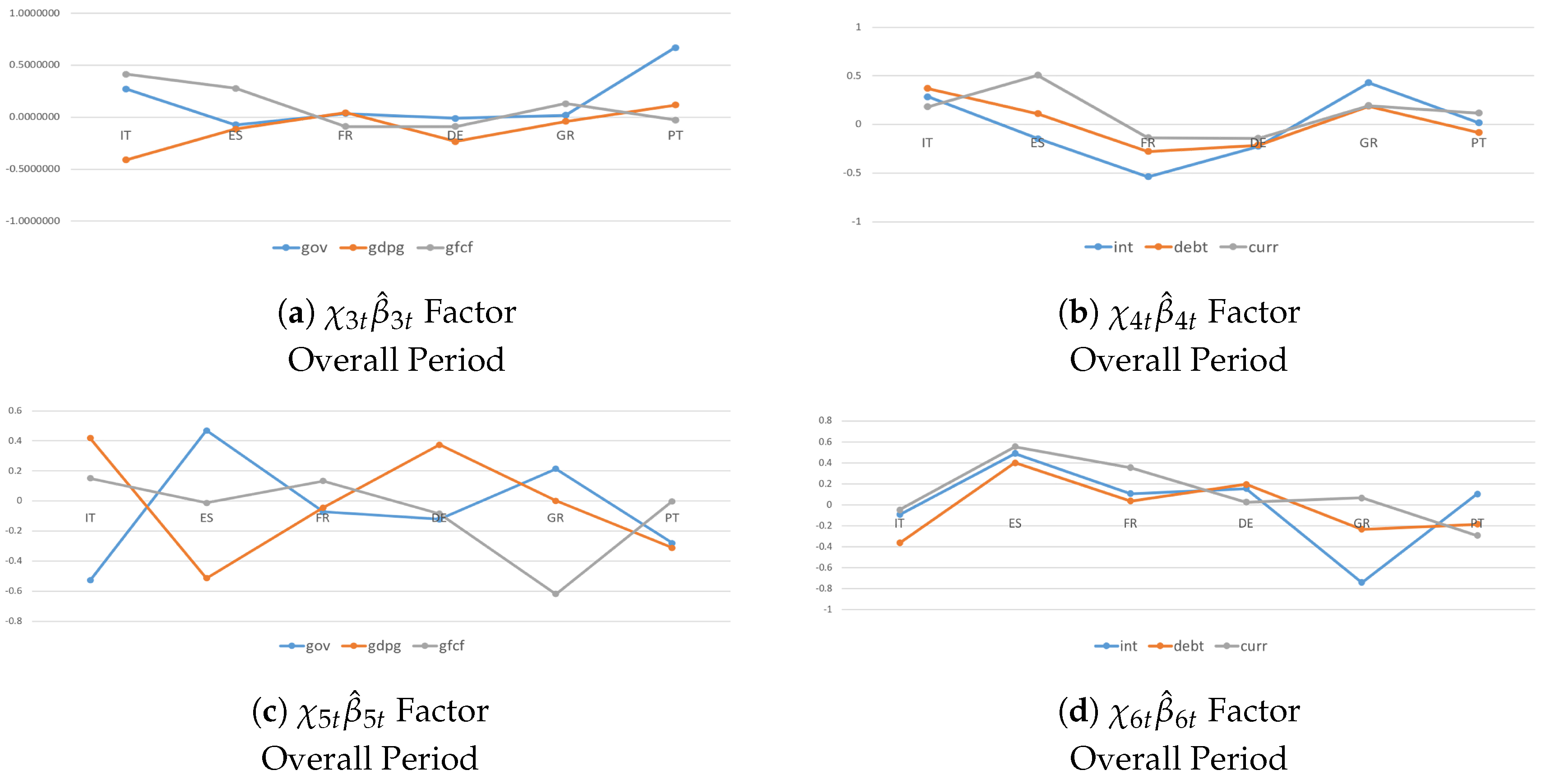
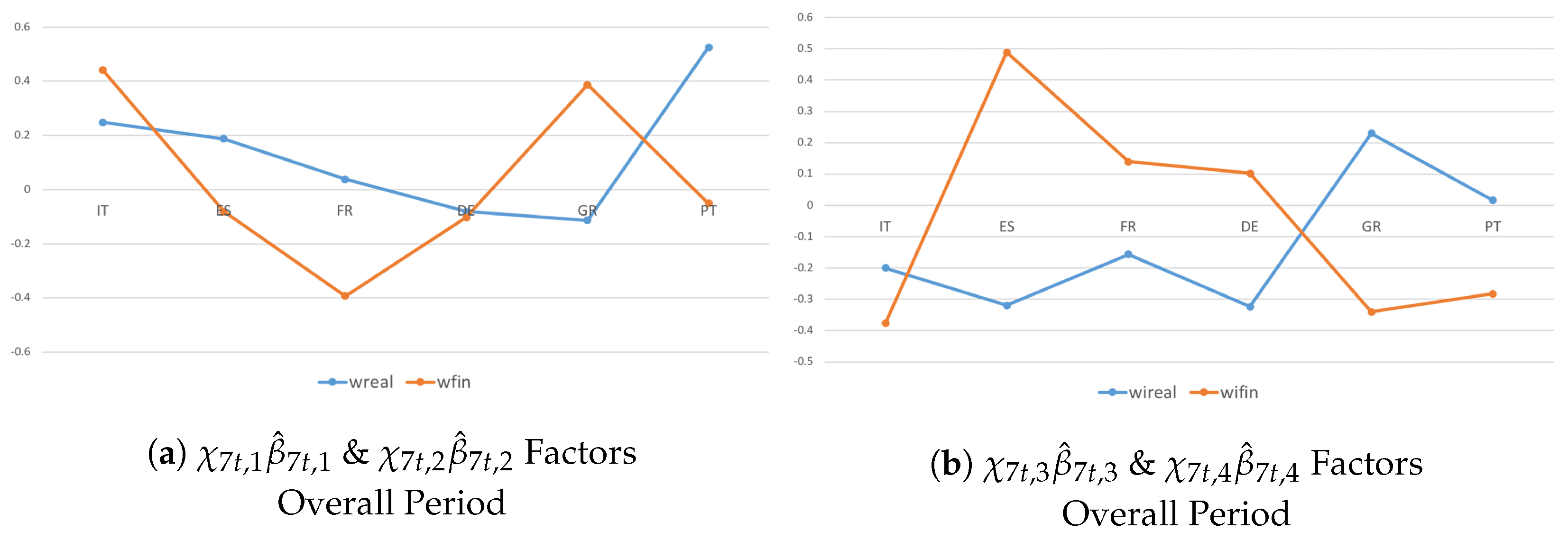
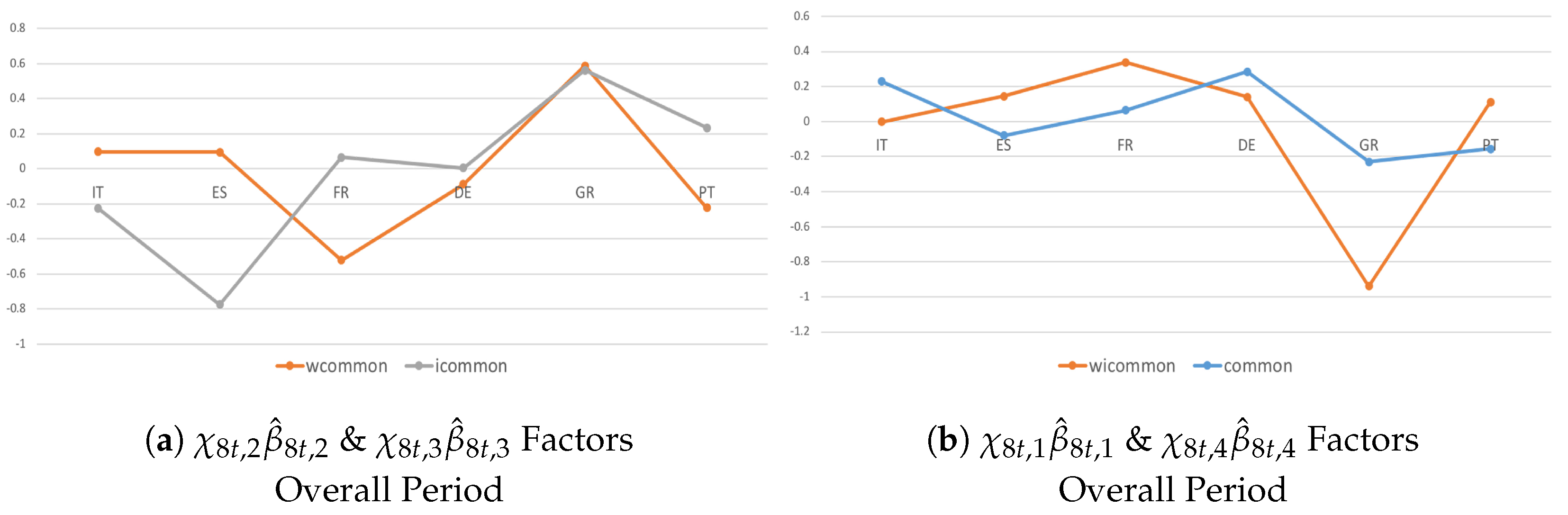
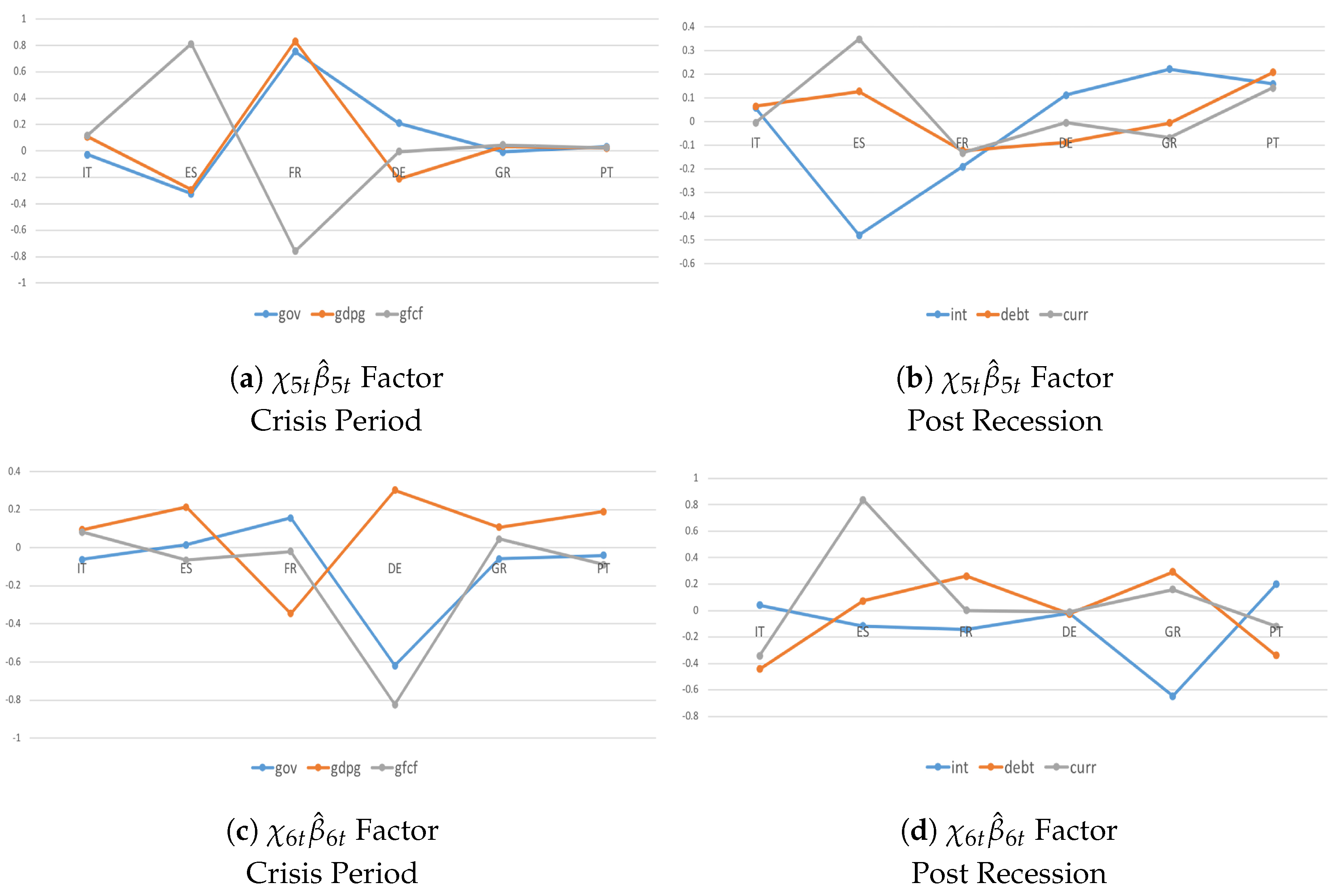
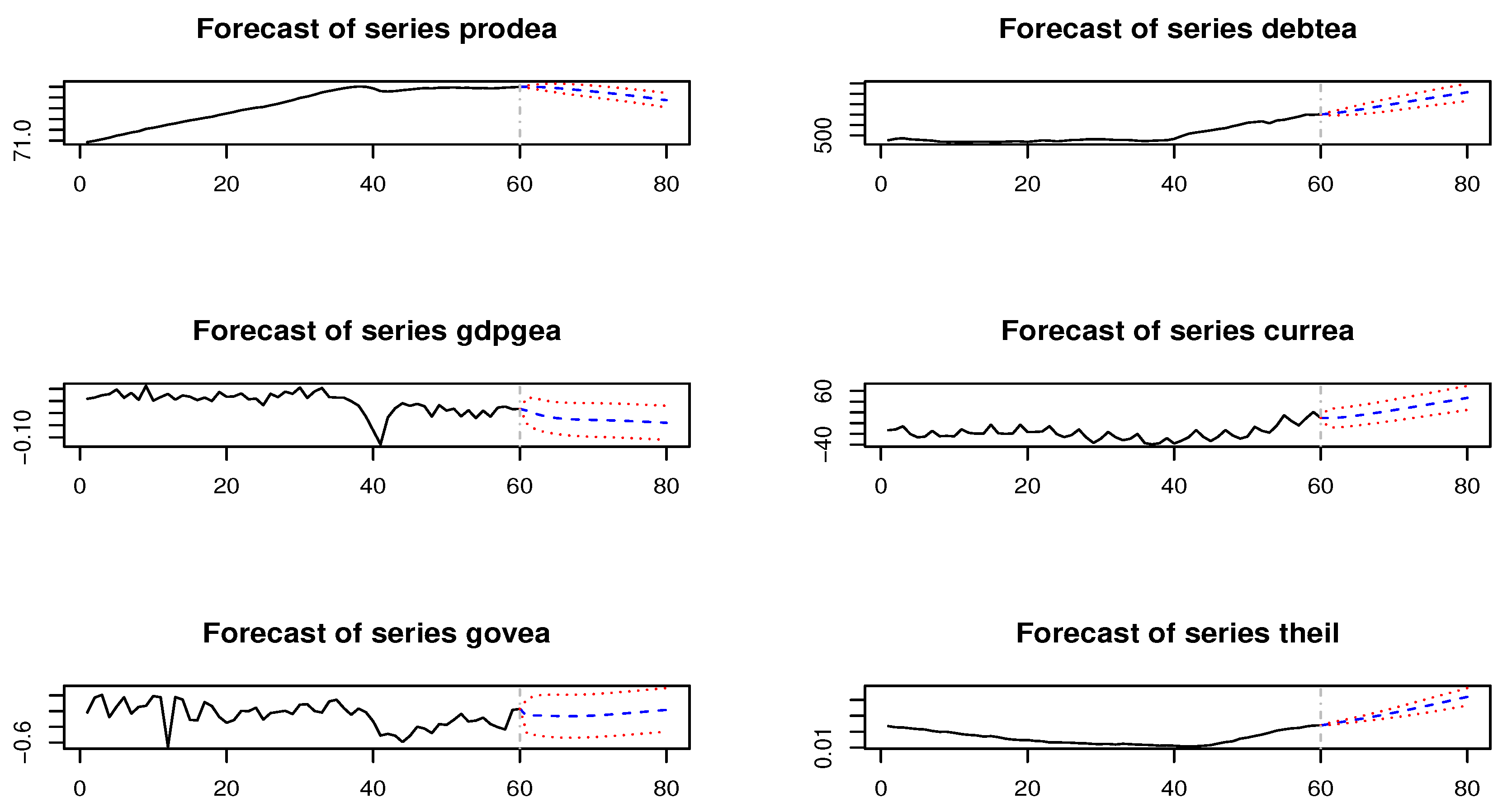
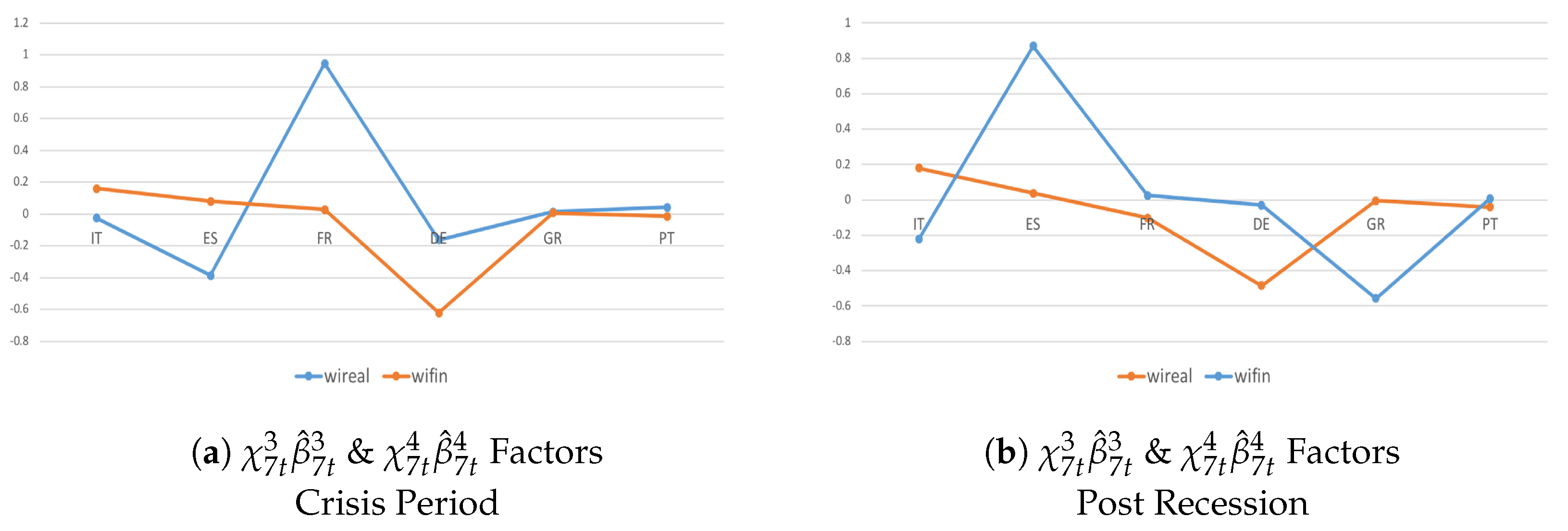
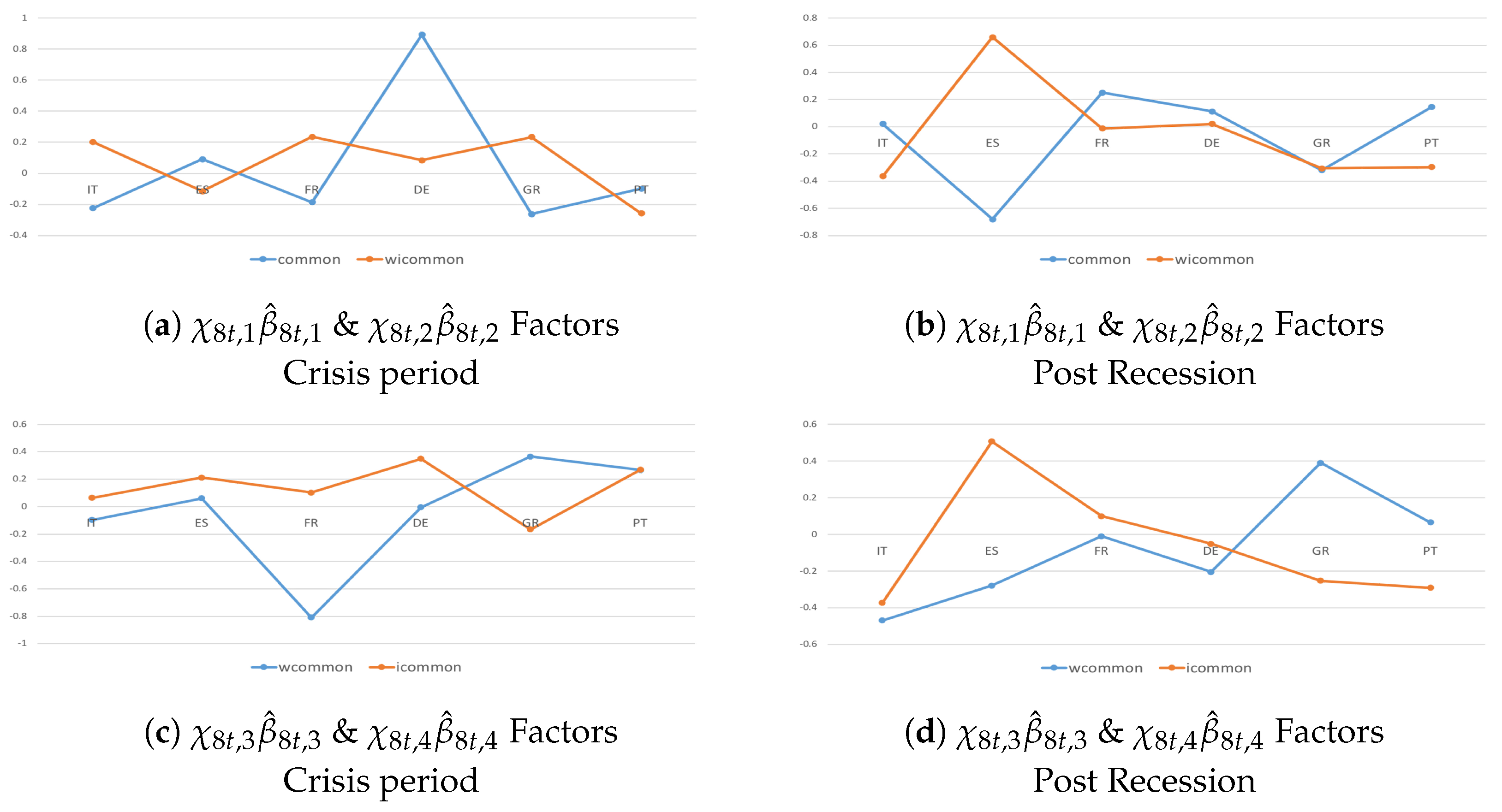
| Test | Test Statistics | Degrees of Freedom | p-Value |
|---|---|---|---|
| 5665 | 2430 | 0.00 | |
| 526.51 | 540 | 0.6531 | |
| 29.41 | 12 | 0.00342 |
| Shock/Response | … | To Others | |||
|---|---|---|---|---|---|
| … | |||||
| … | |||||
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ | ⋮ |
| … | |||||
| From Others | … |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacifico, A. Structural Panel Bayesian VAR Model to Deal with Model Misspecification and Unobserved Heterogeneity Problems. Econometrics 2019, 7, 8. https://doi.org/10.3390/econometrics7010008
Pacifico A. Structural Panel Bayesian VAR Model to Deal with Model Misspecification and Unobserved Heterogeneity Problems. Econometrics. 2019; 7(1):8. https://doi.org/10.3390/econometrics7010008
Chicago/Turabian StylePacifico, Antonio. 2019. "Structural Panel Bayesian VAR Model to Deal with Model Misspecification and Unobserved Heterogeneity Problems" Econometrics 7, no. 1: 8. https://doi.org/10.3390/econometrics7010008
APA StylePacifico, A. (2019). Structural Panel Bayesian VAR Model to Deal with Model Misspecification and Unobserved Heterogeneity Problems. Econometrics, 7(1), 8. https://doi.org/10.3390/econometrics7010008





