Financial Big Data Solutions for State Space Panel Regression in Interest Rate Dynamics
Abstract
1. Introduction
1.1. Multifactor Models for Yield Curve Dynamics
1.2. Feature Extraction Methods for Financial Data
1.3. Contributions and Structure
2. International Macroeconomic and Financial Big Datasets
- Domestic economies:
- Germany (DE), France (FR), Portugal (PO), Spain (ES), Italy (IT), Ireland (IR) and the United Kingdom (GB);
- International economies:
- Japan (JP), United States (U.S.), Australia (AU), Brazil (BR) and South Africa (SA).
- GOV:
- the panel valued time series, which measure the interactions between country-specific sovereign yield curves;
- INF:
- the panel valued time series, which measures the influence of country-specific inflation risks represented by inflation-linked yield curves and Consumer Price Indexes;
- PRD:
- the time series that measures the influence of country-specific productivity proxies represented by Gross Domestic Product (GDP), unemployment rates and Labour productivity;
- FX:
- the time series that measures the interactions between leading foreign exchange markets and the Euro Zone market given by exchange rates for the Euro (EUR) and Japanese Yen (JPY), United States dollar (USD) and Australian dollar (AUD);
- LIQ:
- the time series that serves as a proxy of Euro Zone liquidity represented by 3M Euro Repo and Euribor rates and German Bund Open Interest;
- CR:
- the time series that are used as proxies of the credit quality of the Euro Zone given by the 5YMarkit Intraxx Index.
3. Novel Feature Extraction via Probabilistic Principal Component Methods Using the t-Student Formulation
3.1. Introduction to Probabilistic Principal Component Analysis
3.2. t-Student Principal Component Analysis
3.3. Novel Extension of Probabilistic Principal Component Analysis for a Missing Data Setting
4. EM Algorithm for the Probabilistic Principal Component with t-Student Distribution
- Step 1:
- Expectation step (E-step):The expectation of the conditional distribution over the logarithm of the joint probability function of the observed and hidden variables of the model (1) given N realisations of the variables as a function of the two vectors with static parameters and , that is:
- Step 2:
- Maximisation step (M-step):Re-estimation of the vector of static parameters is carried out via maximisation of the resulting function Q with respect to the vector :
4.1. EM Algorithm for the Probabilistic Principal Component with the Independent t-Student Distribution in the Presence of Missing Data
4.2. EM Algorithm for the Probabilistic Principal Component with the Identical and Conditionally Independent t-Student Distribution in the Presence of Missing Data
5. Multifactor Model with Macroeconomic Factors for the EUR Libor Yield Curve
5.1. The Dynamic Nelson–Siegel Model
5.2. Extending the Dynamic Nelson–Siegel to the Macroeconomic Factor Model
5.3. Estimation Based on the Kalman Filter
5.3.1. Kalman Filter Estimation of Missing Data
5.4. Model Selection Methodology for the Nelson–Siegel Class of Models
| Model 1: diagonal | Model 3: diagonal , | |
| Model 2: diagonal , | Model 4: diagonal . |
6. Feature Extraction Using Cross-Country Macroeconomic Datasets
- D2
- the country-specific government yield curves for countries listed in Table S2 in Appendix A in the Supplementary Material;
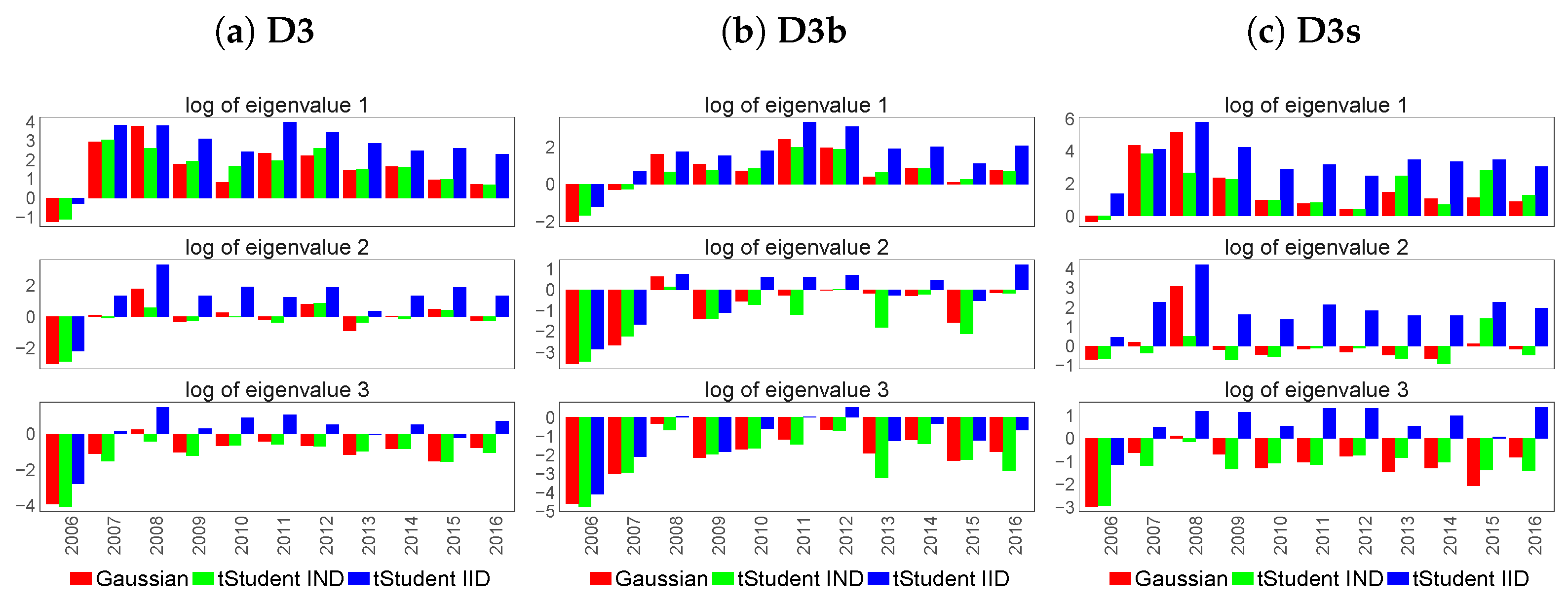
- D3
- the set of country-specific inflation-linked sovereign yield curves for Germany, France, the United Kingdom, Italy, Japan and the United States of America, mixed with inflation-linked swap curves for countries in which inflation-linked government instruments are not available, that is Australia and Spain;
- D3b
- the set of country-specific inflation-linked sovereign yield curves;
- D3s
- the set of country-specific inflation-linked swap curves;
- D4
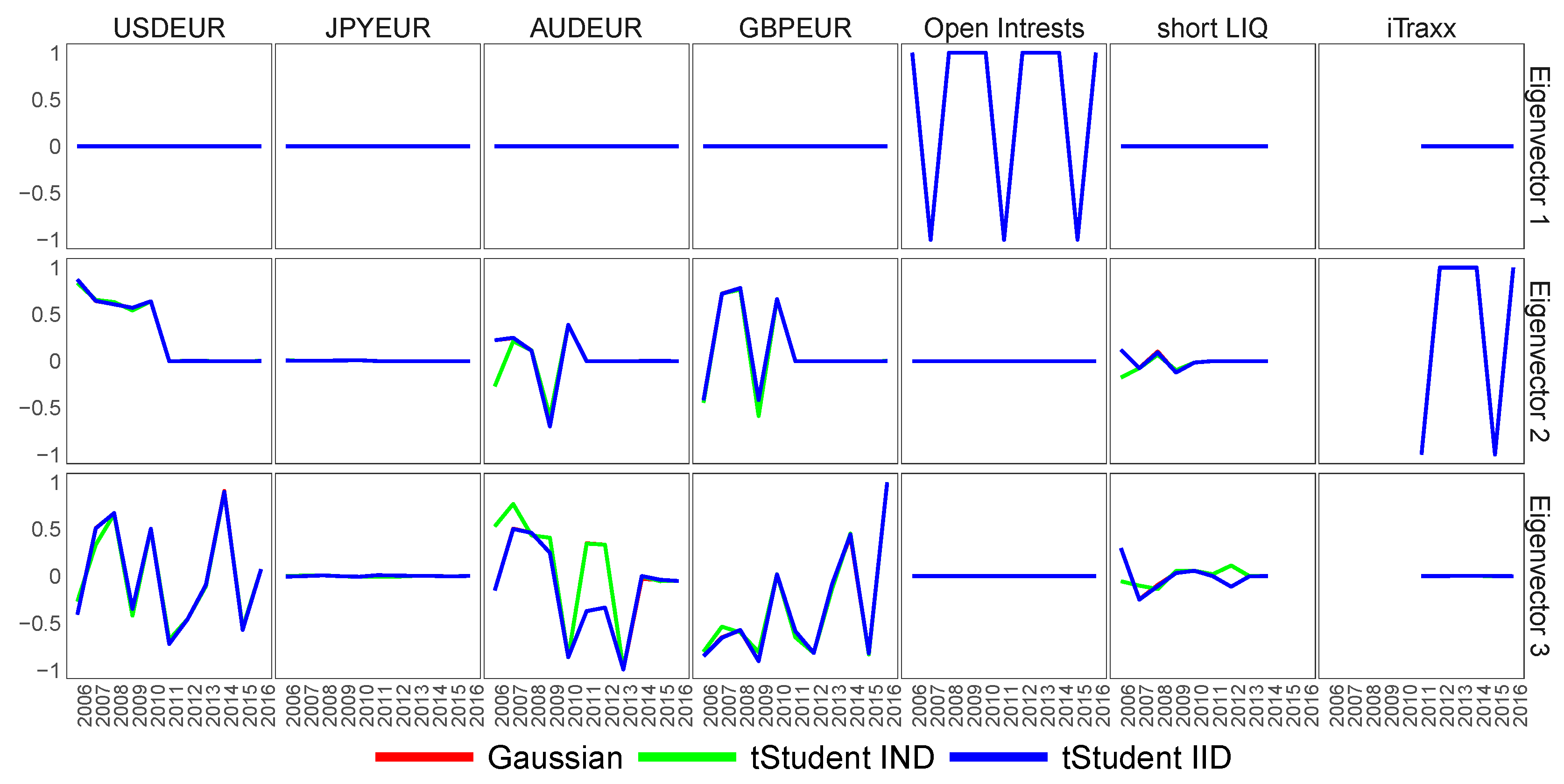
- the set of the Euro Zone activity proxies: the four FX rates against EUR: AUDEUR, JPYEUR, GBPEUR and USDEUR; the proxies for Euro Zone liquidity risk: the open interest of the front future contract on Euro Bund and the spread between three-month Euribor and three-month Euro Repo rate; and the proxy for the credit risk of the Euro Zone: the 5Y Markit iTraxx Index.
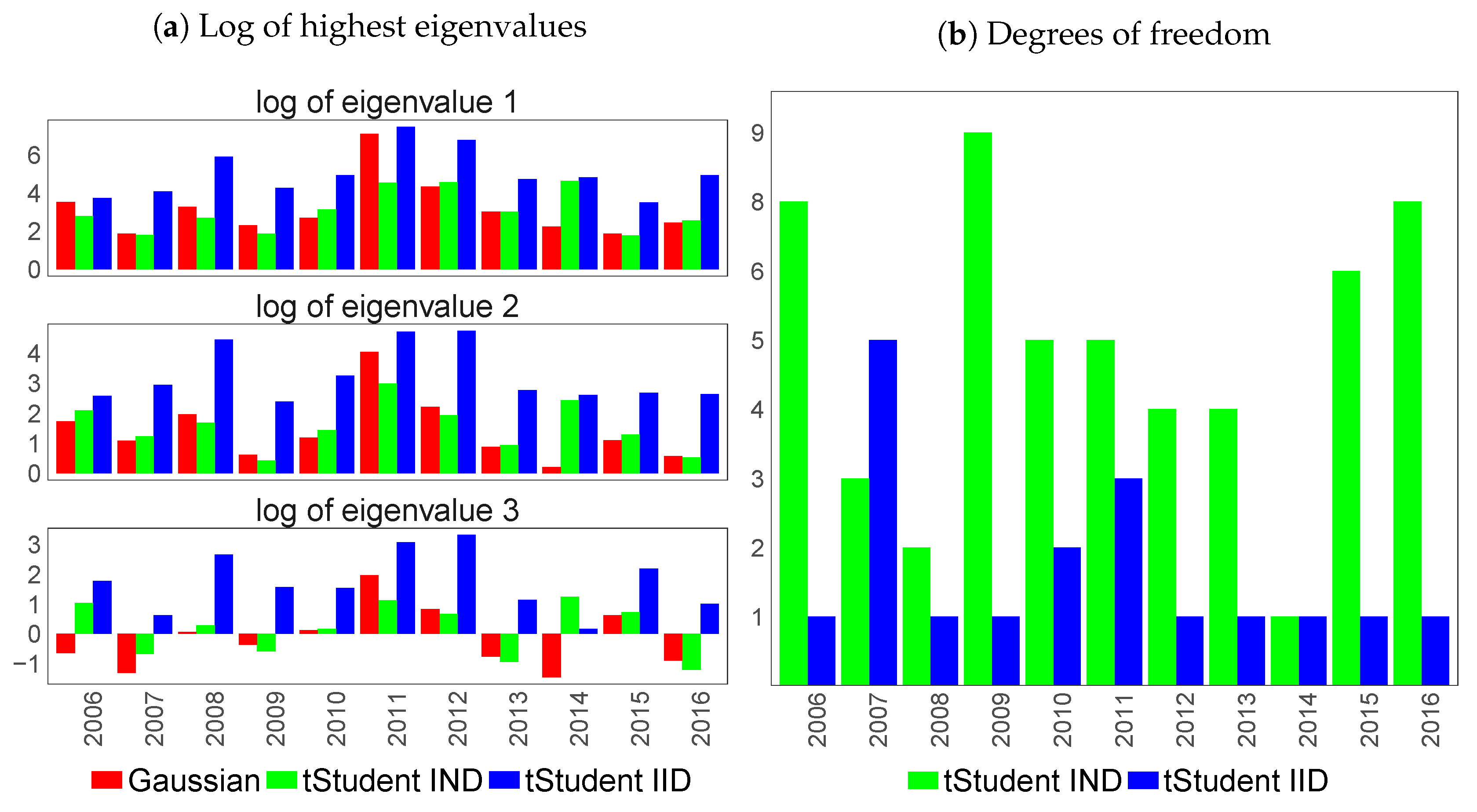
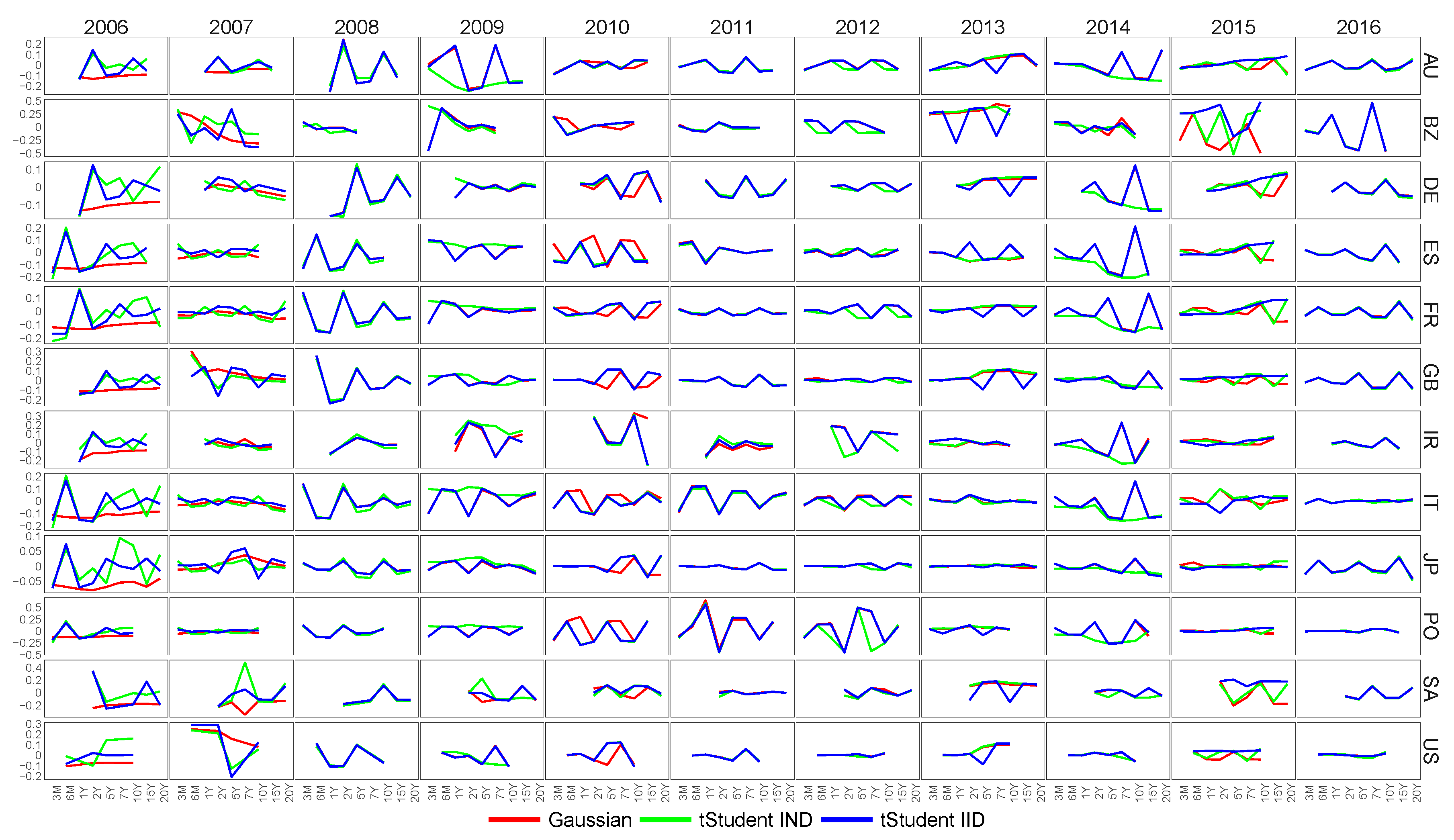
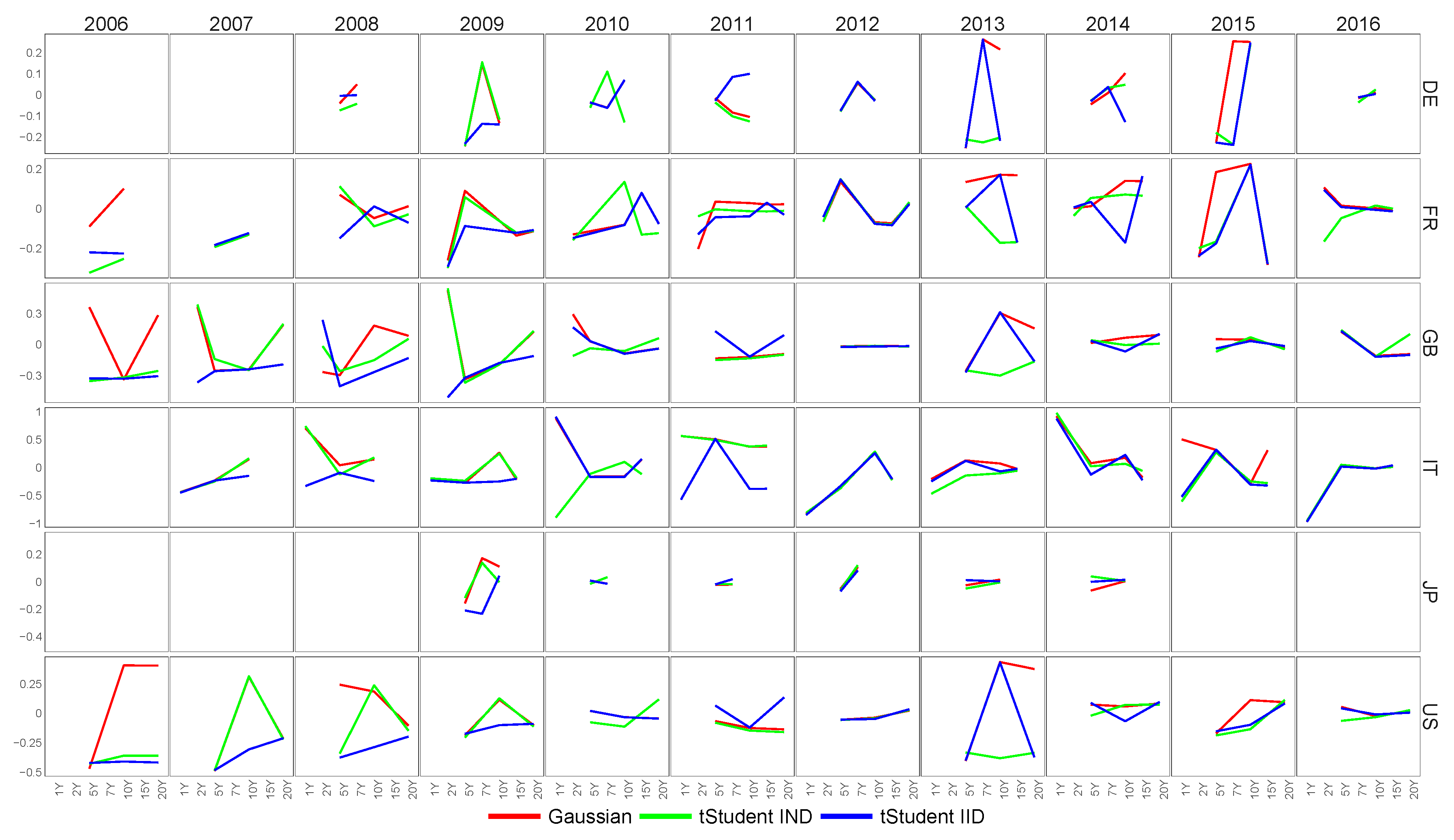
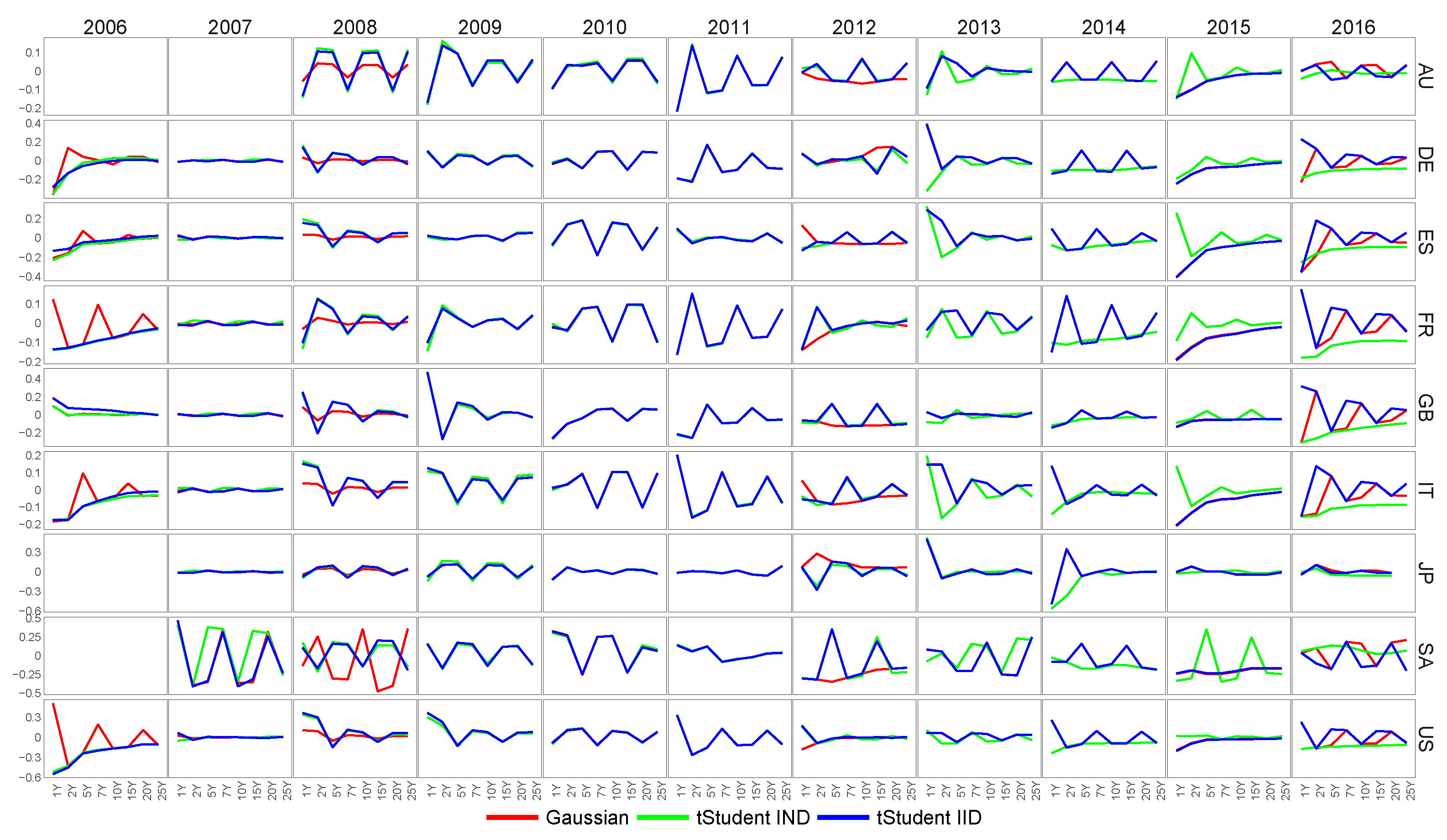
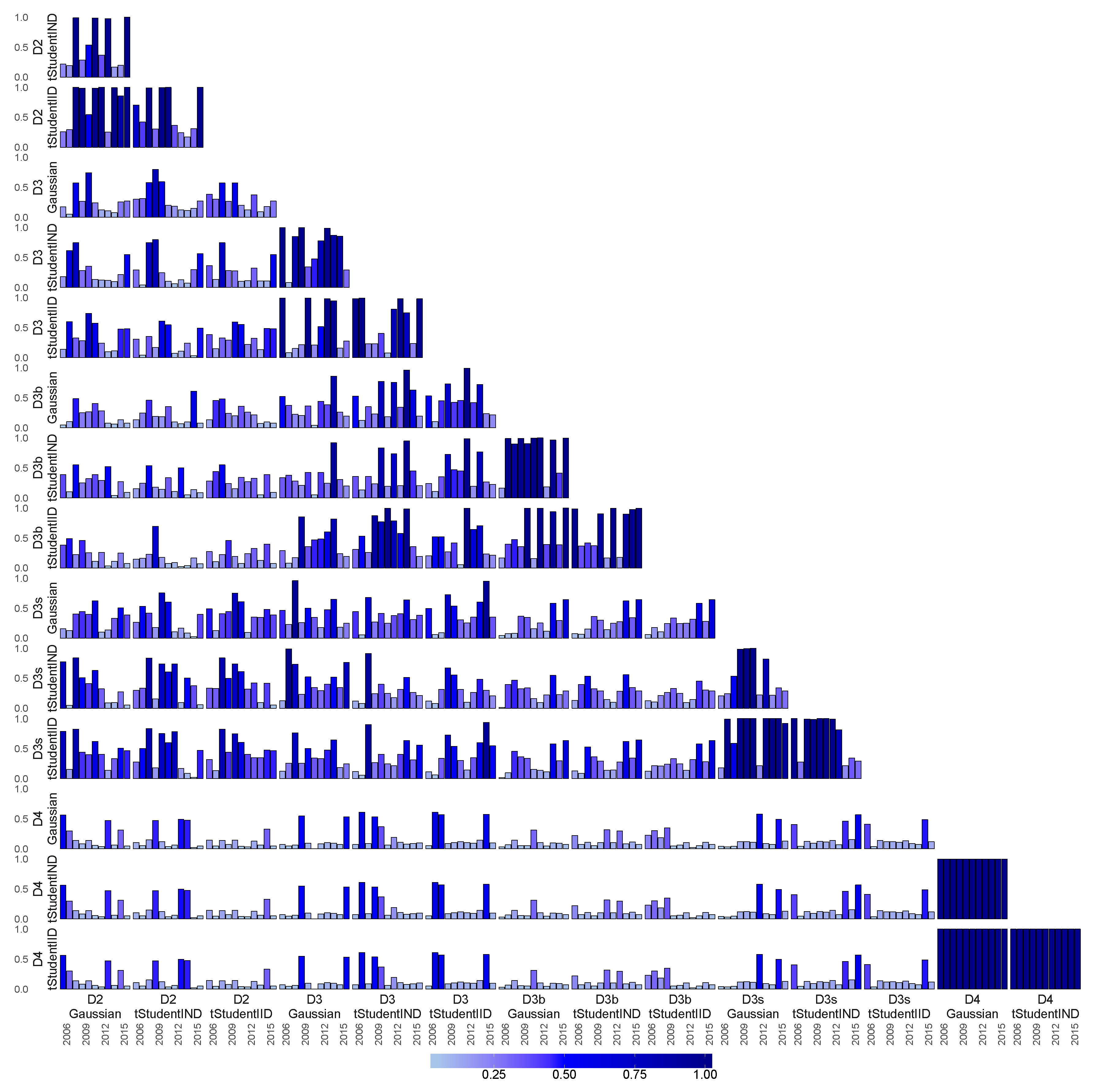
6.1. Feature Extraction for Country-Specific Sovereign Yield Curves
6.2. Feature Extraction for Country-Specific Inflation-Linked Yield Curves
6.3. Feature Extraction for Macroeconomic Proxies of Euro Zone Activity
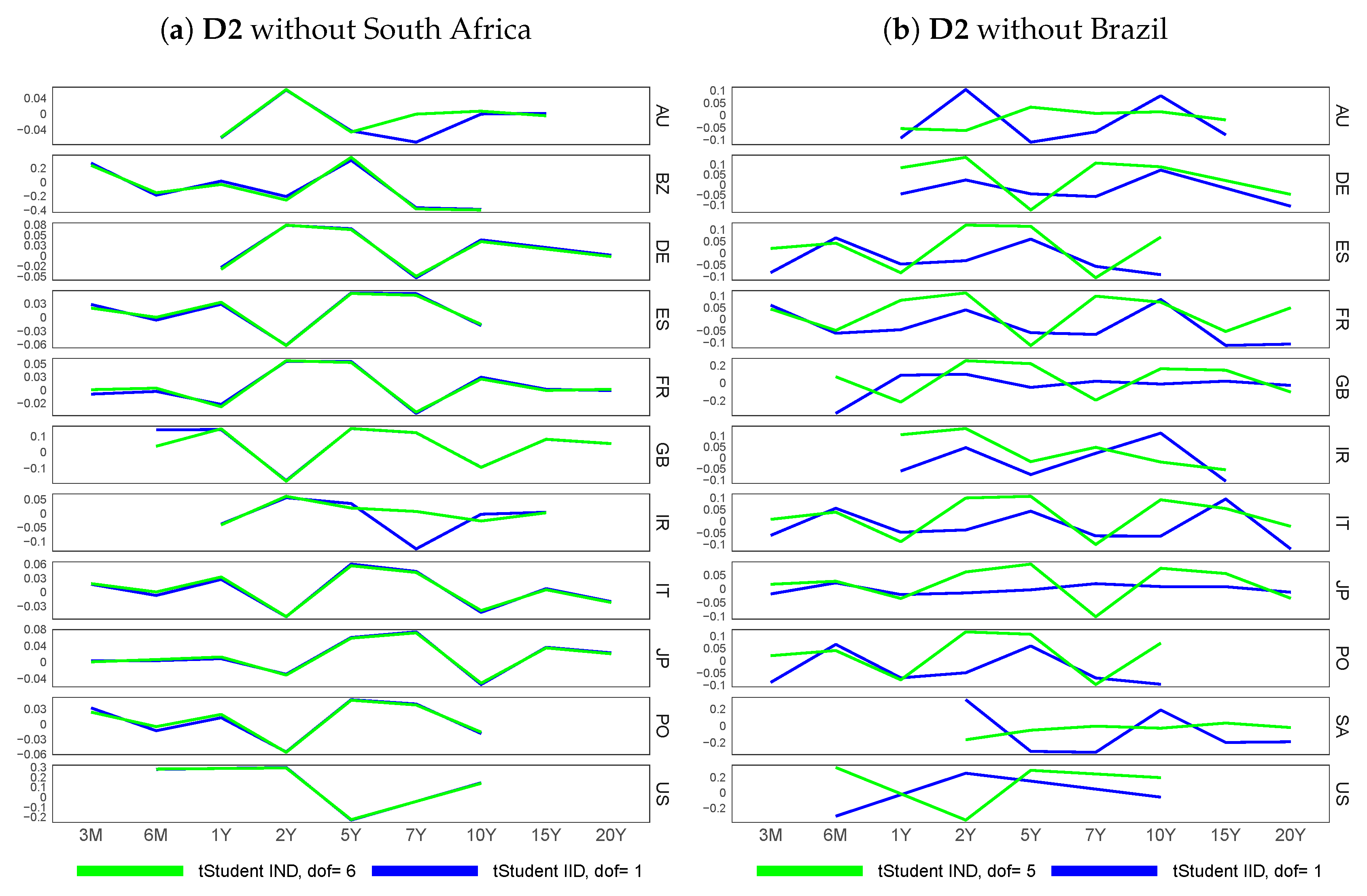
6.4. Similarity of Extracted Features across Various Financial Datasets
7. Hybrid Multi-Factor Dynamic Nelson–Siegel Yield Curve Model of Euro Libor
7.1. The Specification of the Optimal Models for EUR Libor Yield Dynamic Analysis
- 1. minAIC
- We select two standard Nelson–Siegel models with different restrictions on the static parameters that provided the lowest AIC;
- 2. diagAll
- We choose two models with a low complexity (the number of parameters to estimate) per year: the matrices of the model (10) are all diagonal; the covariance matrix is heterogeneous; the covariance matrix is heterogeneous or homogeneous.
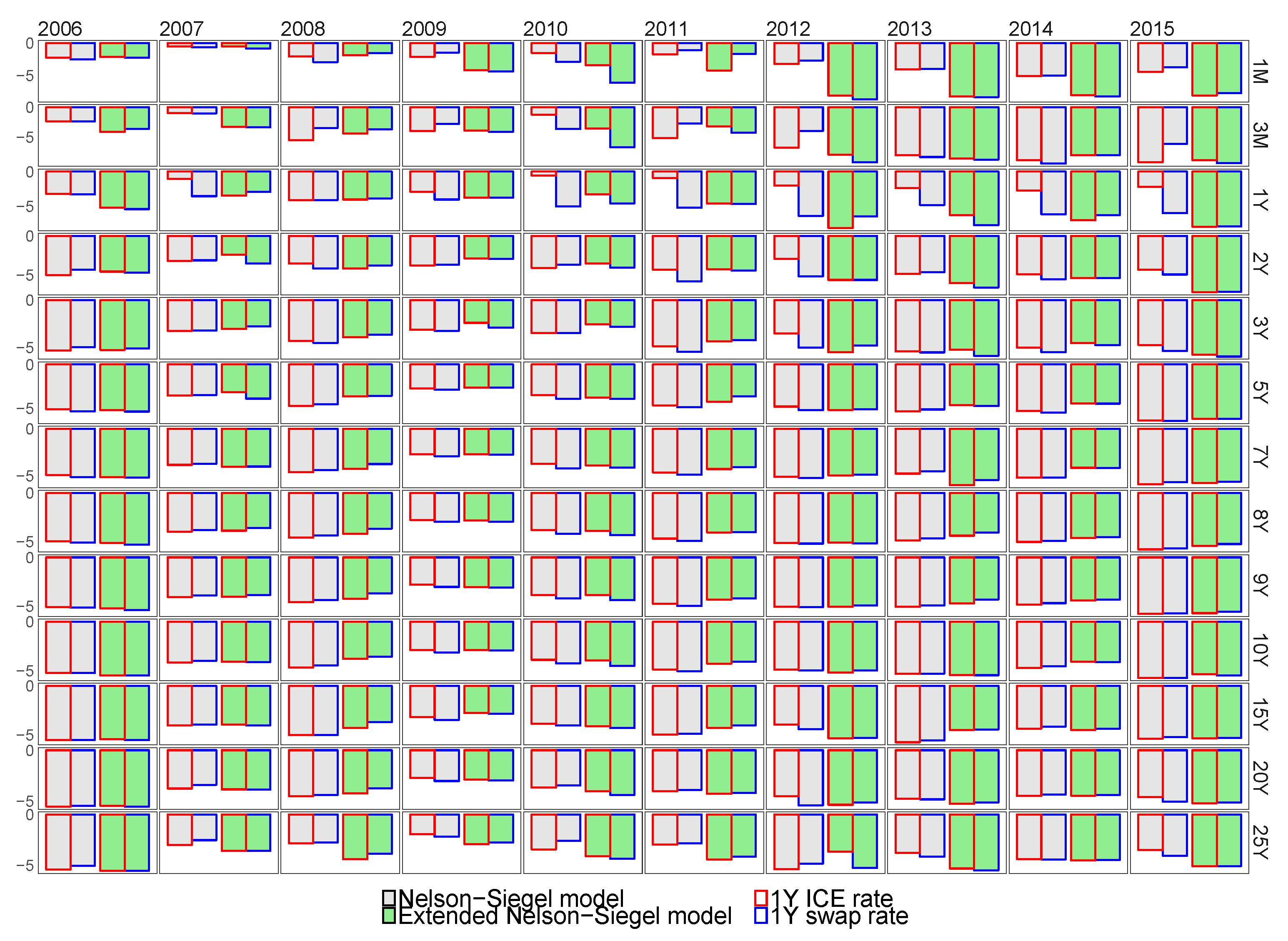
7.2. The Comparison of the Baseline Model Selection Methodologies
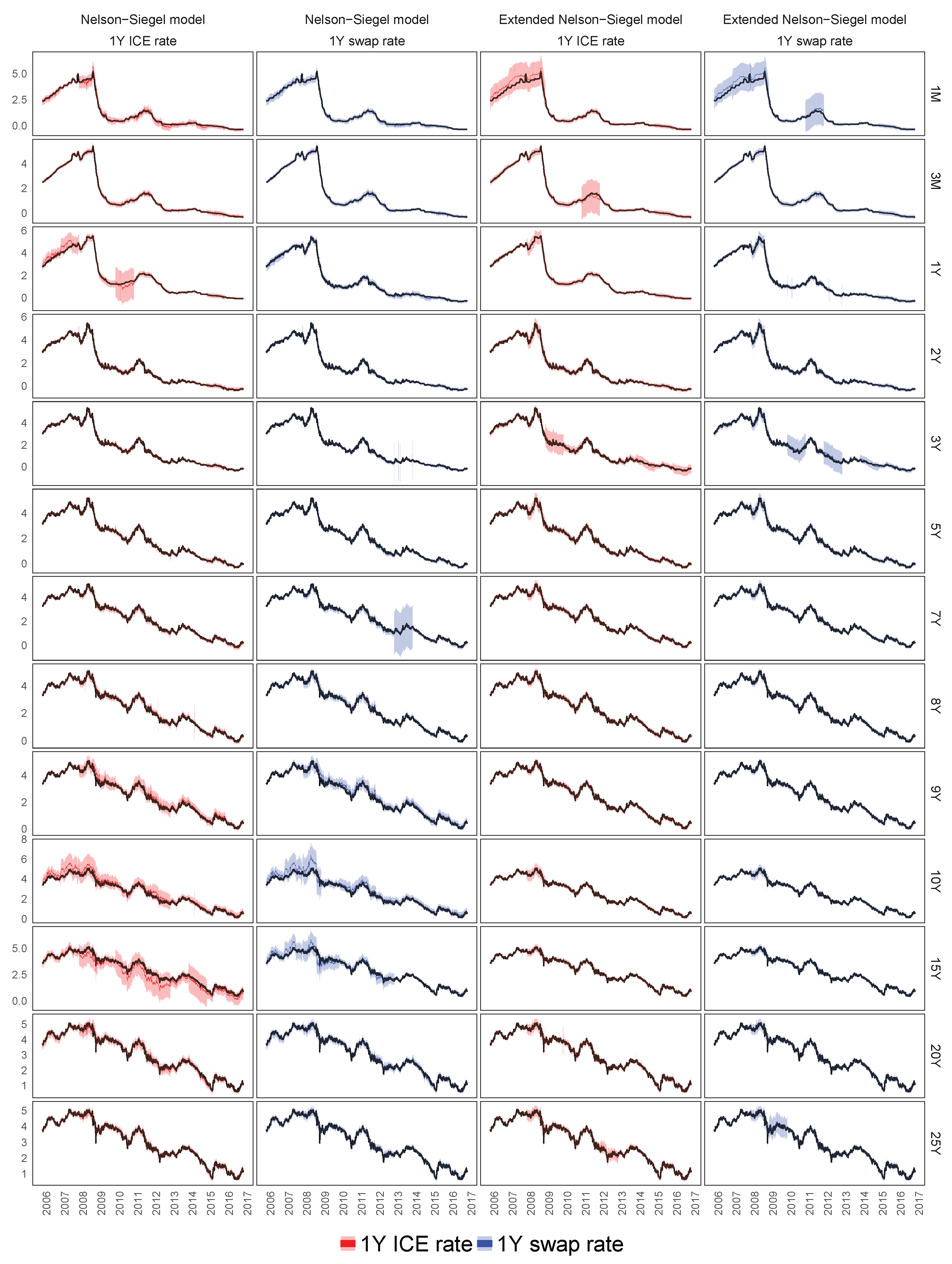
7.3. In-Sample Fit of the Best Models for the Euro Libor Yield Curve
7.3.1. The Calibration of the Euro Libor Yield Curve Using the 1Y ICE Euro Libor or 1Y Swap Rates
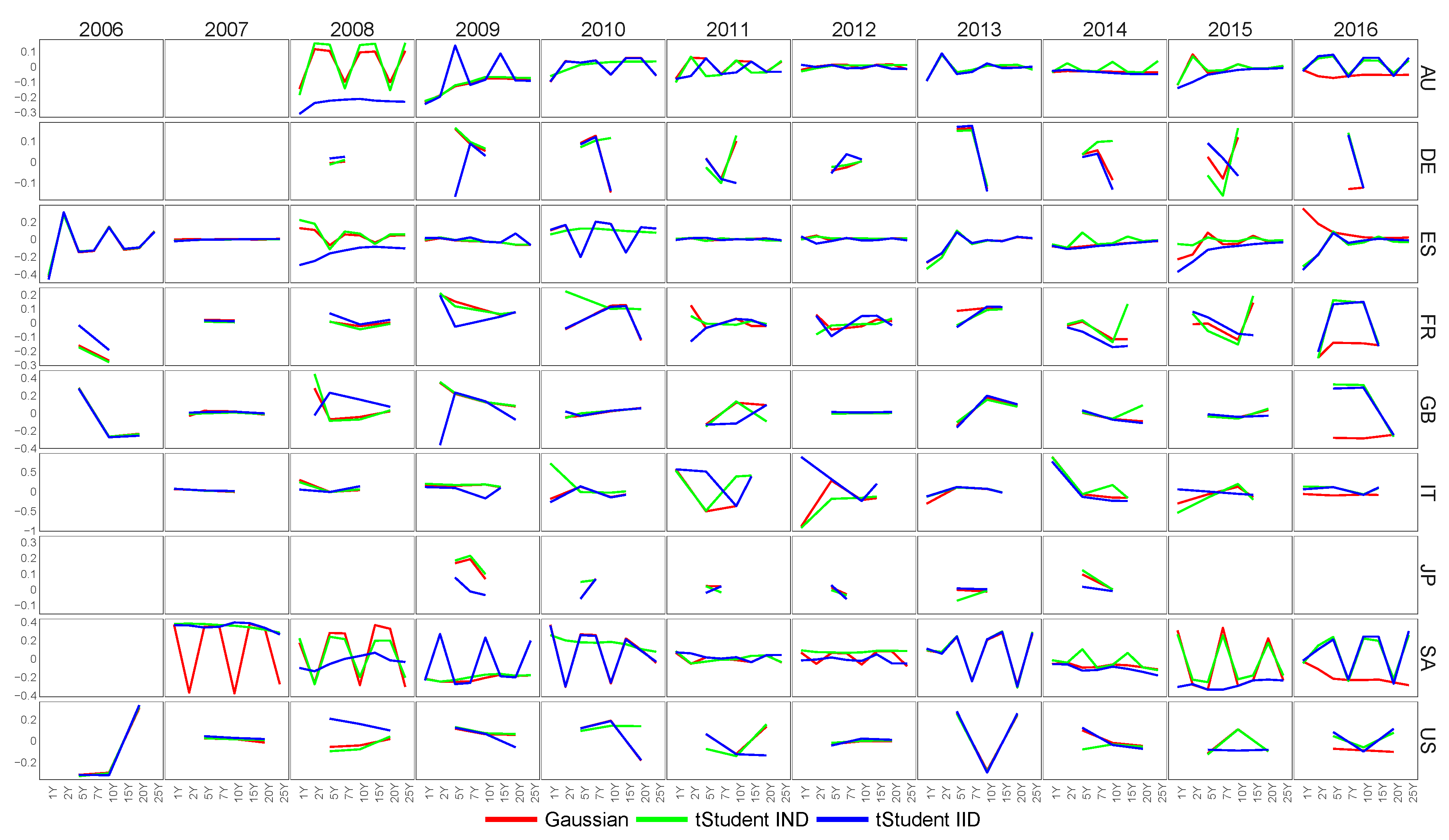
7.3.2. Filtering of Latent Variables
7.4. Forecasting Performance of the Extended Nelson–Siegel Models with Macroeconomic Factors
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbritti, Mirko, Salvatore Dell’Erba, Antonio Moreno, and Sergio Sola. 2013. Global Factors in the Term Structure of Interest Rates. Washington, DC: International Monetary Fund. [Google Scholar]
- Akaike, Hirotogu. 1973. Information theory and an extension of the maximum likelihood principle. Paper presented at 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, September 2–8. [Google Scholar]
- Ang, Andrew, and Monika Piazzesi. 2003. A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables. Journal of Monetary Economics 50: 745–87. [Google Scholar] [CrossRef]
- Archambeau, Cédric, Nicolas Delannay, and Michel Verleysen. 2006. Robust Probabilistic Projections. Paper presented at the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, June 25–29; pp. 33–40. [Google Scholar]
- Armano, Giuliano, Michele Marchesi, and Andrea Murru. 2005. A hybrid genetic-neural architecture for stock indexes forecasting. Information Sciences 170: 3–33. [Google Scholar] [CrossRef]
- Bianchi, Francesco, Haroon Mumtaz, and Paolo Surico. 2009. Dynamics of the Term Structure of UK Interest Rates. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Borovykh, Anastasia, Sander Bohte, and Cornelis W. Oosterlee. 2017. Conditional Time Series Forecasting with Convolutional Neural Networks. arXiv, arXiv:1703.04691. [Google Scholar]
- Cairns, Andrew J. G., and Delme J. Pritchard. 2001. Stability of Descriptive Models for the Term Structure of Interest Rates with Applications to German Market Data. British Actuarial Journal 7: 467–507. [Google Scholar] [CrossRef]
- Candès, Emmanuel J., Xiaodong Li, Yi Ma, and John Wright. 2009. Robust principal component analysis? Neural Computation 21: 3179–213. [Google Scholar]
- Cao, Li-Juan, and Francis Eng Hock Tay. 2003. Support vector machine with adaptive parameters in financial time series forecasting. IEEE Transactions on Neural Networks 14: 1506–18. [Google Scholar] [CrossRef] [PubMed]
- Chen, Tao, Elaine Martin, and Gary Montague. 2009. Robust probabilistic PCA with missing data and contribution analysis for outlier detection. Computational Statistics and Data Analysis 53: 3706–16. [Google Scholar] [CrossRef]
- Chib, Siddhartha, and Bakhodir Ergashev. 2009. Analysis of Multi-Factor Affine Yield Curve. Journal of American Statistical Association 104: 1324–37. [Google Scholar] [CrossRef]
- Coroneo, Laura, Domenico Giannone, and Michele Modugno. 2016. Unspanned macroeconomic factors in the yield curve. Journal of Business & Economic Statistics 34: 472–85. [Google Scholar]
- Cuchiero, Christa, Claudio Fontana, and Alessandro Gnoatto. 2016a. A general HJM framework for multiple yield curve modeling. Finance and Stochastics 20: 267–320. [Google Scholar] [CrossRef]
- Cuchiero, Christa, Claudio Fontana, and Alessandro Gnoatto. 2016b. Affine multiple yield curve models. arXiv, arXiv:1603.00527v1. [Google Scholar]
- De la Torre, Fernando, and Michael J. Black. 2001. Robust Principal Component Analysis for Computer Vision. Paper presented at Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, July 7–14. [Google Scholar]
- Dempster, Arthur P., Nan M. Laird, and Donald B. Rubin. 1977. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of Royal Statistical Society. Series B (Methodological) 39: 1–38. [Google Scholar]
- Diebold, Francis X., and Canlin Li. 2006. Forecasting the term structure of government bond yields. Journal of Econometrics 130: 337–64. [Google Scholar] [CrossRef]
- Ding, Chris, Ding Zhou, Xiaofeng He, and Hongyuan Zha. 2006. R1-PCA: Rotational Invariant L1-norm Principal Component Analysis for Robust Subspace Factorization. Paper presented at the 23rd International Conference on Machine Learning, ICML 2006, Pittsburgh, PA, USA, June 25–29; pp. 281–88. [Google Scholar]
- Mönch, Emanuel. 2008. Forecasting the Yield Curve in a Data-Rich Environment: A No-Arbitrage Factor-Augmented VAR Approach. Journal of Econometrics 146: 26–43. [Google Scholar]
- Eriksson, Anders, and Anton van den Hengel. 2012. Efficient Computation of Robust Weighted Low-Rank Matrix Approximations Using the L 1 Norm. IEEE Transactions on Pattern Analysis and Machine Intelligence 34: 1681–90. [Google Scholar] [CrossRef] [PubMed]
- Fang, Yi, and Myong K. Jeong. 2008. Robust Probabilistic Multivariate Calibration Model. Technometrics 50: 305–16. [Google Scholar] [CrossRef]
- Filipović, Damir, and Anders B. Trolle. 2013. The Term Structure of Interbank Risk. Journal of Financial Economics 109: 707–33. [Google Scholar]
- Geva, Tomer, and Jacob Zahavi. 2014. Empirical evaluation of an automated intraday stock recommendation system incorporating both market data and textual news. Decision Support Systems 57: 212–23. [Google Scholar] [CrossRef]
- Grbac, Zorana, and Wolfgang J. Runggaldier. 2015. Interest Rate Modeling: Post-Crisis Challenges and Approaches. New York: Springer. [Google Scholar]
- Gupta, Arjun K., and Nagar Daya K. 1999. Matrix Variate Distributions. Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- Harvey, Andrew C. 1990. Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge: Cambridge University Press. [Google Scholar]
- Huber, Peter J. 1964. Robust Estimation of a Location Parameter. The Annals of Mathematical Statistics 35: 73–101. [Google Scholar] [CrossRef]
- Huber, Peter J., and Elvezio M. Ronchetti. 2009. Robust Statistics. Wiley Series in Probability and Statistics; Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Hubert, Mia, Peter J. Rousseeuw, and Karlien Vanden Branden. 2005. ROBPCA: A New Approach to Robust Principal Component Analysis. Technometrics 47: 64–79. [Google Scholar] [CrossRef]
- Joslin, Scott, Marcel Priebsch, and Kenneth J. Singleton. 2014. Risk Premiums in Dynamic Term Structure Models with Unspanned Macro Risks. The Journal of Finance 69: 1197–1233. [Google Scholar] [CrossRef]
- Joslin, Scott, Kenneth J. Singleton, and Haoxiang Zhu. 2010. A New Perspective on Gaussian Dynamic Term Structure Models. Review of Financial Studies 24: 926–70. [Google Scholar] [CrossRef]
- Kalman, Rudolph E., and Richard S. Bucy. 1961. New Results in Linear Filtering and Prediction Theory. Journal of Basic Engineering 83: 95–108. [Google Scholar] [CrossRef]
- Karimalis, Emmanouil, Ioannis Kosmidis, and Gareth Peters. 2017. Multi Yield Curve Stress-Testing Framework Incorporating Temporal and Cross Tenor Structural Dependencies. Working Paper No. 655. London, UK: Bank of England. [Google Scholar]
- Ke, Qifa, and Takeo Kanade. 2005. Robust L1 Norm Factorization in the Presence of Outliers and Missing Data by Alternative Convex Programming. Paper presented at IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, June 20–25; pp. 739–46. [Google Scholar]
- Kercheval, Alec N., and Yuan Zhang. 2015. Modeling high-frequency limit order book dynamics with support vector machines. Quantitative Finance 15: 1–36. [Google Scholar] [CrossRef]
- Khan, Zia, and Frank Dellaert. 2003. Robust Generative Subspace Modeling: The Subspace t Distribution. Paper presented at British Machine Vision Conference 2003, Norwich, UK, September 9–11; pp. 1–17. [Google Scholar]
- Kwon, Yung-Keun, and Byung-Ro Moon. 2007. A Hybrid Neurogenetic Approach for Stock Forecasting. IEEE Transactions on Neural Networks 18: 851–64. [Google Scholar]
- Lange, Kenneth L., Roderick J. A. Little, and Jeremy M. G. Taylor. 1989. Robust Statistical Modeling Using the t Distribution. Journal of the American Statistical Association 84: 881–96. [Google Scholar] [CrossRef]
- Little, Roderick J. A., and Donald B. Rubin. 2002. Statistical Analysis with Missing Data, 2nd ed. Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Ludvigson, Sydney C., and Serena Ng. 2010. A Factor Analysis of Bond Risk Premia. In Handbook of Empirical Economics and Finance. Cambridge: National Bureau of Economic Research, pp. 313–72. [Google Scholar]
- Maronna, Ricardo. 2005. Principal Components and Orthogonal Regression Based on Robust Scales. Technometrics 47: 264–73. [Google Scholar] [CrossRef]
- Nelson, Charles R., and Andrew F. Siegel. 1987. Parsimoniuos Modeling of Yield Curves. The Journal of Business 60: 473–89. [Google Scholar] [CrossRef]
- Robert, Paul, and Yves Escoufier. 1976. A Unifying Tool for Linear Multivariate Statistical Methods: The RV- Coefficient. Applied Statistics 25: 257–65. [Google Scholar] [CrossRef]
- Rousseeuw, Peter J. 1985. Multivariate Estimation with High Breakdown Point. Mathematical Statistic and Applications 8: 37. [Google Scholar]
- Rousseeuw, Peter, and Victor Yohai. 1984. Robust Regression by Means of S-Estimators. In Robust and Nonlinear Time Series Analysis. New York: Springer, pp. 256–72. [Google Scholar]
- Sirignano, Justin. 2016. Deep Learning for Limit Order Books. arXiv, arXiv:1601.01987. [Google Scholar]
- Teichmann, Josef, and Mario V. Wüthrich. 2016. Consistent Yield Curve Prediction. The Journal of IAA 46: 181–224. [Google Scholar] [CrossRef]
- Tibshirani, Robert. 1996. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B (Methodological) 58: 267–88. [Google Scholar]
- Tipping, Michael E., and Christopher M. Bishop. 1999. Probabilistic Principal Component Analysis. Journal of the Royal Statistical Society 61: 622–61. [Google Scholar] [CrossRef]
- Tyler, David E. 1987. Statistical Analysis for the Angular Central Gaussian Distribution on the Sphere. Biometrika 74: 579–89. [Google Scholar] [CrossRef]
- Wright, Jonathan H. 2011. Term Premia and Inflation Uncertainty: Empirical Evidence from an International Panel Dataset. American Economic Review 101: 1514–34. [Google Scholar] [CrossRef]
- Xie, Pengtao, and Eric Xing. 2015. Cauchy Principal Component Analysis. arXiv, arXiv:1412.6506. [Google Scholar]
- Zhou, Zihan, Xiaodong Li, John Wright, Emmanuel Candes, and Yi Ma. 2010. Stable Principal Component Pursuit. Paper presented at IEEE International Symposium on Information Theory, Austin, TX, USA, July 13. [Google Scholar]








| Instrument | Cat | Freq. | Availability | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EU | DE | FR | PO | ES | IT | IR | GB | JP | U.S. | AU | BR | SA | |||
| Libor Curve | daily | ✓ | |||||||||||||
| Sovereign Curve | GOV | daily | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Inflation Curve | INF | daily | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| FXRates | FX | daily | ✓ | ✓ | ✓ | ✓ | |||||||||
| CPI | INF | monthly | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| GDP | PRD | yearly | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Unemployment Rates | PRD | yearly | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Labour Productivity | PRD | yearly | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| German Bund OI | LIQ | daily | |||||||||||||
| Euro Repo and Euribor 3M | LIQ | daily | |||||||||||||
| Markit iTraxx 5Y | CR | daily | |||||||||||||
| Year | 1Y ICE Euro Libor Rate | 1Y Swap Rate | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | PPCA | R | l | AIC | log MSE | Model | PPCA | R | L | AIC | log MSE | |||
| 2006 | M0 | hete | −1.42 | 5922.73 | −11,843.46 | −3.99 | M0 | hete | −1.42 | 6164.91 | −12,327.83 | −4.07 | ||
| M2 | 2 | hete | −1.42 | 7898.12 | −15,794.25 | −4.30 | M2 | 2 | hete | −1.42 | 8101.40 | −16,200.80 | −4.36 | |
| 2007 | M0 | hete | −0.76 | 5965.95 | −11,929.90 | −3.16 | M0 | hete | −0.96 | 6256.79 | −12,511.59 | −3.23 | ||
| M2 | 1 | hete | −0.76 | 7305.62 | −14,609.24 | −3.67 | M2 | 1 | hete | −0.96 | 7114.59 | −14,227.19 | −3.99 | |
| 2008 | M0 | hete | −0.52 | 3331.25 | −6660.50 | −3.03 | M0 | hete | −0.48 | 3581.24 | −7160.47 | −2.64 | ||
| M3 | 3 | hete | −0.52 | 4841.08 | −9680.15 | −3.98 | M3 | 3 | hete | −0.48 | 5077.73 | −10,153.47 | −3.81 | |
| 2009 | M0 | hete | −0.52 | 5184.72 | −10,367.44 | −4.27 | M0 | hete | −0.48 | 5679.58 | −11,357.15 | −4.47 | ||
| M2 | 2 | hete | −0.52 | 6764.61 | −13,527.22 | −5.64 | M2 | 2 | hete | −0.48 | 7108.11 | −14,214.22 | −5.77 | |
| 2010 | M0 | hete | −2.18 | 5422.09 | −10,842.19 | −3.66 | M0 | hete | −0.64 | 6027.31 | −12,052.63 | −4.31 | ||
| M2 | 2 | hete | −2.18 | 7650.23 | −15,298.46 | −6.20 | M2 | 2 | hete | −0.64 | 7450.24 | −14,898.48 | −5.81 | |
| 2011 | M0 | hete | −0.52 | 4357.33 | −8712.66 | −3.40 | M0 | hete | −0.56 | 5191.04 | −10,380.08 | −4.26 | ||
| M3 | 1 | hete | −0.52 | 6502.81 | −13,003.63 | −5.19 | M3 | 1 | hete | −0.56 | 6513.74 | −13,025.47 | −5.07 | |
| 2012 | M0 | hete | −0.52 | 4368.44 | −8734.87 | −2.90 | M0 | hete | −0.74 | 4377.26 | −8752.52 | −4.66 | ||
| M2 | 2 | hete | −0.52 | 7773.09 | −15,544.17 | −6.23 | M2 | 2 | hete | −0.74 | 7535.36 | −15,068.73 | −5.76 | |
| 2013 | M0 | hete | −0.83 | 5738.36 | −11,474.72 | −4.69 | M0 | hete | −0.74 | 5390.17 | −10,778.33 | −5.29 | ||
| M2 | 3 | hete | −0.83 | 7854.03 | −15,706.06 | −6.55 | M2 | 3 | hete | −0.74 | 8128.64 | −16,255.27 | −6.72 | |
| 2014 | M0 | hete | −0.91 | 5225.34 | −10,448.68 | −4.43 | M0 | hete | −0.96 | 5638.23 | −11,274.46 | −5.40 | ||
| M2 | 2 | hete | −0.91 | 8462.48 | −16,922.96 | −6.42 | M2 | 2 | hete | −0.96 | 8525.73 | −17,049.46 | −6.47 | |
| 2015 | M0 | hete | −0.99 | 6243.56 | −12,485.13 | −4.93 | M0 | hete | −0.96 | 6639.60 | −13,277.21 | −5.87 | ||
| M2 | 1 | hete | −0.99 | 8886.02 | −17,770.05 | −6.63 | M2 | 1 | hete | −0.96 | 8927.51 | −17,853.02 | −6.67 | |
| 2016 | M0 | hete | −0.99 | 5150.36 | −10,298.73 | −4.69 | M0 | hete | −1.09 | 6108.33 | −12,214.66 | −5.54 | ||
| M2 | 1 | hete | −0.99 | 8595.78 | −17,189.57 | −6.98 | M2 | 1 | hete | −1.09 | 8908.23 | −17,814.46 | −7.15 | |
| Year | 1Y ICE Euro Libor Rate | 1Y Swap Rate | ||||||
|---|---|---|---|---|---|---|---|---|
| Model | log MSEP | Model | log MSEP | |||||
| 1D | 1W | 1M | 1D | 1W | 1M | |||
| 2006 | M0 | −3.93 | −3.78 | −2.94 | M0 | −4.01 | −3.85 | −3.26 |
| M2 | −6.35 | −4.93 | −3.41 | M2 | −6.20 | −4.96 | −3.59 | |
| 2007 | M0 | −1.95 | −2.09 | −1.88 | M0 | −2.24 | −2.36 | −1.75 |
| M2 | −4.90 | −3.33 | −2.01 | M2 | −4.92 | −3.42 | −1.94 | |
| 2008 | M0 | −4.10 | −3.74 | −2.81 | M0 | −4.43 | −3.89 | −2.65 |
| M3 | −5.70 | −3.96 | −2.57 | M3 | −5.46 | −3.56 | −2.05 | |
| 2009 | M0 | −3.77 | −2.77 | −1.26 | M0 | −3.80 | −2.76 | −1.38 |
| M2 | −5.60 | −3.07 | −1.45 | M2 | −5.66 | −3.16 | −1.53 | |
| 2010 | M0 | −2.29 | −2.29 | −1.78 | M0 | −4.18 | −3.62 | −2.34 |
| M2 | −5.52 | −3.69 | −2.22 | M2 | −6.02 | −4.51 | −2.68 | |
| 2011 | M0 | −2.90 | −2.90 | −2.23 | M0 | −3.49 | −3.18 | −2.12 |
| M3 | −6.16 | −4.23 | −1.99 | M3 | −6.02 | −3.98 | −1.70 | |
| 2012 | M0 | −3.86 | −3.69 | −3.03 | M0 | −4.79 | −4.43 | −3.52 |
| M2 | −7.31 | −5.79 | −4.13 | M2 | −7.26 | −5.82 | −4.17 | |
| 2013 | M0 | −4.30 | −4.24 | −2.97 | M0 | −4.91 | −4.81 | −2.85 |
| M2 | −7.18 | −5.74 | −3.73 | M2 | −7.19 | −5.88 | −3.74 | |
| 2014 | M0 | −4.86 | −4.42 | −2.92 | M0 | −5.83 | −4.93 | −2.92 |
| M2 | −7.05 | −5.25 | −3.17 | M2 | −7.01 | −5.21 | −3.01 | |
| 2015 | M0 | −4.34 | −4.17 | −3.55 | M0 | −5.32 | −5.05 | −3.97 |
| M2 | −7.77 | −6.31 | −4.49 | M2 | −7.69 | −6.29 | −4.38 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toczydlowska, D.; Peters, G.W. Financial Big Data Solutions for State Space Panel Regression in Interest Rate Dynamics. Econometrics 2018, 6, 34. https://doi.org/10.3390/econometrics6030034
Toczydlowska D, Peters GW. Financial Big Data Solutions for State Space Panel Regression in Interest Rate Dynamics. Econometrics. 2018; 6(3):34. https://doi.org/10.3390/econometrics6030034
Chicago/Turabian StyleToczydlowska, Dorota, and Gareth W. Peters. 2018. "Financial Big Data Solutions for State Space Panel Regression in Interest Rate Dynamics" Econometrics 6, no. 3: 34. https://doi.org/10.3390/econometrics6030034
APA StyleToczydlowska, D., & Peters, G. W. (2018). Financial Big Data Solutions for State Space Panel Regression in Interest Rate Dynamics. Econometrics, 6(3), 34. https://doi.org/10.3390/econometrics6030034




