Decomposing the Bonferroni Inequality Index by Subgroups: Shapley Value and Balance of Inequality
Abstract
:1. Introduction
2. The Gini and the Bonferroni Inequality Index
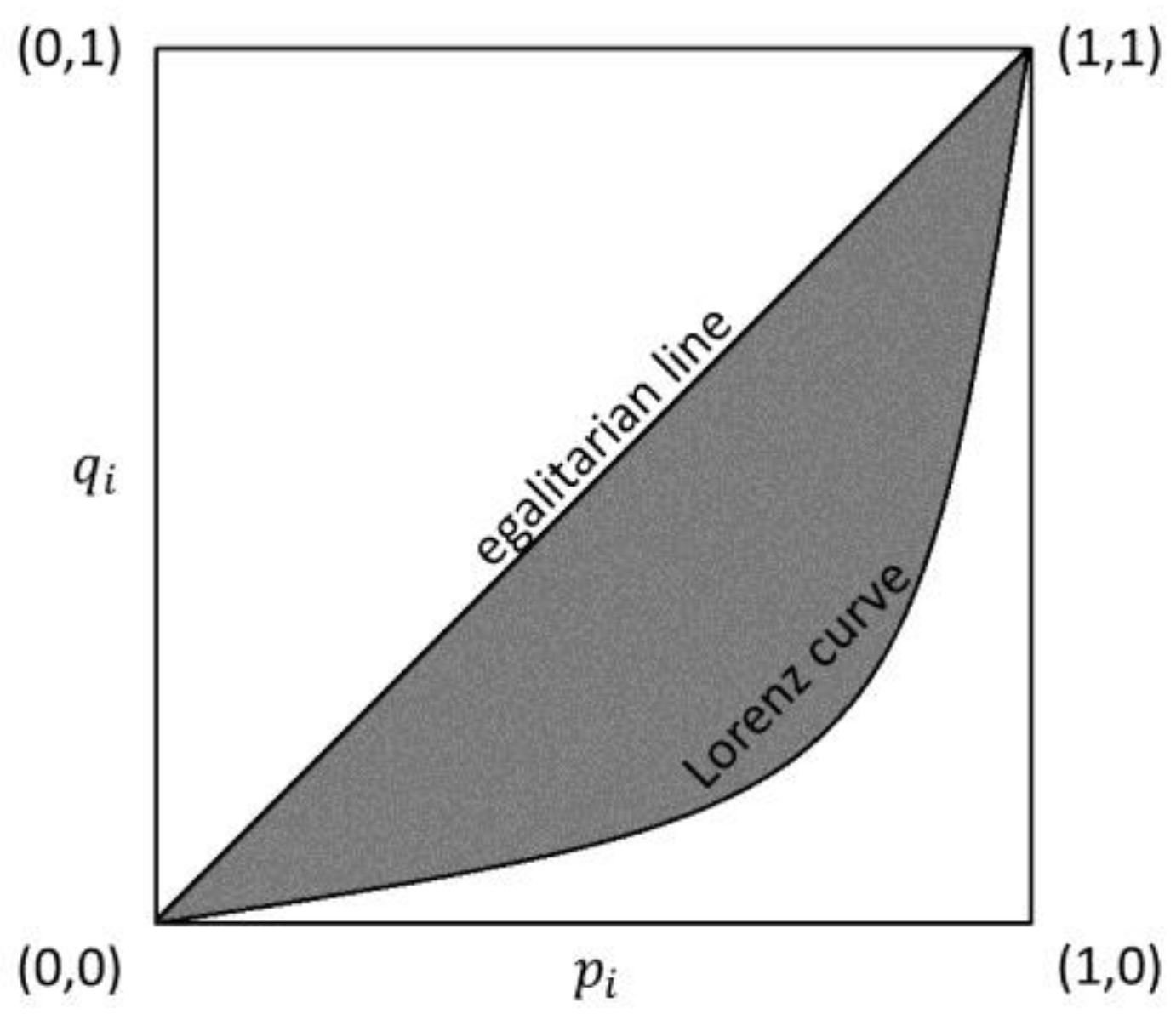
2.1. The Gini Concentration Index
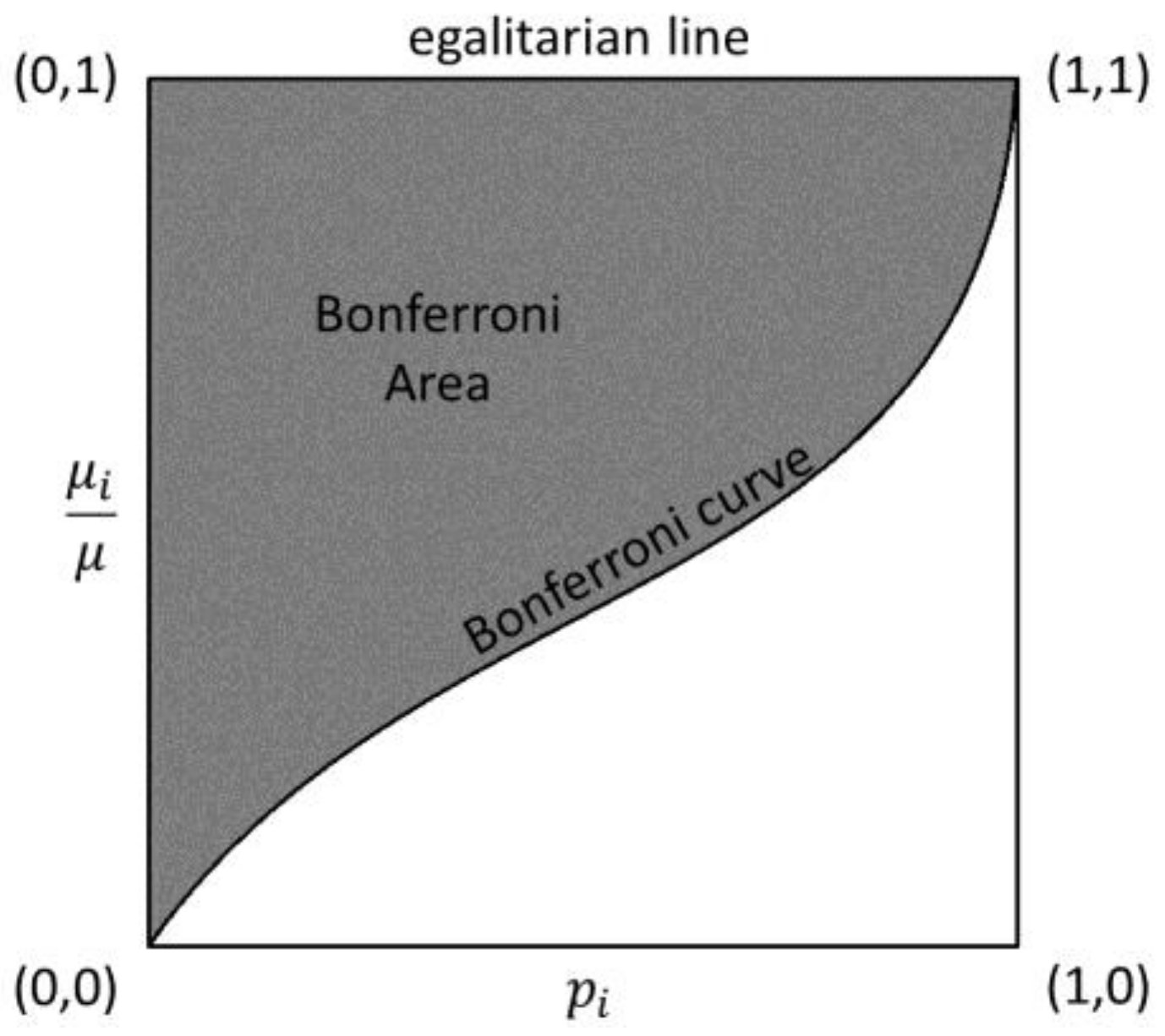
2.2. The Bonferroni Inequality Index
3. A Brief Overview on Inequality Index Decomposition
4. The Shapley Decomposition
A Numerical Illustration
5. The Balance of Inequality Approach
A Numerical Illustration
6. An Application to the Italian Income Distribution
Some Considerations on the Shapley Decomposition and the Balance of Inequality
7. Conclusions and Further Research
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Population Size | Relative Difference | ||||||
|---|---|---|---|---|---|---|---|
| Number of Replications | Number of Replications | ||||||
| No Replication | 2 | 10 | 100 | 2 | 10 | 100 | |
| (a) | (b) | (c) | (d) | (b − a)/a | (c − a)/a | (d − a)/a | |
| Low level of concentration ( 0.20) | |||||||
| 10 | 0.30789 | 0.30394 | 0.30183 | 0.30147 | −0.01285 | −0.01971 | −0.02085 |
| 100 | 0.29684 | 0.29692 | 0.29700 | 0.29702 | 0.00025 | 0.00054 | 0.00061 |
| 1000 | 0.29289 | 0.29291 | 0.29292 | 0.29292 | 0.00006 | 0.00011 | 0.00012 |
| 10,000 | 0.28858 | 0.28859 | 0.28860 | 0.28860 | 0.00002 | 0.00004 | 0.00004 |
| Medium level of concentration ( 0.50) | |||||||
| 10 | 0.68310 | 0.67073 | 0.66296 | 0.66145 | −0.01812 | −0.02949 | −0.03170 |
| 100 | 0.64458 | 0.64382 | 0.64323 | 0.64310 | −0.00119 | −0.00210 | −0.00230 |
| 1000 | 0.63418 | 0.63411 | 0.63405 | 0.63404 | −0.00011 | −0.00019 | −0.00021 |
| 10,000 | 0.62732 | 0.62732 | 0.62731 | 0.62731 | −0.00001 | −0.00002 | −0.00002 |
| High level of concentration ( 0.80) | |||||||
| 10 | 0.94323 | 0.91843 | 0.90107 | 0.89744 | −0.02630 | −0.04470 | −0.04855 |
| 100 | 0.88648 | 0.88452 | 0.88298 | 0.88263 | −0.00221 | −0.00395 | −0.00434 |
| 1000 | 0.88150 | 0.88131 | 0.88116 | 0.88113 | −0.00022 | −0.00039 | −0.00043 |
| 10,000 | 0.87653 | 0.87651 | 0.87649 | 0.87649 | −0.00002 | −0.00004 | −0.00004 |
References
- Aaberge, Rolf. 2000. Characterizations of Lorenz Curves and Income Distributions. Social Choice and Welfare 17: 639–53. [Google Scholar] [CrossRef]
- Bárcena-Martin, Elena, and Luis J. Imedio Olmedo. 2008. The Bonferroni, Gini and De Vergottini Indices. Inequality, Welfare and Deprivation in the European Union in 2000. Research on Economic Inequality 16: 231–57. [Google Scholar]
- Bárcena-Martin, Elena, and Jacques Silber. 2011. On the Concepts of Bonferroni Segregation Index Curve. Rivista Italiana di Economia, Demografia e Statistica 62: 57–74. [Google Scholar]
- Bárcena-Martin, Elena, and Jacques Silber. 2013. On the Generalization and Decomposition of the Bonferroni Index. Social Choice and Welfare 41: 763–87. [Google Scholar] [CrossRef]
- Benedetti, Carlo. 1986. Sulla Interpretazione Benesseriale di Noti Indici di Concentrazione e di altri. Metron 45: 421–29. [Google Scholar]
- Bhattacharya, N., and B. Mahalanobis. 1967. Regional Disparities in Household Consumption in India. Journal of the American Statistical Association 62: 143–61. [Google Scholar] [CrossRef]
- Bonferroni, Carlo E. 1930. Elementi Di Statistica Generale. Firenze: Libreria Seber. [Google Scholar]
- Chakravarty, Satya R. 2007. A Deprivation-Based Axiomatic Characterization of the Absolute Bonferroni Index of Inequality. Journal of Economic Theory 5: 339–51. [Google Scholar] [CrossRef]
- Dalton, Hugh D. 1925. Some Aspects of the Inequality of Incomes in Modern Communities. London: Routledge. [Google Scholar]
- De Vergottini, Mario. 1950. Sugli Indici di Concentrazione. Statistica 10: 445–54. [Google Scholar]
- Deutsch, Joseph, and Jacques Silber. 1999. Inequality Decomposition by Population Subgroups and the Analysis of Interdistributional Inequality. In Handbook on Income Inequality Measurement. Edited by Silber Jacques. Boston: Kluwer Academic Publisher, vol. 71, pp. 363–97. [Google Scholar]
- Deutsch, Joseph, and Jacques Silber. 2007. Decomposing Income Inequality by Population Subgroups: A Generalization. In Research on Economic Inequality: Inequality and Poverty. Edited by Bishop John and Amiel Yoram. Berlin: Springer, vol. 14, pp. 237–53. [Google Scholar]
- Di Maio, Giorgio, and Paolo Landoni. 2017. The Balance of Inequality: A Rediscovery of The Gini’s R Concentration Ratio and a New Inequality Decomposition by Population Subgroups Based on Physical Rationale. Paper presented at Seventh Meeting of The Society for the Study of Economic Inequality (Ecineq), New York City, NY, USA, July 17–19. [Google Scholar]
- Ferrari, Guido, and Pietro Rigo. 1987. Sulla Scomposizione del Rapporto di Concentrazione di Gini. In La Distribuzione Personale del Reddito: Problemi di Formazione, di Ripartizione e di Misurazione. Edited by Zenga Michele. Milano: Vita e Pensiero, pp. 347–63. [Google Scholar]
- Fields, Gary S. 1979a. Income Inequality in Urban Colombia: A Decomposition Analysis. Review of Income and Wealth 25: 327–41. [Google Scholar] [CrossRef]
- Fields, Gary S. 1979b. Decomposing LDC Inequality. Oxford Economic Papers 31: 437–59. [Google Scholar] [CrossRef]
- Frick, Joachim R., and Jan Goebel. 2007. Regional Income Stratification in Unified Germany Using a Gini Decomposition Approach. Discussion paper. Berlin, Germany: Germany Institute for Economich Research, 1–32. [Google Scholar]
- Gini, Corrado. 1912. Studi Economico-Giuridici della Facoltà di Giurisprudenza della Regia Università di Cagliari. In Variabilità e Mutabilità: Contributo Allo Studio Delle Distribuzioni e Delle Relazioni Statistiche. Bologna: Cuppini, vol. 3. [Google Scholar]
- Gini, Corrado. 1914. Sulla Misura della Concentrazione e della Variabilità dei Caratteri. Atti Del Reale Istituto Veneto Di Scienze, Lettere ed Arti 73: 1203–48, English Translation In Metron 2005, 63: 3–38. [Google Scholar]
- Giordani, Paolo, and Giovanni M. Giorgi. 2010. A Fuzzy Logic Approach to Poverty Analysis Based on the Gini and Bonferroni Inequality Indices. Statistical Methods and Applications 19: 587–607. [Google Scholar] [CrossRef]
- Giorgi, Giovanni M. 1990. Bibliographic Portrait of the Gini Concentration Ratio. Metron 48: 183–221. [Google Scholar]
- Giorgi, Giovanni M. 1992. Il Rapporto di Concentrazione di Gini. Genesi, Evoluzione ed una Bibliografia Commentata. Siena: Libreria Editrice Ticci. [Google Scholar]
- Giorgi, Giovanni M. 1993. A Fresh Look at the Topical Interest of the Gini Concentration Ratio. Metron 51: 83–98. [Google Scholar]
- Giorgi, Giovanni M. 1998. Concentration Index, Bonferroni. In Encyclopedia of Statistical Sciences. Updated Series; Edited by Kotz Samuel, Read Campbell B. and Banks David L. New York: Wiley-Intersciences, vol. 2, pp. 141–46. [Google Scholar]
- Giorgi, Giovanni M. 1999. Income Inequality Measurement: The Statistical Approach. In Handbook on Income Inequality Measurement. Edited by Silber Jacques. Boston: Kluwer Academic Publishers, pp. 245–60. [Google Scholar]
- Giorgi, Giovanni M. 2005. Gini’s Scientific Work: An Evergreen. Metron 63: 299–315. [Google Scholar]
- Giorgi, Giovanni M. 2011a. The Gini Inequality Index Decomposition, an Evolutionary Study. In The Measurement of Individual Well-Being and Group Inequality: Essay In Memory Of Z.M. Berrebi. London: Routledge, pp. 185–218. [Google Scholar]
- Giorgi, Giovanni M. 2011b. Corrado Gini: The Man and the Scientist. Metron 69: 1–28. [Google Scholar] [CrossRef]
- Giorgi, Giovanni M., and Michele Crescenzi. 2001a. Bayesian Estimation of the Bonferroni Index in a Pareto-Type I Population. Statistical Methods and Applications 10: 41–48. [Google Scholar] [CrossRef]
- Giorgi, Giovanni M., and Michele Crescenzi. 2001b. A Look at the Bonferroni Inequality Measure in a Reliability Framework. Statistica 61: 571–83. [Google Scholar]
- Giorgi, Giovanni M., and Michele Crescenzi. 2001c. A Proposal of Poverty Measures Based on the Bonferroni Inequality Index. Metron 59: 3–15. [Google Scholar]
- Giorgi, Giovanni M., and Alessio Guandalini. 2013. A Sampling Estimator of the Bonferroni Inequality Index. Rivista Italiana di Economia, Demografia e Statistica 67: 151–58. [Google Scholar]
- Giorgi, Giovanni M., and Riccardo Mondani. 1995. Sampling Distribution of Bonferroni Inequality Index from an Exponential Population. Sankhya 57: 10–18. [Google Scholar]
- Imedio Olmedo, Luis J., Elena Bárcena-Martin, and Encarnación M. Parrado-Gallardo. 2012. Income Inequality Indices Interpreted as Measures of Relative Deprivation/Satisfaction. Social Indicator Research 109: 471–91. [Google Scholar] [CrossRef]
- Istat. 2015. Indagine Sulle Condizioni di Vita (UDB IT—SILC). Available online: https://www.istat.it/it/archivio/4152 (accessed on 4 December 2017).
- Kakwani, Nanak C. 1980. Income Inequality and Poverty: Methods of Estimation and Policy Applications. Oxford: Oxford University Press. [Google Scholar]
- Lorenz, Max O. 1905. Method of Measuring the Concentration of Wealth. Publication of the American Statistical Association 9: 209–19. [Google Scholar] [CrossRef]
- Mehran, Farhad. 1975. A Statistical Analysis of Income Inequality Based on a Decomposition of the Gini Index. Bulletin of the International Statistical Institute 46: 145–50, Contributed Paper, 40th Session, Warsaw, Poland. [Google Scholar]
- Mussard, Stéphane, Françoise Seyte, and Michel Terrazza. 2006. La Décomposition de l’Indicateur de Gini en Sous Groupes: Une Revue de la Littérature. GRÉDI Working paper 06-11. Sherbrooke, QC, Canada: Université De Sherbrooke. [Google Scholar]
- Nygård, Fredrik, and Arne Sandström. 1981. Measuring Income Inequality. Stockholm: Almqvist & Wiksell International. [Google Scholar]
- Osberg, Lars. 2017. On the Limitations of Some Current Usages of the Gini Index. Review of Income and Wealth 63: 574–84. [Google Scholar] [CrossRef]
- Osier, Guillaume. 2009. Variance Estimation for Complex Indicators of Poverty and Inequality Using Linearization Techniques. Survey Research Methods 3: 167–95. [Google Scholar]
- Piesch, Walter. 1975. Statistische Konzentrationsmasse. Tübingen: J.B.C. Mohr (Paul Siebeck). [Google Scholar]
- Piketty, Thomas. 2014. Capital in the Twenty-First Century. Cambridge: Harvard University Press. [Google Scholar]
- Pizzetti, Ernesto. 1951. Relazioni fra Indici di Concentrazione. Statistica 11: 294–316. [Google Scholar]
- Rao, V. 1969. Two Decompositions of Concentration Ratio. Journal of the Royal Statistical Society 132: 418–25. [Google Scholar] [CrossRef]
- Shapley, Lloyd. 1953. A Value for N-Person Games. In Contributions to the Theory of Games (AM-28). Edited by Kuhn Harold W. and Tucker Albert W. Princeton: Princeton University Press, vol. 2, pp. 307–18. [Google Scholar]
- Shorrocks, Anthony F. 1980. The Class of Additively Decomposable Measures. Econometrica 48: 613–25. [Google Scholar] [CrossRef]
- Shorrocks, Anthony F. 1999. Decomposition Procedures for Distributional Analysis: A Unified Framework Based on the Shapley Value. Essex, UK: Department of Economics, University of Essex. [Google Scholar]
- Shorrocks, Anthony F. 2013. Decomposition Procedures for Distributional Analysis: A Unified Framework Based on the Shapley Value. The Journal of Economic Inequality 11: 99–126. [Google Scholar] [CrossRef]
- Silber, Jacques, and Hyun Son. 2010. On the Link between the Bonferroni Index and the Measurement of Inclusive Growth. Economics Bulletin 30: 421–28. [Google Scholar]
- Tarsitano, Agostino. 1990. The Bonferroni Index of Income Inequality. In Income and Wealth Distribution, Inequality and Poverty. Edited by Dagum Camilo and Zenga Michele. Berlin: Springer, pp. 228–42. [Google Scholar]
- Yitzhaki, Shlomo. 1998. More than a dozen alternative ways of spelling Gini. Research on Economic Inequality 8: 13–30. [Google Scholar]
| 1 | In expression (3) the summation is limited to and then divided by . This formulation is different from the one used in other papers mentioned in the Introduction (where the summation is up to the division by is used). Of course, increasing , and the last term in the summation is null. |
| 2 | For the expressions of , and in the case of income classes, see Tarsitano (1990), while for the matrix decomposition of see Bárcena-Martin and Silber (2013). |
| 3 | In expressions (5)–(8), because all the inequality factors have been removed. |
| 4 | Di Maio and Landoni (2017) consider the asymmetry and the irregularity as a unique factor but, to investigate the differences between and , it could be useful to consider them separately. |
| 5 | For more detail on see Di Maio and Landoni (2017). |
| Removed Factor | Income Distribution | |||
|---|---|---|---|---|
| 1 | 2, 6, 10, 18, 20, 25, 30, 50, 55, 84 | 0.490 | 0.609 | |
| 2 | 11, 11, 38, 38.25, 38, 11, 38.25, 38.25, 38.25, 38 | 0.151 | 0.252 | |
| 3 | 5.45, 16.36, 7.89, 14.12, 15.79, 68.18, 23.53, 39.22, 43.14, 66.32 | 0.360 | 0.475 | |
| 4 | 2, 2, 2, 2, 6, 6, 6, 6, 10, 10, 10, 10, 18, 18, 18, 20, 20, 20, 20, 25, 25, 25, 25, 30, 30, 30, 50, 50, 50, 55, 55, 55, 84, 84, 84, 84 | 0.474 | 0.612 | |
| 5 | 2, 6, 25, 10, 20, 84, 18, 30, 50, 55 | 0.333 | 0.481 | |
| 6 | 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30 | 0.000 | 0.000 | |
| 7 | 11, 11, 11, 11, 11, 11, 11, 11, 11, 38, 38, 38, 38.25, 38.25, 38.25 38, 38, 38, 38, 11, 11, 11, 11, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38, 38, 38 | 0.167 | 0.283 | |
| 8 | 11, 11, 11, 38, 38, 38, 38.25, 38.25, 38.25, 38.25 | 0.212 | 0.331 | |
| 9 | 5.45, 5.45, 5.45, 5.45, 16.36, 16.36, 16.36, 16.36, 27.27, 7.89, 7.89, 7.89, 14.12, 14.12, 14.12, 15.79, 15.79, 15.79, 15.79, 68.18, 68.18, 68.18, 68.18, 23.53, 23.53, 23.53, 39.22, 39.22, 39.22, 43.14, 43.14, 43.14, 65.88, 66.32, 66.32, 66.32 | 0.334 | 0.466 | |
| 10 | 5.45, 16.36, 68.18, 7.89, 15.79, 66.32, 14.12, 23.53, 39.22, 43.14 | 0.128 | 0.233 | |
| 11 | 2, 2, 2, 2, 6, 6, 6, 6, 25, 25, 25, 25, 10, 10, 10, 10, 20, 20, 20, 20, 84, 84, 84, 84, 18, 18, 18, 30, 30, 30, 50, 50, 50, 55, 55, 55 | 0.331 | 0.501 | |
| 12 | 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30 | 0.000 | 0.000 | |
| 13 | 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30 | 0.000 | 0.000 | |
| 14 | 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25, 38.25 | 0.214 | 0.343 | |
| 15 | 5.45, 5.45, 5.45, 5.45, 16.36, 16.36, 16.36, 16.36, 68.18, 68.18, 68.18, 68.18, 7.89, 7.89, 7.89, 7.89, 15.79, 15.79, 15.79, 15.79, 66.32, 66.32, 66.32, 66.32, 14.12, 14.12, 14.12, 23.53, 23.53, 23.53, 39.22, 39.22, 39.22, 43.14, 43.14, 43.14 | 0.127 | 0.259 | |
| 16 | 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30 | 0.000 | 0.000 | |
| Factor | Contribution to | Contribution to | ||
|---|---|---|---|---|
| % | % | |||
| within inequality | 0.230 | 47.02 | 0.305 | 50.07 |
| between inequality | 0.176 | 35.90 | 0.244 | 40.13 |
| size | 0.005 | 1.00 | −0.007 | −1.22 |
| ranking | 0.079 | 16.07 | 0.067 | 11.02 |
| Total | 0.490 | 100.00 | 0.609 | 100.00 |
| Factor | Contribution to | Contribution to | ||
|---|---|---|---|---|
| % | % | |||
| within inequality | 0.256 | 52.38 | 0.365 | 59.95 |
| between inequality | 0.151 | 30.86 | 0.252 | 41.42 |
| asymmetry | −0.007 | −1.35 | −0.025 | −4.10 |
| irregularity | 0.010 | 2.05 | 0.017 | 2.73 |
| Total | 0.490 | 100.00 | 0.609 | 100.00 |
| Geographical Area | Households | First Quartile | Median | Mean | Third Quartile | Fisher Asymmetry Coefficient | R | B | |
|---|---|---|---|---|---|---|---|---|---|
| Sample Size | Population Size | ||||||||
| North | 8922 | 12,294,699 | 25,809 | 39,180 | 47,621 | 59,749 | 4.273 | 0.346 | 0.439 |
| Center | 4223 | 5,295,623 | 23,114 | 36,459 | 44,626 | 56,524 | 2.379 | 0.360 | 0.457 |
| South | 4840 | 8,185,550 | 16,939 | 26,617 | 32,561 | 40,400 | 10.861 | 0.372 | 0.482 |
| Italy | 17,985 | 25,775,872 | 22,007 | 34,199 | 42,223 | 53,480 | 5.143 | 0.367 | 0.462 |
| Factor | Contribution to | Contribution to | ||
|---|---|---|---|---|
| Absolute Value | % | Absolute Value | % | |
| Shapley decomposition | ||||
| within inequality | 0.2348 | 63.99 | 0.3065 | 66.30 |
| [0.2281, 0.2415] | [62.16, 65.80] | [0.2956, 0.3174] | [63.94, 68.66] | |
| between inequality | 0.0530 | 14.44 | 0.0626 | 13.55 |
| [0.0439, 0.0621] | [11.95, 16.93] | [0.0522, 0.0730] | [11.28, 15.80] | |
| size | −0.0002 | −0.05 | 0.0090 | 1.95 |
| [−0.0037, 0.0033] | [−1.00, 0.89] | [0.0046, 0.0134] | [0.99, 2.90] | |
| ranking | 0.0793 | 21.62 | 0.0841 | 18.20 |
| [0.0700, 0.0886] | [19.08, 24.13] | [0.0757, 0.0925] | [16.37, 20.01] | |
| Total | 0.3670 | 100.00 | 0.4623 | 100.00 |
| [0.3568, 0.3772] | [0.4505, 0.4741] | |||
| Balance of Inequality () | ||||
| within inequality | 0.3483 | 94.98 | 0.4007 | 81.07 |
| [0.3384, 0.3582] | [94.89, 95.02] | [0.3908, 0.4106] | [79.07, 83.09] | |
| between inequality | 0.0239 | 6.54 | 0.0385 | 7.79 |
| [0.0182, 0.0296] | [5.11, 7.85] | [0.0293, 0.0477] | [6.05, 9.65] | |
| asymmetry | 0.0020 | 0.55 | 0.4405 | 89.13 |
| [0.0008, 0.0032] | [0.24, 0.84] | [0.4393, 0.4417] | [90.78, 89.36] | |
| irregularity | −0.0076 | −2.07 | −0.3855 | −78.00 |
| [−0.0095, −0.0057] | [−2.65, −1.52] | [−0.3874, −0.3836] | [−80.04, −77.62] | |
| Total | 0.3668 | 100.00 | 0.4942 | 100.00 |
| [0.3566, 0.3770] | [0.3908, 0.4106] | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorgi, G.M.; Guandalini, A. Decomposing the Bonferroni Inequality Index by Subgroups: Shapley Value and Balance of Inequality. Econometrics 2018, 6, 18. https://doi.org/10.3390/econometrics6020018
Giorgi GM, Guandalini A. Decomposing the Bonferroni Inequality Index by Subgroups: Shapley Value and Balance of Inequality. Econometrics. 2018; 6(2):18. https://doi.org/10.3390/econometrics6020018
Chicago/Turabian StyleGiorgi, Giovanni M., and Alessio Guandalini. 2018. "Decomposing the Bonferroni Inequality Index by Subgroups: Shapley Value and Balance of Inequality" Econometrics 6, no. 2: 18. https://doi.org/10.3390/econometrics6020018
APA StyleGiorgi, G. M., & Guandalini, A. (2018). Decomposing the Bonferroni Inequality Index by Subgroups: Shapley Value and Balance of Inequality. Econometrics, 6(2), 18. https://doi.org/10.3390/econometrics6020018




