Abstract
The underlying idea behind the construction of indices of economic inequality is based on measuring deviations of various portions of low incomes from certain references or benchmarks, which could be point measures like the population mean or median, or curves like the hypotenuse of the right triangle into which every Lorenz curve falls. In this paper, we argue that, by appropriately choosing population-based references (called societal references) and distributions of personal positions (called gambles, which are random), we can meaningfully unify classical and contemporary indices of economic inequality, and various measures of risk. To illustrate the herein proposed approach, we put forward and explore a risk measure that takes into account the relativity of large risks with respect to small ones.
Keywords:
economic inequality; reference measure; personal gamble; inequality index; risk measure; relativity JEL Classification:
D63; D81; C46
1. Introduction
The Gini mean difference and its normalized version, known as the Gini index, have aided decision makers since their introduction by Corrado Gini more than a hundred years ago (Gini 1912, 1914, 1921); see also (Giorgi 1990, 1993, 1921); Ceriani and Verme 2012; and references therein). In particular, the Gini index has been widely used by economists and sociologists to measure economic inequality. Measures inspired by the index have been employed to assess the equality of opportunity (e.g., Weymark 2003; Kovacevic 2010; Roemer 2013) and estimate income mobility (e.g., Shorrocks 1978). Policymakers have used the Gini index in quantitative development policy analysis (e.g., Sadoulet and de Janvry 1995) and in particular for assessing the impact of carbon tax on income distribution (e.g., Oladosu and Rose 2007). The index has been employed for analysing inequality in the use of natural resources (e.g., Thompson 1976) and for developing informed policies for sustainable consumption and social justice (e.g., Druckman and Jackson 2008). Various extensions and generalizations of the index have been used to evaluate social welfare programs (e.g., Duclos 2000; Kenworthy and Pontusson 2005; Korpi and Palme 1998; Ostry et al. 2014) and to improve the knowledge of tax-base and tax-rate effects, as well as of temporal repercussions of distinct patterns of taxation and public finance on the society (e.g., Pfähler 1990; Slemrod 1992; Yitzhaki 1994; Van De Ven et al. 2001). Furthermore, Denneberg (1990) has advocated the use of the Gini mean difference as a safety loading for insurance premiums, with recent developments in the area by Furman and Zitikis (2017), and Furman et al. (2017).
Naturally, a multitude of interpretations, mathematical expressions, and generalizations of the index have manifested in the literature. As noted by Ceriani and Verme (2012), Corrado Gini himself proposed no less than thirteen formulations of his original index. Yitzhaki (1998, 2003), and Yitzhaki and Schechtman (2013) have discussed a great variety of interpretations of the Gini index. Many monographs and handbooks have been written on measuring economic inequality, where the Gini index and its various extensions and generalizations have played prominent roles: Amiel and Cowell (1999), Atkinson and Bourguignon (2000, 2015), Atkinson and Piketty (2007), Banerjee and Duflo (2011), Champernowne and Cowell (1998), Cowell (2011), Kakwani (1980a), Lambert (2001), Nygård and Sandström (1981), Ostry et al. (2014), Piketty (2014), Sen (1997), Silber (1999), Yitzhaki and Schechtman (2013), to name a few.
Given the diversity, one naturally wonders if there is one underlying thread that unifies all these indices. The population Lorenz function, as well as its various distances from the hypotenuse of the right triangle into which every Lorenz function falls, have traditionally provided such a thread. However, recent developments in the area of measuring economic inequality (e.g., Palma 2006; Zenga 2007; Greselin 2014; Gastwirth 2014; Kośny and Yalonetzky 2015) have highlighted the need for departure from the population mean, which is inherent in the definition of the Lorenz function as the benchmark, or reference point, for measuring economic inequality. The newly developed indices have deviated from the aforementioned unifying thread and thus initiated a fresh rethinking of the problem of measuring inequality.
Bennett and Zitikis (2015) ventured in this direction by suggesting a way to bridge the Harsanyi (1953) and Rawls (1971) conceptual frameworks via a spectrum of random societal positions. In this paper, we make a further step by developing a mathematically rigorous approach for unifying and interpreting numerous classical and contemporary indices of economic inequality, as well as those of risk. Briefly, the approach we have developed is based on appropriately chosen
- societal references such as the population mean, median, or some population distribution-tail based measures, and
- distributions of random personal positions, or gambles, that determine person’s position on a certain population-based function.
Certainly, the literature is permeated by discussions related to points 1 and 2. Relativity issues have been explored in virtually every work, empirical and theoretical, due to the simple reason that they are a fact of life (e.g., Amiel and Cowell 1997, 1999). Naturally, fundamental measures of inequality, such as the Lorenz function, are also relative quantities, e.g., with respect to the population mean income. For discussions of various choices of reference measures and inherent relativity issues, we refer to, e.g., Sen (1983, 1998); Amiel and Cowell (1997, 1999); Zoli (1999, 2012); Duclos (2000); and references therein. To illustrate the point, which will become pivotal in our following deliberations, we recall a remark by Claudio Zoli, who wrote:
This remark leads us towards the use of what we call relative-value functions, which, as we shall see later in this paper, offer a flexible way for coupling fundamental measures of economic inequality, or risk, with appropriate reference points, such as the mean (e.g., Equation (7) below). This is very much in the spirit of Definition 3 by Cowell (2003). We shall come back to the latter work in the second half of Section 4.In particular, Amiel and Cowell (1997, 1999) find evidence that “the appropriate inequality equivalence concept depends on the income levels at which inequality comparisons are made.” Moreover, they show that, as income increases, the equivalence concept moves from the relative attitude to the absolute one, a pattern consistent with our intuition.(Zoli 2012, p. 4)
Finally, we note that the construction of distributions that govern personal random positions on population-based functions have been explored within the dual or rank-dependent utility theory (Quiggin 1982, 1993; Schmeidler 1986, 1989; Yaari 1987), other non-expected utility theories (e.g., Puppe 1991; Machina 1987, 2008; and references therein), distortion risk measures (Wang 1995, 1998), and weighted insurance premium calculation principles (Furman and Zitikis 2008, 2009).
The rest of the paper is organized as follows. In Section 2, we revisit the classical Gini index and, in particular, express it in two ways—absolute and relative—within the framework of expected utility theory using appropriately chosen gambles and societal functions (i.e., Lorenz and Bonferroni). In Section 3, we step aside from the Lorenz and Bonferroni functions and, crucially for this paper, suggest using a (financial) average value at risk as the underlying societal function on which various personal gambles are played; however, the reference measure remains the mean income . In Section 4, we depart from the latter reference and introduce a general index that accommodates any population-based reference measure. In Section 5 and Section 6, we show how the Donaldson-Weymark-Kakwani index and the Wang (or distortion) risk measure, as well as their generalizations, fall into the expected utility framework with collective mean-income references and appropriately chosen personal gambles. In Section 7, we argue for the need for incorporating personal preferences into reference measures, and, in Section 8, we demonstrate how this yields a new measure of risk that takes into account the relativity of large risks with respect to smaller ones. Section 9 finishes the paper with a general index of inequality and risk.
2. The Classical Gini Index Revisited
Naturally, we begin our arguments with the classical index of Gini (1914). Let X be a random variable (think of ‘income’) with non-negatively supported cdf and finite mean . The Gini index, which we denote by , is usually interpreted as twice the area between the actual population Lorenz function (Lorenz 1905; Pietra 1915; Gastwirth 1971)
and the egalitarian Lorenz function , , which is the hypotenuse of the right triangle that we have alluded to in the abstract. For parametric expressions of , we refer to Gastwirth (1971), Kakwani and Podder (1973), as well as to more recent works of Sarabia (2008), Sarabia et al. (2010), and references therein. Hence, the Gini index is
where the gamble follows the uniform density on the unit interval , that is, for all . Intuitively, governs person’s position in terms of income percentiles, and we thus call it personal gamble. In other words, barring the normalizing constant 2, the Gini index is the expected absolute-deviation of person’s position on the actual Lorenz function from his/her position on the reference (egalitarian) Lorenz function . Naturally, the position is random, and we have already seen in the case of the Gini index that it follows the uniform on distribution. This means that the person has an equal chance of receiving any income among all the available incomes which are, in terms of percentiles, identified with the unit interval .
In general, the personal gamble can follow various distributions on , and we shall see a variety of examples throughout this paper. The choice of distribution of carries information about person’s probable positions and is thus inevitably subjective, but many of the examples that we have encountered in the literature follow the beta distribution
which we have visualized in Figure 1. We succinctly write and so, for example, the Gini index (cf. Equation (1)) is based on . For illuminating statistical and historical notes on the beta and other related distributions in the context of measuring economic inequality, we refer to Kleiber and Kotz (2003). For very general yet remarkably tractable beta-generated families of distributions for greater modeling flexibility, we refer to Alexander et al. (2012), and references therein.
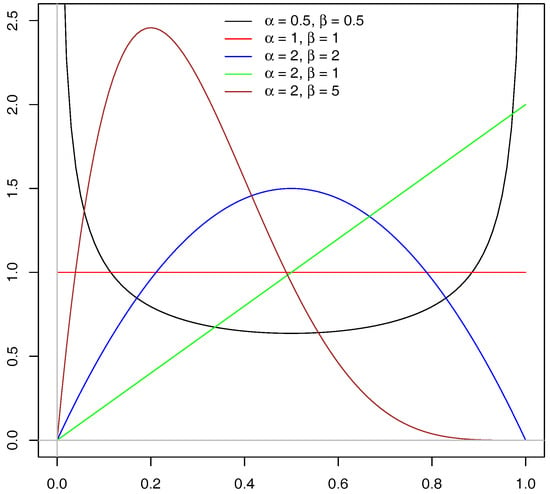
Figure 1.
Beta densities of gambles for various values of and .
Importantly for our following discussion, the Gini index can also be viewed as the expected relative-deviation of person’s position on the actual Lorenz function from his/her position on the reference Lorenz function , as seen from the equations:
where , which is a considerable change from used in the absolute-deviation based representation (1) of the Gini index. Note that the right-hand side of Equation (2) can be succinctly written as , where
is the Bonferroni function of inequality (cf. Bonferroni 1930), which is also known in the literature as the Gini function of inequality because it appeared in Gini (1914). For details on the Bonferroni function and the corresponding Bonferroni index, we refer to Tarsitano (1990) and references therein.
In addition to its role when studying income and poverty, the Bonferroni function has also found many uses in other fields such as reliability, demography, insurance, and medicine (e.g., Giorgi and Crescenzi 2001; and references wherein). For detailed historical notes and references with explicit expressions of the Lorenz and Bonferroni functions, as well as of the Gini and Bonferroni indices, for many parametric distributions, we refer to Giorgi and Nadarajah (2010). The role of the Bonferroni function within the framework of L-functions for measuring economic inequality and actuarial risks can be found in Tarsitano (2004), and Greselin et al. (2009).
3. From Egalitarian Lorenz to the Mean Reference
Not only the classical Gini index but also a multitude of other indices of economic inequality can be viewed as deviation measures (e.g., functional distances) between the actual and egalitarian Lorenz functions (cf., e.g., Zitikis 2002). Note, however, that the actual Lorenz function itself is a relative measure that compares lowest incomes with the population mean income . This two-stage relativity—first with respect to the egalitarian Lorenz function and then with the mean income—warrants a rethinking of the inequality measurement.
Toward this end, we next rephrase the definition of the Gini index by first rewriting the Bonferroni function as follows:
where
is the (financial) average value at risk of X. Indeed, with a little mathematical caveat, is the conditional expectation , which is the mean income of those who are below the ‘poverty line’ . In summary, Equation (2) becomes
with the gamble . If, instead of the latter gamble, we use on the right-hand side of Equation (5), then the expectation turns into the Bonferroni index
For details on the Bonferroni index, we refer to Tarsitano (1990) and references therein. For a comparison of the two weighting schemes, that is, of the gambles employed in the Gini and Bonferroni cases, we refer to De Vergottini (1940). Implications of using the Bonferroni index on welfare measurement have been studied by, e.g., (Benedetti 1986; Aaberge 2000; Chakravarty 2007). Nygård and Sandström (1981) give a wide-ranging discussion of the use of Bonferroni-type concepts in the measurement of economic inequality. Giorgi and Crescenzi (2001), and Chakravarty and Muliere (2004) propose poverty measures based on the fact that the Bonferroni index exhibits greater sensitivity on lower levels of the income distribution than the Gini index. A general class of inequality measures inspired by the Bonferroni index has been explored by Imedio-Olmedo et al. (2011). Giorgi (1998) provides a list of Bonferroni’s publications.
Equations (5) and (6) suggest that the Gini and Bonferroni indices are members of the following general class of indices
where can be any function for which the expectation is well-defined and finite. In the case of the Gini and Bonferroni indices (e.g., Greselin 2014), we have , which is the relative value of x with respect to y. We call any function used in expressions like (7) a relative-value function throughout this paper. Hence, we can view the index as the expected utility of being in the society whose income distribution is depicted by the function and compared with the reference mean income using an appropriately chosen relative-value function . We should note at this point that even though the class of relative-value functions may look large, it is nevertheless prudent to restrict our attention to those that are of the form
for some function . Indeed, under the natural assumption of positive homogeneity, which means that the equation holds for all , Euler’s classical theorem says that we must have Equation (8) for some function . The Gini and Bonferroni indices give rise to .
Another example of the function arises from the E-Gini index of Chakravarty (1988):
where the reference-value function is , that is, , and the gamble . Zitikis (2002) suggests using instead of 2 in the definition of the E-Gini index (see also Zitikis (2003) for additional notes) in which case the right-hand side of Equation (9) turns into the index
In either case, note from the expressions of and that it is sometimes useful to transform the index by some function . We shall elaborate on this point in the next section.
Coming now back to the index , we note that, with the generic relative-value function , the index can be rewritten as , where . Hence, we are dealing with the distorted Bonferroni function , , which is analogous to the distorted Lorenz function upon which Sordo et al. (2014) have built their research (see Aaberge (2000) for earlier results on the topic). We do not pursue this research venue in the present paper because the Bonferroni function, just like that of Lorenz, incorporates a pre-specified reference measure, which is the mean income . In what follows, we argue in favour of more flexibility when choosing reference measures, which may even include personal preferences in addition to those of the entire population.
4. From the Mean to Generic Societal References
We now extend the index to arbitrary references, which we denote by . Namely, let
where is a normalizing function whose main role is to fit the index into the unit interval , with the value 0 meaning perfect equality (i.e., everybody has the same amount) and 1 meaning extreme inequality (i.e., only one person has something, and thus everything, with the others having nothing). Having the flexibility to manipulate references is important due to a variety of reasons. For example, the use of the mean can become questionable when population skewness increases, and this has already been noted by, e.g., Gastwirth (2014) who, in his research on the changing income inequality in the U.S. and Sweden, has suggested replacing the mean by the median .
Another example of that differs from is provided by the Palma index; we refer to Cobham and Sumner (2013a, 2013b, 2014) for details. Namely, let be the average of the top 10% of the population incomes, that is, . Furthermore, let the normalizing function be , the relative-value function , and the (deterministic) gamble . Under these specifications, the index becomes the Palma index of economic inequality:
Instead of the underlying random variable (e.g., income) X, the researcher might be primarily interested in its transformation (e.g., utility of income) . To tackle this situation, we first incorporate the transformed incomes into our framework by extending the definition of the (financial) average value at risk as follows:
Note that , which we can view as the expected utility of X. We have arrived at the extension
of the index .
The index appears to be a minor generalization of the extended intermediate index of Cowell (2003) (see Equation (12) therein), which has been shown to include a large number of well-known indices (in particular, the Generalized Entropy class of indices) and far-reaching new ones. Namely, reduces to the index of Cowell (2003), which for referencing purposes we denote by , by choosing for a certain constant , for a certain function , the reference , the relative-value function , and the (deterministic) gamble ; here are the aforementioned quantities that we have not yet specified:
where , , and are parameters. Hence, even though the reason for our use of the letter for index (10) is alphabetical, it would only be natural to call the Cowell general intermediate index, whose special case, called extended intermediate index, appears in Cowell (2003).
The Atkinson (1970) index, which we denote by , is a special case of . (For many other special cases, we refer to Cowell (2003).) Namely, let the utility function be for some . Furthermore, let the (deterministic) gamble be , the reference , and the relative-value function . Under these specifications, the index turns into , which after the transformation with the function becomes the Atkinson index
This index has been highly influential in measuring economic inequality (e.g., Cowell (2011), and references therein) and inspired a variety of extensions and generalization of the Gini index. In addition, Mimoto and Zitikis (2008) have found the Atkinson index useful for developing a statistical inference theory for testing exponentiality, which has been a prominent problem in life-time analysis and, particularly, in reliability engineering.
5. The Donaldson-Weymark-Kakwani Index Revisited and Extended
The Donaldson-Weymark-Kakwani index (Donaldson and Weymark 1980, 1983; Kakwani 1980a, 1980b; Weymark 1981)
which is also known as the S-Gini index, has arisen following Atkinson (1970) observation that the Gini index does not take into account social preferences. Via the parameter , the index can reflect different social preferences, with the classical Gini index arising by setting . We note in this regard that a justification for a family of indices to be based on the theory of relative deprivation has been provided by Yitzhaki (1979, 1982).
Just like the Gini index , the index can also be placed within the framework of expected relative value. Indeed, using Equations (3) and (4), we have
with the relative-value function and the gamble , whose density is visualized in Figure 2.
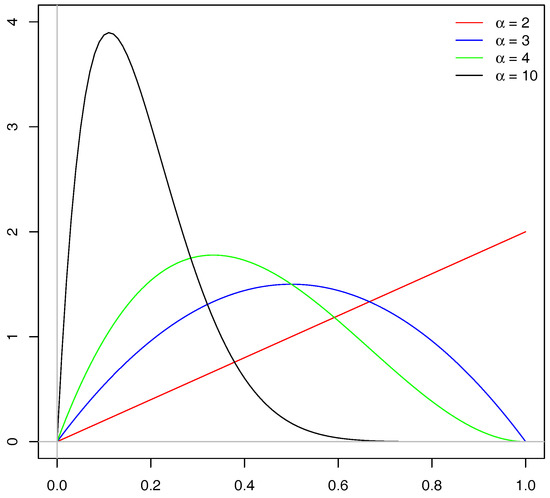
Figure 2.
The density of for various values of .
We next introduce a more flexible index than that allows us to employ more general gambles than . For this, we first introduce a class of generating functions:
- (H)
- Let be any twice differentiable and convex function (i.e., for all ) that satisfies the boundary conditions and , and such that .
Let denote the gamble whose density is given by the formula
for all , and elsewhere. With the relative-value function , we have (details in Appendix A)
To illustrate, we choose the function with any , in which case the gamble follows the density ; that is, , which means that has the same distribution as the earlier noted gamble . Consequently, reduces to , and thus Equation (13) reduce to the following expressions of the Donaldson-Weymark-Kakwani index:
(cf. Donaldson and Weymark (1980, 1983); Yitzhaki (1983); Muliere and Scarsini (1989)).
6. The Wang Risk Measure Revisited and Extended
The index is based on gambles generated by convex functions h. A similar index but based on concave generating functions g is called the Wang (or distortion) risk measure, which has been used in actuarial science and financial mathematics for measuring risks. In detail, the risk measure is defined by the formula
where is a distortion function, meaning that it is non-decreasing and satisfies the boundary conditions and .
Hence, unlike in the previous section, we now work with concave distortion functions, denoted by g, under which the risk measure is coherent (Wang et al. 1997; Wang and Young 1998; Wirch and Hardy 1999; see Artzner et al. (1999) for a general discussion). A classical example of such a distortion function is for any , in which case the Wang risk measure reduces to the proportional-hazards-transform risk measure (Wang 1995)
For more information on concave versus convex distortion functions in the context of measuring risks, their variability and orderings, we refer to Sordo and Suárez-Llorens (2011), Giovagnoli and Wynn (2012), and references therein.
We next show that the Wang risk measure can be placed within the framework of expected relative value. When compared with the index , there are two major changes: First, the function of interest is now the (insurance) average value at risk:
(Note that when , then is equal to the mean .) Second, the function g that generates the distribution of the random position is concave. Specifically, we introduce the following class of generating functions:
- (G)
- Let be twice differentiable and concave function (i.e., for all ) that satisfies the boundary conditions and , and such that .
Any such function g generates the density of the gamble given by the formula
for all , and elsewhere. With the relative-value function , we have (details in Appendix)
Consequently, the Wang risk measure can be expressed in terms of the expected relative value as follows:
When the generating function is for any , then the gamble follows whose density function is depicted in Figure 3.
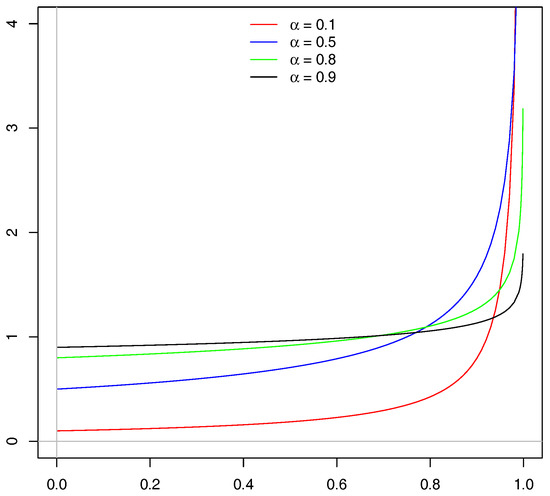
Figure 3.
The density of when for various values of .
From Equation (16), we have
Finally, we note the following expression for the proportional-hazards-transform risk measure:
7. From Collective to Individual References
So far, we have worked with collective references. They do not depend on the outcomes of personal gambles and thus apply to all members of the society. Such references may not, however, be always desirable or justifiable. For example, given the outcome of the gamble , meaning that the person is considered to be among the lowest income earners, the person may wish to compare the current position with the hypothetical one of being among the highest income earners. In such situations, we are dealing with individual references: their values may depend on outcomes of the personal gamble .
Hence, for example, the mean and the median are collective references, but is an individual reference because its value depends on the outcome of . Would the quantile be a good reference? There are at least two major reasons against the use of the quantile, which is known in the risk literature as the value-at-risk:
- The quantile is not robust with respect to realized values p of the random gamble , in the sense that the quantile may change drastically even for very small changes of p.
- For a realized value p of , the quantile is not informative about the values of for . Indeed, we may have the same value of irrespective of whether the cdf F is heavy- or light-tailed.
These are serious issues when constructing sound measures of economic inequality and risk. In the risk literature (cf., e.g., McNeil et al. (2005); Meucci (2007); Pflug and Römisch (2007); Cruz (2009); Sandström (2010); Cannata and Quagliariello (2011); and references therein), the problem with quantiles has been overcome by using whose definition was given in the previous section. For example, adopting as our (individual) reference and using the normalizing function , the earlier introduced index turns into the Zenga (2007) index
with the relative-value function and the gamble . Hence, the Zenga index is the average with respect to all percentiles of the relative deviations of the mean income of the poor (i.e., those whose incomes are below the poverty line ) from the corresponding mean income of the rich, that is, of those whose incomes are above the poverty line . We refer to Greselin et al. (2013) for a more detailed discussion of the relative nature of the Gini and Zenga indices, and their comparison.
8. Relative Measure of Risk
Many risk measures that we find in the literature are designed to measure absolute heaviness of the right-hand tail of the underlying loss distribution. Suppose now that we wish to measure the severity of large (e.g., insurance) losses relative to small ones. Note that this problem is very similar to that tackled by Zenga (2007) in the context of economic inequality. Hence, following the same path but now using the relative-value function and generic gamble , we arrive at the relative measure of risk
which, in the spirit of expected utility, can be rewritten as
where the role of utility function is played by the risk function
In what follows, we explore properties of this risk measure, using the notation instead of to simplify the presentation.
Proposition 1.
We have the following statements:
- If the risk X is constant, that is, for some constant , then .
- Multiplying X by any constant does not change the relative measure of risk, that is, .
- Adding any constant to the risk X decreases the relative measure of risk, that is, .
We have relegated the proof of Proposition 1 to Appendix. We next comment on the meaning of the three properties spelled out in the proposition. First, given that we are dealing with a relative measure of risk, properties 1 and 2 are self-explanatory. As to property 3, it says that lifting up the risk by any positive constant decreases its riskiness. This is natural because lifting up diminishes the relative variability of the risk. This, in turn, suggests that ordering of the relative risk measures should be done, for example, in terms of the Lorenz ordering, which is one of the most used tools for comparing the variability of economic-size distributions. This leads to the following property:
Proposition 2.
If risks X and Y follow the Lorenz ordering , then .
The proof of Property 2 is provided in Appendix, where the basic definition of Lorenz ordering can also be found. It is related to the notion of ordering based on the generalized, also called absolute, Lorenz curve (e.g., Ramos et al. 2000; Sriboonchita et al. 2010; and references therein). This leads us directly to a closely related property called the Pigou-Dalton principle of transfers. In the context of economic inequality, the principle says that progressive (i.e., from rich to poor) rank-order and mean-preserving transfers should decrease the value of inequality measures. Hence, in the context of risk, the transfers should be risk decreasing. Formally (cf., Vergnaud 1997), X is less risk-unequal than Y in the Pigou-Dalton sense, denoted by , if and only if and . Hence, is sometimes denoted by (cf. Denuit et al. 2005). The following property is now obvious.
Proposition 3.
If a Pigou-Dalton risk-increasing transfer turns risk X into Y so that , then .
To have an idea of how the Pigou-Dalton transfers act, we recall (e.g., Shaked and Shanthikumar 2007; Sriboonchita et al. 2010) that given X and Y with densities and , respectively, and assuming that their means are equal, if the sign of the difference changes twice according to the pattern , then . Examples of parametric distributions with such pdf’s can be found in, e.g., Kleiber and Kotz (2003); see also references therein.
In what follows, we discuss an example based on the Zenga (2010) distribution that has shown remarkably good performance in terms of goodness-of-fit on a number of real income data sets. It is a very flexible three-parameter distribution with Pareto-type right-hand tail and whose density is
where is the scale parameter, which also happens to be the mean of the distribution, and and are two shape parameters that affect, respectively, the center and the tails of the distribution. We have depicted the Zenga density in Figure 4. For further details on this distribution and its uses, we refer to Zenga (2010), Zenga et al. (2011), Zenga et al. (2012), and Arcagni and Zenga (2013).
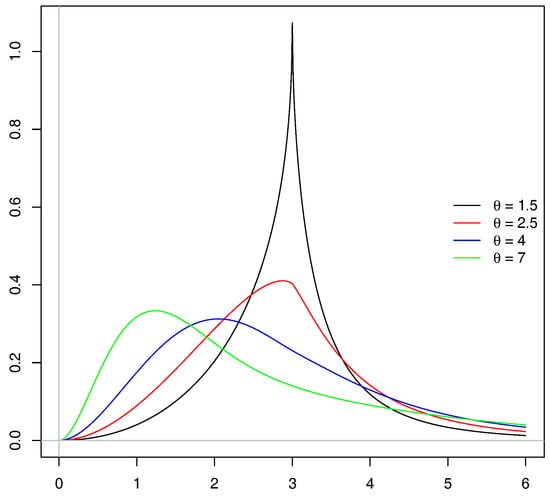
Figure 4.
density for various values of .
To see the effects of the Pigou-Dalton transfers in the case of the Zenga distribution, the following theorem is particularly useful.
Theorem 1
(Arcagni and Porro 2013). Assume and , where all the parameters are positive. When and , then .
9. Conclusions: A General Index of Inequality and Risk
The right-hand sides of Equations (19) and (20), which are identical, barring their different relative-value functions , give rise to a very general measure of inequality:
where and are two gambles, which could be dependent or independent, degenerate or not. Obviously, when , then we have either the Zenga index of economic inequality or the relative measure of risk, depending on the choice of the relative-value function. Furthermore, if , then we have and thus , which is the Bonferroni index . By appropriately choosing relative-value functions and personal gambles, we can reproduce a number of other measures of economic inequality and risk, but the Chakravarty and Atkinson indices require some little extension:
where u and are two utility functions, and
Note that . All the examples that we have mentioned in this paper, and also many other ones that appear in the literature, are special cases of the just introduced index . Table 1 provides a summary.

Table 1.
Special cases of index (22) with in all the rows.
We conclude with the note that, in the examples throughout this paper, the gambles and have been such that either they are identical (i.e., ) or one of them is degenerate (e.g., or ). There is no reason why this should always be the case: the two gambles can be dependent but not necessarily identical or degenerate. This suggests that, in general, modeling probability distributions of the pair can be conveniently achieved by, for example, specifying marginal distributions of the gambles and , as well as dependence structures between them using, e.g., appropriately chosen copulas. For methodological and applications-driven developments related to copulas, we refer to the monographs of Nelsen (2006), Jaworski et al. (2010), Jaworski et al. (2013), and references therein.
Acknowledgments
We are indebted to Academic Editors and anonymous reviewers for suggestions, insightful comments, and constructive criticism that guided our work on the revision. The second author is grateful to the University of Milano-Bicocca for making his most inspiring scientific visit at the university possible. The research has been supported by the grant “From Data to Integrated Risk Management and Smart Living: Mathematical Modelling, Statistical Inference, and Decision Making” awarded by the Natural Sciences and Engineering Research Council of Canada to the second author.
Author Contributions
Both authors, with the consultation of each other, carried out this work and drafted the manuscript together. Both authors read and approved the final manuscript.
Conflicts of Interest
The authors declare that they have no competing interests.
Appendix A. Technicalities
Proof of Equation (13).
Proof of Equation (16).
Since the relative-value function is , we have
where is the density function of the gamble defined by Equation (15). The following are straightforward calculations:
Applying definition (15) of the density function , we obtain
Combining Equations (A3) and (A4), we obtain the first equation of (16). Using Equation (A2) with g instead of h, we arrive at the second equation of (16). ☐
Remark A1.
From the mathematical point of view, Equation (A4) is elementary, but it was a pivotal observation that allowed Jones and Zitikis (2003) to initiate the development of statistical inference for the Wang (or distortion) risk measure. Since then, numerous statistical results have appeared on risk measures: parametric and non-parametric, light- and heavy-tailed cases have been explored in great detail by many authors. To illustrate the challenges that arise in the heavy-tailed context, we refer to Necir and Meraghni (2009), and Necir et al. (2007) for the proportional hazards transform; Necir et al. (2010), and Rassoul (2013) for the tail conditional expectation; and Brahimi et al. (2012) for general distortion risk measures.
Proof of Proposition 1.
Property 1 follows from the fact that, if for any constant , then and so for every . Property 2 follows from the fact that if , then and so for every . Property 3 follows from the fact that for every d, and so the bound together with the assumed positivity of d imply
The latter bound is equivalent to for every , which establishes the bound . ☐
Proof of Proposition 2.
We first recall (Arnold 1987; Aaberge 2000) that the Lorenz ordering means the bound for all . Since
the Lorenz ordering is equivalent to the R-ordering , which means for all . The latter bound and Equation (21) conclude the verification of Proposition 2. ☐
Remark A2.
With the above introduced notion of R-ordering, we can rephrase Proposition 2 as follows: if , then . For detailed treatments of various notions of stochastic orders, we refer to Shaked and Shanthikumar (2007); Li and Li (2013); and Sriboonchita et al. (2010).
References
- Aaberge, Rolf. 2000. Characterizations of Lorenz curves and income distributions. Social Choice and Welfare 17: 639–53. [Google Scholar] [CrossRef]
- Alexander, Carol, Gauss M. Cordeiro, Edwin M. M. Ortega, and José María Sarabia. 2012. Generalized beta-generated distributions. Computational Statistics and Data Analysis 56: 1880–97. [Google Scholar] [CrossRef]
- Amiel, Yoram, and Frank A. Cowell. 1997. Income Transformation and Income Inequality. Discussion Paper DARP 24. London, UK: London School of Economics. [Google Scholar]
- Amiel, Yoram, and Frank A. Cowell. 1999. Thinking About Inequality. Cambridge: Cambridge University Press. [Google Scholar]
- Arcagni, Alberto, and Francesco Porro. 2013. On the parameters of Zenga distribution. Statistical Methods and Applications 22: 285–303. [Google Scholar] [CrossRef]
- Arcagni, Alberto, and Michele Zenga. 2013. Application of Zenga’s distribution to a panel survey on household incomes of European Member States. Statistica and Applicazioni 11: 79–102. [Google Scholar]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Arnold, Barry C. 1987. Majorization and the Lorenz Order: A Brief Introduction. New York: Springer. [Google Scholar]
- Atkinson, Anthony B. 1970. On the measurement of inequality. Journal of Economic Theory 2: 244–63. [Google Scholar] [CrossRef]
- Atkinson, Anthony B., and Francois Bourguignon. 2000. Handbook of Income Distribution. Amsterdam: Elsevier, vol. 1. [Google Scholar]
- Atkinson, Anthony B., and Francois Bourguignon. 2015. Handbook of Income Distribution. Amsterdam: Elsevier, vol. 2. [Google Scholar]
- Atkinson, Anthony B., and Thomas Piketty. 2007. Top Incomes Over the Twentieth Century: A Contrast between Continental European and English-Speaking Countries. Oxford: Oxford University Press. [Google Scholar]
- Banerjee, A.V., and Esther Duflo. 2011. Poor Economics: A Radical Rethinking of the Way to Fight Global Poverty. New York: Public Affairs. [Google Scholar]
- Bennett, Christopher J., and Ricardas Zitikis. 2015. Ignorance, lotteries, and measures of economic inequality. Journal of Economic Inequality 13: 309–16. [Google Scholar] [CrossRef]
- Benedetti, C. 1986. Sulla interpretazione benesseriale di noti indici di concentrazione e di altri. Metron 44: 421–29. [Google Scholar]
- Bonferroni, C. E. 1930. Elementi di Statistica Generale. Firenze: Libreria Seeber. [Google Scholar]
- Brahimi, B., F. Meddi, and A. Necir. 2012. Bias-corrected estimation in distortion risk premiums for heavy-tailed losses. Afrika Statistika 7: 474–90. [Google Scholar] [CrossRef]
- Cannata, F., and M. Quagliariello. 2011. Basel III and Beyond. London: Risk Books. [Google Scholar]
- Ceriani, Lidia, and Paolo Verme. 2012. The origins of the Gini index: Extracts from Variabilità e Mutabilità (1912) by Corrado Gini. Journal of Economic Inequality 10: 421–43. [Google Scholar] [CrossRef]
- Chakravarty, Satya R. 1988. Extended Gini indices of inequality. International Economic Review 29: 147–56. [Google Scholar] [CrossRef]
- Chakravarty, Satya R. 2007. A deprivation-based axiomatic characterization of the absolute Bonferroni index of inequality. Journal of Economic Inequality 5: 339–51. [Google Scholar] [CrossRef]
- Chakravarty, Satya R., and Piero Muliere. 2004. Welfare indicators: A review and new perspectives. 2. Measurement of poverty. Metron 62: 247–81. [Google Scholar]
- Champernowne, D. G., and F. A. Cowell. 1998. Economic Inequality and Income Distribution. Cambridge: Cambridge University Press. [Google Scholar]
- Cobham, Alex, and Andy Sumner. 2013a. Putting the Gini Back in the Bottle? ‘The Palma’ As a Policy-Relevant Measure of Inequality. Working Paper 2013-5. London, UK: King’s College. [Google Scholar]
- Cobham, Alex, and Andy Sumner. 2013b. Is It All about the Tails? The Palma Measure of Income Inequality. Working Paper 343. Washington, DC, USA: Center for Global Development. [Google Scholar]
- Cobham, Alex, and Andy Sumner. 2014. Is inequality all about the tails?: The Palma measure of income inequality. Significance 11: 10–13. [Google Scholar] [CrossRef]
- Cowell, Frank A. 2003. Theil, Inequality and the Structure of Income Distribution. Discussion Paper DARP 67. London, UK: London School of Economics. [Google Scholar]
- Cowell, Frank A. 2011. Measuring Inequality, 3rd ed. Oxford: Oxford University Press. [Google Scholar]
- Cruz, M. 2009. The Solvency II Handbook. London: Risk Books. [Google Scholar]
- Denneberg, Dieter. 1990. Premium calculation: Why standard deviation should be replaced by absolute deviation. ASTIN Bulletin 20: 181–90. [Google Scholar] [CrossRef]
- Denuit, Michel, Jan Dhaene, Marc Goovaerts, and Rob Kaas. 2005. Actuarial Theory for Dependent Risks: Measures, Orders and Models. Chichester: Wiley. [Google Scholar]
- De Vergottini, Mario. 1940. Sul significato di alcuni indici di concentrazione. Giornale degli Economisti e Annali di Economia 11: 317–47. [Google Scholar]
- Donaldson, David, and John A. Weymark. 1980. A single-parameter generalization of the Gini indices of inequality. Journal of Economic Theory 22: 67–86. [Google Scholar] [CrossRef]
- Donaldson, David, and John A. Weymark. 1983. Ethically flexible Gini indices for income distributions in the continuum. Journal of Economic Theory 29: 353–58. [Google Scholar] [CrossRef]
- Druckman, A., and T. Jackson. 2008. Measuring resource inequalities: The concepts and methodology for an area-based Gini coefficient. Ecological Economics 65: 242–52. [Google Scholar] [CrossRef]
- Duclos, Jean-Yves. 2000. Gini indices and the redistribution of income. International Tax and Public Finance 7: 141–62. [Google Scholar] [CrossRef]
- Furman, Edward, Ruodu Wang, and Ricardas Zitikis. 2017. Gini-type measures of risk and variability: Gini shortfall, capital allocations, and heavy-tailed risks. Journal of Business and Finance 83: 70–84. [Google Scholar] [CrossRef]
- Furman, Edward, and Ricardas Zitikis. 2008. Weighted premium calculation principles. Insurance: Mathematics and Economics 42: 459–65. [Google Scholar] [CrossRef]
- Furman, Edward, and Ricardas Zitikis. 2009. Weighted pricing functionals with applications to insurance: An overview. North American Actuarial Journal 13: 483–96. [Google Scholar] [CrossRef]
- Furman, Edward, and Ricardas Zitikis. 2017. Beyond the Pearson correlation: Heavy-tailed risks, weighted Gini correlations, and a Gini-type weighted insurance pricing model. ASTIN Bulletin 47: 919–42. [Google Scholar] [CrossRef]
- Gastwirth, Joseph L. 1971. A general definition of the Lorenz curve. Econometrica 39: 1037–39. [Google Scholar] [CrossRef]
- Gastwirth, Joseph L. 2014. Median-based measures of inequality: Reassessing the increase in income inequality in the U.S. and Sweden. Journal of the IAOS 30: 311–20. [Google Scholar]
- Gini, Corrado. 1912. Variabilità e Mutabilità: Contributo allo Studio delle Distribuzioni e delle Relazioni Statistiche. Bologna: Tipografia di Paolo Cuppini. [Google Scholar]
- Gini, Corrado. 1914. On the measurement of concentration and variability of characters (English translation from Italian by Fulvio de Santis). Metron 63: 3–38. [Google Scholar]
- Gini, Corrado. 1921. Measurement of inequality of incomes. Economic Journal 31: 124–26. [Google Scholar] [CrossRef]
- Giorgi, Giovanni M. 1990. Bibliographic portrait of the Gini concentration ratio. Metron 48: 183–221. [Google Scholar]
- Giorgi, Giovanni M. 1993. A fresh look at the topical interest of the Gini concentration ratio. Metron 51: 83–98. [Google Scholar]
- Giorgi, Giovanni M. 1998. Concentration index, Bonferroni. In Encyclopedia of Statistical Sciences. Edited by S. Kotz, D. L. Banks and C. B. Read. New York: Wiley, vol. 2, pp. 141–46. [Google Scholar]
- Giorgi, Giovanni Maria, and M. Crescenzi. 2001. A look at the Bonferroni inequality measure in a reliability framework. Statistica 91: 571–83. [Google Scholar]
- Giorgi, Giovanni Maria, and Saralees Nadarajah. 2010. Bonferroni and Gini indices for various parametric families of distributions. Metron 68: 23–46. [Google Scholar] [CrossRef]
- Giovagnoli, Alessandra, and Henry P. Wynn. 2012. (U, V)-Ordering and a Duality Theorem for Risk Aversion and Lorenz-Type Orderings. LSE Philosophy Papers. London, UK: London School of Economics and Political Science. [Google Scholar]
- Greselin, Francesca. 2014. More equal and poorer, or richer but more unequal? Economic Quality Control 29: 99–117. [Google Scholar] [CrossRef]
- Greselin, Francesca, Leo Pasquazzi, and Ricardas Zitikis. 2013. Contrasting the Gini and Zenga indices of economic inequality. Journal of Applied Statistics 40: 282–97. [Google Scholar] [CrossRef]
- Greselin, Francesca, Madan L. Puri, and Ricardas Zitikis. 2009. L-functions, processes, and statistics in measuring economic inequality and actuarial risks. Statistics and Its Interface 2: 227–45. [Google Scholar] [CrossRef]
- Harsanyi, John C. 1953. Cardinal utility in welfare economics and in the theory of risk-taking. Journal of Political Economy 61: 434–35. [Google Scholar] [CrossRef]
- Imedio-Olmedo, Luis J., Elena Bárcena-Martín, and Encarnacion M. Parrado-Gallardo. 2011. A class of Bonferroni inequality indices. Journal of Public Economic Theory 13: 97–124. [Google Scholar] [CrossRef]
- Jaworski, Piotr, Fabrizio Durante, and Wolfgang Karl Härdle. 2013. Copulae in Mathematical and Quantitative Finance. Berlin: Springer. [Google Scholar]
- Jaworski, Piotr, Fabrizio Durante, Wolfgang Härdle, and Tomasz Rychlik. 2010. Copula Theory and Its Applications. Berlin: Springer. [Google Scholar]
- Jones, Bruce L., and Ricardas Zitikis. 2003. Empirical estimation of risk measures and related quantities. North American Actuarial Journal 7: 44–54. [Google Scholar] [CrossRef]
- Kakwani, Nanak C. 1980. Income Inequality and Poverty: Methods of Estimation and Policy Applications. New York: Oxford University Press. [Google Scholar]
- Kakwani, Nanak. 1980. On a class of poverty measures. Econometrica 48: 437–46. [Google Scholar] [CrossRef]
- Kakwani, N.C., and N. Podder. 1973. On the estimation of Lorenz curves from grouped observations. International Economic Review 14: 278–92. [Google Scholar] [CrossRef]
- Kenworthy, Lane, and Jonas Pontusson. 2005. Rising inequality and the politics of redistribution in affluent countries. Perspectives on Politics 3: 449–71. [Google Scholar] [CrossRef]
- Kleiber, Christian, and Samuel Kotz. 2003. Statistical Size Distributions in Economics and Actuarial Sciences. Hoboken: Wiley. [Google Scholar]
- Korpi, Walter, and Joakim Palme. 1998. The paradox of redistribution and strategies of equality: Welfare state institutions, inequality, and poverty in the Western countries. American Sociological Review 63: 661–87. [Google Scholar] [CrossRef]
- Kośny, Marek, and Gaston Yalonetzky. 2015. Relative income change and pro-poor growth. Economia Politica 32: 311–27. [Google Scholar] [CrossRef]
- Kovacevic, Milorad. 2010. Measurement of Inequality in Human Development—A Review. Human Development Research Paper 2010/35. New York, NY, USA: United Nations Development Programme. [Google Scholar]
- Lambert, Peter J. 2001. The Distribution and Redistribution of Income, 3rd ed. Manchester: Manchester University Press. [Google Scholar]
- Li, Haijun, and Xiaohu Li. 2013. Stochastic Orders in Reliability and Risk: In Honor of Professor Moshe Shaked. New York: Springer. [Google Scholar]
- Lorenz, M. O. 1905. Methods of measuring the concentration of wealth. Publications of the American Statistical Association 9: 209–19. [Google Scholar] [CrossRef]
- Machina, Mark J. 1987. Choice under uncertainty: Problems solved and unsolved. Economic Perspectives 1: 121–54. [Google Scholar] [CrossRef]
- Machina, Mark J. 2008. Non-expected utility theory. In The New Palgrave Dictionary of Economics, 2nd ed. Edited by S. N. Durlauf and L. E. Blume. New York: Palgrave Macmillan, pp. 74–84. [Google Scholar]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management. Princeton: Princeton University Press. [Google Scholar]
- Mimoto, Nao, and Ricardas Zitikis. 2008. The Atkinson index, the Moran statistic, and testing exponentiality. Journal of the Japan Statistical Society 38: 187–205. [Google Scholar] [CrossRef]
- Meucci, Attilio. 2007. Risk and Asset Allocation. Berlin: Springer. [Google Scholar]
- Muliere, Pietro, and Marco Scarsini. 1989. A note on stochastic dominance and inequality measures. Journal of Economic Theory 49: 314–23. [Google Scholar] [CrossRef]
- Necir, Abdelhakim, and Djamel Meraghni. 2009. Empirical estimation of the proportional hazard premium for heavy-tailed claim amounts. Insurance: Mathematics and Economics 45: 49–58. [Google Scholar] [CrossRef]
- Necir, Abdelhakim, Djamel Meraghni, and Fatima Meddi. 2007. Statistical estimate of the proportional hazard premium of loss. Scandinavian Actuarial Journal 2007: 147–61. [Google Scholar] [CrossRef]
- Necir, Abdelhakim, Abdelaziz Rassoul, and Ricardas Zitikis. 2010. Estimating the conditional tail expectation in the case of heavy-tailed losses. Journal of Probability and Statistics 2010: 596839. [Google Scholar] [CrossRef]
- Nelsen, Roger B. 2006. An Introduction to Copulas, 2nd ed. New York: Springer. [Google Scholar]
- Nygård, Fredrik, and Arne Sandström. 1981. Measuring Income Inequality. Stockholm: Almqvist and Wiksell. [Google Scholar]
- Oladosu, Gbadebo, and Adam Rose. 2007. Income distribution impacts of climate change mitigation policy in the Susquehanna River Basin Economy. Energy Economics 29: 520–44. [Google Scholar] [CrossRef]
- Ostry, Jonathan D., Andrew Berg, and Charalambos G. Tsangarides. 2014. Redistribution, Inequality, and Growth. In IMF Staff Discussion Note SDN/14/02. Washington: International Monetary Fund. [Google Scholar]
- Palma, José Gabriel. 2006. Globalizing inEquality: ‘centrifugal’ and ‘centripetal’ Forces at Work. DESA Working Paper No 35. Washington, DC, USA: United Nations Department of Economics and Social Affairs. [Google Scholar]
- Pfähler, Wilhelm. 1990. Redistributive effect of income taxation: decomposing tax base and tax rates effects. Bulletin of Economic Research 42: 121–29. [Google Scholar] [CrossRef]
- Pflug, Georg Ch, and Werner Römisch. 2007. Modeling, Measuring and Managing Risk. Singapore: World Scientific. [Google Scholar]
- Pietra, Gaetano. 1915. On the relationship between variability indices (Note I). (English translation from Italian by P. Brutti and S. Gubbiotti). Metron 72: 5–16. [Google Scholar] [CrossRef]
- Piketty, Thomas. 2014. Capital in the Twenty-First Century. Cambridge: Harvard University Press. [Google Scholar]
- Puppe, Clemens. 1991. Distorted Probabilities and Choice under Risk. Berlin: Springer. [Google Scholar]
- Quiggin, John. 1982. A theory of anticipated utility. Journal of Economic Behavior and Organization 3: 323–43. [Google Scholar] [CrossRef]
- Quiggin, John. 1993. Generalized Expected Utility Theory: The Rank-Dependent Model. Dordrecht: Kluwer. [Google Scholar]
- Ramos, Hector M., Jorge Ollero, and Miguel A. Sordo. 2000. A sufficient condition for generalized Lorenz order. Journal of Economic Theory 90: 286–92. [Google Scholar] [CrossRef]
- Rassoul, Abdelaziz. 2013. Kernel-type estimator of the conditional tail expectation for a heavy-tailed distribution. Insurance: Mathematics and Economics 53: 698–703. [Google Scholar] [CrossRef]
- Rawls, John. 1971. A Theory of Justice. Cambridge: Harvard University Press. [Google Scholar]
- Roemer, John E. 2013. Economic development as opportunity equalization. World Bank Economic Review 28: 189–209. [Google Scholar] [CrossRef]
- Sadoulet, Elisabeth, and Alain de Janvry. 1995. Quantitative Development Policy Analysis. Baltimore: John Hopkins University Press. [Google Scholar]
- Sandström, Arne. 2010. Handbook of Solvency for Actuaries and Risk Managers: Theory and Practice. Boca Raton: Chapman and Hall. [Google Scholar]
- Sarabia, José María. 2008. Parametric Lorenz curves: Models and applications. In Modeling Income Distributions and Lorenz Curves. Edited by D. Chotikapanich. Berlin: Springer, pp. 167–90. [Google Scholar]
- Sarabia, José María, Faustino Prieto, and María Sarabia. 2010. Revisiting a functional form for the Lorenz curve. Economics Letters 107: 249–52. [Google Scholar] [CrossRef]
- Schmeidler, David. 1986. Integral representation without additivity. Proceedings of the American Mathematical Society 97: 255–61. [Google Scholar] [CrossRef]
- Schmeidler, David. 1989. Subjective probability and expected utility without additivity. Econometrica 57: 571–87. [Google Scholar] [CrossRef]
- Sen, Amartya. 1983. Poor, relatively speaking. Oxford Economic Papers 35: 153–69. [Google Scholar] [CrossRef]
- Sen, Amartya. 1997. On Economic Inequality (expanded Edition With a Substantial Annexe by J. E. Foster and A. Sen). Oxford: Clarendon Press. [Google Scholar]
- Sen, Amartya. 1998. Choice, Welfare and Measurement. Cambridge: Harvard University Press. [Google Scholar]
- Shaked, Moshe, and J. George Shanthikumar. 2007. Stochastic Orders. New York: Springer. [Google Scholar]
- Shorrocks, Anthony. 1978. Income inequality and income mobility. Journal of Economic Theory 19: 376–93. [Google Scholar] [CrossRef]
- Silber, Jacques. 1999. Handbook on Income Inequality Measurement. Boston: Kluwer. [Google Scholar]
- Slemrod, Joel. 1992. Taxation and inequality: A time-exposure perspective. In Tax Policy and the Economy. Edited by J. M. Poterba. Chicago: University of Chicago Press, vol. 6, pp. 105–27. [Google Scholar]
- Sordo, Miguel A., and Alfonso Suárez-Llorens. 2011. Stochastic comparisons of distorted variability measures. Insurance: Mathematics and Economics 49: 11–17. [Google Scholar] [CrossRef]
- Sordo, Miguel A., Jorge Navarro, and José María Sarabia. 2014. Distorted Lorenz curves: Models and comparisons. Social Choice and Welfare 42: 761–80. [Google Scholar] [CrossRef]
- Sriboonchita, Songsak, Wing-Keung Wong, Sompong Dhompongsa, and Hung T. Nguyen. 2010. Stochastic Dominance and Applications to Finance, Risk and Economics. Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- Tarsitano, Agostino. 1990. The Bonferroni index of income inequality. In Income and Wealth Distribution, Inequality and Poverty. Edited by C. Dagum and M. Zenga. New York: Springer, pp. 228–42. [Google Scholar]
- Tarsitano, Agostino. 2004. A new class of inequality measures based on a ratio of L-statistics. Metron 62: 137–60. [Google Scholar]
- Thompson, W. A., Jr. 1976. Fisherman’s luck. Biometrics 32: 265–71. [Google Scholar] [CrossRef]
- Van De Ven, Justin, John Creedy, and Peter J. Lambert. 2001. Close equals and calculation of the vertical, horizontal and reranking effects of taxation. Oxford Bulletin of Economics and Statistics 63: 381–94. [Google Scholar] [CrossRef]
- Vergnaud, J. C. 1997. Analysis of risk in a non expected utility framework and application to the optimality of the deductible. Revue Finance 18: 155–67. [Google Scholar]
- Wang, Shaun. 1995. Insurance pricing and increased limits ratemaking by proportional hazards transforms. Insurance: Mathematics and Economics 17: 43–54. [Google Scholar] [CrossRef]
- Wang, Shaun. 1998. An actuarial index of the right-tail risk. North American Actuarial Journal 2: 88–101. [Google Scholar] [CrossRef]
- Wang, Shaun S., and Virginia R. Young. 1998. Ordering risks: Expected utility theory versus Yaari’s dual theory of risk. Insurance: Mathematics and Economics 22: 145–61. [Google Scholar] [CrossRef]
- Wang, Shaun S., Virginia R. Young, and Harry H. Panjer. 1997. Axiomatic characterization of insurance prices. Insurance: Mathematics and Economics 21: 173–83. [Google Scholar] [CrossRef]
- Weymark, John A. 1981. Generalized Gini inequality indices. Mathematical Social Sciences 1: 409–30. [Google Scholar] [CrossRef]
- Weymark, John. A. 2003. Generalized Gini indices of equality of opportunity. Journal of Economic Inequality 1: 5–24. [Google Scholar] [CrossRef]
- Wirch, Julia Lynn, and Mary R. Hardy. 1999. A synthesis of risk measures for capital adequacy. Insurance: Mathematics and Economics 25: 337–47. [Google Scholar]
- Yaari, Menahem E. 1987. The dual theory of choice under risk. Econometrica 55: 95–115. [Google Scholar] [CrossRef]
- Yitzhaki, Shlomo. 1979. Relative deprivation and the Gini coefficient. Quarterly Journal of Economics 93: 321–24. [Google Scholar] [CrossRef]
- Yitzhaki, Shlomo. 1982. Stochastic dominance, mean variance, and Gini’s mean difference. American Economic Review 72: 178–85. [Google Scholar]
- Yitzhaki, Shlomo. 1983. On an extension of the Gini inequality index. International Economic Review 24: 617–28. [Google Scholar] [CrossRef]
- Yitzhaki, Shlomo. 1994. On the progressivity of commodity taxation. In Models and Measurement of Welfare and Inequality. Edited by W. Eichhorn. Berlin: Springer, pp. 448–66. [Google Scholar]
- Yitzhaki, Shlomo. 1998. More than a dozen alternative ways of spelling Gini. Research on Economic Inequality 8: 13–30. [Google Scholar]
- Yitzhaki, Shlomo. 2003. Gini’s mean difference: A superior measure of variability for non-normal distributions. Metron 51: 285–16. [Google Scholar]
- Yitzhaki, Shlomo, and Edna Schechtman. 2013. The Gini Methodology: A Primer on a Statistical Methodology. New York: Springer. [Google Scholar]
- Zenga, Michele. 2007. Inequality curve and inequality index based on the ratios between lower and upper arithmetic means. Statistica and Applicazioni 5: 3–27. [Google Scholar]
- Zenga, Michele. 2010. Mixture of Polisicchio’s truncated Pareto distributions with beta weights. Statistica and Applicazioni 8: 3–25. [Google Scholar]
- Zenga, Michele, Leo Pasquazzi, M. Polisicchio, and Mariangela Zenga. 2011. More on M. M. Zenga’s new three-parameter distribution for non-negative variables. Statistica and Applicazioni 9: 5–33. [Google Scholar]
- Zenga, Michele, Leo Pasquazzi, and Mariangela Zenga. 2012. First applications of a new three-parameter distribution for non-negative variables. Statistica and Applicazioni 10: 131–47. [Google Scholar]
- Zitikis, Ricardas. 2002. Analysis of indices of economic inequality from a mathematical point of view. Matematika 8: 772–82. [Google Scholar]
- Zitikis, Ricardas. 2003. Asymptotic estimation of the E-Gini index. Econometric Theory 19: 587–601. [Google Scholar] [CrossRef]
- Zoli, Claudio. 1999. A generalized version of the inequality equivalence criterion: A surplus sharing characterization, complete and partial orderings. In Logic, Game Theory and Social Choice. Edited by H. C. M. de Swart. Tilburg: Tilburg University Press, pp. 427–41. [Google Scholar]
- Zoli, Claudio. 2012. Characterizing Inequality Equivalence Criteria. Working Paper 32. Verona, Italy: Department of Economics, University of Verona. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).