Abstract
This paper offers a general and comprehensive definition of the day-of-the-week effect. Using symbolic dynamics, we develop a unique test based on ordinal patterns in order to detect it. This test uncovers the fact that the so-called “day-of-the-week” effect is partly an artifact of the hidden correlation structure of the data. We present simulations based on artificial time series as well. While time series generated with long memory are prone to exhibit daily seasonality, pure white noise signals exhibit no pattern preference. Since ours is a non-parametric test, it requires no assumptions about the distribution of returns, so that it could be a practical alternative to conventional econometric tests. We also made an exhaustive application of the here-proposed technique to 83 stock indexes around the world. Finally, the paper highlights the relevance of symbolic analysis in economic time series studies.
JEL Classification:
C14; C19; C58
1. Introduction
The static capital asset pricing model (CAPM), developed independently by Sharpe (1964), Lintner (1965) and Mossin (1966), has been widely used for a number of financial matters. In its standard form, the CAPM states that the expected risk to security i can be separated into two components: the risk free rate and the risk premium. The latter, in turn, can be explained as the product between the market premium and a modulating coefficient :
According to Equation (1), return on security i depends only on the risk free rate, market return, and beta. Consequently, return should not be altered by any other circumstances (such as the particular day of the week or the time of the year in which the return is measured). According to Fama (1970) a market is informationally efficient if it fully reflects all available information. In fact, as LeRoy (1989) asserts, the efficient market hypothesis (EMH) is just the idea of competitive equilibrium applied to the securities market.
Although early empirical studies (e.g., Blume and Friend 1973; Fama and MacBeth 1973) support the validity of the CAPM, later research documents depart from this equilibrium model. These departures are called “anomalies”1. Among them, there is one especially puzzling feature: the day-of-the-week effect. This anomaly refers to the heterogeneous behavior of returns along the week. Testing the the day-of-the-week effect requires the joint consideration of an equilibrium model, such as Equation (1), and of the efficient market hypothesis (EMH).
Empirical research on markets’ daily seasonality can be traced back to Fields (1931, 1934). These papers have the merit of investigating the issue before a market equilibrium model was formally developed. Cross (1973) detects differences in expected S&P 500 on Fridays and Mondays. Gibbons and Hess (1981) finds lower S&P 500 returns on Mondays relative to other days. The effect is subdivided by French (1980) into a Monday effect (abnormal negative return on this day) and a Friday effect (abnormal positive result on this day). Rogalski (1984) analyzes the effect during trading and non-trading hours for the American market. This effect has been widely surveyed and, for brevity, we refer to Keim and Ziemba (2000) and Ziemba (2012) for further discussion on empirical works about this effect. Keloharju et al. (2016) find return seasonalities in commodities and stock indices arround the world.
The standard approach for detecting the day-of-the week effect is based on the following regression equation (or some variations thereof):
where is the return on day t and , are dichotomous dummy variables for each day of the week from Tuesday through Friday. The coefficient represents the mean return on Monday, while , , is the excess return on day i, and is an error term. This traditional approach is based on different hypothesis testing on values (for an overview see, for instance, Bariviera and de Andrés Sánchez (2005) and references therein). Working based on Equation (2) forces several (sometimes unjustified) assumptions about parameters. For example, Zhang et al. (2017) applies a rolling sample test with a GARCH model in 28 stock indices. Precisely, our original approach, based on ordinal patterns, bypasses this shortcome.
The aim of this paper is to provide a more general definition of the day-of-the-week effect and to develop an alternative test to assess the existence of seasonal effects in daily returns. This paper contributes to the literature in several ways. First, it generalizes the definition of the day-of-the-week effect. Second, it develops an alternative non-parametric test to detect it. Third, it shows that the results of the tests are not obtained by chance, since time causality is taken into consideration. Fourth, most of the day-of-the-week findings in the literature are related with the underlying return-generating process, and not with the causes indicated previously in the literature. Consequently, from a theoretical point of view, this paper introduces a new non-parametric test that is able to detect the intrinsic characteristics of the time series, and uncovers spurious seasonality detection causes. We would like to point out that the methodology we use here is unique in that it is nonlinear, ordinal, requires no model, and provides statistical results in terms of a probability density function. Ours is a statistical methodology that, to the extent of our knowledge, no one using time series analysis has used before.
The remaining of the paper is organized as follows. Section 2 presents the notion of ordinal patterns. Section 3 redefines the day-of-the-week effect and proposes a non-parametric test. Section 4 displays results of the test on theoretical simulations of different stochastic processes. Section 5 performs an empirical application to the New York Stock Exchange. Finally, some conclusions are drawn in Section 6.
2. Ordinal Pattern Analysis
Estimations based on Equation (2) require the assumption of an underlying stochastic process for returns. For these processes, symbolic analysis becomes a suitable alternative to study the dynamics of a time series. Bandt and Pompe (2002) developed a method for estimating the probability distribution function (PDF) based on counting ordinal patterns. The comparison of neighboring values of a time series requires no model assumption. The advantage of this method is that can be applied to any time series, and takes into account time causality Bandt and Pompe (1993). If returns fulfill the efficient markethypothesis (EMH), there should be no privileged pattern. If there were to be a privileged pattern, it would be exploited by arbitrageurs and any possibility of abnormal return should be rapidly wiped out. Thus, if the time series is random, pattern frequency should be the same, provided If patterns are not equally present in the sample, three anomalous situations might be the cause:
- (1)
- Forbidden pattern: a pattern that does not appear within the sample.
- (2)
- Rare pattern: a pattern that seldom appears.
- (3)
- Preferred pattern: a pattern that emerges more often than expected by the uniform distribution.
In any of these cases, we are in presence of a time series with daily seasonal behavior. Consequently, the day-of-the week effect needs to be redefined.
In this line, Zanin (2008) applies the concept of forbidden patterns in order to assess market efficiency, and shows that different financial instruments could achieve different informational efficiency. According to Amigó et al. (2006), forbidden patterns can be used as a means of distinguishing chaotic and random trajectories and constitute a satisfactory alternative to more conventional techniques.
Ordinal patterns have been previously used by Zunino et al. (2010, 2011, 2012) in order to compute quantifiers like permutation entropy and permutation complexity, which, in turn, allow one to quantify the degree of informational efficiency of different markets. Rosso et al. (2012) demonstrates that forbidden patterns are a deterministic feature of nonlinear systems. Bariviera (2011), and Bariviera et al. (2012) show that the correlation structure and informational efficiency are not constant through time and could be affected by several factors such as liquidity or economic shocks.
Given a time series of daily returns2 beginning on Monday, . With a pattern length , following the Bandt and Pompe (2002) method, partitions of the time series could be generated. Each partition is a five-dimensional vector , which represents a whole trading week. Each return is associated with a day of the week. For simplicity, we have standing for Monday through Friday. The method sets the elements of each vector in increasing order. Doing so, each vector of returns is converted into a symbol. For example, if in a given week , where represents return on day , the pattern is . There are possible permutations. Each permutation produces a different pattern (P) and the associated frequencies can be easily computed. Each pattern has a frequency of appearance in the time series. Carpi et al. (2010) asserts that in correlated stochastic processes, pattern-frequency observations do not depend only on the time series’ length but also on the underlying correlation structure. Amigó et al. (2007, 2008) show that in uncorrelated stochastic processes, every ordinal pattern has an equal probability of appearance. Given that the ordinal pattern’s associated PDF is invariant with respect to nonlinear monotonous transformations, the method of Bandt and Pompe (2002) results suitable for experimental data (see e.g., Parlitz et al. 2012; Saco et al. 2010). A graphical meaning of the ordinal pattern can be seen in Parlitz et al. (2012).
3. Day-of-the-Week Effect: A Redefinition of the Problem
As recalled in Section 1, the conventional definition of the day-of-the-week effect refers to the abnormal negative or abnormal positive returns on Monday and Friday, respectively. Since not all the markets are open on the same days, comparisons among countries could be difficult. For example, the Israeli market is open from Sunday through Thursday (Lauterbach and Ungar (1992)) and the first day of the week in the Kuwait Stock Exchange is Saturday (Al-Loughani and Chappell 2001). Additionally, markets are not open simultaneously, due to the different time zones (Koh and Wong 2000). Consequently, spill-over effects can influence returns and could distort results if such influence is not incorporated into the model.
In order to overcome these difficulties, we develop here a more general definition of the day-of-the-week effect that exploits the potential of the symbolic analysis of time series. Instead of estimating the return on each day by means of Equation (2), we will look at the relative position of the return on each day within its week. If there is no seasonal effect, the order in which the days appear in each position (from the worst until the best return of the week), should be random. Otherwise, a seasonal pattern would be detected.
First, we need to give an specific definition of our seasonal effect. It must be emphasized that, according to our proposal, we are not interested in detecting abnormal negative or positive returns on a given day. Instead, we are looking for the features of the return on a given day within its week, from the worst return of the week to the best return, independently of its sign. Thus, a new definition of the day-of-the-week effect is required.
Definition 1.
The day-of-the-week effect occurs whenever a pattern appears much more or less frequently than expected by the uniform distribution.
From this definition a natural null hypotheses arises:
Hypothesis 1.
where , , stands for “absolute frequency of pattern k”.
Since we are interested in studying the day-of-the week effect, testing this hypothesis is insufficient for our purposes.
We should count the number of times in which a given day exhibits the worst return of the week, the next to worst return, and so on, until the best return of the week is detected. In other words, we should count the number of times a given day i occupies the first, second, third, fourth, or fifth position in a pattern and place the absolute frequencies in a matrix as follows:
Definition 2.
Let be a 5 × 5 matrix. Element is the absolute frequency of return on day i at the position j.
Displaying results in this way, we count how many times a given day is in position 0 (the worst return of the week), position 1, position 2, position 3, and position 4 (the best return of the week). As a consequence, we advance two additional hypotheses:
Hypothesis 2.
This hypothesis says that a given day i could occupy any position, from the worst to the best return, within a week.
Hypothesis 3.
This hypothesis says that a given position in the week j could be occupied by any day of the week.
All these null hypotheses could be tested using Pearson’s chi-squared test. This test is useful to verify if there is a significant difference between an expected frequency distribution and an observed frequency distribution. Following Fernández Loureiro (2011) the test statistic is:
where is the observed frequency of day i at position j, and is the expected frequency . Q is distributed asymptotically as a with 4 degrees of freedom.
We advance two additional hypotheses focused on the so-called “Monday effect”.
Hypothesis 4.
This hypothesis tests whether patterns with Monday having the largest return are preferred patterns or not. Pattern numbers correspond to those displayed in Table 1.

Table 1.
Ordinal patterns. Each number of a pattern represents a day of the week, beginning on Monday. The position of the numbers in a pattern represents the increasing order of returns within a week.
Hypothesis 5.
This hypothesis tests whether the patterns with Monday exhibiting the lowest weekly return and Friday the largest are preferred patterns or not.
These hypotheses are tested using the binomial test, which for large samples can be approximated by the normal distribution. The test statistic is:
where is the observed frequency, , is the expected frequency, and N is the number of “weeks”, i.e., the number of 5-day patterns in the sample.
Our definition assumes that the day-of-the-week effect could be produced by the dependence among days of the same week. However, by splitting time series into weeks, we implicitly assume the independence among weeks. Even though this later assumption may be questionable, we do it this way in order to emphasize the order of the returns within the week. We could relax this assumption by moving data daily, instead of weekly. In this way, we could compare if, e.g., Friday in week t influences Monday in week However, it could result in a more confused analysis, and we thus leave this for further research.
4. Simulation of Fractional Brownian Motion
In this section we apply the above-outlined technique to simulated time series. We used the MATLAB wfbm function in order to simulate fractional Brownian motion for , where is the Hurst exponent. Then, we take first differences in the time series in order to obtain the corresponding fractional Gaussian noise (fGn). The Hurst exponent H characterizes the scaling behavior of the range of cumulative departures of a time series from its mean. The study of long-range dependence can be traced back to a seminal paper by Hurst (1951), whose original methodology was applied to detect long memory in hydrologic time series. This method was also explored by Mandelbrot and Wallis (1968) and later introduced in the study of economic time series by Mandelbrot (1972). If the series of first differences is a white noise, then its . Alternatively, Hurst exponents greater than 0.5 reflect persistent processes and less than 0.5 define antipersistent processes.
We perform 1000 simulations consisting of 10,000 data-points for each value of . Accordingly, we obtain 2000 “weeks”, which will be classified into one of the possible patterns. If the underlying stochastic process is purely random and uncorrelated, the frequency of patterns should be uniform. On the contrary, if some correlation is present, some patterns could be preferred over others. All the tests are performed at a significance level.
In Table 2 we test the equality of patterns (Hypothesis 1). When (ordinary Gaussian noise), we cannot reject, on average, the null hypothesis of equal appearance of patterns. Out of the 1000 simulations, only in 50 cases is the null hypothesis rejected. When we move away from , in both directions, rejection increases almost symmetrically. This clearly shows that some kind of correlation affects the distribution of ordinal patterns.

Table 2.
Test of Hypothesis 1 on simulated series.
As commented in the previous section, this analysis is not sufficient. Therefore, we proceed to test Hypothesis 2 and present the pertinent results in Table 3. We test the hypothesis (for every value) for each of the samples and for the average of the samples. We find that for we cannot reject the null hypothesis. In fact, rejection occurs in only 51–59 times out of 1000 samples. In other words, when the generating stochastic process is a white noise, any day is equally prone to occupying any of the positions in the pattern. This is the same as saying that any day could exhibit the best or the worst return of the week, or any intermediate value among them. When we move away from the value 0.5, rejections increase. However, the effect is stronger for than for . This could mean that a positive long -range correlation (i.e., a persistent time series) is more likely to exhibit a day-of-the-week behavior than anti-persistent time series. Additionally, Monday, Wednesday, and Friday are the days most affected by the value-change of .

Table 3.
Test of Hypothesis 2 on simulated series.
Regarding Hypothesis 3, results are displayed in Table 4. In the case of the uncorrelated process (), one encounters that how good or bad the return is within a trading week is independent of the day of the week. This hypothesis is only rejected only 59 times out of the 1000 simulations. When we move away, and then correlations become stronger, and patterns exhibit some degree of preference, increasing the number of rejections. As in the case of Hypothesis 3, rejections are more frequent in the case of persistent time series.

Table 4.
Test of Hypothesis 3 in simulated series.
Hypothesis 4 tests whether the presence of patterns with Monday as the largest return is in agreement with the uniform distribution. There are 24 patterns with Monday as the last element. Consequently, the expected frequency is 0.2. Table 5 displays the results of the simulations. In the case of a pure Gaussian noise, we cannot reject the null hypothesis, as in only 117 out of the 1000 trials we reject it. However, increasing the Hurst exponent produces an increment in the number of rejections. Additionally, we observe that larger Hurst values are associated with greater observed frequency of patterns with Monday as largest return. However, we cannot reject the null hypothesis until or higher.

Table 5.
Test of Hypothesis 4 in simulated series.
Hypothesis 5 tests the presence of a weekly seasonality with Monday as the smallest return of the week and Friday as the largest. There are six patterns with this structure. In analogy with the preceding finding, for an uncorrelated noise, this pattern is neither a preferred nor a rare one. Nevertheless, the increase of the Hurst exponent produces a quick increase in the number of rejections: 309 out of 1000 when . More impressive is how preferred this pattern is in most of the simulations. For , in 698 simulations, the observed frequency of these six patterns was above expectations, and for , in 873 simulations (see Table 6).

Table 6.
Test of Hypothesis 5 in simulated series.
Symbolic analysis is powerful for detecting nontrivial hidden correlations in data. As shown by Carpi et al. (2010); Rosso et al. (2012), a correlated structure as produced by fractional Gaussian noise processes generates an uneven presence of patterns. Provided a sufficiently long time series, no pattern is forbidden. However, a strongly correlated structure produces the emergence of preferred and rare patterns.
Our artificial time series are larger than the usual data sets used in economics. Consequently, the presence of preferred patterns such as the ones evaluated in Hypothesis 5 casts doubts on the validity of previous findings of day-of-the-week. In particular, we claim that, in view of our results, the day-of-the-week effect is mainly produced by a complex correlation structure of the pertinent data.
5. Empirical Application
We used daily data of the NYSE Composite Price Index from 3 January 1966 to 8 December 2017, with a total of 13,550 observations. All data used in this paper was retrieved from Datastream. We split the sample into four non-overlapping periods of equal length (3050 data points), and a final period of 1350 datapoints, in order to verify the temporal evolution of the seasonal effect. We compute daily log returns in order to apply our test.
Regarding Hypothesis 1 (see Table 7), we find, in the whole sample, no forbidden patterns. Under these circumstances, we should discard chaotic behavior in the time series (Rosso et al. 2012). The least frequent pattern, with an absolute frequency equal to 7, is 42013 (i.e., ). The most frequent patterns, with an absolute frequency equal to 34, are 03421 and 04312 (i.e., and , respectively). As stated in Section 2, if data was generated at random, i.e., if no seasonal effect exists, patterns should uniformly appear, configurating the histogram of a uniform distribution. However, as seen in Figure 1, ours is a far from uniform distribution.

Table 7.
Absolute frequency of each pattern. Whole period: 3 January 1966–8 December 2017. Each number of a pattern represents a day of the week, beginning on Monday. The position of the numbers in a pattern represents the increasing order of returns within a week.
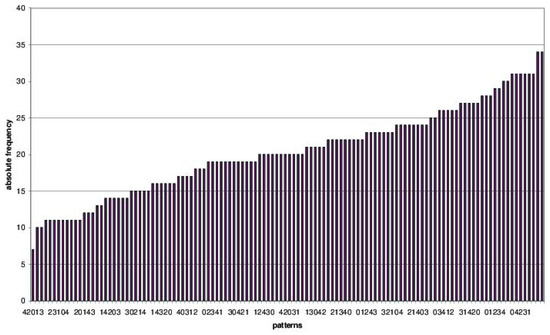
Figure 1.
Histogram of pattern frequency for the whole period.
Table 8 exhibits frequencies and tests for Hypotheses 2 and 3. Following the horizontal lines of the table, we test whether a given day indifferently occupies any position in the returns of the week. Along the vertical sense of the table, we test whether a given position within a week is indifferently occupied by any day.

Table 8.
Absolute frequency of each day in each position. Whole period: 3 January 1966–8 December 2017. Columns 2 to 6 reflect the frequency a given day in terms of the worst return of its week, the next to worst return, etc. until the best return of its week. Q is the statistic defined in Equation (6). Hurst = 0.5471.
Regarding the whole period, we observe that we cannot accept the null hypothesis of equal distribution of returns across the week. In fact, if we observe Table 8, Monday acquires the lowest return of the week more frequently than any other week-day.
In order to justify the fact that intrinsic temporal correlations play a significant role in the ordinal patterns, we have also estimated the frequency of the patterns for the shuffled return data. “Shuffled” realizations of the original data are obtained by permuting them in random order, and eliminating, consequently, all non-trivial temporal correlations. From Table 9, we observe that patterns are distributed in a more or less uniform fashion and, consequently, we cannot reject the null hypotheses. Therefore, the results of our test are not due to chance.

Table 9.
Absolute frequency of each day in each position with shuffled data for the whole period. Columns 2 to 6 reflect the frequency a given day in terms of the worst return of its week, the next to worst return, etc. until the best return of its week. Q is the statistic defined in Equation (6).
If we analyze the evolution of the daily seasonal behavior through time, it is clear that the day-of-the-week effect disappears in daily returns of the NYSE Composite index. Results are reflected in Table 10, Table 11, Table 12, Table 13 and Table 14. Considering the last subperiod, only Tuesday’s effect remains. Tuesday is the most frequent day in the worst position and Friday tends to occupy the best return within each week. However, we cannot reject that the worst return of the week can be occupied by any other week- day. According to this analysis we observe, in agreement with the literature, a disappearing weekly effect in daily returns in the US market. This disappearing effect is related to the hidden underlying dynamics of data, rather than markets participant behavior, as was classically envisaged in the literature. We would like to emphasize that our test unveils the hidden correlation structure of daily returns. As in the case of the artificial generated series, the pattern behavior in real time series is strongly affected by the long memory of data.

Table 10.
Absolute frequency of each day in each position. Subperiod 1: 3 January 1966–9 September 1977. Columns 2 to 6 reflect the frequency a given day in terms of the worst return of its week, the next to worst return, etc. until the best return of its week. Q is the statistic defined in Equation (6). Hurst = 0.5633.

Table 11.
Absolute frequency of each day in each position. Subperiod 2: 12 September 1977–19 May 1989. Columns 2 to 6 reflect the frequency a given day is the worst return of its week, the next to worst return, etc. until the best return of its week. Q is the statistic defined in Equation (6). Hurst = 0.5168.

Table 12.
Absolute frequency of each day in each position. Subperiod 3: 22 May 1989–26 January 2001. Columns 2 to 6 reflect the frequency a given day in terms of the worst return of the week, the next to worst return, etc. until the best return of its week. Q is the statistic defined in Equation (6). Hurst = 0.4453.

Table 13.
Absolute frequency of each day in each position. Subperiod 4: 29 January 2001–5 October 2012. Columns 2 to 6 reflect the frequency a given day in terms of the worst return of the week, the next to worst return, etc. until the best return of its week. Q is the statistic defined in Equation (6). Hurst = 0.4983

Table 14.
Absolute frequency of each day in each position. Subperiod 5: 8 October 2012–8 December 2017. Columns 2 to 6 reflect the frequency a given day in terms of the worst return of the week, the next to worst return, etc. until the best return of its week. Q is the statistic defined in Equation (6). Hurst = 0.4914.
An important difference between real and simulated data is that, whereas in the controlled experiment the Hurst exponent is, by definition, constant across all the time series, in the case of real data, the Hurst exponent tends to vary across time (see e.g., Bariviera et al. 2012; Cajueiro and Tabak 2004a, 2004b). This situation makes a direct comparison between both results difficult. Moreover, we can observe that the power of the test is more sensitive for in detecting the Monday effect (see Table 6 ). In fact, for , the test rejects 856 out of the 1000 simulated series. Another factor that influences results is the time series length. As recalled by Rosso et al. (2012), short time series could result in the incorrect detection of forbidden patterns.
In the Supplementary Material file we present the simulation and test of hypotheses for shorter time series. Additionally, we perform an exhaustive analysis of 83 stock indices with different Hurst levels. We can observe that greater Hurst levels are associated with more significant presence of preferred patterns.
It is clear that theoretical and empirical analyses exhibit some differences. We have to acknowledge that real stock markets dynamics do not follow a pure fGn . In fact, long-range dependence is not only seen in financial time series, but also in volatility, as shown recently by Bariviera (2017). Precisely, more advanced models such as the fractional normal tempered stable process presented by Kim (2012, 2015), allow for long-range dependence in both volatility and noise, and asymmetric dependence structure for the joint distribution. There are many economic variables that influence behaviors known as “stylized facts” of financial time series: volatility clustering, fat tails, asymmetric dependence, etc. For example, Kim (2016) found that long-range dependence increased more in volatile markets during the Lehman Brothers collapse.
We try to emphasize in this paper that, even using a simple model such as a fGn, some part of the seasonal effect is simply due to the correlation structure of data, and not only due to economic reasons. This finding could be used as a starting point in further research in order to apply prewhitening to time series prior to its analysis in order to obtain more reliable results.
6. Conclusions
We propose a more general definition of the day-of-the-week effect. We use symbolic time series analysis in order to develop a test to detect it. According to Definition 1, this effect takes place when a pattern is much more or much less frequent than expected from the uniform distribution. The nature of the seasonal effect is reflected in a frequency matrix (Definition 2), and a test is performed. The new definition allows for a more general and comprehensive study on return seasonality. We would like to highlight that the methodology we use here is unique in that it is nonlinear, ordinal, and requires no a priori model. Additionally, it provides statistical results in terms of a probability density function. To the extent of our knowledge, time series analysis has not been used in a similar methodology before.
Both theoretical and empirical applications show that this method could be useful to discriminate between rare and preferred patterns of a time series. We show that the so-called day-of-the-week effect is influenced not only by traders’ behavior or economic variables. It could be also be induced by the stochastic generating process of data. The findings in this paper could be taken into account in future research, aiming at the separation between the economics causes and the long-range correlation causes of this financial phenomenon.
Acknowledgments
The authors thank two anonymous referees for their helpful comments and suggestions.
Author Contributions
A.F.B. conceived, designed and performed the experiments; A.F.B., A.P. and J.G. analyzed the data and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Al-Loughani, Nabeel, and David Chappell. 2001. Modelling the day-of-the-week effect in the kuwait stock exchange: A nonlinear garch representation. Applied Financial Economics 11: 353–59. [Google Scholar] [CrossRef]
- Amigó, José M., Ljupco Kocarev, and Janusz Szczepanski. 2006. Order patterns and chaos. Physics Letters A 355: 27–31. [Google Scholar] [CrossRef]
- Amigó, José. M., Samuel Zambrano, and Miguel A. F. Sanjuán. 2007. True and false forbidden patterns in deterministic and random dynamics. EPL (Europhysics Letters) 79: 50001. [Google Scholar] [CrossRef]
- Amigó, José. M., Samuel Zambrano, and Miguel A. F. Sanjuán. 2008. Combinatorial detection of determinism in noisy time series. EPL (Europhysics Letters) 83: 60005. [Google Scholar] [CrossRef]
- Bandt, Christoph, and Bernd Pompe. 1993. The entropy profile—A function describing statistical dependences. Journal of Statistical Physics 70: 967–83. [Google Scholar] [CrossRef]
- Bandt, Christoph, and Bernd Pompe. 2002. Permutation entropy: A natural complexity measure for time series. Physical Review Letters 88: 174102. [Google Scholar] [CrossRef] [PubMed]
- Bariviera, Aurelio Fernández. 2011. The influence of liquidity on informational efficiency: The case of the thai stock market. Physica A: Statistical Mechanics and its Applications 390: 4426–32. [Google Scholar] [CrossRef]
- Bariviera, Aurelio Fernández. 2017. The inefficiency of bitcoin revisited: A dynamic approach. Economics Letters 161 SC: 1–4. [Google Scholar] [CrossRef]
- Bariviera, Aurelio Fernández, and Jorge de Andrés Sánchez. 2005. Existe estacionalidad diaria en el mercado de bonos y obligaciones del estado evidencia empírica en el período 1998–2003. Análisis Financiero 98: 16–21. [Google Scholar]
- Bariviera, Aurelio F., M. Belén Guercio, and Lisana B. Martinez. 2012. A comparative analysis of the informational efficiency of the fixed income market in seven european countries. Economics Letters 116: 426–28. [Google Scholar] [CrossRef]
- Blume, Marshall E., and Irwin Friend. 1973. A new look at the capital asset pricing model. The Journal of Finance 28: 19–33. [Google Scholar] [CrossRef]
- Cajueiro, Daniel O., and Benjamin M. Tabak. 2004a. Evidence of long range dependence in asian equity markets: The role of liquidity and market restrictions. Physica A: Statistical Mechanics and Its Applications 342: 656–64. [Google Scholar] [CrossRef]
- Cajueiro, Daniel O., and Benjamin M. Tabak. 2004b. The hurst exponent over time: Testing the assertion that emerging markets are becoming more efficient. Physica A: Statistical and Theoretical Physics 336: 521–37. [Google Scholar] [CrossRef]
- Carpi, Laura C., Patricia M. Saco, and O. A. Rosso. 2010. Missing ordinal patterns in correlated noises. Physica A: Statistical Mechanics and Its Applications 389: 2020–29. [Google Scholar] [CrossRef]
- Cross, Frank. 1973. The behavior of stock prices on fridays and mondays. Financial Analysts Journal 29: 67–69. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417, Papers presented at the Twenty-Eighth Annual Meeting of the American Finance Association New York, NY, USA, December 28–30, 1969. [Google Scholar]
- Fama, Eugene F., and James D. MacBeth. 1973. Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81: 607–36. [Google Scholar] [CrossRef]
- Fernández Loureiro, Emma. 2011. Estadística no Paramétrica: A Modo De Introducción. Buenos Aires: Ediciones Cooperativas. [Google Scholar]
- Fields, M. J. 1931. Stock prices: A problem in verification. The Journal of Business of the University of Chicago 4: 415–18. [Google Scholar] [CrossRef]
- Fields, M. J. 1934. Security prices and stock exchange holidays in relation to short selling. The Journal of Business of the University of Chicago 7: 328–38. [Google Scholar] [CrossRef]
- French, Kenneth R. 1980. Stock returns and the weekend effect. Journal of Financial Economics 8: 55–69. [Google Scholar] [CrossRef]
- Gibbons, Michael R., and Patrick Hess. 1981. Day of the week effects and asset returns. The Journal of Business 54: 579–96. [Google Scholar] [CrossRef]
- Hurst, Harold E. 1951. Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers 116: 770–808. [Google Scholar]
- Keim, Donald B., and William T. Ziemba, eds. 2000. Security Market Imperfections in Worldwide Equity Markets. Cambridge: Cambridge University Press. [Google Scholar]
- Keloharju, Matti, Juhani T. Linnainmaa, and Peter Nyberg. 2016. Return seasonalities. The Journal of Finance 71: 1557–90. [Google Scholar] [CrossRef]
- Kim, Young Shin. 2012. The fractional multivariate normal tempered stable process. Applied Mathematics Letters 25: 2396–401. [Google Scholar] [CrossRef]
- Kim, Young Shin. 2015. Multivariate tempered stable model with long-range dependence and time-varying volatility. Frontiers in Applied Mathematics and Statistics 1: 1. [Google Scholar] [CrossRef]
- Kim, Young Shin. 2016. Long-range dependence in the risk-neutral measure for the market on lehman brothers collapse. Applied Mathematical Finance 23: 309–22. [Google Scholar]
- Koh, Seng-Kee, and Wong Kie-Ann. 2000. Anomalies in asian emerging stock markets. In Security Market Imperfections in Worldwide Equity Markets. Edited by Donald Bruce Keim and William T. Ziemba. Cambridge: Cambridge University Press, pp. 353–59. [Google Scholar]
- Kuhn, Thomas S. 1968. The Structure of Scientific Revolutions. Chicago: University of Chicago. [Google Scholar]
- Lauterbach, Beni, and Meyer Ungar. 1992. Calendar anomalies: Some perspectives from the behaviour of the israeli stock market. Applied Financial Economics 2: 57–60. [Google Scholar] [CrossRef]
- LeRoy, Stephen F. 1989. Efficient capital markets and martingales. Journal of Economic Literature 27: 1583–621. [Google Scholar]
- Lintner, John. 1965. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. The Review of Economics and Statistics 47: 13–37. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B. 1972. Statistical methodology for nonperiodic cycles: From the covariance to rs analysis. In Annals of Economic and Social Measurement, Volume 1, Number 3. NBER Chapters. Cambridge: National Bureau of Economic Research, pp. 259–90. December. [Google Scholar]
- Mandelbrot, Benoit B., and James R. Wallis. 1968. Noah, joseph, and operational hydrology. Water Resources Research 4: 909–18. [Google Scholar] [CrossRef]
- Mossin, Jan. 1966. Equilibrium in a capital asset market. Econometrica 34: 768–83. [Google Scholar] [CrossRef]
- Parlitz, Ulrich, Sebastian Berg, Stefan Luther, Alexander Schirdewan, Jürgen Kurths, and Niels Wessel. 2012. Classifying cardiac biosignals using ordinal pattern statistics and symbolic dynamics. Computers in Biology and Medicine 42: 319–27. [Google Scholar] [CrossRef] [PubMed]
- Rogalski, Richard J. 1984. New findings regarding day-of-the-week returns over trading and non-trading periods: A note. The Journal of Finance 39: 1603–14. [Google Scholar] [CrossRef]
- Rosso, Osvaldo A., Laura C. Carpi, Patricia M. Saco, Martin Gómez Ravetti, Hilda A. Larrondo, and Angelo Plastino. 2012. The amigó paradigm of forbidden/missing patterns: A detailed analysis. The European Physical Journal B 85: 1–12. [Google Scholar] [CrossRef]
- Saco, Patricia M., Laura C. Carpi, Alejandra Figliola, Eduardo Serrano, and Osvaldo A. Rosso. 2010. Entropy analysis of the dynamics of el niño/southern oscillation during the holocene. Physica A: Statistical Mechanics and Its Applications 389: 5022–27. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance 19: 425–42. [Google Scholar]
- Zanin, Massimiliano. 2008. Forbidden patterns in financial time series. Chaos 18: 936–47. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Jilin, Yongzeng Lai, and Jianghong Lin. 2017. The day-of-the-week effects of stock markets in different countries. Finance Research Letters 20 SC: 47–62. [Google Scholar] [CrossRef]
- Ziemba, William T., ed. 2012. Calendar Anomalies and Arbitrage. Singapore: World Scientific. [Google Scholar]
- Zunino, Luciano, Aurelio Fernández Bariviera, M. Belén Guercio, Lisana B. Martinez, and Osvaldo A. Rosso. 2012. On the efficiency of sovereign bond markets. Physica A: Statistical Mechanics and its Applications 391: 4342–49. [Google Scholar] [CrossRef]
- Zunino, Luciano, Benjamin M. Tabak, Francesco Serinaldi, Massimiliano Zanin, Darío G. Pérez, and Osvaldo A. Rosso. 2011. Commodity predictability analysis with a permutation information theory approach. Physica A: Statistical Mechanics and Its Applications 390: 876–90. [Google Scholar] [CrossRef]
- Zunino, Luciano, Massimiliano Zanin, Benjamin M. Tabak, Darío G. Pérez, and Osvaldo A. Rosso. 2010. Complexity-entropy causality plane: A useful approach to quantify the stock market inefficiency. Physica A: Statistical Mechanics and Its Applications 389: 1891–901. [Google Scholar] [CrossRef]
| 1 | According to Kuhn (1968), an anomaly is a fact that puts into question an established paradigm. |
| 2 | Let us assume that the time series is characterized by a continuous distribution. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).