1. Introduction
Changes in housing prices, and in turn changes in housing wealth, exert substantial effects on the economy: increased housing wealth is strongly associated with increased aggregate consumption, cf.
Case et al. (
2005), and vice versa, cf.
Case et al. (
2013). Housing wealth has (together with pension wealth) also been found to be a primary driver of the share of total wealth accruing to the middle class,
1 cf.
Saez and Zucman (
2016). For example, higher housing prices have historically been associated with the middle class owning a greater share of total wealth, and thereby with a lower level of inequality. Consequently, understanding the drivers and dynamics of housing prices is of material importance to economists and policy makers alike.
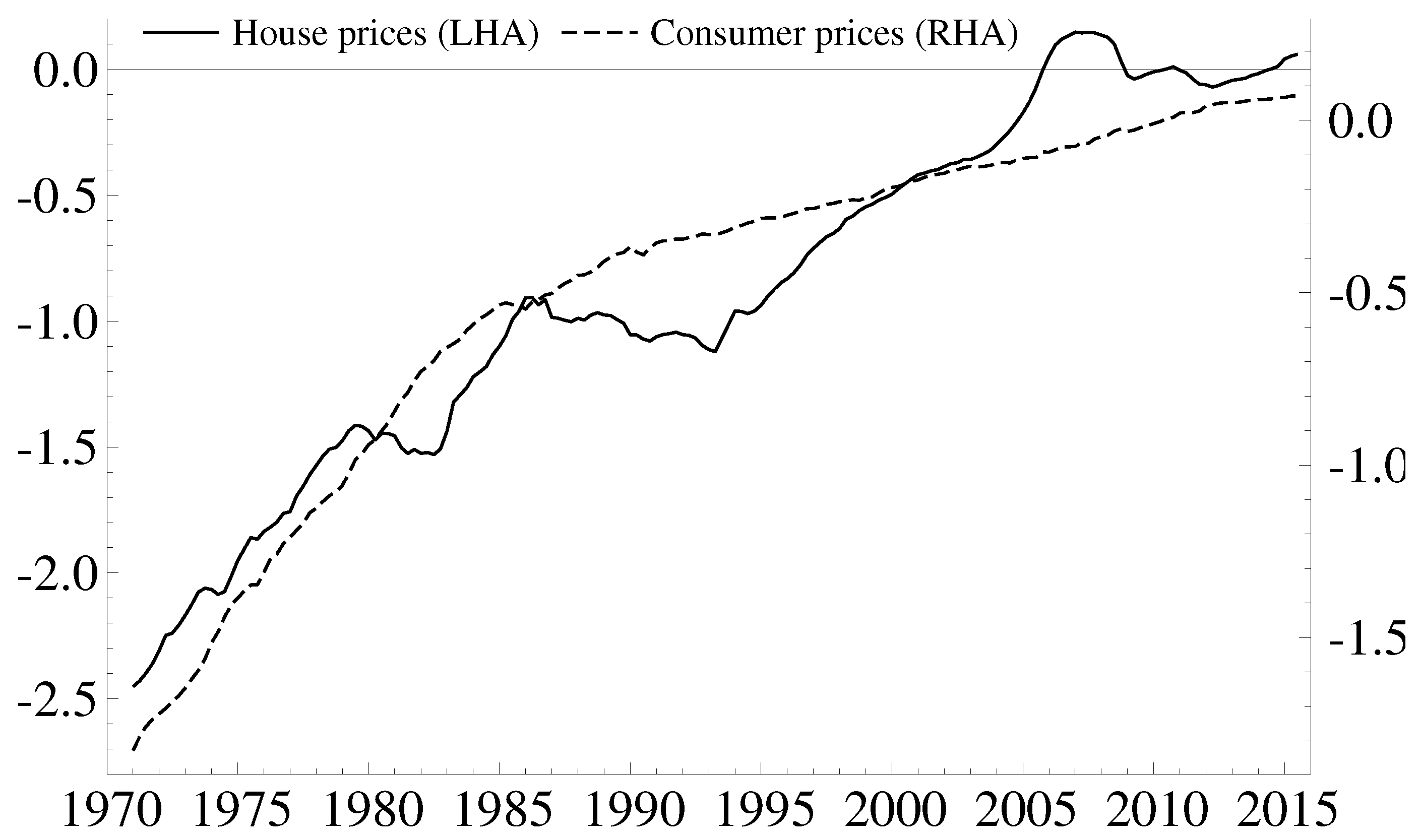
The market price of housing has a tendency to undergo prolonged periods of increases that outpace both incomes and other prices, see e.g.,
Case et al. (
2003) for a study of the US housing market. We have observed similar long-swings patterns in the Danish housing market, see
Figure 1.
2 The Danish national price index for housing increased by 65% between 2003:Q1 and 2007:Q4, while the general price level increased by only 8% over the same period, meaning that housing outpaced inflation by 57 percentage points. In 2008, the housing boom turned to bust as the global economy fell in to recession. Danish house prices fell by 17% between 2008:Q1 and 2012:Q4, while the general price level increased by 10%, closing most of the gap created during the boom years. Moreover, prolonged deviations are not just a phenomenon of the relatively recent past. Housing price changes have either persistently outpaced or fallen behind consumer price inflation since the late 1970s. For example, housing prices slumped during the late 1980s and early 1990s, with inflation outpacing house price increases by 43 percentage points between 1986:Q1 and 1993:Q2. The house price increases then accelerated and had completely closed the gap by 1998:Q2.
Given that housing prices play an important role in the wider economy, the determinants of the market price of housing have been the focus of numerous studies. In this paper, we focus on the approach which treats housing as a carry-generating physical asset that can be reproduced at the cost of construction, cf.
Poterba (
1984). This approach falls under the general asset pricing theory, which typically represents the uncertainty associated with the future value of an asset in the form of a probability distribution, cf. e.g.,
Björk (
2009). Investors’ expectation of the future value of the asset is then assumed to follow the mathematical expectation with respect to this probability distribution. This is known as rational expectations in the wider context of economic modelling, cf. e.g.,
Muth (
1961) and
Sargent and Wallace (
1975). However, in the case of housing, several studies from the US have found evidence in support of individual investors forming their expectations based on extrapolation of recent price changes, see
Case and Shiller (
1989),
Poterba (
1991),
Case et al. (
2003),
Shiller (
2008), and
Piazzesi and Schneider (
2009). As remarked in these studies, the observed momentum-based expectation formation appears incompatible with the assumption of rational expectations.
Some have argued that rational expectations-based approaches conflate the fundamentally different notions of risk and uncertainty, where the former may be expressed as a probability distribution while the latter cannot, see e.g.,
Savage (
1951),
Rutherford (
1984),
Lawson (
1988) and
Binmore (
2009). This distinction has important implications for the appropriateness of rational expectations, and has gained traction with central bank economists in recent years, see e.g.,
King (
2004),
Carney (
2016) and
ECB (
2016). More generally this type of thinking has led to alternative paradigms for expectation formation. For example,
Akerlof and Shiller (
2009) argue that investor psychology is driven by “animal spirits” such as confidence, money illusion and narratives.
Frydman et al. (
2007) advances the imperfect knowledge economics theory, in which individuals change their forecasting strategies in ways that need not be given by expectations with respect to a model-implied probability distribution. Elsewhere in the field of psychology, large-scale forecasting experiments have led to the finding that while “forecasting is often viewed as a statistical problem, [...] forecasts can be improved with behavioural interventions [... such as] training, teaming, and tracking.”, cf.
Mellers et al. (
2014), which suggests that, in practice, expectation formation for macroeconomic outcomes goes beyond the problem of identifying an appropriate statistical model.
In this paper we seek to explain the long-swings dynamic in Danish housing prices (
Figure 1). We do this by developing an asset market model based on uncertainty rather than risk, which allows other forms of forecasting behavior than rational expectations, such as momentum-based forecasting (cf. e.g.,
Case et al. (
2003)). However, since we do not have survey data of individual expectations in the Danish housing market, we introduce the assumption that the expectation errors are stationary (Assumption A in
Juselius (
2017b)). Additionally, we introduce the notion of a gap effect as a measure of the required uncertainty premium, cf.
Frydman et al. (
2007), specified in terms of Tobin’s q, cf.
Tobin (
1969). This uncertainty-based asset market approach produces a set of testable hypotheses on the long-run relationships governing the Danish housing prices, which we confront with the data via a cointegrated vector autoregressive (CVAR) model, see e.g.,
Juselius (
2007) and
Johansen (
1996). The CVAR model provides a general-to-specific framework, which allows us to start the empirical analysis with a sufficiently well-specified, unrestricted VAR model of the Danish housing market, and then impose restrictions corresponding to hypotheses arising from the theoretical model, cf. e.g.,
Hoover et al. (
2008). Importantly, this approach also allows us to infer the process by which the market adjusts when out of equilibrium; specifically, the interplay between long-run and medium-run dynamics may be able to explain long swings around the equilibrium, cf.
Juselius and Assenmacher (
2016, Section 5).
The paper proceeds as follows: in
Section 2, we introduce the theoretical framework for the uncertainty-based no-arbitrage condition, and derive a set of empirically testable hypotheses.
Section 3 specifies an
I(2) CVAR model and tests the hypotheses presented in
Section 2. Finally, we conclude in
Section 4.
3. Specifying an I(2) CVAR Model for the Danish Housing Market
We now turn our attention to confronting the hypotheses derived from the theoretical framework presented in
Section 2 with historical data for the Danish housing market. Specifically, to investigate the empirical relevance of the cointegrating relations in
Section 2.4, we here introduce the
I(2) cointegrated vector autoregressive (CVAR) model. The method applied to arrive at a well-specified, properly identified system is outlined in
Juselius (
2007), while a mathematical exposition of the model, estimation and inference can be found in
Johansen (
1996). An appealing feature of the CVAR framework is that through testing and subsequently imposing restrictions on an unrestricted VAR, such as rank restrictions, zero parameter restrictions, and other restrictions, we arrive at a more parsimonious model with economically interpretable coefficients. As such, specifying a CVAR with an over-identified long-run structure adheres to the general-to-specific procedure outlined in e.g.,
Campos et al. (
2005).
3.1. The Information Set
Our empirical analysis is based on variables that are part of the “MONA” database maintained by the Danish Central Bank, cf.
Danmarks Nationalbank (
2003). This database contains quarterly observations of variables for the Danish economy from 1971:Q1 to 2015:Q3.
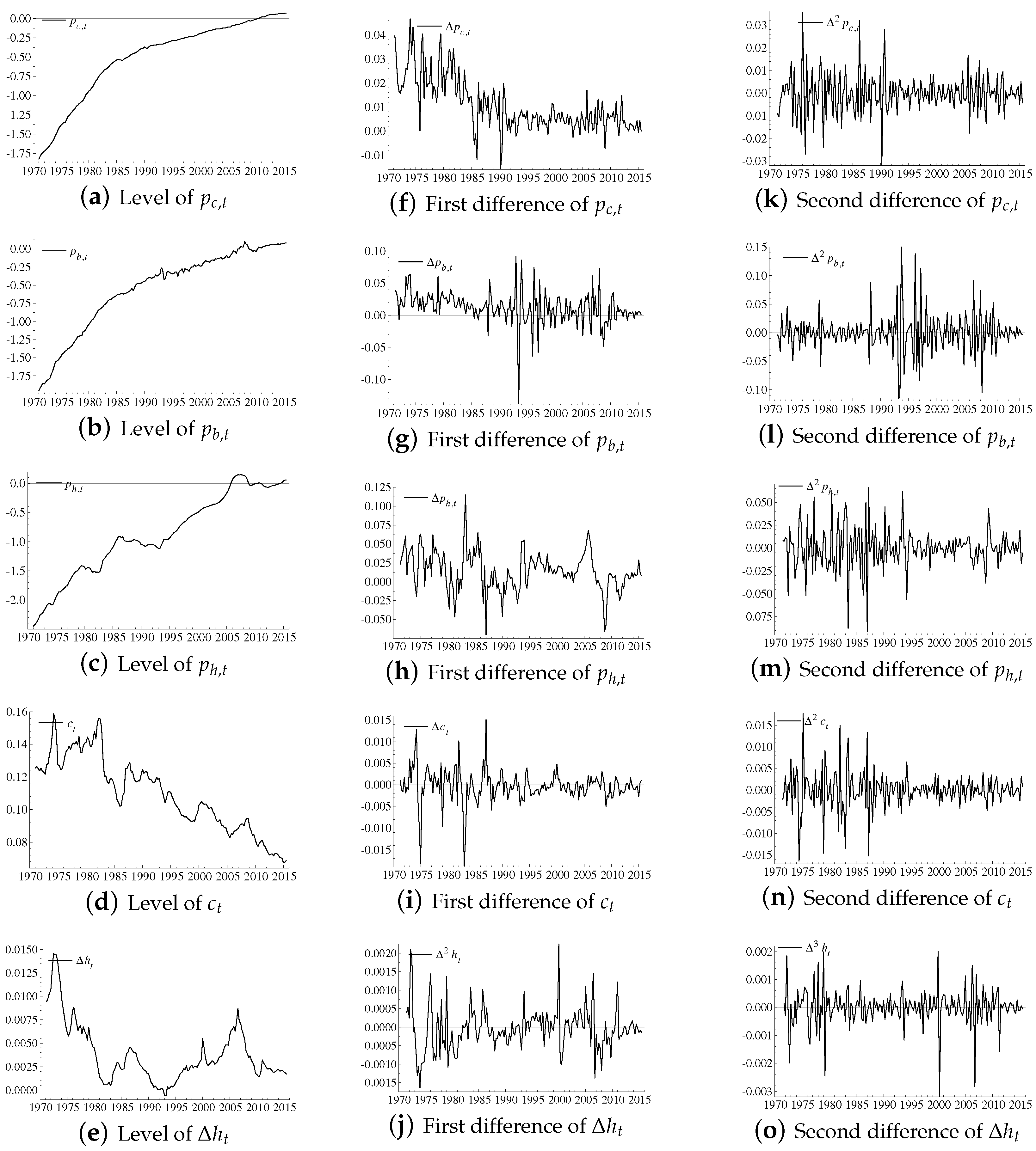
4 We define the information set for our empirical analysis as: the nominal price index for goods, measured as the GDP deflator, denoted
; the nominal price index for construction costs,
; and the nominal price index for single family houses in Denmark,
. We also include the user cost rate of housing investments,
, which is the post-tax nominal interest rate on a highly rated bond. Since this rate represents the opportunity costs of investing in housing (i.e., the carry), depreciation and convenience yield are included and have been assumed to stay constant at
and
, respectively; an assumption similar to those made in
Danmarks Nationalbank (
2003, chp. 3). Finally, we also include the net investments in housing in fixed prices,
, i.e., the first-differenced real housing stock in log terms,
. All variables, apart from the user cost rate,
, are transformed with the natural logarithm. We combine these five variables in our data column vector,
, which we define as
The levels, first-, and second differences of the data is shown in
Figure A1 in
Appendix A.
3.2. The I(2) Cointegrated VAR Model
We formulate the
I(2) CVAR model in terms of acceleration rates, changes and levels (see
Juselius (
2007)), and use the maximum likelihood parametrization introduced by
Johansen (
1997). The model is shown here with
lags to simplify the presentation
Here
is a
matrix of adjustment coefficients,
is a
matrix describing long-run relationships among the variables,
p is the dimension of the data vector,
r is the number of multicointegration relations,
is the number of cointegration relations that only become stationary by differencing,
is the number of stochastic
I(2) trends, and
. Moreover,
is a
matrix of coefficients, where
. The
d matrix is determined such that
. Additionally,
is a
matrix which describe stationary relationships among the differenced variables, where
is the orthogonal complement of
. Finally,
is a
matrix of restricted medium-run adjustment coefficients. We follow
Rahbek et al. (
1999) and restrict the constant term to be in
and the deterministic trend to be in
.
3.3. Lag Length Selection
Given the data vector defined in Equation (
16) for the period 1971:Q1–2015:Q3 we determine the appropriate number of lags and deterministic components required to obtain a sufficiently well-specified model. First, we choose the lag length by starting with a model with
lags and then reduce the number of lags by removing one at a time until a LM-test is rejected and the Schwarz, Hannan-Quinn and Akaike information criteria are minimized (these are given in
Table A1 in
Appendix A). Based on this procedure, we choose the lag length
. Secondly, fitting the CVAR model commonly requires a number of deterministic components to obtain a sufficiently well-specified model, e.g., shift, permanent, and/or transitory dummies. These components become necessary when the structure captured by the unrestricted VAR model falls short of explaining large movements in the data. Such a large movement could for instance be the enactment of a political reform, which changes the institutional features of the economy, or it could be a natural event affecting the economy.
3.4. Dummy Specification
We follow the method of
Juselius (
2007, chp. 6.6) to determine which dummies to include. This approach is based on the sequential identification of large outliers (defined as a standardized residual greater than
) until a sufficiently well-specified model has been obtained. In an iterative manner, we include one dummy at a time to investigate if the specified dummy results in a well-specified model. Following this method, our final specification includes six permanent intervention dummies,
5 two transitory dummies, and three centered quarterly dummies to control for seasonality at the quarterly frequency. We specify the dummies as follows (omitting seasonal dummies)
Reassuringly, most of the dummies coincide with economic events that we would not expect to be captured by the structure of the unrestricted VAR model. The dummies
and
are included to reduce skewness in
; the latter is included due to a big drop in the interest rate following the transition to a fixed exchange rate regime in 1983, whereas the former accounts for a correction from a spike in interest rates in 1975 following turbulence in the money market. The dummy
accounts for the tax reform enacted that year, which is significant in both
and
. The dummy
is included to correct for a large outlier in
in the third quarter of 1993, which coincides with the abolishment of mixed loans. The dummy,
, accounts for the December storm of 1999, which caused a rise and a drop in
. The final dummy,
accounts for the initial shocks of the financial crisis which caused a large transitory shock to
. As a robustness measure, we have also estimated the model without any dummies (included in
Appendix B), where we are able to retrace the main conclusions from the analysis.
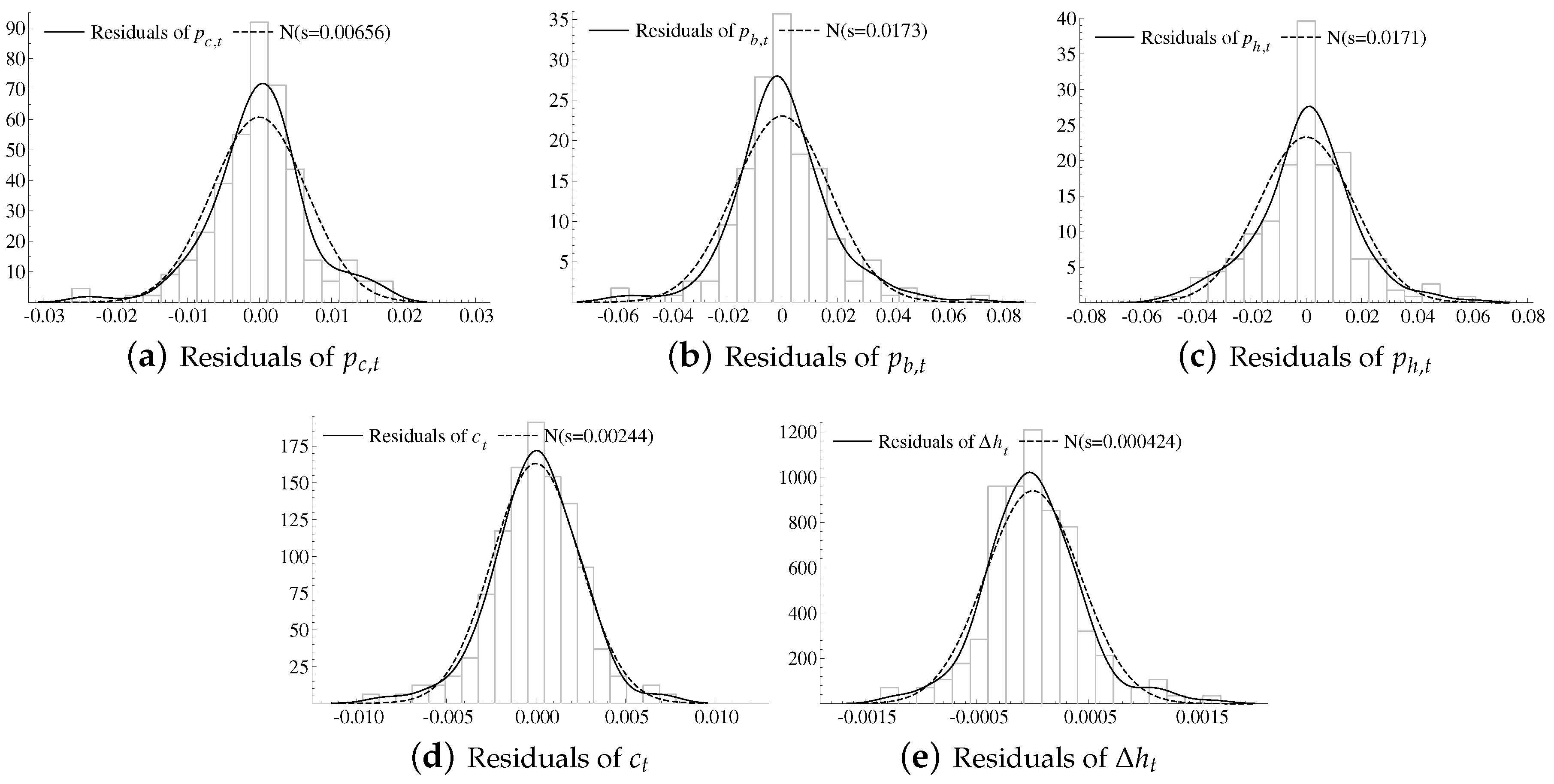
3.5. Misspecification Tests
Once the lag length and deterministic components have been chosen, we examine if the assumption on IID multivariate normality of the model innovations holds. To this end, we present a selection of common misspecification tests for the unrestricted VAR(2) in
Table 1.
The hypotheses of no residual autocorrelation of order 1 and 2 are not rejected, which is necessary for a model to be dynamically complete. The residuals for the construction costs,
, and housing price,
, show no signs of ARCH effects. However, the residuals for the consumer price index,
, the user cost rate,
, and the net investments,
, do not pass the no-ARCH test. The ARCH effects in the consumer prices,
, may in part be attributed to the regime change in 1983, before which there were higher, more volatile price changes than after. The inference is robust to moderate ARCH effects, cf.
Rahbek et al. (
2002) and
Cavaliere et al. (
2010), and as such the presence ARCH effects should not invalidate inference based on our unrestricted VAR model. We note that the presence of ARCH effects is likely to contribute to excess kurtosis, and as such it is not surprising that the univariate tests of non-normality are rejected primarily due to excess kurtosis. Non-normality due to skewness is, on the other hand, a concern for inference, cf.
Juselius (
2007, chp. 4.3). That said, not much skewness remains in the residuals, indicating that the rejection of normality is not sufficient to invalidate inference. In sum, considering that the unrestricted VAR model is only misspecified in terms of ARCH effects and kurtosis-induced non-normality, to which the inference is robust, and given that inclusion of further dummies does not resolve these issues, we conclude that this specification constitutes an appropriate basis for further analysis.
3.6. Rank Determination
Given our sufficiently well-specified unrestricted VAR model, we proceed to determine the appropriate reduced ranks of the
and
matrices. Similar to the
I(1) analysis, exploring whether
is facilitated by the reduced rank hypothesis
, implicitly assuming that
is full rank. Examining whether
is facilitated by the additional reduced rank hypothesis
, where
and
are the orthogonal complements of
and
, respectively. The determination of the reduced rank indices is based on the maximum likelihood trace test procedure proposed by
Bohn Nielsen and Rahbek (
2007).
6 As an alternative to the analytical distribution of the rank test, one can also use critical values from a bootstrap procedure, which is outlined for the
I(1) model in
Cavaliere et al. (
2012). We refrain from using the bootstrap procedure here, as the asymptotic properties have not been shown for the
I(2) model yet.
Table 2 presents the
I(2) trace tests for rank
r equal to 2 and 3, as well as the modulus of the six largest characteristic roots of the model. The trace test starts with the most restricted model
, recalling that
is the number of
I(2) trends, and proceeds until a reduced rank specification not rejected, and is nested in models that are also not rejected. The most restricted model we show in
Table 2 is
. The models become less and less restricted as the table is read row-wise.
The trace test suggests either or . The first specification is borderline rejected (p-value of 4.6%), and it is nested in two models that are rejected (p-values of 4.0% and 0.0% respectively). The second specification is not rejected (p-value of 12.6%) and is nested in models that are also not rejected. Both specifications leave no large characteristic roots; the largest remaining root has modulus and , respectively, indicating no residual unit roots. The first specification points to five unit roots, whereas the second specification points to four unit roots. The modulus of the unrestricted VAR points to four unit roots, corresponding to the second specification.
Taking this into account, we proceed with the second specification, as the rank test is not rejected nor nested in models which are rejected. Moreover, there is significant error correction and stationarity in all cointegrating relations (we return to this point in
Section 3.8). The chosen specification implies two stochastic
I(2) trends (
) and three polynomially cointegrating relations (
),
, which achieve stationarity.
3.7. Hypothesis Testing
Before identifying a long-run structure, we examine if certain variables, or linear combinations of variables, relating to the UANA condition outlined in Equations (
13)–(
15), are found to be
I(1). This is done by estimating the CVAR under the reduced rank conditions,
, also using the numerical maximum likelihood procedure outlined by
Johansen (
1997). Following the estimation, we impose restrictions on the
vectors (see
Johansen (
2006, Proposition II)). This lets us examine the persistency properties of the different variables in the information set and allows us to examine how the UANA condition outlined in
Section 2.4 may hold.
First, we examine if any of the variables are
I(1), by imposing restrictions on one
vector. The test results are displayed in the upper half of
Table 3 and we note all variables seem to be driven by one or more
I(2) trends, as all the hypotheses are rejected. This indicates that
,
, and
are driven by
I(2) trends, and that they may cointegrate from
I(2) to
I(1) to form the right hand side of the UANA condition in Equation (
15).
Next, by imposing restrictions on multiple
vectors, we examine if any linear combinations of the variables in
are
I(1). The test results are shown in the bottom half of
Table 3. The first test is a joint test for long-run price homogeneity; that is, we test whether
and
hold jointly. The nominal price indices would then share the same nominal
I(2) trend, while the real house and construction prices would be
I(1), which corresponds to classical dichotomy holding in the long-run, cf.
Kongsted (
2005). However, the joint test for long-run price homogeneity is rejected with a test statistic of
and a
p-value of practically zero. Testing the hypothesis for
returns a test statistic of
with a
p-value of
, which we reject at a
critical level. The hypothesis for
is rejected with a test statistic of
and a
p-value of practically zero. The hypothesis for
corresponds to the second scenario for the UANA condition, given in Equation (
14). In this scenario
would cointegrate from
I(2) to
I(1), which could cointegrate with
and
to stationarity. This scenario is based on the premise that
, which we have already rejeced, and we likewise reject the test for
with a test statistic of
and the
p-value of
. Therefore, the hypothesis for the UANA condition in Equation (
14) is rejected.
The final hypothesis test corresponds to the third scenario for the UANA condition in
Section 2.4, seen in Equation (
15). Given the premises that
,
, and
, we may still find that there is cointegration between the user cost rate and the relation for Tobin’s q expressed in the price indices. The test for whether
is not rejected with a
p-value of
. Based on this test, it appears that there is support for the UANA condition proposed in Equation (
15). However, we still have to establish that
cointegrates with
from
to
for the UANA condition in Equation (
15) not to be rejected by the data.
We are now ready to specify an over-identified long-run structure. This will allow us to investigate if the UANA condition in Equation (
15) holds empirically, and we may examine if the equilibrium-correcting behavior of the UANA condition can explain the long-swings dynamic in the housing prices introduced in
Section 1.
3.8. An Over-Identified Long-Run Structure
For the chosen rank specification,
, there will be three polynomially cointegrating relations,
for
, but no stationary medium-run relations in the growth rates,
, due to no cointegration in the differences,
. We impose over-identifying restrictions on
by testing reduced rank hypotheses on
in a fashion parallel to that of an
I(1) analysis. We obtain an identified long-run structure by first imposing the UANA condition from
Section 2.4. The UANA condition in itself is is not rejected, and we identify the second and third cointegrating relations by applying an inductive approach, in which we restrict a single variable at a time until we cannot restrict the system further.
The data lends support to a relation between the user cost rate,
, the price of construction,
, and the price of housing,
, in line with Equation (
15); a relation between the net housing investments,
, the price of construction,
, and the price of housing,
; and a relation between the net housing investments,
, the consumer price level,
, and the user cost rate,
. We determine the over-identified long-run structure to be
with the test statistic
, corresponding to
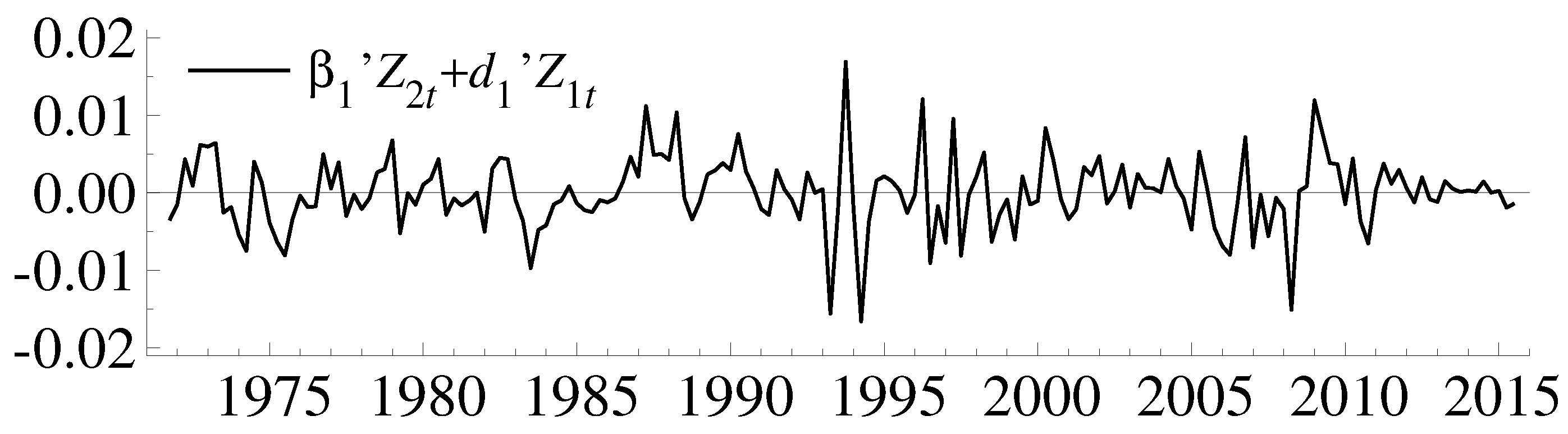
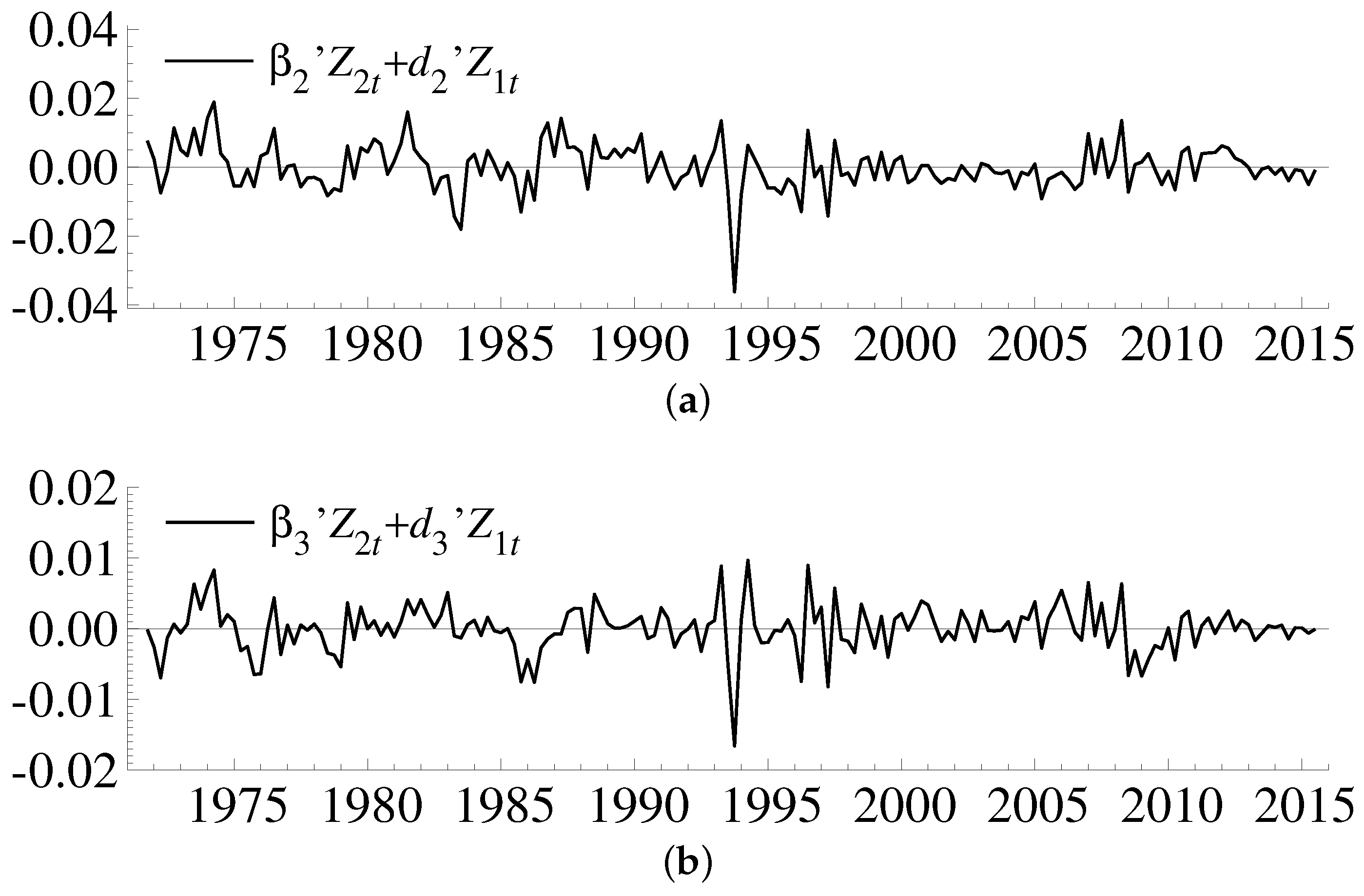
. The cointegrating relations are shown graphically in
Figure 2 and
Figure 3. We return to the intuition of this specification in the interpretations of the cointegrating relations in
Section 3.9.
Imposing the identification scheme on the
I(2) model in Equation (
17) results in the estimated long-run structure presented in
Table 4. The asymptotic distribution of the standard errors for
are derived in
Johansen (
1997) and the standard errors for
d are calculated using the delta method in
Doornik (
2016). Unfortunately, we are unable to test joint restrictions on the elements in
d, which prevents us from assessing whether we can reduce the presence of first differences further.
7 3.9. Interpreting the Long-Run Structure
We interpret a polynomially cointegrating relation as a dynamic equilibrium the same way as
Juselius (
2007): if
, then
and we can interpret it as an equilibrium error with a high degree of persistence. This means that we can interpret
and
d as two levels of equilibrium correction:
describes how the acceleration rates,
, adjust to the dynamic equilibrium relations,
, and
d describes how the growth rates,
, adjust to the long-run equilibrium error,
(i.e., describing a medium-run adjustment, conditional on
). We say that a variable
, for
, is equilibrium error correcting in the long run if
and/or
, and it is error correcting in the medium run if
. If we reverse the inequalities, the system is equilibrium error increasing. It is of particular interest that a variable can be error correcting in the long run (
), while being error increasing in the medium run (
), or vice versa. This type of interplay between long-run and medium-run dynamics can lead to persistent swings around the long-run equilibrium, which we refer to as “long-swings dynamics” in line with
Juselius and Assenmacher (
2016, Section 5).
We translate the parameter estimates in
Table 4 into three univariate equations, which govern the long-run error-correction mechanisms of the system, i.e., the cointegrating relations. These can be rearranged to facilitate interpretation. We do this in the following subsections.
3.9.1. The Uncertainty-Adjusted No-Arbitrage Condition
We interpret the first of the three cointegrating relations in terms of the uncertainty-adjusted no-arbitrage condition presented in
Section 2.4, specifically Equation (
15). The first cointegrating relation is given by
where we include the levels from
and first differences from
that are significant at the 95% critical level. We rearrange the terms in Equation (
20) to relate it to the UANA condition in Equation (
15):
where
denotes the stationary error component. As suggested by the uncertainty-based asset price approach presented in
Section 2.3, the price level of housing,
, and the cost of construction,
, enter with the same coefficient and opposite sign to form Tobin’s q. The user cost rate,
, is also present but enters with a negative coefficient. Based on asset pricing theory the user cost rate,
, should have entered with a positive coefficient as it represents the carry, or opportunity cost, of buying the asset. We may attempt to understand the negative coefficient on
by the dynamic that, in practice, a higher user cost rate would make housing less affordable, which in turn would preclude some investors from entering the housing market as they will be able to borrow less, all else equal. In addition to the levels predicted by the theory, we also find that the changes in net housing investments,
, and the user cost rate
are significant.
As such, we reject the exact specification of the UANA condition as it is presented in Equation (
15), noting that the primary implication from the original framework resulting in Equation (
2) appears to be inconsistent with the data. However, we do find that realized changes in the price of housing,
, are positively related to Tobin’s q. This is in support of the contribution made to the theory by specifying the uncertainty premium in terms of a gap effect. That said, while there are more terms present in Equation (
21) than predicted, the cointegrating relation does indicate that the UANA condition in Equation (
15) provides an empirically relevant characterization of the price formation in the Danish housing market over the period under consideration.
Turning our attention to the medium- and long-term dynamics, the
and
coefficients reveal that the price of housing,
, is strongly error correcting in the long run with respect to this cointegrating relation, but the
coefficient suggests that the change in the price of housing,
, is error increasing in the medium run. This dynamic implies that the price of housing is prone to overshooting its long-term equilibrium level given by Equation (
21). This type of overshooting is consistent with momentum-based forecasting behavior. That is, if investors base their expectations on recent price changes, then the persistence in the realized price changes will increase, cf. e.g.,
Shiller (
2008), leading to overshooting behavior in the medium run. We return to this point in
Section 3.10. We also note that the construction price index,
, is error increasing in the long run, and the change in the housing stock,
is (borderline) error correcting in the long run. Finally, the user cost rate,
, is (borderline) error correcting in both the medium- and long run. Moreover, graphical inspection of the cointegrating relation in the sample reveals that the relation is stationary and it exhibits relatively little persistence, see
Figure 2.
3.9.2. Net Housing Investments
We interpret the second and third cointegrating relations as characterizing the long-run equilibrium of net housing investments. These relations are not implied by our theoretical framework in
Section 2, instead we have identified them inductively by imposing zero restrictions on the long-run structure. In the Equations (
22) and (
23), we include the levels from
and differences from
that are significant at the 95% critical level.
The second of the three cointegrating relations is given by,
where
denotes the stationary error component. We interpret Equation (
22) as characterizing the net housing investment in equilibrium as approximately proportional to Tobin’s q. The levels of the variables
cointegrate from
I(2) to
I(1), and in turn with the significant first-differences,
, from
I(1) to
I(0) to achieve stationarity. While
and
do not enter with the same coefficient, they are of roughly the same magnitude and enter with opposite signs. The
and
coefficients reveal that the net housing investments,
, exhibits error-increasing behavior with respect to this cointegrating relation in both the long and medium run. If there is a positive deviation from the cointegrating relation as a result of Tobin’s q being above unity, then we would expect this to cause the net investments to increase. We note that the price level of housing,
, is error increasing with respect to the this cointegrating relation in the long run. On the other hand, the price index of building costs,
, is error correcting in both the long and medium run. Finally, the user cost,
is (borderline) error correcting in the long run.
Figure 3a shows this cointegrating relation.
The third and final cointegration relation is a linear combination of the housing prices,
, the building costs,
, and the net investment in housing,
, which cointegrate to cancel out the
I(2) trends, and in turn cointegrate with the first differences to
I(0). The cointegrating relation is given by,
where
denotes the stationary error component. Equation (
23) is somewhat difficult to interpret in isolation. Considering the error-correcting properties,
and
reveal that the housing investments,
, error correct in the long run, and error increases in the medium run with respect to this cointegrating relation. Furthermore, the user cost rate,
is error increasing in the long run, and error correcting in the medium run. Intuitively, if the user cost rate rises above its long-run value relative to the housing investments, we expect a negative effect on the housing investments, as a higher user cost rate will discourage investments. Finally, the construction price index,
, is error increasing in the long run, while the house price index,
, error corrects in the long run.
Figure 3b shows this cointegrating relation.
3.10. Summary of Empirical Findings
In summary, we find strong evidence in support of the housing price, as well as remaining variables in our information set, defined in Equation (
16), being integrated of order two, i.e., highly persistent. Moreover, we strongly reject that the
I(2) dynamics can be appropriately accounted for by simply transforming to real variables, i.e., we reject long-run price homogeneity. Rather, we find that the uncertainty-adjusted no-arbitrage (UANA) condition, given in Equation (
15), provides an empirically relevant characterization of the long-run house price equilibrium. Furthermore, the error-correction dynamics estimated via the cointegrated VAR model can help explain the long-swings behavior in the housing price, observed in
Figure 1.
On the last point, it is instructive to construct an informal example of how long-swings behavior associated with the cointegrating relation in Equation (
21) relates to our theoretical framework in
Section 2 in combination with momentum-based forecasting. Suppose that, at some point in time, the expected future price change is greater than the sum of the current user cost rate and the uncertainty premium; that is, there is arbitrage according to the UANA condition in Equation (
12). Investors will then respond by buying housing, pushing the housing price up in the process, which increases Tobin’s q (all else equal), and in turn the required uncertainty premium in the next quarter.
This pattern may continue quarter after quarter until Tobin’s q has been increased to the point where the expected price change for the next quarter is less than or equal to the sum of the user cost rate and the uncertainty premium. Given the momentum in the price of housing and individual forecasts, the result can be a persistent swing upwards in the price until the required uncertainty premium has become too large relative to investors’ expectations of the price change in the next quarter. At this point, further price increases will result in overshooting relative to the long-run equilibrium as well as further increases in the uncertainty premium. In this situation there is also arbitrage, but in the other direction, which will lead to investors selling housing. In turn, the momentum in housing prices will decrease, or even turn (all else equal), and the process will go into reverse. The result is in this case a persistent swing downwards in the price of housing until the required uncertainty premium has become small enough for investors to find housing attractive again relative to their expectations of future price changes.
In practice, all else is not equal, and changes in the user cost rate, building costs, and housing investments will also affect the price of housing. For example, if Tobin’s q is greater than unity then the housing stock is smaller than what is demanded by investors, and so net investments will increase to generate profit from the discrepancy between the price at which housing is sold relative to its cost of construction. That is, we would expect a positive association between Tobin’s q and net investments, which aligns well with our interpretation of the second cointegration relation in Equation (
22).