Evaluating Ingenious Instruments for Fundamental Determinants of Long-Run Economic Growth and Development
Abstract
1. Introduction
2. Ingenious Instruments for Fundamental Determinants of Economic Development
3. Instrumental Variables Estimation and Reduced Forms
4. Testing Statistical Adequacy
5. Results
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources
References
- Acemoglu, Daron, Simon Johnson, and James A. Robinson. 2001. The colonial origins of comparative development: An empirical investigation. American Economic Review 91: 1369–401. [Google Scholar] [CrossRef]
- Acemoglu, Daron, Simon Johnson, and James A. Robinson. 2002. Reversal of fortune: Geography and institutions in the making of the modern world income distribution. Quarterly Journal of Economics 117: 1231–94. [Google Scholar] [CrossRef]
- Acemoglu, Daron, Simon Johnson, and James A. Robinson. 2005. Institutions as a fundamental cause of long-run growth. In Handbook of Economic Growth. Edited by Philippe Aghion and Steven N. Durlauf. Amsterdam: Elsevier North-Holland, Volume 1A, pp. 385–472. [Google Scholar]
- Andrews, Donald W.K., and James H. Stock. 2007. Inference with weak instruments. In Advances in Economics and Econometrics, Theory and Applications: 9th Congress of the Econometric Society, vol 3. Edited by Richard Blundell, Whitney K. Newey and Torsten Persson. Cambridge: Cambridge University Press, pp. 122–73. [Google Scholar]
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2009. Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton: Princeton University Press. [Google Scholar]
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2010. The credibility revolution in empirical economics: How better research design is taking the con out of econometrics. Journal of Economic Perspectives 24: 3–30. [Google Scholar] [CrossRef]
- Anselin, Luc, and Raymond J.G.M. Florax. 1995. Small sample properties of tests for spatial dependence in regression models: Some further results. In New Directions in Spatial Econometrics. Edited by Luc Anselin and Raymond J.G.M. Florax. Berlin: Springer, pp. 21–74. [Google Scholar]
- Anselin, Luc, Anil K. Bera, Raymond Florax, and Mann J. Yoon. 1996. Simple diagnostic tests for spatial dependence. Regional Science and Urban Economics 26: 77–104. [Google Scholar] [CrossRef]
- Ashraf, Quamrul, and Oded Galor. 2011. Dynamics and stagnation in the Malthusian epoch. American Economic Review 101: 2003–41. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, Quamrul, and Oded Galor. 2013. The “out of Africa” hypothesis, human genetic diversity, and comparative economic development. American Economic Review 103: 1–46. [Google Scholar] [CrossRef] [PubMed]
- Bazzi, Samuel, and Michael A. Clemens. 2013. Blunt instruments: Avoiding common pitfalls in identifying the causes of economic growth. American Economic Journal: Macroeconomics 5: 152–86. [Google Scholar] [CrossRef]
- Belsley, David A., Edwin Kuh, and Roy E. Welsch. 2005. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. Hoboken: John Wiley. [Google Scholar]
- Bloom, David E., and Jeffrey D. Sachs. 1998. Geography, demography, and economic growth in Africa. Brookings Papers on Economic Activity 1998: 207–73. [Google Scholar] [CrossRef]
- Bockstette, Valerie, Areendam Chanda, and Louis Putterman. 2002. States and markets: The advantage of an early start. Journal of Economic Growth 7: 347–69. [Google Scholar] [CrossRef]
- Brock, William A., and Steven N. Durlauf. 2001. What have we learned from a decade of empirical research on growth? Growth empirics and reality. World Bank Economic Review 15: 229–72. [Google Scholar] [CrossRef]
- Casey, Gregory, and Marc Klemp. 2016. Instrumental variables in the long run. MPRA Working Paper 68696. Munich, Germany: University Library of Munich. [Google Scholar]
- Chanda, Areendam, and Louis Putterman. 2007. Early starts, reversals and catch-up in the process of economic development. Scandinavian Journal of Economics 109: 387–413. [Google Scholar] [CrossRef]
- Cliff, Andrew D., and J.K. Ord. 1973. Spatial Autocorrelation. London: Pion. [Google Scholar]
- Conley, Timothy G., and Ethan Ligon. 2002. Economic distance and cross-country spillovers. Journal of Economic Growth 7: 157–87. [Google Scholar] [CrossRef]
- Cragg, John G., and Stephen G. Donald. 1993. Testing identifiability and specification in instrumental variable models. Econometric Theory 9: 222–40. [Google Scholar] [CrossRef]
- Deaton, Angus. 2010. Instruments, randomization, and learning about development. Journal of Economic Literature 48: 424–55. [Google Scholar] [CrossRef]
- Diamond, Jared. 1997. Guns, Germs, and Steel: The Fates of Human Societies. New York: W.W. Norton. [Google Scholar]
- Doornik, Jurgen A., and Henrik Hansen. 2008. An omnibus test for univariate and multivariate normality. Oxford Bulletin of Economics and Statistics 70: 927–39. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., and David F. Hendry. 2013a. Empirical Econometric Modelling, PcGive 14, Volume I. London: Timberlake Consultants Ltd. [Google Scholar]
- Doornik, Jurgen A., and David F. Hendry. 2013b. Modelling Dynamic Systems, PcGive 14, Volume II. London: Timberlake Consultants Ltd. [Google Scholar]
- Durlauf, Steven N., Paul A. Johnson, and Jonathan R.W. Temple. 2005. Growth econometrics. In Handbook of Economic Growth. Edited by Philippe Aghion and Steven N. Durlauf. Amsterdam: Elsevier North-Holland, Volume 1A, pp. 555–677. [Google Scholar]
- Easterly, William. 2007. Inequality does cause underdevelopment: Insights from a new instrument. Journal of Development Economics 84: 755–76. [Google Scholar] [CrossRef]
- Easterly, William, and Ross Levine. 2003. Tropics, germs, and crops: How endowments influence economic development. Journal of Monetary Economics 50: 3–39. [Google Scholar] [CrossRef]
- Easterly, William, and Ross Levine. 2016. The European origins of economic development. Journal of Economic Growth 21: 225–57. [Google Scholar] [CrossRef]
- Eberhardt, Markus, and Francis Teal. 2017. The magnitude of the task ahead: Macro implications of heterogeneous technology. Unpublished manuscript. UK: School of Economics, University of Nottingham. [Google Scholar]
- Engerman, Stanley L., and Kenneth L. Sokoloff. 1997. Factor endowments, institutions, and differential paths of growth among New World economies. In How Latin America Fell Behind. Edited by Stephen Haber. Stanford: Stanford University Press, pp. 260–304. [Google Scholar]
- Ertur, Cem, and Wilfried Koch. 2007. Growth, technological interdependence and spatial externalities: Theory and evidence. Journal of Applied Econometrics 22: 1033–62. [Google Scholar] [CrossRef]
- Feyrer, James, and Bruce Sacerdote. 2009. Colonialism and modern income: Islands as natural experiments. Review of Economics and Statistics 91: 245–62. [Google Scholar] [CrossRef]
- Fingleton, Bernard, and Julie Le Gallo. 2008. Estimating spatial models with endogenous variables, a spatial lag and spatially dependent disturbances: Finite sample properties. Papers in Regional Science 87: 319–39. [Google Scholar] [CrossRef]
- Frankel, Jeffrey A. 2003. Comments and discussion on: Bosworth, B.P., Collins, S.M., The empirics of growth: An update. Brookings Papers on Economic Activity 2003: 189–99. [Google Scholar]
- Frankel, Jeffrey A., and David Romer. 1999. Does trade cause growth? American Economic Review 89: 379–99. [Google Scholar] [CrossRef]
- Freedman, David A. 2006. Statistical models for causation: What inferential leverage do they provide? Evaluation Review 30: 691–713. [Google Scholar] [CrossRef] [PubMed]
- Fuchs-Schuendeln, Nicola, and Tarek Alexander Hassan. 2015. Natural experiments in macroeconomics. National Bureau of Economic Research Working Paper 21228. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Gallup, John Luke, Jeffrey D. Sachs, and Andrew D. Mellinger. 1999. Geography and economic development. International Regional Science Review 22: 179–232. [Google Scholar] [CrossRef]
- Hahn, Jinyong, and Jerry Hausman. 2002. Notes on bias in estimators for simultaneous equation models. Economics Letters 75: 237–41. [Google Scholar] [CrossRef]
- Hall, Robert E., and Charles I. Jones. 1999. Why do some countries produce so much more output per worker than others? Quarterly Journal of Economics 114: 83–116. [Google Scholar] [CrossRef]
- Hansen, Lars Peter. 1982. Large sample properties of generalized method of moments estimators. Econometrica 50: 1029–54. [Google Scholar] [CrossRef]
- Heckman, James J., and Sergio Urzúa. 2010. Comparing IV with structural models: What simple IV can and cannot identify. Journal of Econometrics 156: 27–37. [Google Scholar] [CrossRef] [PubMed]
- Hendry, David F. 1995. Dynamic Econometrics. Oxford: Oxford University Press. [Google Scholar]
- Hendry, David F. 2009. The methodology of empirical econometric modeling: Applied econometrics through the looking-glass. In Palgrave Handbook of Econometrics: Volume 2: Applied Econometrics. Edited by Terence C. Mills and Kerry Patterson. Basingstoke: Palgrave Macmillan, pp. 3–67. [Google Scholar]
- Hendry, David F., and Bent Nielsen. 2007. Econometric Modeling: A Likelihood Approach. Princeton: Princeton University Press. [Google Scholar]
- Imbens, Guido W. 2010. Better LATE than nothing: Some comments on Deaton (2009) and Heckman and Urzua (2009). Journal of Economic Literature 48: 399–423. [Google Scholar] [CrossRef]
- Imbens, Guido W., and Michal Kolesár. 2016. Robust standard errors in small samples: Some practical advice. Review of Economics and Statistics 98: 701–12. [Google Scholar] [CrossRef]
- Iyer, Lakshmi. 2010. Direct versus indirect colonial rule in India: Long-term consequences. Review of Economics and Statistics 92: 693–713. [Google Scholar] [CrossRef]
- Jeanty, P. Wilner. 2010. Anketest: Stata module to perform diagnostic tests for spatial autocorrelation in the residuals of OLS, SAR, IV, IV-SAR, probit, and logit models. Available online: ideas.repec.org/c/boc/bocode/s457113.html (accessed on 25 March 2014).
- Kraay, Aart C. 2015. Weak instruments in growth regressions: Implications for recent cross-country evidence on inequality and growth. World Bank Policy Research Working Paper 7494. Washington, DC, USA: World Bank Group. [Google Scholar]
- Knowles, Stephen, and P. Dorian Owen. 2010. Which institutions are good for your health? The deep determinants of comparative cross-country health status. Journal of Development Studies 46: 701–23. [Google Scholar] [CrossRef]
- King, Gary, and Margaret E. Roberts. 2015. How robust standard errors expose methodological problems they do not fix, and what to do about it. Political Analysis 23: 159–79. [Google Scholar] [CrossRef]
- La Porta, Rafael, Florencio Lopez-de-Silanes, Andrei Shleifer, and Robert Vishny. 1999. The quality of government. Journal of Law, Economics, and Organization 15: 222–79. [Google Scholar] [CrossRef]
- Le Cam, Lucien. 1986. Asymptotic Methods in Statistical Decision Theory. New York: Springer. [Google Scholar]
- Leamer, Edward E. 2010. Tantalus on the road to Asymptopia. Journal of Economic Perspectives 24: 31–46. [Google Scholar] [CrossRef]
- LeSage, James, and Robert Kelley Pace. 2009. Introduction to Spatial Econometrics. Boca Raton: CRC Press. [Google Scholar]
- MacKinnon, James G. 2013. Thirty years of heteroskedasticity-robust inference. In Recent Advances and Future Directions in Causality, Prediction, and Specification Analysis. Edited by Xiaohong Chen and Norman R. Swanson. New York: Springer, pp. 437–461. [Google Scholar]
- MacKinnon, James G., and Halbert White. 1985. Some heteroskedasticity-consistent covariance matrix estimators with improved finite sample properties. Journal of Econometrics 29: 305–25. [Google Scholar] [CrossRef]
- Malik, Adeel, and Jonathan R.W. Temple. 2009. The geography of output volatility. Journal of Development Economics 90: 163–78. [Google Scholar] [CrossRef]
- Mauro, Paolo. 1995. Corruption and growth. Quarterly Journal of Economics 110: 681–712. [Google Scholar] [CrossRef]
- Mayer, Thierry, and Soledad Zignago. 2011. Notes on CEPII’s distances measures: The GeoDist database. CEPII Working Paper 2011-25. Paris, France: CEPII. [Google Scholar]
- Michalopoulos, Stelios. 2012. The origins of ethnolinguistic diversity. American Economic Review 102: 1508–39. [Google Scholar] [CrossRef] [PubMed]
- Moran, P.A.P. 1948. The interpretation of statistical maps. Journal of the Royal Statistical Society. Series B (Methodological) 10: 243–51. [Google Scholar]
- Moreno, Ramon, and Bharat Trehan. 1997. Location and the growth of nations. Journal of Economic Growth 2: 399–418. [Google Scholar] [CrossRef]
- Murray, Michael P. 2006. Avoiding invalid instruments and coping with weak instruments. Journal of Economic Perspectives 20: 111–32. [Google Scholar] [CrossRef]
- Olsson, Ola. 2005. Geography and institutions: Plausible and implausible linkages. Journal of Economics 86 Supplement: 167–94. [Google Scholar]
- Olsson, Ola, and Douglas A. Hibbs, Jr. 2005. Biogeography and long-run economic development. European Economic Review 49: 909–38. [Google Scholar] [CrossRef]
- Putterman, Louis, and David N. Weil. 2010. Post-1500 population flows and the long-run determinants of economic growth and inequality. Quarterly Journal of Economics 125: 1627–82. [Google Scholar] [CrossRef] [PubMed]
- Qin, Duo. 2015. Resurgence of the endogeneity-backed instrumental variable methods. Economics: The Open-Access, Open-Assessment E-Journal 9: 1–35. [Google Scholar] [CrossRef]
- Qin, Duo, Sophie van Huellen, and Qing-Chao Wang. 2016. How credible are shrinking wage elasticities of married women labour supply? Econometrics 4: 1. [Google Scholar] [CrossRef]
- Ramsey, J.B. 1969. Tests for specification errors in classical linear least-squares regression analysis. Journal of the Royal Statistical Society. Series B 31: 350–71. [Google Scholar]
- Rodrik, Dani, Arvind Subramanian, and Francesco Trebbi. 2004. Institutions rule: The primacy of institutions over geography and integration in economic development. Journal of Economic Growth 9: 131–65. [Google Scholar] [CrossRef]
- Sachs, Jeffrey D. 2003. Institutions don’t rule: Direct effects of geography on per capita income. National Bureau of Economic Research Working Paper 9490. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Sachs, Jeffrey D., and Andrew M. Warner. 1995. Economic reform and the process of global integration. Brookings Papers on Economic Activity 1995: 1–95. [Google Scholar] [CrossRef]
- Sargan, J.D. 1958. The estimation of economic relationships using instrumental variables. Econometrica 26: 393–415. [Google Scholar] [CrossRef]
- Shea, John. 1997. Instrument relevance in multivariate linear models: A simple measure. Review of Economics and Statistics 79: 348–52. [Google Scholar] [CrossRef]
- Sims, Christopher A. 2010. But economics is not an experimental science. Journal of Economic Perspectives 24: 59–68. [Google Scholar] [CrossRef]
- Spanos, Aris. 1990. The simultaneous-equations model revisited: Statistical adequacy and identification. Journal of Econometrics 44: 87–105. [Google Scholar] [CrossRef]
- Spanos, Aris. 2006. Econometrics in retrospect and prospect. In Palgrave Handbook of Econometrics. Edited by T.C. Mills and K. Patterson. Basingstoke: Palgrave MacMillan, Vol. 1, Econometric Theory. pp. 3–58. [Google Scholar]
- Spanos, Aris. 2007. The instrumental variables method revisited: On the nature and choice of optimal instruments. In The Refinement of Econometric Estimation and Test Procedures: Finite Sample and Asymptotic Analysis. Edited by G.D.A. Phillips and E. Tzavalis. Cambridge: Cambridge University Press, pp. 34–59. [Google Scholar]
- Spanos, Aris. 2010. Akaike-type criteria and the reliability of inference: Model selection versus statistical model specification. Journal of Econometrics 158: 204–20. [Google Scholar] [CrossRef]
- Spanos, Aris. 2015. Revisiting Haavelmo’s structural econometrics: Bridging the gap between theory and data. Journal of Economic Methodology 22: 171–96. [Google Scholar] [CrossRef]
- Spanos, Aris. 2017. Mis-specification testing in retrospect. Journal of Economic Surveys. [Google Scholar] [CrossRef]
- Spanos, Airs, and James J. Reade. 2016. Heteroskedasticity/autocorrelation consistent standard errors and reliability of inference. Working Paper for the 17th Annual Oxmetrics Conference. Washington, DC, USA: George Washington University. [Google Scholar]
- Spolaore, Enrico, and Romain Wacziarg. 2009. The diffusion of development. Quarterly Journal of Economics 124: 469–529. [Google Scholar] [CrossRef]
- Spolaore, Enrico, and Romain Wacziarg. 2013. How deep are the roots of economic development? Journal of Economic Literatur 51: 325–69. [Google Scholar] [CrossRef]
- Spolaore, Enrico, and Romain Wacziarg. 2014. Long-term barriers to economic development. In Handbook of Economic Growth. Edited by P. Aghion and S.N. Durlauf. Amsterdam: Elsevier North-Holland, Volume 2A, pp. 121–76. [Google Scholar]
- Stock, James H., and Motohiro Yogo. 2005. Testing for weak instruments in linear IV regression. In Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg. Edited by D.W.K. Andrews and J.H. Stock. Cambridge: Cambridge University Press. [Google Scholar]
- Swamy, P.A.V.B., George S. Tavlas, and Stephen G. Hall. 2015. On the interpretation of instrumental variables in the presence of specification errors. Econometrics 3: 55–64. [Google Scholar] [CrossRef]
- The Economist. 2006. Winds of change. The Economist. November 4th, p. 84. Available online: http://www.economist.com/node/8104169 (accessed on 26 October 2013).
- White, Halbert. 1980. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 48: 817–38. [Google Scholar] [CrossRef]
- Wooldridge, Jeffrey M. 2010. Econometric Analysis of Cross Section and Panel Data, 2nd ed. Cambridge: MIT Press. [Google Scholar]
- Zietz, Joachim. 2001. Heteroskedasticity and neglected parameter heterogeneity. Oxford Bulletin of Economics and Statistics 63: 263–73. [Google Scholar] [CrossRef]
| 1 | A small minority of studies adopt other measures of development as the dependent variable, either as a complement to examining income per capita, e.g., infant mortality (Feyrer and Sacerdote 2009), or as an alternative, e.g., life expectancy (Knowles and Owen 2010) or output volatility (Malik and Temple 2009). |
| 2 | To simplify the notation, observed variables are assumed to have zero means. Assumptions (a)–(d) are the relevant finite-sample conditions; most formal treatments of the properties of IV estimation focus on the corresponding asymptotic conditions: (a)′: plim(N−1Z′ε) = 0; (b)′: plim(N−1X1′Z) = ΣXZ ≠ 0; (c)′: plim(N−1Z′Z) = ΣZZ > 0, and (d)′: plim(N−1Z′y) ≠ 0, where Z = (Z1, Z2, …, ZN)′, X1 = (X11, X12, …, X1N)′, y = (y1, y2, …, yN)′ and ε = (ε1, ε2, …, εN)′ (Spanos 2007, pp. 37–8). |
| 3 | If the structural model is exactly identified (p = m1), this involves a pure reparameterization with a one-to-one correspondence between reduced form and structural parameters. If the structural model is overidentified (p > m1), it involves a reparameterization/restriction; in this case, Equation (3a), despite its ‘reduced-form’ label, is more general than the structural model in Equation (1). |
| 4 | Details of the mapping between structural and MLR/RF parameters are provided by Spanos (2007, pp. 41–4). Note that the restrictions γ0 = 0 are non-testable identifying restrictions imposed together with B1 ≠ 0 and β1 ≠ 0 to identify the structural parameters in α1. Imposing γ0 = 0 independent of B1 ≠ 0 and β1 ≠ 0 is equivalent to treating X1i as exogenous, which leads to a contradiction. |
| 5 | Although rarely discussed explicitly in the fundamental determinants literature, some applied researchers also weaken the linearity assumption, interpreting linear regression as providing a best linear predictor that approximates some nonlinear conditional expectation function (CEF) of the observable variables (Angrist and Pischke 2009). On this interpretation, how well the regression line fits the nonlinear CEF will vary with the values of the explanatory variables, with the consequent residual heteroskedasticity regarded as a natural feature of this characterization. This further shifts the focus to reliance on asymptotic results and heteroskedastic-robust inference. |
| 6 | One response to concerns about validity of underlying statistical assumptions is the development and application of Generalized Method of Moments (GMM) estimation, which requires less restrictive assumptions. However, as Spanos (2015, p. 183) argues, this comes at a price: “weaker premises will always give rise to less precise inferences without any guarantee that they will be more adequate for the particular data, especially when the inference is unduly reliant on asymptotics … Even if one has to rely on asymptotic results, the adequacy of the premises renders such results a lot more reliable for the given n. In contrast, asymptotic properties such as [consistent and asymptotically normal], stemming from nonvalidated premises, provide no guarantee for reliable inferences in practice.” In any case, all the studies examined rely on 2SLS estimation, applied to relatively small samples, fitting simple linear-in-parameters models with additive errors and constant parameters across countries. |
| 7 | This choice is consistent with Conley and Ligon’s (2002) finding of positive spillovers of GDP per capita on neighbours’ growth performance. Qualitatively similar results are obtained if the study’s main explanatory variable, e.g., institutional quality, is used as the economic variable in the weighting scheme. Latitude and longitude data are from CEPII’s database of geographical variables (Mayer and Zignago 2011). The spatial weights matrices are constructed using spwmatrix and the tests computed using anketest (Jeanty 2010), both Stata routines written by Wilner Jeanty. |
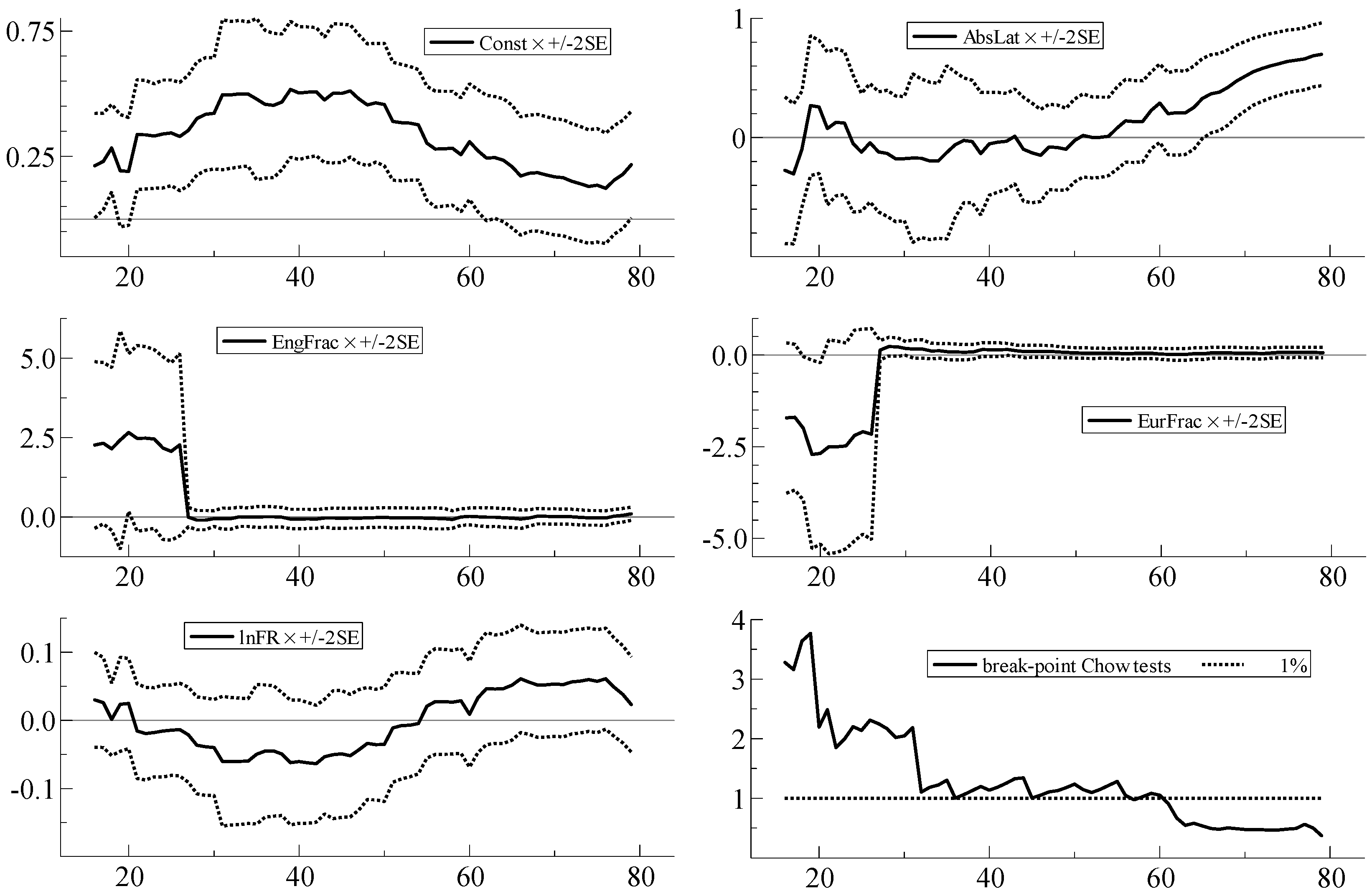
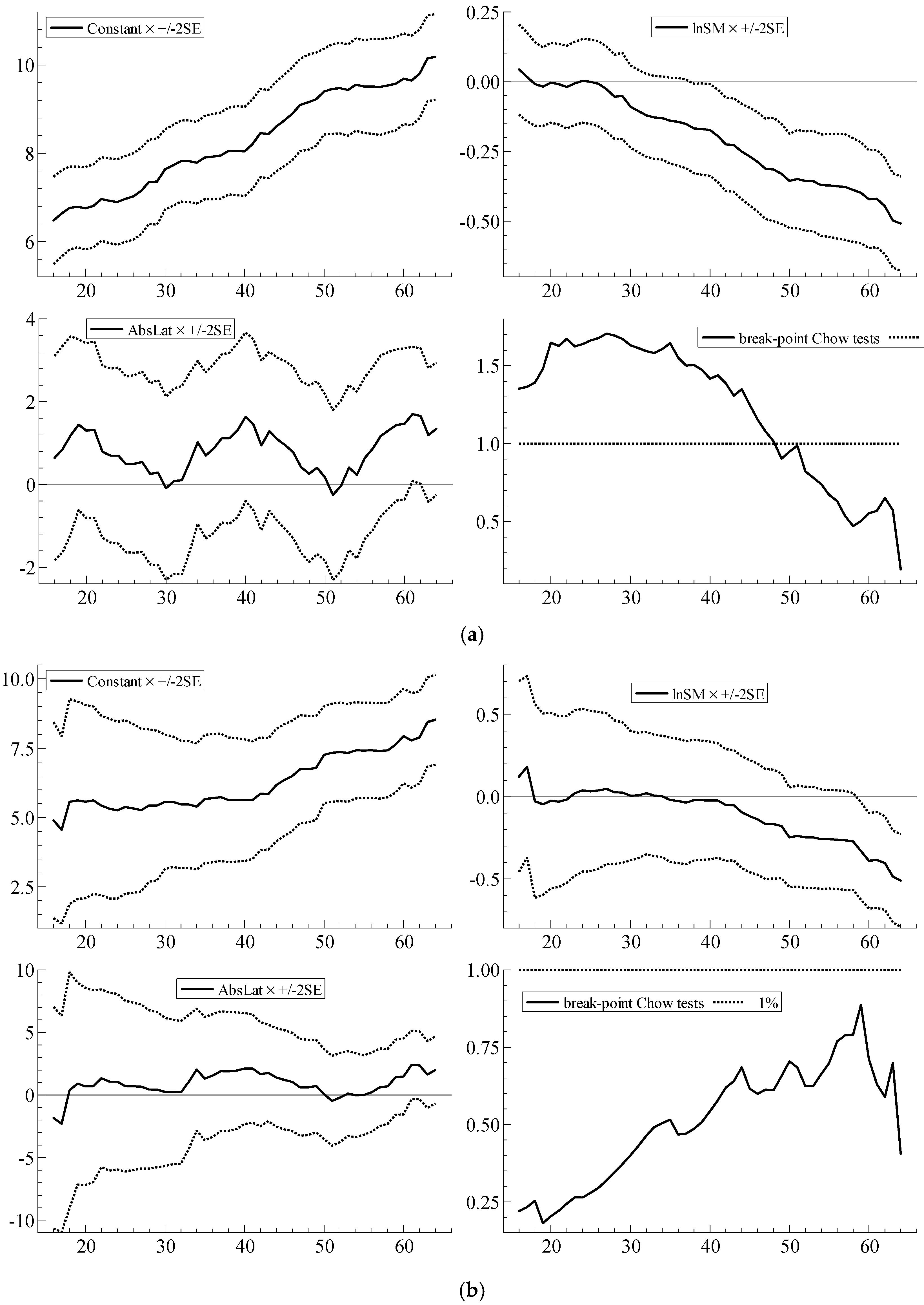
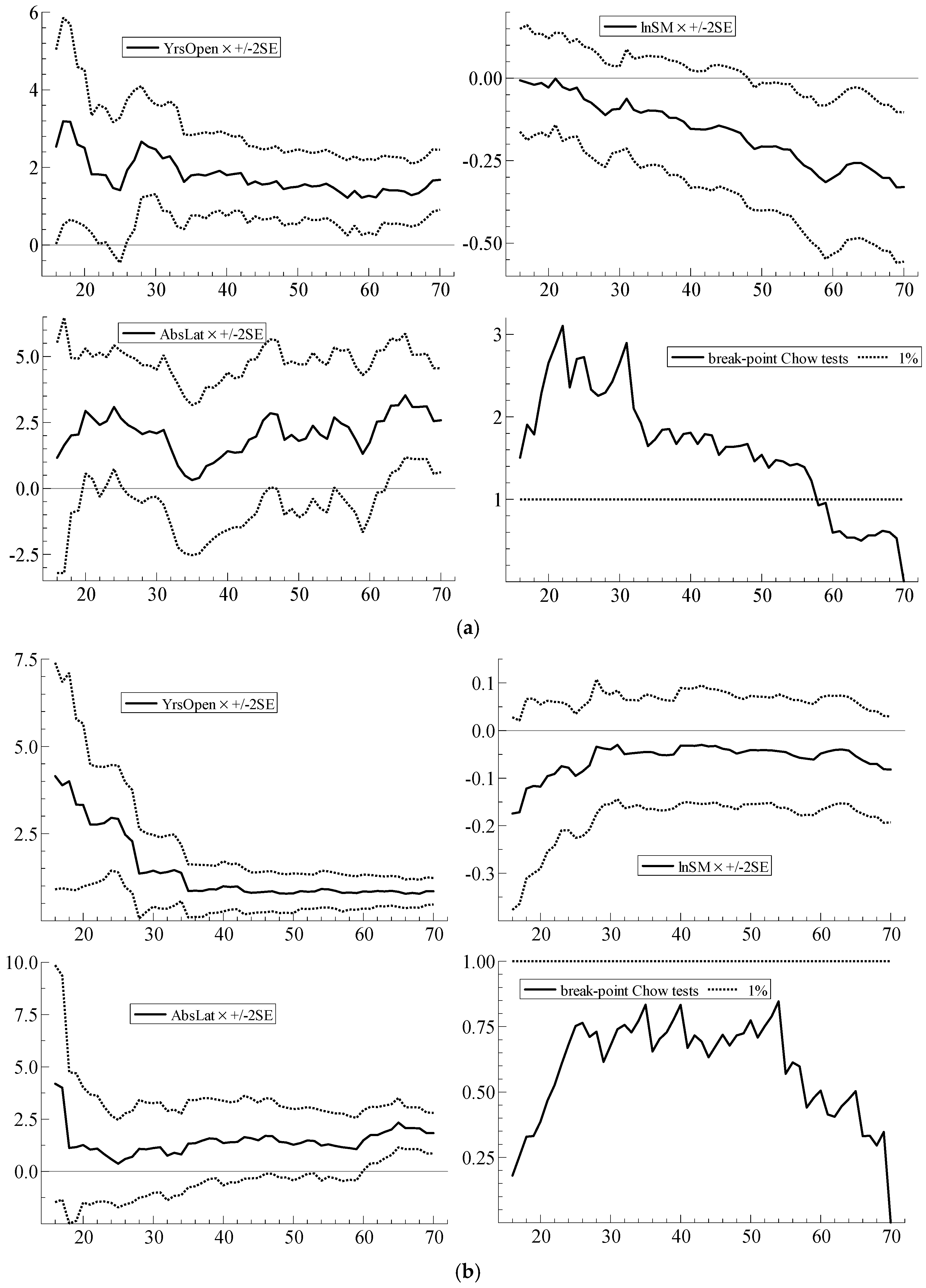
| 8 | With parameter constancy, the sequence of coefficient estimates should stabilize, with no sharp breaks, as N increases; the ideal is to be able to see, from left to right, through the ‘tunnel’ formed by the narrowing standard error bands. Qin et al. (2016), for example, provide a recent example of the usefulness of recursive plots as a diagnostic device. In the recursive graphs, the Chow test statistic values are scaled by the relevant critical values from the F-distribution at the 1% significance level; scaled test values greater than unity in the graphs (represented by the dotted line) therefore indicate statistical significance at the 1% level. |
| 9 | As Hendry (2009, p. 31) emphasizes, “[s]uitable tests for the absence of dependence would seem essential before too great weight is placed on results that [are based] on the claim of random sampling, especially when the units are large entities like countries.” |
| 10 | Although examination of the different potential sources of parameter non-constancy in the individual models is beyond the scope of the current paper, identification of influential observations and outliers using, for example, jackknife estimation and associated DFBETAS (Belsley et al. 2005) could provide additional insights on the sensitivity of coefficient estimates to individual observations. |
| 11 | |
| 12 | |
| 13 | Ashraf and Galor (2011, p. 2016) express the view that “variations in land productivity and other geographical characteristics are inarguably exogenous to the cross-country variation in population density” (emphasis added). This is surprising given the emphasis on potential omitted variables as a source of endogeneity for lyst; omitted variables may also be correlated with the geographical controls, which would potentially bias OLS estimates for all the coefficients. |
| 14 | The version of the model fitted by Spolaore and Wacziarg (2013) includes different geographical control variables (absolute latitude, percentage of land area in the tropics, a landlocked dummy and an island dummy). These are therefore included with the additional instruments, Plants (the number of prehistoric wild grasses) and Animals (the number of prehistoric domesticable large mammals), in the instrument set appearing in each RF. |
| 15 | Correlation of explanatory variables with omitted variables is, however, still a source of endogeneity, which is considered to varying degrees. Spolaore and Wacziarg (2009) use genetic distance as of 1500 to instrument for current genetic distance in their bilateral income difference regressions. Putterman and Weil (2010) emphasize the importance of including appropriate controls to reduce the possibility of omitted variables bias. |
| 16 | In the fundamental determinants literature, the country is the usual unit of geographical aggregation, as is the case for all the studies considered here. An interesting question, left for future investigation, is whether spatially correlated residuals are also present in sub-national empirical studies, such as Michalopoulos’ (2012) exploration of the determinants of ethnolinguistic diversity at different levels of spatial aggregation, including ‘virtual countries’ and adjacent regions. Noting that cross-country studies are based on relatively small sample sizes, a referee poses the question of whether statistical assumptions are more likely to be violated with small samples. Sub-national studies would also provide a larger number of observations, which may shed light on this question, but, in general, misspecification is just as likely with models fitted to large as to small samples and its adverse effects (e.g., due to heterogeneity) may be even more damaging in large samples (Spanos 2017). |
| 17 | Casey and Klemp’s (2016) recent study is an exception to the widespread neglect of dynamics in this literature. They examine the use of historical instruments for contemporary endogenous explanatory variables and explicitly consider the persistence of the latter, in aiming to quantify the long-run causal effect of historical values of the endogenous fundamental determinant, such as institutional quality, on contemporary levels of development. Their approach, using system GMM, suggests that conventional IV estimation overestimates the effect of institutions on development. |


| Test | Reference | Null | Description |
|---|---|---|---|
| Norm NormVec | Doornik & Hansen (2008) | Normality | Norm = under the null, where z1 and z2 are transformed skewness and kurtosis measures correcting for finite-sample dependence between sample skewness and kurtosis (computed using OxMetrics 7 (Doornik and Hendry 2013a, p. 276)). NormVec is the multivariate equivalent (Doornik and Hansen 2008, Section III) (computed using OxMetrics 7 (Doornik and Hendry 2013b, p. 227)). |
| Hetero HeteroVec | White (1980) | Homoskedasticity | Degrees-of-freedom-adjusted F-approximation to an asymptotically distributed χ2 test statistic under the null, calculated as NR2 from an auxiliary regression of the squared residuals on a constant, the original regressors, and their squares (computed using OxMetrics 7 (Doornik and Hendry 2013a, p. 277)). HeteroVec is obtained from a multivariate regression of all error variances and covariances on the original regressors and their squares (computed using OxMetrics 7 (Doornik and Hendry 2013b, p. 227)). |
| HeteroX HeteroXVec | White (1980) | Homoskedasticity | As for Hetero, but also including cross-products of the regressors in the auxiliary regression; reported only if there are sufficient observations (computed using OxMetrics 7 (Doornik and Hendry 2013a, p. 277)). HeteroXVec is the multivariate equivalent (computed using OxMetrics 7 (Doornik and Hendry 2013b, p. 227)). |
| RESET RESETVec | Ramsey (1969) | Correct functional form | Includes squares and cubes of the fitted values from the original regression as additional regressors. Under the null of zero coefficients on these additional regressors, the F-test is approximately F distributed (computed using OxMetrics 7 (Doornik and Hendry 2013a, p. 278)). RESETVec is the multivariate equivalent (computed using OxMetrics 7). |
| Moran’s I | Moran (1948) | Lack of spatial autocorrelation | I = (e′We/S)/(e′e/N), where e is a vector of OLS residuals, W is a spatial weights matrix and S = A standardized version of I is approximately normally distributed under the null of no spatial autocorrelation (Cliff and Ord 1973) (computed using Jeanty’s (2010) anketest routine in Stata 14.2). |
| LMρλ | Anselin et al. (1996) | Lack of spatial autocorrelation | LMρλ is a joint test of lack of spatial error and spatial lag dependence and is asymptotically χ2(2) distributed under the null of absence of both spatial error and spatial lag dependence (Anselin et al. 1996, Equation (15)) (computed using Jeanty’s (2010) anketest routine in Stata 14.2). |
| Parameter Constancy | Doornik & Hendry (2013b) | i-invariance of parameters | Recursive graph of estimated coefficients for coefficient j for i = 1, …, M, with M increasing to N. Sequences of break-point Chow tests assessing whether model based on first M observations yields good forecasts of the remaining observations (Doornik and Hendry 2013a, Equation (18.2)) (computed using OxMetrics 7 (Doornik and Hendry 2013a, p. 264–5)). |
| Study | Table/Row or Column | Estimation Method (N) | Dependent Variable | Explanatory Variables (Endogenous Variables in Bold) | Additional Instruments | Diagnostics |
|---|---|---|---|---|---|---|
| Hall and Jones (1999) | Table II, row 3 | 2SLS (N = 79) | ln(Y/L) | SocInf | AbsLat, EurFrac, EngFrac, lnFR | OverID |
| Hall and Jones (1999) | Table II, row 3# | 2SLS (N = 79) | ln(Y/L) | GADP, YrsOpen | AbsLat, EurFrac, EngFrac, lnFR | |
| Acemoglu et al. (2001) | Table 4, column 2 | 2SLS (N = 64) | lnGDPpc | AvExpr, AbsLat, | lnSM | |
| Acemoglu et al. (2001) | Table 4, column 8 | 2SLS (N = 64) | lnGDPpc | AvExpr, AbsLat, continent dvs | lnSM | |
| Acemoglu et al. (2001) | Table 5, column 6 | 2SLS (N = 64) | lnGDPpc | AvExpr, AbsLat, FrLO | lnSM | |
| Acemoglu et al. (2001) | Table 5, column 7 | 2SLS (N = 64) | lnGDPpc | AvExpr, Religion variables | lnSM | |
| Acemoglu et al. (2001) | Table 5, column 8 | 2SLS (N = 64) | lnGDPpc | AvExpr, AbsLat, Religion variables | lnSM | |
| Acemoglu et al. (2001) | Table 5, column 9 | 2SLS (N = 64) | lnGDPpc | AvExpr, AbsLat, FrC, FrLO, Religion variables | lnSM | |
| Easterly and Levine (2003) | Table 4, row 4 | 2SLS (N = 72) | lnGDPpc | Inst, FrLO, Religion variables, EthDiv | lnSM, AbsLat, Landlock | OverID, First-stage F |
| Easterly and Levine (2003) | Table 4, row 6 | 2SLS (N = 72) | lnGDPpc | Inst, FrLO, Religion variables, EthDiv, Oil | lnSM, AbsLat, Landlock, Crops/minerals dvs | OverID, First-stage F |
| Easterly and Levine (2003) | Table 4, row 6## | 2SLS (N = 72) | lnGDPpc | Inst, FrLO, Religion variables, EthDiv, Oil | lnSM, AbsLat, Landlock | na |
| Easterly and Levine (2003) | Table 5, row 4 | 2SLS (N = 70) | lnGDPpc | Inst, YrsOpen, FrLO, Religion variables, EthDiv | lnSM, AbsLat | OverID |
| Sachs (2003) | Table 1, column 10 | 2SLS (N = 69) | lcgdp95 | Rule, Mal94p | lnSM, KGPTemp, ME | |
| Sachs (2003) | Table 1, column 12 | 2SLS (N = 69) | lcgdp95 | Rule, Malfal | lnSM, KGPTemp, ME | |
| Ashraf and Galor (2011) | Table 2, column 6 | 2SLS (N = 96) | lpd1500 | lyst, ln(AbsLat), ln(LandProd), distcr, Land100km, continent dvs | Plants, Animals | OverID, First-stage F |
| Ashraf and Galor (2011) | Table 3, column 6 | 2SLS (N = 94) | lpd1000 | lyst, ln(AbsLat), ln(LandProd), distcr, Land100km, continent dvs | Plants, Animals | OverID, First-stage F |
| Ashraf and Galor (2011) | Table 4, column 6 | 2SLS (N = 83) | lpd1 | lyst, ln(AbsLat), ln(LandProd), distcr, Land100km, continent dvs | Plants, Animals | OverID, First-stage F |
| Spolaore and Wacziarg (2013) | Table 2, column 4 | 2SLS (N = 98) | lpd1500 | lyst, AbsLat, LandTropics, Landlock, Island | Plants, Animals | |
| Ashraf and Galor (2011) | Table 8, column 3 | 2SLS (N = 93) | natech1K | lyst, ln(AbsLat), ln(LandProd), distcr, Land100km, continent dvs | Plants, Animals | OverID, First-stage F |
| Ashraf and Galor (2011) | Table 8, column 6 | 2SLS (N = 93) | natech1 | lyst, ln(AbsLat), ln(LandProd), distcr, Land100km, continent dvs | Plants, Animals | OverID, First-stage F |
| Ashraf and Galor (2011) | Table 9, column 3 | 2SLS (N = 92) | lpd1000 | tech1K, ln(AbsLat), ln(LandProd), distcr, Land100km, continent dvs | Plants, Animals | OverID, First-stage F |
| Ashraf and Galor (2011) | Table 9, column 6 | 2SLS (N = 83) | lpd1 | tech1, ln(AbsLat), ln(LandProd), distcr, Land100km, continent dvs | Plants, Animals | OverID, First-stage F |
| Spolaore and Wacziarg (2013) | Table 5, column 2 | OLS (N = 148) | lpci05 | AdjYrsAg, AbsLat, LandTropics, Landlock, Island | na | |
| Spolaore and Wacziarg (2013) | Table 5, column 4 | OLS (N = 135) | lpci05 | AdjStateHist, AbsLat, LandTropics, Landlock, Island | na | |
| Spolaore and Wacziarg (2013) | Table 6, column 3 | OLS (N = 147) | lpci05 | AdjYrsAg, EuroShare, AbsLat, LandTropics, Landlock, Island | na | |
| Spolaore and Wacziarg (2013) | Table 6, column 4 | OLS (N = 134) | lpci05 | AdjStateHist, EuroShare, AbsLat, LandTropics, Landlock, Island | na | |
| Spolaore and Wacziarg (2013) | Table 6, column 5 | OLS (N = 149) | lpci05 | EuroShare, WtGenDist, AbsLat, LandTropics, Landlock, Island | na | |
| Spolaore and Wacziarg (2013) | Table 7, column 1 | OLS (N = 155) | lpci05 | IndGenDist, AbsLat, LandTropics, Landlock, Island | na | |
| Spolaore and Wacziarg (2013) | Table 7, column 2 | OLS (N = 154) | lpci05 | WtGenDist, AbsLat, LandTropics, Landlock, Island | na | |
| Spolaore and Wacziarg (2013) | Table 7, column 3 | OLS (N = 149) | lpci05 | WtGenDist, EuroShare, AbsLat, LandTropics, Landlock, Island | na | |
| Ashraf and Galor (2013) | Table 2, column 5 | 2SLS (N = 21) | lpd1500 | Div, DivSq, ln(AbsLat), lyst, ln(Arable), ln(AgSuit) | mdistAddis, divhatsq | |
| Ashraf and Galor (2013) | Table 2, column 6 | 2SLS (N = 21) | lpd1500 | Div, DivSq, ln(AbsLat), lyst, ln(Arable), ln(AgSuit), continent dvs | mdistAddis, divhatsq |
| Study | Table/Row or Column | RF Dependent Variables | Normality | Heteroskedasticity | RESET | Spatial Dependence | Parameter Constancy |
|---|---|---|---|---|---|---|---|
| Hall and Jones (1999) | Table II, row 3 | ln(Y/L), SocInf | 1/3 | 2/6 | 2/3 | 4/4 | 2/2 |
| Hall and Jones (1999) | Table II, row 3# | ln(Y/L), GADP, YrsOpen | 1/4 | 2/8 | 2/4 | 5/6 | 3/3 |
| Acemoglu et al. (2001) | Table 4, column 2 | lnGDPpc, AvExpr | 1/3 | 0/6 | 1/3 | 4/4 | 1/2 |
| Acemoglu et al. (2001) | Table 4, column 8 | lnGDPpc, AvExpr | 1/3 | 2/6 | 1/3 | 3/4 | 1/2 |
| Acemoglu et al. (2001) | Table 5, column 6 | lnGDPpc, AvExpr | 2/3 | 0/6 | 0/3 | 4/4 | 1/2 |
| Acemoglu et al. (2001) | Table 5, column 7 | lnGDPpc, AvExpr | 1/3 | 1/6 | 2/3 | 4/4 | 1/2 |
| Acemoglu et al. (2001) | Table 5, column 8 | lnGDPpc, AvExpr | 1/3 | 2/6 | 1/3 | 4/4 | 1/2 |
| Acemoglu et al. (2001) | Table 5, column 9 | lnGDPpc, AvExpr | 0/3 | 1/6 | 0/3 | 4/4 | 1/2 |
| Easterly and Levine (2003) | Table 4, row 4 | lnGDPpc, Inst | 0/3 | 1/6 | 3/3 | 3/4 | 1/2 |
| Easterly and Levine (2003) | Table 4, row 6 | lnGDPpc, Inst | 0/3 | 0/6 | 2/3 | 3/4 | 1/2 |
| Easterly and Levine (2003) | Table 4, row 6## | lnGDPpc, Inst | 0/3 | 1/6 | 2/3 | 3/4 | 2/2 |
| Easterly and Levine (2003) | Table 5, row 4 | lnGDPpc, Inst | 0/3 | 0/6 | 1/3 | 2/4 | 1/2 |
| Sachs (2003) | Table 1, column 10 | lcgdp95, Rule, Mal94p | 1/4 | 3/8 | 2/4 | 4/6 | 2/3 |
| Sachs (2003) | Table 1, column 12 | lcgdp95, Rule, Malfal | 1/4 | 2/8 | 2/4 | 4/6 | 2/3 |
| Ashraf and Galor (2011) | Table 2, column 6 | lpd1500, yst | 2/3 | 3/6 | 0/3 | 4/4 | 2/2 |
| Ashraf and Galor (2011) | Table 3, column 6 | lpd1000, yst | 2/3 | 3/6 | 1/3 | 4/4 | 2/2 |
| Ashraf and Galor (2011) | Table 4, column 6 | lpd1, yst | 3/3 | 1/6 | 0/3 | 4/4 | 1/2 |
| Spolaore and Wacziarg (2013) | Table 2, column 4 | lpd1500, yst | 2/3 | 6/6 | 2/3 | 4/4 | 1/2 |
| Ashraf and Galor (2011) | Table 8, column 3 | natech1K, yst | 3/3 | 4/6 | 1/3 | 4/4 | 1/2 |
| Ashraf and Galor (2011) | Table 8, column 6 | natech1, yst | 2/3 | 2/6 | 0/3 | 4/4 | 0/2 |
| Ashraf and Galor (2011) | Table 9, column 3 | lpd1000, tech1K | 2/3 | 5/6 | 3/3 | 4/4 | 1/2 |
| Ashraf and Galor (2011) | Table 9, column 6 | lpd1, tech1 | 1/3 | 4/6 | 0/3 | 4/4 | 2/2 |
| Spolaore and Wacziarg (2013) | Table 5, column 2 | lpci05 | 0/1 | 0/2 | 0/1 | 2/2 | 1/1 |
| Spolaore and Wacziarg (2013) | Table 5, column 4 | lpci05 | 0/1 | 0/2 | 0/1 | 2/2 | 0/1 |
| Spolaore and Wacziarg (2013) | Table 6, column 3 | lpci05 | 0/1 | 0/2 | 1/1 | 2/2 | 1/1 |
| Spolaore and Wacziarg (2013) | Table 6, column 4 | lpci05 | 0/1 | 0/2 | 0/1 | 1/2 | 0/1 |
| Spolaore and Wacziarg (2013) | Table 6, column 5 | lpci05 | 0/1 | 2/2 | 0/1 | 2/2 | 1/1 |
| Spolaore and Wacziarg (2013) | Table 7, column 1 | lpci05 | 0/1 | 0/2 | 0/1 | 2/2 | 1/1 |
| Spolaore and Wacziarg (2013) | Table 7, column 2 | lpci05 | 0/1 | 0/2 | 0/1 | 2/2 | 1/1 |
| Spolaore and Wacziarg (2013) | Table 7, column 3 | lpci05 | 0/1 | 2/2 | 0/1 | 2/2 | 1/1 |
| Ashraf and Galor (2013) | Table 2, column 5 | lpd1500, Div, DivSq | 0/4 | 1/4 | 1/4 | 0/6 | 0/3 |
| Ashraf and Galor (2013) | Table 2, column 6 | lpd1500, Div, DivSq | 2/4 | 0/3 | 1/4 | 2/6 | 0/3 |
| Test | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Table II, Row 3 | SocInf Components | |||
| ln(Y/L) | SocInf | GADP | YrsOpen | |
| Norm-p | 0.285 | 0.046 | 0.782 | 0.001 |
| NormVec-p | 0.953 | 0.632 | ||
| Hetero-p | 0.022 | 0.774 | 0.613 | 0.791 |
| HeteroVec-p | 0.147 | 0.179 | ||
| HeteroX-p | 0.021 | 0.760 | 0.397 | 0.941 |
| HeteroXVec-p | 0.071 | 0.208 | ||
| RESET-p | 0.114 | 0.011 | 0.000 | 0.180 |
| RESETVec-p | 0.000 | 0.000 | ||
| Moran’s I-p | 0.000 | 0.001 | 0.000 | 0.009 |
| LMρλ-p | 0.002 | 0.017 | 0.003 | 0.080 |
| Parameter Constancy | NC | NC | NC | NC |
| R2 | 0.614 | 0.328 | 0.535 | 0.167 |
| N | 79 | 79 | ||
| Sargan-p | 0.232 | 0.151 | ||
| CD-F | 9.028 | 0.488 | ||
| Partial R2 | 0.328 | 0.535 | 0.167 | |
| Shea partial R2 | 0.328 | 0.084 | 0.026 | |
| Test | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T4C2 | T4C8 | T5C6 | T5C7 | T5C8 | T5C9 | |||||||
| lnGDPpc | AvExpr | lnGDPpc | AvExpr | lnGDPpc | AvExpr | lnGDPpc | AvExpr | lnGDPpc | AvExpr | lnGDPpc | AvExpr | |
| Norm-p | 0.070 | 0.975 | 0.064 | 0.999 | 0.046 | 0.879 | 0.177 | 0.769 | 0.149 | 0.887 | 0.358 | 0.998 |
| NormVec-p | 0.050 | 0.037 | 0.014 | 0.026 | 0.030 | 0.074 | ||||||
| Hetero-p | 0.253 | 0.513 | 0.017 | 0.831 | 0.377 | 0.642 | 0.312 | 0.814 | 0.083 | 0.800 | 0.187 | 0.823 |
| HeteroVec-p | 0.585 | 0.146 | 0.765 | 0.453 | 0.220 | 0.279 | ||||||
| HeteroX-p | 0.272 | 0.654 | 0.030 | 0.859 | 0.345 | 0.733 | 0.079 | 0.333 | 0.035 | 0.727 | 0.066 | 0.698 |
| HeteroXVec-p | 0.641 | 0.209 | 0.740 | 0.035 | 0.022 | 0.010 | ||||||
| RESET-p | 0.407 | 0.006 | 0.061 | 0.014 | 0.198 | 0.068 | 0.042 | 0.044 | 0.093 | 0.026 | 0.064 | 0.063 |
| RESETVec-p | 0.196 | 0.068 | 0.369 | 0.100 | 0.163 | 0.103 | ||||||
| Moran’s I-p | 0.003 | 0.002 | 0.006 | 0.002 | 0.006 | 0.009 | 0.004 | 0.001 | 0.004 | 0.001 | 0.002 | 0.002 |
| LMρλ-p | 0.023 | 0.005 | 0.083 | 0.021 | 0.035 | 0.008 | 0.019 | 0.005 | 0.029 | 0.005 | 0.020 | 0.008 |
| Parameter Constancy | NC | C/NC | NC | C/NC | NC | C/NC | NC | C/NC | NC | C/NC | NC | C/NC |
| R2 | 0.500 | 0.296 | 0.584 | 0.328 | 0.505 | 0.345 | 0.562 | 0.321 | 0.588 | 0.354 | 0.591 | 0.369 |
| N | 64 | 64 | 64 | 64 | 64 | 64 | ||||||
| CD-F | 13.093 | 3.456 | 9.886 | 19.841 | 8.613 | 5.277 | ||||||
| Partial R2 | 0.177 | 0.056 | 0.142 | 0.252 | 0.129 | 0.086 | ||||||
| Test | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
|---|---|---|---|---|---|---|---|---|
| T4R4 | T4R6 | T4R6# | T5R4 | |||||
| lnGDPpc | Inst | lnGDPpc | Inst | lnGDPpc | Inst | lnGDPpc | Inst | |
| Norm-p | 0.268 | 0.842 | 0.908 | 0.157 | 0.374 | 0.931 | 0.349 | 0.958 |
| NormVec-p | 0.119 | 0.903 | 0.173 | 0.425 | ||||
| Hetero-p | 0.123 | 0.494 | 0.938 | 0.970 | 0.088 | 0.657 | 0.485 | 0.872 |
| HeteroVec-p | 0.537 | 0.971 | 0.614 | 0.832 | ||||
| HeteroX-p | 0.006 | 0.301 | 0.489 | 0.884 | 0.001 | 0.235 | 0.944 | 0.638 |
| HeteroXVec-p | 0.252 | 0.947 | 0.158 | 0.784 | ||||
| RESET-p | 0.010 | 0.016 | 0.001 | 0.284 | 0.005 | 0.059 | 0.071 | 0.133 |
| RESETVec-p | 0.008 | 0.004 | 0.016 | 0.015 | ||||
| Moran’s I-p | 0.000 | 0.017 | 0.015 | 0.124 | 0.001 | 0.012 | 0.004 | 0.201 |
| LMρλ-p | 0.011 | 0.150 | 0.005 | 0.006 | 0.012 | 0.121 | 0.026 | 0.393 |
| Parameter Constancy | NC | C | NC | C/NC | NC | NC | NC | C/NC |
| R2 | 0.615 | 0.573 | 0.787 | 0.729 | 0.632 | 0.593 | 0.686 | 0.674 |
| N | 72 | 72 | 72 | 70 | ||||
| Sargan-p | 0.066 | 0.429 | 0.145 | 0.097 | ||||
| CD-F | 11.743 | 5.155 | 10.898 | 12.131 | ||||
| Partial R2 | 0.359 | 0.563 | 0.345 | 0.285 | ||||
| Test | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| T1C10 | T1C12 | |||
| lcgdp95 | Rule | Mal94p | Malfal | |
| Norm-p | 0.147 | 0.420 | 0.303 | 0.072 |
| NormVec-p | 0.002 | 0.001 | ||
| Hetero-p | 0.654 | 0.727 | 0.000 | 0.000 |
| HeteroVec-p | 0.018 | 0.162 | ||
| HeteroX-p | 0.757 | 0.651 | 0.000 | 0.000 |
| HeteroXVec-p | 0.093 | 0.356 | ||
| RESET-p | 0.274 | 0.148 | 0.003 | 0.000 |
| RESETVec-p | 0.018 | 0.000 | ||
| Moran’s I-p | 0.001 | 0.817 | 0.004 | 0.000 |
| LMρλ-p | 0.001 | 0.487 | 0.027 | 0.001 |
| Parameter Constancy | NC | C | NC | NC |
| R2 | 0.603 | 0.541 | 0.581 | 0.637 |
| N | 69 | 69 | ||
| Rule | Mal94p | Rule | Malfal | |
| Partial R2 | 0.541 | 0.581 | 0.541 | 0.637 |
| Shea partial R2 | 0.253 | 0.272 | 0.367 | 0.432 |
| Sargan-p | 0.404 | 0.560 | ||
| CD-F | 6.371 | 11.592 | ||
| Test | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | (15) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ashraf and Galor (2011) | Ashraf and Galor (2011) | Ashraf and Galor (2011) | Spolaore and Wacziarg (2013) | Ashraf and Galor (2011) | Ashraf and Galor (2011) | Ashraf and Galor (2011) | |||||||||
| T2C6 | T3C6 | T4C6 | T2C4 | T8C3 | T8C6 | T9C3 | T9C6 | ||||||||
| lpd1500 | lyst | lpd1000 | lyst | lpd1 | lyst | lpd1500 | lyst | natech1K | lyst | natech1 | lpd1000 | tech1K | lpd1 | tech1 | |
| Norm-p | 0.360 | 0.010 | 0.121 | 0.015 | 0.029 | 0.002 | 0.461 | 0.001 | 0.004 | 0.004 | 0.073 | 0.061 | 0.003 | 0.023 | 0.643 |
| NormVec-p | 0.027 | 0.010 | 0.001 | 0.006 | 0.001 | 0.006 | 0.001 | 0.075 | |||||||
| Hetero-p | 0.323 | 0.096 | 0.283 | 0.085 | 0.039 | 0.425 | 0.001 | 0.001 | 0.000 | 0.150 | 0.049 | 0.329 | 0.002 | 0.050 | 0.001 |
| HeteroVec-p | 0.011 | 0.002 | 0.069 | 0.000 | 0.000 | 0.113 | 0.000 | 0.001 | |||||||
| HeteroX-p | 0.031 | 0.082 | 0.034 | 0.083 | 0.064 | 0.346 | 0.000 | 0.002 | 0.021 | 0.067 | 0.149 | 0.038 | 0.045 | 0.113 | 0.011 |
| HeteroXVec-p | 0.001 | 0.001 | 0.185 | 0.000 | 0.001 | 0.041 | 0.000 | 0.000 | |||||||
| RESET-p | 0.055 | 0.308 | 0.010 | 0.460 | 0.282 | 0.678 | 0.035 | 0.251 | 0.016 | 0.454 | 0.242 | 0.013 | 0.008 | 0.194 | 0.059 |
| RESETVec-p | 0.152 | 0.059 | 0.077 | 0.020 | 0.200 | 0.140 | 0.010 | 0.065 | |||||||
| Moran’s I-p | 0.000 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.001 | 0.002 |
| LMρλ-p | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.012 |
| Parameter Constancy | NC | NC | NC | NC | NC | C/NC | NC | C/NC | NC | C/NC | C/NC | NC | C | NC | NC |
| R2 | 0.686 | 0.685 | 0.650 | 0.698 | 0.617 | 0.712 | 0.474 | 0.721 | 0.720 | 0.674 | 0.555 | 0.624 | 0.711 | 0.614 | 0.511 |
| N | 96 | 94 | 83 | 98 | 93 | 93 | 92 | 83 | |||||||
| Sargan-p | 0.358 | 0.159 | 0.587 | 0.216 | 0.343 | 0.254 | 0.938 | 0.250 | |||||||
| CD-F | 16.299 | 16.067 | 12.458 | 69.911 | 14.484 | 14.484 | 8.595 | 7.105 | |||||||
| Partial R2 | 0.275 | 0.277 | 0.255 | 0.606 | 0.259 | 0.259 | 0.173 | 0.163 | |||||||
| Test | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
|---|---|---|---|---|---|---|---|---|
| T5C2 | T5C4 | T6C3 | T6C4 | T6C5 | T7C1 | T7C2 | T7C3 | |
| lpci05 | lpci05 | lpci05 | lpci05 | lpci05 | lpci05 | lpci05 | lpci05 | |
| Norm-p | 0.917 | 0.499 | 0.438 | 0.322 | 0.072 | 0.148 | 0.269 | 0.072 |
| Hetero-p | 0.249 | 0.431 | 0.115 | 0.214 | 0.034 | 0.097 | 0.097 | 0.034 |
| HeteroX-p | 0.130 | 0.237 | 0.128 | 0.150 | 0.042 | 0.146 | 0.058 | 0.042 |
| RESET-p | 0.636 | 0.739 | 0.025 | 0.531 | 0.220 | 0.590 | 0.365 | 0.220 |
| Moran’s I-p | 0.000 | 0.028 | 0.000 | 0.028 | 0.000 | 0.001 | 0.000 | 0.000 |
| LMρλ-p | 0.000 | 0.006 | 0.000 | 0.098 | 0.000 | 0.001 | 0.001 | 0.000 |
| Parameter Constancy | NC | C/NC | NC | C/NC | NC | NC | NC | NC |
| R2 | 0.523 | 0.588 | 0.580 | 0.656 | 0.545 | 0.499 | 0.496 | 0.545 |
| N | 148 | 135 | 147 | 134 | 149 | 155 | 154 | 149 |
| Test | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| T2C5 | T2C6 | |||||
| lpd1500 | Div | DivSq | lpd1500 | Div | DivSq | |
| Norm-p | 0.545 | 0.947 | 0.930 | 0.876 | 0.019 | 0.007 |
| NormVec-p | 0.909 | 0.224 | ||||
| Hetero-p | 0.847 | 0.044 | 0.071 | 0.136 | 0.521 | 0.669 |
| HeteroVec-p | 0.286 | NF | ||||
| RESET-p | 0.415 | 0.816 | 0.750 | 0.591 | 0.060 | 0.284 |
| RESETVec-p | 0.003 | 0.013 | ||||
| Moran’s I-p | 0.156 | 0.680 | 0.719 | 0.213 | 0.485 | 0.499 |
| LMρλ-p | 0.130 | 0.207 | 0.235 | 0.080 | 0.031 | 0.028 |
| Parameter Constancy | C | C | C | C | C | C |
| R2 | 0.900 | 0.988 | 0.986 | 0.900 | 0.993 | 0.993 |
| N | 21 | 21 | ||||
| CD-F | 19.283 | 18.861 | ||||
| Partial R2 | 0.986 | 0.983 | 0.896 | 0.883 | ||
| Shea partial R2 | 0.740 | 0.738 | 0.815 | 0.804 | ||
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owen, P.D. Evaluating Ingenious Instruments for Fundamental Determinants of Long-Run Economic Growth and Development. Econometrics 2017, 5, 38. https://doi.org/10.3390/econometrics5030038
Owen PD. Evaluating Ingenious Instruments for Fundamental Determinants of Long-Run Economic Growth and Development. Econometrics. 2017; 5(3):38. https://doi.org/10.3390/econometrics5030038
Chicago/Turabian StyleOwen, P. Dorian. 2017. "Evaluating Ingenious Instruments for Fundamental Determinants of Long-Run Economic Growth and Development" Econometrics 5, no. 3: 38. https://doi.org/10.3390/econometrics5030038
APA StyleOwen, P. D. (2017). Evaluating Ingenious Instruments for Fundamental Determinants of Long-Run Economic Growth and Development. Econometrics, 5(3), 38. https://doi.org/10.3390/econometrics5030038





