Abstract
Economic policy agencies produce forecasts with accompanying narratives, and base policy changes on the resulting anticipated developments in the target variables. Systematic forecast failure, defined as large, persistent deviations of the outturns from the numerical forecasts, can make the associated narrative false, which would in turn question the validity of the entailed policy implementation. We establish when systematic forecast failure entails failure of the accompanying narrative, which we call forediction failure, and when that in turn implies policy invalidity. Most policy regime changes involve location shifts, which can induce forediction failure unless the policy variable is super exogenous in the policy model. We propose a step-indicator saturation test to check in advance for invariance to policy changes. Systematic forecast failure, or a lack of invariance, previously justified by narratives reveals such stories to be economic fiction.
JEL Classification:
C22; C51
1. Introduction
The Bank of England’s quarterly Inflation Reports announces its projections of CPI inflation and 4-quarter real GDP growth for the next two years. For example, those made in November 2009 are shown in Figure 1. Accompanying these forecast distributions are textual explanations for the forecasts, an excerpt from which is:1
In his speech on the Report, the Governor stressed:CPI inflation looked set to rise sharply in the near term. Further out, downward pressure from the persistent margin of spare capacity was likely to bear down on inflation for some time to come.
We term the published numerical forecast a ‘direct forecast’, whereas one constructed from the narrative, as in e.g., Ericsson (2016) for the USA, is called a ‘derived forecast’. Taken together, we call the joint production of the numerical forecast and the accompanying narrative a ‘forediction’, intended to convey a forecast made alongside a story (diction) that describes the forecast verbally.2 In this paper, we investigate whether a close link between the direct and derived forecasts sustains an evaluation of the resulting foredictions and their associated policies.It is more likely than not that later this year I will need to write a letter to the Chancellor to explain why inflation has fallen more than 1 percentage point below the target (of 2%).The stimulus to demand, combined with a turnaround in the stock cycle and the effects of the depreciation in sterling, is likely to drive a recovery in activity.
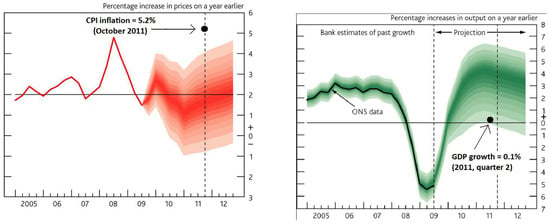
Figure 1.
CPI inflation and 4-quarter real GDP growth forecasts, based on market interest rate expectations and £200 billion asset purchases: November 2009 Bank of England Inflation Report, with October 2011 outturns.
Figure 1 shows the direct forecasts for CPI inflation and 4-quarter real GDP growth from the Bank of England November 2009 Inflation Report, with the outturns in October 2011. The outturn for CPI inflation 2 years out lay well above the central 90% of the distribution for the projected probabilities of CPI inflation outturns, well above the 2% target, yet the outturn for GDP lay in the lowest band. The large forecast error on the direct CPI inflation forecast refutes the above narrative, and would do so more generally when the derived forecast is closely similar, resulting in a forediction failure. The next step would be to investigate the validity of policy decisions made on the basis of the forediction, namely here, the Bank of England decided to hold the Bank Rate at 0.5% and finance a further £25 billion of asset purchases within 3 months.3
The two objectives of this paper are (i) establishing when systematic forecast failure, defined as large, persistent deviations of the outturns from the forecasts, entails forediction failure and when that in turn implies policy invalidity; and (ii) whether failures of invariance in policy models are detectable in advance, which should enable more robust policy models to be developed.
There are four key steps in the process of evaluating foredictions and associated policies. The first is to establish whether the direct and derived forecasts are almost the same. Then forecasts are indeed closely described by the accompanying narrative in the sense formalized by Ericsson (2016), namely accurate estimates of the forecasts can be derived by quantifying the narrative. For example, regressing the derived forecasts on the direct should deliver a highly significant relation with a coefficient near unity. The second step involves testing whether systematic forecast failure of the direct forecasts occurs, for which many tests exist. If the direct and derived forecasts are closely linked, as checked in the first step, then systematic forecast failure of the direct forecasts would imply systematic forecast failure of the derived forecasts. This is forediction failure, checked by testing (a) if the narrative-derived forecasts remain linked to the direct forecasts, and (b) they also differ significantly from the realized outcomes. In that case, the accompanying narrative must also be rejected. In the third step, if a policy implementation had been justified by the forediction, then it too must be invalid after forediction failure. This is harder to quantify unless there is a known policy rule, such as a Taylor rule linking interest rate responses to inflation, but the policy link may be stated explicitly in the narrative. The fourth step is to test if the forediction failure actually resulted from the policy change itself because of a lack of invariance of the model used in the policy analysis to that change. In that case, the policy model is also shown to be invalid.
Evaluating the validity of policy analysis involves two intermediate links. First, genuine causality from policy instruments to target variables is essential for policy effectiveness if changing the policy variable is to affect the target: see e.g., Cartwright (1989). That influence could be indirect, as when an interest rate affects aggregate demand which thereby changes the rate of inflation. Secondly, the invariance of the parameters of the empirical models used for policy to shifts in the distributions of their explanatory variables is also essential for analyses to correctly represent the likely outcomes of policy changes. Thus, a policy model must not only embody genuine causal links in the data generation process (DGP), invariance also requires the absence of links between target parameters and policy-instrument parameters, since the former cannot be invariant to changes in the latter if their DGP parameters are linked, independently of what modellers may assume: see e.g., Hendry (2004) and Zhang et al. (2015). Consequently, weak exogeneity matters in a policy context because its two key requirements are that the relevant model captures the parameters of interest for policy analyses, and that the parameters of the policy instrument and the target processes are unconnected in the DGP, not merely in their assumed parameter spaces. Since changes in policy are involved, valid policy then requires super exogeneity of the policy variables in the target processes: see Engle et al. (1983).
To this end, the paper proposes a step-indicator saturation test to check in advance for invariance to policy changes. Step-indicator saturation (SIS) is designed to detect location shifts of unknown magnitude, location and frequency at any point in the sample, see Castle et al. (2015). Super exogeneity, which is required for policy validity, can be tested by checking whether any significant location shifts in models of the policy instruments are significant in the model of the target variables. The proposed test is an extension of the test for super exogeneity using impulse indicator saturation proposed in Hendry and Santos (2010).
Combining these ideas, forediction evaluation becomes a feasible approach to checking the validity of policy decisions based on forecasts linked to a narrative that the policy agency wishes to convey. Policy decisions can fail because empirical models are inadequate, causal links do not exist, parameters are not invariant, the story is incorrect, or unanticipated events occur. By checking the properties of the direct and derived forecasts and the invariance of the policy model to the policy change envisaged, the source of forediction failure may be more clearly discerned, hopefully leading to fewer bad mistakes in the future.
The structure of the paper is as follows. Section 2 explores the link between direct and derived forecasts with accompanying narratives that are often used to justify policy decisions, where Section 2.1 discusses whether narratives or forecasts come first, or are jointly decided. Section 3 considers what can be learned from systematic forecast failure, and whether there are any entailed implications for forediction failure. More formally, Section 3.1 outlines a simple theoretical policy DGP; Section 3.2 describes what can be learned from systematic forecast failure using a taxonomy of forecast errors for a mis-specified model of that DGP; Section 3.3 provides a numerical illustration; and Section 3.4 notes some of the implications of forediction failure for economic theories using inter-temporal optimization. Parametric time-varying models are not explicitly considered, but Section 6.1 investigates an approach that potentially allows coefficients to change in many periods; our analysis would extend to handling location shifts in models with time-varying coefficients but constant underlying parameters, as in structural time series models which have constant-parameter ARIMA representations. Section 4 presents a two-stage test for invariance using automatic model selection to implement step-indicator saturation, which extends impulse-indicator saturation (IIS): see Hendry et al. (2008). Section 5 reports some simulation evidence on its first-stage null retention frequency of irrelevant indicators (gauge) and its retention frequency of relevant indicators (potency), as well as its second-stage rejection frequencies in the presence or absence of invariance: see Johansen and Nielsen (2016) for an analysis of gauge in IIS. Section 6 applies this SIS-based test to the small artificial-data policy model analyzed in Section 3.1, and Section 6.1 investigates whether a shift in a policy parameter can be detected using multiplicative indicator saturation (MIS), where step indicators are interacted with variables. Section 7 summarizes the forecast error taxonomy and associated relevant tests, and Section 8 considers how intercept corrections can improve forecasts without changing the forecasting model’s policy responses. Section 9 concludes.
2. Forediction: Linking Forecasts, Narratives, and Policies
Links between forecasts and their accompanying narratives have been brought into new salience through innovative research by Stekler and Symington (2016) and Ericsson (2016). The former develop quantitative indexes of optimism/pessimism about the US economy by analyzing the qualitative information in the minutes from Federal Open Market Committee (FOMC) meetings, scaled to match real GDP growth rates in percentages per annum. The latter calibrates the Stekler and Symington (2016) index for real GDP growth, denoted FMI, to past GDP growth outcomes, removing its truncation to , and shows that the resulting index can provide excellent post-casts of the Fed’s ‘Greenbook’ forecasts of 2006–10 (which are only released after a 5-year delay). Clements and Reade (2016) consider whether Bank of England narratives provide additional information beyond their inflation forecasts.
For many years, Central Banks have published narratives both to describe and interpret their forecasts, and often justify entailed policies. Important examples include the minutes from Federal Open Market Committee (FOMC) meetings, the Inflation Reports of the Bank of England, and International Monetary Fund (IMF) Reports. For Banca d’Italia, Siviero and Terlizzese (2001) state that:
Such an approach is what we term forediction: any claims as to its success need to be evaluated in the light of the widespread forecast failure precipitated by the 2008–9 Financial Crisis. As we show below, closely tying narratives and forecasts may actually achieve the opposite of what those authors seem to infer, by rejecting both the narratives and associated policies when forecasts go wrong....forecasting does not simply amount to producing a set of figures: rather, it aims at assembling a fully-fledged view—one may call it a “story behind the figures”—of what could happen: a story that has to be internally consistent, whose logical plausibility can be assessed, whose structure is sufficiently articulated to allow one to make a systematic comparison with the wealth of information that accumulates as time goes by.
Sufficiently close links between direct forecasts and forecasts derived from their accompanying narratives, as highlighted by Stekler and Symington (2016) and Ericsson (2016), entail that systematic forecast failure vitiates any related narrative and its associated policy. This holds irrespective of whether the direct forecasts lead to the narrative, or the forecasts are modified (e.g., by ‘judgemental adjustments’) to satisfy a preconceived view of the future expressed in a narrative deliberately designed to justify a policy, or the two are iteratively adjusted as in the above quote, perhaps to take account of informal information available to a panel such as the Bank of England’s Monetary Policy Committee (MPC). In all three cases, if the direct and derived forecasts are almost the same, and the narratives reflect cognitive models or theories, then the large forecast errors around the ‘Great Recession’ would also refute such thinking, as addressed in Section 3. However, when direct and derived forecasts are not tightly linked, failure in one need not entail failure in the other, but both can be tested empirically.
2.1. Do Narratives or Forecasts Come First?
Forcing internal consistency between forecasts and narratives, as both Siviero and Terlizzese (2001) and Pagan (2003) stress, could be achieved by deciding the story, then choosing add factors to achieve it, or vice versa, or by a combination of adjustments. The former authors appear to suggest the third was common at Banca d’Italia, and the fact that Bank of England forecasts are those of the MPC based on the information it has, which includes forecasts from the Bank’s models, suggests mutual adjustments of forecasts and narratives, as in e.g., (Bank of England 2015, p. 33) (our italics):
Not only could add factors be used to match forecasts to a narrative, if policy makers had a suite of forecasting models at their disposal, then the weightings on different models could be adjusted to match their pooled forecast to the narrative, or both could be modified in an iterative process. Genberg and Martinez (2014) show the link between narratives and forecasts at the International Monetary Fund (IMF), where forecasts are generated on a continuous basis through the use of a spreadsheet framework that is occasionally supplemented by satellite models, as described in Independent Evaluation Office (2014). Such forecasts ‘form the basis of the analysis [...] and of the [IMF’s] view of the outlook for the world economy’ (p.1). Thus, adjustments to forecasts and changes to the associated narratives tend to go hand-in-hand at many major institutions.The projections for growth and inflation are underpinned by four key judgements.
In a setting with several forecasting models used by an agency that nevertheless delivered a unique policy prescription, possibly based on a ‘pooled forecast’, then to avoid implementing policy incorrectly, super exogeneity with respect to the policy instrument would seem essential for every model used in that forecast. In practice, the above quotes suggest some Central Banks act as though there is a unique policy model constrained to match their narrative, where all the models in the forecasting suite used in the policy decision are assumed to be invariant to any resulting changes in policy. This requirement also applies to scenario studies as the parameters of the models being used must be valid across all the states examined. Simply asserting that the policy model is ‘structural’ because it is derived from a theory is hardly sufficient. Akram and Nymoen (2009) consider the role of empirical validity in monetary policy, and caution against over-riding it. Even though policy makers recognise that their policy model may not be the best forecasting model, as illustrated by the claimed trade-off between theory consistency and empirical coherence in Pagan (2003), forecast failure can still entail forediction failure, as shown in Section 3.
2.2. Is There a Link between Forecasts and Policy?
Evaluating policy-based forediction failure also requires there to be a link between the forecasts and policy changes. This can either occur indirectly through the narratives or directly through the forecasts themselves (e.g., through a forward looking Taylor rule). That direct forecasts and forecasts derived from the narratives are closely linked implies that policies justified by those narratives, are also linked to the forecasts.
In their analysis of the differences between the Greenbook and FOMC forecasts, Romer and Romer (2008) find that there is a statistically significant link between differences in these two forecasts and monetary policy shocks. This can be interpreted as evidence suggesting that policy makers forecasts influence their decisions above and beyond other informational inputs. As such, the policy decision is both influenced by and influences the forecasts.
Regardless of this influence, the link between forecasts and policy depends on how the forecasts are used. Ellison and Sargent (2012) illustrate that it is possible for ‘bad forecasters’ to be ‘good policymakers’. In this sense, forecast failure could potentially be associated with policy success. However, this is less likely when focusing on systematic forecast failure. Sinclair et al. (2016) Sinclair, Tien, and Gamber find that forecast failure at the Fed is associated with policy failure. They argue that in 2007–08 the Greenbook’s overpredictions of output and inflation “resulted in a large contractionary [monetary policy] shock” of around 7 percentage points. By their calculations, using a forward-looking Taylor rule, this forecast-error-induced shock reduced real growth by almost 1.5 percentage points. Furthermore, Independent Evaluation Office (2014) illustrates that in IMF Programs, the forecasts are often interpretable as the negotiated policy targets. This suggests that forecasts, narratives and policy are sufficiently closely linked so that systematic forediction failure can be used to refute the validity of policy decisions.
3. Forecast Failure and Forediction Failure
Systematic forecast failure by itself is not a sufficient condition for rejecting an underlying theory or any associated forecasting model, see, e.g., Castle and Hendry (2011). Furthermore, forecasting success may, but need not, ‘corroborate’ the forecasting model and its supporting theory: see Clements and Hendry (2005). Indeed, Hendry (2006) demonstrates a robust forecasting device that can outperform the forecasts from an estimated in-sample DGP after a location shift. Nevertheless, when several rival explanations exist, forecast failure can play an important role in distinguishing between them as discussed by Spanos (2007). Moreover, systematic forecast failure almost always rejects any narrative associated with the failed forecasts and any policy implications therefrom, so inevitably results in forediction failure.
3.1. A Simple Policy Data Generation Process
In this section, we develop a simple theoretical policy model which is mis-specified for its economy’s DGP. At time T, the DGP shifts unexpectedly, so there is forecast failure. However, even if the DGP did not shift, because the policy model is mis-specified, a policy change itself can induce forecast failure. In our model, the policy agency decides on an action at precisely time T, so the two shifts interact. We provide a taxonomy of the resulting sources of failure, and what can be inferred from each component.
Let be a policy target, say inflation, the instrument an agency controls to influence that target, say interest rates, where is the variable that is directly influenced by the instrument, say aggregate excess demand, which in turn directly affects inflation. Also, let represent the net effect of other variables on the target, say world inflation in the domestic currency, and denote additional forces directly affecting domestic demand, where the are super exogenous for the parameters in the DGP. The system is formalized as:
where for simplicity with and ; and :
with where and . In the next period, solving as a function of policy and exogenous variables:
Consequently, a policy shift moving to would, on average and ceteris paribus, move to . We omit endogenous dynamics to focus on the issues around forediction.
In a high-dimensional, wide-sense non-stationary world, where the model is not the DGP, and parameters need to be estimated from data that are not accurately measured, the policy agency’s model of inflation is the mis-specified representation:
where and are obtained as the OLS estimates of the regression of on , thus omitting . Also, its model of demand is mis-specified as:
where and are obtained as the OLS estimates of the regression of on , thus omitting . This system leads to its view of the policy impact of at as being on average and ceteris paribus:
so a policy shift moving to would be expected to move to where and are in-sample estimates of and respectively. If the agency wishes to lower inflation when and , it must set such that (e.g., corresponds to a 1 percentage point reduction in the annual inflation rate).
The equilibrium means in the stationary world before any shifts or policy changes are:
where , and , so that as well from (4), and:
where from (5), . We now consider the effects of the unexpected shift in the DGP in Section 3.1.1, of the policy change in Section 3.1.2, and of mis-specification of the policy model for the DGP in Section 3.1.3.
3.1.1. The DGP Shifts Unexpectedly
Just as the policy change is implemented at time T, the DGP shifts unexpectedly to:
and:
For simplicity we assume the error distributions remain the same, so that:
The equilibrium means after the shift and before the policy change are:
where the expectation is taken at time , and when remain unchanged:
Even using the in-sample DGP (3) with known parameters and known values for the exogenous variables, there will be forecast failure for a large location shift from to since the forecast error is:
so that:
and similarly for , then .
3.1.2. The Policy Change
Next, the policy shift changes to , which is a mistake as that policy leads to the impact instead of as anticipated by an agency using the in-sample DGP parameters. Instead, the policy shift would alter the mean forecast error to:
The additional component in (11) compared to (10) would be zero if , so the failure of super exogeneity of the policy variable for the target augments, or depending on signs, possibly attenuates the forecast failure. Importantly, if so the DGP did not shift, the policy shift by itself could create forecast failure. Section 4 addresses testing for such a failure in advance of a policy-regime shift.
3.1.3. The Role of Mis-Specification
Third, there would be a mis-specification effect from using (6), as the scenario calculated ex ante would suggest the effect to be . Although there is also an estimation effect, it is probably O, but to complete the taxonomy of forecast errors below, we will add estimation uncertainty since the parameters of (6) could not be ‘known’. Denoting such estimates of the model by , then:
where the in-sample expected values of OLS estimated coefficients are shown by a subscript , noting that both and are almost bound to be known to the policy agency. From the DGP in (9):
but from (6), the agency would forecast as:
where is the measured forecast-origin value. An agency is almost certain to know the correct value, but we allow for the possibility of an incorrect forecast-origin value to complete the taxonomy of forecast-failure outcomes in (16) and Table 1. Then the agency anticipates that shifting to would on average revise the outcome to , as against the actual outcome in (12), leading to a forecast error of :

Table 1.
A taxonomy of the implications of systematic forecast failures.
Then (14) has an approximate average value of:
Unless the model is revised, the same average error will occur in the following periods leading to systematic forecast failure. Indeed, even if the policy agency included and appropriately in their forecasting model’s equations, their roles in (14) would be replaced by any shifts in their parameter values, changing (15): see Hendry and Mizon (2012).
3.1.4. The Sources of Forecast Failure
The error in (14) can be decomposed into terms representing mis-estimation (labelled (a)), mis-specification ((b)) and change ((c)) for each of the equilibrium mean (labelled (i)), slope parameter ((ii)) and unobserved terms ((iii)), as in (16). The implications of this 3x3 framework are recorded in Table 1, ignoring covariances, and under the assumption that the derived forecasts are closely similar to the direct.
In (16), the impacts of each of the nine terms can be considered in isolation by setting all the others to zero in turn. Although only i(c) is likely to cause forecast failure, any narrative and associated policy as discussed above may well be rejected by systematic errors arising from any of these nine terms.
3.2. What Can Be Learned from Systematic Forecast Failure?
The three possible mistakes—mis-estimation, mis-specification and change—potentially affect each of the three main components of any forecasting model—equilibrium means, slope parameters and unobserved terms—leading to the nine terms in Table 1. This condensed model-free taxonomy of sources of forecast errors is based on Ericsson (2017), which built on those in Clements and Hendry (1998) for closed models and Hendry and Mizon (2012) for open systems.
As not all sources of systematic forecast failure lead to the same implications, we consider which sources should cause rejection of the forecasting model (denoted FM in the table), the forediction narrative (FN), or impugn policy validity (PV). Systematic failure of the forecasts could arise from any of the terms, but the consequences vary with the source of the mistake. We assume that the derived forecasts are sufficiently close to the direct that both suffer systematic forecast failure, so in almost every case in the table, the entailed forediction and policy are rejected. However, a ‘?’ denotes that systematic forecast failure is less likely in the given case, but if it does occur then the consequences are as shown.
Taking the columns in turn, mis-estimation by itself will rarely lead to systematic forecast failure and should not lead to rejecting the formulation of a forecasting model, or the theory from which it was derived, as appropriate estimation would avoid such problems. For example, when the forecast origin has been mis-measured by a statistical agency resulting in a large forecast error in iii(a), one should not reject either the forecasting model or the underlying theory. Nevertheless, following systematic forecast failure, any policy conclusions that had been drawn and their accompanying narrative should be rejected as incorrect, at least until more accurate data are produced.
Next, mis-specification generally entails that the model should be rejected against a less badly specified alternative, and that foredictions and policy claims must be carefully evaluated as they too will often be invalid. In stationary processes, mis-specification alone will not lead to systematic forecast failure, but the real economic world is not stationary, and policy regime shifts will, and are intended to, alter the distributions of variables. That omitted variables need not induce systematic forecast failure may surprise at first sight, but iii(b) in (16) reveals their direct effect has a zero mean as shown by Hendry and Mizon (2012).
Third, unanticipated changes in the non-zero-mean components of forecasting models will usually cause systematic forecast failure. However, slope shifts on zero-mean influences and changes in innovation error variances need not. Nevertheless, in almost all cases systematic forecast failure will induce both forediction and policy failure if the policy implemented from the mistaken narrative depended on a component that had changed. Finally, the consequences for any underlying theory depend on how that theory is formulated, an issue briefly discussed in Section 3.4. We return to the taxonomy in Section 4, where we propose a test for the elements of forediction failure.
3.3. A Numerical Illustration
The scenario considered is one where in (13), the agency’s direct forecast, , is higher than the policy target value, and as , it announces a rise in of such that aims to be smaller than the target, so will fall. Unfortunately, an unanticipated boom hits, resulting in large rises in and . Below, and denote forecast values from (infeasible) in-sample DGP estimates, whereas and are model-based forecasts, which here also correspond to the agency’s forediction-based forecasts for inflation and output. An example of how a forecast, the associated forediction and a linked policy change could be represented is given in Table 2.

Table 2.
Forediction example.
The numerical values of the parameters in the 5-variable in-sample simulation DGP are recorded in the top two rows of Table 3.

Table 3.
Parameter values for the simulation DGPs.
As and , their projections on and respectively are both zero, so , , , , and . The policy change is and the shifts in the DGP are described in the bottom two rows of Table 3. Now and , but initially x jumps to around 6 because of the lag in its response to the policy change. For y and x these cases are denoted (I) & (II) in Figure 2, whereas cases (III) & (IV) have the same policy implementation and DGP change, but with no location shift, so and .
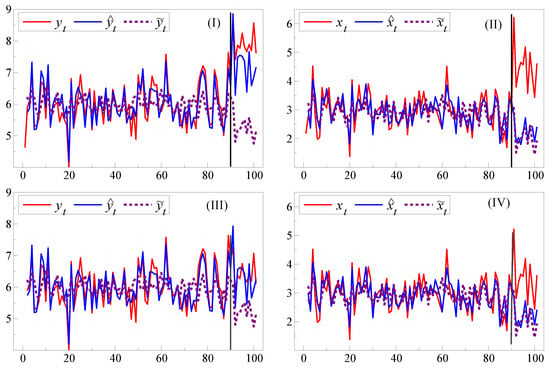
Figure 2.
(I,II) both forediction and policy failures from the forecast failure following a changed DGP with a location shift and a policy change combined; (III,IV) both forediction and policy failures after a changed DGP without a location shift but with a policy change.
For a single simulation, Figure 2(I) illustrates the systematic forecast failure of for when the break in the DGP includes both a location shift and the policy change, together with the much larger failure of the model’s forecast, . When there is no unexpected location shift, so and , then as (III) shows, the in-sample DGP-based forecasts do not suffer failure despite the other changes in the DGP. However, the model mis-specification interacting with still induces both forediction and policy failure from the model’s forecast failing. This occurs because the agency’s model for is mis-specified, so the change acts as an additional location shift, exacerbating the location shift in (I) from the change in , whereas only the policy change occurs in (III). There is little difference between and in either scenario: even if the agency had known the in-sample DGP equation for , there would have been both forediction and policy failure from the changes in the slope parameters caused by as Figure 2(II),(IV) show.
3.4. Implications of Forediction Failure for Inter-Temporal Theories
Whether or not a systematic forecast failure from whatever source impugns an underlying economic theory depends on how directly the failed model is linked to that theory. That link is close for dynamic stochastic general equilibrium (DSGE) theory, so most instances of FM in Table 1 entail a theory failure for the DSGE class. More directly, Hendry and Mizon (2014) show that the mathematical basis of inter-temporal optimization fails when there are shifts in the distributions of the variables involved. All expectations operators must then be three-way subscripted, as in which denotes the conditional expectation of the random variable formed at time t as the integral over the distribution given an available information set . When is the distribution where future changes in are unpredictable, then:
whereas:
so the conditional expectation formed at t is not an unbiased predictor of the outcome , and only a ‘crystal-ball’ predictor based on ‘knowing’ is unbiased.
A related problem afflicts derivations which incorrectly assume that the law of iterated expectations holds even though distributions shift between t and , since then only having information at time t entails:
It is unsurprising that a shift in the distribution of between periods would wreck a derivation based on assuming such changes did not occur, so the collapse of DSGEs like the Bank of England’s Quarterly Econometric Model (BEQEM) after the major endowment shifts occasioned by the ‘Financial Crisis’ should have been anticipated. A similar fate is likely to face any successor built on the same lack of mathematical foundations relevant for a changing world. Indeed, a recent analysis of the replacement model, COMPASS (Central Organising Model for Projection Analysis and Scenario Simulation) confirms that such a fate has already occurred.4
The results of this section re-emphasize the need to test forecasting and policy-analysis models for their invariance to policy changes prior to implementing them. Unanticipated location shifts will always be problematic, but avoiding the policy-induced failures seen in Figure 2(III) and (IV) by testing for invariance seems feasible. Section 4 briefly describes step-indicator saturation, then explains its extension to test invariance based on including in conditional equations the significant step indicators from marginal-model analyses.
4. Step-Indicator Saturation (SIS) Based Test of Invariance
Many tests for super exogeneity have been proposed since Engle et al. (1983): see e.g., (Hendry 1988; Favero and Hendry 1992; Engle and Hendry 1993; Psaradakis and Sola 1996; Jansen and Teräsvirta 1996; Hendry and Santos 2010), including tests based on co-breaking as in Krolzig and Toro (2002), and Hendry and Massmann (2007). Here we propose a test of invariance based on step-indicator saturation (denoted SIS), following Castle et al. (2015). SIS builds on the impulse-indicator saturation (IIS) approach proposed by Hendry et al. (2008) to detect outliers and shifts in a model.
In IIS, an impulse indicator is created for every observation, thereby saturating the model, but indicators are entered in feasibly large blocks for selection of significant departures. Johansen and Nielsen (2009) derive the properties of IIS for dynamic regression models, which may have unit roots, and show that parameter estimator distributions are almost unaffected despite including T impulse indicators for T observations, and Johansen and Nielsen (2016) derive the distribution of the gauge. Hendry and Mizon (2011) demonstrate distortions in modelling from not handling outliers, and Castle et al. (2016) show that outliers can even be distinguished from non-linear reactions as the latter hold at all observations whereas the former only occur at isolated points. Castle et al. (2015) establish that the properties of step-indicator saturation are similar to IIS, but SIS exhibits higher power than IIS when location shifts occur. Ericsson and Reisman (2012) propose combining IIS and SIS in ‘super saturation’ and Ericsson (2016) uses IIS to adjust an ex post mis-match between the truncated FMI Greenbook ’post-casts’ and GDP outcomes.5
The invariance test proposed here is the extension to SIS of the IIS-based test of super exogeneity in Hendry and Santos (2010). SIS is applied to detect location shifts in models of policy instruments, then any resulting significant step indicators are tested in the model for the target variables of interest. Because the ‘size’ of a test statistic is only precisely defined for a similar test, and the word is anyway ambiguous in many settings (such as sample size), we use the term ‘gauge’ to denote the empirical null retention frequency of indicators. The SIS invariance test’s gauge is close to its nominal significance level. We also examine its rejection frequencies when parameter invariance does not hold. When the probability of retention of relevant indicators is based on selection, it no longer corresponds to the conventional notion of ‘power’, so we use the term ‘potency’ to denote the average non-null retention frequency from selection. However, as IIS can detect failures of invariance from variance shifts in the unmodelled processes, ‘super saturation’ could help delineate that source of failure. Neither test requires ex ante knowledge of the timings, signs, numbers or magnitudes of location shifts, as policy-instrument models are selected automatically using Autometrics.
We test for location shifts by adding to the candidate variables a complete set of T step indicators denoted when the sample size is T, where for observations up to j, and zero otherwise (so is the intercept). Using a modified general-to-specific procedure, Castle et al. (2015) establish the gauge and the null distribution of the resulting estimator of regression parameters. A two-block process is investigated analytically, where half the indicators are added and all significant indicators recorded, then that half is dropped, and the other half examined: finally, the two retained sets of indicators are combined. The gauge, g, is approximately when the nominal significance level of an individual test is . Hendry et al. (2008) and Johansen and Nielsen (2009) show that other splits, such as using k splits of size , or unequal splits, do not affect the gauge of IIS.
The invariance test then involves two stages. Denote the variables in the system by , where the are the conditioning variables. Here, we only consider . In the first stage, SIS is applied to the marginal system for all conditioning variables, and the associated significant indicators are recorded. When the intercept and s lags of all n variables are always retained (i.e., not subject to selection), SIS is applied at significance level , leading to the selection of step indicators:
where (20) is selected to be congruent. The coefficients of the significant step indicators are denoted to emphasize their dependence on used in selection. Although SIS could be applied to (20) as a system, we will focus on its application to each equation separately. The gauge of step indicators in such individual marginal models is investigated in Castle et al. (2015), who show that simulation-based distributions for SIS using Autometrics have a gauge, g, close to the nominal significance level . Section 4.1 notes their findings on the potency of SIS at the first stage to determine the occurrence of location shifts. Section 4.2 provides analytic, and Section 4.3 Monte Carlo, evidence on the gauge of the invariance test. Section 4.4 analyses a failure of invariance from a non-constant marginal process. Section 4.5 considers the second stage of the test for invariance. Section 5 investigates the gauges and potencies of the proposed automatic test in Monte Carlo experiments for a bivariate data generation process based on Section 4.4.
4.1. Potency of SIS at Stage 1
Potency could be judged by the selected indicators matching actual location shifts exactly or within periods. How often a shift at (say) is exactly matched by the correct single step indicator is important for detecting policy changes: see e.g., Hendry and Pretis (2016). However, for stage 2, finding that a shift has occurred within a few periods of its actual occurrence could still allow detection of an invariance failure in a policy model.
Analytic power calculations for a known break point exactly matched by the correct step function in a static regression show high power, and simulations confirm the extension of that result to dynamic models. A lower potency from SIS at stage 1 could be due to retained step indicators not exactly matching the shifts in the marginal model, or failing to detect one or more shifts when there are location shifts. The former is not very serious, as stage 1 is instrumental, so although there will be some loss of potency at stage 2, attenuating the non-centrality parameter relative to knowing when shifts occurred, a perfect timing match is not essential for the test to reject when invariance does not hold. Failing to detect one or more shifts would be more serious as it both lowers potency relative to knowing those shifts, and removes the chance of testing such shifts at stage 2. Retention of irrelevant step indicators not corresponding to shifts in the marginal process, at a rate determined by the gauge g of the selection procedure, will also lower potency but the effect of this is likely to be small for SIS.
Overall, Castle et al. (2015) show that SIS has relatively high potency for detecting location shifts in marginal processes at stage 1, albeit within a few periods either side of their starting/ending, from chance offsetting errors. Thus, we now consider the null rejection frequency at stage 2 of the invariance test for a variety of marginal processes using step indicators selected at stage 1.
4.2. Null Rejection Frequency of the SIS Test for Invariance at Stage 2
The m significant step indicators in the equations of (20) are each retained using the criterion:
when is the critical value for significance level . Assuming all m retained step indicators correspond to distinct shifts (or after eliminating any duplicates), for each t combine them in the m vector , and add all to the model for (written here with one lag):
where , which should be under the null, to be tested as an added-variable set in the conditional Equation (22) without selection, using an -test, denoted , at significance level which rejects when . Under the null of invariance, this -test should have an approximate F-distribution, and thereby allow an appropriately sized test. Under the alternative that , will have power, as discussed in Section 4.4.
Although (20) depends on the selection significance level, , the null rejection frequency of should not depend on , although too large a value of will lead to an -test with large degrees of freedom, and too small will lead to few, or even no, step indicators being retained from the marginal models. If no step indicators are retained in (20), so (21) does not occur, then cannot be computed for that data, so must under-reject in Monte Carlos when the null is true. Otherwise, the main consideration when choosing is to allow power against reasonable alternatives to invariance by detecting any actual location shifts in the marginal models.
4.3. Monte Carlo Evidence on the Null Rejection Frequency
To check that shifts in marginal processes like (20) do not lead to spurious rejection of invariance when super exogeneity holds, the Monte Carlo experiments need to estimate the gauges, g, of the SIS-based invariance test in three states of nature for (20): (A) when there are no shifts (Section 4.3.1); (B) for a mean shift (Section 4.3.2); and (C) facing a variance change (Section 4.3.3). Values of g close to the nominal significance level and constant across (A)–(C) are required for a similar test. However, since Autometrics selection seeks a congruent model, insignificant irrelevant variables can sometimes be retained, and the gauge will correctly reflect that, so usually g .
The simulation DGP is the non-constant bivariate first-order vector autoregression (VAR(1)):
where , inducing the valid conditional relation:
with:
In (23), let , so equals before and after. Also , so the marginal process is:
As the analysis in Hendry and Johansen (2015) shows, can be retained without selection during SIS, so we do not explicitly include dynamics as the canonical case is testing:
in (26). Despite shifts in the marginal process, (24) and (25) show that invariance holds for the conditional model.
In the Monte Carlo, the constant and invariant parameters of interest are , , and , with , and . Sample sizes of are investigated with replications, for both (testing for step indicators in the marginal) and (testing invariance in the conditional equation) equal to (, , ), though we focus on both at .
4.3.1. Constant Marginal
The simplest setting is a constant marginal process, which is (23) with , so the parameters of the conditional model are and the parameters of the marginal are . The conditional representation with m selected indicators from (20) is:
and invariance is tested by the -statistic of the null in (28).
Table 4 records the outcomes at facing a constant marginal process, with lags of included in the implementation of (20). Tests for location shifts in marginal processes should not use too low a probability of retaining step indicators, or else the -statistic will have a zero null rejection frequency. For example, at and , under the null, half the time no step indicators will be retained, so only about will be found overall, as simulation confirms. Simulated gauges and nominal null rejection frequencies for were close so long as .

Table 4.
SIS simulations under the null of super exogeneity for a constant marginal process. ‘% no indicators’ records the percentage of replications in which no step indicators are retained, so stage 2 is redundant. Stage 2 gauge records the probability of the -test falsely rejecting for the included step indicators at .
4.3.2. Location Shifts in
The second DGP is given by (23) where , 10 with , and . The results are reported in Table 5. Invariance holds irrespective of the location shift in the marginal, so these experiments check that spurious rejection is not induced thereby. Despite large changes in , when , Table 5 confirms that gauges are close to nominal significance levels. Importantly, the test does not spuriously reject the null, and now is only slightly undersized at for small shifts, as again sometimes no step indicators are retained.

Table 5.
SIS simulations under the null of super exogeneity for a location shift in the marginal process. Stage 1 gauge is for retained step indicators at times with no shifts; and stage 1 potency is for when the exact indicators matching step shifts are retained, with no allowance for mis-timing.
4.3.3. Variance Shifts in
The third DGP given by (23) allows the variance-covariance matrix to change while maintaining the conditions for invariance, where , 10 with , and . Table 6 indicates that gauges are close to nominal significance levels, and again the test does not spuriously reject the null, remaining slightly undersized at for small shifts.

Table 6.
SIS simulations under the null of super exogeneity for a variance shift in the marginal process. Legend as for Table 5.
Overall, the proposed test has appropriate empirical null retention frequencies for both constant and changing marginal processes, so we now turn to its ability to detect failures of invariance.
4.4. Failure of Invariance
In this section, we derive the outcome for an invariance failure in the conditional model when the marginal process is non-constant due to a location shift, and obtain the non-centrality and approximate power of the invariance test in the conditional model for a single location shift in the marginal.
From (23) when invariance does not hold:
so letting leads to the conditional relation:
which depends on when and:
When the dynamics and timings and forms of shifts in (31) are not known, we model using (20). Autometrics with SIS will be used to select significant regressors as well as significant step indicators from the saturating set .
Although SIS can handle multiple location shifts, for a tractable analysis, we consider the explicit single alternative (a non-zero intercept in (32) would not alter the analysis):
Further, we take as constant in (30), so that the location shift is derived from the failure of conditioning when :
The power of a test of the significance of in a scalar process when the correct shift date is known, so selection is not needed, is derived in Castle et al. (2015), who show that the test power rises with the magnitude of the location shift and the length it persists, up to half the sample. Their results apply to testing in (32) and would also apply to testing in (33) when is known or is correctly selected at Stage 1. Section 4.5 considers the impact on the power of the invariance test of of needing to discover the shift indicator at Stage 1. Castle et al. (2015) also examine the effects on the potency at Stage 1 of selecting a step indicator that does not precisely match the location shift in the DGP, which could alter the rejection frequency at Stage 2.
4.5. Second-Stage Test
The gauge of the test at the second stage conditional on locating the relevant step indicators corresponding exactly to the shifts in the marginal was calculated above. A relatively loose will lead to retaining some ‘spurious’ step indicators in the marginal, probably lowering potency slightly. In practice, there could be multiple breaks in different marginal processes at different times, which may affect one or more , but little additional insight is gleaned compared to the one-off break in (32), since the proposed test is an -test on all retained step indicators, so does not assume any specific shifts at either stage. The advantage of using the explicit alternative in (32) is that approximate analytic calculations are feasible. We only consider a bivariate VAR explicitly, where in (30) under the null that the conditional model of is invariant to the shift in .
Let SIS selection applied to the marginal model for yield a set of step indicators defined by:
which together entail retaining . Combine these significant step indicators in a vector , and add to the assumed constant relation:
to obtain the test regression written as:
As with IIS, a difficulty in formalizing the analysis is that the contents of vary between draws, as it matters how close the particular relevant step indicators retained are to the location shift, although which irrelevant indicators are retained will not matter greatly. However, Hendry and Pretis (2016) show that the main reason SIS chooses indicators that are incorrectly timed is that the shift is either initially ‘camouflaged’ by opposite direction innovation errors, or same-sign large errors induce an earlier selection. In both cases, such mistakes should only have a small impact on the second-stage test potency, as simulations confirm. Failing to detect a shift in the marginal model will lower potency when that shift in fact leads to a failure of invariance in the conditional model.
4.6. Mis-Timed Indicator Selection in the Static Bivariate Case
We first consider the impact of mis-timing the selection of an indicator for this location shift in the conditional process in (30) derived from the non-invariant system (29) when . The conditional relation is written for as:
where , which lacks invariance to changes in at in the marginal model (20):
However, (37) is modelled by:
where .
As SIS seeks the best matching step indicator for the location shift, any discrepancy between and is probably because the values of between and induced the mistaken choice. Setting where for a specific formulation, then:
For observations beyond :
so that:
which could be large for and . To a first approximation, least-squares selection would drive estimates to minimize the first two terms in (41). If they vanish, for , (40) becomes:
and between and :
suggesting SIS would find , and that chance draws of must essentially offset during the non-overlapping period to . In such a setting:
so that the estimated equation error variance will not be greatly inflated by the mis-match in timing, and the rejection frequency of a t-test of : will be close to that of the corresponding test of : in (37) despite the selection of the relevant indicator by SIS.
5. Simulating the Potencies of the SIS Invariance Test
The potency of the -test of : in (39) depends on the strength of the invariance violation, ; the magnitude of the location shift, , both directly and through its detectability in the marginal model, which in turn depends on ; the sample size T; the number of periods affected by the location shift; the number of irrelevant step indicators retained (which will affect the test’s degrees of freedom, again depending on ); how close the selected step shift is to matching the DGP shift; and on . These properties are now checked by simulation, and contrasted in experiments with the optimal, but generally infeasible, test based on adding the precisely correct indicator , discussed above.
The simulation analyses used the bivariate relationship in Section 4.3 for violations of super exogeneity due to a failure of weak exogeneity under non-constancy in:
where and , but , with the level shift at in the marginal (in a policy context, it is more convenient to use ) so:
We vary over 1, 2, , 3 and 4; over , 1, and when , reducing the departure from weak exogeneity; a sample size of with a break point at ; and significance levels and in the marginal and conditional, with replications.
5.1. Optimal Infeasible Indicator-Based -Test
The optimal infeasible -test with a known location shift in the marginal process is computable in simulations. Table 7 reports the rejections of invariance, which are always high for large shifts, but fall as departures from weak exogeneity decrease. Empirical rejection frequencies approximate maximum achievable power for this type of test. The correct step indicator is almost always significant in the conditional model for location shifts larger than , even for relatively small values of .

Table 7.
Power of the optimal infeasible -test for a failure of invariance using a known step indicator for at , , .
5.2. Potency of the SIS-Based Test
Table 8 records the Stage 1 gauge and potency at different levels of location shift (d) and departures from weak (and hence super) exogeneity via (). The procedure is slightly over-gauged at Stage 1 for small shifts, when its potency is also low, and both gauge and potency are correctly unaffected by the magnitude of , whereas Stage 1 potency rises rapidly with d.

Table 8.
Stage 1 gauge and potency at for , , and .
Table 9 records Stage 2 potency for the three values of . It shows that for a failure of invariance, even when , test potency can increase at tighter Stage 1 significance levels, probably by reducing the retention rate of irrelevant step indicators. Comparing the central panel with the matching experiments in Table 7, there is remarkably little loss of rejection frequency from selecting indicators by SIS at Stage 1, rather than knowing them, except at the smallest values of d.

Table 9.
Stage 2 potency for a failure of invariance at , , , and .
6. Application to the Small Artificial-Data Policy Model
To simulate a case of invariance failure from a policy change, which could be checked by in-sample, followed by forecast failure, we splice the two scenarios from Figure 2 sequentially in the order of the 100 observations in panels (III+IV) then those used for panels (I+II), creating a sample of .
Next, we estimate (5) with SIS, retaining the policy variable, and test the significance of the selected step-indicators in (6). At Stage 1, using , as the model is mis-specified and the sample is keeping the last 11 observations for the forecast period, two indicators are selected. Testing these in (6) yields , strongly rejecting invariance of the parameters of the model for to shifts in the model of .
Figure 3 reports the outcome graphically, where the ellipses show the period with the earlier break in the DGP without a location shift but with the policy change. Panel (I) shows the time series for with the fitted and forecast values, denoted , from estimating the agency’s model with SIS which delivered the indicators for testing invariance. Panel (II) shows the outcome for after adding the selected indicators denoted SIS from the marginal model for , which had earlier rejected invariance. Panel (III) reports the outcome for a setting where the invariance failure led to an improved model, which here coincides with the in-sample DGP. This greatly reduces the later forecast errors and forediction failures. Finally, Panel (IV) augments the estimated in-sample DGP equation (with all its regressors retained) by selecting using SIS at . This further reduces forecast failure, although constancy can still be rejected from the unanticipated location shift. If the invariance rejection had led to the development of an improved model, better forecasts, and hopefully improved foredictions and policy decisions, would have resulted. When the policy model is not known publicly (as with MPC decisions), the agency alone can conduct these tests. However, an approximate test based on applying SIS to an adequate sequence of published forecast errors could highlight potential problems.
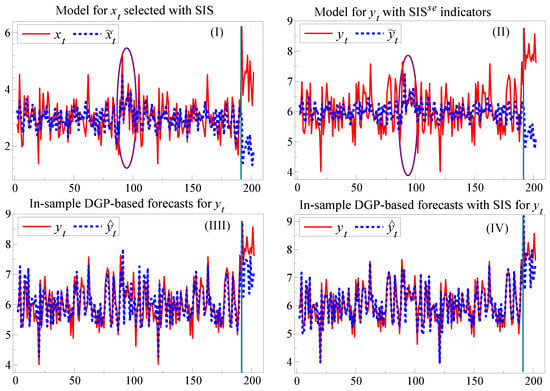
Figure 3.
(I) Forecast failure for by even with SIS; (II) Forecast failure in even augmented by the SIS indicators selected from the margin model for ; (III) Smaller forecast failure from based on the in-sample DGP; (IV) Least forecast failure from based on the in-sample DGP with SIS.
6.1. Multiplicative Indicator Saturation
In the preceding example, the invariance failure was detectable by SIS because the policy change created a location shift by increasing by . A zero-mean shift in a policy-relevant derivative, would not be detected by SIS, but could be by multiplicative indicator saturation (MIS) proposed in Ericsson (2012). MIS interacts step indicators with variables as in , so when and is zero otherwise. Kitov and Tabor (2015) have investigated its performance in detecting changes in parameters in zero-mean settings by extensive simulations. Despite the very high dimensionality of the resulting parameter space, they find MIS has a gauge close to the nominal significance level for suitably tight , and has potency to detect such parameter changes. As policy failure will occur after a policy-relevant parameter shifts, advance warning thereof would be invaluable. Even though the above illustration detected a failure of invariance, it did not necessarily entail that policy-relevant parameters had changed. We now apply MIS to the artificial data example in Section 6 to ascertain whether such a change could be detected, focusing on potential shifts in the coefficient of in (6).
Selecting at as there are more then 200 candidate variables yielded:
with . Thus, the in-sample shift of in is found over , warning of a lack of invariance in the key policy parameter from the earlier policy change, although that break is barely visible in the data, as shown by the ellipse in Figure 3 (II). To understand how MIS is able to detect the parameter change, consider knowing where the shift occurred and splitting your data at that point. Then you would be startled if fitting your correctly specified model separately to the different subsamples did not deliver the appropriate estimates of their DGP parameters. Choosing the split by MIS will add variability, but the correct indicator, or one close to it, should accomplish the same task.
7. Forecast Error Taxonomy and Associated Tests
Table 10 relates the taxonomy in Table 1 to the sources of the forecast errors from (16) to illustrate which indicator-saturation test could be used, where the order (SIS, IIS) etc. shows their likely potency.

Table 10.
The taxonomy of systematic forecast failures with associated tests.
When the source of forecast failure is the equilibrium mean or forecast origin mis-estimation, then SIS is most likely to detect the systematically signed forecast errors, whereas for other unobserved terms IIS is generally best equipped to detect these changes. When the slope parameter is the source of failure for , then SIS is generally best, whereas when , IIS might help. In practice, policy invalidity and forediction failure are probably associated with i(c) and ii(c), where both SIS and IIS tests for super exogeneity are valid. In this setting, policy failure can also be triggered through ii(a) and ii(b) which makes an SIS test for super exogeneity again attractive. Absent a policy intervention, then zero-mean changes result in ii(c), so may best be detected using multiplicative indicator saturation.
8. How to Improve Future Forecasts and Foredictions
Scenarios above treated direct forecasts and those derived from foredictions as being essentially the same. When a major forecast error occurs, the agency can use a robust forecasting device such as an intercept correction (IC), or differencing the forecasts, to set them ‘back on track’ for the next period. Although sometimes deemed ‘ad hoc’, Clements and Hendry (1998) show the formal basis for their success in improving forecasts. However, the foredictions that led to the wrong policy implementation cannot be fixed so easily, even if the agency’s next narrative alters its story. In our example, further increases in will induce greater forecast failure if the policy model is unchanged: viable policy requires invariance of the model to the policy change. Nevertheless, there is a partial ‘fix’ to the forecast failure and policy invalidity. If the lack of invariance is invariant, so policy shifts change the model’s parameters in the same way each time as in (14), the shift associated with a past policy change can be added as an IC to a forecast based on a later policy shift. We denote such an IC by SIS, which has the advantage that it can be implemented before experiencing forecast failure. This is shown in Figure 4(I),(II), focusing on the last 50 periods, where the policy change coincides with the location shift at observation 191. The first panel records the forecasts for a model of which includes the SIS indicator for the period of the first forecast failure, and also includes SIS as an imposed IC, from . Had a location shift not also occurred, SIS would have corrected the forecast for the lack of invariance, and could have been included in the policy analysis and the associated foredictions.
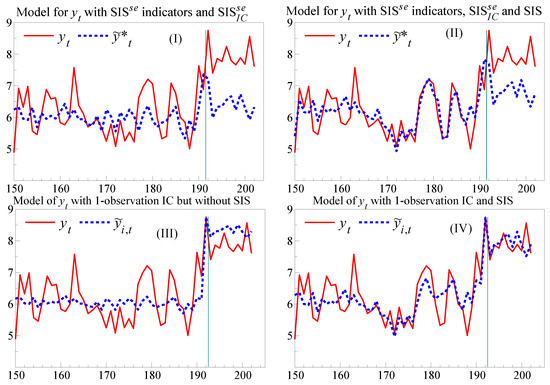
Figure 4.
(I) Forecasts for by , just using SIS for the first policy-induced shift and SIS at observation 191; (II) Forecasts for by also with SIS in-sample; (III) Forecasts from for by with a 1-observation IC but without SIS; (IV) Forecasts for by also with SIS in-sample.
Figure 4 also shows how effective a conventional IC is in the present context after the shift has occurred, using a forecast denoted by . The IC is a step indicator with a value of unity from observation onwards when the forecast origin is , so one observation later, the forecast error is used to estimate the location shift. Compared to the massive forecast failure seen for the models of in Figure 3 (I) & (II), neither of the sets of forecast errors in Figure 4 (III) & (IV) fails a constancy test ( and ). The IC alone corrects most of the forecast failure, but as (IV) shows, SIS improves the in-sample tracking by correcting the earlier location-shift induced failure and improves the accuracy of the resulting forecasts.6
In real-time forecasting, these two steps could be combined, using SIS as the policy is implemented, followed by an IC one-period later when the location shift materialises, although a further policy change is more than likely in that event. Here, the mis-specified econometric models of the relationships between the variables are unchanged, but their forecasts are very different: successful forecasts do not imply correct models.
9. Conclusions
We considered two potential implications of forecast failure in a policy context, namely forediction failure and policy invalidity. Although an empirical forecasting model cannot necessarily be rejected following forecast failure, when the forecasts derived from the narratives of a policy agency are very close to the model’s forecasts, as Ericsson (2016) showed was true for the FOMC minutes, then forecast failure entails forediction failure. Consequently, the associated narrative and any policy decisions based thereon also both fail. A taxonomy of the sources of forecast errors showed what could be inferred from forecast failure, and was illustrated by a small artificial-data policy model.
A test for invariance and the validity of policy analysis was proposed by selecting shifts in all marginal processes using step-indicator saturation and checking their significance in the conditional model. The test was able to detect failures of invariance when weak exogeneity failed and the marginal processes changed from a location shift. Compared to the nearest corresponding experiment in Hendry and Santos (2010), the potency of is considerably higher for SIS at than IIS at (both at ) as shown in Figure 5.
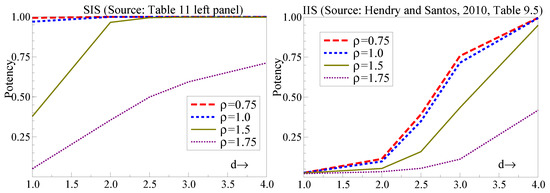
Figure 5.
Comparison of the potency of SIS with IIS.
A test rejection outcome by indicates a dependence between the conditional model parameters and those of the marginals, warning about potential mistakes from using the conditional model to predict the outcomes of policy changes that alter the marginal processes by location shifts, which is a common policy scenario. Combining these two features of forecast failure with non-invariance allows forediction failure and policy invalidity to be established when they occur. Conversely, learning that the policy model is not invariant to policy changes could lead to improved models, and we also showed a ‘fix’ that could help mitigate forecast failure and policy invalidity.
While all the derivations and Monte Carlo experiments here have been for 1-step forecasts from static regression equations, a single location shift and a single policy change, the general nature of the test makes it applicable when there are multiple breaks in several marginal processes, perhaps at different times. Generalizations to dynamic equations, to conditional systems, and to other non-stationary settings, probably leading to more approximate null rejection frequencies, are the focus of our present research.
Acknowledgments
This research was supported in part by grants from the Robertson Foundation (award 9907422), Institute for New Economic Thinking (grant 20029822) and Statistics Norway (through Research Council of Norway Grant 236935). We are indebted to Jurgen A. Doornik, Neil R. Ericsson, Bent Nielsen, Ragnar Nymoen, Felix Pretis, the guest editors Rocco Mosconi and Paolo Paruolo, and two anonymous referees for helpful comments on an earlier version. It is a great pleasure to participate in a Special Issue of Econometrics in honour of Søren Johansen and Katarina Juselius who have both made major contributions to understanding the theory and practice of analysing non-stationary time series, and have been invaluable long-time co-authors. All calculations and graphs used OxMetrics Doornik (2013) and PcGive Doornik and Hendry (2013), which implements Autometrics.
Author Contributions
All authors contributed equally to this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akram, Q. Farooq, and Ragnar Nymoen. 2009. Model Selection for Monetary Policy Analysis: How Important is Empirical Validity? Oxford Bulletin of Economics and Statistics 71: 35–68. [Google Scholar] [CrossRef]
- Bank of England. 2015. Inflation Report, August, 2015. London: Bank of England Monetary Policy Committee. [Google Scholar]
- Cartwright, Nancy. 1989. Nature’s Capacities and their Measurement. Oxford: Clarendon Press. [Google Scholar]
- Castle, Jennifer L., Jurgen A. Doornik, David F. Hendry, and Felix Pretis. 2015. Detecting Location Shifts During Model Selection by Step-Indicator Saturation. Econometrics 3: 240–64. [Google Scholar] [CrossRef]
- Castle, Jennifer L., Jurgen A. Doornik, and David F. Hendry. 2016. Robustness and Model Selection. Unpublished paper. Oxford, UK: Economics Department, University of Oxford. [Google Scholar]
- Castle, Jennifer L., and David F. Hendry. 2011. On Not Evaluating Economic Models by Forecast Outcomes. Istanbul University Journal of the School of Business Administration 40: 1–21. [Google Scholar]
- Clements, Michael P., and David F. Hendry. 1998. Forecasting Economic Time Series. Cambridge: Cambridge University Press. [Google Scholar]
- Clements, Michael P., and David F. Hendry. 2005. Evaluating a Model by Forecast Performance. Oxford Bulletin of Economics and Statistics 67: 931–56. [Google Scholar] [CrossRef]
- Clements, Michael P., and J. James Reade. 2016. Forecasting and Forecast Narratives: The Bank of England Inflation Reports. Discussion paper. Reading, UK: Economics Department, University of Reading. [Google Scholar]
- Doornik, Jurgen A. 2007. Econometric Model Selection With More Variables Than Observations. Working paper. Oxford, UK: Economics Department, University of Oxford. [Google Scholar]
- Doornik, Jurgen A. 2009. Autometrics. In The Methodology and Practice of Econometrics. Edited by Jennifer L. Castle and Neil Shephard. Oxford: Oxford University Press, pp. 88–121. [Google Scholar]
- Doornik, Jurgen A. 2013. OxMetrics: An Interface to Empirical Modelling, 7th ed. London: Timberlake Consultants Press. [Google Scholar]
- Doornik, Jurgen A., and David F. Hendry. 2013. Empirical Econometric Modelling using PcGive: Volume I., 7th ed. London: Timberlake Consultants Press. [Google Scholar]
- Ellison, Martin, and Thomas J. Sargent. 2012. A Defense of the FOMC. International Economic Review 53: 1047–65. [Google Scholar] [CrossRef]
- Engle, Robert F., and David F. Hendry. 1993. Testing Super Exogeneity and Invariance in Regression Models. Journal of Econometrics 56: 119–39. [Google Scholar] [CrossRef]
- Engle, Robert F., David F. Hendry, and Jean-Francois Richard. 1983. Exogeneity. Econometrica 51: 277–304. [Google Scholar] [CrossRef]
- Ericsson, Neil R. 2012. Detecting Crises, Jumps, and Changes in Regime. Working paper. Washington, D.C., USA: Federal Reserve Board of Governors. [Google Scholar]
- Ericsson, Neil R. 2016. Eliciting GDP Forecasts from the FOMC’s Minutes Around the Financial Crisis. International Journal of Forecasting 32: 571–83. [Google Scholar] [CrossRef]
- Ericsson, Neil R. 2017. Economic Forecasting in Theory and Practice: An Interview with David F. Hendry. International Journal of Forecasting 33: 523–42. [Google Scholar] [CrossRef]
- Ericsson, Neil R., and Erica L. Reisman. 2012. Evaluating a Global Vector Autoregression for Forecasting. International Advances in Economic Research 18: 247–58. [Google Scholar] [CrossRef]
- Favero, Carlo, and David F. Hendry. 1992. Testing the Lucas Critique: A Review. Econometric Reviews 11: 265–306. [Google Scholar] [CrossRef]
- Genberg, Hans, and Andrew B. Martinez. 2014. On the Accuracy and Efficiency of IMF forecasts: A Survey and some Extensions. IEO Background Paper BP/14/04. Washington, D.C., USA: Independent Evaluation Office of the International Monetary Fund. [Google Scholar]
- Hendry, David F. 1988. The Encompassing Implications of Feedback versus Feedforward Mechanisms in Econometrics. Oxford Economic Papers 40: 132–49. [Google Scholar] [CrossRef]
- Hendry, David F. 2001. How Economists Forecast. In Understanding Economic Forecasts. Edited by David F. Hendry and Neil R. Ericsson. Cambridge: MIT Press, pp. 15–41. [Google Scholar]
- Hendry, David F. 2004. Causality and Exogeneity in Non-stationary Economic Time Series. In New Directions in Macromodelling. Edited by A. Welfe. Amsterdam: North Holland, pp. 21–48. [Google Scholar]
- Hendry, David F. 2006. Robustifying Forecasts from Equilibrium-Correction Models. Journal of Econometrics 135: 399–426. [Google Scholar] [CrossRef]
- Hendry, David F., and Søren Johansen. 2015. Model Discovery and Trygve Haavelmo’s Legacy. Econometric Theory 31: 93–114. [Google Scholar] [CrossRef]
- Hendry, David F., Søren Johansen, and Carlos Santos. 2008. Automatic Selection of Indicators in a Fully Saturated Regression. Computational Statistics 33: 317–35, Erratum, 337–39. [Google Scholar] [CrossRef]
- Hendry, David F., and Hans-Marti Krolzig. 2005. The Properties of Automatic Gets Modelling. Economic Journal 115: C32–C61. [Google Scholar] [CrossRef]
- Hendry, David F., and Michael Massmann. 2007. Co-breaking: Recent Advances and a Synopsis of the Literature. Journal of Business and Economic Statistics 25: 33–51. [Google Scholar] [CrossRef]
- Hendry, David F., and Grayham E. Mizon. 2011. Econometric Modelling of Time Series with Outlying Observations. Journal of Time Series Econometrics 3: 1–26. [Google Scholar] [CrossRef]
- Hendry, David F., and Grayham E. Mizon. 2012. Open-model Forecast-error Taxonomies. In Recent Advances and Future Directions in Causality, Prediction, and Specification Analysis. Edited by Xiaohong Chen and Norman R. Swanson. New York: Springer, pp. 219–40. [Google Scholar]
- Hendry, David F., and Grayham E. Mizon. 2014. Unpredictability in Economic Analysis, Econometric Modeling and Forecasting. Journal of Econometrics 182: 186–95. [Google Scholar] [CrossRef]
- Hendry, David F., and Felix Pretis. 2016. Quantifying the Uncertainty around Break Dates in Models using Indicator Saturation. Working paper. Oxford, UK: Economics Department, Oxford University. [Google Scholar]
- Hendry, David F., and Carlos Santos. 2010. An Automatic Test of Super Exogeneity. In Volatility and Time Series Econometrics. Edited by Mark W. Watson, Tim Bollerslev and Jeffrey Russell. Oxford: Oxford University Press, pp. 164–93. [Google Scholar]
- Independent Evaluation Office. 2014. IMF Forecasts: Process, Quality, and Country Perspectives. Technical report. Washington: International Monetary Fund. [Google Scholar]
- Jansen, Eilev S., and Timo Teräsvirta. 1996. Testing Parameter Constancy and Super Exogeneity in Econometric Equations. Oxford Bulletin of Economics and Statistics 58: 735–63. [Google Scholar] [CrossRef]
- Johansen, Søren, and Bent Nielsen. 2009. An Analysis of the Indicator Saturation Estimator as a Robust Regression Estimator. In The Methodology and Practice of Econometrics. Edited by Jennifer L. Castle and Neil Shephard. Oxford: Oxford University Press, pp. 1–36. [Google Scholar]
- Johansen, Søren, and Bent Nielsen. 2016. Asymptotic Theory of Outlier Detection Algorithms for Linear Time Series Regression Models. Scandinavian Journal of Statistics 43: 321–48. [Google Scholar] [CrossRef]
- Kitov, Oleg I., and Morten N. Tabor. 2015. Detecting Structural Changes in Linear Models: A Variable Selection Approach using Multiplicative Indicator Saturation. Unpublished paper. Oxford, UK: University of Oxford. [Google Scholar]
- Krolzig, Hans-Martin, and Juan Toro. 2002. Testing for Super-exogeneity in the Presence of Common Deterministic Shifts. Annales d’Economie et de Statistique 67/68: 41–71. [Google Scholar] [CrossRef]
- Pagan, Adrian R. 2003. Report on Modelling and Forecasting at the Bank of England. Bank of England Quarterly Bulletin Spring. Available online: http://www.bankofengland.co.uk/archive/Documents/historicpubs/qb/2003/qb030106.pdf (accessed on 5 October 2015).
- Psaradakis, Zacharias, and Martin Sola. 1996. On the Power of Tests for Superexogeneity and Structural Invariance. Journal of Econometrics 72: 151–75. [Google Scholar] [CrossRef]
- Pretis, Felix, James Reade, and Genaro Sucarrat. 2016. General-to-Specific (GETS) Modelling And Indicator Saturation With The R Package Gets. Working paper, 794. Oxford, UK: Economics Department, Oxford University. [Google Scholar]
- Romer, Christina D., and David H. Romer. 2008. The FOMC versus the Staff: Where can Monetary Policymakers add Value? American Economic Review 98: 230–35. [Google Scholar] [CrossRef]
- Sinclair, Tara M., Pao-Lin Tien, and Edward Gamber. 2016. Do Fed Forecast Errors Matter? CAMA Working Paper No. 47/2016. Canberra, Australia: Centre for Applied Macroeconomic Analysis (CAMA). [Google Scholar]
- Siviero, Stefano, and Daniele Terlizzese. 2001. Macroeconomic Forecasting: Debunking a Few Old Wives’ Tales. Discussion paper 395. Rome, Italy: Research Department, Banca d’Italia. [Google Scholar]
- Spanos, Aris. 2007. Curve-Fitting, the Reliability of Inductive Inference and the Error-Statistical Approach. Philosophy of Science 74: 1046–66. [Google Scholar] [CrossRef]
- Stekler, Herman O., and Hilary Symington. 2016. Evaluating Qualitative Forecasts: The FOMC Minutes, 2006–2010. International Journal of Forecasting 32: 559–70. [Google Scholar] [CrossRef]
- Stenner, Alfred J. 1964. On Predicting our Future. Journal of Philosophy 16: 415–28. [Google Scholar] [CrossRef]
- Zhang, Kun, Jiji Zhang, and Bernhard Schölkopf. 2015. Distinguishing Cause from Effect Based on Exogeneity. Available online: http://arxiv.org/abs/1504.05651 (accessed on 10 October 2015).
| 1 | Bank of England Inflation Report, November 2009, p.47. See http://www.bankofengland.co.uk/publications/Documents/inflationreport/ir09nov.pdf. |
| 2 | Other than the proposal in Hendry (2001), archival search revealed two earlier, somewhat unrelated, uses of ‘forediction’: (1) by Richard Feynman in a letter to Enrico Fermi in 1951 (see CBPF-CS-012/97); and (2) in Stenner (1964). |
| 3 | Bank of England Minutes of the Monetary Policy Committee, November 2009, p.8. See http://www.bankofengland.co.uk/publications/minutes/Documents/mpc/pdf/2009/mpc0911.pdf. |
| 4 | |
| 5 | All of these indicator saturation methods are implemented in the Autometrics algorithm in PcGive: see Doornik (2009) and Doornik and Hendry (2013), which can handle more variables than observations using block path searches with both expanding and contracting phases as in Hendry and Krolzig (2005), and Doornik (2007). An R version is available at https://cran.r-project.org/web/packages/gets/index.html: see Pretis et al. (2016). |
| 6 | As noted above, the lagged impact of the policy change causes to overshoot, so is somewhat above over the forecast horizon, albeit a dramatic improvement over Figure 3 (I): using 2-periods to estimate the IC solves that. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).