Abstract
This paper develops a method to improve the estimation of jump variation using high frequency data with the existence of market microstructure noises. Accurate estimation of jump variation is in high demand, as it is an important component of volatility in finance for portfolio allocation, derivative pricing and risk management. The method has a two-step procedure with detection and estimation. In Step 1, we detect the jump locations by performing wavelet transformation on the observed noisy price processes. Since wavelet coefficients are significantly larger at the jump locations than the others, we calibrate the wavelet coefficients through a threshold and declare jump points if the absolute wavelet coefficients exceed the threshold. In Step 2 we estimate the jump variation by averaging noisy price processes at each side of a declared jump point and then taking the difference between the two averages of the jump point. Specifically, for each jump location detected in Step 1, we get two averages from the observed noisy price processes, one before the detected jump location and one after it, and then take their difference to estimate the jump variation. Theoretically, we show that the two-step procedure based on average realized volatility processes can achieve a convergence rate close to , which is better than the convergence rate for the procedure based on the original noisy process, where n is the sample size. Numerically, the method based on average realized volatility processes indeed performs better than that based on the price processes. Empirically, we study the distribution of jump variation using Dow Jones Industrial Average stocks and compare the results using the original price process and the average realized volatility processes.
Keywords:
high frequency financial data; jump variation; realized volatility; integrated volatility; microstructure noise; wavelet methods; nonparametric methods JEL:
C01; C14; C22; C51; C52; C58; G17
1. Introduction
1.1. Motivation
Volatility analysis plays an important role in finance. For example, portfolio allocation, derivative pricing and risk management all require accurate estimation of volatility. With the advance of technology, financial instruments are traded at frequencies as high as milliseconds, which produces large numbers of trading records each day and enables us to better estimate volatility. Such data are often referred to as high-frequency financial data. There are a growing number of volatility analysis studies based on high-frequency financial data. One popular approach is to use realized volatility, which is the sum of the squared difference of the log prices. See, for example, Barndorff-Nielsen and Shephard (2002) [1], Zhang et al. (2005) [2] and Zhang (2006) [3]. If the observed data are assumed to be a continuous semi-martingale price process, realized volatility yields a consistent estimator of integrated volatility. However, high-frequency financial data are contaminated with market microstructure noise, and the contaminated price observations make the realized volatility inconsistent. If we assume that high-frequency financial data follow semi-martingale price processes with additive microstructure noises, several methods are proposed to consistently estimate integrated volatility based on high-frequency financial data. See, for example, Bandi and Russell (2008) [4], Barndorff-Nielsen et al. (2008) [5], Jacod et al. (2009) [6], Jacod et al. (2010) [7], Xiu (2010) [8] and Zhang et al. (2005) [2].
Jumps are often observed in financial markets due to events happening around the globe or the release of financial reports. See Aït-Sahalia et al. (2002) [9], Barndorff-Nielsen and Shephard (2004) [10]. Actually, a jump-diffusion model has been studied back in Merton (1976) [11]. Such jumps lead to a violation of the continuous assumption and, thus, cause the inconsistency of those established estimators. To accurately estimate and predict volatility, it is important to have methods that estimate jumps and that separate it from the continuous part. Many existing methods have focused on testing for jumps under the strong assumption that we can observe the exact price process (see Aït-Sahalia 2004 [12], Aït-Sahalia and Jacod 2009 [13], Andersen et al. 2012 [14], Barndorff-Nielsen and Shephard 2006 [15], Carr and Wu 2003 [16], Eraker et al. 2003 [17], Eraker 2004 [18], Fan and Fan 2011 [19], Huang and Tauchen 2005 [20], Jiang and Oomen 2008 [21], Lee and Hannig 2010 [22], Lee and Mykland 2008 [23], Bollerslev et al. 2009 [24] and Todorov 2009 [25]). Recently, a few tests started to take microstructure noise into account; for example, the pre-averaging method is used to take care of the microstructure noise, and a test for jumps based on power variation is employed in Aït-Sahalia et al. (2012) [26]. Furthermore, some interesting jump research going on includes, but is not limited to: estimating the degree of jump activities (see Ait-Sahalia and Jacod 2009 [27], Jing et al. 2011 [28], Jing et al. 2012 [29] and Todorov and Tauchen 2011 [30]), modeling return using pure jump process (see Jing et al. 2012 [31] and Kong et al. 2015 [32]), modeling jumps in volatility processes (see Todorov and Tauchen 2011 [33]) and forecasting volatility with the existence of jumps (see Andersen et al. 2007 [34], Andersen et al. 2011 [35] and Andersen et al. 2011 [36]).
The method proposed in this paper mainly focuses on the wavelet-based detection and estimation of jump variation based on high-frequency financial data with market microstructure noise. Wavelet analysis is a tool for decomposing signals and functions into time-frequency contents that can unfold a signal or function over the time-frequency plane to provide information on “when” such “frequency” occurs (Wang 2006 [37]). It enables us to analyze non-stationary time series and to detect local changes. With such features, wavelet methods are developed to detect sudden localized changes in Wang (1995) [38] and to study jump variation based on high-frequency financial data with microstructure noise in Fan and Wang (2007) [39]. In this paper, we are going to take advantage of the nice properties of wavelets and adopt a new approach to improve the wavelet estimation methods.
The paper is organized as follows. In the remaining part of Section 1, we will introduce the basic model and wavelet techniques. In Section 2, we analyze the statistical properties of the original log price process, realized volatility process and average realized volatility process. The simulation is in Section 3, and the empirical study of jump variation is in Section 4. Section 5 provides some concluding remarks about our results. The proofs of the main theorems are in Section 6. More detailed proofs of the lemmas are in Appendix A. Tables and figures for further illustration are in Appendix B.
1.2. Integrated Volatility, Realized Volatility and Jump Variation
Let be the price process of a financial asset. We assume that the log price is a semi-martingale satisfying the stochastic differential equation
where we assume and are both bounded and continuous, is a standard Brownian motion, is a counting process and the total number of jumps in time period is finite. The three terms on the right-hand side of Equation (1) correspond to the drift, diffusion and jump parts of X, respectively.
Integrated volatility, as an important measure of the variation of the return process during a time period , is defined as
In financial practice, the estimation of the integrated volatility is of great interest.
Suppose are n observations of the log price process in time period . Define the realized volatility of X as
Stochastic analysis shows that as ,
where the first term on the right-hand side is the integrated volatility, and the second term is called the jump variation, which is the main focus of this paper. We denote it as Ψ,
Equation (4) says that, as the number of observations n increases, realized volatility converges in probability to integrated volatility plus jump variation Ψ. Thus, to better model and predict volatility, we need methods to estimate jump variation and to separate it from the integrated volatility.
1.3. Market Microstructure Noises
Microstructure noise plays a big role in the analysis of high-frequency financial data. It is often assumed that the observed data are a noisy version of at time points ,
where ϵ’s are the microstructure noises. We assume that ϵ’s are i.i.d. random variables with mean zero and variance . We also assume that ϵ and X are independent.
With noisy observations , now it becomes even more challenging. Let us define the realized volatility based on Y as
It can be shown (Zhang et al., 2005 [2]) that:
where is convergence in law and is a standard normal random variable. The result (8) implies that realized volatility is an inconsistent estimator of integrated volatility.
1.4. Wavelet Basics
Let φ and ψ be the specially-constructed father wavelet and mother wavelet, respectively. Then, the wavelet basis is , . We can expand a function over the wavelet basis as follows. Denote by the wavelet coefficient of associated with location and frequency ,
Then, we have
where .
There are two cases regarding the order of the wavelet coefficients (Daubechies, 1992 [40]):
Case 1: If f is a Hölder continuous function with exponent α, , i.e., for any , then satisfies
That means, for a Hölder continuous function f, the wavelet coefficients decrease at the order of as the frequency level increases. Details are in Lemmas 1 and 2 in Appendix A.
Case 2: If f is a Hölder continuous function with exponent α, , except for a jump of size L at s. Then, for sufficiently large j with , there exists a constant depending on L, such that
where is an interval around zero for some positive constant d. That means, nearby this jump point, the wavelet coefficients decrease no faster than the order of as the frequency level increases. Details are in Lemma 3 in Appendix A. Examples will be shown later in Section 5 for the Daubechies wavelets used in this paper.
Note that with n discrete observations, j takes values , where .
2. Statistical Analysis
2.1. Choosing a Frequency Level to Differentiate Jumps
In this section, we are going to study several different processes and the orders of their wavelet coefficients for both the continuous part and the jump part. For each process, we will determine a frequency level for which the order of the corresponding wavelet coefficients is significantly larger nearby jumps than the continuous part.
2.1.1. Starting from X and [X, X]
We first focus on the processes without noises. We consider and at time points .
From Equation (1), we have
For simplicity, we assume that in Equation (1) is defined in . Define as:
For , by Lemma 7 and Corollary 1 in Appendix A, we have:
where is a standard Brownian motion whose associated diffusion term in the above equation is due to discretization, and is convergence in law.
We let and be the wavelet coefficients of X and associated with location and frequency , respectively.
For , from Equation (13), the drift term is Hölder continuous with exponent . The diffusion term is Hölder continuous with exponent α arbitrarily close to , so the order of the continuous component of is dominated by the diffusion term. The order of the jump component is no less than . Therefore, if we pick a frequency level at , the order of the jump component is significantly larger than the other terms.
For , from Equation (15), the drift term is Hölder continuous with exponent . The diffusion term is Hölder continuous with exponent α arbitrarily close to and multiplied by an extra . Thus, again, if we pick a frequency level at , the order of the jump component is significantly larger than the others.
2.1.2. Moving on to Y and [Y, Y]
We now consider the noisy observations from Equation (6):
We let be the wavelet coefficients of Y, so . ’s are i.i.d with mean zero and variance , so the order of noise component is . If we pick a frequency level at , the order of the jump component is significantly larger than the others (Fan and Wang, 2007 [39]).
Next, let us consider . Similar to the way we rewrite in Equation (13), we rewrite Equation (8) as follows:
where the term is a diffusion term due to discretization, the term is a diffusion term due to noise, and are independent Brownian motions and is a constant (mean of the noise term).
We let be the wavelet coefficients of . The order for the continuous component dominated by the diffusion term due to noise is no greater than , where α is arbitrarily close to 1/2. The order of the jump component is greater than . However, in this situation, since the order of the diffusion term due to noise is too large, we are not able to have a frequency level at which we can differentiate the jumps.
2.1.3. Subsampling and Averaging on [Y, Y]
We now consider subsampling and averaging to reduce the order of the diffusion term due to noise. Subsampling: Create M grids (sub-samples) on the time line so that the distance between two consecutive observations within each grid is and the average size of each grid is . Denote by , the realized volatility of Y using grid m.
Averaging: denotes the average of the realized volatilities of Y using all M grids:
Rewriting the results in Zhang et al. (2005) [2], we have
Let be the wavelet coefficients of . We choose . Then, the order of the continuous component is no greater than , where α is arbitrarily close to 1/2. Therefore, if we pick a frequency level at , the order of the jump component is larger than the others.
2.2. Threshold Selection and Jump Location Estimation
For each process discussed in the above section, we are able to choose a frequency level to differentiate jumps, and thus, we develop a threshold on the wavelet coefficients at such a frequency level to detect those jumps. To accomplish the task, we first standardize the wavelet coefficients at chosen frequency level by dividing them by their median. Given a process, if the continuous component is dominated by the diffusion term at chosen frequency level , by Lemma 5, the standardized wavelet coefficients nearby a jump point are at least of the order , where α is arbitrarily close to 1/2. As volatility process is bounded, using Lemma 6, we can show that with probability tending to one, the maximum of standardized wavelet coefficients for the continuous part can be bounded by , where is some constant that may depend on , and is the median absolute deviation of the standard normal distribution.
For in (19), if we take , the continuous part is dominated by the term, and by Lemma 6, we have that with probability tending to one, the maximum of standardized wavelet coefficients is bounded by . Therefore, we may use threshold
If any standardized wavelet coefficients exceed threshold , then their associated locations are considered to be estimated jump locations. Let be q true jump locations in . Denote those estimated locations by . It is shown in Wang (1995) [38] and Raimondo (1998) [41] that at chosen frequency level , we have as and:
Note that for processes X, , Y and , to differentiate jumps, we have chosen frequency levels , n, and n, respectively. The orders of wavelet coefficients of different components and convergence rates of wavelet jump location estimators are summarized in Table B1 and Table B2 in Appendix B.
2.3. Estimation of Jump Variation
Finally, our goal is to estimate jump variation Ψ. For each estimated jump location , we choose a small neighborhood and calculate the average of the process over and . We estimate the jump size by taking the difference of two averages. The jump variation is estimated by the sum of squares of all jump size estimators.
2.3.1. Without Microstructure Noise Assumption
To estimate jump variation without noises, we have the results using X and in the following two theorems. Since is smoother, its associated method can achieve a convergence rate , which is higher than convergence rate for the method based on X.
Theorem 1.
Assume we observe . Under model (1), let be the average of X over and the average over . For each estimated jump location , let . Define
Choose ; we have
Theorem 2.
Assume we observe . Under model (1), let be the average of over and the average of over . For each estimated jump location , let . Define
Choose ; we have
2.3.2. With the Microstructure Noise Assumption
For noisy observations, we are able to improve the convergence rate in Fan and Wang (2007) [39] by using a smoother to obtain a higher convergence rate .
Theorem 3.
Under models (1) and (6), let be the average of over and be the average of over . For each estimated jump location , let . Define
Let , . If we choose , then we have
Moreover, the convergence rate is arbitrarily close to as γ can get arbitrarily close to for the threshold in Equation (20). For , if we choose the threshold to be for some constant , then the convergence rate is .
See the proof of Theorems 1–3 in Section 6. The orders of the convergence rates of the jump variation estimators are summarized in Table B3 in Appendix B.
3. Simulations
We have conducted a simulation study that assumes 32,768 number of observations for one day. Here are the simulation model and procedure.
- A sample path of is from the geometric OU volatility model
- A sample path of is fromwith .
- Jump locations are randomly selected, and three jumps are added to with size from i.i.d. .
- Noises ϵ’s are from i.i.d. with η at four different levels: 0.01, 0.02, 0.03, 0.04. Then, a sample path of is from .
- Realized volatility processes are calculated using a moving window of 32,768 observations. We actually simulate 65,536 of records, so that we have 32,768 complete observations of all processes for calculating these realized volatility processes. There are eight of such processes: X, , Y, , , , , . Figure 1 displays their sample paths as an example to show how those processes look under our scheme.
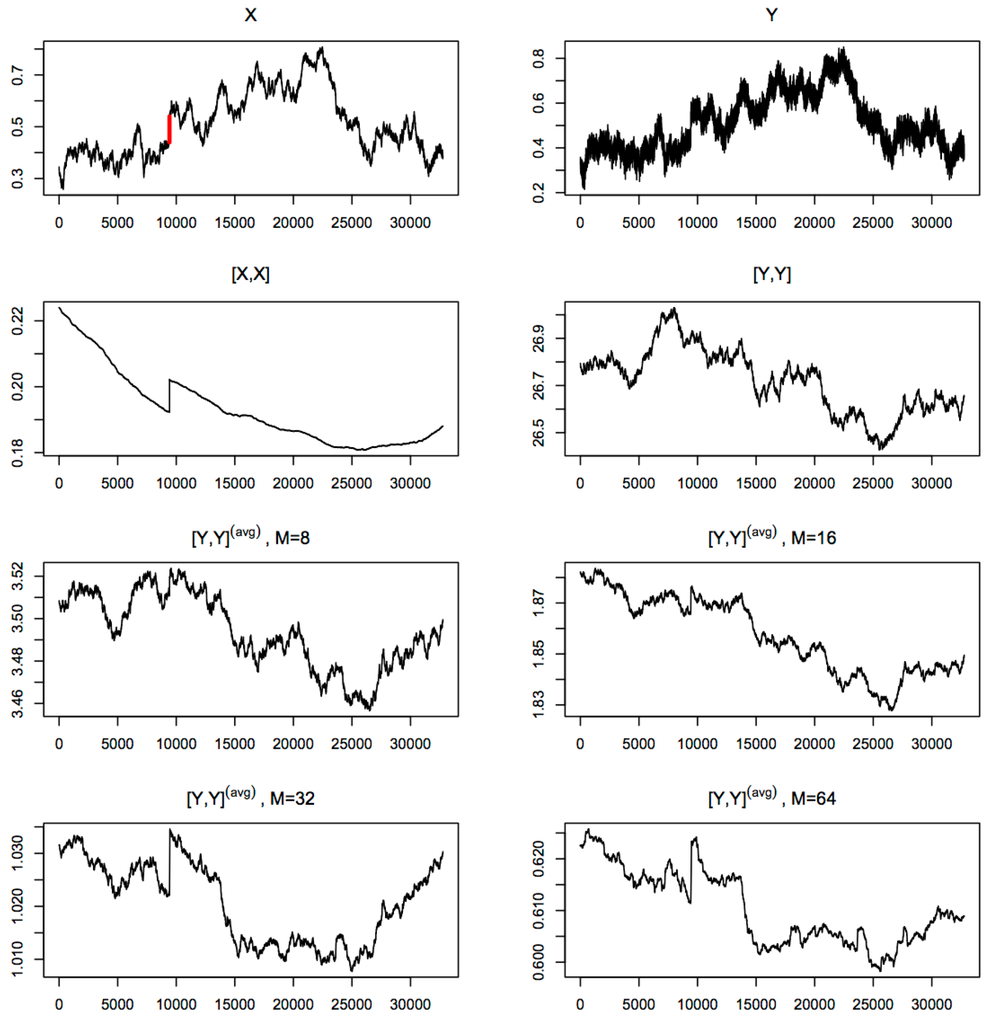 Figure 1. Processes simulated with a true jump at location 9424, noise level .
Figure 1. Processes simulated with a true jump at location 9424, noise level . - Discrete wavelet transformations are performed using Daubechies wavelet D20 on those realized volatility processes. We illustrate the behaviors of the wavelet coefficients at different frequency levels in Figure B1 and Figure B2 in Appendix B using those of the X process and the Y process as an example. We use the notations in Percival and Walden (2000) [42]: W1 represents the highest frequency level, W2 the second highest, and so on and so forth. At each frequency level from W1 to W5, if any standardized wavelet coefficient exceeds the threshold in (20), we declare the location associated with that coefficient as an estimated jump location. Here, we use , since the results in Section 2 and the simulation study show that the method based on is better than others.
- For each estimated jump location, we estimate the jump size and jump variation as described in Section 2. For X and Y, we use intervals of length 64. For , , , , , , we use intervals of length 128.
- The whole simulation procedure is repeated 1000 times.
If we do not assume the existence of market microstructure in the model, we are able to improve our estimation of jump variation using the process from using the X process, as shown in Theorems 1 and 2. The simulation results without adding noises are given in Table 1 and Table 2. Table 1 gives the average number of detected jumps and the corresponding standard deviation. We find that we are able to detect all three jumps most of the time using either X or at any frequency level from W1–W5. Table 2 is the mean squared error (MSE) of jump variation estimation and shows a smaller MSE using at every frequency level from W1 to W5.

Table 1.
Mean number of detected jumps at frequency levels from W1 to W5 using X and with the corresponding standard deviation in parenthesis.

Table 2.
MSE of the jump variation estimation at frequency levels from W1 to W5 using X and .
If we assume the existence of market microstructure in the model, we are able to improve our estimation of jump variation using processes from using the Y process, as shown in Theorem 3. The simulation results are summarized in Table 3 and Table 4. The results are illustrated at frequency levels from W1 to W5 and noise levels for processes Y, , , , and . Table 3 displays the average number of detected jumps and the corresponding standard deviation, with Table 4 for the MSEs of the jump variation estimation.

Table 3.
Mean number of detected jumps at frequency levels from W1 to W5 and noise levels using Y, , , , and , with the corresponding standard deviation in parenthesis.

Table 4.
MSE of the jump variation estimation at frequency levels from W1 to W5 and noise levels using Y, , , , and .
The results show that if we falsely detect some jumps while they are not, it does not affect too much the jump variation estimation since the estimated jump sizes are very small. However, if our detection misses some of the true jumps, it does have a certain effect on jump variation estimation. and X are both able to detect the jumps fairly well. As the noise level increases, the Y- and -based methods start to miss one or two jumps; the method based on can also miss detecting the jumps when M is small and noise is large, but it improves with a bigger M. In terms of the MSE of the jump variation estimation, the methods based on and perform better than those based on X and Y, respectively. As the noise level increases, we need to increase M for the method in order to improve its performance. does poorly compared to other processes.
4. Empirical Study
4.1. Distribution of Jump Variation
We study the distribution of jump variation for returns of each Dow Jones Industrial Average stock in January 2013. We collect the tick by tick prices from 9:30 a.m.–4 p.m. for each trading day from the TAQ database. There are 21 trading days and 30 stocks, which correspond to 630 stock-days. We compare the jump variation estimation of the 630 stock-days using Y, and and at different sampling frequencies: 1 tick, 2 ticks, 4 ticks. Here, we consider tick time equidistant, as discussed in Andersen et al., 2012 [14].
To detect the jump locations, we use Daubechies wavelet D4 at W4, W3, W2 for sampling frequencies at 1 tick, 2 ticks, 4 ticks, respectively, with the thresholds in Equation (20). We take such wavelet frequency levels to make sure of the consistency of jump detection along different sampling frequencies. To estimate the jump variation, at each estimated jump location, we take the difference between the means of intervals with width four. For , we use . We transform the data by the Box–Cox power transformation with power selected by the data, so that the Gaussian assumption of the threshold should be approximately followed.
The histograms of estimated jump variation for these 630 stock-days are illustrated in Figure 2. From left to right, the first column shows the result from using process Y, the second column using and the third column using . From top to bottom, the first row is the result from sampling data at every one tick, the second row at every two ticks and the third row at every four ticks.
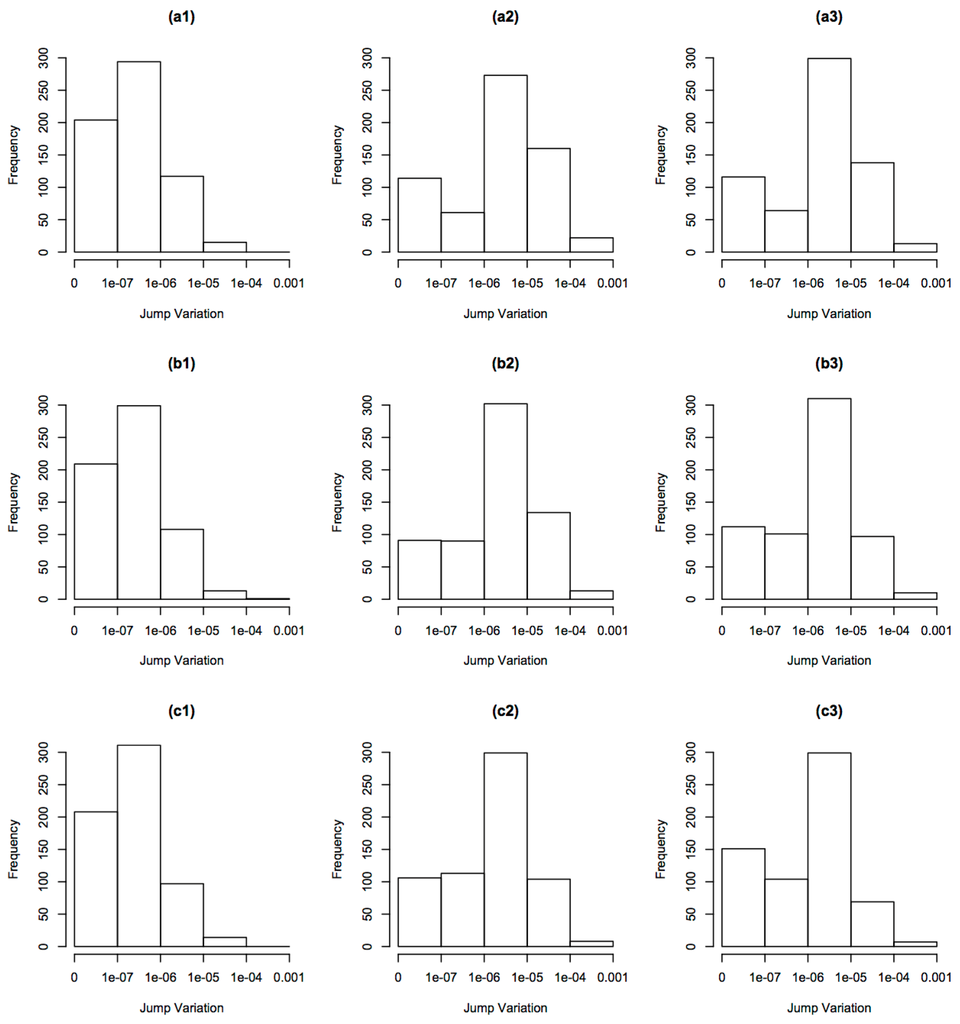
Figure 2.
Histograms of jump variation: The first row from left to right (a1,a2,a3) shows the results using processes Y, and , respectively, sampled at every one tick, the second row (b1,b2,b3) sampled at every two ticks and the third row (c1,c2,c3) sampled at every four ticks.
Compared to Y, processes and are able to pick up much larger jump variation at the same sampling frequency level. We find that around 25% of the jump variation is above 1 × 10 using and , while using Y, we only have around 1.5% (note that a price change from 100 to 99.99 leads to a squared log return change of around 1 × 10). On the other hand, for the same process, the distribution of jump variation looks very similar across different sampling frequencies.
4.2. Evidence of Microstructure Noises
To remove the idiosyncratic effects of each single stock, we plot the weighted average of the daily realized volatility using all stocks in Figure 3. They are before removing jump variation in (a) and after removing jump variation using processes Y, and in (b), (c) and (d), respectively. The solid lines are calculated from sampling at every one tick, the dashed lines at every two ticks and the dotted lines at every four ticks. The weight is decided by the mean level of the realized volatility of each stock. The larger it is, the smaller the weight is, so that each stock will contribute equally to the weighted average.
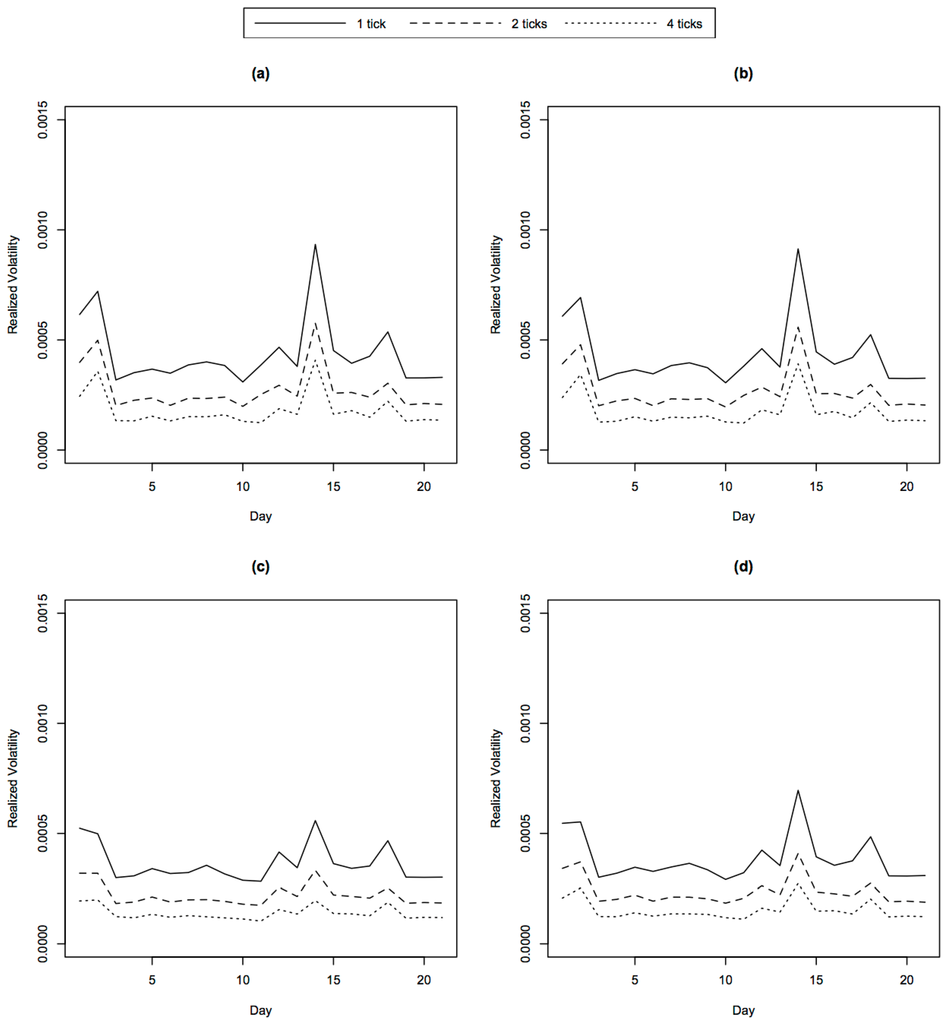
Figure 3.
Realized volatility: (a) before removing jump variation; (b–d) after removing jump variation using processes Y, and , respectively. The solid lines are calculated from sampling at every one tick, the dashed lines at every two ticks and the dotted lines at every four ticks.
We see from Figure 3 that there is clear evidence of microstructure noises, since as the sampling frequency increases, the realized volatility increases, as well, in each case, just as we show in theory. Moreover, the effects of removing jumps are more significant using and than Y.
5. Discussion
We develop a nonparametric method for estimating jump variation with noisy high frequency financial data. With a better approach based on new process and the wavelet techniques, we are able to detect and estimate jump variation more efficiently if the variance of microstructure noise is assumed to be a constant. Numerically, we show that the proposed method indeed has smaller mean square errors.
From the empirical results, we observe that the method based on outperforms that based on Y. This may suggest that is not a constant, so if we modify to be some decreasing function of n, for example, and , then the -based method can achieve a better convergence rate than that for Y.
For the Daubechies wavelets D4 and D20 used in the paper, we display their graphs below in Figure 4, as well as the graphs of the absolute values of their integrations. Using Daubechies wavelet D4, we may pick for , while using Daubechies wavelet D20, we may pick for .
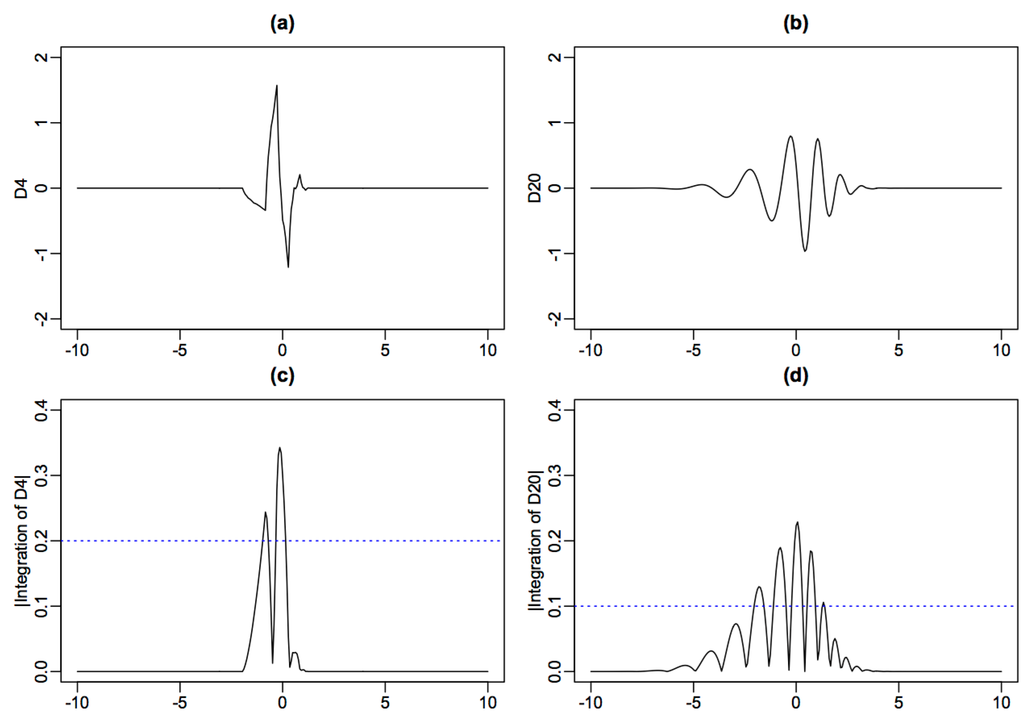
Figure 4.
(a,b) Daubechies wavelets D4 and D20, respectively; (c,d) absolute values of integrated D4 and D20, respectively.
We leave some open problems for future study, including the extension to estimate jump size, optimal frequency level selection in practice, the irregular spaced observations, data-dependent threshold selection and its sensitivity study.
6. Proof of Theorems
Theorem 1.
(Estimation of jump size/variation using X) Let be an estimated jump location. Denote the average of X over and the average of X over . We estimate the jump size by
If we choose , then
and
Proof.
Denote the number of in and , respectively. Then, and . We decompose as
where , and correspond to the drift, diffusion and jump part.
where and .
Because , the total non-zero terms in and is . Furthermore, by maximal martingale inequality,
Therefore, .
For , since
and
and τ independent of , we have
and
Together, we have
Finally,
Thus, if we take , we have
And
☐
Theorem 2.
(Estimation of jump variation using ) Denote the average of over and the average of over . We estimate the jump variation by
If we choose , then
Proof.
Similar to the proof of the previous theorem, we decompose the as
where , , correspond to the drift, diffusion and jump parts.
We still have
and
has changed to
Thus, if we take , we have
☐
Theorem 3.
(Estimation of jump variation using ) Denote the average of over and the average of over . We estimate the jump variation by
Let , . If we choose , then
Moreover, the convergence rate is arbitrarily close to as γ can get arbitrarily close to for the threshold in Equation (20). For , if we choose the threshold to be for some constant , then, the convergence rate is .
Proof.
This time, we have
Thus, if we take , we have
☐
Acknowledgments
Wang’s research is partly supported by NSF Grants DMS-10-5635, DMS-12-65203 and DMS-15-28375. The authors would like to thank the editor, associate editor and referees for suggestions that led to the improvement of the paper.
Author Contributions
Yazhen Wang proposed the project, and Xin Zhang carried out the work. Xin Zhang and Yazhen Wang contributed to the development of methodology and theory. Xin Zhang, Donggyu Kim and Yazhen Wang contributed to the theoretic proof. Xin Zhang contributed the numerical results. Xin Zhang and Yazhen Wang contributed to the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Lemmas
Lemma A1.
(Order of wavelet coefficients in the continuous case) Suppose that . If f is Hölder continuous with exponent α, , i.e., . Then, its wavelet transform satisfies
where
Proof.
First, note that , so we have
Taking the absolute value, we have
Note that the integral in the last equation is finite. The result then follows. ☐
Lemma A2.
(Necessary condition: order of wavelet coefficients in the continuous case) Suppose that ψ is compactly supported. Suppose also that is bounded and continuous. If for some , the wavelet transform of f satisfies
then f is Hölder continuous with exponent α.
See Section 2.9 in Daubechies, 1992 [40].
Lemma A3.
(Order of wavelet coefficients in the jump case) Suppose that . If g is Hölder continuous with exponent α, . Let
Then, for sufficiently large j with , there exists a constant depending on L, such that
where for some positive constant d.
Proof.
For the first part, we have its absolute value
For the second part, by Lemma 1, we have its absolute value
The proof is complete. ☐
Lemma A4.
(Robustness of the median) Let , where is the wavelet coefficient corresponding to the continuous part and to the jump part. Suppose no more than of is nonzero. Let be the q-th quantile of and be the q-th quantile of . Then
Proof.
Suppose there is only one nonzero , so . Let denote this nonzero coefficient. If its corresponding , we have the following three cases:
- Case 1:
- . Since all other , we have .
- Case 2:
- . Then, we have , so
- Case 3:
- . Then, we have , so
Together, we have
If its corresponding , similarly, we can prove
This proves the result when we have only one nonzero . For more than one nonzero coefficient, we can use iteration by adding one at one time. Therefore, the result holds. ☐
Lemma A5.
(Order of the maximum to median ratio of wavelet coefficients in the jump case) Suppose is a Hölder continuous process with exponent α, , except for a jump of size L. Then, for sufficiently large j,
where , and is a constant and increases as L increases.
Proof.
First, we consider . In a neighborhood of point t where is continuous, by Lemmas 1 and 2, wavelet coefficients at such points are at order with α close to 1/2. On the other hand, nearby a jump point in , by Lemma 3, for sufficiently large j, converges no faster than . Since the order is much larger than , we have regulated by the jump part.
Second, we consider . Assume we have discrete observations and that the number of jumps is R. Since the wavelet functions have compact support, among the wavelet coefficients at a fine level, no more than (%) of them will be affected by the jumps, where b is very small. For example, if we use a wavelet of support length S, we have wavelet coefficients at the finest level, and there will be no more than of them affected by jumps. Thus, in this case, we have , which goes to zero as n goes to infinity. Since the number of coefficients affected by jumps is very small compared to the total number of wavelets coefficients, i.e. , if we order the wavelet coefficients at fine levels, by Lemma 4, will be surely regulated by the continuous part.
Together, when j is sufficiently large, the ratio
☐
Lemma A6.
(Order of the maximum to median ratio of wavelet coefficients in the Brownian motion case) Let be a Brownian motion and be the corresponding wavelet coefficients. Then,
where , and is the median of for .
Proof.
For fixed j, is a stationary Gaussian process with mean zero and variance function
Therefore, we have
We have
where the second inequality is derived using the inequality .
By (A15) and (A16), Equation (A14) follows. ☐
Remark.
The covariance function of is
which is zero when is bigger than the range of . That is, , a stationary Gaussian process with the m-dependent covariance structure, and we can derive an asymptotic distribution of .
Lemma A7.
(Equivalent representation of the realized volatility of X) Suppose X follows an Itô process satisfying the stochastic differential equation
The realized volatility of X at is defined by
where is an equidistant partition on . Then, we have
where stable convergence is defined in Rényi, 1963 [43], Aldous and Eagleson, 1978 [44], and Hall and Heyde, 1980 [45].
Proof.
By Itô’s Lemma, we have for any ,
Then, we have
Now, it is enough to show
Let , where and . Simple algebraic manipulations show
For , since is bounded, we have
Then, we have
where the first and last lines are due to (A23) and the boundedness of , respectively.
For , we have
First consider that . is continuous, and so, we have a.s. The boundedness of and dominated convergence theorem imply . Thus, we have
where the first inequality is due to Hölder’s inequality, and the second inequality is by the fact that
where the first and second equalities are due to the Itô isometry and the boundedness of , respectively. For , since are uncorrelated, simple algebraic manipulations show
where the first inequality is due to Hölder’s inequality and the fifth and sixth lines are due to the boundedness of and (A26), respectively. By (A25) and (A27), we have
For , the sequence, , is a martingale difference sequence, and so, we have
where the second equality is due to the Itô isometry and the last equality is from (A23) and the boundedness of . Thus,
For , since is bounded and integrable, . Thus, an application of Theorem 5.1 in Jacod and Protter (1998) [46] leads to:
Collecting (A24), (A28)–(A30), we have (A22). ☐
Corollary 1.
Appendix B. Tables and Figures
Note that in the following tables, we take α close to 1/2 and .

Table B1.
Summary of the order of the wavelet coefficients of different components.
| Component | X | Y | |||
|---|---|---|---|---|---|
| cont. drift (≤) | |||||
| cont. diffusion (≤) | |||||
| jump (≥) | |||||
| noise () | 0 |

Table B2.
Summary of the convergence rate of jump location estimation.
| X | Y | |||
|---|---|---|---|---|
| NA |

Table B3.
Summary of the convergence rate of jump variation estimation.
| X | Y | |||
|---|---|---|---|---|
| NA |
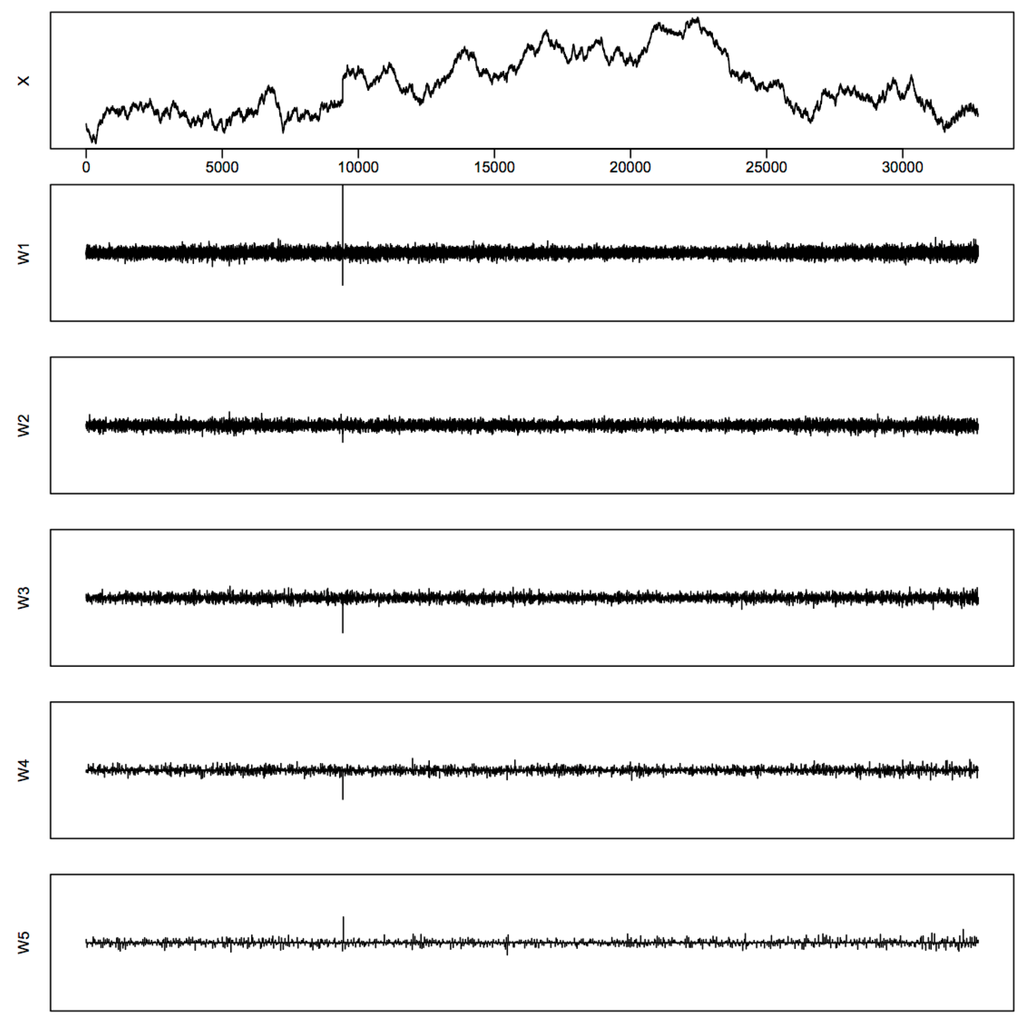
Figure B1.
Wavelet coefficients of X at levels W1–W5, with a jump at location 9424.
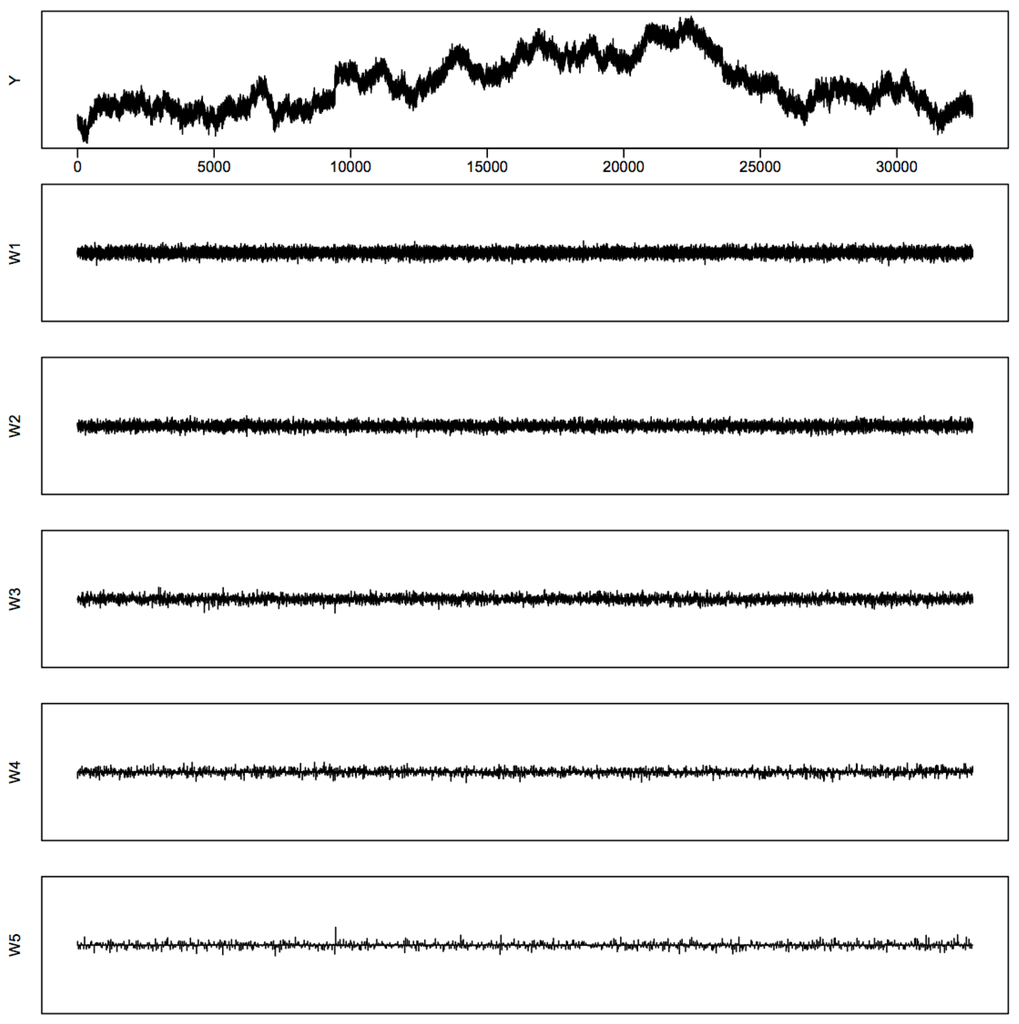
Figure B2.
Wavelet coefficients of Y at levels W1–W5, with a jump at location 9424.
References
- O.E. Barndorff-Nielsen, and N. Shephard. “Econometric Analysis of Realized Volatility and Its Use in Estimating Stochastic Volatility Models.” J. R. Stat. Soc. Ser. B 64 (2002): 253–280. [Google Scholar] [CrossRef]
- L. Zhang, P.A. Mykland, and Y. Aït-Sahalia. “A Tale of Two Time Scales: Determining Integrated Volatility with Noisy High-Frequency Data.” J. Am. Stat. Assoc. 100 (2005): 1394–1411. [Google Scholar] [CrossRef]
- L. Zhang. “Efficient Estimation of Stochastic Volatility Using Noisy Observations: A Multi-Scale Approach.” Bernoulli 12 (2006): 1019–1043. [Google Scholar] [CrossRef]
- F.M. Bandi, and J.R. Russell. “Microstructure Noise, Realized Variance, and Optimal Sampling.” Rev. Econ. Stud. 75 (2008): 339–369. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, P.R. Hansen, A. Lunde, and N. Shephard. “Designing Realized Kernels to Measure Ex-post Variation of Equity Prices in the Presence of Noise.” Econometrica 76 (2008): 1481–1536. [Google Scholar]
- J. Jacod, Y. Li, P.A. Mykland, M. Podolskij, and M. Vetter. “Microstructure Noise in the Continuous Case: The Pre-averaging Approach.” Stoch. Process. Their Appl. 119 (2009): 2249–2276. [Google Scholar] [CrossRef]
- J. Jacod, M. Podolskij, and M. Vetter. “Limit Theorems for Moving Averages of Discretized Processes Plus Noise.” Ann. Stat. 38 (2010): 1478–1545. [Google Scholar] [CrossRef]
- D. Xiu. “Quasi-maximum Likelihood Estimation of Volatility with High Frequency Data.” J. Econ. 159 (2010): 235–250. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia. “Telling from Discrete Data Whether the Underlying Continuous-Time Model Is a Diffusion.” J. Finance 57 (2002): 2075–2121. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, and N. Shephard. “Power and Bipower Variation with Stochastic Volatility and Jumps (with discussion).” J. Financ. Econ. 2 (2004): 1–48. [Google Scholar]
- R.C. Merton. “Option Pricing When Underlying Stock Returns Are Discontinuous.” J. Financ. Econ. 3 (1976): 125–144. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia. “Disentangling Volatility from Jumps.” J. Financ. Econ. 74 (2004): 487–528. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, and J. Jacod. “Testing for Jumps in a Discretely Observed Process.” Ann. Stat. 37 (2009): 184–222. [Google Scholar] [CrossRef]
- T.G. Andersen, D. Dobrev, and E. Schaumburg. “Jump-robust Volatility Estimation Using Nearest Neighbor Truncation.” J. Econ. 169 (2012): 75–93. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, and N. Shephard. “Econometrics of Testing for Jumps in Financial Economics using Bipower Variation.” J. Financ. Econ. 4 (2006): 1–30. [Google Scholar] [CrossRef]
- P. Carr, and L. Wu. “What Type of Process Underlies Options? A Simple Robust Test.” J. Finance 58 (2003): 2581–2610. [Google Scholar] [CrossRef]
- B. Eraker, M. Johannes, and N. Polson. “The Impact of Jumps in Returns and Volatility.” J. Finance 58 (2003): 1269–1300. [Google Scholar] [CrossRef]
- B. Eraker. “Do Stock Prices and Volatility Jump? Reconciling Evidence From Spot and Option Prices.” J. Finance 59 (2004): 1367–1404. [Google Scholar] [CrossRef]
- Y. Fan, and J. Fan. “Testing and Detecting Jumps Based on a Discretely Observed Process.” J. Econom. 164 (2011): 331–344. [Google Scholar] [CrossRef]
- X. Huang, and G.T. Tauchen. “The Relative Contribution of Jumps to Total Price Variance.” J. Financ. Econ. 4 (2005): 456–499. [Google Scholar]
- G.J. Jiang, and R.C. Oomen. “Testing for Jumps When Asset Prices Are Observed with Noise—A “Swap Variance” Approach.” J. Econ. 144 (2008): 352–370. [Google Scholar] [CrossRef]
- S.S. Lee, and J. Hannig. “Detecting Jumps From Lévy Jump Diffusion Processes.” J. Financ. Econ. 96 (2010): 271–290. [Google Scholar] [CrossRef]
- S.S. Lee, and P.A. Mykland. “Jumps in Financial Markets: A New Nonparametric Test and Jump Dynamics.” Rev. Financ. Stud. 21 (2008): 2535–2563. [Google Scholar] [CrossRef]
- T. Bollerslev, U. Kretschmer, C. Pigorsch, and G. Tauchen. “A Discrete-time Model for daily S & P500 Returns and Realized Variations: Jumps and Leverage Effects.” J. Econ. 150 (2009): 151–166. [Google Scholar]
- V. Todorov. “Estimation of Continuous-Time Stochastic Volatility Models with Jumps Using High-Frequency Data.” J. Econ. 148 (2009): 131–148. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, J. Jacod, and J. Li. “Testing for Jumps in Noisy High Frequency Data.” J. Econ. 168 (2012): 207–222. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, and J. Jacod. “Estimating the Degree of Activity of Jumps in High Frequency Data.” Ann. Stat. 37 (2009): 2202–2244. [Google Scholar] [CrossRef]
- B.Y. Jing, X.B. Kong, and Z. Liu. “Estimating the Jump Activity Index of Lévy Processes Under Noisy Observations Using High Frequency Data.” J. Am. Stat. Assoc. 106 (2011): 558–568. [Google Scholar] [CrossRef]
- B.Y. Jing, X.B. Kong, Z. Liu, and P.A. Mykland. “On the Jump Activity Index for Semimartingales.” J. Econ. 166 (2012): 213–223. [Google Scholar] [CrossRef]
- V. Todorov, and G. Tauchen. “Limit Theorems for Power Variations of Pure-Jump Processes with Application to Activity Estimation.” Ann. Appl. Probabil. 21 (2011): 546–588. [Google Scholar] [CrossRef]
- B.Y. Jing, X.B. Kong, and Z. Liu. “Modeling High Frequency Data by Pure Jump Processes.” Ann. Stat. 40 (2012): 759–784. [Google Scholar] [CrossRef]
- X.B. Kong, Z. Liu, and B.Y. Jing. “Testing For Pure-jump Processes For High-Frequency Data.” Ann. Stat. 43 (2015): 847–877. [Google Scholar] [CrossRef]
- V. Todorov, and G. Tauchen. “Volatility Jumps.” J. Bus. Econ. Stat. 29 (2011): 356–371. [Google Scholar] [CrossRef]
- T.G. Andersen, T. Bollerslev, and F.X. Diebold. “Roughing it Up: Including Jump Components in the Measurement, Modeling, and Forecasting of Return Volatility.” Rev. Econ. Stat. 89 (2007): 701–720. [Google Scholar] [CrossRef]
- T.G. Andersen, T. Bollerslev, and X. Huang. “A Reduced Form Framework for Modeling and Forecasting Jumps and Volatility in Speculative Prices.” J. Econ. 160 (2011): 176–189. [Google Scholar] [CrossRef]
- T.G. Andersen, T. Bollerslev, and N. Meddahi. “Realized Volatility Forecasting and Market Microstructure Noise.” J. Econ. 160 (2011): 220–234. [Google Scholar] [CrossRef]
- Y. Wang. “Selected Review on Wavelets.” In Frontier Statistics, a Festschrift for Peter Bickel. Edited by H. Koul and J. Fan. London, UK: Imperial College Press, 2006, pp. 163–179. [Google Scholar]
- Y. Wang. “Jump and Sharp Cusp Detection by Wavelets.” Biometrika 82 (1995): 385–397. [Google Scholar] [CrossRef]
- J. Fan, and Y. Wang. “Multi-scale Jump and Volatility Analysis for High-Frequency Financial Data.” J. Am. Stat. Assoc. 102 (2007): 1349–1362. [Google Scholar] [CrossRef]
- I. Daubechies. Ten Lectures on Wavelets. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, 1992. [Google Scholar]
- M. Raimondo. “Minimax Estimation of Sharp Change Points.” Ann. Stat. 26 (1998): 1379–1397. [Google Scholar] [CrossRef]
- D.B. Percival, and A.T. Walden. Wavelet Methods for Time Series Analysis. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- A. Rényi. “On Stable Sequences of Events.” Sankhyā Ser. A 25 (1963): 293–302. [Google Scholar]
- D.J. Aldous, and G.K. Eagleson. “On Mixing and Stability of Limit Theorems.” Ann. Probab. 6 (1978): 325–331. [Google Scholar] [CrossRef]
- P. Hall, and C.C. Heyde. Martingale Limit Theory and Its Application. Boston, MA, USA: Academic Press, 1980. [Google Scholar]
- J. Jacod, and P. Protter. “Asymptotic Error Distributions for the Euler Method for Stochastic Differential Equations.” Ann. Probab. 26 (1998): 267–307. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).