Removing Specification Errors from the Usual Formulation of Binary Choice Models
Abstract
:1. Introduction
2. Methods of Correctly Specifying Binary Choice Models and Their Estimation
2.1. Model for a Cross-Section of Individuals
2.2. Unique Coefficients and Error Terms of Models
2.2.1. Causal Relations
2.2.2. Derivation of a Model from (1) without Committing a Single Specification Error
2.2.3. A Latent Regression Model with Unique Coefficients and Error Terms
2.2.4. A Correctly Specified Latent Regression Model
2.2.5. What Specification Errors Are (3)–(8) Free from?
2.3. Comparison of (7) with the Yatchew and Griliches (1985) [2], Wooldridge (2002) [5], and Cramer (2006) [4] Latent Regression Models
Parameterization of Model (7)
2.4. Derivation of the Likelihood Function for (11)
- (i)
- The in cannot be estimated, since there is no information about it in the data. To solve this problem, we set equal to 1.
- (iI)
- From (2) it follows that the conditional probability that = 1 (or > 0) given and iswhere the information about the constant term is contained in the proportion of observations for which the dependent variable is equal to 1.
Unconstrained and Constrained Maximum Likelihood Estimation
2.5. Estimation of the Components of the Coefficients of (7)
2.5.1. How to Select the Regressors and Coefficient Drivers Appearing in (11)?
2.5.2. Impure Marginal Effects
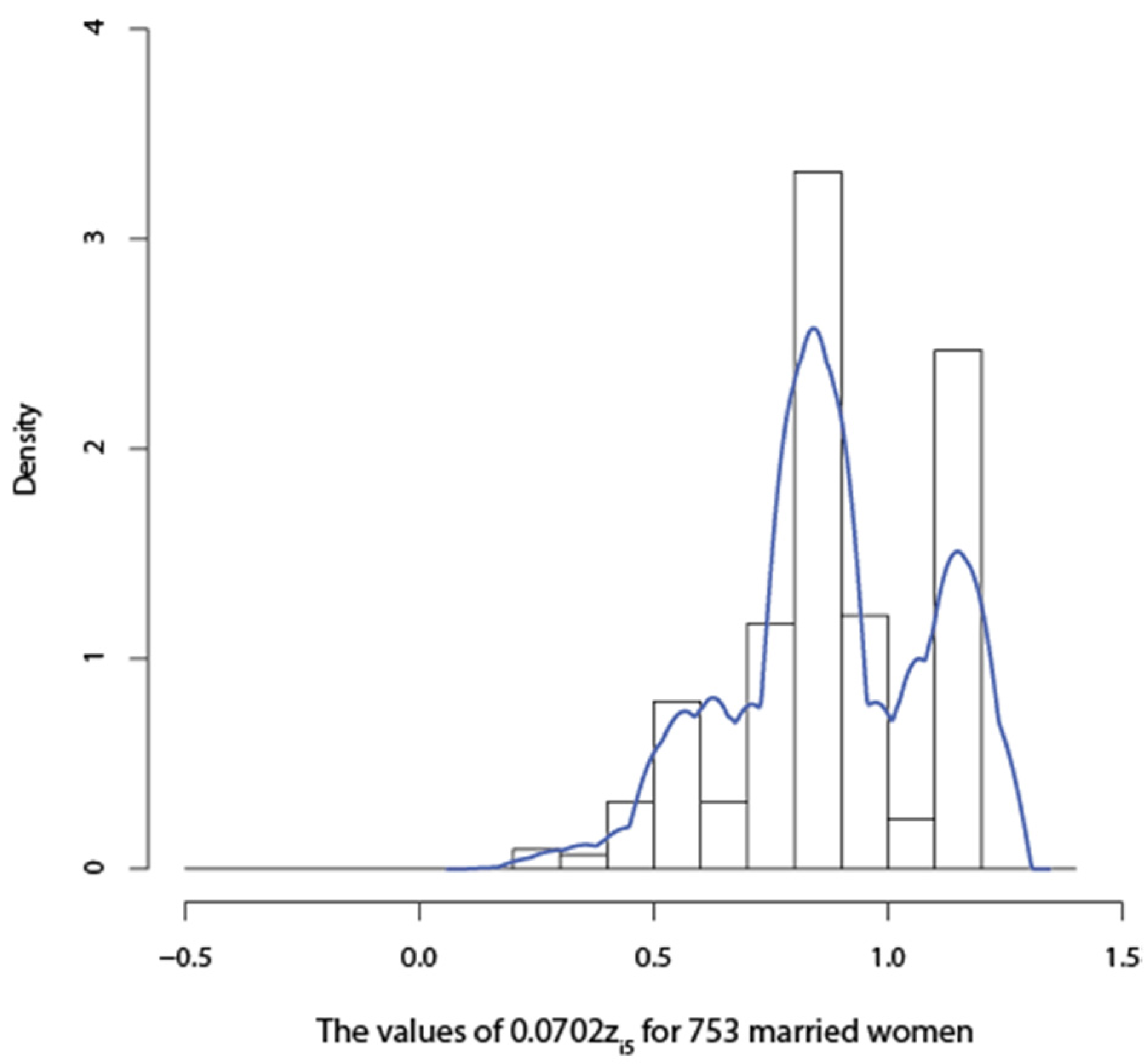
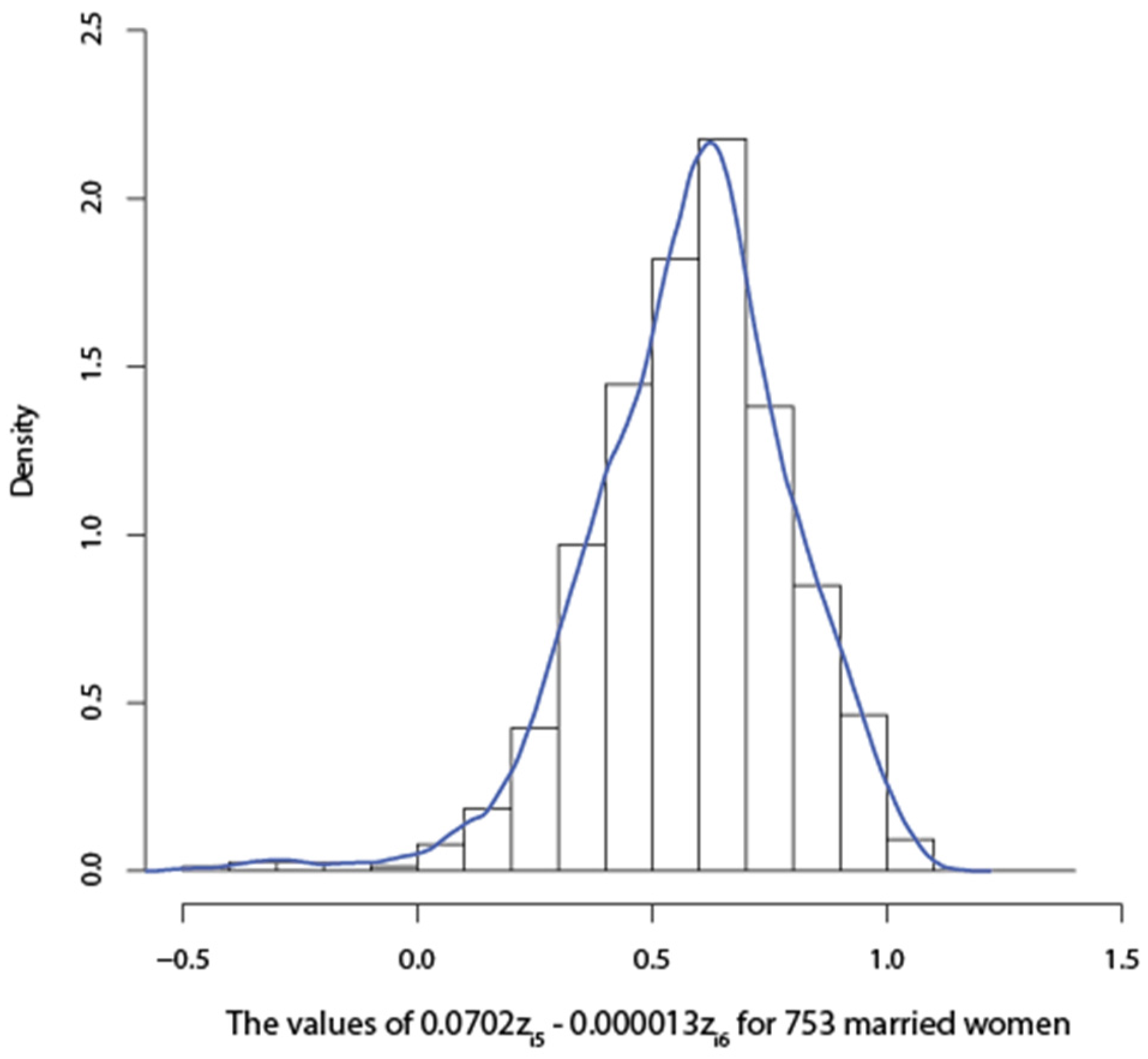
3. Earnings and Education Relationship
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A. Derivation of Linear and Nonlinear Regressions with Additive Error Terms
A.1. Nonunique Coefficients and Error Terms
A.1.1. Beginning Problems—Rigorous Derivation of Models with Additive Error Terms
A.1.2. Full Independence and the Existence of Conditional Expectations
A.1.3. Linear Conditional Means and Variances
B. Derivation of the Information Matrix for (10)
References
- J.W. Pratt, and R. Schlaifer. “On the Interpretation and Observation of Laws.” J. Econom. 39 (1988): 23–52. [Google Scholar] [CrossRef]
- A. Yatchew, and Z. Griliches. “Specification Error in Probit Models.” Rev. Econom. Stat. 66 (1984): 134–139. [Google Scholar] [CrossRef]
- W. Greene. Econometric Analysis, 7th ed. Upper Saddle River, NJ, USA: Pearson, Prentice Hall, 2012. [Google Scholar]
- J.S. Cramer. “Robustness of Logit Analysis: Unobserved Heterogeneity and Misspecified Disturbances, Discussion Paper 2006/07.” Amsterdam, The Netherlands: Department of Quantitative Economics, Amsterdam School of Economics, 2006. [Google Scholar]
- J.M. Wooldridge. Econometric Analysis of Cross-Section and Panel Data. Cambridge, MA, USA: The MIT Press, 2002. [Google Scholar]
- P.A.V.B. Swamy, J.S. Mehta, G.S. Tavlas, and S.G. Hall. “Small Area Estimation with Correctly Specified Linking Models.” In Recent Advances in Estimating Nonlinear Models, with Applications in Economics and Finance. Edited by J. Ma and M. Wohar. New York, NY, USA: Springer, 2014, pp. 193–228. [Google Scholar]
- B. Skyrms. “Probability and Causation.” J. Econom. 39 (1998): 53–68. [Google Scholar] [CrossRef]
- R.L. Basmann. “Causality Tests and Observationally Equivalent Representations of Econometric Models.” J. Econom. 39 (1988): 69–104. [Google Scholar] [CrossRef]
- J.W. Pratt, and R. Schlaifer. “On the Nature and Discovery of Structure (with discussion).” J. Am. Stat. Assoc. 79 (1984): 9–21. [Google Scholar] [CrossRef]
- H.A. Karlsen, T. Myklebust, and D. Tjøstheim. “Nonparametric Estimation in a Nonlinear Cointegration Type Model.” Ann. Stat. 35 (2007): 252–299. [Google Scholar] [CrossRef]
- H. White. “Using Least Squares to Approximate Unknown Regression Functions.” Int. Econ. Rev. 21 (1980): 149–170. [Google Scholar] [CrossRef]
- H. White. “Maximum Likelihood Estimation of Misspecified Models.” Econometrica 50 (1982): 1–25. [Google Scholar] [CrossRef]
- J. Pearl. Causality. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- C.R. Rao. Linear Statistical Inference and Its Applications, 2nd ed. New York, NY, USA: John Wiley & Sons, 1973. [Google Scholar]
- E.L. Lehmann, and G. Casella. Theory of Point Estimation. New York, NY, USA: Spriger Verlag, Inc., 1998. [Google Scholar]
- P.A.V.B. Swamy, G.S. Tavlas, and S.G. Hall. “On the Interpretation of Instrumental Variables in the Presence of Specification Errors.” Econometrics 3 (2015): 55–64. [Google Scholar] [CrossRef]
- J. Felipe, and F.M. Fisher. “Aggregation in Production Functions: What Applied Economists Should Know.” Metroeconomica 54 (2003): 208–262. [Google Scholar] [CrossRef]
- J.J. Heckman, and D. Schmierer. “Tests of Hypotheses Arising in the Correlated Random Coefficient Model.” Econ. Modell. 27 (2010): 1355–1367. [Google Scholar] [CrossRef] [PubMed]
- A.S. Goldberger. Functional Form and Utility: A Review of Consumer Demand Theory. Boulder, CO, USA: Westview Press, 1987. [Google Scholar]
- P. Whittle. Probability. New York, NY, USA: John Wiley & Sons, 1976. [Google Scholar]
- J.J. Heckman, and E.J. Vytlacil. “Structural Equations, Treatment Effects and Econometric Policy Evaluation.” Econometrica 73 (2005): 669–738. [Google Scholar] [CrossRef]
- A.M. Kagan, Y.V. Linnik, and C.R. Rao. Characterization Problems in Mathematical Statistics. New York, NY, USA: John Wiley & Sons, 1973. [Google Scholar]
- P.A.V.B. Swamy, and P. von zur Muehlen. “Further Thoughts on Testing for Causality with Econometric Models.” J. Econom. 39 (1988): 105–147. [Google Scholar] [CrossRef]
- V. Berenguer-Rico, and J. Gonzalo. “Departamento de Economía, Universidad Carlos III de Madrid. Summability of Stochastic Processes: A Generalization of Integration and Co-integration valid for Non-linear Processes.” Unpublished work. , 2013. [Google Scholar]
- 1See, also, Greene (2012, Chapter 17, p. 713) [3].
- 2We will show below that the inconsistency problems Yatchew and Griliches (1984, p. 713) [2] pointed out with the probit and logit models are eliminated by replacing these models by the model in (1) and (2).
- 3We explain in the next paragraph why we have included these conditions.
- 4Some researchers may believe that there is no such thing as the true functional form of (1). Whenever we talk of the correct functional form of (1), we mean the functional form of (1) that is appropriate to the particular binary choice in (2).
- 5Here we are using Skyrms’ (1988, p. 59) [7] definition of the term “all relevant pre-existing conditions.”
- 6This is Basmann’s (1988, pp. 73, 99) [8] statement.
- 8We postpone making stochastic assumptions about measurement errors.
- 9The label “omitted” means that we would remove them from (3).
- 12A similar admissibility condition for covariates is given in Pearl (2000, p. 79) [13]. Pearl (2000, p. 99) [13] also gives an equation that forms a connection between the opaque phrase “the value that the coefficient vector of (3) would take in unit i, had been ” and the physical processes that transfer changes in into changes in .
- 13We illustrate this procedure in Section 3 below.
- 14Pratt and Schlaifer (1988) [1] consider what they call “concomitants” that absorb “proxy effects” and include them as additional regressors in their model. The result in (9) calls for Equation (10) which justifies our label for its right-hand side variables.
- 15An important difference between coefficient drivers and instrumental variables is that a valid instrument is one that is uncorrelated with the error term, which often proves difficult to find, particularly when the error term is nonunique. For a valid driver we need variables which should satisfy Equations (25) and (26). On the problems with instrumental variables, see Swamy, Tavlas, and Hall (2015) [16].
- 16These biases are not involved in Wooldridge’s marginal effects because according to that researcher omitted regressors constituting his model’s error term do not introduce omitted-regressor biases into the coefficients of the included regressors.
- 17The standard errors of estimates are given in parentheses below the estimates for five married women. The estimates and their standard errors for other married women are available from the authors upon request.
- 18According to Geene (2012, p, 708) [3], it would be natural to assume that all the determinants of a wife’s labor force participation would be correlated with the husband’s hours which is defined as a linear stochastic function of the husband’s age and education and the family income. Our inclusion of husband’s variables in (32) is consistent with this assumption.
- 19The standard errors of estimates are given in parentheses below the estimates for five married women. These estimates and standards errors for other married women are available from I-Lok Chang upon request.
- 20Another widely cited work that utilized a set of separability conditions is that of Heckman and Schmierer (2010) [18]. These authors postulated a threshold crossing model which assumes separability between observables Z that affect choice and an unobservable V. They used a function of Z as an instrument and used the distribution of V to define a fundamental treatment parameter known as the marginal treatment effect.
- 21The “uniqueness” is defined in Section 2.2.3.
- 22We have been using the cross-sectional subscript i so far. We change this subscript to the time subscript t wherever the topic under discussion requires the use of the latter subscript.
- 23This proof is relevant to Heckman’s interpretation that in any of his models, the error term is the deviation of the dependent variable from its conditional expectation (see Heckman and Vytlacil (2005) [21]. Conditions (A2.1)–(A2.3) do not always hold and hence this conditional expectation does not always exist.
- 24A nonstationary series is integrated of order d if it becomes stationary after being first differenced d times (see Greene (2012, p. 943) [3]). If in (A1) is a nonstationary series of this type, then it cannot be made stationary by first differencing it once or more than once if is nonlinear. Basmann (1988, p. 98) [8] acknowledged that a model representation is not free of the most serious objection, i.e., nonuniqueness, if stationarity producing transformations of its observable dependent variable are used.
| (Standard Error) | (Standard Error) |
|---|---|
| −13.280 | 1.2811 |
| (6.5787) | (0.5535) |
| −5.2539 | 0.7930 |
| (9.1608) | (0.7830) |
| −15.221 | 1.5029 |
| (4.9202) | (0.4197) |
| −21.577 | 1.8393 |
| (11.213) | (0.9942) |
| −9.2086 | 1.0386 |
| (7.8416) | (0.6504) |
| 0.8419 |
| (0.8110) |
| 0.6314 |
| (0.6083) |
| 0.8419 |
| (0.8110) |
| 0.7016 |
| (0.6758) |
| 0.8419 |
| (0.8110) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swamy, P.A.V.B.; Chang, I.-L.; Mehta, J.S.; Greene, W.H.; Hall, S.G.; Tavlas, G.S. Removing Specification Errors from the Usual Formulation of Binary Choice Models. Econometrics 2016, 4, 26. https://doi.org/10.3390/econometrics4020026
Swamy PAVB, Chang I-L, Mehta JS, Greene WH, Hall SG, Tavlas GS. Removing Specification Errors from the Usual Formulation of Binary Choice Models. Econometrics. 2016; 4(2):26. https://doi.org/10.3390/econometrics4020026
Chicago/Turabian StyleSwamy, P.A.V.B., I-Lok Chang, Jatinder S. Mehta, William H. Greene, Stephen G. Hall, and George S. Tavlas. 2016. "Removing Specification Errors from the Usual Formulation of Binary Choice Models" Econometrics 4, no. 2: 26. https://doi.org/10.3390/econometrics4020026
APA StyleSwamy, P. A. V. B., Chang, I.-L., Mehta, J. S., Greene, W. H., Hall, S. G., & Tavlas, G. S. (2016). Removing Specification Errors from the Usual Formulation of Binary Choice Models. Econometrics, 4(2), 26. https://doi.org/10.3390/econometrics4020026








