Continuous and Jump Betas: Implications for Portfolio Diversification
Abstract
:1. Introduction
2. Data
3. Modeling Framework
3.1. The Estimators in Discrete Time
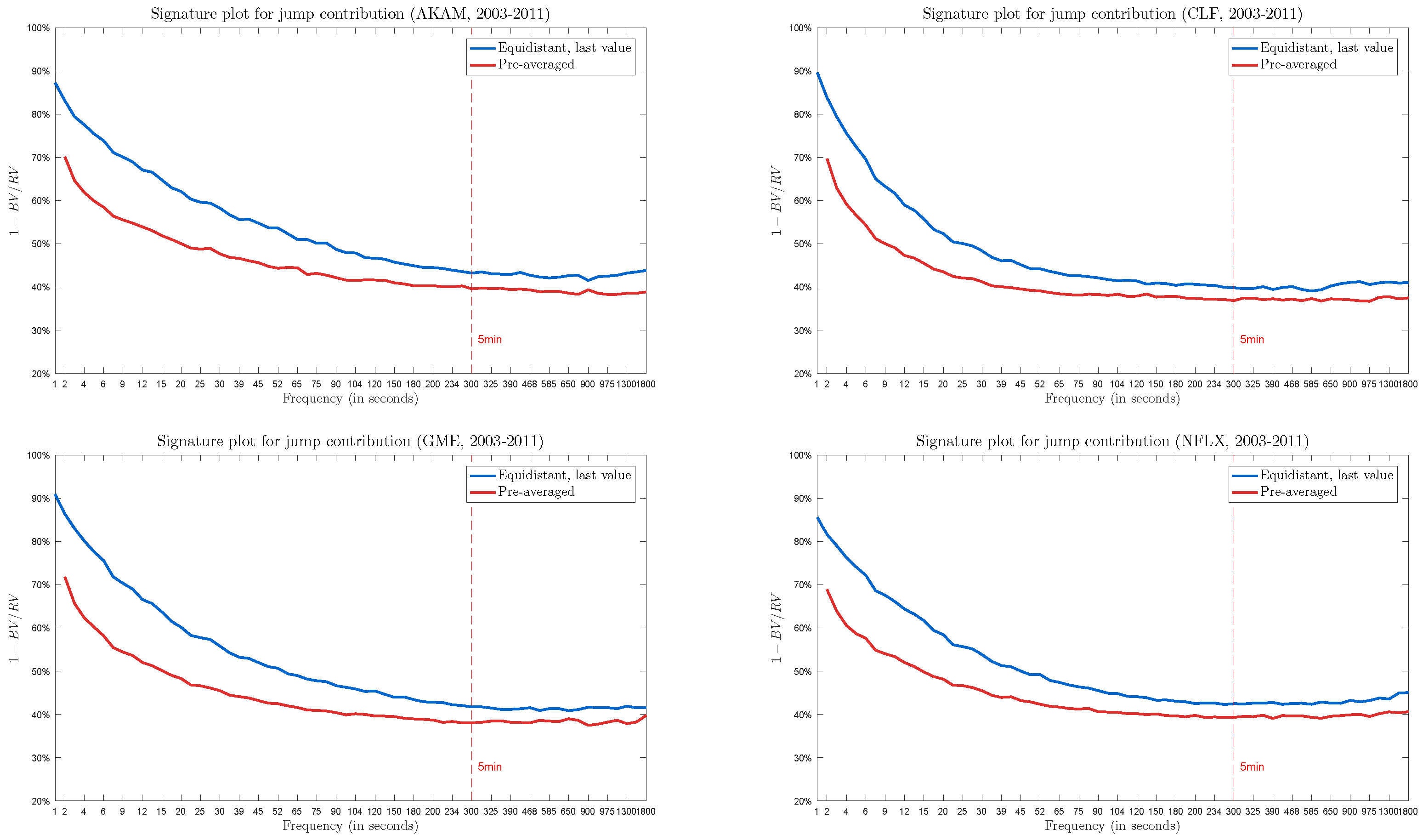
3.2. Testing for Jumps
3.3. Choices of Parameter Values
4. Estimated Betas
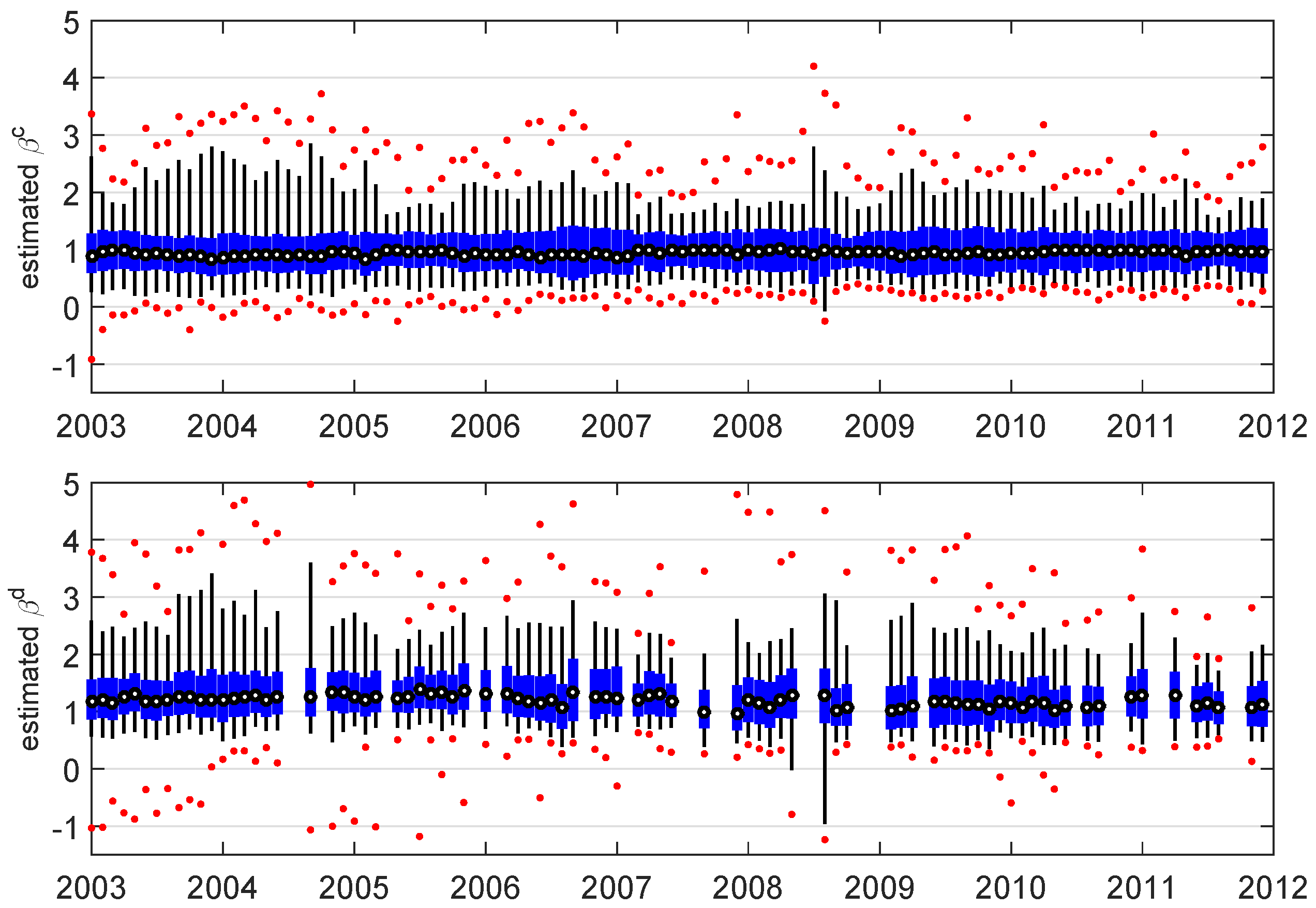
4.1. Summary Statistics of the Estimated Betas
4.2. Robustness Analysis
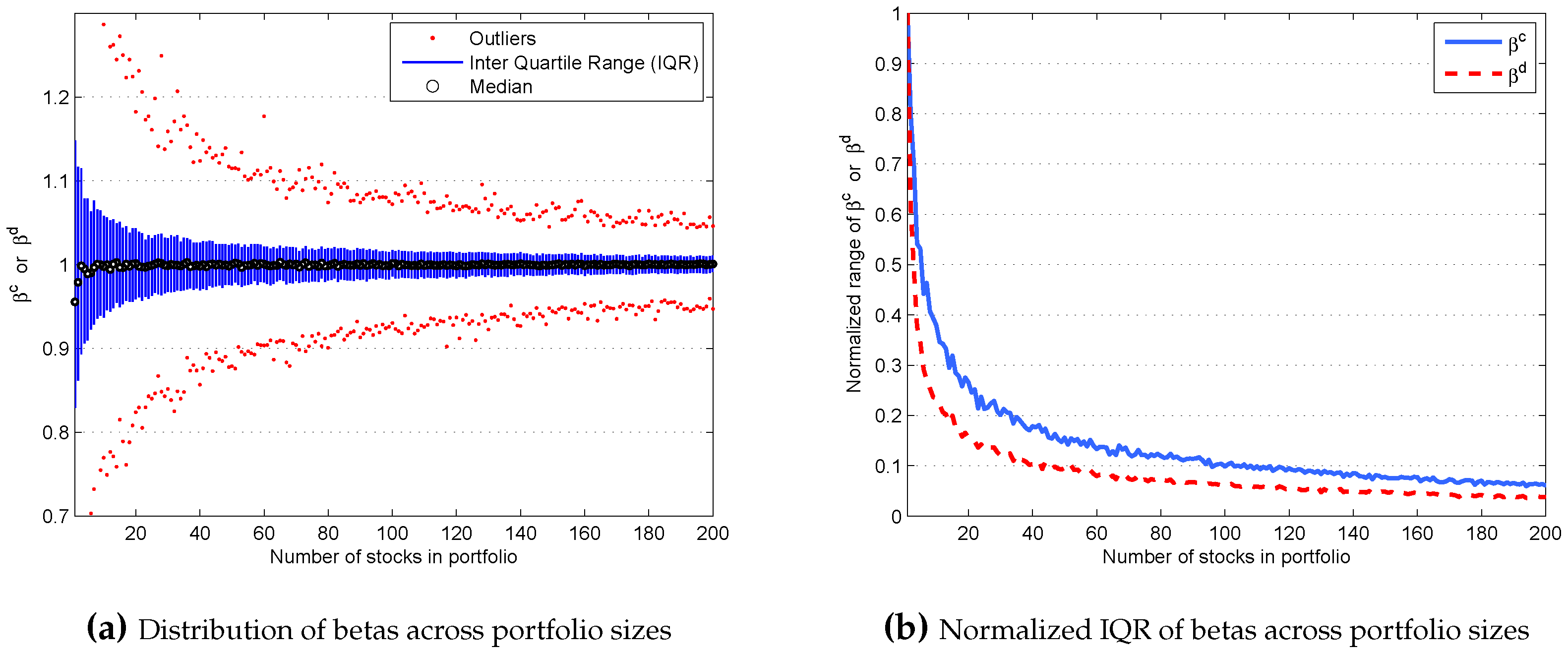
5. Portfolio Diversification with Betas
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
- 1.Existing studies use standard deviation [5,6,7], mean absolute deviation [8,9], semi-variance [10], terminal wealth standard deviation [11,12], residual variance from the CAPM [13,14], mean realised dispersion [15], and realised volatility [16]. For a comprehensive list of different risk measures used in portfolio diversification, see ([17] p. 44).
- 2.There are 900 stocks in the original dataset of stocks that have been represented on the S&P500 at any time during the sample period. We additionally delete stocks that have altered currency of trade, are over-the-counter or listed on alternative exchanges. See Dungey et al. [44] for further database details.
- 5.The small sample properties of the two discrete estimators have been investigated in Alexeev et al. [42]. The authors show that the estimation bias becomes a concern only when the difference between and exceeds unity. This is not the case in the current application.
- 6.Alternatively, if microstructure noise, nonsynchronicity and intraday volatility patterns are persistent, one could use the robust two-time scale estimator of Boudt and Zhang [54] to take these into account. The estimator is implemented using the modified Lee and Mykland [51] jump statistic proposed in Boudt et al. [55].
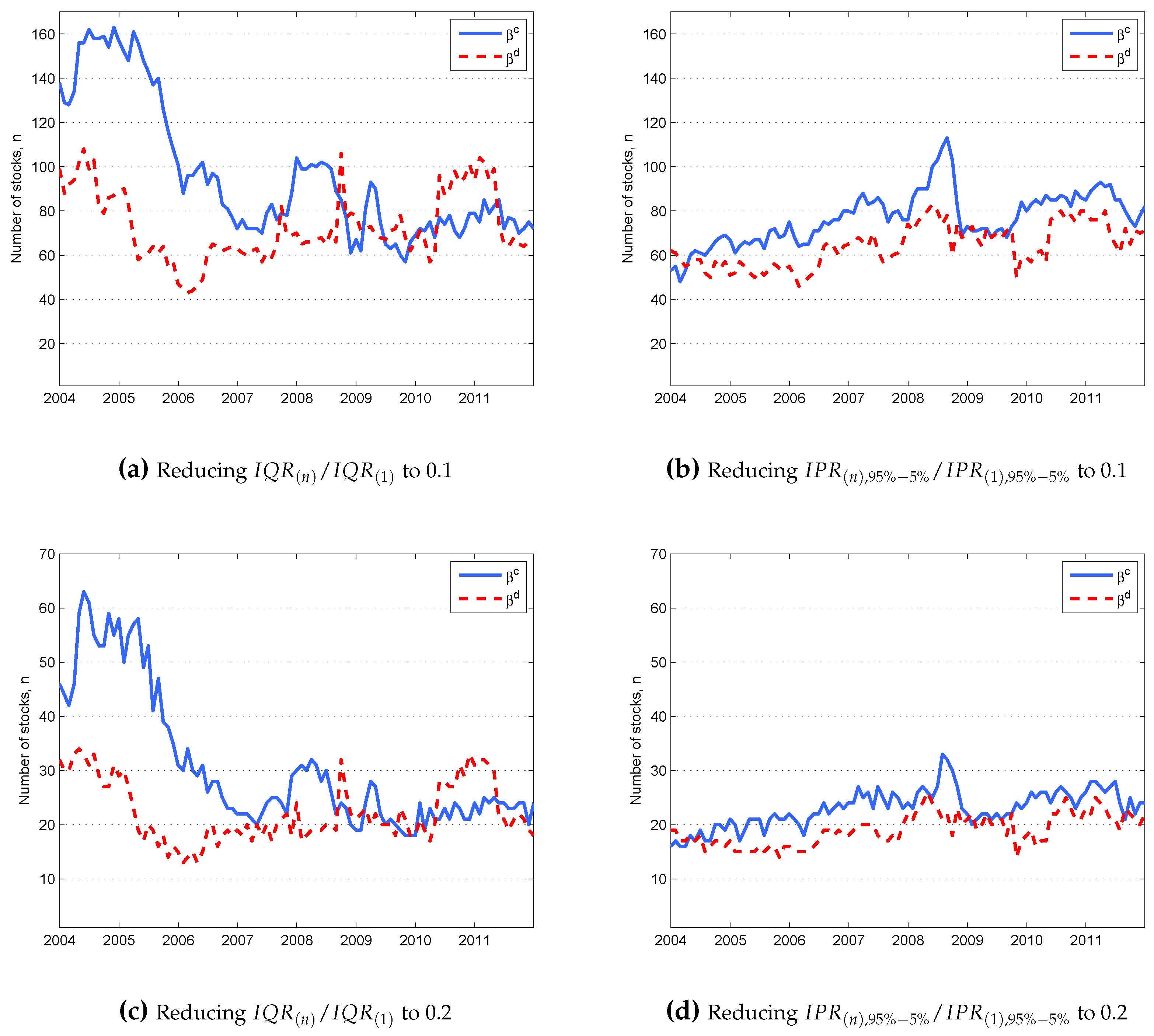
- 7.Given the difference in variability in betas with firm characteristics, future research could explore a stratified sampling scheme to further the diversification benefits.
- 8.A portfolio size resulting in a 10-fold reduction in the normalised IQR can be inferred from Figure 3b through the intersection of the blue and red curves with the horizontal line at 0.1. Figures similar to Figure 3b are constructed for each time period, and the corresponding portfolio sizes are determined from each of these figures and plotted in Figure 4a.
References
- H. Markowitz. “Portfolio Selection.” J. Finance 7 (1952): 77–91. [Google Scholar] [CrossRef]
- H. Markowitz. Portfolio Selection: Efficient Diversification of Investments. New York, NY, USA: John Wiley & Sons, 1959. [Google Scholar]
- P. Artzner, F. Delbaen, J.M. Eber, and D. Heath. “Thinking Coherently.” Risk 10 (1997): 68–71. [Google Scholar]
- P. Artzner, F. Delbaen, J.M. Eber, and D. Heath. “Coherent Measures of Risk.” Math. Finance 9 (1999): 203–228. [Google Scholar] [CrossRef]
- J.L. Evans, and S.H. Archer. “Diversification and the Reduction of Dispersion: An Empirical Analysis.” J. Finance 23 (1968): 761–767. [Google Scholar] [CrossRef]
- B.H. Solnik. “Why Not Diversify Internationally Rather than Domestically? ” Financ. Anal. J. 30 (1974): 48–52, 54. [Google Scholar] [CrossRef]
- M. Statman. “How Many Stocks Make a Diversified Portfolio? ” J. Financ. Quant. Anal. 22 (1987): 353–363. [Google Scholar] [CrossRef]
- L. Fisher, and J.H. Lorie. “Some Studies of Variability of Returns on Investments in Common Stocks.” J. Bus. 43 (1970): 99–134. [Google Scholar] [CrossRef]
- B.D. Fielitz. “Indirect versus Direct Diversification.” Financ. Manag. 3 (1974): 54–62. [Google Scholar] [CrossRef]
- E.S. O’Neal. “How Many Mutual Funds Constitute a Diversified Mutual Fund Portfolio? ” Financ. Anal. J. 53 (1997): 37–46. [Google Scholar] [CrossRef]
- S. Brands, and D.R. Gallagher. “Portfolio selection, diversification and fund-of-funds: A note.” Account. Finance 45 (2005): 185–197. [Google Scholar] [CrossRef]
- H. Benjelloun. “Evans and Archer—Forty years later.” Invest. Manag. Financ. Innov. 7 (2010): 98–104. [Google Scholar]
- W.H. Wagner, and S.C. Lau. “The Effect of Diversification on Risk.” Financ. Anal. J. 27 (1971): 48–53. [Google Scholar] [CrossRef]
- R.C. Klemkosky, and J.D. Martin. “The Effect of Market Risk on Portfolio Diversification.” J. Finance 30 (1975): 147–154. [Google Scholar] [CrossRef]
- L. Kryzanowski, and S. Singh. “Should Minimum Portfolio Sizes Be Prescribed for Achieving Sufficiently Well-Diversified Equity Portfolios? ” Front. Finance Econ. 7 (2010): 1–37. [Google Scholar]
- V. Alexeev, and M. Dungey. “Equity portfolio diversification with high frequency data.” Quant. Finance 15 (2014): 1205–1215. [Google Scholar] [CrossRef]
- V. Alexeev, and F. Tapon. “The number of stocks in your portfolio should be larger than you think: Diversification evidence from five developed markets.” J. Invest. Strateg. 4 (2014): 43–82. [Google Scholar] [CrossRef]
- G.Y. Tang. “How efficient is naive portfolio diversification? An educational note.” Omega 32 (2004): 155–160. [Google Scholar] [CrossRef]
- D. Copp, and S. Cleary. “Diversification with Canadian stocks: How much is enough? ” Can. Invest. Rev. 12 (1999): 21–25. [Google Scholar]
- T. Bloomfield, R. Leftwich, and J.B. Long Jr. “Portfolio strategies and performance.” J. Financ. Econ. 5 (1977): 201–218. [Google Scholar] [CrossRef]
- P. Silvapulle, and C. Granger. “Large returns, conditional correlation and portfolio diversification: A value-at-risk approach.” Quant. Finance 1 (2001): 542–551. [Google Scholar] [CrossRef]
- T. Bollerslev, V. Todorov, and S.Z. Li. “Jump Tails, Extreme Dependencies, and the Distribution of Stock Returns.” J. Econom. 172 (2013): 307–324. [Google Scholar] [CrossRef]
- K. Pukthuanthong, and R. Roll. “Internationally Correlated Jumps.” Rev. Asset Pricing Stud. 5 (2014): 92–111. [Google Scholar] [CrossRef]
- V. Todorov, and T. Bollerslev. “Jumps and Betas: A New Framework for Disentangling and Estimating Systematic Risks.” J. Econom. 157 (2010): 220–235. [Google Scholar] [CrossRef]
- M.E. Blume. “On the Assessment of Risk.” J. Finance 26 (1971): 1–10. [Google Scholar] [CrossRef]
- T.G. Andersen, T. Bollerslev, and F.X. Diebold. “Roughing It Up: Including Jump Components in the Measurement, Modeling, and Forecasting of Return Volatility.” Rev. Econ. Stat. 89 (2007): 701–720. [Google Scholar] [CrossRef]
- M. Dungey, M. McKenzie, and V. Smith. “Empirical Evidence on Jumps in the Term Structure of the US Treasury Market.” J. Empir. Finance 16 (2009): 430–445. [Google Scholar] [CrossRef]
- J. Jacod, and V. Todorov. “Testing for Common Arrivals of Jumps for Discretely Observed Multidimensional Processes.” Ann. Stat. 37 (2009): 1792–1838. [Google Scholar] [CrossRef]
- J. Lahaye, S. Laurent, and C.J. Neely. “Jumps, Cojumps and Macro Announcements.” J. Appl. Econom. 26 (2011): 893–921. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, and J. Jacod. “Analyzing the Spectrum of Asset Returns: Jump and Volatility Components in High Frequency Data.” J. Econ. Lit. 50 (2012): 1007–1050. [Google Scholar] [CrossRef]
- J. Lahaye, S. Laurent, and C.J. Neely. “Bond Yields and the Federal Reserve.” J. Political Econ. 113 (2005): 311–344. [Google Scholar]
- F. Audrino, and Y. Hu. “Volatility Forecasting: Downside Risk, Jumps and Leverage Effect.” Econometrics 4 (2016): 8. [Google Scholar] [CrossRef]
- B. Blair, S.H. Poon, and S. Taylor. “Forecasting S&P500 Volatility: The incremental information content of implied volatilities and high-frequency index returns.” J. Econom. 105 (2001): 5–26. [Google Scholar]
- T.G. Andersen, T. Bollerslev, F.X. Diebold, and P. Labys. “Modelling and Forecasting Realized Volatility.” Econometrica 71 (2003): 579–625. [Google Scholar] [CrossRef]
- D.S. Bates. “The market for crash risk.” J. Econ. Dyn. Control 32 (2008): 2291–2321. [Google Scholar] [CrossRef]
- Y.S. Lai, and H.J. Sheu. “The Incremental Value of a Futures Hedge Using Realized Volatility.” J. Futures Mark. 30 (2010): 874–896. [Google Scholar] [CrossRef]
- R.J. Barro. “Rare Disasters and Asset Markets in the Twentieth Century.” Q. J. Econ. 121 (2006): 823–866. [Google Scholar] [CrossRef]
- A.J. Patton, and M. Verardo. “Does Beta Move with News? Firm-specific Information Flows and Learning About Profitability.” Rev. Financ. Stud. 25 (2012): 2789–2839. [Google Scholar] [CrossRef]
- P. Santa-Clara, and S. Yan. “Crashes, Volatility, and the Equity Premium: Lessons from S&P500 Options.” Rev. Econ. Stat. 92 (2010): 435–451. [Google Scholar]
- M. Cremers, M. Halling, and D. Weinbaum. “Aggregate Jump and Volatility Risk in the Cross-Section of Stock Returns.” J. Finance 70 (2015): 577–614. [Google Scholar] [CrossRef]
- H. Guo, K. Wang, and H. Zhou. “Good Jumps, Bad Jumps, and Conditional Equity Premium.” Working Paper. 2015. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2516074 (accessed on 11 January 2016).
- V. Alexeev, M. Dungey, and W. Yao. “Time-Varying Continuous and Jump Betas: The Role of Firm Characteristics and Periods of Stress.” Technical Report. 2016. Available online: http://valexeev.yolasite.com/resources/papers/BetaPaperNEW.pdf (accessed on 10 January 2016).
- T. Bollerslev, S.Z. Li, and V. Todorov. “Roughing up Beta: Continous vs. Discontinous Beta, and the Cross-Section of Expected Stock Returns.” J. Financ. Econ. 120 (2016): 464–490. [Google Scholar] [CrossRef]
- M. Dungey, M. Luciani, and D. Veredas. “Ranking Systemically Important Financial Institutions.” Working Papers ECARES 2013/130530; ULB—Universite Libre de Bruxelles. 2012. Available online: http://econpapers.repec.org/paper/tinwpaper/20120115.htm (accessed on 7 May 2015).
- W.F. Sharpe. “Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk.” J. Finance 19 (1964): 425–442. [Google Scholar] [CrossRef]
- J. Lintner. “Security Prices, Risk, and Maximal Gains From Diversification.” J. Finance 20 (1965): 587–615. [Google Scholar] [CrossRef]
- J. Lintner. “The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets.” Rev. Econ. Stat. 47 (1965): 13–37. [Google Scholar] [CrossRef]
- C. Mancini. “Disentangling the Jumps of the Diffusion in a Geometric Jumping Brownian Motion.” Giornale dell’Istituto Italiano degi Attuari 64 (2001): 19–47. [Google Scholar]
- X. Huang, and G. Tauchen. “The Relative Contribution of Jumps to Total Price Variance.” J. Financ. Econom. 3 (2005): 456–499. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, and N. Shephard. “Econometrics of Testing for Jumps in Financial Economics Using Bipower Variation.” J. Financ. Econom. 4 (2006): 1–30. [Google Scholar] [CrossRef]
- S.S. Lee, and P.A. Mykland. “Jumps in Financial Markets: A New Nonparametric Test and Jump Dynamics.” Rev. Financ. Stud. 21 (2008): 2535–2563. [Google Scholar] [CrossRef]
- Y. Aït-Sahalia, and J. Jacod. “Testing for jumps in a discretely observed process.” Ann. Stat. 37 (2009): 184–222. [Google Scholar] [CrossRef]
- A.M. Dumitru, and G. Urga. “Identifying Jumps in Financial Assets: A Comparison Between Nonparametric Jump Tests.” J. Bus. Econ. Stat. 30 (2012): 242–255. [Google Scholar] [CrossRef]
- K. Boudt, and J. Zhang. “Jump robust two time scale covariance estimation and realized volatility budgets.” Quant. Finance 15 (2015): 1041–1054. [Google Scholar] [CrossRef]
- K. Boudt, C. Croux, and S. Laurent. “Robust estimation of intraweek periodicity in volatility and jump detection.” J. Empir. Finance 18 (2011): 353–367. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, and N. Shephard. “Power and Bipower Variation with Stochastic Volatility and Jumps.” J. Financ. Econom. 2 (2004): 1–37. [Google Scholar] [CrossRef]
- K. Christensen, R.C. Oomen, and M. Podolskij. “Fact or friction: Jumps at ultra high frequency.” J. Financ. Econ. 114 (2014): 576–599. [Google Scholar] [CrossRef]
- A. Black, J. Chen, O. Gustap, and J.M. Williams. “The Importance of Jumps in Modelling Volatility during the 2008 Financial Crisis.” Technical Report. 2012. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2118486 (accessed on 7 May 2015).
- J. Jacod, Y. Li, P.A. Mykland, M. Podolskij, and M. Vetter. “Microstructure noise in the continuous case: The pre-averaging approach.” Stoch. Process. Their Appl. 119 (2009): 2249–2276. [Google Scholar] [CrossRef]
- A. Ang, J. Chen, and Y. Xing. “Downside Risk.” Rev. Financ. Stud. 19 (2006): 1191–1239. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexeev, V.; Dungey, M.; Yao, W. Continuous and Jump Betas: Implications for Portfolio Diversification. Econometrics 2016, 4, 27. https://doi.org/10.3390/econometrics4020027
Alexeev V, Dungey M, Yao W. Continuous and Jump Betas: Implications for Portfolio Diversification. Econometrics. 2016; 4(2):27. https://doi.org/10.3390/econometrics4020027
Chicago/Turabian StyleAlexeev, Vitali, Mardi Dungey, and Wenying Yao. 2016. "Continuous and Jump Betas: Implications for Portfolio Diversification" Econometrics 4, no. 2: 27. https://doi.org/10.3390/econometrics4020027
APA StyleAlexeev, V., Dungey, M., & Yao, W. (2016). Continuous and Jump Betas: Implications for Portfolio Diversification. Econometrics, 4(2), 27. https://doi.org/10.3390/econometrics4020027




