Social Networks and Choice Set Formation in Discrete Choice Models
Abstract
:1. Introduction
2. Unordered Multiple Choice and Choice Sets
3. Social Networks and Choice Set Formation
3.1. Modeling Social Networks
3.2. Social Network Effects on Alternative Availability
3.3. Social Network Effects on Availability and Utility
4. Estimation of Welfare Impacts
5. Monte Carlo Experiments
5.1. Evaluating Parameter Estimates
5.2. Evaluating Welfare Estimates
6. Results
6.1. SNE Experimets
6.1.1. SNE Parameter Estimates
6.1.2. SNE Market Shares
6.1.3. SNE Welfare Estimates
6.2. DNE Experimets
6.2.1. DNE Parameter Estimates
6.2.2. DNE Market Shares
6.2.3. DNE Welfare Estimates
7. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- J.R. Hauser, O. Toubia, T. Evgeniou, R. Befurt, and D. Dzyabura. “Disjunctions of conjunctions, cognitive simplicity, and consideration sets.” J. Mark. Res. 47 (2010): 485–496. [Google Scholar] [CrossRef]
- J.R. Hauser. “Consideration-set heuristics.” J. Bus. Res. 67 (2014): 1688–1699. [Google Scholar] [CrossRef]
- E. Van Nierop, B. Bronnenberg, R. Paap, M. Wedel, and P.H. Franses. “Retrieving unobserved consideration sets from household panel data.” J. Mark. Res. 47 (2010): 63–74. [Google Scholar] [CrossRef]
- K. Eliaz, and R. Spiegler. “Consideration sets and competitive marketing.” Rev. Econ. Stud. 78 (2011): 235–262. [Google Scholar] [CrossRef] [Green Version]
- J. Swait, and T. Erdem. “Brand effects on choice and choice set formation under uncertainty.” Mark. Sci. 26 (2007): 679–697. [Google Scholar] [CrossRef]
- Forbes. “10 New Findings About The Millennial Consumer.” 2015. Available online: http://www.forbes.com/sites/danschawbel/2015/01/20/10-new-findings-about-the-millennial-consumer/#3528b01828a8 (accessed on 24 June 2016).
- AutoTrader. “The Next Generation Car Buyer: Millennials.” 2013. Available online: http://oemsolutions.agameautotrader.com/wp-content/uploads/2013/05/Millennials-Next-Gen-Car-Buyer.pdf (accessed on 24 June 2016).
- Automotive News. “BMW Tailors its Pitch to the Young and Wealthy.” 2016. Available online: http://www.autonews.com/article/20160113/OEM09/160119822/bmw-tailors-its-pitch-to-the-young-and-wealthy (accessed on 24 June 2016).
- W. Zavoina, and R.D. McKelvey. “A statistical model for the analysis of ordinal level dependent variables.” J. Math. Sociol. 4 (1975): 103–120. [Google Scholar]
- D. McFadden. “Conditional Logit Analysis of Qualitative Choice Behavior.” In Frontiers in Econometrics. Edited by P. Zarembka. London, UK: New York, NY, USA: Academic Press, 1974, pp. 105–142. [Google Scholar]
- J. Swait, and M. Ben-Akiva. “Incorporating random constraints in discrete models of choice set generation.” Transp. Res. B Methodol. 22 (1987): 91–102. [Google Scholar] [CrossRef]
- L. Li, W.L. Adamowicz, and J. Swait. “The effect of choice set misspecification on welfare measures in random utility models.” Resour. Energy Econ. 42 (2015): 71–92. [Google Scholar] [CrossRef]
- M. Bierlaire, R. Hurtubia, and G. Flötteröd. “Analysis of implicit choice set generation using a constrained multinomial logit model.” Transp. Res. Rec. 2175 (2010): 92–97. [Google Scholar] [CrossRef]
- J. Andreoni. “Impure altruism and donations to public goods: A theory of warm-glow giving.” Econ. J. 100 (1990): 464–477. [Google Scholar] [CrossRef]
- M. Rabin. “Incorporating fairness into game theory and economics.” Am. Econ. Rev. 5 (1993): 1281–1302. [Google Scholar]
- S.D. Levitt, and J.A. List. “What do laboratory experiments measuring social preferences reveal about the real world? ” J. Econ. Perspect. 21 (2007): 153–174. [Google Scholar] [CrossRef]
- W. Neilson, and B. Wichmann. “Social networks and non-market valuations.” J. Environ. Econ. Manag. 67 (2014): 155–170. [Google Scholar] [CrossRef]
- E. Duflo, and E. Saez. “Participation and investment decisions in a retirement plan: The influence of colleagues choices.” J. Public Econ. 85 (2002): 121–148. [Google Scholar] [CrossRef]
- S.M. Chowdhury, and J.Y. Jeon. “Impure altruism or inequality aversion?: An experimental investigation based on income effects.” J. Public Econ. 118 (2014): 143–150. [Google Scholar] [CrossRef]
- W.A. Brock, and S.N. Durlauf. “Discrete choice with social interactions.” Rev. Econ. Stud. 68 (2001): 235–260. [Google Scholar] [CrossRef]
- L.-F. Lee, J. Li, and X. Lin. “Binary choice models with social network under heterogeneous rational expectations.” Rev. Econ. Stat. 96 (2014): 402–417. [Google Scholar] [CrossRef]
- A.R. Soetevent, and P. Kooreman. “A discrete-choice model with social interactions: With an application to high school teen behavior.” J. Appl. Econ. 22 (2007): 599–624. [Google Scholar] [CrossRef]
- T.J. Richards, S.F. Hamilton, and W.J. Allender. “Social networks and new product choice.” Am. J. Agric. Econ. 96 (2014): 489–516. [Google Scholar] [CrossRef]
- B. Wichmann. “Social Structure, Non-Market Valuation, and Bargaining.” Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2012. [Google Scholar]
- C.F. Manski. “The structure of random utility models.” Theory Decis. 8 (1977): 229–254. [Google Scholar] [CrossRef]
- J. Swait. “Probabilistic Choice Set Formation in Transportation Demand Models.” Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1984. [Google Scholar]
- J. Swait, and M. Ben-Akiva. “Empirical test of a constrained choice discrete model: Mode choice in Sao Paulo, Brazil.” Transp. Res. B Methodol. 22 (1987): 103–115. [Google Scholar] [CrossRef]
- M. Ben-Akiva, and S.R. Lerman. Discrete Choice Analysis: Theory and Application to Travel Demand, 4th ed. Cambridge, MA, USA: The MIT Press, 1991. [Google Scholar]
- F. Martínez, F. Aguila, and R. Hurtubia. “The constrained multinomial logit: A semi-compensatory choice model.” Transp. Res. B Methodol. 43 (2009): 365–377. [Google Scholar] [CrossRef]
- M. Sovinsky Goeree. “Limited information and advertising in the us personal computer industry.” Econometrica 76 (2008): 1017–1074. [Google Scholar]
- M. Draganska, and D. Klapper. “Choice set heterogeneity and the role of advertising: An analysis with micro and macro data.” J. Mark. Res. 48 (2011): 653–669. [Google Scholar] [CrossRef]
- J.B. Chang, J.L. Lusk, and F.B. Norwood. “How closely do hypothetical surveys and laboratory experiments predict field behavior? ” Am. J. Agric. Econ. 91 (2009): 518–534. [Google Scholar] [CrossRef]
- T.C. Haab, and R.L. Hicks. “Accounting for choice set endogeneity in random utility models of recreation demand.” J. Environ. Econ. Manag. 34 (1997): 127–147. [Google Scholar] [CrossRef]
- K.N. Habib, C. Morency, M. Trépanier, and S. Salem. “Application of an independent availability logit model (IAL) for route choice modelling: Considering bridge choice as a key determinant of selected routes for commuting in montreal.” J. Choice Model. 9 (2013): 14–26. [Google Scholar] [CrossRef]
- R.L. Andrews, and T. Srinivasan. “Studying consideration effects in empirical choice models using scanner panel data.” J. Mark. Res. 32 (1995): 30–41. [Google Scholar] [CrossRef]
- M. Jackson, and A. Watts. “The evolution of social and economic networks.” J. Econ. Theory 106 (2002): 265–295. [Google Scholar] [CrossRef]
- M. Jackson, and B. Rogers. “Meeting strangers and friends of friends: How random are social networks? ” Am. Econ. Rev. 97 (2007): 890–915. [Google Scholar] [CrossRef]
- M.H. DeGroot. “Reaching a consensus.” J. Am. Stat. Assoc. 69 (1974): 118–121. [Google Scholar] [CrossRef]
- P.M. DeMarzo, D. Vayanos, and J. Zwiebel. “Persuasion bias, social influence, and unidimensional opinions.” Q. J. Econ. 118 (2003): 909–968. [Google Scholar] [CrossRef]
- P.R. Milgrom, and R.J. Weber. “A theory of auctions and competitive bidding.” Econometrica 50 (1982): 1089–1122. [Google Scholar] [CrossRef]
- P. Eso, and L. White. “Precautionary bidding in auctions.” Econometrica 72 (2004): 77–92. [Google Scholar] [CrossRef]
- C.F. Manski. “Identification of endogenous social effects: The reflection problem.” Rev. Econ. Stud. 60 (1993): 531–542. [Google Scholar] [CrossRef]
- Y. Bramoullé, H. Djebbari, and B. Fortin. “Identification of peer effects through social networks.” J. Econom. 150 (2009): 41–55. [Google Scholar] [CrossRef]
- X. Lin. “Identifying peer effects in student academic achievement by spatial autoregressive models with group unobservables.” J. Labor Econ. 28 (2010): 825–860. [Google Scholar] [CrossRef]
- E. Patacchini, and G. Venanzoni. “Peer effects in the demand for housing quality.” J. Urban Econ. 83 (2014): 6–17. [Google Scholar] [CrossRef]
- J.A. Smith, M. McPherson, and L. Smith-Lovin. “Social distance in the united states sex, race, religion, age, and education homophily among confidants, 1985 to 2004.” Am. Sociol. Rev. 79 (2014): 432–456. [Google Scholar] [CrossRef]
- L. Leszczensky, and S. Pink. “Ethnic segregation of friendship networks in school: Testing a rational-choice argument of differences in ethnic homophily between classroom-and grade-level networks.” Soc. Netw. 42 (2015): 18–26. [Google Scholar] [CrossRef]
- J. Benhabib, A. Bisin, and M.O. Jackson. Handbook of Social Economics, Volume 1B. New York, USA: Elsevier, 2010, Volume 1. [Google Scholar]
- A. Banerjee, A.G. Chandrasekhar, E. Duflo, and M.O. Jackson. “The diffusion of microfinance.” Science 341 (2013): 1236498. [Google Scholar] [CrossRef] [PubMed]
- N. Magnan, D.J. Spielman, T.J. Lybbert, and K. Gulati. “Leveling with friends: Social networks and Indian farmers’ demand for a technology with heterogeneous benefits.” J. Dev. Econ. 116 (2015): 223–251. [Google Scholar] [CrossRef]
- D. Karlan, M. Mobius, T. Rosenblat, and A. Szeidl. “Trust and social collateral.” Q. J. Econ. 124 (2009): 1307–1361. [Google Scholar] [CrossRef]
- R. McMillan, and B. Parlee. “Dene hunting organization in fort good hope, northwest territories: “ Ways we help each other and share what we can”.” Arctic 66 (2013): 435–447. [Google Scholar] [CrossRef]
- M. Fafchamps, and F. Gubert. “The formation of risk sharing networks.” J. Dev. Econ. 83 (2007): 326–350. [Google Scholar] [CrossRef]
- A. Ambrus, M. Mobius, and A. Szeidl. “Consumption risk-sharing in social networks.” Am. Econ. Rev. 104 (2014): 149–182. [Google Scholar] [CrossRef]
- C.F. Manski. “Measuring expectations.” Econometrica 72 (2004): 1329–1376. [Google Scholar] [CrossRef]
- W. Van der Klaauw. “On the use of expectations data in estimating structural dynamic choice models.” J. Labor Econ. 30 (2012): 521–554. [Google Scholar] [CrossRef]
- X. Qu, and L.-F. Lee. “Estimating a spatial autoregressive model with an endogenous spatial weight matrix.” J. Econom. 184 (2015): 209–232. [Google Scholar] [CrossRef]
- 1Ben-Akiva and Lerman [28] offer a discussion about the properties of the Gumbel distribution.
- 2The primitive set can be thought of as the MNL’s global choice set.
- 3The literature offers several approaches to incorporate choice sets in discrete choice models. For example, the Constrained Multinomial Logit introduces a penalty to the utility of alternatives outside the consumer’s consideration set (Martinez et al. [29]). Other papers examine the role of choice set formation with a focus on advertising. Sovinsky Goeree [30] presents a discrete-choice model of limited consumer information; where advertising influences the set of products from which consumers choose to purchase. Draganska and Klapper [31] examine the dual role of advertising, consumer preferences and choice set formation, and propose an approach to disentangle the two effects using individual-level data on brand awareness (i.e., consideration sets).
- 4The graph-theoretic approach proves to be useful when modeling networks of multiple relationships. Jackson and Watts [36] and Jackson and Rogers [37] are examples of papers that use the graph-theoretic approach. Neilson and Wichmann [17] use sociometric approach to develop a valuation model in which social networks influence the utility that individuals obtain from public goods. The sociometric approach is also used by DeGroot [38] and DeMarzo et al. [39] to model social influence in unidimensional opinion models.
- 5Theoretically, this standardized normalization can be easily relaxed by allowing connections to have different weights. The standardized normalization captures the extensive margin of social effects. In practice, it requires pairwise data about the existence of social links. A more sophisticated normalization may capture the intensive margin of social effects; however, it would require data not only on the existence of social links, but also on the strengths of social contacts.
- 6To see why, recall that the diagonal of the matrix W is equal to zero.
- 7We implicitly assume that there is one social network influencing both choice set formation and utility. This is just a simplification assumption and it is straightforward to extend this model to one in which the network that influences choice set formation in the first stage is different from the network that influences choice in the second stage.
- 8The subscripts n (indexing the decision maker) and j (indexing the alternative) are suppressed to simplify notation.
- 9In fact, Equation (14) corresponds to the expression for the MNL model.
- 10Both prices and quality differ not only between alternatives but also between individuals capturing decision-maker heterogeneity in quality perceptions and prices (due to, for example, accessibility).
- 11Network density is the share of the potential links in a network that are actual links.
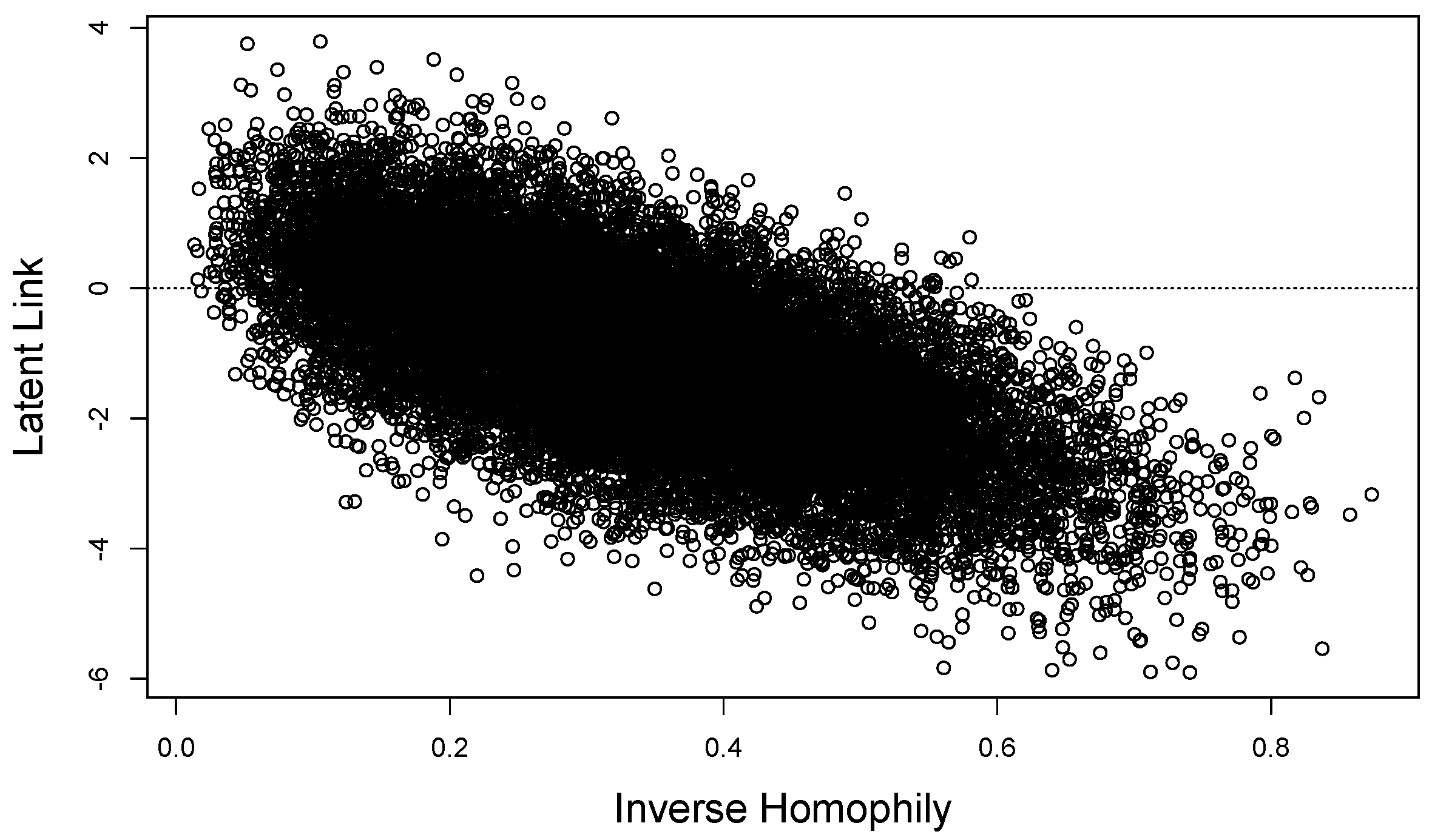
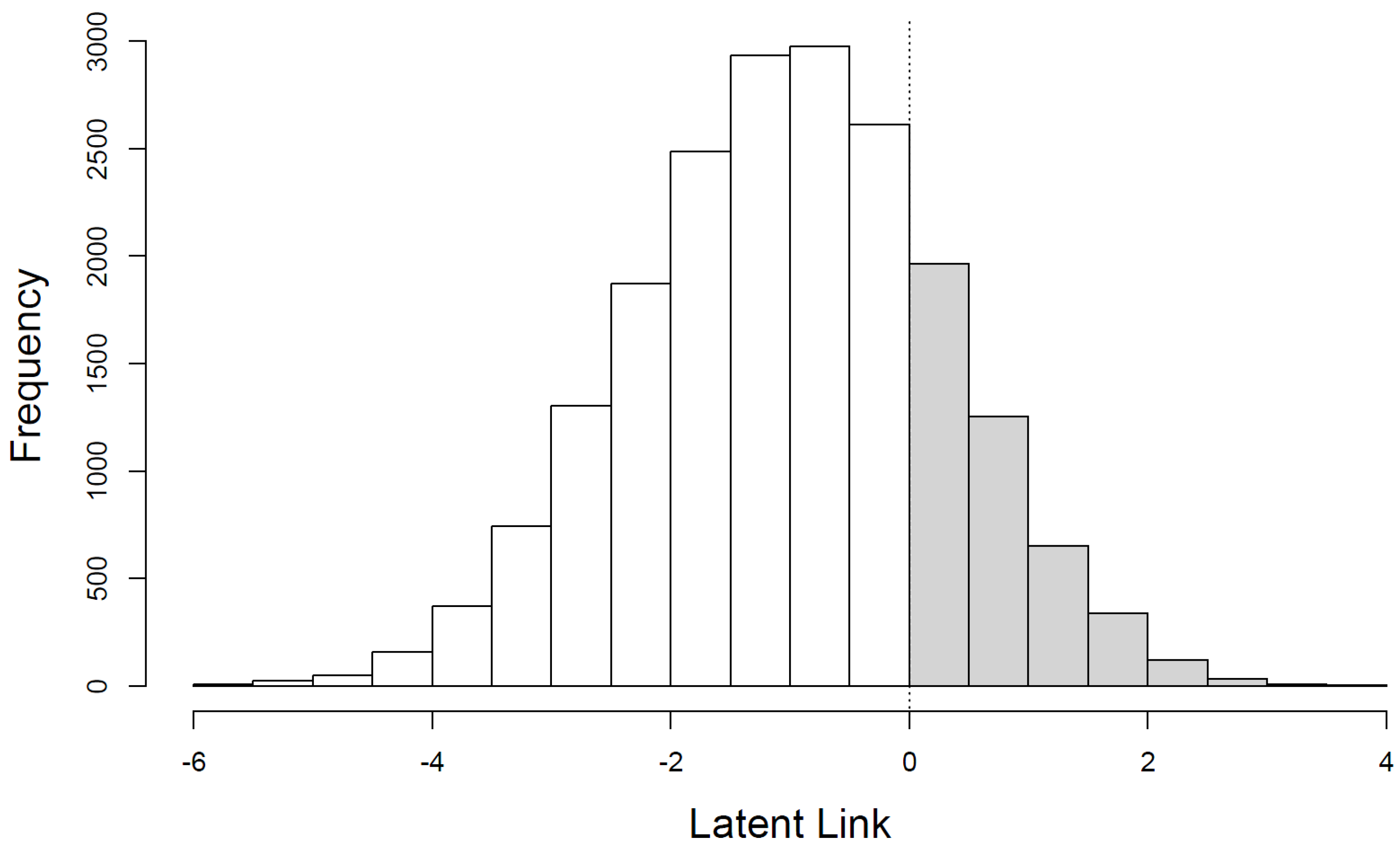
- 12The first stage alternative rule-out process determines the distribution of choice sets. Indexing choice sets by , the universe of choice sets is , , , , , , , and the empty set. Therefore, there is a possibility that none of the three alternatives satisfies the availability condition and choices are therefore not observed. In order to keep the sample size constant throughout the simulation, we redraw the error for individual n if all alternatives are ruled out. The parametrization of the experiment was such that the re-drawing was done only in approximately 3%–5% of the replications. This procedure enables us to compare estimates from different models with the assurance that (possibly observed) biases or inefficiencies are not driven by sample size differences.
- 13Note that the chosen alternative after the project may be the same alternative chosen before the policy, therefore may (or may not) be different from , and the same is true for the error term.
- 14The one exception is the estimate of in the experiment with .
- 15Refer to the Supplementary Materials for a discussion about the distribution of choice sets.
- 16“Available estimates” refers to estimates obtained using pre-project (real, not hypothetical) data.
- 17Recall that the IAL ignores network effects and does not estimate the and parameters.
- 18Experiments with are experiments where (, ), i.e., 20% of the combined quality effect () is assigned to network quality (see Equation (11)). Similarly, corresponds to (, ).
- 19Note that the top two panels of Table 7 present estimates of experiments in which the DGP has () and (), and the bottom two panels presents results for the DGPs with () and ().
| Number of Decision Makers (N) | 2000 |
| Number of Global Alternatives (Alternatives in B) | 3 |
| Random Terms | |
| Parameters of the Logistic Distribution (mean, scale) | 0, 10 |
| Parameters of the Gumbel Distribution (location, scale) | 0, 1 |
| Attributes of Each Alternative | |
| SNE model | price, own quality |
| DNE model | price, own quality, and network quality |
| Value of True Parameters of the SNE Experiments | |
| Fixed CSF threshold parameter () | 0.5 |
| Varying degree of social interaction in CSF | |
| Fixed utility parameters (ASC1, ASC2, , , ) | 2, 1, −3, 5, 0 |
| Value of True Parameters of the DNE Experiments | |
| Fixed CSF threshold parameter () | 0.5 |
| Varying degree of social interaction in CSF | |
| Fixed utility parameters (ASC1, ASC2, , β) | 2, 1, −3, 5 |
| Varying degree of social interaction in choice | c |
| Number of Replications (datasets within an experiment) | 400 |
| SNE: | |||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | |
| ASC1 {2} | 2.0068 (0.0512) | 2.0046 (0.0453) | 2.0057 (0.0438) | 1.9988 (0.0470) | 1.9892 (0.0397) |
| ASC2 {1} | 0.9986 (0.0580) | 0.9956 (0.0547) | 1.0029 (0.0495) | 1.0061 (0.0432) | 1.0012 (0.0387) |
| Price {−3} | −3.0217 (0.0573) | −3.0112 (0.0553) | −2.9991 (0.0523) | −3.0182 (0.0483) | −3.0135 (0.0427) |
| Quality {5} | 5.0148 (0.0583) | 5.0115 (0.0630) | 4.9913 (0.0579) | 5.0081 (0.0478) | 5.0521 (0.0431) |
| {0.5} | 0.5003 (0.0380) | 0.4999 (0.0410) | 0.5000 (0.0390) | 0.5001 (0.0365) | 0.5011 (0.0370) |
| {varied} | 0.1988 (0.0206) | 0.4023 (0.0363) | 0.4992 (0.0413) | 0.5994 (0.0401) | 0.8052 (0.0404) |
| μ {10} | 10.0404 (0.0425) | 10.0680 (0.0426) | 10.0199 (0.0426) | 10.0279 (0.0390) | 10.0270 (0.0416) |
| IAL: | |||||
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | |
| ASC1 {2} | 2.0001 (0.0599) | 1.9671 (0.0653) | 1.9051 (0.0817) | 1.8170 (0.1146) | 1.6460 (0.2157) |
| ASC2 {1} | 0.9917 (0.0751) | 0.9590 (0.0908) | 0.9310 (0.1118) | 0.8798 (0.1436) | 0.7718 (0.2671) |
| Price {−3} | −3.0289 (0.0704) | −2.9707 (0.0867) | −2.8956 (0.0974) | −2.7878 (0.1153) | −2.6186 (0.1992) |
| Quality {5} | 4.9830 (0.0710) | 4.9823 (0.0856) | 4.9689 (0.0857) | 4.9383 (0.0980) | 4.8769 (0.1361) |
| {0.5} | 0.5025 (0.0430) | 0.5000 (0.0522) | 0.4953 (0.0569) | 0.4847 (0.0643) | 0.4525 (0.1517) |
| μ {10} | 8.9504 (0.1057) | 7.7838 (0.2216) | 7.2074 (0.2793) | 6.6611 (0.3339) | 5.3400 (0.4660) |
| ( = 0.2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Consumer Choice | Before | After | Change | ||||||
| True | SNE | IAL | True | SNE | IAL | True | SNE | IAL | |
| {1} | 0.407 | 0.407 (0.015) | 0.407 (0.014) | 0.245 | 0.245 (0.032) | 0.251 (0.036) | −0.163 | −0.162 (0.022) | −0.157 (0.044) |
| {2} | 0.327 | 0.326 (0.013) | 0.327 (0.015) | 0.644 | 0.643 (0.014) | 0.630 (0.023) | 0.317 | 0.317 (0.017) | 0.304 (0.044) |
| {3} | 0.266 | 0.266 (0.020) | 0.266 (0.018) | 0.111 | 0.112 (0.031) | 0.119 (0.075) | −0.155 | −0.155 (0.019) | −0.147 (0.050) |
| ( = 0.8) | |||||||||
| Consumer Choice | Before | After | Change | ||||||
| True | SNE | IAL | True | SNE | IAL | True | SNE | IAL | |
| {1} | 0.402 | 0.401 (0.020) | 0.403 (0.020) | 0.224 | 0.221 (0.045) | 0.248 (0.114) | −0.179 | −0.179 (0.018) | −0.154 (0.137) |
| {2} | 0.325 | 0.325 (0.012) | 0.324 (0.022) | 0.678 | 0.681 (0.016) | 0.615 (0.093) | 0.353 | 0.355 (0.024) | 0.291 (0.177) |
| {3} | 0.273 | 0.274 (0.024) | 0.273 (0.026) | 0.098 | 0.098 (0.021) | 0.136 (0.393) | −0.175 | −0.176 (0.038) | −0.137 (0.218) |
| Models | |||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | |
| True | 0.3784 | 0.3895 | 0.3956 | 0.4025 | 0.4181 |
| SNE | 0.3728 (0.0814) | 0.3814 (0.0843) | 0.3865 (0.0842) | 0.3906 (0.0747) | 0.4076 (0.0737) |
| IAL | 0.3649 (0.0984) | 0.3721 (0.1113) | 0.3822 (0.1166) | 0.3950 (0.1311) | 0.4254 (0.2066) |
| Estimates of | |||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | |
| 0.2 | 0.2001 (0.0130) | 0.4011 (0.0308) | 0.5005 (0.0408) | 0.5974 (0.0411) | 0.8018 (0.0393) |
| 0.5 | 0.2015 (0.0178) | 0.4015 (0.0327) | 0.5002 (0.0376) | 0.5980 (0.0401) | 0.8008 (0.0363) |
| 0.8 | 0.1996 (0.0137) | 0.4029 (0.0309) | 0.4999 (0.0321) | 0.5990 (0.0359) | 0.8021 (0.0355) |
| Estimates of | |||||
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | |
| 0.2 | 0.1998 (0.0395) | 0.2014 (0.0376) | 0.2007 (0.0401) | 0.2020 (0.0383) | 0.2012 (0.0318) |
| 0.5 | 0.5002 (0.0163) | 0.4997 (0.0144) | 0.4995 (0.0190) | 0.5001 (0.0153) | 0.5008 (0.0108) |
| 0.8 | 0.7978 (0.0063) | 0.7989 (0.0067) | 0.7992 (0.0055) | 0.7992 (0.0036) | 0.7997 (0.0025) |
| Estimates of β | |||||
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | |
| 0.2 | 5.0327 (0.0450) | 4.9930 (0.0388) | 5.0208 (0.0447) | 4.9847 (0.0449) | 4.9955 (0.0349) |
| 0.5 | 5.0119 (0.0309) | 5.0151 (0.0246) | 5.0017 (0.0257) | 4.9734 (0.0227) | 5.0177 (0.0216) |
| 0.8 | 4.9980 (0.0293) | 5.0397 (0.0290) | 4.9807 (0.0271) | 4.9858 (0.0245) | 5.0016 (0.0168) |
| Price Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| {, } | Models | |||||
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | ||
| {4, 1} | DNE | −2.9827 (0.0495) | −3.0090 (0.0507) | −2.9933 (0.0475) | −3.0005 (0.0449) | −2.9981 (0.0471) |
| IAL | −3.0054 (0.0659) | −2.9831 (0.0842) | −2.8890 (0.1009) | −2.7934 (0.1258) | −2.7541 (0.1909) | |
| {2.5, 2.5} | DNE | −2.9979 (0.0480) | −3.0108 (0.0476) | −2.9912 (0.0432) | −3.0163 (0.0421) | −3.0011 (0.0357) |
| IAL | −3.0791 (0.0771) | −3.0421 (0.0826) | −2.9807 (0.1032) | −2.9439 (0.1287) | −2.8302 (0.1613) | |
| {1, 4} | DNE | −3.0064 (0.0488) | −2.9968 (0.0473) | −2.9926 (0.0416) | −3.0041 (0.0413) | −3.0035 (0.0334) |
| IAL | −3.2701 (0.1088) | −3.1576 (0.0815) | −3.1677 (0.1062) | −3.1762 (0.1330) | −3.5588 (0.2295) | |
| Own Quality Parameter Estimates | ||||||
| {, } | Models | |||||
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | ||
| {4, 1} | DNE | 4.0323 (0.0550) | 3.9928 (0.0493) | 4.0200 (0.0544) | 3.9845 (0.0474) | 3.9949 (0.0425) |
| IAL | 4.2493 (0.0903) | 4.3142 (0.1117) | 4.3561 (0.1244) | 4.3446 (0.1307) | 4.2888 (0.1635) | |
| {2.5, 2.5} | DNE | 2.5074 (0.0408) | 2.5119 (0.0362) | 2.4995 (0.0346) | 2.4900 (0.0356) | 2.5068 (0.0300) |
| IAL | 3.0340 (0.2148) | 3.1055 (0.2445) | 3.3559 (0.3465) | 3.4283 (0.3818) | 3.4482 (0.3896) | |
| {1, 4} | DNE | 1.0045 (0.0192) | 1.0074 (0.0202) | 0.9949 (0.0189) | 0.9982 (0.0154) | 1.0000 (0.0103) |
| IAL | 1.3030 (0.3030) | 1.2917 (0.2917) | 1.5384 (0.5385) | 1.9042 (0.9050) | 2.1963 (1.2043) | |
| Network Quality Parameter Estimates | ||||||
| {, } | Models | |||||
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | ||
| {4, 1} | 1.0004 (0.0075) | 1.0002 (0.0075) | 1.0008 (0.0076) | 1.0002 (0.0058) | 1.0007 (0.0055) | |
| {2.5, 2.5} | DNE | 2.5044 (0.0261) | 2.5032 (0.0184) | 2.5023 (0.0220) | 2.4834 (0.0177) | 2.5109 (0.0164) |
| {1, 4} | 3.9935 (0.0342) | 4.0323 (0.0348) | 3.9858 (0.0303) | 3.9876 (0.0272) | 4.0017 (0.0187) | |
| ( = 4, = 1, = 0.2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Consumer Choice | Before | After | Change | ||||||
| True | DNE | IAL | True | DNE | IAL | True | DNE | IAL | |
| {1} | 0.410 | 0.410 (0.017) | 0.409 (0.014) | 0.238 | 0.238 (0.035) | 0.259 (0.089) | −0.171 | −0.172 (0.021) | −0.150 (0.125) |
| {2} | 0.326 | 0.327 (0.014) | 0.327 (0.016) | 0.657 | 0.659 (0.013) | 0.620 (0.057) | 0.331 | 0.332 (0.016) | 0.293 (0.115) |
| {3} | 0.264 | 0.264 (0.022) | 0.263 (0.020) | 0.104 | 0.104 (0.034) | 0.120 (0.153) | −0.160 | −0.160 (0.019) | −0.143 (0.104) |
| ( = 4, = 1, = 0.8) | |||||||||
| Consumer Choice | Before | After | Change | ||||||
| True | DNE | IAL | True | DNE | IAL | True | DNE | IAL | |
| {1} | 0.405 | 0.404 (0.020) | 0.406 (0.020) | 0.217 | 0.216 (0.046) | 0.258 (0.194) | −0.188 | −0.188 (0.017) | −0.147 (0.216) |
| {2} | 0.325 | 0.326 (0.011) | 0.324 (0.023) | 0.693 | 0.694 (0.016) | 0.604 (0.129) | 0.368 | 0.368 (0.022) | 0.280 (0.239) |
| {3} | 0.270 | 0.271 (0.025) | 0.270 (0.025) | 0.090 | 0.090 (0.026) | 0.138 (0.524) | −0.180 | −0.180 (0.035) | −0.133 (0.263) |
| ( = 1, = 4, = 0.2) | |||||||||
| Consumer Choice | Before | After | Change | ||||||
| True | DNE | IAL | True | DNE | IAL | True | DNE | IAL | |
| {1} | 0.415 | 0.415 (0.014) | 0.411 (0.017) | 0.215 | 0.216 (0.041) | 0.300 (0.395) | −0.200 | −0.200 (0.026) | −0.111 (0.447) |
| {2} | 0.325 | 0.326 (0.013) | 0.326 (0.017) | 0.699 | 0.698 (0.015) | 0.562 (0.195) | 0.373 | 0.373 (0.017) | 0.236 (0.368) |
| {3} | 0.260 | 0.259 (0.018) | 0.263 (0.024) | 0.086 | 0.086 (0.042) | 0.137 (0.597) | −0.174 | −0.173 (0.016) | −0.125 (0.279) |
| ( = 1, = 4, = 0.8) | |||||||||
| Consumer Choice | Before | After | Change | ||||||
| True | DNE | IAL | True | DNE | IAL | True | DNE | IAL | |
| {1} | 0.412 | 0.411 (0.017) | 0.411 (0.019) | 0.194 | 0.193 (0.044) | 0.296 (0.527) | −0.218 | −0.218 (0.014) | −0.115 (0.472) |
| {2} | 0.324 | 0.325 (0.011) | 0.325 (0.020) | 0.736 | 0.737 (0.013) | 0.558 (0.242) | 0.412 | 0.412 (0.016) | 0.233 (0.433) |
| {3} | 0.264 | 0.264 (0.020) | 0.264 (0.028) | 0.070 | 0.070 (0.030) | 0.146 (1.080) | −0.193 | −0.194 (0.026) | −0.118 (0.390) |
| {, } | Models | |||||
|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | ||
| {4, 1} | True | 0.3882 | 0.3991 | 0.4015 | 0.4112 | 0.4269 |
| DNE | 0.3904 (0.0772) | 0.3928 (0.0730) | 0.4003 (0.0792) | 0.4018 (0.0709) | 0.4156 (0.0764) | |
| IAL | 0.3197 (0.1943) | 0.3264 (0.1948) | 0.3404 (0.1873) | 0.3517 (0.1854) | 0.3600 (0.2394) | |
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | ||
| {2.5, 2.5} | True | 0.4040 | 0.4151 | 0.4209 | 0.4268 | 0.4411 |
| DNE | 0.4056 (0.0663) | 0.4124 (0.0609) | 0.4177 (0.0634) | 0.4167 (0.0614) | 0.4336 (0.0599) | |
| IAL | 0.2372 (0.4162) | 0.2424 (0.4165) | 0.2633 (0.3753) | 0.2740 (0.3583) | 0.2923 (0.3835) | |
| 0.2 | 0.4 | 0.5 | 0.6 | 0.8 | ||
| {1, 4} | True | 0.4224 | 0.4339 | 0.4397 | 0.4452 | 0.4582 |
| DNE | 0.4245 (0.0637) | 0.4382 (0.0609) | 0.4373 (0.0576) | 0.4411 (0.0606) | 0.4515 (0.0496) | |
| IAL | 0.1294 (0.6938) | 0.1297 (0.7012) | 0.1413 (0.6787) | 0.1640 (0.6349) | 0.1569 (0.6576) | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wichmann, B.; Chen, M.; Adamowicz, W. Social Networks and Choice Set Formation in Discrete Choice Models. Econometrics 2016, 4, 42. https://doi.org/10.3390/econometrics4040042
Wichmann B, Chen M, Adamowicz W. Social Networks and Choice Set Formation in Discrete Choice Models. Econometrics. 2016; 4(4):42. https://doi.org/10.3390/econometrics4040042
Chicago/Turabian StyleWichmann, Bruno, Minjie Chen, and Wiktor Adamowicz. 2016. "Social Networks and Choice Set Formation in Discrete Choice Models" Econometrics 4, no. 4: 42. https://doi.org/10.3390/econometrics4040042
APA StyleWichmann, B., Chen, M., & Adamowicz, W. (2016). Social Networks and Choice Set Formation in Discrete Choice Models. Econometrics, 4(4), 42. https://doi.org/10.3390/econometrics4040042






