Testing Symmetry of Unknown Densities via Smoothing with the Generalized Gamma Kernels

Abstract

This paper improves a kernel-smoothed test of symmetry through combining it with a new class of asymmetric kernels called the generalized gamma kernels. It is demonstrated that the improved test statistic has a normal limit under the null of symmetry and is consistent under the alternative. A test-oriented smoothing parameter selection method is also proposed to implement the test. Monte Carlo simulations indicate superior finite-sample performance of the test statistic. It is worth emphasizing that the performance is grounded on the first-order normal limit and a small number of observations, despite a nonparametric convergence rate and a sample-splitting procedure of the test.

1. Introduction

Symmetry and conditional symmetry play a key role in numerous fields of economics and finance. Economists’ focuses are often on asymmetry of price adjustments (Bacon [1]), innovations in asset markets (Campbell and Hentschel [2]) or policy shocks (Clarida and Gertler [3]). In addition, the mean-variance analysis in finance is consistent with investors’ portfolio decision making if and only if asset returns are elliptically distributed (e.g., Chamberlain [4]; Owen and Rabinovitch [5]; Appendix B in Chapter 4 of Ingersoll [6]). Moreover, conditional symmetry in the distribution of the disturbance is often a key regularity condition for regression analysis. In particular, convergence properties of adaptive estimation and robust regression estimation are typically explored under this condition. For the former, Bickel [7] and Newey [8] demonstrate that conditional symmetry of the disturbance distribution in the contexts of linear regression and moment-condition models, respectively, suffices for adaptive estimators to attain their efficiency bounds. For the latter, Carroll and Welsh [9] warn invalidity in inference based on robust regression estimation when the regression disturbance is asymmetrically distributed. Indeed, symmetry of the disturbance distribution is often a key assumption for consistency of parameter estimators in certain versions of robust regression estimation (e.g., Lee [10,11]; Zinde-Walsh [12]; Bondell and Stefanski [13]). Based on their simulation studies, Baldauf and Santos Silva [14] also argue that lack of conditional symmetry in the disturbance distribution may lead to inconsistency of parameter estimates via robust regression estimation.

In view of the importance in the existence of symmetry, a number of tests for symmetry and conditional symmetry have been proposed. The tests can be classified into kernel and non-kernel methods. Examples for the former include Fan and Gencay [15], Ahmad and Li [16], Zheng [17], Diks and Tong [18], and Fan and Ullah [19]. The latter falls into the tests based on: (i) sample moments (Randles et al. [20]; Godfrey and Orme [21]; Bai and Ng [22]; Premaratne and Bera [23]); (ii) regression percentile (Newey and Powell [24]); (iii) martingale transformation (Bai and Ng [25]); (iv) empirical processes (Delgado and Escanciano [26]; Chen and Tripathi [27]); and (v) Neyman’s smooth test (Fang et al. [28]). Our focus is on the test by Fernandes, Mendes and Scaillet [29] (abbreviated as “FMS” hereafter). While this test can be viewed as the kernel-smoothed one, it has a unique feature. When a probability density function (“pdf”) is symmetric about zero, its shapes on positive and negative sides must be mirror images each other. Then, after estimating pdfs on positive and negative sides separately using positive and absolute values of negative observations, respectively, FMS examine whether symmetry holds through gauging closeness between two density estimates. By this nature, we call the test the split-sample symmetry test (“SSST”) hereafter. One of the features of the SSST is that it relies on asymmetric kernels with support on $\left[0,\infty \right)$ such as the gamma (“G”) kernel by Chen [30]. Asymmetric kernel estimators are nonnegative and boundary bias-free, and achieve the optimal convergence rate (in the mean integrated squared error sense) within the class of nonnegative kernel estimators. It is also reported (e.g., p. 597 of Gospodinov and Hirukawa [31]; p. 651 of FMS) that asymmetric kernel-based estimation and inference possess nice finite-sample properties. The split-sample approach is expected to result in efficiency loss. However, it can attain the same convergence rate as the smoothed symmetry tests using symmetric kernels do. Furthermore, unlike these tests, the SSST does not require continuity of density derivatives at the origin.

The aim of this paper is to ameliorate the SSST further through combining it with the generalized gamma (“GG”) kernels, a new class of asymmetric kernels with support on $\left[0,\infty \right)$ that have been proposed recently by Hirukawa and Sakudo [32]. Our particular focus is on two special cases of the GG kernels, namely, the modified gamma (“MG”) and Nakagami-m (“NM”) kernels. While superior finite-sample performance of the MG kernel has been reported in the literature, the NM kernel is also anticipated to have an advantage when applied to the SSST. It is known that finite-sample performance of a kernel density estimator depends on proximity in shape between the underlying density and the kernel chosen. As shown in Section 2, the NM kernel collapses to the half-normal pdf when smoothing is made at the origin, and the shape of the density is likely to be close to those on the positive side of single-peaked symmetric distributions. We also pay particular attention to the smoothing parameter selection. While existing articles on asymmetric kernel-smoothed tests (e.g., Fernandes and Grammig [33]; FMS) simply borrow the choice method based on optimality for density estimation, we tailor the idea of test-oriented smoothing parameter selection by Kulasekera and Wang [34,35] to the SSST.

The SSST with the GG kernels plugged in preserves all appealing properties documented in FMS. First, the SSST has a normal limit under the null of symmetry and it is also consistent under the alternative. Hence, unlike the tests by Delgado and Escanciano [26] and Chen and Tripathi [27], no simulated critical values are required. Second, Monte Carlo simulations indicate superior finite-sample performance of the SSST smoothed by the GG kernels. The performance is confirmed even when the entire sample size is 50, despite a nonparametric convergence rate and a sample-splitting procedure. Remarkably, the superior performance is based simply on first-order asymptotic results, and thus the assistance of bootstrapping appears to be unnecessary, unlike most of the smoothed tests employing fixed, symmetric kernels. This result complements previous findings on asymmetric kernel-smoothed tests by Fernandes and Grammig [33] and FMS.

The remainder of this paper is organized as follows. In Section 2 a brief review of a family of the GG kernels is provided. Section 3 proposes symmetry and conditional symmetry tests based on the GG kernels. Their limiting null distributions and power properties are also explored. As an important practical problem, Section 4 discusses the smoothing parameter selection. Our particular focus is on the choice method for power optimality. Section 5 conducts Monte Carlo simulations to investigate finite-sample properties of the test statistics. Section 6 summarizes the main results of the paper. Proofs are provided in the Appendix.

This paper adopts the following notational conventions: $\Gamma \left(a\right)={\int }_0^{\infty }{y}^{a-1}exp\left(-y\right)dy$ $\left(a>0\right)$ is the gamma function; $\mathbf{1}\left\{·\right\}$ signifies an indicator function; $⌊·⌋$ denotes the integer part; $∥A∥={\left\{tr\left(A^{\prime }A\right)\right\}}^{1/2}$ is the Euclidian norm of matrix A; and $c\left(>0\right)$ denotes a generic constant, the quantity of which varies from statement to statement. The expression “$X\stackrel{d}{=}Y$” reads “A random variable X obeys the distribution Y.” The expression “$X_n\sim Y_n$” is used whenever $X_n/Y_n\to 1$ as $n\to \infty$. Lastly, in order to describe different asymptotic properties of an asymmetric kernel estimator across positions of the design point $x\left(>0\right)$ relative to the smoothing parameter $b\left(>0\right)$ that shrinks toward zero, we denote by “interior x” and “boundary x” a design point x that satisfies $x/b\to \infty$ and $x/b\to \kappa$ for some $0<\kappa <\infty$ as $b\to 0$, respectively.

2. Family of the GG Kernels: A Brief Review

Before proceeding, we provide a concise review on a family of the GG kernels. The family constitutes a new class of asymmetric kernels, and it consists of a specific functional form and a set of common conditions, as in Definition 1 below. The name “GG kernels” comes from the fact that the pdf of a GG distribution by Stacy [36] is chosen as the functional form. A major advantage of the family is that for each asymmetric kernel generated from this class, asymptotic properties of the kernel estimators (e.g., density and regression estimators) can be delivered by manipulating the conditions directly, as with symmetric kernels.

Definition 1. 

(Hirukawa and Sakudo [32], Definition 1) Let $\left(\alpha ,\beta ,\gamma \right)=\left({\alpha }_b\left(x\right),{\beta }_b\left(x\right),{\gamma }_b\left(x\right)\right)\in {\mathbb{R}}_{+}^3$ be a continuous function of the design point x and the smoothing parameter b. For such$\left(\alpha ,\beta ,\gamma \right)$ , consider the pdf of $GG\left(\alpha ,\beta \Gamma \left(\alpha /\gamma \right)/\Gamma \left\{\left(\alpha +1\right)/\gamma \right\},\gamma \right)$ , i.e.,

$$K_{GG}\left(u;x,b\right)=\frac{\gamma u^{\alpha -1}exp\left[-{\left\{\frac{u}{\beta \Gamma \left(\frac{\alpha }{\gamma }\right)/\Gamma \left(\frac{\alpha +1}{\gamma }\right)}\right\}}^{\gamma }\right]}{{\left\{\beta \Gamma \left(\frac{\alpha }{\gamma }\right)/\Gamma \left(\frac{\alpha +1}{\gamma }\right)\right\}}^{\alpha }\Gamma \left(\frac{\alpha }{\gamma }\right)}\mathbf{1}\left\{u\ge 0\right\}.$$

(1)

This pdf is said to be a family of the GG kernels if it satisfies each of the following conditions:

Condition 1. 

$\beta =\left\{\begin{array}{cc}x\hfill & \mathit{\text{for}}x\ge C_{1}b\hfill \\ {\phi }_b\left(x\right)\hfill & \mathit{\text{for}}x\in \left[0,C_{1}b\right)\hfill \end{array}\right.$ , where $0<C_1<\infty$ is some constant, the function ${\phi }_b\left(x\right)$ satisfies $C_{2}b\le {\phi }_b\left(x\right)\le C_{3}b$ for some constants $0<C_2\le C_3<\infty$ , and the connection between x and ${\phi }_b\left(x\right)$ at $x=C_{1}b$ is smooth.

Condition 2. 

$\alpha ,\gamma \ge 1$ , and for $x\in \left[0,C_{1}b\right)$ , α satisfies $1\le \alpha \le C_4$ for some constant $1\le C_4<\infty$ . Moreover, connections of α and γ at $x=C_{1}b$ , if any, are smooth.

Condition 3. 

$M_b\left(x\right):=\frac{\Gamma \left(\frac{\alpha }{\gamma }\right)\Gamma \left(\frac{\alpha +2}{\gamma }\right)}{{\left\{\Gamma \left(\frac{\alpha +1}{\gamma }\right)\right\}}^2}=\left\{\begin{array}{cc}1+\left(C_5/x\right)b+o\left(b\right)\hfill & \mathit{\text{for}}x\ge C_{1}b\hfill \\ O\left(1\right)\hfill & \mathit{\text{for}}x\in \left[0,C_{1}b\right)\hfill \end{array}\right.$ , for some constant $0<\left|C_5\right|<\infty$.

Condition 4. 

$H_b\left(x\right):=\frac{\Gamma \left(\frac{\alpha }{\gamma }\right)\Gamma \left(\frac{2\alpha }{\gamma }\right)}{2^{1/\gamma }\Gamma \left(\frac{\alpha +1}{\gamma }\right)\Gamma \left(\frac{2\alpha -1}{\gamma }\right)}=\left\{\begin{array}{cc}1+o\left(1\right)\hfill & \mathit{\text{for}}\mathit{\text{interior}}x\hfill \\ O\left(1\right)\hfill & \mathit{\text{for}}\mathit{\text{boundary}}x\hfill \end{array}\right.$.

Condition 5. 

$A_{b,\nu }\left(x\right):={\left\{\frac{\gamma \Gamma \left(\frac{\alpha +1}{\gamma }\right)}{\beta }\right\}}^{\nu -1}\frac{\Gamma \left\{\frac{\nu \left(\alpha -1\right)+1}{\gamma }\right\}}{{\nu }^{\frac{\nu \left(\alpha -1\right)+1}{\gamma }}{\left\{\Gamma \left(\frac{\alpha }{\gamma }\right)\right\}}^{2\nu -1}}\sim \left\{\begin{array}{cc}{V}_I\left(\nu \right){\left(xb\right)}^{\frac{1-\nu }{2}}\hfill & \mathit{\text{for}}\mathit{\text{interior}}x\hfill \\ V_B\left(\nu \right)b^{1-\nu }\hfill & \mathit{\text{for}}\mathit{\text{boundary}}x\hfill \end{array}\right.$, $\nu \in {\mathbb{R}}_{+}$, where constants $0<V_I\left(\nu \right),V_B\left(\nu \right)<\infty$ depend only on ν.

The family embraces the following two special cases1. Putting

$$\left(\alpha ,\beta \right)=\left\{\begin{array}{cc}\left(\frac{x}{b},x\right)\hfill & \text{for}x\ge 2b\hfill \\ \left(\frac{1}{4}{\left(\frac{x}{b}\right)}^2+1,\frac{x^2}{4b}+b\right)\hfill & \text{for}x\in \left[0,2b\right)\hfill \end{array}\right.$$

and $\gamma =1$ in (1) generates the MG kernel

$$K_{MG}\left(u;x,b\right)=\frac{u^{\alpha -1}exp\left\{-u/\left(\beta /\alpha \right)\right\}}{{\left(\beta /\alpha \right)}^{\alpha }\Gamma \left(\alpha \right)}\mathbf{1}\left\{u\ge 0\right\}.$$

It can be found that this is equivalent to the one proposed by Chen [30] by recognizing that $\alpha ={\rho }_b\left(x\right)$ on p. 473 of Chen [30] and $\beta /\alpha =b$. The same $\left(\alpha ,\beta \right)$ and $\gamma =2$ also yields the NM kernel

$$K_{NM}\left(u;x,b\right)=\frac{2u^{\alpha -1}exp\left[-{\left\{u/\left(\beta \Gamma \left(\frac{\alpha }{2}\right)/\Gamma \left(\frac{\alpha +1}{2}\right)\right)\right\}}^2\right]}{{\left\{\beta \Gamma \left(\frac{\alpha }{2}\right)/\Gamma \left(\frac{\alpha +1}{2}\right)\right\}}^{\alpha }\Gamma \left(\frac{\alpha }{2}\right)}\mathbf{1}\left\{u\ge 0\right\}.$$

The GG kernels are designed to inherit all appealing properties that the MG kernel possesses. We conclude this section by referring to the properties. Two properties below are basic ones. First, by construction, the GG kernels are free of boundary bias and always generate nonnegative density estimates everywhere. Second, the shape of each GG kernel varies according to the position at which smoothing is made; in other words, the amount of smoothing changes in a locally adaptive manner. To illustrate this property, Figure 1 plots the shapes of the MG and NM kernels at four different design points ($x=0.0,0.5,1.0,2.0$) at which the smoothing is performed. For reference, the G kernel is also drawn in each panel. When smoothing is made at the origin (Panel (A)), the NM kernel collapses to a half-normal pdf, whereas others reduce to exponential pdfs. As the design point moves away from the boundary (Panels (B–D)), the shape of each kernel becomes flatter and closer to symmetry. We should stress that Figure 1 is drawn with the value of the smoothing parameter fixed at $b=0.2$. Unlike variable bandwidth methods for fixed, symmetric kernels (e.g., Abramson [37]), adaptive smoothing of these kernels can be achieved by a single smoothing parameter, which makes them much more appealing in empirical work.

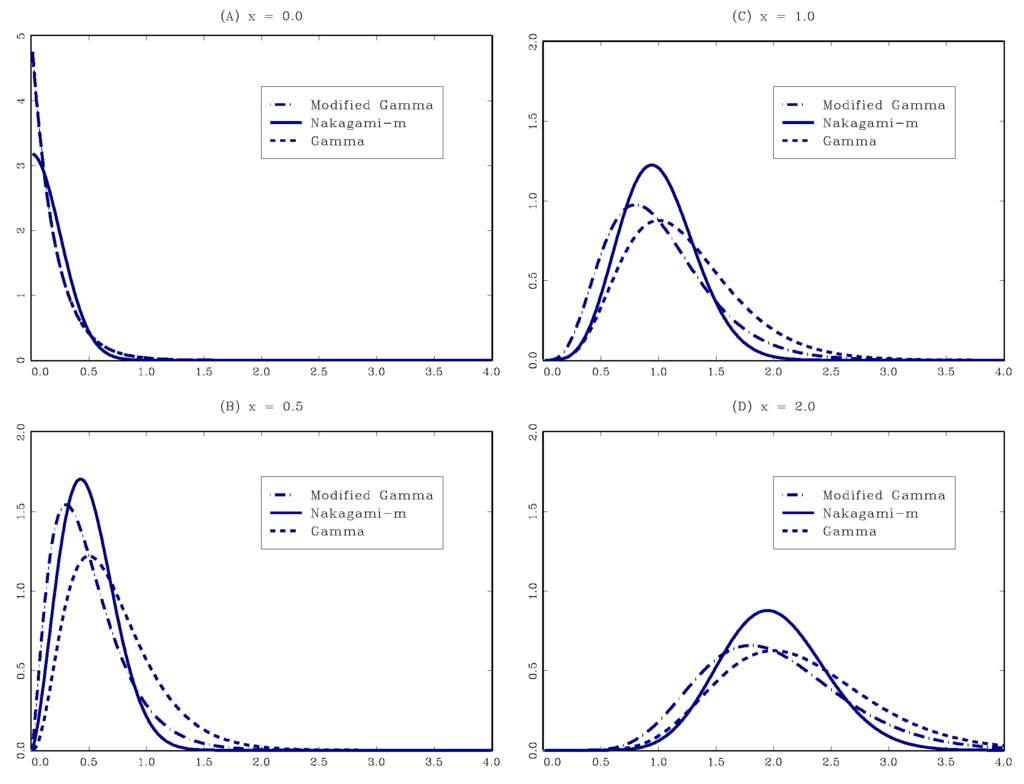
Figure 1. Shapes of the GG Kernels When $b=0.2$.

The remaining three properties are on density estimates using the GG kernels. Third, when best implemented, each GG density estimator attains Stone’s [38] optimal convergence rate in the mean integrated squared error within the class of nonnegative kernel density estimators. Fourth, the leading bias of each GG density estimator contains only the second-order derivative of the true density over the interior region, unlike many other asymmetric kernels including the G kernel. Fifth, the variance of the GG estimator tends to decrease as the design point moves away from the boundary. This property is particularly advantageous to estimating the distributions that have long tails with sparse data.

3. Tests for Symmetry and Conditional Symmetry Smoothed by the GG Kernels

3.1. SSST as a Special Case of Two-Sample Goodness-of-Fit Tests

This section proposes to combine the SSST with the GG kernels, explores asymptotic properties of the test statistic, and finally expands the scope of the test to testing the null of conditional symmetry. The SSST can be characterized as a special case of two-sample tests for equality of two unknown densities investigated by Anderson, Hall and Titterington [39]. Suppose that we are interested in testing symmetry of the distribution of a random variable $U\in \mathbb{R}$. Without loss of generality, we hypothesize that the distribution is symmetric about zero. If U has a pdf, then under the null, its shapes on positive and negative sides of the entire real line $\mathbb{R}$ must be mirror images each other. Let f and g be the pdfs to the right and left from the origin, respectively. Then, we would like to test the null hypothesis

$$H_0:f\left(u\right)=g\left(u\right)\text{for}\text{almost}\text{all}u\in {\mathbb{R}}_{+}$$

against the alternative

$$H_1:f\left(u\right)\ne g\left(u\right)\text{on}\mathrm{a}\text{set}\text{of}\text{positive}\text{measure}\text{in}{\mathbb{R}}_{+}.$$

Accordingly, a natural test statistic should be built on the integrated squared error (“ISE”)

$$\begin{array}{cc}\hfill I& ={\int }_0^{\infty }{\left\{f\left(u\right)-g\left(u\right)\right\}}^{2}du\hfill \\ & ={\int }_0^{\infty }\left\{f\left(u\right)-g\left(u\right)\right\}dF\left(u\right)-{\int }_0^{\infty }\left\{f\left(u\right)-g\left(u\right)\right\}dG\left(u\right),\hfill \end{array}$$

where F and G are cumulative distribution functions corresponding to f and g, respectively.

The name of the SSST comes from the way to construct a sample analog to I. A random sample of N observations ${\left\{U_i\right\}}_{i=1}^N$ is split into two sub-samples, namely, ${\left\{X_i\right\}}_{i=1}^{n_1}:={\left\{U_i:U_i\ge 0\right\}}_{i=1}^{n_1}$ and ${\left\{Y_i\right\}}_{i=1}^{n_2}:={\left\{-U_i:U_i<0\right\}}_{i=1}^{n_2}$, where $N=n_1+n_2$. Given the sub-samples, f and g can be estimated using a GG kernel with the smoothing parameter b as

$$\widehat{f}\left(u\right)=\frac{1}{n_1}\sum _{i=1}^{n_1}{K}_{GG}\left(X_i;u,b\right)\text{and}\widehat{g}\left(u\right)=\frac{1}{n_2}\sum _{i=1}^{n_2}{K}_{GG}\left(Y_i;u,b\right),$$

respectively2. Similarly, $\left(F,G\right)$ is replaced with their empirical measures $\left(F_{n_1},G_{n_2}\right)$. In addition, because $n_1\sim n_2$ under $H_0$, without loss of generality and for ease of exposition, we assume that N is even and that $n:=n_1=n_2=N/2$. Using a short-handed notation $K_X\left(Y\right)=K_{GG}\left(Y;X,b\right)$ finally yields the sample analog to I as

$$\begin{array}{cc}\hfill {\overline{I}}_n& =\frac{1}{n}\sum _{i=1}^n\left\{\widehat{f}\left(X_i\right)+\widehat{g}\left(Y_i\right)-\widehat{g}\left(X_i\right)-\widehat{f}\left(Y_i\right)\right\}\hfill \\ & =\sum _{i=1}^n\frac{1}{n^2}\left\{K_{X_i}\left(X_i\right)+K_{Y_i}\left(Y_i\right)-K_{Y_i}\left(X_i\right)-K_{X_i}\left(Y_i\right)\right\}\hfill \\ & +\sum _{j=1}^n\sum _{i=1,i\ne j}^n\frac{1}{n^2}\left\{K_{X_j}\left(X_i\right)+K_{Y_j}\left(Y_i\right)-K_{Y_j}\left(X_i\right)-K_{X_j}\left(Y_i\right)\right\}\hfill \\ & =I_{1n}+I_n.\hfill \end{array}$$

Although we could use ${\overline{I}}_n$ itself as the test statistic, the probability limit of $I_{1n}$ plays a role in a non-vanishing center term of the asymptotic null distribution. Because the term is likely to cause size distortions in finite samples, we focus only on $I_n$ to construct the testing statistic. Now $I_n$ can be rewritten as

$$I_n:=\sum _{1\le i<j\le n}{\Phi }_n\left(Z_i,Z_j\right):=\sum _{1\le i<j\le n}\frac{1}{n^2}\left\{{\varphi }_n\left(Z_i,Z_j\right)+{\varphi }_n\left(Z_j,Z_i\right)\right\},$$

where $Z_i:=\left(X_i,Y_i\right)$ and ${\varphi }_n\left(Z_i,Z_j\right):=K_{X_j}\left(X_i\right)+K_{Y_j}\left(Y_i\right)-K_{Y_j}\left(X_i\right)-K_{X_j}\left(Y_i\right)$. Observe that ${\Phi }_n\left(Z_i,Z_j\right)$ is symmetric between $Z_i$ and $Z_j$ and that $E\left\{\left.{\Phi }_n\left(Z_i,Z_j\right)\right|Z_i\right\}=0$ almost surely under $H_0$. It follows that $I_n$ is a degenerate U-statistic, and thus we may apply a martingale central limit theorem (e.g., Theorem 1 of Hall [40]; Theorem 4.7.3 of Koroljuk and Borovskich [41]).

Before describing the asymptotic properties of $I_n$, we make two remarks. First, applying the idea of two-sample goodness-of-fit tests to the symmetry test is not new. Ahmad and Li [16] and Fan and Ullah [19] have also studied the symmetry test based on closeness of two density estimates measured by the ISE. They estimate densities using two samples, namely, the original entire sample ${\left\{X_i\right\}}_{i=1}^N:={\left\{U_i\right\}}_{i=1}^N$ and the one obtained by flipping the sign of each observation ${\left\{Y_i\right\}}_{i=1}^N:={\left\{-U_i\right\}}_{i=1}^N$ in our notations. Because each of X and Y has support on $\left(-\infty ,\infty \right)$ by construction, a standard symmetric kernel is employed for density estimation unlike the SSST. Second, if X and Y are taken from two different distributions with support on $\left[0,\infty \right)$, then $I_n$ can be viewed as a pure two-sample goodness-of-fit test. It can be immediately applied to the testing for equality of two unknown distributions of nonnegative economic and financial variables such as incomes, wages, short-term interest rates, and insurance claims.

To present the convergence properties of $I_n$, we make the following assumptions.

Assumption 1. 

Two random samples ${\left\{X_i\right\}}_{i=1}^{n_1}$ and ${\left\{Y_i\right\}}_{i=1}^{n_2}$ are drawn independently from univariate distributions that have pdfs f and g with support on $\left[0,\infty \right)$, respectively.

Assumption 2. 

f and g are twice continuously differentiable on $\left[0,\infty \right)$, and $E{\left|X{f}^{\prime \prime }\left(X\right)\right|}^2$, $E\left|X^2{f}^{\prime \prime }\left(X\right)g^{\prime \prime }\left(X\right)\right|$, $E\left|Y^2{f}^{\prime \prime }\left(Y\right)g^{\prime \prime }\left(Y\right)\right|$, $E{\left|Y{g}^{\prime \prime }\left(Y\right)\right|}^2<\infty$.

Assumption 3. 

The smoothing parameter $b\left(=b_n\right)$ satisfies $b+{\left(nb\right)}^{-1}\to 0$ as $n\to \infty$.

Assumption 4. 

Let $\left(X_1,X_2\right)$ and $\left(Y_1,Y_2\right)$ be two independent copies of X and Y, respectively. Then, the followings hold:

(a)

$E\left\{K_{X_2}\left(X_1\right)K_{Y_2}\left(X_1\right)\right\}\sim E\left\{f\left(X\right)g\left(X\right)\right\}$; and $E\left\{K_{Y_2}\left(Y_1\right)K_{X_2}\left(Y_1\right)\right\}\sim E\left\{f\left(Y\right)g\left(Y\right)\right\}$.

(b)

$E\left\{K_{X_2}\left(X_1\right)K_{X_1}\left(X_2\right)\right\}\sim b^{-1/2}{V}_I\left(2\right)E\left\{X^{-1/2}f\left(X\right)\right\}$; $E\left\{K_{X_2}\left(Y_1\right)K_{Y_1}\left(X_2\right)\right\}\sim$

$b^{-1/2}{V}_I\left(2\right)$$E\left\{X^{-1/2}g\left(X\right)\right\}$; $E\left\{K_{Y_2}\left(X_1\right)K_{X_1}\left(Y_2\right)\right\}\sim b^{-1/2}{V}_I\left(2\right)E\left\{Y^{-1/2}f\left(Y\right)\right\}$;

and $E\left\{K_{Y_2}\left(Y_1\right)K_{Y_1}\left(Y_2\right)\right\}$ $\sim b^{-1/2}{V}_I\left(2\right)E\left\{Y^{-1/2}g\left(Y\right)\right\}$, where $V_I\left(2\right)$ is a kernel-specific constant given in Condition 5 of Definition 1.

Assumptions 1–3 are standard in the literature of asymmetric kernel smoothing. On the other hand, Assumption 4 has a different flavor. Convergence results on $I_n$ are built on several different moment approximations. While Definition 1 implies the statements in Lemma A2 in the Appendix, it is unclear whether the definition may even admit such approximations as in Assumption 4. The difficulty comes from the fact that unlike symmetric kernels, roles of design points and data points are nonexchangeable in asymmetric kernels. What makes the problem more complicated is that functional forms of $\left(\alpha ,\beta ,\gamma \right)=\left({\alpha }_b\left(x\right),{\beta }_b\left(x\right),{\gamma }_b\left(x\right)\right)$ in the GG kernels are not fully specified in Definition 1. Considering that not all GG kernels may admit the moment approximations (a) and (b), we choose to make an extra assumption. Note that the MG and NM kernels fulfill Assumption 4, as documented in the next lemma.

Lemma 1. 

If Assumptions 1–3 hold, then each of the MG and NM kernels satisfies Assumption 4.

The theorem below delivers the convergence properties of $I_n$ and provides a consistent estimator of its asymptotic variance.

Theorem 1. 

Suppose that Assumptions 1–4 and $n_1=n_2=n$ hold.

(i) 

Under $H_0$, $n{b}^{1/4}{I}_n\stackrel{d}{\to }N\left(0,{\sigma }^2\right)$ as $n\to \infty$, where

$${\sigma }^2=2V_I\left(2\right)E\left[X^{-1/2}\left\{f\left(X\right)+g\left(X\right)\right\}+Y^{-1/2}\left\{f\left(Y\right)+g\left(Y\right)\right\}\right],$$

which reduces to ${\sigma }^2=8V_I\left(2\right)E\left\{X^{-1/2}f\left(X\right)\right\}$ under $H_0$, and $V_I\left(2\right)$ is a kernel-specific constant given in Condition 5 of Definition 1.

(ii) 

A consistent estimator of ${\sigma }^2$ is given by

$${\widehat{\sigma }}^2=2V_I\left(2\right)\frac{1}{n}\sum _{i=1}^n\left[X_i^{-1/2}\left\{\widehat{f}\left(X_i\right)+\widehat{g}\left(X_i\right)\right\}+Y_i^{-1/2}\left\{\widehat{f}\left(Y_i\right)+\widehat{g}\left(Y_i\right)\right\}\right].$$

(2)

We make a few remarks. First, it follows from Lemma 1 and Theorem 1 that the MG and NM kernels can be safely employed for the SSST, where values of $V_I\left(2\right)$ for these kernels are $\left(V_{I,MG}\left(2\right),V_{I,NM}\left(2\right)\right)=\left(1/\left(2\sqrt{\pi }\right),1/\sqrt{2\pi }\right)$. It also follows from Proposition 1 of FMS and Theorem 1 that limiting null distributions of $n{b}^{1/4}{I}_n$ using the G and MG kernels coincide, as expected. Second, while a similar form to the asymptotic variance ${\sigma }^2$ can be found in Proposition 1 of FMS, ${\sigma }^2$ takes a more general form. Accordingly, the variance estimator ${\widehat{\sigma }}^2$ is consistent under both $H_0$ and $H_1$. Third, it can be inferred from Theorem 1 that the test statistic becomes $T_n:=n{b}^{1/4}{I}_n/\widehat{\sigma }$. As a consequence, the SSST is a one-sided test that rejects $H_0$ in favor of $H_1$ if $T_n>z_{\alpha }$, where $z_{\alpha }$ is the upper α-percentile of $N\left(0,1\right)$.

The next proposition refers to consistency of the SSST. Observe that the power approaches one for local alternatives with convergence rates no faster than $n{b}^{1/4}$, as well as for fixed alternatives.

Proposition 1. 

If Assumptions 1–4 hold, then under $H_1$, $Pr\left(T_n>B_n\right)\to 1$ as $n\to \infty$ for any non-stochastic sequence $B_n$ satisfying $B_n=o\left(n{b}^{1/4}\right)$.

3.2. SSST When Two Sub-Samples Have Unequal Sample Sizes

Convergence results in the previous section rely on the assumption that the sample sizes of two sub-samples ${\left\{X_i\right\}}_{i=1}^{n_1}$ and ${\left\{Y_i\right\}}_{i=1}^{n_2}$ are the same, i.e., so far $n_1=n_2$ has been maintained. In reality, $n_1\ne n_2$ is often the case, in particular, when the entire sample size $N=n_1+n_2$ is odd or when $H_1$ is true.

Handling this case requires more tedious calculation. When $n_1\ne n_2$, $I_n$ can be rewritten as

$$\begin{array}{cc}\hfill I_{n_1,n_2}& =\sum _{j=1}^{n_1}\sum _{i=1,i\ne j}^{n_1}\frac{1}{n_1^2}{K}_{X_j}\left(X_i\right)+\sum _{j=1}^{n_2}\sum _{i=1,i\ne j}^{n_2}\frac{1}{n_2^2}{K}_{Y_j}\left(Y_i\right)\hfill \\ & -\sum _{j=1}^{n_2}\sum _{i=1,i\ne j}^{n_1}\frac{1}{n_1{n}_2}{K}_{Y_j}\left(X_i\right)-\sum _{j=1}^{n_1}\sum _{i=1,i\ne j}^{n_2}\frac{1}{n_1{n}_2}{K}_{X_j}\left(Y_i\right).\hfill \end{array}$$

(3)

Following Fan and Ullah [19], we deliver convergence results under the assumption that two sample sizes $n_1$ and $n_2$ diverge at the same rate. The asymptotic variance of $n_1{b}^{1/4}{I}_{n_1,n_2}$ and its consistent estimate are also provided. Because the essential arguments are the same as those for Theorem 1 and Proposition 1, we omit the proofs of Theorem 2 and Proposition 2 and simply state the results. Observe that when $n_1=n_2=n$, these results collapse to Theorem 1 and Proposition 1, respectively.

Theorem 2. 

Suppose that Assumptions 1–4 and $n_1/n_2\to \lambda$ for some constant $\lambda \in \left(0,\infty \right)$ hold.

(i) 

Under $H_0$, $n_1{b}^{1/4}{I}_{n_1,n_2}\stackrel{d}{\to }N\left(0,{\sigma }_{\lambda }^2\right)$ as $n_1\to \infty$, where

$$\begin{array}{cc}\hfill {\sigma }_{\lambda }^2& =2V_I\left(2\right)\left[E\left\{X^{-1/2}f\left(X\right)\right\}+\lambda E\left\{X^{-1/2}g\left(X\right)\right\}\right.\hfill \\ & \left.+\lambda E\left\{Y^{-1/2}f\left(Y\right)\right\}+{\lambda }^{2}E\left\{Y^{-1/2}g\left(Y\right)\right\}\right],\hfill \end{array}$$

which reduces to ${\sigma }_{\lambda }^2=2{\left(1+\lambda \right)}^2{V}_I\left(2\right)E\left\{X^{-1/2}f\left(X\right)\right\}$ under $H_0$.

(ii) 

A consistent estimator of ${\sigma }_{\lambda }^2$ is given by

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_{\lambda }^2& =2V_I\left(2\right)\left\{\frac{1}{n_1}\sum _{i=1}^{n_1}{X}_i^{-1/2}\widehat{f}\left(X_i\right)+\left(\frac{n_1}{n_2}\right)\frac{1}{n_1}\sum _{i=1}^{n_1}{X}_i^{-1/2}\widehat{g}\left(X_i\right)\right.\hfill \\ & \left.+\left(\frac{n_1}{n_2}\right)\frac{1}{n_2}\sum _{i=1}^{n_2}{Y}_i^{-1/2}\widehat{f}\left(Y_i\right)+{\left(\frac{n_1}{n_2}\right)}^2\frac{1}{n_2}\sum _{i=1}^{n_2}{Y}_i^{-1/2}\widehat{g}\left(Y_i\right)\right\}.\hfill \end{array}$$

(4)

Proposition 2. 

If Assumptions 1–4 and $n_1/n_2\to \lambda \in \left(0,\infty \right)$ hold, then under $H_1$, $Pr\left(T_{n_1,n_2}>B_{n_1}\right):=Pr\left(n_1{b}^{1/4}{I}_{n_1,n_2}/{\widehat{\sigma }}_{\lambda }>B_{n_1}\right)\to 1$ as $n_1\to \infty$ for any non-stochastic sequence $B_{n_1}$ satisfying $B_{n_1}=o\left(n_1{b}^{1/4}\right)$.

The next corollary is a natural outcome from Theorem 2 and comes from the fact that under $H_0$, $n_1\sim n_2$ or $\lambda =1$ holds. Because N could be odd in this context, n should read $n=⌊N/2⌋$.

Corollary 1. 

If Assumptions 1–4 and $n_1/n_2\to 1$ hold, then $n_1,n_2\sim n=⌊N/2⌋$ so that $n_1{b}^{1/4}{I}_{n_1,n_2}=n{b}^{1/4}{I}_n+o_p\left(1\right)$.

3.3. Extension to a Test for Conditional Symmetry

So far we have maintained the assumption that the random variable U is observable and has a distribution that is symmetric about zero. However, often U is unobservable or the axis of symmetry is not zero. The former is typical when we are interested in symmetry of the distribution of the disturbance conditional on regressors in regression analysis. In this scenario, the test is conducted after U is replaced with the residual. For the latter, the test should be based on location-adjusted observations, i.e., transformed observations with an estimate of the axis of symmetry (e.g., the sample mean or the sample median) subtracted from U. These aspects motivate us to generalize the SSST to the testing for conditional symmetry.

Following FMS, we consider a testing for symmetry in the conditional distribution of $\left.V_1\right|V_2$ with $\left(V_1,V_2\right)\in \mathbb{R}\times {\mathbb{R}}^d$ within the framework of a semiparametric context. Specifically, for a parameter space ${\Theta }_1$ and a function ${\xi }_1:{\mathbb{R}}^d\times {\Theta }_1\to \mathbb{R}$, it suffices to check whether the conditional distribution of $\left.V_1\right|V_2$ is symmetric about ${\xi }_1\left(V_2;{\theta }_1^0\right)$ for some ${\theta }_1^0\in$ ${\Theta }_1$. Observe that this is equivalent to test whether there is ${\theta }_1^0\in$ ${\Theta }_1$ such that the conditional distribution of $\left.V\right|V_2:=$ $\left.V_1-{\xi }_1\left(V_2;{\theta }_1^0\right)\right|V_2$ is symmetric about zero.

However, implementing this type of testing strategy requires to estimate the conditional pdf of $\left.V\right|V_2$ nonparametrically. This is cumbersome, considering the curse of dimensionality in $V_2$ and another smoothing parameter choice. Instead, as in Zheng [17], Bai and Ng [25] and Delgado and Escanciano [26], we assume that there are a parameter space ${\Theta }_2$ and a function ${\xi }_2:{\mathbb{R}}^{d+1}\times {\Theta }_2\to \mathbb{R}$ that can attain symmetry of the marginal distribution of $U:={\xi }_2\left(V_1,V_2;{\theta }_2^0\right)$ about zero for some ${\theta }_2^0\in$ ${\Theta }_2$. Given the dependence of V (and thus U) on ${\Theta }_1$, we can finally rewrite our testing scheme as the one that tests, for a suitable parameter space Θ and a function $\xi :{\mathbb{R}}^{d+1}\times \Theta \to \mathbb{R}$, symmetry of the marginal distribution of $U=\xi \left(V_1,V_2;{\theta }_0\right)$ about zero for some ${\theta }_0\in$ Θ.

Accordingly, the procedure of the conditional symmetry test takes the following two steps. First, we estimate $\xi \left(·,·;{\theta }_0\right)$ given N observations ${\left\{\left(V_{1i},V_{2i}\right)\right\}}_{i=1}^N$ and denote a consistent estimator of $\left(\xi ,{\theta }_0\right)$ as $\left(\widehat{\xi },\widehat{\theta }\right)$. Second, the test is conducted using ${\left\{{\widehat{U}}_i\right\}}_{i=1}^N:=$ ${\left\{\widehat{\xi }\left(V_1,V_2;\widehat{\theta }\right)\right\}}_{i=1}^N$. As before, the entire sample is split into two sub-samples ${\left\{{\widehat{X}}_i\right\}}_{i=1}^{n_1}:={\left\{{\widehat{U}}_i:{\widehat{U}}_i\ge 0\right\}}_{i=1}^{n_1}$ and ${\left\{{\widehat{Y}}_i\right\}}_{i=1}^{n_2}:={\left\{-{\widehat{U}}_i:{\widehat{U}}_i<0\right\}}_{i=1}^{n_2}$. Then, the test statistics, namely, $I_n\left(\widehat{\xi },\widehat{\theta }\right)$ and $I_{n_1,n_2}\left(\widehat{\xi },\widehat{\theta }\right)$ for equal ($n_1=n_2=n$) and unequal ($n_1\ne n_2$) sample sizes, can be obtained by replacing $\left(X,Y\right)=\left(X\left(\xi ,{\theta }_0\right),Y\left(\xi ,{\theta }_0\right)\right)$ in $I_n\left(\xi ,{\theta }_0\right)$ and $I_{n_1,n_2}\left(\xi ,{\theta }_0\right)$ with $\left(\widehat{X},\widehat{Y}\right)$, respectively.

Our remaining task is to demonstrate that there is no asymptotic cost in the test statistics with $\left(\xi ,{\theta }_0\right)$ replaced by its estimator $\left(\widehat{\xi },\widehat{\theta }\right)$, as long as $\left(\widehat{\xi },\widehat{\theta }\right)\stackrel{p}{\to }\left(\xi ,{\theta }_0\right)$ at a suitable rate of convergence. To control the convergence rate, we make Assumption 5 below. Observe that it allows for nonparametric rates of convergence; see Hansen [42], for instance, for uniform convergence rates of kernel estimators.

Assumption 5. 

$N^r∥\widehat{\theta }-{\theta }_0∥\stackrel{p}{\to }0$ and $N^r\left|\widehat{\xi }-\xi \right|\stackrel{p}{\to }0$ uniformly over ${\mathbb{R}}^{d+1}\times \Theta$ for some $r\in \left(0,1/2\right]$.

Theorem 3 below provides combinations of the shrinking rate q for b and the convergence rate r for $\left(\widehat{\xi },\widehat{\theta }\right)$ that can establish the first-order asymptotic equivalence between $n{b}^{1/4}{I}_n\left(\xi ,{\theta }_0\right)$ ($n_1{b}^{1/4}{I}_{n_1,n_2}\left(\xi ,{\theta }_0\right)$) and $n{b}^{1/4}{I}_n\left(\widehat{\xi },\widehat{\theta }\right)$ ($n_1{b}^{1/4}{I}_{n_1,n_2}\left(\widehat{\xi },\widehat{\theta }\right)$) when two sub-samples have equal (unequal) sample sizes.

Theorem 3. 

If Assumptions 1–5 hold, then under $H_0$,

$$n{b}^{1/4}{I}_n\left(\widehat{\xi },\widehat{\theta }\right)=n{b}^{1/4}{I}_n\left(\xi ,{\theta }_0\right)+o_p\left(1\right)$$

as $n\to \infty$ when $n_1=n_2=n$ and

$$n_1{b}^{1/4}{I}_{n_1,n_2}\left(\widehat{\xi },\widehat{\theta }\right)=n_1{b}^{1/4}{I}_{n_1,n_2}\left(\xi ,{\theta }_0\right)+o_p\left(1\right)$$

as $n_1\to \infty$ when $n_1/n_2\to \lambda \in \left(0,\infty \right)$, provided that $\left(q,r\right)$ belong to the set $\left\{\left(q,r\right):r>-5q/4+1,r>q/2,r\le 1/2\right\}$.

The set given in the theorem can be expressed as the triangular region formed by the corners $\left(2/5,1/2\right)$, $\left(4/7,2/7\right)$ and $\left(1,1/2\right)$ on the $q-r$ plane. The theorem also indicates that we must employ the sub-optimal smoothing parameter $b=o\left(n^{-2/5}\right)$ or undersmooth the observations to avoid additional cost of estimating $\left(\xi ,{\theta }_0\right)$, as is the case with other kernel-smoothed tests. Moreover, FMS set $b=o\left(n^{-4/9}\right)$ and obtain the lower bound of r as $4/9$. Indeed, the set provided in Theorem 3 overlaps the one derived by FMS $\left\{\left(q,r\right):q>4/9,r>4/9\right\}$.

4. Smoothing Parameter Selection

How to choose the value of the smoothing parameter b is an important practical problem. Nonetheless, it appears that the issue has not been well addressed in the literature on testing problems using asymmetric kernels. While Fernandes and Grammig [33] adopt a method inspired by Silverman’s [43] rule-of-thumb, FMS adjust the value chosen via cross validation. Both methods choose the smoothing parameter value from the viewpoint of optimality for density estimation. Such choices cannot be justified in theory or practice, because estimation-optimal values may not be equally optimal for testing purposes. In contrast, there are a few works on test-oriented smoothing parameter selection. For the test of equality in two unknown regression curves, Kulasekera and Wang [34,35], analytically explore the idea of choosing the smoothing parameter value that maximizes the power with the size preserved. Gao and Gijbels [44] combine this idea with the Edgeworth expansion for a bootstrap specification test of parametric regression models.

Below we tailor the procedure by Kulasekera and Wang [35] to the SSST. For a realistic setup, the case of $n_1\ne n_2$ is exclusively considered. Their basic idea is from sub-sampling. Without loss of generality assume that ${\left\{X_i\right\}}_{i=1}^{n_1}$ and ${\left\{Y_i\right\}}_{i=1}^{n_2}$ are ordered samples. Then, the entire sample $\left\{{\left\{X_i\right\}}_{i=1}^{n_1},{\left\{Y_i\right\}}_{i=1}^{n_2}\right\}$ can be split into M sub-samples, where $M=M_{n_1}$ is a non-stochastic sequence that satisfies $1/M+M/n_1\to 0$ as $n_1\to \infty$. Given such M and $\left(k_1,k_2\right):=\left(⌊n_1/M⌋,⌊n_2/M⌋\right)$, the mth sub-sample is defined as $\left\{{\left\{X_{m+\left(i-1\right)M}\right\}}_{i=1}^{k_1},{\left\{Y_{m+\left(i-1\right)M}\right\}}_{i=1}^{k_2}\right\},m=1,\dots ,M$. This sub-sample yields the analogues to (3) and (4) as

$$\begin{array}{cc}\hfill I_{k_1,k_2}\left(m\right)& =\sum _{j=1}^{k_1}\sum _{i=1,i\ne j}^{k_1}\frac{1}{k_1^2}{K}_{X_{m+\left(j-1\right)M}}\left(X_{m+\left(i-1\right)M}\right)+\sum _{j=1}^{k_2}\sum _{i=1,i\ne j}^{k_2}\frac{1}{k_2^2}{K}_{Y_{m+\left(j-1\right)M}}\left(Y_{m+\left(i-1\right)M}\right)\hfill \\ & -\sum _{j=1}^{k_2}\sum _{i=1,i\ne j}^{k_1}\frac{1}{k_1{k}_2}{K}_{Y_{m+\left(j-1\right)M}}\left(X_{m+\left(i-1\right)M}\right)-\sum _{j=1}^k\sum _{i=1,i\ne j}^{k_2}\frac{1}{k_1{k}_2}{K}_{X_{m+\left(j-1\right)M}}\left(Y_{m+\left(i-1\right)M}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_{\lambda }^2\left(m\right)& =2V_I\left(2\right)\left\{\frac{1}{k_1}\sum _{i=1}^{k_1}{X}_{m+\left(i-1\right)M}^{-1/2}{\widehat{f}}_m\left(X_{m+\left(i-1\right)M}\right)\right.+\left(\frac{k_1}{k_2}\right)\frac{1}{k_1}\sum _{i=1}^{k_1}{X}_{m+\left(i-1\right)M}^{-1/2}{\widehat{g}}_m\left(X_{m+\left(i-1\right)M}\right)\hfill \\ & +\left(\frac{k_1}{k_2}\right)\frac{1}{k_2}\sum _{i=1}^{k_2}{Y}_{m+\left(i-1\right)M}^{-1/2}{\widehat{f}}_m\left(Y_{m+\left(i-1\right)M}\right)\left.+{\left(\frac{k_1}{k_2}\right)}^2\frac{1}{k_2}\sum _{i=1}^{k_2}{Y}_{m+\left(i-1\right)M}^{-1/2}{\widehat{g}}_m\left(Y_{m+\left(i-1\right)M}\right)\right\},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\widehat{f}}_m\left(u\right)& =\frac{1}{k_1}\sum _{i=1}^{k_1}{K}_{GG}\left(X_{m+\left(i-1\right)M};u,b\right)\text{and}\hfill \\ \hfill {\widehat{g}}_m\left(u\right)& =\frac{1}{k_2}\sum _{i=1}^{k_2}{K}_{GG}\left(Y_{m+\left(i-1\right)M};u,b\right).\hfill \end{array}$$

It follows that the test statistic using the mth sub-sample becomes

$$T_{k_1,k_2}\left(m\right):=\frac{k_1{b}^{1/4}{I}_{k_1,k_2}\left(m\right)}{{\widehat{\sigma }}_{\lambda }\left(m\right)},m=1,\dots ,M.$$

Also denote the set of admissible values for $b=b_{n_1}$ as $H_{n_1}:=\left[\underline{B}{n}_1^{-q},\overline{B}{n}_1^{-q}\right]$ for some prespecified exponent $q\in \left(0,1\right)$ and two constants $0<\underline{B}<\overline{B}<\infty$. Moreover, let

$${\widehat{\pi }}_M\left(b_{k_1}\right):=\frac{1}{M}\sum _{m=1}^M\mathbf{1}\left\{T_{k_1,k_2}\left(m\right)>c_m\left(\alpha \right)\right\},$$

where $c_m\left(\alpha \right)$ is the critical value for the size α test using the mth sub-sample. We pick the power-maximized ${\widehat{b}}_{k_1}=\widehat{B}{k}_1^{-q}=arg{max}_{b_{k_1}\in H_{k_1}}{\widehat{\pi }}_M\left(b_{k_1}\right)$, and the smoothing parameter value ${\widehat{b}}_{n_1}:=\widehat{B}{n}_1^{-q}$ follows.

The behavior of ${\widehat{\pi }}_M\left(b_{k_1}\right)$ can be examined by considering the local alternative

$$H_1^{\prime }:f\left(u\right)=g\left(u\right)+\frac{h\left(u\right)}{\sqrt{n_1{b}^{1/4}}},$$

where $h\left(u\right)$ satisfies ${\int }_0^{\infty }h\left(u\right)du=0$ and $I_h:=$ ${\int }_0^{\infty }{h}^2\left(u\right)du\in \left(0,\infty \right)$. Also let $\pi \left(b_{n_1}\right):=Pr\left\{T_{n_1,n_2}>c\left(\alpha \right)\right\}$, where $c\left(\alpha \right)$ is the critical value for the size α test using the entire sample. For such $\pi \left(b_{n_1}\right)$, define $b_{n_1}^{*}:=B^{*}{n}_1^{-q}=arg{max}_{b_{n_1}\in H_{n_1}}\pi \left(b_{n_1}\right)$. Then, ${\widehat{b}}_{n_1}$ is optimal in the sense of Proposition 3. The proof is omitted, because it is a minor modification of the one for Theorem 2.1 of Kulasekera and Wang [35]; indeed it can be established by recognizing that $T_{n_1,n_2}\stackrel{d}{\to }N\left(I_h/{\sigma }_{\lambda },1\right)$ under $H_1^{\prime }$, as in Proposition 3 of Fernandes and Grammig [33].

Proposition 3. 

If Assumptions 1–4, $1/M+M/n_1\to 0$ and $n_1/n_2\to \lambda \in \left(0,\infty \right)$ hold, then $B^{*}/\widehat{B}\stackrel{p}{\to }1$ as $n_1\to \infty$.

We conclude this section by stating how to obtain ${\widehat{b}}_{n_1}$ in practice. Step 1 reflects that M should be divergent but smaller than both $n_1$ and $n_2$ in finite samples. Step 3 follows from the implementation methods in Kulasekera and Wang [34,35]. Finally, Step 4 considers that there may be more than one maximizer of ${\widehat{\pi }}_M\left(b_{k_1}\right)$.

Step 1: Choose some $\delta \in \left(0,1\right)$ and specify $M=min\left\{⌊n_1^{\delta }⌋,⌊n_2^{\delta }⌋\right\}$.

Step 2: Make M sub-samples of sizes $\left(k_1,k_2\right)=\left(⌊n_1/M⌋,⌊n_2/M⌋\right)$.

Step 3: Pick two constants $0<\underline{H}<\overline{H}<1$ and define $H_{k_1}=\left[\underline{H},\overline{H}\right]$.

Step 4: Set $c_m\left(\alpha \right)\equiv z_{\alpha }$ and find ${\widehat{b}}_{k_1}=inf\left\{arg{max}_{b_{k_1}\in H_{k_1}}{\widehat{\pi }}_M\left(b_{k_1}\right)\right\}$ by a grid search.

Step 5: Obtain $\widehat{B}={\widehat{b}}_{k_1}{k}_1^q$ and calculate ${\widehat{b}}_{n_1}=\widehat{B}{n}_1^{-q}$.

5. Finite-Sample Performance

5.1. Setup

It is widely recognized that asymptotic results on kernel-smoothed tests are not well transmitted to their finite-sample distributions, which reflects that omitted terms in the first-order asymptotics on the test statistics are highly sensitive to their smoothing parameter values in finite samples. On the other hand, Fernandes and Grammig [33] and FMS report superior finite-sample properties of asymmetric kernel-smoothed tests. To see which perspective dominates, this section investigates finite-sample performance of the test statistic for the SSST via Monte Carlo simulations.

To make a direct comparison with the results by FMS, we specialize in the conditional symmetry test using the same linear regression model $y={\beta }_0+{\beta }_{1}x+u$ as used in FMS. The data are generated in the following manner. First, the regressor x is drawn from $N\left(0,1\right)$. Second, the disturbance u, which is independent of x, is drawn from one of eight distributions with means of zero given in Table 1. Distributions with “S” (symmetric) and “A” (asymmetric) are used to investigate size and power properties of the test statistic, respectively. All the distributions are popularly chosen in the literature; the generalized lambda distribution (“GLD”) by Ramberg and Schmeiser [45], in particular, is known to nest a wide variety of symmetric and asymmetric distributions3. Finally, the dependent variable y is generated by setting ${\beta }_0={\beta }_1=1$.

Table 1. Distributions of the Disturbance u in the Simulation Study.

	Distribution	Skewness	Kurtosis
S1	$N\left(0,1\right)$	$0.00$	$3.00$
S2	$t_{10}$	$0.00$	$4.00$
S3	$DE\left(0,1\right)$ or Standard Laplace	$0.00$	$24.00$
S4	$U\left[-1,1\right]$ or GLD with $\left({\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\right)=\left(0,1,1,1\right)$	$0.00$	$1.80$
A1	$LN\left(0,1\right)-exp\left(1/2\right)$	$6.18$	$113.94$
A2	${\chi }_3^2-3$	$1.63$	$7.00$
A3	GLD with $\left({\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\right)=\left(12.601,-0.00980045,-0.11,-0.0001\right)$	$-2.92$	$19.52$
A4	GLD with $\left({\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\right)=\left(-9.7726,-0.0151878,-0.001,-0.13\right)$	$3.16$	$23.75$

Note: “S” and “A” stand for symmetric and asymmetric distributions, respectively. “GLD” denotes the generalized lambda distribution by Ramberg and Schmeiser [45]. The distribution is defined in terms of the inverse of the cumulative distribution function $F^{-1}\left(u\right)={\lambda }_1+\left\{u^{{\lambda }_3}+{\left(1-u\right)}^{{\lambda }_4}\right\}/{\lambda }_2$ for $u\in \left[0,1\right]$.

We are interested in testing symmetry of the conditional distribution of y given x. For this purpose the SSST is applied for the least-squares residual ${\widehat{u}}_i:=y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{x}_i$ using the sample ${\left\{\left(y_i,x_i\right)\right\}}_{i=1}^N$, where $\left({\widehat{\beta }}_0,{\widehat{\beta }}_1\right)$ are least-squares estimates of $\left({\beta }_0,{\beta }_1\right)$. Finite-sample size and power properties of the test statistic $T_{n_1,n_2}$ for two sub-samples with unequal sample sizes are examined against nominal 5% and 10% levels. The MG and NM kernels (denoted as “$T_{n_1,n_2}$-MG” and “$T_{n_1,n_2}$-NM”, respectively) are employed as examples of the GG kernels.

Finite-sample properties of $T_{n_1,n_2}$-MG and $T_{n_1,n_2}$-NM are evaluated in comparison with other versions of the SSST. First, two versions of FMS’s original test statistic built on an equivalence to our $I_n$ using the G kernel are considered. “FMS-G-O” is FMS’s truly original statistic, whereas “FMS-G-AltVar” is the one with the variance estimator replaced by ${\widehat{\sigma }}_{\lambda }^2$ given in Theorem 2. Second, $T_{n_1,n_2}$ using the G kernel (denoted as “$T_{n_1,n_2}$-G”) is also calculated. Notice that FMS-G-AltVar and $T_{n_1,n_2}$-G take exactly the same form. The only difference is the method of choosing the smoothing parameter b, which will be discussed shortly. Effects of changing the variance estimator, the method of choosing b, and the kernel choice can be examined by weighing FMS-G-O with FMS-G-AltVar, FMS-G-AltVar with $T_{n_1,n_2}$-G, and $T_{n_1,n_2}$-G with $T_{n_1,n_2}$-MG or $T_{n_1,n_2}$-NM, respectively.

The smoothing parameter b for FMS-G-O and FMS-G-AltVar is determined via making an adjustment for the value chosen by a cross-validation criterion; see p. 657 of FMS for details. On the other hand, the values of b for $T_{n_1,n_2}$-G, $T_{n_1,n_2}$-MG and $T_{n_1,n_2}$-NM are selected by the power-optimality criterion in the previous section. Implementation details are as follows: (i) all critical values in ${\widehat{\pi }}_M\left(b_{k_1}\right)$ are set at $z_{0.05}=1.645$; (ii) the shrinking rate of b is set at $q=4/9$ because of $N^{1/2}$-consistency of least-squares estimates and Theorem 3; (iii) three different values are considered for δ, namely, $\delta \in \left\{0.3,0.5,0.7\right\}$; and (iv) the interval for $b_{k_1}$ is set equal to $H_{k_1}=\left[0.01,0.64\right]$. The sample size is $N\in \left\{50,100,200\right\}$, and 1000 replications are drawn for each combination of the sample size N and the distribution of u.

5.2. Simulation Results

Table 2 presents finite-sample rejection frequencies of each test statistic against nominal 5% and 10% levels across 1000 Monte Carlo samples. Critical values are simply based on the first-order normal limit, i.e., $1.645$ and $1.280$ correspond to the 5% and 10% levels, respectively.

Table 2. Size and Power of the SSST.

(A) Size														(%)
N	Test	δ		Distribution
				S1			S2			S3			S4
				5%	10%		5%	10%		5%	10%		5%	10%
50	FMS-G-O	−		4.8	9.4		4.9	9.5		6.0	10.8		7.4	12.6
	FMS-G-AltVar	−		4.7	9.3		4.4	8.9		5.8	10.9		6.9	12.6
	$T_{n_1,n_2}$-G	0.3		3.5	7.5		3.1	7.0		4.5	8.7		5.2	9.6
		0.5		3.8	6.8		3.0	7.3		4.4	7.9		5.4	10.2
		0.7		3.4	6.7		3.4	7.3		4.5	8.9		5.4	10.5
	$T_{n_1,n_2}$-MG	0.3		3.6	7.7		3.9	7.5		4.9	9.5		5.3	9.7
		0.5		4.0	7.2		3.7	7.2		4.9	8.7		5.4	10.2
		0.7		3.3	6.8		3.8	7.3		4.7	9.1		5.3	10.7
	$T_{n_1,n_2}$-NM	0.3		3.4	7.3		3.1	6.7		4.3	8.3		5.2	9.3
		0.5		3.9	6.7		3.1	6.4		4.2	7.9		5.2	9.8
		0.7		3.3	7.0		3.1	6.4		4.4	8.1		5.2	10.3
100	FMS-G-O	−		5.2	9.8		6.7	10.8		5.6	10.1		7.4	12.5
	FMS-G-AltVar	−		4.9	8.9		6.4	10.6		5.3	9.9		6.6	12.6
	$T_{n_1,n_2}$-G	0.3		4.0	7.0		6.1	9.3		5.1	8.8		7.3	11.9
		0.5		3.6	7.3		5.8	9.1		5.2	8.9		7.1	11.4
		0.7		3.8	7.6		5.9	9.5		4.8	9.3		6.6	11.8
	$T_{n_1,n_2}$-MG	0.3		4.5	7.4		6.2	9.5		5.8	9.6		7.3	12.1
		0.5		3.7	7.7		6.1	9.6		5.7	9.0		7.2	11.6
		0.7		3.8	8.1		5.8	9.6		5.1	9.4		6.7	12.1
	$T_{n_1,n_2}$-NM	0.3		4.2	6.8		5.3	8.9		4.3	8.4		7.1	12.4
		0.5		4.0	6.6		5.3	8.7		4.9	8.7		7.2	11.6
		0.7		4.2	6.8		5.3	8.8		4.9	8.4		7.3	11.7
200	FMS-G-O	−		4.1	7.3		6.0	9.3		5.8	8.9		8.9	14.1
	FMS-G-AltVar	−		4.1	7.0		6.1	8.9		5.4	9.3		8.7	15.1
	$T_{n_1,n_2}$-G	0.3		3.3	6.3		4.9	8.0		4.9	8.7		8.9	12.9
		0.5		3.2	6.4		4.9	8.6		5.3	8.7		8.7	13.3
		0.7		3.5	6.8		5.2	9.2		5.4	8.9		8.4	13.9
	$T_{n_1,n_2}$-MG	0.3		3.5	6.7		5.5	8.4		5.5	9.4		9.0	13.4
		0.5		3.5	6.8		5.2	9.0		5.7	8.8		8.7	13.6
		0.7		3.5	7.0		5.5	9.8		5.7	9.1		8.6	13.7
	$T_{n_1,n_2}$-NM	0.3		3.5	6.0		4.0	7.5		4.4	8.5		8.7	13.3
		0.5		3.6	5.9		4.4	7.6		4.4	8.4		8.7	13.3
		0.7		3.6	5.8		4.6	7.4		4.5	8.4		8.8	13.1
(B) Power														(%)
N	Test	δ		Distribution
				A1			A2			A3			A4
				5%	10%		5%	10%		5%	10%		5%	10%
50	FMS-G-O	−		42.0	51.6		21.4	30.3		26.3	37.2		28.8	40.8
				[43.7]	[52.4]		[22.7]	[31.0]		[27.6]	[38.1]		[30.5]	[42.0]
	FMS-G-AltVar	−		24.9	37.0		13.3	22.4		39.8	52.2		43.1	55.3
				[27.5]	[39.0]		[13.9]	[24.1]		[41.5]	[53.6]		[44.9]	[57.4]
	$T_{n_1,n_2}$-G	0.3		31.3	41.5		17.3	24.7		30.8	41.3		33.8	44.3
				[35.4]	[46.6]		[20.8]	[29.5]		[35.1]	[46.3]		[38.7]	[50.8]
		0.5		29.5	39.7		16.0	23.8		29.4	39.1		31.4	42.9
		0.7		27.8	38.7		14.5	22.6		28.0	36.8		30.2	40.6
	$T_{n_1,n_2}$-MG	0.3		32.1	42.2		17.9	25.8		31.6	41.8		35.5	45.5
				[35.2]	[45.7]		[20.9]	[29.3]		[35.0]	[45.8]		[39.1]	[49.5]
		0.5		30.1	40.8		16.5	24.5		30.2	40.3		32.2	43.1
		0.7		28.0	38.9		15.1	23.0		28.5	37.5		30.8	41.1
	$T_{n_1,n_2}$-NM	0.3		33.8	42.5		18.2	25.2		32.9	42.5		35.2	46.5
				[36.6]	[48.8]		[20.7]	[30.4]		[36.8]	[48.5]		[39.2]	[53.5]
		0.5		33.5	42.2		17.7	24.9		32.4	42.2		34.6	45.8
		0.7		33.0	41.4		17.4	24.2		32.2	41.6		34.5	45.7
100	FMS-G-O	−		73.0	81.5		41.4	51.4		59.1	71.2		64.2	74.6
				[72.7]	[81.8]		[40.7]	[52.3]		[58.7]	[71.8]		[63.8]	[74.6]
	FMS-G-AltVar	−		56.4	70.2		30.3	43.4		73.7	80.7		77.2	83.7
				[58.1]	[71.6]		[32.2]	[44.4]		[74.4]	[81.8]		[78.1]	[84.4]
	$T_{n_1,n_2}$-G	0.3		72.3	80.5		37.9	48.6		70.3	78.4		74.1	80.5
				[75.4]	[84.4]		[40.2]	[54.9]		[72.8]	[82.3]		[76.1]	[84.1]
		0.5		67.1	77.2		33.9	45.0		65.2	75.7		69.5	78.2
		0.7		62.9	73.6		31.9	42.5		61.7	72.3		65.2	75.8
	$T_{n_1,n_2}$-MG	0.3		73.1	80.2		38.3	49.3		70.5	78.3		73.6	81.0
				[74.8]	[83.6]		[40.9]	[53.5]		[72.4]	[80.7]		[75.4]	[83.3]
		0.5		67.4	77.5		34.6	45.4		65.6	75.4		69.5	77.9
		0.7		62.9	73.5		32.0	42.3		62.2	72.5		65.3	75.2
	$T_{n_1,n_2}$-NM	0.3		76.8	84.0		41.7	51.9		75.5	82.1		76.8	84.0
				[79.6]	[87.2]		[44.8]	[58.0]		[77.6]	[85.0]		[79.7]	[86.9]
		0.5		77.0	84.0		40.1	51.0		75.1	82.0		75.7	83.0
		0.7		76.4	83.7		39.6	50.1		74.9	81.9		75.6	82.9
200	FMS-G-O	−		97.4	98.3		71.5	80.7		95.6	98.1		97.1	97.8
				[97.8]	[98.6]		[75.0]	[84.2]		[96.9]	[98.6]		[97.4]	[98.4]
	FMS-G-AltVar	−		93.4	96.3		60.4	72.8		98.7	99.0		98.4	99.1
				[95.2]	[97.5]		[69.1]	[78.5]		[98.8]	[99.2]		[99.0]	[99.2]
	$T_{n_1,n_2}$-G	0.3		97.7	99.1		77.0	84.8		98.6	99.1		98.6	99.2
				[98.7]	[99.4]		[82.7]	[90.3]		[98.8]	[99.4]		[98.9]	[99.2]
		0.5		97.2	98.1		71.3	80.9		97.7	98.9		97.9	98.7
		0.7		96.4	97.6		65.4	75.8		96.7	98.8		97.2	98.3
	$T_{n_1,n_2}$-MG	0.3		97.9	99.1		76.2	85.3		98.6	99.1		98.5	99.1
				[98.6]	[99.4]		[81.8]	[89.8]		[98.7]	[99.4]		[98.7]	[99.2]
		0.5		97.3	98.1		71.4	80.3		97.6	98.9		97.9	98.6
		0.7		96.5	97.6		65.5	75.9		96.7	98.7		97.2	98.3
	$T_{n_1,n_2}$-NM	0.3		98.9	99.0		84.8	91.1		98.8	99.2		98.6	98.9
				[99.0]	[99.2]		[91.1]	[95.8]		[99.4]	[99.7]		[99.5]	[99.7]
		0.5		96.8	97.0		81.2	88.2		98.3	98.6		98.4	98.6
		0.7		95.6	95.7		80.9	88.3		98.3	98.6		98.4	98.6

Note: Numbers in brackets are size-adjusted powers.

Panel (A) reports size properties. At first glance, we can find that the results of FMS-G-O are close to what is reported in Table 3 of FMS. It has the tendency of over-rejecting the null slightly against the nominal size. Comparing FMS-G-O with FMS-G-AltVar reveals that replacing the variance formula is likely to decrease the rejection frequencies. Changing the choice method of b further reduces the rejection frequencies, and $T_{n_1,n_2}$-G tends to result in mild under-rejection of the null. Effects of alternative kernel choices are mixed. While $T_{n_1,n_2}$-G and $T_{n_1,n_2}$-MG have similar size properties, $T_{n_1,n_2}$-NM looks more conservative in the sense that its rejection frequencies are slightly smaller. Impacts of varying δ are found to be minor at best. A concern is that all test statistics exhibit size distortions for S4. However, the distribution is platykurtic and has sharp boundaries at $\pm 1$. A platykurtic distribution is an exception rather than a rule in economics and finance, and a distribution with a compact support violates Assumption 1. In sum, all test statistics exhibit good size properties, although their convergence rates are nonparametric ones, effective sample sizes are (roughly) a half of the entire sample size N, and no size correction devices such as bootstrapping are used.

Panel (B) refers to power properties. We can immediately see that the rejection frequencies of each test statistic approach to one with the sample size N, which confirms consistency of the SSST. There is substantial improvement in power as the sample size increases from $N=50$ to 100. Most of rejection frequencies become nearly one for as small as $N=200$. After a closer look, we can find it hard to judge whether changing the variance formula from FMS-G-O to FMS-G-AltVar may affect power properties favorably or adversely. However, once the smoothing parameter value is chosen via the power-optimality criterion, power properties are improved in general. Power properties of $T_{n_1,n_2}$-G and $T_{n_1,n_2}$-MG again look alike, whereas $T_{n_1,n_2}$-NM appears to be more powerful than these two. Because the power tends to decrease with δ, it could be safe to choose $\delta =0.3$ from the viewpoint of power-maximization. Indeed, for $N=200$ and $\delta =0.3$, each of $T_{n_1,n_2}$-G, $T_{n_1,n_2}$-MG and $T_{n_1,n_2}$-NM exhibits better power properties than FMS-G-O and FMS-G-AltVar.

For convenience, Panel (B) presents size-adjusted powers, where the best case scenario (i.e., $\delta =0.3$) is considered for $T_{n_1,n_2}$-G, $T_{n_1,n_2}$-MG and $T_{n_1,n_2}$-NM. These three test statistics again outperform FMS’s original statistics in terms of size-adjusted powers, and $T_{n_1,n_2}$-NM appears to have the best power properties among three. All in all, Monte Carlo results indicate superior size and power properties of the SSST with the GG kernels plugged in.

6. Conclusions

The SSST developed by FMS is built on the idea of gauging the closeness between right and left sides of the axis of symmetry of an unknown pdf. To implement the test, we split the entire sample into two sub-samples and estimate both sides of the pdf nonparametrically using asymmetric kernels with support on $\left[0,\infty \right)$. This paper has improved the SSST by combining it with the newly proposed GG kernels. The test statistic can be interpreted as a standardized version of a degenerate U-statistic. We deliver convergence properties of the test statistic and provide the asymptotic variance formulae for the cases of two sub-samples with equal and unequal sample sizes separately. It is demonstrated that the SSST smoothed by the GG kernels has a normal limit under the null of symmetry and is consistent under the alternative. As a part of the implementation method we also propose to select the smoothing parameter in a power-optimality criterion. Monte Carlo simulations indicate that the GG kernel-smoothed SSST with the power-maximized smoothing parameter value plugged in enjoys superior finite-sample properties. It should be stressed that the good performance of the SSST is grounded on the first-order normal limit and a small number of observations, despite its nonparametric convergence rate and sample-splitting procedure.

Appendix A.1. Proof of Lemma 1

Because the proof for the MG kernel is basically the same as those for Lemmata 1(e) and 2 of FMS, we prove the case of the NM kernel. Among all statements, we concentrate on demonstrating that

$$\begin{array}{cc}\hfill E\left\{K_{X_2}\left(X_1\right)K_{Y_2}\left(X_1\right)\right\}& \sim E\left\{f\left(X\right)g\left(X\right)\right\},\text{and}\hfill \end{array}$$

(A1)

$$\begin{array}{cc}\hfill E\left\{K_{X_2}\left(Y_1\right)K_{Y_1}\left(X_2\right)\right\}& \sim b^{-1/2}{V}_I\left(2\right)E\left\{X^{-1/2}g\left(X\right)\right\}.\hfill \end{array}$$

(A2)

All the remaining statements can be shown in the same manner. To approximate the gamma function, we frequently refer to the following well-known formulae:

• Stirling’s formula (“SF”):

  $$\Gamma \left(z+1\right)=\sqrt{2\pi }{z}^{z+1/2}{e}^{-z}\left\{1+\frac{1}{12z}+\frac{1}{288z^2}+O\left(z^{-3}\right)\right\}\text{as}z\to \infty .$$
• Legendre’s duplication formula (“LDF”):

  $$\Gamma \left(z\right)\Gamma \left(z+\frac{1}{2}\right)=\frac{\sqrt{\pi }}{2^{2z-1}}\Gamma \left(2z\right)\text{for}z>0.$$

In addition, proofs of the above statements require the following lemma. Its proof is virtually the same as those for Lemmata A.1 and A.2 of Fernandes and Monteiro [46], and thus it is omitted.

Lemma A1. 

For a constant $D>0$ and two numbers $x,y>0$,

$$exp\left\{-\frac{{\left(y-x\right)}^2}{Dx}\right\}\le {\left(\frac{x}{y}\right)}^{\frac{y-x}{D}}\le exp\left\{-\frac{{\left(y-x\right)}^2}{Dx}+\frac{{\left(y-x\right)}^3}{2D{x}^2}\right\}$$

(A3)

if $x\le y$, and

$$exp\left\{-\frac{{\left(y-x\right)}^2}{Dx}+\frac{{\left(y-x\right)}^3}{2D{y}^2}\right\}\le {\left(\frac{x}{y}\right)}^{\frac{y-x}{D}}\le exp\left\{-\frac{{\left(y-x\right)}^2}{Dx}\right\}$$

(A4)

if $y<x$.

Proof of (A1). 

We apply the trimming argument as on p. 476 of Chen [30]. For some $ϵ\in \left(0,1/2\right)$,

$$\begin{array}{cc}& E\left\{K_{X_2}\left(X_1\right)K_{Y_2}\left(X_1\right)\right\}\hfill \\ & ={\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{b^{1-ϵ}}^{\infty }\left\{{\int }_0^{\infty }{L}_b\left(u;x,y\right)f\left(x_1\right)d{x}_1\right\}g\left(y\right)dy\right]f\left(x\right)dx+O\left(b^{1-ϵ}\right),\hfill \end{array}$$

where $L_b\left(u;x,y\right):=K_{NM}\left(u;x,b\right)K_{NM}\left(u;y,b\right)$ for interior $x,y$. Then, the proof takes a multi-step approach including the following steps:

Step 1: approximating $J\left(x,y\right):={\int }_0^{\infty }{L}_b\left(u;x,y\right)f\left(u\right)du.$

Step 2: approximating $J:={\int }_{b^{1-ϵ}}^{\infty }\left\{{\int }_{b^{1-ϵ}}^{\infty }J\left(x,y\right)g\left(y\right)dy\right\}f\left(x\right)dx.$

Step 1:  Define

$$P_z\left(b\right):=\frac{z\Gamma \left(\frac{z}{2b}\right)}{\Gamma \left(\frac{z}{2b}+\frac{1}{2}\right)}$$

(A5)

for $z=x,y,x+y$. Then,

$$\begin{array}{cc}\hfill L_b\left(u;x,y\right)& =\frac{2{\left\{P_x\left(b\right)P_y\left(b\right)/\sqrt{P_x^2\left(b\right)+P_y^2\left(b\right)}\right\}}^{\frac{x+y}{b}-1}\Gamma \left(\frac{x+y}{2b}-\frac{1}{2}\right)}{P_x^{x/b}\left(b\right)\Gamma \left(\frac{x}{2b}\right)P_y^{y/b}\left(b\right)\Gamma \left(\frac{y}{2b}\right)}\hfill \\ & \times \frac{2u^{\left(\frac{x+y}{b}-1\right)-1}exp\left[-{\left\{\frac{u}{P_x\left(b\right)P_y\left(b\right)/\sqrt{P_x^2\left(b\right)+P_y^2\left(b\right)}}\right\}}^2\right]}{{\left\{P_x\left(b\right)P_y\left(b\right)/\sqrt{P_x^2\left(b\right)+P_y^2\left(b\right)}\right\}}^{\frac{x+y}{b}-1}\Gamma \left(\frac{x+y}{2b}-\frac{1}{2}\right)},\hfill \end{array}$$

(A6)

where the first term is denoted as $B_b\left(x,y\right)$, and the second term can be viewed as the pdf of $GG\left(\left(x+y\right)/b-1,P_x\left(b\right)P_y\left(b\right)/\sqrt{P_x^2\left(b\right)+P_y^2\left(b\right)},2\right)$. Moreover, $B_b\left(x,y\right)$ can be further rewritten as

$$B_{1b}{B}_{2b}{B}_{3b}:=\frac{2\Gamma \left(\frac{x+y}{2b}-\frac{1}{2}\right)}{\Gamma \left(\frac{x}{2b}\right)\Gamma \left(\frac{y}{2b}\right)}\frac{{\left\{P_x^2\left(b\right)+P_y^2\left(b\right)\right\}}^{1/2}}{P_x\left(b\right)P_y\left(b\right)}\frac{P_x^{y/b}\left(b\right)P_y^{x/b}\left(b\right)}{{\left\{P_x^2\left(b\right)+P_y^2\left(b\right)\right\}}^{\frac{x+y}{2b}}},$$

(A7)

and an approximation to each of $B_{1b}$, $B_{2b}$ and $B_{3b}$ is provided separately.

By LDF, $B_{1b}$ becomes

$$B_{1b}=\left(\frac{2}{\frac{x+y}{2b}-\frac{1}{2}}\right)\frac{\Gamma \left(\frac{x+y}{2b}+\frac{1}{2}\right)}{\Gamma \left(\frac{x}{2b}\right)\Gamma \left(\frac{y}{2b}\right)}=\frac{b\sqrt{\pi }}{2^{\frac{x+y}{b}-3}\left(x+y-b\right)}\frac{\Gamma \left(\frac{x+y}{2b}\right)}{\Gamma \left(\frac{x}{2b}\right)\Gamma \left(\frac{y}{2b}\right)\Gamma \left(\frac{x+y}{2b}\right)}.$$

Then, by SF, an approximation to $B_{1b}$ is given by

$$B_{1b}=\sqrt{\frac{2}{\pi }}\left(\frac{\sqrt{xy}}{x+y}\right){\left(\frac{x+y}{x}\right)}^{\frac{x}{2b}}{\left(\frac{x+y}{y}\right)}^{\frac{y}{2b}}\left\{1+o\left(1\right)\right\}.$$

(A8)

Next, it follows from LDF and SF that

$$P_z\left(b\right)=\frac{2^{z/b-1}}{\sqrt{\pi }}\frac{z{\Gamma }^2\left(\frac{z}{2b}\right)}{\Gamma \left(\frac{z}{b}\right)}={\left(2bz\right)}^{1/2}\left\{1+\frac{b}{4z}+O\left(b^2\right)\right\}.$$

(A9)

Hence,

$$B_{2b}^2=\frac{1}{P_x^2\left(b\right)}+\frac{1}{P_y^2\left(b\right)}=\frac{b^{-1}}{2}\left(\frac{x+y}{xy}\right)\left\{1+o\left(1\right)\right\},$$

and thus

$$B_{2b}=\frac{b^{-1/2}}{\sqrt{2}}\left(\frac{\sqrt{x+y}}{\sqrt{xy}}\right)\left\{1+o\left(1\right)\right\}.$$

(A10)

Furthermore, (A9) also implies that

$$\begin{array}{cc}\hfill P_x^{y/b}\left(b\right)& ={\left(2bx\right)}^{\frac{y}{2b}}exp\left(\frac{y}{4x}\right)\left\{1+o\left(1\right)\right\};\hfill \\ \hfill P_y^{x/b}\left(b\right)& ={\left(2by\right)}^{\frac{x}{2b}}exp\left(\frac{x}{4y}\right)\left\{1+o\left(1\right)\right\};\text{and}\hfill \\ \hfill {\left\{P_x^2\left(b\right)+P_y^2\left(b\right)\right\}}^{\frac{x+y}{2b}}& ={\left\{2b\left(x+y\right)\right\}}^{\frac{x+y}{2b}}exp\left(\frac{1}{2}\right)\left\{1+o\left(1\right)\right\}.\hfill \end{array}$$

Then,

$$B_{3b}=x^{\frac{y}{2b}}{y}^{\frac{x}{2b}}{\left(x+y\right)}^{-\frac{x+y}{2b}}exp\left\{\frac{1}{4}\left(\frac{y}{x}-1\right)\right\}exp\left\{\frac{1}{4}\left(\frac{x}{y}-1\right)\right\}\left\{1+o\left(1\right)\right\}.$$

(A11)

Substituting (A8), (A10) and (A11) into (A7) finally yields

$$B_b\left(x,y\right):=b^{-1/2}{\tilde{B}}_b\left(x,y\right){\left(\frac{x}{y}\right)}^{\frac{y-x}{2b}}\left\{1+o\left(1\right)\right\},$$

where

$${\tilde{B}}_b\left(x,y\right)=\frac{1}{\sqrt{\pi }\sqrt{x+y}}exp\left\{\frac{1}{4}\left(\frac{y}{x}-1\right)\right\}exp\left\{\frac{1}{4}\left(\frac{x}{y}-1\right)\right\}.$$

Then, for a random variable ${\zeta }_x\stackrel{d}{=}GG\left(\left(x+y\right)/b-1,P_x\left(b\right)P_y\left(b\right)/\sqrt{P_x^2\left(b\right)+P_y^2\left(b\right)},2\right)$,

$$\begin{array}{cc}\hfill J\left(x,y\right)& ={\int }_0^{\infty }{L}_b\left(u;x,y\right)f\left(u\right)du\left\{1+o\left(1\right)\right\}\hfill \\ & =b^{-1/2}{\tilde{B}}_b\left(x,y\right){\left(\frac{x}{y}\right)}^{\frac{y-x}{2b}}E\left\{f\left({\zeta }_x\right)\right\}\left\{1+o\left(1\right)\right\}.\hfill \end{array}$$

By the property of GG random variables, (A5), (A9), and (A10),

$$E\left({\zeta }_x\right)=B_{2b}^{-1}\frac{\Gamma \left(\frac{x+y}{2b}\right)}{\Gamma \left(\frac{x+y}{2b}-\frac{1}{2}\right)}=\sqrt{xy}\left\{1+O\left(b\right)\right\}.$$

In the end, a first-order Taylor expansion of $f\left({\zeta }_x\right)$ around ${\zeta }_x=\sqrt{xy}$ gives

$$J\left(x,y\right)=b^{-1/2}{\tilde{B}}_b\left(x,y\right)f\left(\sqrt{xy}\right){\left(\frac{x}{y}\right)}^{\frac{y-x}{2b}}\left\{1+o\left(1\right)\right\},$$

which completes Step 1.

Step 2:  For some $t\in \left(0,1\right)$, we split the interval for y into four subintervals as follows:

$$\begin{array}{cc}\hfill J& ={\int }_{b^{1-ϵ}}^{\infty }\left\{{\int }_{b^{1-ϵ}}^{\left(1-t\right)x}+{\int }_{\left(1-t\right)x}^x+{\int }_x^{\left(1+t\right)x}+{\int }_{\left(1+t\right)x}^{\infty }J\left(x,y\right)g\left(y\right)dy\right\}f\left(x\right)dx\hfill \\ & =J_1+J_2+J_3+J_4\text{(say)}.\hfill \end{array}$$

Also denote $h\left(x,y\right):={\tilde{B}}_b\left(x,y\right)f\left(\sqrt{xy}\right)g\left(y\right)$. Then, by (A4) and the change of variable $v:=\left(y-x\right)/\sqrt{2bx}$,

$$\begin{array}{cc}\hfill J_1& \le {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_0^{\left(1-t\right)x}{b}^{-1/2}h\left(x,y\right)exp\left\{-\frac{{\left(y-x\right)}^2}{2bx}\right\}\left\{1+o\left(1\right)\right\}dy\right]f\left(x\right)dx\hfill \\ & \le {\int }_{b^{1-ϵ}}^{\infty }\sqrt{2x}\left[{\int }_{-\frac{1}{\sqrt{2}}\sqrt{\frac{x}{b}}}^{-\frac{t}{\sqrt{2}}\sqrt{\frac{x}{b}}}h\left(x,x+v\sqrt{2bx}\right)e^{-v^2}\left\{1+o\left(1\right)\right\}dv\right]f\left(x\right)dx\to 0\hfill \end{array}$$

as $b\to 0$.

Next, it follows from (A4) that

$$\begin{array}{cc}\hfill J_2& \ge {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{\left(1-t\right)x}^x{b}^{-1/2}h\left(x,y\right)exp\left\{-\frac{{\left(y-x\right)}^2}{2bx}+\frac{{\left(y-x\right)}^3}{4b{y}^2}\right\}\left\{1+o\left(1\right)\right\}dy\right]f\left(x\right)dx\hfill \\ & \ge {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{\left(1-t\right)x}^x{b}^{-1/2}h\left(x,y\right)exp\left\{-\frac{{\left(y-x\right)}^2}{2bx}\left(1+{\tau }_1\right)\right\}\left\{1+o\left(1\right)\right\}dy\right]f\left(x\right)dx,\hfill \end{array}$$

where ${\tau }_1:=t\left(2-t\right)/\left\{2{\left(1-t\right)}^2\right\}$. By the change of variable $w:=\left(y-x\right)\sqrt{\left(1+{\tau }_1\right)/\left(2bx\right)}$, the right-hand side becomes

$${\int }_{b^{1-ϵ}}^{\infty }\sqrt{\frac{2x}{1+{\tau }_1}}\left[{\int }_{-t\sqrt{\frac{1+{\tau }_1}{2}}\sqrt{\frac{x}{b}}}^{0}h\left(x,x+w\sqrt{\frac{2bx}{1+{\tau }_1}}\right)e^{-w^2}\left\{1+o\left(1\right)\right\}dw\right]f\left(x\right)dx.$$

Because ${\int }_{-\infty }^0{e}^{-v^2}dv=\sqrt{\pi }/2$ and $h\left(x,x\right)=f\left(x\right)g\left(x\right)/\sqrt{2\pi x}$, we have

$$lim\underset{b\to 0}{inf}{J}_2=\frac{1}{2}\sqrt{\frac{1}{1+{\tau }_1}}{\int }_0^{\infty }f\left(x\right)g\left(x\right)dF\left(x\right)\to \frac{1}{2}E\left\{f\left(X\right)g\left(X\right)\right\}$$

by letting t shrink toward zero. On the other hand, again by (A4) and the change of variable $v=\left(y-x\right)/\sqrt{2bx}$,

$$\begin{array}{cc}\hfill J_2& \le {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{\left(1-t\right)x}^x{b}^{-1/2}h\left(x,y\right)exp\left\{-\frac{{\left(y-x\right)}^2}{2bx}\right\}\left\{1+o\left(1\right)\right\}dy\right]f\left(x\right)dx\hfill \\ & \le {\int }_{b^{1-ϵ}}^{\infty }\sqrt{2x}\left[{\int }_{-\frac{t}{\sqrt{2}}\sqrt{\frac{x}{b}}}^{0}h\left(x,x+v\sqrt{2bx}\right)e^{-v^2}\left\{1+o\left(1\right)\right\}dv\right]f\left(x\right)dx,\hfill \end{array}$$

so that

$$lim\underset{b\to 0}{sup}{J}_2=\frac{1}{2}{\int }_0^{\infty }f\left(x\right)g\left(x\right)dF\left(x\right)=\frac{1}{2}E\left\{f\left(X\right)g\left(X\right)\right\}.$$

Hence, we can conclude that $J_2\to \left(1/2\right)E\left\{f\left(X\right)g\left(X\right)\right\}$.

It can be also demonstrated that $J_3\to \left(1/2\right)E\left\{f\left(X\right)g\left(X\right)\right\}$ and $J_4\to 0$ with the assistance of (A3). Therefore, $J\to E\left\{f\left(X\right)g\left(X\right)\right\}$, and thus (A1) is established.   □

Proof of (A2).  Again for some $ϵ\in \left(0,1/2\right)$,

$$E\left\{K_{X_2}\left(Y_1\right)K_{Y_1}\left(X_2\right)\right\}={\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{b^{1-ϵ}}^{\infty }{M}_b\left(x,y\right)g\left(y\right)dy\right]f\left(x\right)dx+O\left(b^{-ϵ}\right),$$

where ${\Lambda }_b\left(x,y\right):=K_{NM}\left(y;x,b\right)K_{NM}\left(x;y,b\right)$ for interior $x,y$ and the order of the remainder term is $O\left(b^{-ϵ}\right)=o\left(b^{-1/2}\right)$ by construction. Observe that

$${\Lambda }_b\left(x,y\right)=\frac{4y^{x/b-1}{x}^{y/b-1}}{P_x^{x/b}\left(b\right)P_y^{y/b}\left(b\right)\Gamma \left(\frac{x}{2b}\right)\Gamma \left(\frac{y}{2b}\right)}exp\left\{-\frac{y^2}{P_x^2\left(b\right)}\right\}exp\left\{-\frac{x^2}{P_y^2\left(b\right)}\right\}.$$

(A12)

It follows from (A9) that

$$P_z^{z/b}\left(b\right)={\left(2bz\right)}^{\frac{z}{2b}}exp\left(\frac{1}{4}\right)\left\{1+o\left(1\right)\right\}$$

(A13)

for $z=x,y$. Similarly,

$$\begin{array}{cc}\hfill exp\left\{-\frac{y^2}{P_x^2\left(b\right)}\right\}& =exp\left(-\frac{y^2}{2bx}\right)exp\left\{\frac{1}{4}{\left(\frac{y}{x}\right)}^2\right\}\left\{1+o\left(1\right)\right\},\text{and}\hfill \end{array}$$

(A14)

$$\begin{array}{cc}\hfill exp\left\{-\frac{x^2}{P_y^2\left(b\right)}\right\}& =exp\left(-\frac{x^2}{2by}\right)exp\left\{\frac{1}{4}{\left(\frac{x}{y}\right)}^2\right\}\left\{1+o\left(1\right)\right\}.\hfill \end{array}$$

(A15)

Substituting (A13)–(A15) into (A12) and using SF, we have

$$\begin{array}{cc}\hfill {\Lambda }_b\left(x,y\right)& =\frac{b^{-1}}{\pi \sqrt{x}\sqrt{y}}{\left(\frac{x}{y}\right)}^{\left(y-x\right)/b}exp\left\{-\frac{\left(y+x\right){\left(y-x\right)}^2}{2bxy}\right\}\hfill \\ & \times exp\left[\frac{1}{4}\left\{{\left(\frac{y}{x}\right)}^2-1\right\}\right]exp\left[\frac{1}{4}\left\{{\left(\frac{x}{y}\right)}^2-1\right\}\right]\left\{1+o\left(1\right)\right\}.\hfill \end{array}$$

As before, for some $t\in \left(0,1\right)$, consider

$$\begin{array}{cc}\hfill \Lambda & ={\int }_{b^{1-ϵ}}^{\infty }\left\{{\int }_{b^{1-ϵ}}^{\left(1-t\right)x}+{\int }_{\left(1-t\right)x}^x+{\int }_x^{\left(1+t\right)x}+{\int }_{\left(1+t\right)x}^{\infty }{\Lambda }_b\left(x,y\right)g\left(y\right)dy\right\}f\left(x\right)dx\hfill \\ & ={\Lambda }_1+{\Lambda }_2+{\Lambda }_3+{\Lambda }_4\text{(say)}.\hfill \end{array}$$

It follows from (A4) that

$$\begin{array}{cc}\hfill {\Lambda }_1& \le {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_0^{\left(1-t\right)x}\frac{b^{-1}}{\pi \sqrt{x}\sqrt{y}}exp\left\{-\frac{{\left(y-x\right)}^2}{bx}-\frac{\left(y+x\right){\left(y-x\right)}^2}{2bxy}\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{y}{x}\right)}^2-1\right)\right\}exp\left\{\frac{1}{4}\left({\left(\frac{x}{y}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(y\right)dy\right]f\left(x\right)dx\hfill \\ & \le {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_0^{\left(1-t\right)x}\frac{b^{-1}}{\pi \sqrt{x}\sqrt{y}}exp\left\{-\frac{{\tau }_2{\left(y-x\right)}^2}{2bx}\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{y}{x}\right)}^2-1\right)\right\}exp\left\{\frac{1}{4}\left({\left(\frac{x}{y}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(y\right)dy\right]f\left(x\right)dx,\hfill \end{array}$$

where ${\tau }_2:=\left(4-t\right)/\left(1-t\right)$. Then, by the change of variable $\eta :=\left(y-x\right)\sqrt{{\tau }_2/\left(2bx\right)}$,

$$\begin{array}{cc}\hfill b^{1/2}{\Lambda }_1& \le {\int }_{b^{1-ϵ}}^{\infty }\frac{1}{\pi }\sqrt{\frac{2}{{\tau }_2}}\left[{\int }_{-\sqrt{\frac{{\tau }_2}{2}}\sqrt{\frac{x}{b}}}^{-t\sqrt{\frac{{\tau }_2}{2}}\sqrt{\frac{x}{b}}}\frac{1}{\sqrt{x+\eta \sqrt{\frac{2bx}{{\tau }_2}}}}{e}^{-{\eta }^2}exp\left\{\frac{1}{4}\left({\left(\frac{x+\eta \sqrt{\frac{2bx}{{\tau }_2}}}{x}\right)}^2-1\right)\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{x}{x+\eta \sqrt{\frac{2bx}{{\tau }_2}}}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(x+\eta \sqrt{\frac{2bx}{{\tau }_2}}\right)d\eta \right]f\left(x\right)dx\hfill \\ & \to 0,\hfill \end{array}$$

or ${\Lambda }_1=o\left(b^{-1/2}\right)$.

Next, (A4) implies that

$$\begin{array}{cc}\hfill {\Lambda }_2& \ge {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{\left(1-t\right)x}^x\frac{b^{-1}}{\pi \sqrt{x}\sqrt{y}}exp\left\{-\frac{{\left(y-x\right)}^2}{bx}+\frac{{\left(y-x\right)}^3}{2b{y}^2}-\frac{\left(y+x\right){\left(y-x\right)}^2}{2bxy}\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{y}{x}\right)}^2-1\right)\right\}exp\left\{\frac{1}{4}\left({\left(\frac{x}{y}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(y\right)dy\right]f\left(x\right)dx\hfill \\ & \ge {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{\left(1-t\right)x}^x\frac{b^{-1}}{\pi \sqrt{x}\sqrt{y}}exp\left\{-\frac{{\left(y-x\right)}^2}{2bx}\left(3+{\tau }_3\right)\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{y}{x}\right)}^2-1\right)\right\}exp\left\{\frac{1}{4}\left({\left(\frac{x}{y}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(y\right)dy\right]f\left(x\right)dx,\hfill \end{array}$$

where ${\tau }_3:={\left(1-t\right)}^{-2}$. By the change of variable $\mu :=\left(y-x\right)\sqrt{\left(3+{\tau }_3\right)/\left(2bx\right)}$, the right-hand side becomes

$$\begin{array}{cc}& {\int }_{b^{1-ϵ}}^{\infty }\frac{b^{-1/2}}{\pi }\sqrt{\frac{2}{3+{\tau }_3}}\left[{\int }_{\sqrt{\frac{3+{\tau }_3}{2}}\sqrt{\frac{x}{b}}}^0\frac{1}{\sqrt{x+\mu \sqrt{\frac{2bx}{3+{\tau }_3}}}}{e}^{-{\mu }^2}exp\left\{\frac{1}{4}\left({\left(\frac{x+\mu \sqrt{\frac{2bx}{3+{\tau }_3}}}{x}\right)}^2-1\right)\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{x}{x+\mu \sqrt{\frac{2bx}{3+{\tau }_3}}}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(x+\mu \sqrt{\frac{2bx}{3+{\tau }_3}}\right)d\mu \right]f\left(x\right)dx,\hfill \end{array}$$

so that

$$lim\underset{b\to 0}{inf}{b}^{1/2}{\Lambda }_2=\frac{1}{2\sqrt{\pi }}\sqrt{\frac{2}{3+{\tau }_3}}{\int }_0^{\infty }{x}^{-1/2}g\left(x\right)dF\left(x\right)\to \frac{1}{2}{V}_{I,NM}\left(2\right)E\left\{X^{-1/2}g\left(X\right)\right\}$$

by letting t shrink toward zero, where $V_{I,NM}\left(2\right):=1/\sqrt{2\pi }$. Notice that we may safely assume that $E\left\{X^{-1/2}g\left(X\right)\right\}<\infty$: Assumption 2 ensures that f and g are bounded, and thus it must be the case that $x^{-1/2}f\left(x\right)g\left(x\right)\le c{x}^{-1/2}$ in the vicinity of the origin. On the other hand, (A4) also yields

$$\begin{array}{cc}\hfill {\Lambda }_2& \le {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{\left(1-t\right)x}^x\frac{b^{-1}}{\pi \sqrt{x}\sqrt{y}}exp\left\{-\frac{{\left(y-x\right)}^2}{bx}-\frac{\left(y+x\right){\left(y-x\right)}^2}{2bxy}\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{y}{x}\right)}^2-1\right)\right\}exp\left\{\frac{1}{4}\left({\left(\frac{x}{y}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(y\right)dy\right]f\left(x\right)dx\hfill \\ & \le {\int }_{b^{1-ϵ}}^{\infty }\left[{\int }_{\left(1-t\right)x}^x\frac{b^{-1}}{\pi \sqrt{x}\sqrt{y}}exp\left\{-\frac{2{\left(y-x\right)}^2}{bx}\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{y}{x}\right)}^2-1\right)\right\}exp\left\{\frac{1}{4}\left({\left(\frac{x}{y}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(y\right)dy\right]f\left(x\right)dx.\hfill \end{array}$$

By the change of variable $\omega :=\left(y-x\right)\sqrt{2/\left(bx\right)}$,

$$\begin{array}{cc}\hfill {\Lambda }_2& \le {\int }_{b^{1-ϵ}}^{\infty }\frac{b^{-1/2}}{\sqrt{2}\pi }\left[{\int }_{-t\sqrt{2}\sqrt{\frac{x}{b}}}^0\frac{1}{\sqrt{x+\omega \sqrt{\frac{bx}{2}}}}{e}^{-{\omega }^2}exp\left\{\frac{1}{4}\left({\left(\frac{x+\omega \sqrt{\frac{bx}{2}}}{x}\right)}^2-1\right)\right\}\right.\hfill \\ & \left.\times exp\left\{\frac{1}{4}\left({\left(\frac{x}{x+\omega \sqrt{\frac{bx}{2}}}\right)}^2-1\right)\right\}\left\{1+o\left(1\right)\right\}g\left(x+\omega \sqrt{\frac{bx}{2}}\right)d\omega \right]f\left(x\right)dx,\hfill \end{array}$$

and thus

$$lim\underset{b\to 0}{sup}{b}^{1/2}{\Lambda }_2=\frac{1}{2\sqrt{2\pi }}{\int }_0^{\infty }{x}^{-1/2}g\left(x\right)dF\left(x\right)=\frac{1}{2}{V}_{I,NM}\left(2\right)E\left\{X^{-1/2}g\left(X\right)\right\}.$$

Hence, we can conclude that ${\Lambda }_2\sim b^{-1/2}\left(1/2\right)V_{I,NM}\left(2\right)E\left\{X^{-1/2}g\left(X\right)\right\}$.

It also follows from (A3) that ${\Lambda }_3\sim b^{-1/2}{V}_{I,NM}\left(2\right)\left(1/2\right)E\left\{X^{-1/2}g\left(X\right)\right\}$ and ${\Lambda }_4=o\left(b^{-1/2}\right)$. Therefore, $\Lambda \sim b^{-1/2/}{V}_{I,NM}\left(2\right)E\left\{X^{-1/2}g\left(X\right)\right\}$, and thus (A2) is also established.   □

Appendix A.2. Proof of Theorem 1

Because (ii) is obvious given that (i) is true, we concentrate only on (i). The proof strategy for (i) largely follows the one for Theorem 1.1 of Fernandes and Monteiro [46]. The proof of (i) also requires three lemmata below.

Lemma A2. 

Let $\left(X_1,X_2\right)$ and $\left(Y_1,Y_2\right)$ be two independent copies of X and Y, respectively. Then, under Assumptions 1–3, the followings hold:

(a) 

$E\left\{K_{X_2}^2\left(X_1\right)\right\}\sim b^{-1/2}{V}_I\left(2\right)E\left\{X^{-1/2}f\left(X\right)\right\}$; $E\left\{K_{X_2}^2\left(Y_1\right)\right\}\sim b^{-1/2}{V}_I\left(2\right)E\left\{X^{-1/2}g\left(X\right)\right\}$;

$E\left\{K_{Y_2}^2\left(X_1\right)\right\}\sim b^{-1/2}{V}_I\left(2\right)E\left\{Y^{-1/2}f\left(Y\right)\right\}$; and $E\left\{K_{Y_2}^2\left(Y_1\right)\right\}\sim b^{-1/2}{V}_I\left(2\right)E\left\{Y^{-1/2}g\left(Y\right)\right\},$ where $V_I\left(2\right)$ is given in Condition 5 of Definition 1.

(b) 

$E\left\{K_{X_2}\left(X_1\right)K_{Y_2}\left(Y_1\right)\right\}\sim E\left\{f\left(X\right)\right\}E\left\{g\left(Y\right)\right\}$; $E\left\{K_{X_2}\left(Y_1\right)K_{Y_2}\left(X_1\right)\right\}\sim E\left\{g\left(X\right)\right\}E\left\{f\left(Y\right)\right\}$;

$E\left\{K_{X_2}\left(Y_1\right)K_{X_1}\left(Y_2\right)\right\}\sim E^2\left\{g\left(X\right)\right\}$; and $E\left\{K_{Y_2}\left(X_1\right)K_{Y_1}\left(X_2\right)\right\}\sim E^2\left\{f\left(Y\right)\right\}$.

(c) 

$E\left\{K_{X_2}\left(X_1\right)K_{X_2}\left(Y_1\right)\right\}\sim E\left\{f\left(X\right)g\left(X\right)\right\}$; and $E\left\{K_{Y_2}\left(Y_1\right)K_{Y_2}\left(X_1\right)\right\}\sim E\left\{g\left(Y\right)f\left(Y\right)\right\}$.

(d) 

$E\left\{K_{X_2}\left(X_1\right)K_{X_1}\left(Y_2\right)\right\}\sim E\left\{f\left(X\right)g\left(X\right)\right\}$; $E\left\{K_{Y_1}\left(X_2\right)K_{X_2}\left(X_1\right)\right\}\sim E\left\{f^2\left(Y\right)\right\}$;

$E\left\{K_{X_1}\left(Y_2\right)K_{Y_2}\left(Y_1\right)\right\}\sim E\left\{g^2\left(X\right)\right\}$; and $E\left\{K_{Y_2}\left(Y_1\right)K_{Y_1}\left(X_2\right)\right\}\sim E\left\{f\left(Y\right)g\left(Y\right)\right\}$.

Lemma A3. 

If Assumptions 1–4 and $n_1=n_2=n$ hold, then

$$E\left\{{\Phi }_n^2\left(Z_1,Z_2\right)\right\}\sim \frac{4V_I\left(2\right)}{n^4{b}^{1/2}}E\left[X^{-1/2}\left\{f\left(X\right)+g\left(X\right)\right\}+Y^{-1/2}\left\{f\left(Y\right)+g\left(Y\right)\right\}\right].$$

Lemma A4. 

If Assumptions 1–4 and $n_1=n_2=n$ hold, then $E\left\{{\Phi }_n^{2k}\left(Z_1,Z_2\right)\right\}<\infty$ and

$$\frac{E\left\{{\mathsf{{\rm Y}}}_n^k\left(Z_1,Z_2\right)\right\}+n^{1-k}E\left\{{\Phi }_n^{2k}\left(Z_1,Z_2\right)\right\}}{E^k\left\{{\Phi }_n^2\left(Z_1,Z_2\right)\right\}}\to 0$$

for some $k\in \left(1,3/2\right)$, where ${\mathsf{{\rm Y}}}_n\left(x,y\right):=E\left\{{\Phi }_n\left(Z_1,x\right){\Phi }_n\left(y,Z_1\right)\right\}$.

Appendix A.2.1. Proof of Lemma A2

The variance approximation in Theorem 1 of Hirukawa and Sakudo [32] and the trimming argument on p.476 of Chen [30] yield (a). On the other hand, the bias approximation in Theorem 1 of Hirukawa and Sakudo [32] is applied to (b)–(d). As a consequence, (b) can be established by recognizing that $E\left\{K_{X_2}\left(X_1\right)K_{Y_2}\left(Y_1\right)\right\}=E\left\{K_{X_2}\left(X_1\right)\right\}E\left\{K_{X_2}\left(X_1\right)\right\}$, for instance. Moreover, (c) and (d) follow from the proofs for (d) and (f) in Lemma A1 of FMS. □

Appendix A.2.2. Proof of Lemma A3

Because ${\varphi }_n\left(Z_1,Z_2\right)\stackrel{d}{=}{\varphi }_n\left(Z_2,Z_1\right)$, we have

$$E\left\{{\Phi }_n^2\left(Z_1,Z_2\right)\right\}=\frac{2}{n^4}\left[E\left\{{\varphi }_n^2\left(Z_1,Z_2\right)\right\}+E\left\{{\varphi }_n\left(Z_1,Z_2\right){\varphi }_n\left(Z_2,Z_1\right)\right\}\right].$$

With the assistance of Assumption 4 and Lemma A2, we can pick out the leading terms of $E\left\{{\varphi }_n^2\left(Z_1,Z_2\right)\right\}$ and $E\left\{{\varphi }_n\left(Z_1,Z_2\right){\varphi }_n\left(Z_2,Z_1\right)\right\}$ as:

$$\begin{array}{cc}& E\left\{{\varphi }_n^2\left(Z_1,Z_2\right)\right\}\hfill \\ & =E\left\{K_{X_2}^2\left(X_1\right)\right\}+E\left\{K_{X_2}^2\left(Y_1\right)\right\}+E\left\{K_{Y_2}^2\left(X_1\right)\right\}+E\left\{K_{Y_2}^2\left(Y_1\right)\right\}+O\left(1\right)\hfill \\ & =b^{-1}{V}_I\left(2\right)E\left[X^{-1/2}\left\{f\left(X\right)+g\left(X\right)\right\}+Y^{-1/2}\left\{f\left(Y\right)+g\left(Y\right)\right\}\right]+o\left(b^{-1}\right);\text{and}\hfill \\ & E\left\{{\varphi }_n\left(Z_1,Z_2\right){\varphi }_n\left(Z_2,Z_1\right)\right\}\hfill \\ & =E\left\{K_{X_2}\left(X_1\right)K_{X_1}\left(X_2\right)\right\}+E\left\{K_{X_2}\left(Y_1\right)K_{Y_1}\left(X_2\right)\right\}\hfill \\ & +E\left\{K_{Y_2}\left(X_1\right)K_{X_1}\left(Y_2\right)\right\}+E\left\{K_{Y_2}\left(Y_1\right)K_{Y_1}\left(Y_2\right)\right\}+O\left(1\right)\hfill \\ & =b^{-1}{V}_I\left(2\right)E\left[X^{-1/2}\left\{f\left(X\right)+g\left(X\right)\right\}+Y^{-1/2}\left\{f\left(Y\right)+g\left(Y\right)\right\}\right]+o\left(b^{-1}\right).\hfill \end{array}$$

The result immediately follows. □

Appendix A.2.3. Proof of Lemma A4

It follows from Lemma A3 that

$$E^k\left\{{\Phi }_n^2\left(Z_1,Z_2\right)\right\}=O\left(n^{-4k}{b}^{-k/2}\right).$$

(A16)

Next, by Jensen’s and $C_r$-inequalities,

$$\begin{array}{cc}& E\left\{{\mathsf{{\rm Y}}}_n^k\left(Z_1,Z_2\right)\right\}\hfill \\ & =E_{Z_1,Z_2}\left[E_{Z_3}^k\left\{{\Phi }_n\left(Z_3,Z_1\right){\Phi }_n\left(Z_2,Z_3\right)\right\}\right]\hfill \\ & \le E_{Z_1,Z_2}\left[E_{Z_3}{\left\{{\Phi }_n\left(Z_3,Z_1\right){\Phi }_n\left(Z_2,Z_3\right)\right\}}^k\right]\hfill \\ & \le n^{-4k}{E}_{Z_1,Z_2}\left\{E_{Z_3}\left|{\varphi }_n\left(Z_3,Z_1\right){\varphi }_n\left(Z_2,Z_3\right)+{\varphi }_n\left(Z_3,Z_1\right){\varphi }_n\left(Z_3,Z_2\right)\right.\right.\hfill \\ & \left.+{\left.{\varphi }_n\left(Z_1,Z_3\right){\varphi }_n\left(Z_2,Z_3\right)+{\varphi }_n\left(Z_1,Z_3\right){\varphi }_n\left(Z_3,Z_2\right)\right|}^k\right\}\hfill \\ & \le n^{-4k}{2}^{2\left(k-1\right)}{E}_{Z_1,Z_2}\left[E_{Z_3}{\left|{\varphi }_n\left(Z_3,Z_1\right){\varphi }_n\left(Z_2,Z_3\right)\right|}^k+E_{Z_3}{\left|{\varphi }_n\left(Z_3,Z_1\right){\varphi }_n\left(Z_3,Z_2\right)\right|}^k\right.\hfill \\ & \left.+E_{Z_3}{\left|{\varphi }_n\left(Z_1,Z_3\right){\varphi }_n\left(Z_2,Z_3\right)\right|}^k+E_{Z_3}{\left|{\varphi }_n\left(Z_1,Z_3\right){\varphi }_n\left(Z_3,Z_2\right)\right|}^k\right]\hfill \\ & =n^{-4k}{2}^{2\left(k-1\right)}\left({\mathsf{{\rm Y}}}_1+{\mathsf{{\rm Y}}}_2+{\mathsf{{\rm Y}}}_3+{\mathsf{{\rm Y}}}_4\right)\text{(say)}.\hfill \end{array}$$

Furthermore, applying $C_r$-inequality repeatedly yields

$${\mathsf{{\rm Y}}}_1\le 2^{4\left(k-1\right)}·8\left[E\left\{K_{X_1}^k\left(X_3\right)K_{X_3}^k\left(X_2\right)\right\}+E^2\left\{K_{X_1}^k\left(X_3\right)\right\}\right]$$

under $H_0$. Essentially the same arguments as in the proofs of Lemmata 1 and A2 establish that $E\left\{K_{X_1}^k\left(X_3\right)K_{X_3}^k\left(X_2\right)\right\}$ is bounded by $c{b}^{1-k}{\int }_0^{\infty }{x}^{1-k}{f}^3\left(x\right)dx$. It follows from $k<3/2$ that $x^{1-k}{f}^3\left(x\right)\le c{x}^{-1/2}$ in the neighborhood of the origin, and thus ${\int }_0^{\infty }{x}^{1-k}{f}^3\left(x\right)dx<\infty$ holds. Hence, $E\left\{K_{X_1}^k\left(X_3\right)K_{X_3}^k\left(X_2\right)\right\}\le O\left(b^{1-k}\right)$. Similarly, $E^2\left\{K_{X_1}^k\left(X_3\right)\right\}\le O\left\{{\left(b^{\left(1-k\right)/2}\right)}^2\right\}=O\left(b^{1-k}\right)$, and thus ${\mathsf{{\rm Y}}}_1\le O\left(b^{1-k}\right)$. It can be also shown that each of ${\mathsf{{\rm Y}}}_2$, ${\mathsf{{\rm Y}}}_3$ and ${\mathsf{{\rm Y}}}_4$ is bounded by $O\left(b^{1-k}\right)$. As a result,

$$E\left\{{\mathsf{{\rm Y}}}_n^k\left(Z_1,Z_2\right)\right\}\le O\left(n^{-4k}{b}^{1-k}\right).$$

(A17)

Using $C_r$-inequality and ${\varphi }_n\left(Z_1,Z_2\right)\stackrel{d}{=}{\varphi }_n\left(Z_2,Z_1\right)$, we also have

$$\begin{array}{cc}\hfill E\left\{{\Phi }_n^{2k}\left(Z_1,Z_2\right)\right\}& \le n^{-4k}E{\left|{\varphi }_n\left(Z_1,Z_2\right)+{\varphi }_n\left(Z_2,Z_1\right)\right|}^{2k}\hfill \\ & \le n^{-4k}{2}^{2k-1}\left\{E{\left|{\varphi }_n\left(Z_1,Z_2\right)\right|}^{2k}+E{\left|{\varphi }_n\left(Z_2,Z_1\right)\right|}^{2k}\right\}\hfill \\ & =n^{-4k}{2}^{2k}E{\left|{\varphi }_n\left(Z_1,Z_2\right)\right|}^{2k}.\hfill \end{array}$$

Again, by $C_r$-inequality,

$$E{\left|{\varphi }_n\left(Z_1,Z_2\right)\right|}^{2k}\le 4·2^{2\left(2k-1\right)}E\left\{K_{X_2}^{2k}\left(X_1\right)\right\}\le c{b}^{\frac{1-2k}{2}}{\int }_0^{\infty }{x}^{\frac{1-2k}{2}}{f}^2\left(x\right)dx,$$

where $x^{\left(1-2k\right)/2}{f}^2\left(x\right)\le c{x}^{-\left(1-\epsilon \right)}$ for some $\epsilon \in \left(0,1/2\right)$ as $x\to 0$ so that ${\int }_0^{\infty }{x}^{\left(1-2k\right)/2}{f}^2\left(x\right)dx<\infty$ is ensured. Therefore,

$$E\left\{{\Phi }_n^{2k}\left(Z_1,Z_2\right)\right\}\le O\left(n^{-4k}{b}^{\frac{1-2k}{2}}\right)=o\left(1\right)$$

(A18)

and thus $E\left\{{\Phi }_n^{2k}\left(Z_1,Z_2\right)\right\}<\infty$ is demonstrated.

In the end, by (A16)–(A18),

$$\begin{array}{cc}\hfill \frac{E\left\{{\mathsf{{\rm Y}}}_n^k\left(Z_1,Z_2\right)\right\}}{E^k\left\{{\Phi }_n^2\left(Z_1,Z_2\right)\right\}}& =O\left(b^{1-k/2}\right)\to 0,\text{and}\hfill \\ \hfill \frac{n^{1-k}E\left\{{\Phi }_n^{2k}\left(Z_1,Z_2\right)\right\}}{E^k\left\{{\Phi }_n^2\left(Z_1,Z_2\right)\right\}}& =O\left\{{\left(n{b}^{1/2}\right)}^{1-k}\right\}\to 0,\hfill \end{array}$$

as long as $1<k<3/2$. This completes the proof. □

Appendix A.2.4. Proof of Theorem 1

It follows from Lemma A4 that a martingale central limit theorem for a degenerate U-statistic (Theorem 4.7.3 of Koroljuk and Borovskich [41], to be precise) applies. Moreover, by Lemma A3, the asymptotic variance of the normal limit becomes

$$\begin{array}{cc}\hfill {\sigma }^2& =\underset{n\to \infty }{lim}{n}^2{b}^{1/2}Var\left(I_n\right)\hfill \\ & =\underset{n\to \infty }{lim}{n}^2{b}^{1/2}\frac{n\left(n-1\right)}{2}E\left\{{\Phi }_n^2\left(Z_1,Z_2\right)\right\}\hfill \\ & =2V_I\left(2\right)E\left[X^{-1/2}\left\{f\left(X\right)+g\left(X\right)\right\}+Y^{-1/2}\left\{f\left(Y\right)+g\left(Y\right)\right\}\right]\hfill \\ & =8V_I\left(2\right)E\left\{X^{-1/2}f\left(X\right)\right\}\text{under}{H}_0.\hfill \end{array}$$

□

Appendix A.3. Proof of Proposition 1

The proof closely follows the one for Theorem 2.2 of Fan and Ullah [19]. Under $H_1$, $E\left(I_n\right)={\int }_0^{\infty }{\left\{f\left(u\right)-g\left(u\right)\right\}}^{2}du+O\left(b\right)=I+O\left(b\right)$. Moreover, $Var\left(I_n\right)=O\left(n^{-2}{b}^{-1/2}\right)$ and ${\widehat{\sigma }}^2\stackrel{p}{\to }{\sigma }^2$, regardless of whether $H_0$ or $H_1$ may be true. Therefore, $I_n=I+O\left(b\right)+O_p\left(n^{-1}{b}^{-1/4}\right)\stackrel{p}{\to }I>0$, and thus $n{b}^{1/4}{I}_n/\widehat{\sigma }$ is a divergent stochastic sequence with an expansion rate of $n{b}^{1/4}$. The result immediately follows. □

Appendix A.4. Proof of Theorem 3

For brevity, we focus only on the case of equal sample sizes in two sub-samples. The proof largely follow the one for Proposition 5 of FMS. FMS consider the Taylor expansion

$$I_n\left(\widehat{\xi },\widehat{\theta }\right)-I_n\left(\xi ,{\theta }_0\right)={\Delta }_1\left(\xi ,{\theta }_0\right)\left(\widehat{\xi }-\xi \right)+{\Delta }_2\left(\xi ,{\theta }_0\right)\left(\widehat{\theta }-{\theta }_0\right)+R_n,$$

where ${\Delta }_1\left(\xi ,{\theta }_0\right)$ and ${\Delta }_2\left(\xi ,{\theta }_0\right)$ are partial derivatives of $I_n$ with respect to the first and second arguments evaluated at $\left(\xi ,{\theta }_0\right)$, respectively, and $R_n$ is the remainder term of a smaller order. The only difference between their proof and ours is that we derive the range of $\left(q,r\right)$ within which

$$n{b}^{1/4}\left\{{\Delta }_1\left(\xi ,{\theta }_0\right)\left(\widehat{\xi }-\xi \right)+{\Delta }_2\left(\xi ,{\theta }_0\right)\left(\widehat{\theta }-{\theta }_0\right)\right\}=o_p\left(1\right)$$

is the case. Because each of ${\Delta }_1$ and ${\Delta }_2$ is $O\left(b\right)+O_p\left(n^{-1}{b}^{-3/4}\right)$, the left-hand side is bounded by

$$O\left(n^{1-r}{b}^{5/4}\right)+O_p\left(n^{-r}{b}^{-1/2}\right)=O\left(n^{1-r-5q/4}\right)+O_p\left(n^{-r+q/2}\right).$$

This becomes $o_p\left(1\right)$ if $\left(q,r\right)$ satisfy $r>-5q/4+1$, $r>q/2$ and $r\le 1/2$. □