Abstract
We develop a procedure for removing four major specification errors from the usual formulation of binary choice models. The model that results from this procedure is different from the conventional probit and logit models. This difference arises as a direct consequence of our relaxation of the usual assumption that omitted regressors constituting the error term of a latent linear regression model do not introduce omitted regressor biases into the coefficients of the included regressors.
JEL:
C13; C51
1. Introduction
It is well-known that binary choice models are subject to certain specification errors. It can be shown that the usual approach of adding an error term to a mathematical function leads to a model with nonunique coefficients and error term. In this model, the conditional expectation of the dependent variable given the included regressors does not always exist. Even when it exists, its functional form may be unknown. The nonunique error term is interpreted as representing the net effect of omitted regressors on the dependent variable. Pratt and Schlaifer (1988, p. 34) [1] pointed out that omitted regressors are not unique and as a result, the condition that the included regressors be independent of “the” excluded variables themselves is “meaningless”. There are cases where the correlation between the nonunique error term and the included regressors can be made to appear and disappear at the whim of an arbitrary choice between two observationally equivalent models. To avoid these problems, we specify models with unique coefficients and error terms without misspecifying their correct functional forms. The unique error term of a model is a function of certain “sufficient sets” of omitted regressors. We derive these sufficient sets for a binary choice model in this paper. In the usual approach, omitted regressors constituting the error term of a model do not introduce omitted-regressor biases into the coefficients of the included regressors. In our approach, they do so.
Following the usual approach, Yatchew and Griliches (1984) [2]1 showed that if one of two uncorrelated regressors included in a simple binary choice model is omitted, then the estimator of the coefficient on the remaining regressor will be inconsistent. They also showed that, if the disturbances in a latent regression model are heteroscedastic, then the maximum likelihood estimators that assume homoscedasticity are inconsistent and the covariance matrix is inappropriate. In this paper, we show that the use of a latent regression model with unique coefficients and error term changes their results. Our binary choice model is different from those of such researchers as Yatchew and Griliches [2], Cramer (2006) [4], and Wooldridge (2002, Chapter 15) [5]. The concept of unique coefficients and error term is distinctive to our work. Specifically, we do not assume any incorrect functional form, and we account for relevant omitted regressors, measurement errors, and correlations between excluded and the included regressors. Our model features varying coefficients (VCs) in which we interpret the VC on a continuous regressor as a function of three quantities: (i) bias-free partial derivative of the dependent variable with respect to the continuous regressor; (ii) omitted-regressor biases; and (iii) measurement-error biases. This interpretation of the VCs is unique to our work and allows us to focus on the bias-free (i.e., partial derivatives) parts of the VCs.
The remainder of this paper is comprised of three sections. Section 2 summarizes a recent derivation of Swamy, Mehta, Tavlas and Hall (2014) [6] of all the terms involved in a binary choice model with unique coefficients and error term. The section also provides the conditions under which such a model can be consistently estimated. Section 3 presents an empirical example. Section 4 concludes. An Appendix at the end of the paper has two sections. The first section compares the relative generality of assumptions underlying different linear and nonlinear models. The second section derives the information matrix for a binary choice model with unique coefficients and error term.
2. Methods of Correctly Specifying Binary Choice Models and Their Estimation
2.1. Model for a Cross-Section of Individuals
Greene (2012, pp. 681–683) [3] described various situations under which the use of discrete choice models is called for. In what follows, we develop a discrete choice model that is free of several specification errors. To explain, we begin with the following specification:
where i indexes n individuals, is a mathematical function, and its arguments are mathematical variables. Let be short hand for this function. We do not observe but view the outcome of a discrete choice as a reflection of the underlying mathematical function in Equation (1). We only observe whether a choice is made or not (see Greene (2012, p. 686) [3]).
Therefore, our observation is
where the choice “not made” is indicated by the value 0 and the choice “made” is indicated by the value 1, i.e., takes either 0 or 1. An example of model (2), provided in Greene (2012, Example 17.1, pp. 683–684) [3], is a situation involving labor force participation where a respondent either works or seeks work ( = 1) or does not ( = 0) in the period in which a survey was taken.2
In Equation (1), is , denotes the total number of the arguments of ; there are no omitted arguments needing an error term. Equation (1) is a mathematical equation that holds exactly. Inexactness and stochastic error term enters into (1) when we derive the appropriate error term and make distributional assumption about it. The reasons for this are explained below. The number may depend on i. This dependence occurs when the number of arguments of is different for different individuals. For example, before deciding whether or not to make a large purchase, each consumer makes a marginal benefit/marginal cost calculations based on the utilities achieved by making the purchase and by not making the purchase, and by using the available funds for the purchase of something else. The difference between benefit and cost as an unobserved variable can vary across consumers if they have different utility functions with different arguments. These variations can show up in the form of different arguments of for different consumers.
It should be noted that (1) represents our departure from the usual approach of adding a nonunique error term to a mathematical function and making a “meaningless” assumption about the error term. Pratt and Schlaifer (1988, p. 34) [1] severely criticized this approach. To avoid this criticism, what we have done in (1) is that we have taken all the x-variables and the variables constituting the error term in Cramer’s (2006) [4] (or e in Wooldridge’s (2002, p. 457) [5]) latent regression model, and included them in as its arguments. In addition, we also included in all relevant pre-existing conditions as its arguments.3.
The problem that researchers face is that of uncovering the correct functional form of .4 However, any false relations can be shown to have been eliminated when we control for all relevant pre-existing conditions. To make use of this observation due to Skyrms (1988, p. 59) [7], we incorporate these pre-existing conditions into by letting some of the elements of represent these conditions.5 Clearly, we have no way of knowing what these pre-existing conditions might be, how to measure them (if we knew them), or how many there may be. To control for these conditions, we use the following approach. We assume that all relevant pre-existing conditions appear as arguments of the function in Equation (1). This is a straightforward approach. Therefore, when we take the partial derivatives of with respect to , a determinant of included in as its argument, the values of all pre-existing conditions are automatically held constant. This action is important because it sets the partial derivative equal to zero whenever the relation of to , an element , is false (see Skyrms (1988, p. 59) [7]).
The function in (1) is exact and mathematical in nature, without any relevant omitted arguments. Moreover, its unknown functional form is not misspecified. Therefore, it does not require an error term; indeed, it would be incorrect to add an error term to . We refer to (1) as “a minimally restricted mathematical equation,” the reason being that no restriction other than the normalization rule, that the coefficient of is unity, is imposed on (1). Without this restriction, the function is difficult to identify. The reason why no other restriction is imposed on it is that we want (1) to be a real-world relationship. With such a relationship we can estimate the causal effects of a treatment. Basmann (1988, pp. 73, 99) [8] argued that causality is a property of the real world. We define that real-world relations are those that are not misspecified. Causal relations are unique in the real world. This is the reason why we insist that the coefficients and error term of our model be unique. From Basmann’s (1988, p. 98) [8] definition it follows that (1) is free of the most serious objection, i.e., non-uniqueness, which occurs when stationarity producing transformation of observable variables are used.6 We do not use such variables in (1).
2.2. Unique Coefficients and Error Terms of Models
2.2.1. Causal Relations
Basmann (1988, pp. 73, 99) [8] emphasized that the word “causality” designates a property of the real world. Hence we work only with appropriate real-world relationships to evaluate causal effects.
We define that the real-world relationships are those that are not subject to any specification errors. It is possible to avoid some of those errors, as we show below. The real-world relationships and their properties are always true and unique. Such relationships cannot be found, however, by imposing severe restrictions because they can be false. Examples of these restrictions are given in the Appendix to the paper. For example, certain separability conditions are imposed on (1) to obtain (A1) in the Appendix. These conditions are so severe that their truth is doubtful. For this reason, (A1) may not be a real-world relationship and may not possess the causality property. Again in the Appendix, (A2) is a general condition of statistical independence which is very strong. Model (A5) of the Appendix with a linear functional form could be misspecified.7
2.2.2. Derivation of a Model from (1) without Committing a Single Specification Error
To avoid misspecifications of the unknown correct functional form of (1), we change the problem of estimating (1) to the problem of estimating some of its partial derivatives in
where, for , … , , if is continuous and = with the right sign if is discrete having zero as one of its possible values, ∆ is the first-difference operator, and the intercept . In words, this intercept is the error of approximation due to approximating by (). Therefore, model (3) with zero intercept does not misspecify the unknown functional form of (1) if the error of approximation is truly zero and model (3) with nonzero intercept is the same as (1) with no misspecifications of its functional form, since . This is how we deal with the problem of the unknown functional form of (1). Note that no separability conditions need to be imposed on (1) to write it in the form of (3). This is the advantage of (3) over (A1).
Note that in the above definition of the partial derivative (), the values of all the arguments of (including all relevant pre-existing conditions) other than are held constant. These partial derivatives are different from those that can be derived from (A1) with suppressed. This is because in taking the latter derivatives the values of are not held constant.
Equation (3) is not a false relationship, since we held the values of all relevant pre-exiting conditions constant in deriving its coefficients. The regression in (3) has the minimally restricted equation in (1) as its basis. The coefficients of (3) are constants if (1) is linear and are variables otherwise. In the latter case, the coefficients of (3) can be the functions of all of the arguments of . Any function of the form (1) with unknown functional form can be written as linear in variables and nonlinear in coefficients, as in (3). We have already established that this linear-in-variables and nonlinear-in-coefficients model has the correct functional form if its intercept is zero and is the same as (1) otherwise. In either case, (3) does not have a misspecified functional form. In this paper, we take advantage of this procedure.
Not all elements of are measured; suppose that the first K of them are measured. This assumption needs the restriction that min. Even these measurements may contain errors so that the observed argument is equal to the sum of the true value and a measurement error, denoted by .8 The arguments, , = K + 1, … , , for which no data are available, are treated as regressors omitted from (3).9 These are of two types: (i) unobserved determinants of and (ii) all relevant pre-existing conditions. We know nothing of these two types of variables. With these variables being present in (3), we cannot estimate it. Again without misspecifying (1) these variables should be eliminated from (3). To do so, we consider the “auxiliary” relations of each to . Such relations are: For g = K + 1,…, ,
where if is continuous holding the values of all the regressors of (A8) other than that of constant and = with the right sign if is discrete taking zero as one of its possible values and . This intercept is the portion of remaining after the effect () of on has been subtracted from it.
In (4), there are relationships. The intercept is the error due to approximating the relationship between the gth omitted regressor and all the included regressors (“the correct relationship”) by . If this error of approximation is truly zero, then Equation (4) with zero intercept has the same functional form as the correct relationship. In the alternative case where the error of approximation is not zero, (4) is the same as the correct relationship, i.e., . In either case (4) does not misspecify the correct functional form. According to Pratt and Schlaifer (1988, p. 34) [1], the condition that the included regressors be independent of “the” omitted regressors themselves is meaningless. This statement supports (4) but not the usual assumption that the error term of a latent regression model is uncorrelated with or independent of the included regressors.10 The problem is that omitted regressors are not unique, as Pratt and Schlaifer (1988, p. 34) [1] proved.
2.2.3. A Latent Regression Model with Unique Coefficients and Error Terms
Substituting the right-hand side of Equation (4) for in (3) gives
The error term, the intercept, and the coefficients of the nonconstant regressors of this model are , , and , j = 1, … ,K, respectively.
Bias-free partial derivatives:
These partial derivatives have the correct functional form if the ’s are continuous.
“Sufficient” sets of omitted regressors: The regressors, , are called “omitted regressors” because they are included in (3) but not in Equation (5). The regressors are called “the included regressors.” It can be seen from (5) that the portions of omitted regressors, , respectively, in conjunction with the included regressors are sufficient to determine the value of exactly. For this reason, Pratt and Schlaifer (1988, p. 34) [1] called “certain “sufficient sets” of omitted regressors.” The second term () on the right-hand side of (5) is called “a function of these sufficient sets of omitted regressors ” Pratt and Schlaifer (1988, 1984) [1,9] pointed out that this function can be taken as the error term of (5). It remains as a mathematical function until we make a distributional assumption about it. Note that the problem with the error terms of the usual latent regression models including those of (A1), Karlsen, Myklebust and Tjøstheim’s (2007) [10] and White’s (1980, 1982) [11,12] models is that they are not the appropriate functions of the sufficient sets of omitted regressors and hence are not unique and/or are arbitrary.11
Deterministic omitted-regressors bias: The term contained in the coefficient of in (5) measures such a bias.
Swamy et al. (2014, pp. 197, 199, 217–219) [6] proved that the coefficients and the error term of (5) are unique in the following sense:
Uniqueness: The coefficients and error term of model (5) are unique if they are invariant under the addition and subtraction of the coefficient of any regressor omitted from (5) times any regressor included in (5) on the right-hand side of (3) (see Swamy et al. 2014, pp. 199, 219) [6].
The equations in (4) play a crucial role in Swamy et al.’s (2014) [6] proof of the uniqueness of the coefficients and error term of (5). If we had taken the sum + + of the last terms on the right-hand side of (3) as its error term, then we would have obtained a nonunique error term. The reason why this would have happened is that omitted regressors are not unique. What (4) has done is that it has split each gth omitted regressor into a “sufficient set” and an included-regressors’ effect. This sufficient set times the coefficient of the gth omitted regressor has become a term in the (unique) error term of (5) and the included-regressors’ effect times the coefficient of the gth omitted regressor has become a term in omitted-regressor biases of the coefficients of (5). This is not the usual procedure where the whole of each omitted regressor goes into the formation of an error term and no part of it becomes a term in omitted-regressor biases. The usual procedure leads to nonunique coefficients and error term. In the YG procedure, only some of the included regressors which, when omitted, introduce omitted-regressor biases into the (nonunique) coefficients on the remaining included regressors. Yatchew and Griliches (1984) [2], Wooldridge (2002) [5], and Cramer (2006) [4] followed the usual procedure. Without using (4) it is not possible to derive a model with unique coefficients and error term.
2.2.4. A Correctly Specified Latent Regression Model
Substituting the terms on the right-hand sides of equations , j = 1, … ,K, for , j = 1, … ,K, respectively, in (5) gives a model of the form
where the intercept is defined as
and the other terms are defined as
where the set contains all the regressors of Equation (7) that are continuous, the set contains all the regressors of (7) that can take the value zero with positive probability, the ratio of in the first line of Equation (9) comes from the equation , and this ratio does not appear in the second line of Equation (9) because can take the value zero with positive probability.
Equation (7) implies that a model is correctly specified if it is derived by inserting measurement errors at the appropriate places in a model with unique coefficients and error term (see Swamy et al. (2014, p. 199) [6]).
Deterministic measurement-error biases: The formula in (8) measures the sum of measurement-error biases in the coefficients of and the formula in the first line of (9) measures such a bias in the coefficient of .
Under our approach, measurement errors do not become random variables until distributional assumptions are made about them.
2.2.5. What Specification Errors Are (3)–(8) Free from?
(i) The unknown functional form of (1) is not allowed to become the source of a specification error in (3); (ii) The uniqueness of the coefficients and error term of (5) eliminates the specification error resulting from non-unique coefficients and error term; (iii) Pratt and Schlaifer (1988, p. 34) [1] pointed out that the requirement that the included regressors be independent of the excluded regressors themselves is “meaningless”. The specification error introduced by making this meaningless assumption is avoided by taking a correct function of certain “sufficient sets” of omitted regressors as the error term of (5); (iv) The specification error of ignoring measurement errors when they are present is avoided by placing them at the appropriate places in (5). It should be noted that when we affirm that (7) is free of specification errors, we mean that it is free of specification-errors (i)–(iv). Using (3)–(6) we have derived a real-world relationship in (7) that is free of specification-errors (i)–(iv). Thus, our approach affirms that any relationship suffering from anyone of these specification errors is definitely not a real-world relationship.
2.3. Comparison of (7) with the Yatchew and Griliches (1985) [2], Wooldridge (2002) [5], and Cramer (2006) [4] Latent Regression Models
In Section 2.2.3, we have seen that the relationships between each omitted regressor and the included regressors in (4) introduce omitted-regressor biases into the coefficients on the regressors of (5). We have pointed out in the last paragraph of that section that this is not how Yatchew and Griliches (YG) derived omitted-regressor biases. They work with models in which the coefficients and error terms do not satisfy our definition of uniqueness. YG considered a simple binary choice model and omitted one of its two included regressors. According to YG, this omission introduces omitted regressor bias into the coefficient on the regressor that is allowed to remain. The results proved by YG are: (i) even if the omitted regressor is uncorrelated with the remaining included regressor, the coefficient on the latter regressor will be inconsistent; (ii) If the errors in the underlying regression are heteroscedastic, then the maximum likelihood estimators that ignore the heteroscedasticity are inconsistent and the covariance matrix is inappropriate (see also Greene (2012, p. 713) [3]). We do not omit any of the included regressors from (5) to generate omitted-regressor biases. For YG, omitted regressors in (4) are those that generate the error term in their latent regression model. Equation (5)’s error term is a function of those variables that satisfy Pratt and Schlaifer’s definition of “sufficient sets” of our omitted regressors. Thus, YG’ concepts of omitted-regressors, included regressors, and error terms are different from ours. Their model is subject to specification errors (i)–(iv) listed in the previous section. YG’s assumptions about the error term of their model are questionable because of its non-uniqueness. Unless its coefficients and error term are unique no model can represent any real-world relationship which is unique. According to YG, Wooldridge, and Cramer, the regressors constituting the error term of a latent regression model do not produce omitted-regressors biases. Their omitted-regressor bias is not the same as those in (5). YG’s results cannot be obtained from our model (7). Their nonunique heteroscedastic error term is different from our unique heteroscedastic error term in (7). It can be shown that the results of YG arose as a direct consequence of ignoring our omitted-regressor and measurement-error biases in (9). Omitted regressors constituting the YG model’s (non-unique) error term also introduce omitted-regressor biases in our sense but not in their sense. Furthermore, the YG model suffers from all the four specification errors (i)–(iv) which equations (3)–(5), (7)–(9) avoid.
To recapitulate, misspecifications of the correct functional form of (1) are avoided by expressing it in the form of Equation (3). If the sum,, of the last terms on the right-hand side of (3) is treated as its error term, then this error term is not unique (see Swamy et al. (2014, p. 197) [6]). Suppose that the coefficients of (3) are constants. Then the correlation between the nonunique error term and the first K regressors of (3) can be made uncertain and certain, at the whim of an arbitrary choice between two observationally equivalent forms of (3), as shown by Swamy et al. (2014, pp. 217–218) [6]. To eliminate this difficulty, a model with unique coefficients and error term is derived by substituting the right-hand side of Equation (4) for the omitted regressor, , in (3) for every . Equation (7) shows how the terms of an equation look like if this equation is made free of specification errors (i)–(iv). For each continuous with j > 0 in (7), its coefficient contains the bias-free partial derivative () and omitted-regressor and measurement-error biases.
Parameterization of Model (7)
The partial derivative () components of the coefficients (, j = 1, … , K) of (7) are the objects of our estimation. For this purpose, we parameterize (7) using our knowledge of the probability model governing the observations in (7). We assume that for j = 0, 1, … , K:
where , the ’s are fixed parameters, the z’s drive the coefficients of (7) and are, therefore, called “coefficient drivers.” These drivers are observed. We will explain below how to select these drivers. The errors (’s) are included in Equation (10) because the p + 1 drivers may not be able to explain all variation in .
Admissible drivers: For j = 0, 1, … , K, the vector in (10) is an admissible set of coefficient drivers if given , the value that the vector of the coefficients of (7) would take in unit i had been is independent of for all i.12
We use the following matrix notation: is , is , is , is a scalar, is the (K + 1) ( + 1) matrix having as its jth row, and is . Substituting the right-hand side of (10) for in (7) gives
Assumption 1.
The regressors of Equation (7) are conditionally independent of their coefficients given the coefficient drivers.
Assumption 2.
For all i, let be a Borel function of , , and .
Assumption 3.
For i, = 1, …,n, , , and if .
In terms of homoscedastic error term, Equation (11) can be written as
where is positive definite.
Under Assumptions 1–3, the conditional expectation
exists (see Rao (1973, p. 97) [14].
2.4. Derivation of the Likelihood Function for (11)
The parameters of model (11) to be estimated are and . Due to the lack of observations on the dependent variable not all of these parameters are identified. Therefore, we need to impose some restrictions. The following two restrictions are imposed on model (11):
- (i)
- The in cannot be estimated, since there is no information about it in the data. To solve this problem, we set equal to 1.
- (iI)
- From (2) it follows that the conditional probability that = 1 (or > 0) given and iswhere the information about the constant term is contained in the proportion of observations for which the dependent variable is equal to 1.
For symmetric distributions like normal,
where F(.|.) is the conditional distribution function of . The conditional probability that (or ) given and is . The conditional probability that (or ) given and is . F(.|.) in (15) denotes the conditional normal distribution function of the random variable with mean zero and unit variance; is the density function of the standard normal. Let be the column stack of . To exploit the symmetry property of , we add together the two elements of corresponding to the (j, ) and (, j) elements of in and eliminate the (, j) element of from for j = 0, 1, … , K . These operations change the (1 × (K + 1)2) vector to the (1 × (K + 1)(K + 2)/2) vector, denoted by , and change the (K + 1)2 × 1 vector to the [(K + 1)(K + 2)/2] × 1 vector, denoted by .
The maximum likelihood (ML) method is used to estimate the elements of and . To do so, each observation is treated as a single draw from a binomial distribution. The model with success probability and independent observations leads to the likelihood function,
The likelihood function for a sample of n observations can be written as
This equation gives
where is a Kronecker product and is the column stack of .
Unconstrained and Constrained Maximum Likelihood Estimation
In the case where is identified, then its positive definite estimate may not be obtained unless the log likelihood function in (18) is maximized subject to the restriction that is positive definite. Furthermore, these constrained estimates of and do not satisfy the following likelihood equations.
where stands for and is the derivative of .
We now show that is not identified. The log likelihood function in (18) has the property that it does not change when is multiplied by a positive constant and inside the square root by . This can be seen clearly from
An implication of this property is that if ln L in (18) attains a maximum value at , then yields another point at which ln L attains its maximum value. Consequently, solving Equations (19) and (20) for and gives an infinity of solutions, respectively. None of these solutions is consistent because is not identified. For this reason we set = . After inserting this value in Equation (19), it is solved for . This solution is taken as the maximum likelihood estimate of .
The information matrix, denoted by , is
where the elements of this matrix are given in equation (A8) with = .
Suppose that = I. Then the positive definiteness of (22) is a necessary condition for to be identifiable on the basis of the observed variables in (17). If the likelihood equations in (19) have a unique solution, then the inverse of the information matrix in (22) will give the covariance matrix of the limiting distribution of the ML estimator of . Suppose that the solution of (19) is not unique. In this case, if Lehmann and Casella’s (1998, p. 467, (5.5)) [15] method of solving (19) for is followed, then the square roots of the diagonal elements of (22) when evaluated at Lehmann and Casella’s solutions of (19), give the large sample standard errors of the estimate of .
2.5. Estimation of the Components of the Coefficients of (7)
The estimates of the coefficients of (7) are obtained by replacing the ’s and of (10) by their maximum likelihood estimates and the mean value zero, respectively. We do not get the correct estimates of the components of in (9) from its estimate unless its two different functional forms in (8) and (9) and (10) are reconciled. For a continuous with j > 0, we recognize that its coefficient in (9) and in (10) are the same. Therefore, the sum in (10) is equal to the function in (9). We have already shown that is equal to and the sum of omitted-regressor and measurement-error biases (ORMEB) is equal to .
Equation (9) has the form
where , , .
Equations (9) and (10) imply that
where the ’s are the ML estimates of the ’s derived in Section 2.4. We do not know how to predict and, therefore, we set it equal to its mean value which is equal to zero. Equation (24) reconciles the discrepancies between the functional forms of (9) and (10). We have the ML estimates of all the unknown parameters on the left-hand side of Equation (24). From these estimates, it can be determined that for individual i and regressors , j = 1,…, K:
The estimate of the partial derivative
The estimate of omitted-regressor bias
The estimate of measurement-error bias
where the p + 1 coefficient drivers are allocated either to a group, denoted by , or to a group, denoted by ; . The unknowns in formulas (25)–(27) are and . We discuss how to determine these unknowns below.
The type of data Greene (2012, pp. 244–246, Example 8.9) [3] used can tell us about . Which of the terms in , should go into , can be decided after examining the sign and magnitude of each term in If we are not sure of any particular value of , then we can present the estimated kernel functions for , i = 1, … , n, for various values of .
Regarding we can make the following assumption:
Assumption 4.
For all i and j: (i) The measurement error forms a negligible proportion of .
Alternatively, the percentage point × 100 can be specified if we have the type of data Greene (2012, pp. 244–246, Example 8.9) [3] had. If such data are not available, then we can make Assumption 4. Under this assumption, in (25) and (26) gets equated to 1 and the number of unknown quantities in formulas (25) and (26) is reduced to 1.
Under these assumptions, we can obtain the estimates of and their standard errors. These standard errors are based on those of ’s involved in . If the estimate of given by formula (25) is accurate, then our estimate of the partial derivative is free of omitted-regressor and measurement-error biases, and also of specification errors (i)–(iv) listed in Section 2.2.5.
2.5.1. How to Select the Regressors and Coefficient Drivers Appearing in (11)?
The choice of the dependent variable and regressors to be included in (7) is entirely dictated by the partial derivatives we want to learn. The learning of a partial derivative, say , requires (i) the use of and as the dependent variable and a regressor of (7), respectively; (ii) the use of z’s in (25) and (26) as the coefficient drivers in (10); and (iii) the use of the values of and in (25). These requirements show that the learning about one partial derivative is more straightforward than learning about more than one partial derivative. Therefore, in our practical work we will include in our basic model (7) only one non-constant regressor besides the intercept.
It should be remembered that the coefficient drivers in (10) are different from the regressors in (7). There are also certain requirements that the coefficient drivers should satisfy. They explain variations in the components of the coefficients of (7), as is clear from Equations (25) and (26). After deciding that we want to learn about and knowing from (23) that this is only a part of the coefficient of the regressor in the (, )-relationship, we need to include in (10) those coefficient drivers that facilitate accurate evaluation of the formulas (25)–(27). Initially, we do not know what such coefficient drivers are. We have decided to use as coefficient drivers those variables that economists include in their models of the (, )-relationship as additional explanatory variables. Specifically, instead of using them as additional regressors we use them as coefficient drivers in (10).13,14 It follows from Equations (25) and (26) that among all the coefficient drivers included in (10) there should be one subset of coefficient drivers that is highly correlated with the bias-free partial derivative part and another subset of coefficient drivers that is highly correlated with the omitted-regressor bias of the jth coefficient of (7).15
If and are unknown, as they usually are, then we should make alternative assumptions about them and compare the results obtained under these alternative assumptions.
2.5.2. Impure Marginal Effects
The marginal effect of any one of the included regressors on the probability that is
where we set = .
These effects are impure because they involve omitted-regressor and measurement-error biases. It is not easy to integrate omitted-regressor and measurement-error biases out of the probability in (15).16
3. Earnings and Education Relationship
This section is designed to give some specific empirical examples on the type of misspecification that usually found in actual data sets. Several authors studied this relationship. We are also interested in learning about the partial derivative of earnings with respect to education of individuals. For this purpose, we set up the model
where denotes unobserved earnings, denotes unobserved education, and the components of and are given in (8) and (9), respectively. Equation (29) is derived in the same way that (7) is derived. Like (7), Equation (29) is devoid of four specification errors. In our empirical work, we use = years of schooling as a proxy for education.
Greene (2012, p. 14) [3] used model (29) after changing it to a fixed coefficient model with added error term, in which the dependent variable is the log of earnings (hourly wage times hours worked). He pointed out that this model neglects the fact that most people have higher incomes when they are older than when they are young, regardless of their education. Therefore, Greene argued that the coefficient on education will overstate the marginal impact of education on earnings. He further pointed out that if age and education are positively correlated, then his regression model will associate all the observed increases in income with increases in education. Greene concluded that a better specification would account for the effect of age. He also pointed out that income tends to rise less rapidly in the later earning years than in the early ones. To accommodate this phenomena and the age effect, Greene (2012, p. 14) [3] included in his model the variables age and age2.
Recognizing the difficulties in measuring education pointed out by Greene (2012, p. 221) [3], we measure education as hours of schooling plus measurement error. Another problem Greene discussed is that of the endogeneity of education. We handle this problem by making Assumptions II and III. Under these assumptions, the conditional expectation exists. Other regressors Greene (2012, p. 708) [3] included in his labor supply model include kids, husband’s age, husband’s education and family income.
The question that arises is the following: How should we handle the variables mentioned in the previous two paragraphs? Researchers who studied earnings-education relationship have often included these variables as additional explanatory variables in earnings and education equation with fixed coefficients. Greene (2012, p. 699) [3] also included the interaction between age and education as an additional explanatory variable. Previous studies, however, have dealt with fixed coefficient models and did not have anything to do with VCs of the type in (29). The coefficients of the earnings-education relationship in (29) have unwanted omitted-regressor and measurement-error biases as their portions. We need to separate them from the corresponding partial derivatives, as shown in (7) and (9). How do we perform this separation? Based on the above derivation in (1)–(9), we use the variables identified in the previous two paragraphs as the coefficient drivers.
When these coefficient drivers are included, the following two equations get added to Equation (29):
where = 1 for all i, = Wife’s Age, = Wife’s , = Kids, = Husband’s age, = Husband’s education, and = Family income.
It can be seen from (11) that Equation (30) with j = 0 makes the coefficient drivers act as additional regressors in (29) and Equation (30) with j = 1 introduces the interactions between education and each of the coefficient drivers. Greene (2012, p. 699) [3] informed us that binary choice models with interaction terms received considerable attention in recent applications. Note that for j = 1, h = 1, … , 6, should not be equated to because is not equal to .
Appendix Table F5.1 of Greene (2012) [3] contains 753 observations used in the Mroz study of the labor supply behavior of married women. We use these data in this section. Of the 753 married women in the sample, 428 were participants and the remaining 325 were nonparticipants in the formal labor market. This means that = 1 for 428 observations and = 0 for 325 observations. The data on and the z’s for these 753 married women are obtained from Greene’s Appendix Table F5.1. Using these data and applying an iteratively rescaled generalized least squares method to (29) and (30) we obtain
From these equations we have computed the estimates of and and their standard errors. To conserve space, Table 1 below is restricted to contain these quantities only for five married women.

Table 1.
Estimates of and with their standard errors for five married women17.
From (23) we obtain
Our interest is in the partial derivative which is the bias-free portion of . This partial derivative measures the “impact” of the ith married woman’s education on her earnings. Our prior belief is that the right sign for this bias-free portion is positive. Now it is appropriate to use the formula in (25) with j = 1 to estimate. We assume that is negligible. We need to choose the terms in the sum from the terms on the right-hand side of Equation (32). It can be seen from this equation that if we retain the estimate = − in the sum , then this sum does not give positive estimate of for any combination of the six coefficient drivers in (32). Therefore, we remove from . We expect the impact of education on earnings to be small. To obtain the smallest possible positive estimate of , we choose the smallest positive term on the right-hand side of (32). This term is + . Hence we set the z’s other than in equal to zero. Thus, we obtain = 1 and = + . The value of times 0.0702 gives the estimate of the impact of the ith married woman’s education on her earnings.
To conserve space, we present the values of = + only for only i = 1, …, 5 in Table 2. The impact estimates for all 753 married women are presented in the form of a histogram or a kernel density function in Figure 1 below. We interpret the estimate to imply that an additional year of schooling is associated with a × 100 percent increase in earnings. This impact of education on earnings is different for different married women. The impact of a wife’s education on her earnings is 0.0702 times her husband’s education.18 Our results in Table 2 and Figure 1 below show that the greater are the years of schooling of a husband, the larger is the impact of his wife’s education on her earnings. However, the estimates of appear to be high at least for some married women whose husbands had larger years of schooling. Therefore, they may contain some omitted-regressor biases.

Table 2.
Estimates of the bias-free portion of for five married women19.
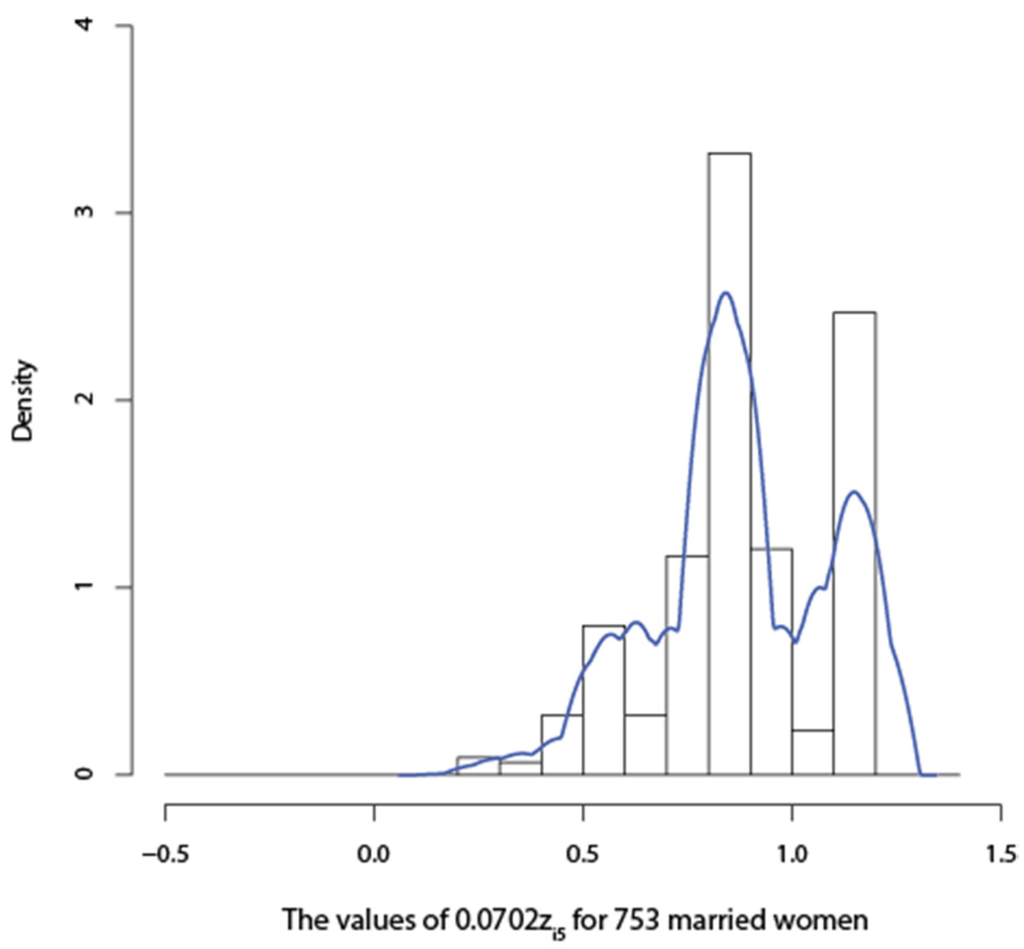
Figure 1.
Estimates of the “impacts” of education on the earnings for 753 married women.
A histogram and a kernel density function presented in Figure 1 are much more revealing than a table containing the values, , i = 1,…, 753, and their standard errors would. Also, such a table occupies a lot of space without telling us mush. We are using Figure 1 as a descriptive device. The kernel function in Figure 1 is multimodal. All the estimates in this figure have the correct signs.
Greene’s (2012, p. 708) [3] estimate 0.0904 of the coefficient of education in his estimated labor supply model is not comparable to the estimates in Figure 1 because (i) his model is different from our model; (ii) the dependent variable of his labor supply model in Greene (2012, p. 683) [3] is the log of the dependent variable of our model (29); and (iii) our definition of in (3) is different from Greene’s (2012, p. 14) [3] definition of . Greene’s estimate is some kind of average estimate applicable to all 753 married women. It is unreasonable to expect his average estimate to be close to the estimate for each married women. We will now show that given the 6 coefficient drivers in (32), it is not possible to reduce the magnitudes of all the estimates in Figure 1 without changing the positive sign of some of these estimates in the left tail end of Figure 1 to the negative sign. This is what has happened in Figure 2. To reduce the magnitudes of the estimates of bias-free parts of the ’s given in Figure 1 for all i, we use the alternative estimates, − of the bias-free parts of the ’s called “modified , i = 1 ,…, 753.” The histogram and kernel density function for the modified is given in Figure 2 below.
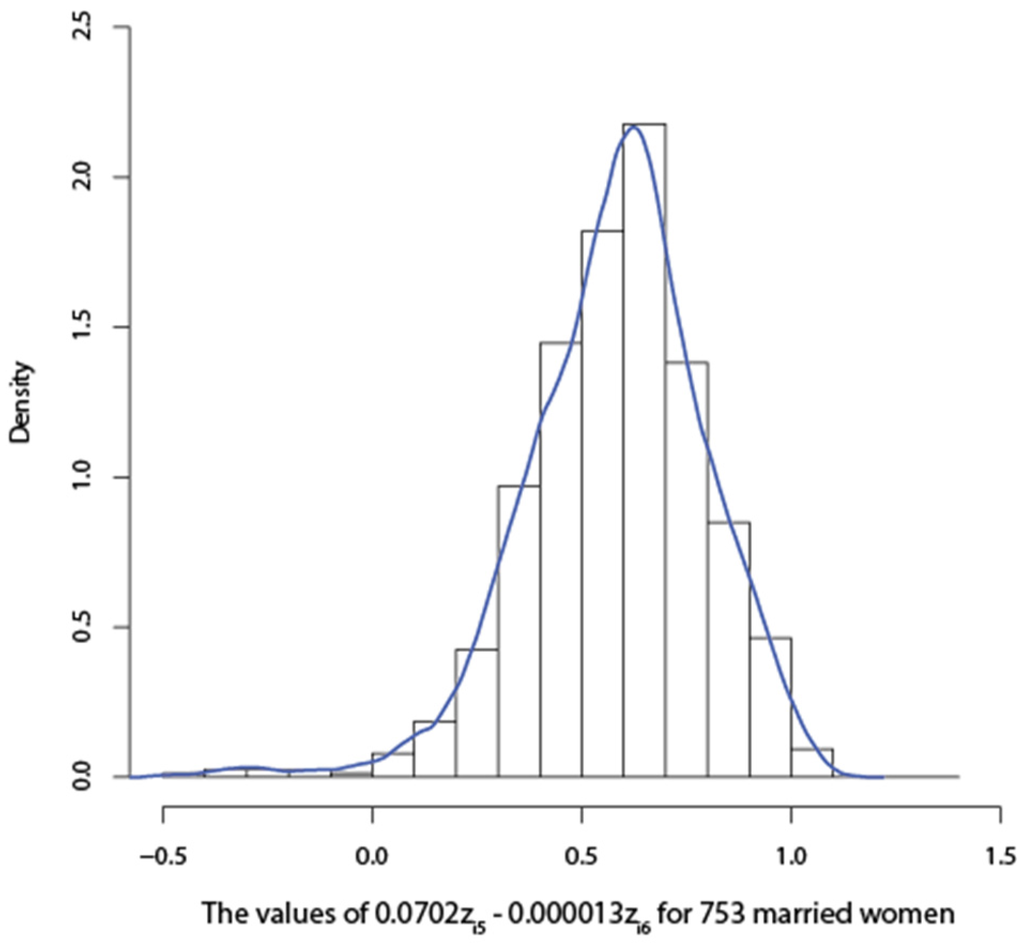
Figure 2.
Modified estimates of the “impacts” of education on the earnings for 753 married women.
Five of the estimates in the left-tail end of this figure have the wrong (negative) sign. More number of wrong signs will occur if we try to further reduce the magnitudes of the modified estimates. The kernel density function of the modified estimates is unimodal unlike the kernel density function in Figure 1. The range of the modified estimates is smaller than that of the estimates in Figure 1.
From these results it is incorrect to conclude that the conventional discrete choice models and their method of estimation give better and unambiguous results than the latent regression model in (11) and (14) and formula (25). The reasons for this circumstance are the following: (i) The conventional models including discrete choice models suffer from four specification errors listed in Section 2.2.5 and the model in (11) and (14) is free of these errors; (ii) The conventional latent regression models have nonunique coefficients and error terms and the model in (11) and (14) is based on model (5) which has unique coefficients and error term. How can a model with nonunique coefficients and error term give unambiguous results? (iii) The conventional method of estimating the discrete choice models appears to be simple because these models are based on the assumption that “the” omitted regressors constituting their error terms do not introduce omitted-regressor biases into the coefficients of their included regressors. The model in (11) and (14) is not based on any such assumption; (iv) Pratt and Schlaifer pointed out that in the conventional model the condition that its regressors be independent of “the” omitted regressors constituting its error term is meaningless. The error terms of the model in (11) and (14) are not the functions of “the” omitted-regressors.
4. Conclusions
We have removed four major specification errors from the conventional formulation of probit and logit models. A reformulation of Yatchew and Griliches’ probit model so that it is devoid of these specification errors changes their results. We also find that their model has nonunique coefficients and error term. YG make the assumption that omitted regressors constituting the error term of their model do not introduce omitted-regressor biases into the coefficients of the included regressors. We have developed a method of calculating the bias-free partial derivative portions of the coefficients of a correctly specified probit model.
Acknowledgments
We are grateful to four referees for their thoughtful comments.
Author Contributions
All authors contributed equally to the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
In this Appendix, we show that any of the models estimated in the econometric literature is more restrictive than (1). We also show that these restrictions, when imposed on (1), lead to several specification errors.
A. Derivation of Linear and Nonlinear Regressions with Additive Error Terms
A.1. Nonunique Coefficients and Error Terms
A.1.1. Beginning Problems—Rigorous Derivation of Models with Additive Error Terms
It is widely assumed that the error term in an econometric model arises because of omitted regressors influencing the dependent variable. We can use appropriate Felipe and Fisher’s (2003) [17] separability and other conditions to separate the included regressors, , from omitted regressors, , so that (1) can be written as
where = is a function of omitted regressors. Let be the random error term and let be equal to which is an unknown function of .20 Let be the fixed parameters representing the constant features of model (A1). From the above derivation we know what type of conditions which, when imposed on (1), give exactly the model in Greene (2012, p. 181, (7-3)) [3].
The separability conditions used to rewrite (1) in the form of (A1) are very restrictive, as shown by Felipe and Fisher (2003) [17]. Furthermore, in his scrutiny of the Rotterdam School demand models, Goldberger (1987) [19] pointed out that the treatment of any features of (1) as constant parameters such as may be questioned and these parameters are not unique.21 Use of non-unique parameters is a specification error. Therefore, the functional form of (A1) is most probably misspecified.
Skyrms (1988, p. 59) [7] made the important point that spurious correlations disappear when we control for all relevant pre-existing conditions.22 Even though some of the regressors, , represent all relevant pre-existing conditions in our formulation of (A1), they cannot be controlled for, as we should to eliminate false (spurious) correlations, since they are included in the error term of (A1). Therefore, in (A1), the correlations between and some of can be spurious.
Karlsen, Myklebust and Tjøstheim (KMT) (2007) [10] considered a model of the type (A1) for time series data. They assumed that is an unobserved stationary process and and are both observed nonstationary processes and are of unit-root type. White (1980, 1982) [11,12] also considered (A1) for time-series data and assumed that the ’s are serially independent and are distributed with mean zero and constant variance. He also assumed that is uncorrelated with for all t. Pratt and Schlaifer (1988, 1984) [1,9] criticized that these assumptions are meaningless because they are about which is not unique and is composed of variables of which we know nothing. Any distributional assumption about a nonunique error term is arbitrary.
A.1.2. Full Independence and the Existence of Conditional Expectations
Consider (A1) again. Let X = , Y = and M = , be three random variables. Then X and M are statistically independent if their joint distribution can be expressed as the product of their marginal distributions. It is not possible to verify this condition.
Let H(X) and K(M) be the functions of X and , respectively. As Whittle (1976) [20] pointed out, we must live with the idea that, for the given random variables like M and X, we may be only able to assert the validity of the condition
where the functions H and K are such that E[H(X)] < and E[K(M)] < . If condition (A2) holds only for certain functions, H and K, then we cannot say that X and M are independent. Suppose that Equation (A2) holds only for linear K, so that E[H(X)M] = E(M)E[H(X)] for any H for which E[H(X)] < . This equation is equivalent to which shows that the disturbance at observation i is mean independent of x at i. This may be true for all i in the sample. This mean independence implies Greene’s (2012, p. 183) [3] assumption (3).
E[H(X)K(M)] = E[H(X)]E[K(M)]
Let us now drop condition (A2) and let us assume instead that
Using these assumptions, Rao (1973, p. 97) [14] proved that
Equations (A3) and (A4) prove that under conditions (A2.1)–(A2.3), E (Y |x) exists.23
H(X) be a Borel function of X,
E|Y| < ∞,
E|YH(X)| < ∞.
E[H(X)Y | X = x] = H(x)E(Y |x)
E{H(X)[Y – E(Y |X)]} = 0
A.1.3. Linear Conditional Means and Variances
Under the necessary and sufficient conditions of Kagan, Linnik and Rao’s (KLR’s) (1973, pp. 11–12) [22] lemma (reproduced in Swamy and von zur Muehlen (1988, pp. 114–115) [23]), the following two equations hold almost certainly:
and
If the conditions of KLR’s lemma are not satisfied, then (A5) and (A6) are not the correct first and second conditional moments of . The problem is that we cannot know a priori whether or not these conditions are satisfied. The conditions of KLR’s Lemma are not satisfied if and are integrated series.24 Furthermore, cannot be made stationary by first differencing it once or more than once because of the nonlinearity of . In these cases, we can use, as Berenguer-Rico and Gonzalo (2013) [24] do, the concepts of summability, cosummability and balanced relationship to analyze model (A1). Clearly the conditions of KLR’s lemma are stronger than White’s assumptions which, in turn, are stronger than KMT’s (2007) [10] assumptions. It is clear that KMT’s assumptions are not always satisfied.
B. Derivation of the Information Matrix for (10)
Consider the log likelihood function in (18). For this function,
where is the partial derivative of with respect to .
. Using this result in (A7) gives
where the condition that n > (K + 1)(p + 1) is needed for the matrix on the right-hand side of this equation to be positive definite.
Taking the expectation of both sides of Equation (A11) gives
where the condition that n > (K + 1)(K + 1) is needed for the matrix on the right-hand side of this equation to be positive definite.
References
- J.W. Pratt, and R. Schlaifer. “On the Interpretation and Observation of Laws.” J. Econom. 39 (1988): 23–52. [Google Scholar] [CrossRef]
- A. Yatchew, and Z. Griliches. “Specification Error in Probit Models.” Rev. Econom. Stat. 66 (1984): 134–139. [Google Scholar] [CrossRef]
- W. Greene. Econometric Analysis, 7th ed. Upper Saddle River, NJ, USA: Pearson, Prentice Hall, 2012. [Google Scholar]
- J.S. Cramer. “Robustness of Logit Analysis: Unobserved Heterogeneity and Misspecified Disturbances, Discussion Paper 2006/07.” Amsterdam, The Netherlands: Department of Quantitative Economics, Amsterdam School of Economics, 2006. [Google Scholar]
- J.M. Wooldridge. Econometric Analysis of Cross-Section and Panel Data. Cambridge, MA, USA: The MIT Press, 2002. [Google Scholar]
- P.A.V.B. Swamy, J.S. Mehta, G.S. Tavlas, and S.G. Hall. “Small Area Estimation with Correctly Specified Linking Models.” In Recent Advances in Estimating Nonlinear Models, with Applications in Economics and Finance. Edited by J. Ma and M. Wohar. New York, NY, USA: Springer, 2014, pp. 193–228. [Google Scholar]
- B. Skyrms. “Probability and Causation.” J. Econom. 39 (1998): 53–68. [Google Scholar] [CrossRef]
- R.L. Basmann. “Causality Tests and Observationally Equivalent Representations of Econometric Models.” J. Econom. 39 (1988): 69–104. [Google Scholar] [CrossRef]
- J.W. Pratt, and R. Schlaifer. “On the Nature and Discovery of Structure (with discussion).” J. Am. Stat. Assoc. 79 (1984): 9–21. [Google Scholar] [CrossRef]
- H.A. Karlsen, T. Myklebust, and D. Tjøstheim. “Nonparametric Estimation in a Nonlinear Cointegration Type Model.” Ann. Stat. 35 (2007): 252–299. [Google Scholar] [CrossRef]
- H. White. “Using Least Squares to Approximate Unknown Regression Functions.” Int. Econ. Rev. 21 (1980): 149–170. [Google Scholar] [CrossRef]
- H. White. “Maximum Likelihood Estimation of Misspecified Models.” Econometrica 50 (1982): 1–25. [Google Scholar] [CrossRef]
- J. Pearl. Causality. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- C.R. Rao. Linear Statistical Inference and Its Applications, 2nd ed. New York, NY, USA: John Wiley & Sons, 1973. [Google Scholar]
- E.L. Lehmann, and G. Casella. Theory of Point Estimation. New York, NY, USA: Spriger Verlag, Inc., 1998. [Google Scholar]
- P.A.V.B. Swamy, G.S. Tavlas, and S.G. Hall. “On the Interpretation of Instrumental Variables in the Presence of Specification Errors.” Econometrics 3 (2015): 55–64. [Google Scholar] [CrossRef]
- J. Felipe, and F.M. Fisher. “Aggregation in Production Functions: What Applied Economists Should Know.” Metroeconomica 54 (2003): 208–262. [Google Scholar] [CrossRef]
- J.J. Heckman, and D. Schmierer. “Tests of Hypotheses Arising in the Correlated Random Coefficient Model.” Econ. Modell. 27 (2010): 1355–1367. [Google Scholar] [CrossRef] [PubMed]
- A.S. Goldberger. Functional Form and Utility: A Review of Consumer Demand Theory. Boulder, CO, USA: Westview Press, 1987. [Google Scholar]
- P. Whittle. Probability. New York, NY, USA: John Wiley & Sons, 1976. [Google Scholar]
- J.J. Heckman, and E.J. Vytlacil. “Structural Equations, Treatment Effects and Econometric Policy Evaluation.” Econometrica 73 (2005): 669–738. [Google Scholar] [CrossRef]
- A.M. Kagan, Y.V. Linnik, and C.R. Rao. Characterization Problems in Mathematical Statistics. New York, NY, USA: John Wiley & Sons, 1973. [Google Scholar]
- P.A.V.B. Swamy, and P. von zur Muehlen. “Further Thoughts on Testing for Causality with Econometric Models.” J. Econom. 39 (1988): 105–147. [Google Scholar] [CrossRef]
- V. Berenguer-Rico, and J. Gonzalo. “Departamento de Economía, Universidad Carlos III de Madrid. Summability of Stochastic Processes: A Generalization of Integration and Co-integration valid for Non-linear Processes.” Unpublished work. , 2013. [Google Scholar]
- 1See, also, Greene (2012, Chapter 17, p. 713) [3].
- 2We will show below that the inconsistency problems Yatchew and Griliches (1984, p. 713) [2] pointed out with the probit and logit models are eliminated by replacing these models by the model in (1) and (2).
- 3We explain in the next paragraph why we have included these conditions.
- 4Some researchers may believe that there is no such thing as the true functional form of (1). Whenever we talk of the correct functional form of (1), we mean the functional form of (1) that is appropriate to the particular binary choice in (2).
- 5Here we are using Skyrms’ (1988, p. 59) [7] definition of the term “all relevant pre-existing conditions.”
- 6This is Basmann’s (1988, pp. 73, 99) [8] statement.
- 7Cramer (2006, p. 2) [4] and Wooldridge (2002, p. 457) [5] assume that their latent regression models are linear. This is a usual assumption. We are simply justifying our unusual assumptions without criticizing the usual assumptions.
- 8We postpone making stochastic assumptions about measurement errors.
- 9The label “omitted” means that we would remove them from (3).
- 10Cramer (2006, p. 4) [4] and Wooldridge (2002, p. 457) [5] make the usual assumption.
- 11Cramer (2006, p. 4) [4] and Wooldridge (2002, p. 457) [5] adopt the usual latent regression models with nonunique coefficients and error terms.
- 12A similar admissibility condition for covariates is given in Pearl (2000, p. 79) [13]. Pearl (2000, p. 99) [13] also gives an equation that forms a connection between the opaque phrase “the value that the coefficient vector of (3) would take in unit i, had been ” and the physical processes that transfer changes in into changes in .
- 13We illustrate this procedure in Section 3 below.
- 14Pratt and Schlaifer (1988) [1] consider what they call “concomitants” that absorb “proxy effects” and include them as additional regressors in their model. The result in (9) calls for Equation (10) which justifies our label for its right-hand side variables.
- 15An important difference between coefficient drivers and instrumental variables is that a valid instrument is one that is uncorrelated with the error term, which often proves difficult to find, particularly when the error term is nonunique. For a valid driver we need variables which should satisfy Equations (25) and (26). On the problems with instrumental variables, see Swamy, Tavlas, and Hall (2015) [16].
- 16These biases are not involved in Wooldridge’s marginal effects because according to that researcher omitted regressors constituting his model’s error term do not introduce omitted-regressor biases into the coefficients of the included regressors.
- 17The standard errors of estimates are given in parentheses below the estimates for five married women. The estimates and their standard errors for other married women are available from the authors upon request.
- 18According to Geene (2012, p, 708) [3], it would be natural to assume that all the determinants of a wife’s labor force participation would be correlated with the husband’s hours which is defined as a linear stochastic function of the husband’s age and education and the family income. Our inclusion of husband’s variables in (32) is consistent with this assumption.
- 19The standard errors of estimates are given in parentheses below the estimates for five married women. These estimates and standards errors for other married women are available from I-Lok Chang upon request.
- 20Another widely cited work that utilized a set of separability conditions is that of Heckman and Schmierer (2010) [18]. These authors postulated a threshold crossing model which assumes separability between observables Z that affect choice and an unobservable V. They used a function of Z as an instrument and used the distribution of V to define a fundamental treatment parameter known as the marginal treatment effect.
- 21The “uniqueness” is defined in Section 2.2.3.
- 22We have been using the cross-sectional subscript i so far. We change this subscript to the time subscript t wherever the topic under discussion requires the use of the latter subscript.
- 23This proof is relevant to Heckman’s interpretation that in any of his models, the error term is the deviation of the dependent variable from its conditional expectation (see Heckman and Vytlacil (2005) [21]. Conditions (A2.1)–(A2.3) do not always hold and hence this conditional expectation does not always exist.
- 24A nonstationary series is integrated of order d if it becomes stationary after being first differenced d times (see Greene (2012, p. 943) [3]). If in (A1) is a nonstationary series of this type, then it cannot be made stationary by first differencing it once or more than once if is nonlinear. Basmann (1988, p. 98) [8] acknowledged that a model representation is not free of the most serious objection, i.e., nonuniqueness, if stationarity producing transformations of its observable dependent variable are used.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).