Abstract
Financial time-series data often exhibit statistically significant skewness and heavy tails, and numerous flexible distributions have been proposed to model them. In the context of the Log-linear Realized GARCH model with Skew-t (ST) distributions, our objective is to explore how the choice of prior distributions in the Adaptive Random Walk Metropolis method and initial parameter values in the Generalized Reduced Gradient (GRG) Solver method affect ST parameter and log-likelihood estimates. An empirical study was conducted using the FTSE 100 index to evaluate model performance. We provide a comprehensive step-by-step tutorial demonstrating how to perform estimation and sensitivity analysis using data tables in Microsoft Excel. Among seven ST distributions—namely, the asymmetric, epsilon, exponentiated half-logistic, Hansen, Jones–Faddy, Mittnik–Paolella, and Rosco–Jones–Pewsey distributions—Hansen’s ST distribution is found to be superior. This study also applied the GRG method to estimate new approaches, including Realized Real-Time GARCH, Realized ASHARV, and GARCH@CARR models. An empirical study showed that the GARCH@CARR model with the feedback effect provides the best goodness of fit. Out-of-sample forecasting evaluations further confirm the predictive dominance of models incorporating real-time information, particularly Realized Real-Time GARCH for volatility forecasting and Realized ASHARV for 1% VaR estimation. The findings offer actionable insights for portfolio managers and risk analysts, particularly in improving volatility forecasts and tail-risk assessments during market crises, thereby enhancing risk-adjusted returns and regulatory compliance. Although the GRG method is sensitive to initial values, its presence in the spreadsheet method can be a powerful and promising tool in working with probability density functions that have explicit forms and are unimodal, high-dimensional, and complex, without the need for programming experience.
1. Introduction
Financial time-series data often exhibit statistically significant skewness and heavy tails, characteristics that conventional volatility models struggle to capture accurately. These features are not merely statistical nuances; they have profound implications for risk management, asset pricing, and financial stability. For instance, during the 2008 Global Financial Crisis, traditional models underestimated tail risks because they failed to account for extreme skewness and kurtosis, which led to significant losses for investors and institutions (Nadarajah et al., 2015). Similarly, unexpected volatility spikes, such as those observed during the COVID-19 market turmoil, further underscore the need for models that can better adapt to asymmetric and heavy-tailed distributions (Alfeus & Harvey, 2025).
The foundation of modern volatility modelling lies in the Generalized Autoregressive Conditionally Heteroskedastic (GARCH) framework, which has evolved significantly since its inception. A pivotal advancement was the introduction of the Realized GARCH (RealG) model on linear and log-linear specifications by Hansen et al. (2012), which demonstrated that incorporating high-frequency realized volatility measures could substantially improve volatility forecasts compared to the standard GARCH model. This innovation builds upon earlier work by Andersen et al. (2003), who established realized volatility as a robust predictor of future volatility. The RealG model has gained considerable attention in the literature on financial econometrics (see, e.g., Abounoori and Zabol (2020); Cai et al. (2021); Wang et al. (2020); Xie and Yu (2020)). Recent work by Matei et al. (2019); Nugroho et al. (2023c) has shown that the Log-linear RealG (LogRealG) model outperforms its linear counterpart in in-sample estimation, particularly in capturing the nuanced dynamics of financial markets during periods of stress.
The practical stakes of accurate volatility modelling are high. For example, Mugerman et al. (2020) demonstrated how exogenous events like daylight savings time shifts can disrupt market returns and volatility, highlighting the broader importance of understanding volatility dynamics. In risk management, mis-modelling volatility can lead to inaccurate value-at-risk estimates, flawed margin settings, and inadequate capital reserves, with potentially severe consequences for financial institutions and regulators (Gerlach & Wang, 2016). Accurate volatility forecasts are also critical for derivative pricing, portfolio optimization, and algorithmic trading strategies, where even minor deviations can translate into significant financial losses (Sharma, 2015).
On the distributional front, the literature has long recognized the limitations of Gaussian assumptions in financial modelling. Seminal contributions, such as that by Christoffersen et al. (2010), have highlighted the importance of non-normality in option pricing, paving the way for skewed and heavy-tailed distributions in volatility models. The Skewed Student-t (ST) distribution, in particular, has become a cornerstone for addressing asymmetry and leptokurtosis in financial returns. Our work builds on these foundations by conducting a comprehensive comparison of seven ST distributions, including Hansen’s ST (H) in Liu et al. (2015); Nugroho et al. (2021), Mittnik–Paolella ST (MP) in Li and Nadarajah (2020), Jones–Faddy ST (JF) in Acitas et al. (2021), Epsilon ST (E) as a special case of scale-shape mixtures of normal skew in Jamalizadeh and Lin (2017), Asymmetric ST (A) in Rubio and Steel (2015), Rosco–Jones–Pewsey ST (RJP) in Li (2019), and Exponentiated Half-Logistic ST (EHL) as proposed recently in Adubisi et al. (2022). These seven error distributions were selected to comparatively evaluate their performance within the LogRealG model framework, particularly noting that E, JF, and RJP have not previously been applied to the analysis of GARCH-type models.
The estimation methods used in recent studies to estimate parameters of GARCH-type and realized models include Maximum Likelihood Estimation (MLE), such as in Hansen and Huang (2016); Matei et al. (2019); Xie and Yu (2020); Bayesian MCMC (Markov chain Monte Carlo) estimation, such as in C. W. Chen et al. (2023); C. W. S. Chen and Watanabe (2019); Nugroho et al. (2023b,2023c); Machine Learning (ML) methods, such as in Amirshahi and Lahmiri (2023); Zahid et al. (2022); and Excel’s Solver, such as in Farida et al. (2019); Listyan et al. (2022). The MCMC method is the most popular and widely used sampling method to sample from an unknown high-dimensional distribution and to avoid problems with computational issues in volatility estimation. Two Bayesian MCMC estimators—namely, robust adaptive Metropolis and standard random walk Metropolis—were shown in Tendenan et al. (2020) to produce more favourable results than MLE estimators in a simulation study. Further support for the efficacy of MCMC approaches comes from studies such as Djeddi (2022), which indicates that MCMC algorithms can successfully capture complex GARCH model components and yield accurate estimates, even in scenarios where MLE might fail. Djeddi (2022) further highlights a critical limitation of MLE, noting that MLE estimates may not be consistent when the returns series contains spikes or its volatility is highly persistent. However, MCMC methods possess significant drawbacks. Their primary limitations include the substantial programming expertise required for implementation and longer computation times compared to alternative optimization methods, such as Excel’s Solver or MLE.
While advanced ML techniques offer powerful predictive capabilities, our choice of the Bayesian MCMC method is based on its distinctive and crucial advantages for econometric modelling. Unlike many ‘black-box’ ML models that primarily focus on point predictions (Bharadiya, 2023), MCMC provides a full probabilistic inference of model parameters (van Ravenzwaaij et al., 2018). This allows for comprehensive quantification of parameter uncertainty through posterior distributions and credible intervals, which is essential for robust risk management and informed decision-making in financial contexts. Furthermore, MCMC’s ability to seamlessly integrate prior knowledge about model parameters, combined with its effectiveness in handling complex, structured econometric models like GARCH, offers a transparent and interpretable framework for understanding underlying financial dynamics. This interpretability and emphasis on parameter inference differentiate MCMC as a more suitable tool for our specific research objectives compared to purely predictive ML methodologies.
To address MCMC’s limitations—its reliance on programming expertise and computationally intensive sampling—we employ Excel’s Solver as an accessible alternative. The key advantages of Excel’s Solver are threefold: its user-friendly interface requires no programming knowledge (de los Rios & Ramos, 2020), making it accessible to non-technical practitioners; its Generalized Reduced Gradient (GRG) method is robust, effective, and reliable for solving smooth nonlinear optimization problems (Maia et al., 2017; Msabawy & Mohammad, 2021; Parkinson et al., 2018; Terregrossa & Sener, 2023); and it delivers rapid solutions for unimodal likelihood functions (Msabawy & Mohammad, 2021). However, these advantages must be weighed against critical disadvantages: as a heuristic method, GRG cannot guarantee global optima (Plevris et al., 2021), and its solutions are sensitive to initial values—a limitation thoroughly examined in our sensitivity analysis. These disadvantages necessitate validation using MCMC as a statistical benchmark. By including both methods, this study bridges a critical gap between theoretical rigour and practical applicability: MCMC serves as the gold standard for parameter estimation, while GRG provides a viable alternative for practitioners who prioritize accessibility and speed but still require validated results.
This study employs an Adaptive Random Walk Metropolis (ARWM) approach for estimation of the LogRealG model, with the method worked out in the MCMC scheme implemented in Matlab. Studies by Listyan et al. (2022); Nugroho et al. (2023a) empirically confirmed the validity of the ARWM method as efficient in the estimation of GARCH-type and RealG models. To assess the performance of the ARWM method, we evaluate the efficiency of the estimation method by calculating the Integrated Autocorrelation Time (IAT), as well as the Effective Sample Size (ESS). To assess the robustness of the empirical results, we investigate the sensitivity analysis of MCMC output to the choice of prior distributions. The choice of the prior distribution on the degrees-of-freedom parameter in the Student-t and ST-version distributions was shown by da Fonseca et al. (2021); Nakajima and Omori (2012) to affect the final results.
With this in mind and focusing on the seven types of ST distributions as probability distributions for the errors in a LogRealG model, the novelty and contributions of this study are twofold, designed to provide a comprehensive analysis of volatility modelling. First, we conduct an extensive comparison of seven ST distributions within the LogRealG framework, employing both Bayesian MCMC and GRG estimation methods. This includes a detailed sensitivity analysis of prior distributions for MCMC and initial values for GRG to assess their impact on parameter and log-likelihood estimates, as well as a rigorous comparison of distributional performance using information criteria. Critically, those distributions differ in how they model tail risks and asymmetries. Importantly, three distributions—E, JF, and RJP—have never been applied to GARCH-type volatility models, despite their theoretical promise, leaving a significant gap in understanding their empirical performance. Second, we extend the current RealG modelling approaches by developing and empirically evaluating three new model variants: Realized Real-Time GARCH, Realized Asymmetric Stochastic Heteroskedastic Autoregressive Volatility, and Conditional AutoRegressive Realized Volatility with a feedback effect. These dual contributions collectively address both theoretical refinement (through distributional comparisons) and practical innovation (through model extensions), offering actionable insights for financial econometrics. For empirical validation, we use daily returns and realized kernel measures of the FTSE 100 (UK) index, spanning major market events to ensure rigorous stress testing.
The remainder of this paper is organized as follows: Section 2 introduces the methodology, including the LogRealG model, ST distributions, and estimation techniques. Section 3 presents our core empirical findings, including a comprehensive comparison of seven ST distributions applied to the LogRealG model, in-sample performance evaluation of competing RealG variants, and out-of-sample forecasting comparisons of volatility and value-at-risk predictions. Section 4 discusses policy implications and conclusions. Technical sensitivity analyses of prior distributions (MCMC) and initial parameter values (GRG) are provided in Appendix A and Appendix B, respectively.
2. Materials and Methods
To ground our comparative analysis, this section details the LogRealG framework, the seven ST distributions, and the estimation methods (MCMC and GRG).
2.1. LogRealG Model
In order to improve the adequacy of the Exponential GARCH (EGARCH) model in measuring volatility and increasing the accuracy of prediction, Matei et al. (2019) and Nugroho et al. (2023c) studied the LogRealG model by incorporating a realized measure of volatility into the volatility process and by defining the log-realized measure as a normal process. The daily asset return is denoted as , and the realized measure is denoted as . The LogRealG model is expressed as follows:
where quadratic functions and , for , are referred to as the leverage function, accounting for dependence between return and volatility, which is empirically important. The model requires and does not require any constraints for the others.
Notice that the assumption of the distribution on the innovations of the GARCH volatility model directly impacts the accuracy of volatility predictions. Hence, the rest of this section is dedicated to the models with standardized skew and heavy-tailed densities. The standardized density is derived via the transformation expressed as .
2.2. Standardized Skew Student-t Densities
In the context of the GARCH model, Nadarajah et al. (2015) showed that the A distribution provides the best fit distribution for cocoa bean price returns, compared with Fernandez–Steel’s ST distribution in Trottier and Ardia (2016) and ten non-ST distributions, including normal, Student-t, and generalized error distributions. For the A-distributed errors, the standardized density function is expressed as follows:
where is the skewness parameter; and are the left and right tail parameters, respectively; (where is the gamma function), and is defined as .
For the E-distributed errors, the standardized density function is expressed as follows:
where is the skewness parameter and represents the degrees of freedom, which control the height and tails of the density. A left-skewed density function is indicated by , whereas a right-skewed density function is indicated by .
For the EHL distributed errors, the standardized density function is expressed as follows:
where and . Here, . The superiority of the EHL distribution over eleven other distributions, excluding the six distributions mentioned in the previous section, was validated for both the GARCH and GJR-GARCH models.
For the H-distributed error, the standardized density function is expressed as follows:
where and . The density function is skewed to the left when and vice-versa when .
For the JF-distributed error, the standardized density function is expressed as follows:
where , , and denotes the beta function. When or , the density function is left- or right-skewed, respectively. Liu et al. (2015) and Nugroho et al. (2021) showed the superiority of the H distribution compared to the Fernandez–Steel’s ST distribution, the skewed generalized error distribution reported by Theodossiou (2015), and the SVG distribution of Christoffersen et al. (2010) for the EGARCH model.
For the MP-distributed error, the standardized density function is expressed as follows:
where . For , the density function is skewed to the right (left).
For the RJP-distributed error, the standardized density function is expressed as follows:
where and is a skewness parameter. The density functions are skewed to the left (right) if .
The seven ST distributions discussed here employ distinct mathematical approaches to model skewness and heavy tails. A detailed comparison of their theoretical properties and financial applications is provided in Appendix A.
2.3. Log-Likelihood Function for the Model
The log-likelihood function for the LogRealG(1,1) model is the sum of the log likelihood of return and the log likelihood of measurement . Let and , and since the equation of is normally distributed with a mean of and variance of , the log-likelihood function for measurement equation is
Therefore, the log-likelihood function for the LogRealG(1,1) model is
where denotes the parameter vector of the model and PDF denotes the density function of return errors.
2.4. ARWM Method
MCMC is a general strategy for generating a sequence of random samples that satisfy the Markov property based on a complex high-dimensional target probability distribution (even the target distribution may not have a closed form), from which integrals over the parameter, as its expected value or variance describing the distribution of the parameter of interest, can be approximated using the generated Markov chain via Monte Carlo integration. The ARWM algorithm generates a Markov chain based on the Random Walk Metropolis algorithm (Spencer, 2021). The algorithm is adaptive because it updates the proposal sample during the simulation in order to better match the target distribution. This is done by using the history of the Markov chain to estimate the covariance matrix of the target distribution. The algorithm is easy to implement and can be used to sample from a wide variety of target distributions.
In this study, we employed the following ARWM method in the MCMC scheme and implemented it in Matlab.
- Initialize the algorithm. Set some starting values for and a step size of at iteration .
- Generate a proposal. At iteration n, generate a proposal sample () from a Gaussian distribution with a small covariance matrix:
- Check parameter conditions. If the proposal satisfies constraints, then go to the next step; otherwise, keep as the current state and go to step 6.
- Calculate the acceptance probability. Calculate the standard Metropolis acceptance ratio:where L is the total likelihood function based on Equation (10) and is the prior distribution.
- Accept/reject a proposal. If , where u is a uniform random number on , then accept the proposed state and set . Otherwise, reject the proposed state and keep as the current state.
- Update the step size. The step size is updated adaptively based on the following formula:where a represents the number of accepted proposals per iteration (n) and is the target acceptance rate, which is commonly set to or (for our case; see Gelman et al. (1996)).
- Repeat steps 2 and 5 until the samples “converge”. This process is known as the “burn-in” period, and convergence will be defined later on in this article.
To prevent from converging to a poor proposal variance, a deterministic sequence of positive real numbers () should be chosen so that satisfies the following properties (Baker, 2014):
For example, Chimisov et al. (2018); Nugroho et al. (2023c) chose the harmonic series of order k, i.e., for some .
2.5. Excel’s Solver
The most popular spreadsheet optimization tool is, perhaps, Solver in Microsoft Excel (Dasovic & Klansek, 2021), an optimization package included within Microsoft Excel. By changing the values of decision-variable cells that satisfy the given constraint, Solver finds an optimal value for the formula in the objective cell. There are three choices of solution methods provided by Solver—namely, GRG, Evolutionary, and Simplex LP. The best approaches for nonlinear problems are GRG and Evolutionary, whereas Simplex LP can only be used for linear problems. This study chooses GRG, since this method is the fastest compared to the other nonlinear solution method (de los Rios & Ramos, 2020). Moreover, the likelihood functions of the models considered in this study, referred to as objective functions, are smooth (differentiable) functions, which is a requirement of the GRG method. Put simply, Excel Solver’s GRG examines the gradient or slope of the objective function as the input values (or parameters such as decision variables in our case) vary and decides that it has found the best solution when its partial derivative equals zero.
The steps of the GRG algorithm for a general problem are described in Parkinson et al. (2018). Here is a brief overview of how Excel Solver’s GRG method works in estimating the parameters of the GARCH-type model:
- Initialize the algorithm. The algorithm starts by specifying the initial values of the model parameters and calculating the log-likelihood function for each data point as an objective function
- Define the problem. Once the problem is set up, we can open the Solver Parameters dialogue box, define the problem, select the GRG Nonlinear method.
- The GRG algorithm runs. The GRG algorithm iterates until it reaches a stopping condition.
- Solver completion message. When the Solver stops running, the Solver Results dialogue displays a message that describes or discusses one of several stopping conditions (see McFedries (2022)).
2.6. Model Selection Criteria
To compare the fitting performance of models with different conditional distribution specifications, this study selects a suitable model based on four Information Criteria (IC)—namely, Akaike’s Information Criterion (AIC), Consistent AIC (CAIC), the Bayesian Information Criterion (BIC), and Adjusted BIC (ABIC)—since different criteria sometimes support different models. These are the easiest and most commonly used criteria for testing how well a statistical model fits the data. This is reasonable, and since they may be expressed as log-likelihood functions with simple penalties and can be used to compare many models simultaneously, not all of them are nested. The study in Dziak et al. (2020) presents perspectives that may provide insights into how to interpret the practical implications of the four ICs, in addition to a summary of criteria that include the penalty weight, quality, and type of error that may occur. The ICs can be computed as
where is the log-likelihood value of the entire dataset under the model evaluated for the parameter estimates, T is the number of observations, and k is the number of estimated parameters in the model. The optimal model is selected based on lowest IC value.
3. Results
Building on the LogRealG framework and estimation methods outlined in the previous section, we now present empirical results in two stages: first, a comparative evaluation of Skew-t distributions and, second, an assessment of extended models incorporating real-time data and feedback effects.
This section presents the core empirical findings of our study, structured to clearly delineate our two main contributions. First, we evaluate the performance of seven ST distributions in the LogRealG model, using the FTSE 100 index as a case study. This comparison highlights the importance of distributional assumptions in volatility modelling. Second, we introduce and assess three extended models that utilize real-time data and feedback mechanisms, demonstrating their superiority in forecasting volatility and tail risk.
3.1. Observed Data
The empirical analysis presented in this study utilizes daily returns and the RK of the FTSE 100 index from January 2000 to December 2017, comprising 4503 observations. The RK measure, introduced by Barndorff-Nielsen et al. (2008), is robust to microstructure noise bias and makes efficient use of the available data. The dataset spans 18 years and captures several major market disruptions that are critical for evaluating volatility models. First, the Global Financial Crisis (2007–2009) serves as a key stress test, exposing the FTSE 100 index to extreme volatility and structural breaks, which are essential for assessing model robustness. Second, the European Sovereign Debt Crisis (2010–2012) provides insights into prolonged market turbulence that are particularly relevant for the UK due to its economic ties with the Eurozone. Third, the flash crashes of 6 May 2010 and 24 August 2015 offer extreme, short-lived volatility spikes, testing the models’ ability to adapt to sudden market shocks. While the dataset ends in 2017, our primary focus is on advancing volatility modelling techniques rather than analysing recent market conditions. The methodological framework developed here is designed to be transferable to contemporary datasets. It is worth noting that the Oxford-Man Institute’s realized volatility library, one of the most comprehensive public sources for high-frequency financial data, ceased updates after the COVID-19 pandemic began, making this study particularly valuable as one of the last comprehensive analyses using this benchmark dataset. Although the dataset is no longer publicly available, its inclusion of these events ensures that our findings remain methodologically rigorous and applicable to future crises, reinforcing the contribution to volatility forecasting under diverse market conditions.
Figure 1 displays the time plot of the daily returns and logarithm of RKs (log(RK)) in percentage for the observed stock index. The mean of returns is negative, suggesting that returns decrease slightly over time. The returns process varies around its mean, indicating that the series is stationary. This stationarity is necessary before applying the volatility model.
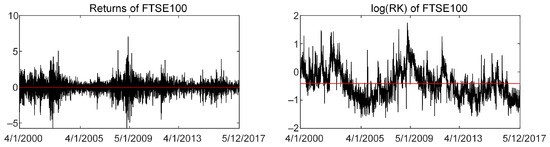
Figure 1.
Plots of daily return and log(RK). The red line denotes the average time-series data.
Table 1 presents the summary statistics of the daily returns and log(RK). The returns data exhibit kurtosis of more than 3, indicating that the distribution is heavy-tailed and negatively skewed. The non-normality of the distribution of returns is confirmed by a Jarque–Bera (JB) test, which rejects the null hypothesis of normality at the 5% significance level. To check for conditional heteroskedasticity, the Ljung–Box (LB) Q-test is conducted on the first five lags of the squared returns. The null hypothesis of the absence of autocorrelation at the 5% significance level is rejected, which suggests the incorporation of the AR(1) term into RealG-type models. The LB p-value of log(RK) rejects the null hypothesis of the absence of autocorrelation, which results in the high persistence of volatility (Takahashi et al., 2023). Consequently, the characteristic of the observed data—specifically, skewness and heavy tails—render it highly suitable for analysis employing various ST distributions as a primary comparative framework.

Table 1.
Statistical description for returns and log(RK).
3.2. Performance of ST Distributions in the LogRealG Model
3.2.1. Based on the Estimation in the MCMC Scheme
First, the estimation of the LogRealG-type model with ST distributions is conducted by the ARWM method in the MCMC scheme. MCMC chains start from the following initial values:
Following Sherlock et al. (2017), we start the ARWM method with the initial proposal variance of , where d is the number of estimated parameters. First, investigations of the IAT (see Nugroho et al. (2021) for the algorithm and https://github.com/mjlaine/mcmcstat/blob/master/iact.m (accessed on 5 October 2012) for the Matlab code written by Marko Laine) of our MCMC sample show that the chains converge within about 50,000 iterations. In this case, all IAT values are less than 400, leading to ESSs (the chain length divided by the IAT (Turek et al., 2017)) exceeding 100; hence, the ARWM method is statistically efficient, as recommended by Givens (2015). According to these observations, we use the first 5000 iterations for a burn-in period and build a posterior sample of 50,000. For example, Figure 2 displays the trace plots of the Markov chain samples. This figure visually shows rapid convergence and chain mixing. Thus, based on the trace plots, it is not necessary to lengthen the burn-in period for all parameters, and the initial values seem to be reasonable.
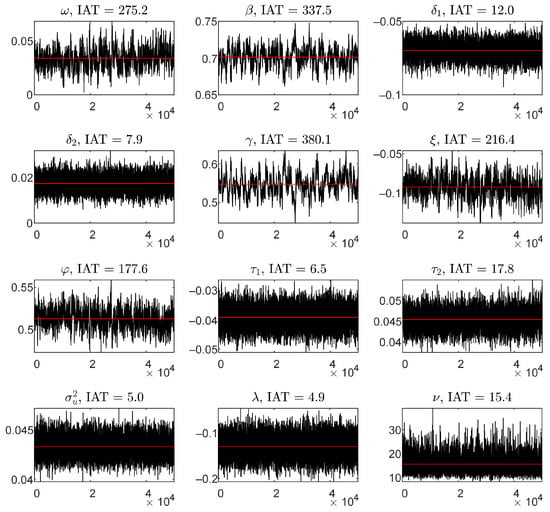
Figure 2.
Trace plots of the ARWM chains for the LogRealG model with H distribution. The red line represents an estimated average or the posterior mean.
Bayesian modelling concerns prior distribution over model parameters. In this context, Depaoli et al. (2020); Kruschkes (2015) recommended the importance of fully examining the impact of the prior distribution to the final model estimates through a sensitivity analysis, since this impact may produce biased results. Since there exists no study that has investigated how the prior for the ST parameters should be specified, this study assesses the sensitivity of MCMC outputs to the choice of prior distributions for the parameters. A detailed discussion regarding the sensitivity analysis is provided in Appendix B.
To investigate the robustness of the distribution comparison, we calculate four selection criteria for the highest log likelihoods, which are presented in Table 2. Excluding the AIC, the H distribution is favoured over the A distribution under the four above-mentioned priors for . Excluding the A distribution, the H distribution outperforms the others, regardless of the choice of prior. Therefore, it is reasonable to choose the four above-mentioned priors for the ST parameters in the implementation of the MCMC algorithm.

Table 2.
Selection criteria under the priors in the MCMC algorithm that give the highest log likelihood.
After evaluating the sensitivity of the prior distribution in the MCMC scheme, we turn to estimation analysis using the GRG method to compare the consistency of the results.
3.2.2. Based on the Estimation in the GRG Scheme
The performance of the seven ST distributions is also analysed based on the estimation results from the GRG method in Excel’s Solver, with the sensitivity analysis of the initial values of the method discussed in Appendix C. Based on the highest log likelihood, Table 3 presents log likelihood and four IC values for the estimated LogRealG models. It can be seen that the LogRealG model with H distribution has an upper hand in all six distribution specifications. The only exception is that the AIC value of model with A is slightly smaller than that of model with H. These results are similar to previously reported MCMC results.

Table 3.
Selection criteria under the initial values in Excel’s Solver that give the highest log likelihood.
The GRG method’s sensitivity to initial values, while notable, can be effectively managed by adopting empirically validated initialization strategies that prioritize both maximum log-likelihood attainment and stability across parameter variations. Our analysis reveals that for most skew-t distributions—particularly A H, JF, MP, and RJP—the log-likelihood values exhibit remarkable robustness, with variations of less than 0.5% across a broad range of initial values (e.g., , ). For instance, H demonstrates negligible differences in log likelihood ( vs. ), whether initialized with or , underscoring its insensitivity to moderate changes in starting points. However, the E distribution demands greater caution, as its log likelihood can vary by over 1% (e.g., for vs. for ), highlighting the need for constrained grid searches (e.g., ) to avoid suboptimal solutions. To generalize, initializing skewness parameters () near zero (symmetry) and tail parameters () at moderate values (e.g., ) consistently yields stable optimum, while validation against MCMC results further safeguards against initialization bias. These findings not only mitigate GRG’s local-optimization limitations but also provide practitioners with actionable guidelines for reliable implementation.
To find out how different the estimation values obtained from the MCMC and GRG are, the MCMC results are used as a benchmark. Figure 3 displays the relative errors in estimated parameters and ICs. The figure shows that relatively large differences for some parameter estimates occur in the case of models with E, EHL, and MP. In the E and EHL specifications, GRG resulted negative estimates for the constant parameters of and , in contrast to MCMC, which produces a positive and significant estimate. The only exception is for the E specification, where the estimates of by the two methods have the same negative sign. These results indicate that the lower bounds for the conditional log variances of the two methods may differ. In the EHL specification, although the coefficients of leverage functions estimated by the two methods look different, each coefficient has the same sign, which indicates that the two methods provide leveraged estimates with the same effect. Furthermore, in the MP specification, the estimated values of obtained by the two methods differ considerably. As previously reported, the estimated value of depends on the initial value of , but this does not change the log-likelihood estimate. In terms of log likelihood and ICs, the two estimation approaches produce relatively very similar values for each model.
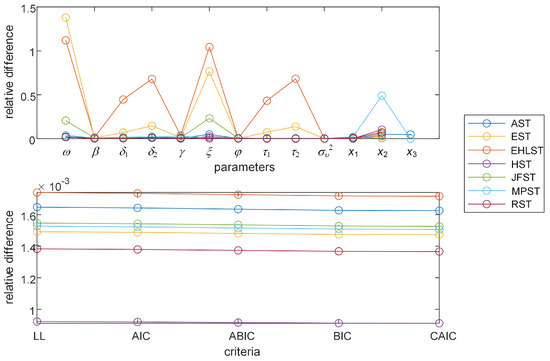
Figure 3.
Plots of relative error. Parameters , , and denote the ST parameters.
The finding of consistency between MCMC and GRG reinforces the reliability of the HST distribution. Based on these results, we now extend our analysis to explore structural innovations in volatility modelling. The following section introduces three extended RealG variants designed to incorporate real-time information and feedback mechanisms based on insights gained from the distribution comparison.
3.3. Using Excel’s Solver to Estimate the Extended Models
Studies by Smetanina (2017); Smetanina and Wu (2020) proposed a new model by incorporating the current return in the GARCH volatility specification: Real-Time GARCH (RTG). Considering the model with leverage and feedback effects (the different effects of the past positive and negative returns on conditional variance), we propose the Realized RTG(1,1) model with leverage and feedback effects (Real-RTG-LF hereafter):
Following Smetanina and Wu (2020), the log-likelihood function of is expressed as follows:
with
where
Recently, based upon the idea of RTG, which is able to capture the time-varying volatility of volatility, Ding (2023) proposed the Asymmetric Stochastic Heteroskedastic Autoregressive Volatility (ASHARV) model. This model can be extended to a Realized ASHARV model (RealAS hereafter), which is expressed as follows:
where . The term of is called drift. Similar to the log-likelihood function of the Real-RTG-LF model, the log-likelihood function of is expressed as follows:
with
where
Meanwhile, Xie et al. (2019); Xie and Yu (2020) developed the GARCH@CARR model, which has a simpler specification than the LogRealG model. Moreover, a comprehensive empirical study by Xie and Yu (2020) showed that the proposed model outperforms the LogRealG model. By adding a feedback effect, we propose the GARCH@CARR model with a feedback effect (G@C-F hereafter), which is characterized by
where and denotes the log-normal distribution. The log-likelihood function for the model is then defined as
3.3.1. In-Sample Fitting
The distributional comparison in Section 3.2 highlighted the critical role of ST specifications in volatility forecasting. We now evaluate whether structural enhancements to the LogRealG model—through real-time returns (Real-RTG-LF), volatility-of-volatility dynamics (RealAS), and feedback mechanisms (G@C-F)—can further improve in-sample fit, utilizing the H distribution’s established superiority.
To perform this evaluation, Excel’s Solver was employed to estimate all RealG variants. Table 4 reports the parameter estimates, log likelihood, and four ICs for five competing models. It is clearly visible that the Real-RTG-LF model has the worst goodness-of-fit. In other words, the model could not improve the performance of the LogRealG model. Two ICs of the RealAS model are smaller in value than those of the LogRealG model, meaning two competing models achieve the same performance. Meanwhile, the G@C model has significantly better goodness of fit than the LogRealG, Real-RTG-LF, and RealAS models. The interesting result is that we clearly see an improved log likelihood and ICs after adding a feedback effect in the process of the conditional mean of the range in the G@C model. This gives a particularly strong indication that the specification of the feedback effect provides an improvement for the G@C model.

Table 4.
Parameter estimates of competing models with H distribution using Excel’s Solver.
3.3.2. Out-of-Sample Forecasting
While the in-sample results demonstrate the efficacy of the extended models, their practical utility depends on out-of-sample predictive accuracy. The following analysis bridges the gap between theoretical innovation and real-world application, testing whether models incorporating real-time information can reliably forecast volatility and tail risk in financial markets.
Based on the goodness-of-fit analysis in the previous section, several models demonstrated superior performance in capturing the volatility dynamics of historical data. However, the true evaluation of a volatility model lies in its forecasting ability. Still, using the GRG method in Excel’s Solver for model estimation, this subsection examines the out-of-sample forecasting performance of each model. Reliable volatility forecasting plays a central role in modern financial practices, ranging from investment decision-making and risk management to the pricing of financial assets (Alfeus & Harvey, 2025; Sharma, 2015). Therefore, this evaluation will focus on one-step-ahead volatility forecasting and the accuracy of market risk measurement through Value-at-Risk (VaR) to determine which model is most useful in practical applications.
This study assesses the predictive accuracy of competing models from two perspectives: volatility forecasting and tail-risk forecasting. To evaluate volatility forecasting performance, we employ two types of measures. The first type includes three standard loss functions—the Mean Absolute Error (MAE), the Mean Square Error (MSE), and the Mean Absolute Percentage Error (MAPE)—following Al Rahahleh and Kao (2018). The second is the Predictive Log-Likelihood (PLL) approach, as utilized by Chan and Grant (2016); Gerlach and Wang (2016); Le (2023). Consistent with the RealG framework, this study uses the realized kernel as a proxy for the unobservable true volatility. For the tail-risk perspective, the performance of VaR forecasts is evaluated using the Violation Rate (VRate) (Gerlach & Wang, 2016) and Lopez’s Quadratic Loss Function (RQL) (Zamani et al., 2022), as these metrics allow for a relative ranking of the models.
Table 5 reports one-day-ahead forecast performance for the five models. The period from January 2000 to December 2014 is used as the initial learning period to generate the first day’s forecasts, i.e., for 2 January 2015, which is then recursively used to calculate forecasts up to December 2017.

Table 5.
Out-of-sample forecasting performance of competing models with H distribution: January 2015 to December 2017.
The out-of-sample volatility forecasting performance reveals distinct advantages of the Real-RTG-LF-HST model. It achieves the lowest errors across all standard loss functions, indicating superior precision in predicting volatility compared to alternatives. Notably, the RealAS-HST model ranks second, while the G@C variants exhibit significantly higher errors, suggesting limitations in their adaptability to volatility dynamics.
The predictive likelihood results, however, present an interesting contrast: the G@C-HST and G@C-F-HST models yield markedly higher PLL values compared to alternatives. This difference implies that while the G@C models may better capture the distributional shape of volatility, their point forecasts are less accurate. This tension underscores the importance of selecting evaluation metrics aligned with research objectives—standard loss functions for point estimates versus likelihood for density forecasting.
The Violation Rate (VRate) serves as a key metric for evaluating the accuracy of VaR forecasts, with an ideal model producing a VRate that closely matches the nominal significance level of the VaR. The Violation Rate (VRate) and Quadratic Loss (RQL) metrics highlight the RealAS-HST model as the most reliable for 1% VaR forecasts, with the closest violation rate to the nominal 1% level and the lowest RQL. This indicates that the model provides precise coverage of extreme tail risks without being overly conservative. At the 5% VaR level, however, Real-RTG-LF-HST demonstrates the most balanced performance, with a near-ideal violation rate (3.51% nominal) and competitive RQL (0.0448). The LogRealG-HST model, while achieving the tightest 5% VaR violation rate (5.80%), incurs higher RQL losses (0.0772), indicating a trade-off between frequency and magnitude of deviations.
4. Conclusions and Policy Implications
This study illustrated the use of Excel’s Solver and the MCMC method implemented in Matlab to estimate LogRealG models with seven ST-error distributions, namely A, E, EHL, H, JF, MP, and RJP. The estimation method is employed using the GRG and ARWM methods, which have been shown to be statistically efficient and easy to implement, respectively. This allows the reader to observe and compare the implementation of these methods through the sensitivity analysis of the ST parameters and log likelihood. Although not reported, notice that both estimation methods were able to rapidly find a solution—about 8 min for the MCMC algorithm and less than 1 min for Excel’s Solver.
This study found, in application, that posterior estimates of the skewness parameter are robust to four prior specifications—namely, normal, beta, exponential, and gamma—while the parameter(s) controlling tail thickness are influenced by different priors and their variances. The exception is for the parameter estimates of in EHL, which are affected by the choice of its own prior distribution, and for in JF, which are affected by the different variances of each prior distribution.
Compared with the ARWM method, Solver (GRG) from Microsoft Excel was shown to be a powerful alternative method to achieve the maximum value for log likelihood, although this is affected by the initial values of the ST parameters. This study found that the degree-of-freedom parameter only is robust to the initial value in order to obtain a feasible solution, although the parameter estimates are affected by the choice of its initial value. Excluding E, the estimates of log likelihood are robust to different initial values of the ST parameters.
In each case of the estimation method, the models with six distribution specifications were compared on the basis of four information criteria. The estimation results are robust and show strong evidence of H specification provided by ABIC, BIC, and CAIC. Thus, the current EHL model cannot outperform the H model in terms of the information criteria. Therefore, based on the previously mentioned literature study, we weakly conclude that the H model outperforms thirteen ST and ten non-ST distributions.
Finally, this study used Excel’s Solver to estimate the three extensions of the Realized GARCH variants: Realized Real-Time GARCH with leverage and feedback effects, Realized ASHARV, and GARCH@CARR with a feedback effect. By comparing these models against each other and two benchmark models (Log-linear Realized GARCH and GARCH@CARR), we showed that the GARCH@CARR model with a feedback effect has the best fit.
The out-of-sample forecasting evaluation results consistently demonstrate the predictive superiority of the Realized Real-Time GARCH-LF and Realized ASHARV models over the other three competing models. Specifically, the Realized Real-Time GARCH-LF model significantly outperforms its counterparts in volatility forecasting. Meanwhile, the Realized ASHARV model shows the best performance in VaR forecasting, particularly at the 1% VaR level. The dominance of these two models underscores the important contribution of information derived from real-time returns. These findings provide empirical evidence that incorporating real-time information enables more accurate capture of volatility dynamics and generates more reliable risk forecasts compared to models relying solely on historical data.
The demonstrated capability and practicality of Excel Solver’s GRG in estimating models with explicit likelihood formulas highlight an accessible tool that can empower policymakers—even those without advanced programming expertise—to implement and understand sophisticated econometric models for critical financial analysis and decision-making. However, while the GRG method implemented in Excel’s Solver offers a practical and efficient approach for smooth, nonlinear optimization, its limitations must be acknowledged. As a heuristic method, GRG cannot guarantee convergence to a globally optimal solution, and its performance is highly sensitive to initial parameter values—a limitation rigorously examined in our sensitivity analysis. Suboptimal initial values may lead to local optimum or, in some cases, failure to converge to any feasible solution. This dependence on initialization underscores the importance of validation against robust benchmarks (e.g., MCMC) and careful calibration in applied settings.
The findings from our study offer direct practical guidance for policymakers and financial practitioners, such as portfolio managers and risk analysts. First, the superior in-sample fit demonstrated by Hansen’s Skew-t distribution within the Log-linear Realized GARCH framework, along with the finding that the simplest GARCH@CARR model provides the best overall fit, indicates that effective volatility modelling does not always necessitate overly complex specifications. This allows policymakers to select robust and interpretable models for internal assessments and regulatory frameworks, while portfolio managers can utilize these models to enhance risk-adjusted returns through more accurate volatility forecasts during market stress (e.g., crises or flash crashes). Second, the out-of-sample forecasting dominance of models incorporating real-time information (e.g., Realized Real-Time GARCH and Realized ASHARV) underscores the critical role of high-frequency data in risk management. For risk analysts, these models—particularly Realized ASHARV’s 1% VaR accuracy—provide a reliable tool for setting margin requirements and capital reserves. While Excel’s GRG Solver provides an accessible tool for practitioners lacking programming expertise, its sensitivity to initial values and local optimum limitations, as observed in our sensitivity analysis, suggest that its use should be paired with validation against benchmark methods like MCMC.
For future research, we recommend exploring alternative optimization methods that can overcome the limitations of GRG. One promising direction is the use of stochastic global optimization methods, such as evolutionary algorithms, which are available in Excel’s Solver. These methods are designed to find globally optimal solutions and can reduce dependence on initial values. In addition, further research could focus on developing systematic guidelines for the selection of optimal initial values for GRG, thereby improving the consistency and reliability of the results in the context of GARCH modelling.
Author Contributions
Conceptualization, D.B.N.; Methodology, D.B.N.; Software, D.B.N.; Validation, A.S.; Formal Analysis, D.B.N. and A.S.; Data Curation, A.S.; Writing—Original Draft Preparation, D.B.N.; Writing—Review and Editing, A.S. and T.M.; Supervision, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Vice-Rector of Research, Innovation, and Entrepreneurship at Universitas Kristen Satya Wacana, Indonesia, through the Directorate of Research and Community Service (DRPM) under the Applied Research scheme (Fiscal Year 2025, Contract No. 160/SPK-PT/RIK/08/2025). The publication fee of this work was supported by Kwansei Gakuin University, Japan. The funders had no role in study design; data collection, analysis, or interpretation; or the preparation of the manuscript.
Data Availability Statement
All data, materials, and codes that support the findings of this study are available from the corresponding author upon reasonable request. The real datasets were downloaded from the Oxford-Man Institute’s Quantitative Finance Realized Library (https://realized.oxford-man.ox.ac.uk/data (accessed on 3 September 2018)), but this database was recently removed from public availability.
Acknowledgments
We would like to thank Andreas Setiawan, member of SeMARTy, for his expertise in the development of the research proposal.
Conflicts of Interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Appendix A. Theoretical Differences Between Skewed Student-t Distributions
The seven ST distributions examined in this study differ fundamentally in their parameterizations of skewness and tail behaviour, which critically impact their ability to model financial returns. Table A1 presents their key theoretical distinctions.

Table A1.
Comparative theoretical properties of seven ST distributions: Skewness mechanisms and tail parameters.
Table A1.
Comparative theoretical properties of seven ST distributions: Skewness mechanisms and tail parameters.
| Distribution | Skewness | Tail Behaviour | Financial Application |
|---|---|---|---|
| A | controls asymmetry direction; separate left/right tails | (left tail), (right tail) | GARCH-type volatility modelling |
| E | Single scales both tails equally | Single controls both tails | First application in this study |
| EHL | Nonlinear tarnsformation via | controls tail thickness | GARCH-type volatility modelling |
| H | Linear transform with | Single with scaled tails | GARCH-type volatility modelling, option pricing |
| JF | Beta parameters bound skewness | Implicit via beta function | First application in this study |
| MP | Power-law decay () with | with power-adjusted tails | GARCH-type volatility modelling |
| RJP | Hyperbolic transform (cosh/sinh) | Hyperbolic transform (cosh/sinh) | First application in this study |
Appendix B. Prior Sensitivity Analysis in MCMC Method
Sensitivity is examined by considering four possible prior distributions—namely, normal, beta, exponential, and gamma—by either modifying the mean or/and increasing the variances relative to our initial prior. These prior conditions are listed in Table A2, including narrowed variation and more variation. Following Nugroho and Morimoto (2015), to sample the b parameter, which has a range of to 1, we define , where ; hence, the prior on b is
with a prior mean of .
The selection of normal and beta priors follows established Bayesian practice for financial volatility models. Normal distributions serve as weakly informative priors for unbounded parameters (e.g., in H and RJP), where large variances (e.g., ) ensure the data dominate posterior inference. For bounded parameters (e.g., in A), beta priors provide natural conjugacy and flexibility: represents a uniform prior, while gently centres mass near without being restrictive. These choices align with recommendations for the RealG model (Nakajima & Omori, 2012) and ensure priors are sufficiently diffuse to avoid unintended information while preventing numerical instability in tail regions (e.g., ).

Table A2.
Alternativeprior distributions, other than the normal distribution, with hyperparameters on ST parameters.
Table A2.
Alternativeprior distributions, other than the normal distribution, with hyperparameters on ST parameters.
| Exp | Exp | ||||
| Mean | 0.5 | 0.5 | 4 | 10 | |
| SD | 0.1 | 0.29 | 0.14 | 4 | 14.1 |
| Exp | |||||
| Mean | 10 | 20 | 40 | 1 | 20 |
| SD | 141.4 | 5 | 8.2 | 10 | 25.8 |
SD: standard deviation.
Table A3 and Table A4 present the parameter estimates (posterior mean and standard deviation), IAT for the ST parameters, and log-likelihood values. Notice that given the specified priors, the estimates for the other parameters turn out to be nearly identical, except . In all cases, the estimates for the skewness parameter () and shape parameters are not affected by changing the prior for the parameter itself or the others. As a consequence, changing the priors for those parameters does not affect the other parameter(s) in each distribution, and vice-versa.
The degree-of-freedom parameters of the A distribution; degree-of-freedom parameter () of E, H, MP, and RJP; zero-location and unit-scale parameters of JF distribution; and parameter of EHL can be greatly influenced by the type of prior itself, as well as by the amount of variance. Under the same prior, the posterior standard deviation becomes larger as the dispersion of the prior increases.
Excluding the JF and EHL specifications, the above results indicate that the skewness and heavy-tailed parameters are independent of each other. This finding is consistent with the findings of an earlier study. For example, Leisen et al. (2017) argues the heaviness of the left (or right) tail of A is controlled by (or ) only. For EHL and JF distributions, notice that the behaviour of the tail is simultaneously reflected by the and parameters, respectively. Thus, our finding on parameters the parameters is consistent with the result reported by Adubisi et al. (2022), who argue that the skewness and kurtosis values of EHL are not affected by .

Table A3.
Prior sensitivity analysis for the ST parameters in A, EHL, EST, and HST distributions.
Table A3.
Prior sensitivity analysis for the ST parameters in A, EHL, EST, and HST distributions.
| A | ||||||
| ∼ | ||||||
| ∼ | Exp | Exp | ||||
| 0.517 | 0.516 | 0.515 | 0.514 | 0.518 | 0.522 | |
| 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |
| 8.4 | 14.1 | 9.9 | 16.6 | 8.7 | 10.0 | |
| 7.6 | 8.8 | 8.4 | 9.3 | 12.1 | 21.7 | |
| 1.1 | 1.6 | 1.4 | 1.7 | 2.4 | 6.0 | |
| 96.6 | 57.9 | 49.3 | 40.6 | 30.9 | 39.7 | |
| 12.4 | 21.5 | 20.9 | 39.2 | 24.2 | 39.7 | |
| 1.6 | 4.6 | 5.3 | 14.4 | 4.5 | 7.9 | |
| 11.5 | 23.4 | 29.1 | 76.7 | 19.2 | 31.3 | |
| 4288.4 | 4284.2 | 4284.0 | 4283.3 | 4284.7 | 4290.5 | |
| E | ||||||
| ∼ | ||||||
| ∼ | Exp | Exp | ||||
| 0.044 | 0.046 | 0.051 | 0.053 | 0.047 | 0.049 | |
| 0.009 | 0.009 | 0.009 | 0.009 | 0.009 | 0.009 | |
| 5.6 | 5.3 | 8.9 | 7.6 | 6.5 | 6.2 | |
| 10.7 | 14.2 | 14.1 | 16.0 | 16.4 | 27.2 | |
| 1.2 | 2.5 | 2.5 | 3.4 | 2.9 | 6.1 | |
| 8.1 | 17.0 | 10.9 | 11.9 | 16.8 | 33.2 | |
| 4292.0 | 4290.2 | 4290.0 | 4290.4 | 4289.9 | 4293.8 | |
| EHL | ||||||
| ∼ | Exp | Exp | ||||
| ∼ | Exp | Exp | Exp | |||
| ∼ | Exp | Exp | ||||
| 3.2 | 3.2 | 3.2 | 3.2 | 3.5 | 3.2 | |
| 0.099 | 0.144 | 0.121 | 0.109 | 0.112 | 0.096 | |
| 120.3 | 192.5 | 151.5 | 107.5 | 190.5 | 161.9 | |
| 3.0 | 3.0 | 3.0 | 3.0 | 3.7 | 3.0 | |
| 0.192 | 0.285 | 0.234 | 0.215 | 0.275 | 0.183 | |
| 122.5 | 193.2 | 153.6 | 105.2 | 201.7 | 154.7 | |
| 5.2 | 9.3 | 6.0 | 5.1 | 8.2 | 5.0 | |
| 0.626 | 1.777 | 0.632 | 0.491 | 0.810 | 0.517 | |
| 283.4 | 250.7 | 160.1 | 110.5 | 193.5 | 218.9 | |
| 4314.6 | 4314.0 | 4314.7 | 4314.9 | 4317.1 | 4314.5 | |
| H | ||||||
| ∼ | ||||||
| ∼ | Exp | Exp | ||||
| 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | |
| 5.3 | 7.2 | 5.8 | 5.5 | 5.2 | 10.2 | |
| 10.8 | 13.7 | 13.3 | 15.5 | 16.5 | 25.7 | |
| 1.3 | 2.5 | 2.2 | 3.2 | 2.9 | 5.4 | |
| 7.9 | 17.2 | 9.2 | 15.1 | 12.4 | 21.9 | |
| 4285.9 | 4284.1 | 4284.2 | 4284.0 | 4284.3 | 4287.2 | |
The first row: posterior mean. The second row: standard deviation. The third row: IAT. The bold values indicate log-likelihood values that are nearly the same.
Next, we asses the impact of a change in prior on the log likelihood. Excluding the EHL and JF distributions, the smallest log-likelihood value is obtained when the prior of is or , which has a standard deviation greater than 8. In these cases, the estimate of has a larger mean and standard deviation. When the prior of is , which has a standard deviation of 5, the log-likelihood values are competitive with those produced by other priors. For the MP and RJP distributions, all priors yield almost the same log likelihoods. Overall, very close log-likelihood values are produced by priors , Exp, Exp, and . In these cases, the maximum log likelihood may be achieved.

Table A4.
Prior sensitivity analysis for the ST parameters in JF, MP, and RJP distributions.
Table A4.
Prior sensitivity analysis for the ST parameters in JF, MP, and RJP distributions.
| JF | ||||||
| ∼ | Exp | Exp | ||||
| ∼ | Exp | Exp | ||||
| 4.2 | 5.3 | 5.7 | 5.9 | 7.5 | 5.6 | |
| 0.28 | 0.703 | 0.587 | 0.697 | 0.469 | 0.511 | |
| 179.9 | 237.7 | 260.2 | 281.8 | 243.7 | 245.7 | |
| 5.4 | 6.4 | 5.8 | 6.1 | 7.7 | 5.8 | |
| 0.286 | 0.716 | 0.597 | 0.709 | 0.476 | 0.520 | |
| 177.5 | 237.2 | 259.5 | 282.2 | 244.9 | 245.6 | |
| 4298.0 | 4295.2 | 4294.4 | 4294.7 | 4294.8 | 4294.5 | |
| MP | ||||||
| ∼ | Exp | Exp | ||||
| ∼ | Exp | Exp | ||||
| 0.956 | 0.956 | 0.956 | 0.955 | 0.955 | 0.955 | |
| 0.009 | 0.009 | 0.009 | 0.009 | 0.009 | 0.009 | |
| 7.1 | 6.2 | 6.8 | 7.9 | 6.8 | 5.8 | |
| d | 2.0 | 1.9 | 1.9 | 1.7 | 1.8 | 1.8 |
| 0.099 | 0.102 | 0.105 | 0.078 | 0.047 | 0.092 | |
| 198.3 | 215.2 | 127.2 | 247.8 | 115.6 | 168.9 | |
| 6.6 | 11.5 | 8.9 | 43.1 | 19.5 | 20.2 | |
| 1.7 | 4.7 | 3.5 | 30.5 | 4.9 | 14.9 | |
| 58.9 | 63.6 | 16.3 | 319.3 | 27.8 | 229.8 | |
| 4292.0 | 4291.7 | 4291.3 | 4291.8 | 4290.95 | 4291.9 | |
| RJP | ||||||
| ∼ | ||||||
| ∼ | Exp | Exp | ||||
| 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |
| 7.3 | 7.9 | 6.7 | 6.3 | 7.4 | 8.9 | |
| 11.1 | 15.0 | 14.7 | 17.1 | 17.4 | 28.1 | |
| 1.3 | 2.9 | 2.6 | 4.4 | 3.1 | 6.5 | |
| 6.9 | 14.5 | 15.5 | 30.7 | 14.4 | 22.6 | |
| 4290.4 | 4289.2 | 4289.3 | 4289.0 | 4288.9 | 4291.3 | |
The first row: posterior mean. The second row: standard deviation. The third row: IAT. The bold values indicate log-likelihood values that are nearly the same.
Appendix C. Sensitivity Analysis of Initial Values in GRG Method
An illustrative example of the suitability of the Excel Solver’s GRG in applying the LogRealG model with H distribution is outlined as follows.
- Initializing the parameter values. The initial values of the model parameters are stored in D3:D14. These are changing variable cells. The value of each parameter cell will be changed by Solver interatively, at the same time, until the optimum has been found.
- Defining the objective cells. We assign cell D17 to the objective function (total log likelihood in this case). Then, in cells D18:D21, we enter the function of AIC, ABIC, BIC, and CAIC.
- Defining data cells. The historical data series (called return and log realized ) are stored in cells B26:D4528.
- Initializing the volatility and measurement process. To implement volatility and measurement equations, the initial value () is set to be equal to the log of the variance of returns, and is set to be equal zero. We calculate , , , and in cells D25:G25 by placing the formulas expressed as “=LN(VAR(B26:B4528))”, “=EXP(D25)”, “0”, and “=$D$5*F25+$D$6*(F252-1)”, respectively.
- Calculating the volatility and measurement process. At time point , processes (not including the exogenous variable), , , , and in cells D26:H26 are calculated by the formulas expressed as “=$D$3 + $D$4*D25 + G25”, “=EXP(D26)”, “=B26/SQRT(E26)”, “=$D$5*F26 + $D$6*(F262-1)”, and “=$D$10*F26 + $D$11*(F262-1)”, respectively. The formulas in E26:G26 can now be copied down to compute the complete processes at each time point. Meanwhile, process , for includes an exogenous variable. Starting from in cell D26 with the formula expressed as “=$D$3 + $D$4*D26 + G26 + $D$7*C26”; then, this formula can be copied down at each time point.
- Calculating the log density function. We can first calculate the constant parts of the H density function in Equation (5)—namely, , a and b. These parts are calculated in cells J16:J18 by the formulas expressed as “=GAMMA((D14+1)/2)/(GAMMA(D14/2)* SQRT(PI()*D14))”, “=4*D13*J17*(D14-2)/(D14-1)”, and “=SQRT(1 + 3*D132-J182)”, respectively. The part containing the condition is calculated in cell I26 by the formula expressed as “=-0.5*($D$14+1)*IF(F26<-$J$18/$J$19,LN(1+1/$D$14*(($J$19* F26+$J$18)/(1-$D$13))2),LN(1+1/$D$14*(($J$19*F26+$J$18)/(1+$D$13))2))”; then, this formula can be copied down at each time point.
- Calculating the log likelihood. Based on model (1), the log-likelihood of return and measurement at time point are calculated in cells J26:K26 by the formulas expressed as “=-0.5*LN(E26) + LN($J$19) + LN($J$17) + I26” and “=-0.5*LN(2*PI()*$D$12)-0.5*(C26-$D$8-$D$9* D26-H26)2/$D$12”, respectively. The log likelihood for the fitted model is the sum of the two log likelihoods and is calculated in cell L26 by the formula expressed as “=J26 + K26”. Those formulas can now be copied down at each time point to obtain the total log likelihood for the fitted model stored in cell D17.
- Applying the Solver. Open Solver window and define the problem. Applying the GRG method, the iterative calculation takes less than one minute.
Figure A1 displays an Excel screenshot showing the above process.
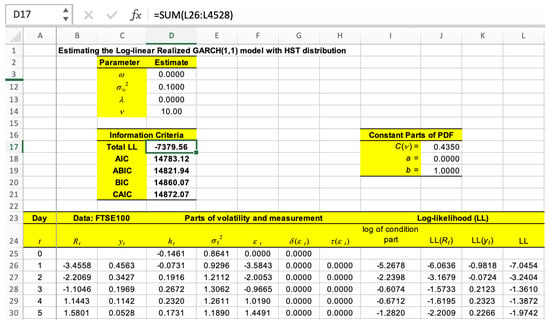
Figure A1.
Workbook for modelling of LogRealG with H distribution.
In this example, we illustrate the process of sensitivity analysis to see how various initial values of the ST distribution parameters would affect the estimated cells (for parameters and log likelihood). According to the parameter constraints, the analysis is performed by changing the initial value of one parameter and fixing the initial value of the other(s). Sensitivity is calculated by dividing the percentage change in the output variable by the percentage change in the input variable. In Table A5 we can observe the results of our experiment. Observations are made on the existence of solutions, changes in parameter estimates, and changes in estimated log-likelihood values. This analysis helps determine the combination of a set of initial values on all ST parameters in the model.
First, considering the model with the A distribution, the initial values of , , and range from 0.1 to 0.9 at an increment of 0.1, those of range from 2 to 18 at an increment of 0.2, and those of range from 5 to 40 at an increment of 5. The result shows that the Solver could not find a feasible solution when the value of was initially set to 0.1, 0.2, 0.3, and 0.8 for fixed initial values of and . The estimates of were found to depend on its initial value and tend to increase as the initial value increases. In this case, the sensitivity of increased by 31%. The estimates of , and log likelihood do not appear to be affected by the initial values of each parameter. Hence, the initial values of can be used to compare the estimated values obtained by the ARWM method.
Second, the initial values of and in the model with the E distribution were set in increments of 0.1 using and in increments of 4 using . The result shows that the Solver could not find a feasible solution when the value of was initially set to 0.9 for the fixed initial values . The different initial values of had less of affect on the estimation of , with a sensitivity of 2.9%, and a great affect on the estimation of and log likelihood, with sensitivity greater than 100%. When the initial value of is fixed at 0, different initial values of have less of an affect on the estimation of and greatly affect the estimation of and log likelihood, with sensitivity values of greater than 35%. In addition, the maximum log likelihood was achieved with initial values of .

Table A5.
Sensitivity analysis for Excel’s Solver.
Table A5.
Sensitivity analysis for Excel’s Solver.
| Initial Value | Estimated Value | |||
|---|---|---|---|---|
| Fixed Value | Changing Value | |||
| A | ||||
| 0.514 | (9, 35) | |||
| 0.514 | (9, 26 to 37) | |||
| 0.514 | (9, 33 to 35) | |||
| E | ||||
| 0.038 to 0.087 | 14 to 24 | to | ||
| 0.046 to 0.049 | 14 to 28 | to | ||
| EHL | ||||
| (3.2, 2.9) | 3.8 | |||
| (3.2, 2.9) | 3.7 to 4.1 | to | ||
| (3.2, 2.9) | 2.1 to 7.7 | to | ||
| H | ||||
| to 0.5 | 14 | |||
| to 40 | 12 to 16 | to | ||
| JF | ||||
| 6.2 | 6.4 | |||
| 6.0 to 6.3 | 6.2 to 6.5 | |||
| MP | ||||
| (1.8, 0.955) | 21 | |||
| (1.8, 0.955) | 15 to 22 | |||
| (1.6 to 2.0, 0.955) | 7 to 40 | to | ||
| RJP | ||||
| 14 to 16 | ||||
| 15 | ||||
Third, the initial value of each parameter in the model with the EHL distribution was varied from 1 to 10 in increments of 1. The Solver results are very sensitive to the initial values of , as indicated by the small number of choices of initial values for both parameters that provide feasible solutions. When the optimal solution is achieved, the estimates of the parameters are not affected by different initial values of each parameter. For the parameter, the estimated value is slightly less affected by different initial values of , with a sensitivity of 20%, and greatly affected by its own different initial values, with a sensitivity of 62%. Meanwhile, the estimated log likelihood is greatly affected by different initial values of , with sensitivity greater than 60%. In this case, the estimates of and log likelihood tend to grow as the initial value of rises, with initial values of providing the maximum log likelihood.
Fourth, regarding the parameters of the model with the H distribution, taking initial values of ranging from to in increments of 0.1 results in considerable sensitivity to feasible solutions, since these are only provided by values within the range of to . Such values do not affect the estimation of the parameters and log likelihood. Taking initial values of ranging from to in increments of 0.1 results in considerable sensitivity to feasible solutions, as these are only provided by values ranging from to 0.5. Such values do not affect on the estimation of the parameters and log likelihood. Meanwhile, changing the initial values of in increments of 4 in the range of does not affect on the estimation of and log likelihood, but it has less of an effect on the estimation of log likelihood (), with sensitivity values of less than 12%. Hence, we can choose initial values of to maximize the log-likelihood value.
Fifth, in the case of the model with the JF distribution, there are several combinations of initial values of that do not yields feasible solutions—namely (6, 1), (2, 7), and (2, 8)—when the initial values are set in increments of 1 using . These different values do not appear to affect the parameter and log-likelihood estimates. Thus, we can choose any combination that produces a feasible solution, such as .
Sixth, the optimal solution for the model with the MP distribution is not found for initial values of when changing by increments of 0.1 in the range of [0.1, 2]. The same situation also occurs when changing the initial value of d within the range 0.1 to 3 in increments of 0.1. When it has a solution, the parameter and log-likelihood estimates are not affected by different initial values of each parameter. Meanwhile, the estimated value of is greatly affected by different initial values of d and , where the initial value of changes in increments of 4 within the range of . It was found that the estimated value of increases as its initial value increases. Here, the maximizer of log likelihood is provided by the initial values of .
Finally, the model with RJP is considered. When the initial values of are changed by increments of 1 within the range of , the feasible solution is found in the range of to . These different values affect the estimation of only, with a sensitivity of 0.25%. Meanwhile, different initial values of in increments of 1 do not appear to affect the parameter and log-likelihood estimates. The two conditions produce very similar log-likelihood values, so we can choose as the initial values for .
References
- Abounoori, E., & Zabol, M. (2020). Modeling gold volatility: Realized GARCH approach. Iranian Economic Review, 24(1), 299–311. [Google Scholar]
- Acitas, S., Yenilmez, I., Senoglu, B., & Kantar, Y. M. (2021). Modified maximum likelihood estimator under the Jones and Faddy’s skew t-error distribution for censored regression model. Journal of Applied Statistics, 48(12), 2136–2151. [Google Scholar] [CrossRef]
- Adubisi, O. D., Abdulkadir, A., Farouk, U. A., & Chiroma, H. (2022). The exponentiated half logistic skew-t distribution with GARCH-type volatility models. Scientific African, 16, e01253. [Google Scholar] [CrossRef]
- Alfeus, M., & Harvey, J. (2025). Improving realised volatility forecast for emerging markets. Journal of Economics and Finance, 49(1), 299–342. [Google Scholar] [CrossRef]
- Al Rahahleh, N., & Kao, R. (2018). Forecasting volatility: Evidence from the Saudi Stock Market. Journal of Risk and Financial Management, 11(4), 84. [Google Scholar] [CrossRef]
- Amirshahi, B., & Lahmiri, S. (2023). Hybrid deep learning and GARCH-family models for forecasting volatility of cryptocurrencies. Machine Learning with Applications, 12, 100465. [Google Scholar] [CrossRef]
- Andersen, T. G., Bollerslev, T., Diebold, F. X., & Labys, P. (2003). Modeling and forecasting realized volatility. Econometrica, 71(2), 579–625. [Google Scholar] [CrossRef]
- Baker, M. J. (2014). Adaptive Markov Chain Monte Carlo sampling and estimation in Mata. The Stata Journal, 14(3), 623–661. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O. E., Hansen, P., Lunde, A., & Shephard, N. (2008). Designing realised kernels to measure the ex-post variation of equity prices in the presence of noise. Econometrica, 6(76), 1481–1536. [Google Scholar] [CrossRef]
- Bharadiya, J. P. (2023). A review of Bayesian Machine Learning Principles, methods, and applications. International Journal of Innovative Science and Research Technology, 8(5), 2033–2038. [Google Scholar]
- Cai, G., Wu, Z., & Peng, L. (2021). Forecasting volatility with outliers in Realized GARCH models. Journal of Forecasting, 40(4), 667–685. [Google Scholar] [CrossRef]
- Chan, J. C., & Grant, A. L. (2016). Modeling energy price dynamics: GARCH versus stochastic volatility. Energy Economics, 54, 182–189. [Google Scholar] [CrossRef]
- Chen, C. W., Watanabe, T., & Lin, E. M. (2023). Bayesian estimation of realized GARCH-type models with application to financial tail risk management. Econometrics and Statistics, 28, 30–46. [Google Scholar] [CrossRef]
- Chen, C. W. S., & Watanabe, T. (2019). Bayesian modeling and forecasting of Value-at-Risk via threshold realized volatility. Applied Stochastic Models in Business and Industry, 35(3), 747–765. [Google Scholar] [CrossRef]
- Chimisov, C., Latuszynski, K., & Roberts, G. (2018). Air markov chain monte carlo. arXiv, arXiv:1801.09309. [Google Scholar] [CrossRef]
- Christoffersen, P., Elkamhi, R., Feunou, B., & Jacobs, K. (2010). Option valuation with conditional heteroskedasticity and nonnormality. The Review of Financial Studies, 23(5), 2139–2183. [Google Scholar] [CrossRef]
- da Fonseca, T. C. O., Cerqueira, V. S., Migon, H. S., & Torres, C. A. C. (2021). Evaluating the performance of degrees of freedom estimation in asymmetric GARCH models with t-student innovations. Brazilian Review of Econometrics, 40(2), 347–373. [Google Scholar] [CrossRef]
- Dasovic, B., & Klansek, U. (2021). Comparison of spreadsheet-based optimization tools applied to construction site layout problem. In P. Mesaros, V. Jothiprakash, K. Kotrasova, & M. Zelenakova (Eds.), Proceedings of young scientist 2021 (Vol. 1209, p. 012010). IOP Publishing. [Google Scholar]
- de los Rios, M. D., & Ramos, E. H. (2020). Determination of the Hansen solubility parameters and the Hansen sphere radius with the aid of the solver add-in of Microsoft Excel. SN Applied Sciences, 2(4), 676. [Google Scholar] [CrossRef]
- Depaoli, S., Winter, S. D., & Visser, M. (2020). The importance of prior sensitivity analysis in Bayesian statistics: Demonstrations using an interactive Shiny App. Frontiers in Psychology, 11, 608045. [Google Scholar] [CrossRef]
- Ding, Y. D. (2023). A simple joint model for returns, volatility and volatility of volatility. Journal of Econometrics, 232(2), 521–543. [Google Scholar] [CrossRef]
- Djeddi, A. (2022). Bayesian MCMC approach to the multicomponent volatility jump-augmented models [Ph.D. thesis, University of York]. Available online: https://etheses.whiterose.ac.uk/id/eprint/31293/1/Djeddi_204036258_AcceptedThesis.pdf (accessed on 26 July 2025).
- Dziak, J. J., Coffman, D. L., Lanza, S. T., Li, R., & Jermiin, L. S. (2020). Sensitivity and specificity of information criteria. Briefings in Bioinformatics, 21(2), 553–565. [Google Scholar] [CrossRef]
- Farida, F., Makaje, N., & Phon-On, A. (2019). A simplified approach to eestimating parameter of the GARCH (1,1) model. Applied Science and Engineering Progress, 12(3), 158–163. [Google Scholar] [CrossRef]
- Gelman, A., Roberts, G. O., & Gilks, W. R. (1996). Efficient metropolis jumping rules. In Bayesian statistics 5: Proceedings of the fifth valencia international meeting. Oxford University Press. [Google Scholar]
- Gerlach, R., & Wang, C. (2016). Forecasting risk via realized GARCH, incorporating the realized range. Quantitative Finance, 16(4), 501–511. [Google Scholar] [CrossRef]
- Givens, G. (2015). Computational statistic. John Wiley & Sons. [Google Scholar]
- Hansen, P. R., & Huang, Z. (2016). Exponential GARCH modeling with realized measures of volatility. Journal of Business & Economic Statistics, 34, 269–287. [Google Scholar] [CrossRef]
- Hansen, P. R., Huang, Z., & Shek, H. H. (2012). Realized GARCH: A joint model for returns and realized measures of volatility. Journal of Applied Econometrics, 27(6), 877–906. [Google Scholar] [CrossRef]
- Jamalizadeh, A., & Lin, T.-I. (2017). A general class of scale-shape mixtures of skew-normal distributions: Properties and estimation. Computational Statistics, 32, 451–474. [Google Scholar] [CrossRef]
- Kruschkes, J. K. (2015). Doing bayesian analysis: A tutorial with R, Jags, and STAN. Academic Presss. [Google Scholar]
- Le, H. (2023). Modelling inflation dynamics: A Bayesian comparison between GARCH and stochastic volatility. Economic Research-Ekonomska Istrazivanja, 36(1), 2112–2136. [Google Scholar] [CrossRef]
- Leisen, F., Marin, J. M., & Villa, C. (2017). Objective Bayesian modelling of insurance risks with the skewed Student-t distribution. Applied Stochastic Models in Business and Industry, 33(2), 136–151. [Google Scholar] [CrossRef]
- Li, R. (2019). Some contributions to distribution theory [Ph.D. thesis, University of Manchester]. Available online: https://pure.manchester.ac.uk/ws/portalfiles/portal/84031132/FULL_TEXT.PDF (accessed on 9 June 2025).
- Li, R., & Nadarajah, S. (2020). A review of Student’s t distribution and its generalizations. Empirical Economics, 58(3), 1461–1490. [Google Scholar] [CrossRef]
- Listyan, G. R. A., Nugroho, D. B., & Mahatma, T. (2022). Modeling the volatility of FTSE100 index returns using realized GARCH model with jumps (Vol. 2542, p. 040002). AIP Publishing. [Google Scholar]
- Liu, Y., Li, J. S.-H., & Ng, A. C.-Y. (2015). Option pricing under GARCH models with Hansen’s skewed-t distributed innovations. The North American Journal of Economics and Finance, 31, 108–125. [Google Scholar] [CrossRef]
- Maia, A., Ferreira, E., Oliveira, M., Menezes, L., & Andrade-Campos, A. (2017). Numerical optimization strategies for springback compensation in sheet metal forming. In J. Paulo Davim (Ed.), Computational methods and production engineering (pp. 51–82). Woodhead Publishing. [Google Scholar]
- Matei, M., Rovira, X., & Agell, N. (2019). Bivariate volatility modeling with high-frequency data. Econometrics, 7(3), 41. [Google Scholar] [CrossRef]
- McFedries, P. (2022). Excel data analysis for dummies (5th ed.). John Wiley & Sons. [Google Scholar]
- Msabawy, A., & Mohammad, F. (2021). Continuous sizing optimization of cold-formed steel portal frames with semi-rigid joints using generalized reduced gradient algorithm. Materials Today: Proceedings, 42, 2290–2300. [Google Scholar] [CrossRef]
- Mugerman, Y., Yidov, O., & Wiener, Z. (2020). By the light of day: The effect of the switch to winter time on stock markets. Journal of International Financial Markets, Institutions and Money, 65, 101197. [Google Scholar] [CrossRef]
- Nadarajah, S., Afuecheta, E., & Chan, S. (2015). GARCH modeling of five popular commodities. Empirical Economics, 48(4), 1691–1712. [Google Scholar] [CrossRef]
- Nakajima, J., & Omori, Y. (2012). Stochastic volatility model with leverage and asymmetrically heavy-tailed error using GH skew Student’s t-distribution. Computational Statistics & Data Analysis, 56(11), 3690–3704. [Google Scholar]
- Nugroho, D. B., Mahatma, T., & Pratomo, Y. (2021). Applying the non-linear transformation families to the lagged-variance of EGARCH and GJR models. IAENG International Journal of Applied Mathematics, 51(4), 1–12. [Google Scholar]
- Nugroho, D. B., & Morimoto, T. (2015). Estimation of realized stochastic volatility models using Hamiltonian Monte Carlo-Based methods. Computational Statistics, 30(2), 491–516. [Google Scholar] [CrossRef]
- Nugroho, D. B., Wibowo, H., & Saragih, A. (2023a). Modeling daily return volatility through GJR(1,1) model and realized volatility measure. Thailand Statistician, 22(1), 50–62. [Google Scholar]
- Nugroho, D. B., Wicaksono, B. A. A., & Larwuy, L. (2023b). GARCH-X(1,1) model allowing a non-linear function of the variance to follow an AR(1) process. Communications for Statistical Applications and Methods, 30(2), 163–178. [Google Scholar] [CrossRef]
- Nugroho, D. B., Wijaya, J., & Setiawan, A. (2023c). Modeling of returns volatility through EGARCH model using high-frequency data. Journal of Applied Probability and Statistics, 18(2), 55–73. [Google Scholar]
- Parkinson, A. R., Balling, R., & Hedengren, J. D. (2018). Optimization methods for engineering design (2nd ed.). Brigham University Press. [Google Scholar]
- Plevris, V., Bakas, N. P., & Solorzano, G. (2021). Pure Random Orthogonal Search (PROS): A plain and elegant parameterless algorithm for global optimization. Applied Sciences, 11(11), 5053. [Google Scholar] [CrossRef]
- Rubio, F. J., & Steel, M. F. J. (2015). Bayesian modelling of skewness and kurtosis with Two-Piece Scale and shape distributions. Electronic Journal of Statistics, 9(2), 1884–1912. [Google Scholar] [CrossRef]
- Sharma, P. (2015). Forecasting stock index volatility with GARCH models: International evidence. Studies in Economics and Finance, 32(4), 445–463. [Google Scholar] [CrossRef]
- Sherlock, C., Golightly, A., & Henderson, D. A. (2017). Adaptive, delayed-acceptance MCMC for targets with expensive likelihoods. Journal of Computational and Graphical Statistics, 26(2), 434–444. [Google Scholar] [CrossRef]
- Smetanina, E. (2017). Real-time GARCH. Journal of Financial Econometrics, 15(4), 561–601. [Google Scholar] [CrossRef]
- Smetanina, E., & Wu, W. B. (2020). Asymptotic theory for QMLE for the real-time GARCH(1,1) model. Journal of Time Series Analysis, 42(5–6), 752–776. [Google Scholar] [CrossRef]
- Spencer, S. E. F. (2021). Accelerating adaptation in the adaptive Metropolis–Hastings random walk algorithm. Australian & New Zealand Journal of Statistics, 63(3), 468–484. [Google Scholar] [CrossRef]
- Takahashi, M., Omori, Y., & Watanabe, T. (2023). Realized stochastic volatility model. In Stochastic volatility and realized stochastic volatility models (pp. 79–113). Springer Nature Singapore. [Google Scholar]
- Tendenan, V., Gerlach, R., & Wang, C. (2020). Tail risk forecasting using Bayesian realized EGARCH models. arXiv, arXiv:2008.05147. [Google Scholar] [CrossRef]
- Terregrossa, S. J., & Sener, U. (2023). Employing a generalized reduced gradient algorithm method to form combinations of steel price forecasts generated separately by ARIMA-TF and ANN models. Cogent Economics & Finance, 11(1), 2169997. [Google Scholar] [CrossRef]
- Theodossiou, P. (2015). Skewed generalized error distribution of financial assets and option pricing. Multinational Finance Journal, 19(4), 223–266. [Google Scholar] [CrossRef]
- Trottier, D.-A., & Ardia, D. (2016). Moments of standardized Fernandez–Steel skewed distributions: Applications to the estimation of GARCH-type models. Finance Research Letters, 18, 311–316. [Google Scholar] [CrossRef]
- Turek, D., de Valpine, P., Paciorek, C. J., & Anderson-Bergman, C. (2017). Automated parameter blocking for efficient Markov Chain Monte Carlo sampling. Bayesian Analysis, 12(2), 465–490. [Google Scholar] [CrossRef]
- van Ravenzwaaij, D., Cassey, P., & Brown, S. D. (2018). A simple introduction to Markov Chain Monte-Carlo sampling. Psychonomic Bulletin & Review, 25, 143–154. [Google Scholar]
- Wang, J., Jiang, Y., Zhu, Y., & Yu, J. (2020). Prediction of volatility based on realized-GARCH-kernel-type models: Evidence from China and the U.S. Economic Modelling, 91, 428–444. [Google Scholar] [CrossRef]
- Xie, H., Qi, N., & Wang, S. (2019). A new variant of RealGARCH for volatility modeling. Finance Research Letters, 28, 438–443. [Google Scholar] [CrossRef]
- Xie, H., & Yu, C. (2020). Realized GARCH models: Simpler is better. Finance Research Letters, 33, 101221. [Google Scholar] [CrossRef]
- Zahid, M., Iqbal, F., & Koutmos, D. (2022). Forecasting bitcoin volatility using hybrid GARCH models with machine learning. Risks, 10(12), 237. [Google Scholar] [CrossRef]
- Zamani, S., Chaghazardi, A., & Arian, H. (2022). Pathwise grid valuation of fixed-income portfolios with applications to risk management. Heliyon, 8(7), e09880. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).