Image Processor and RISC MCU Embedded Single Chip Fingerprint Sensor
Abstract
1. Introduction
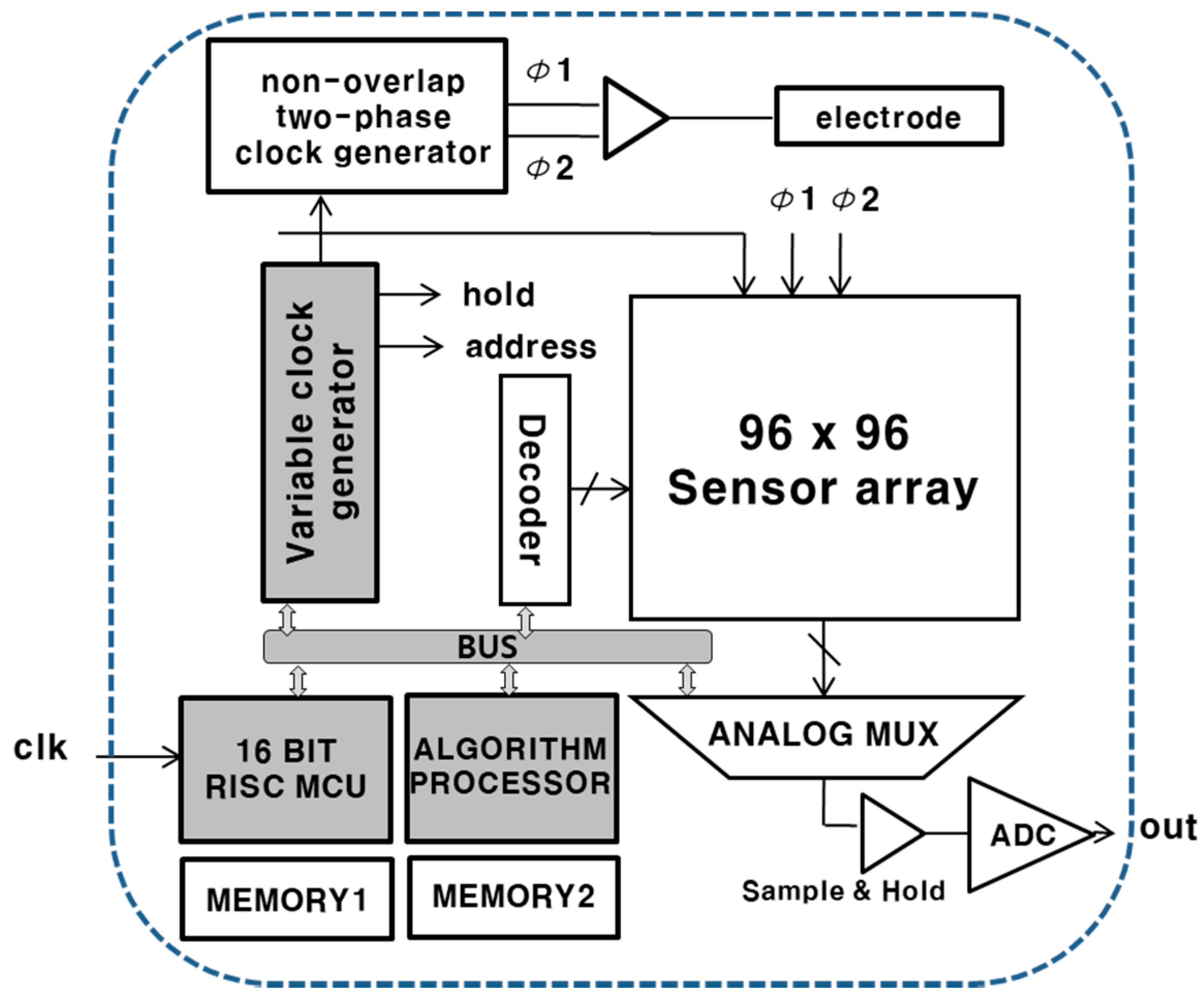
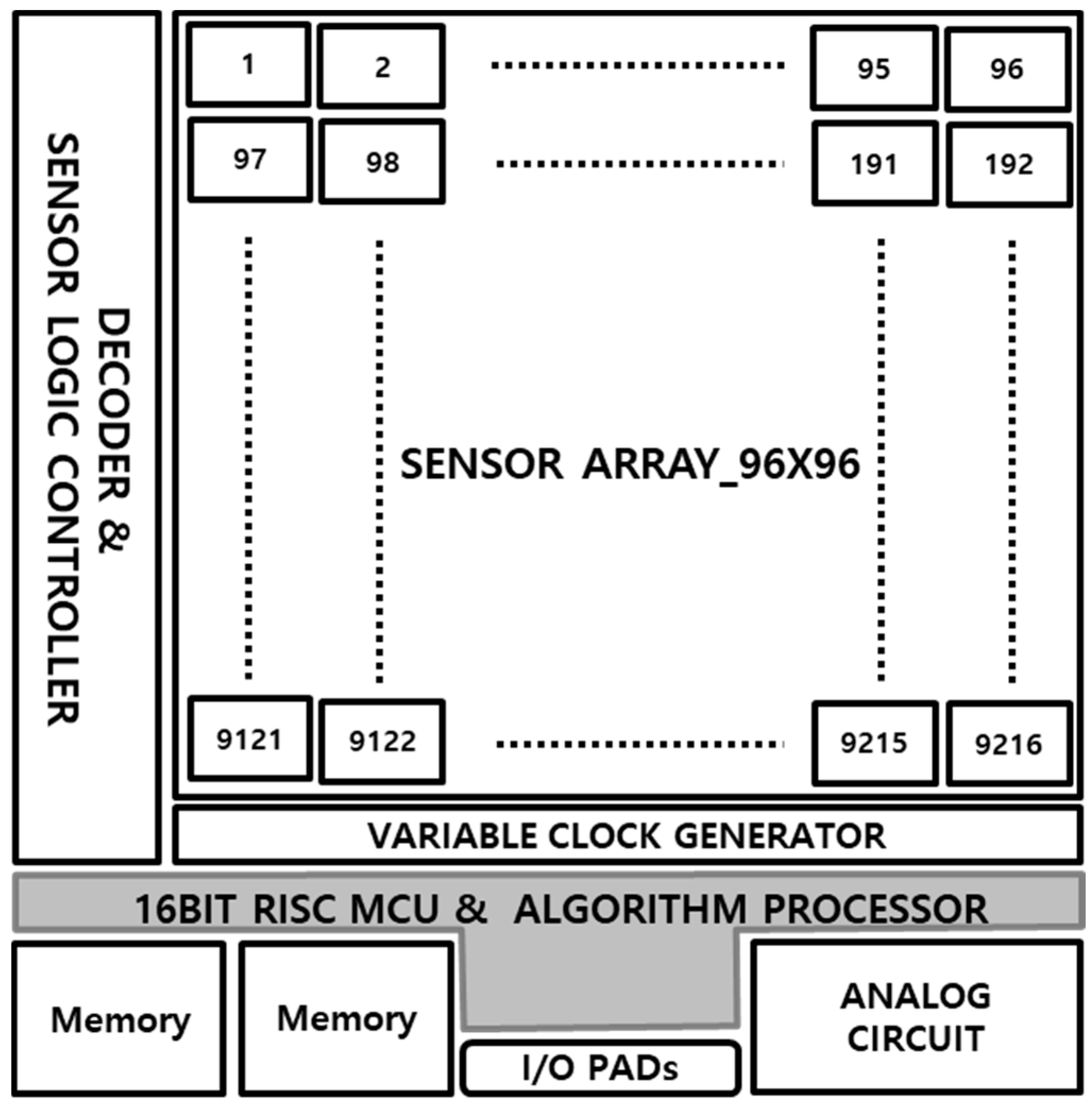
2. Sensor Array Design
2.1. Sensor Design
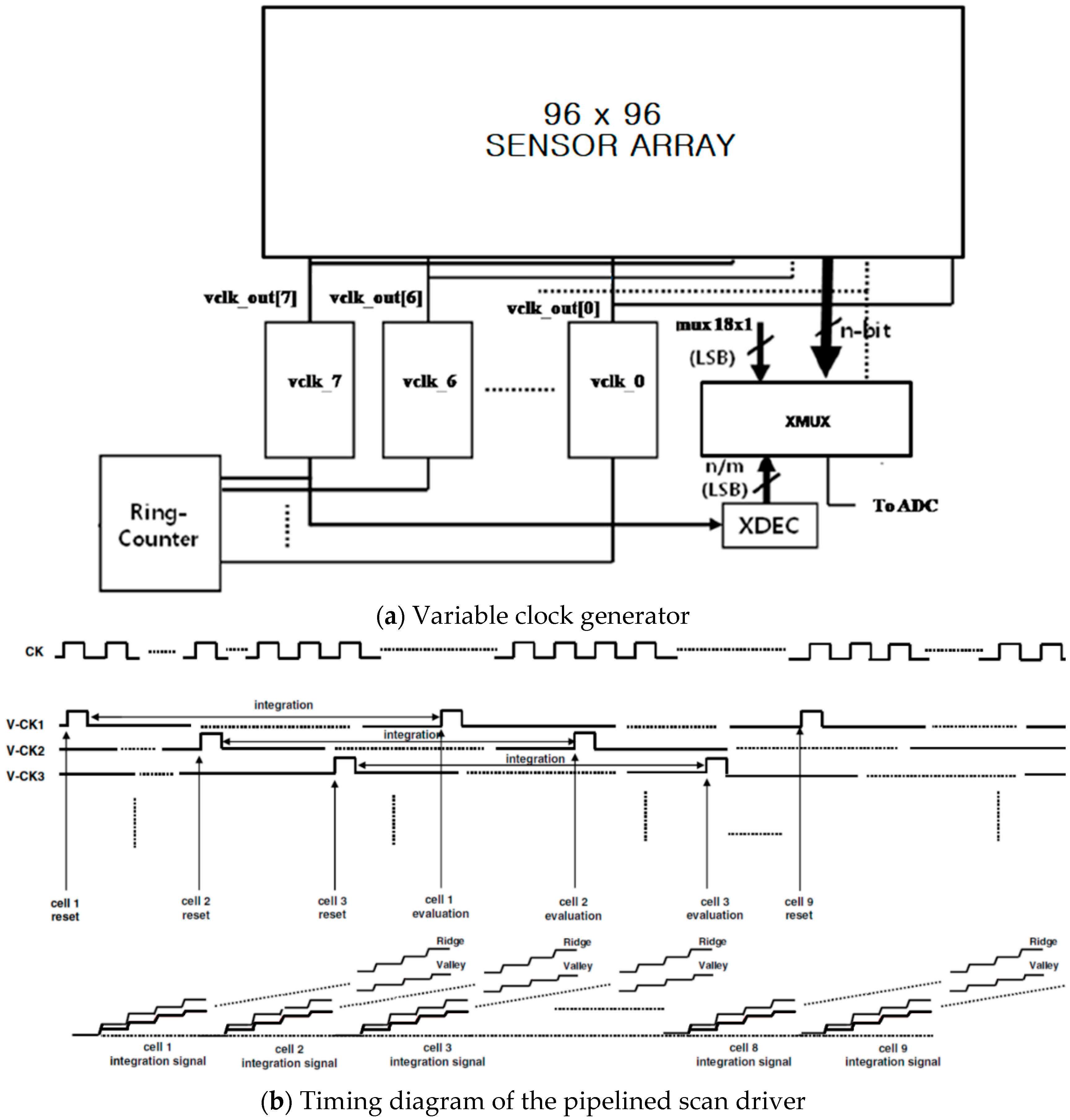
2.2. Sensor Array Design
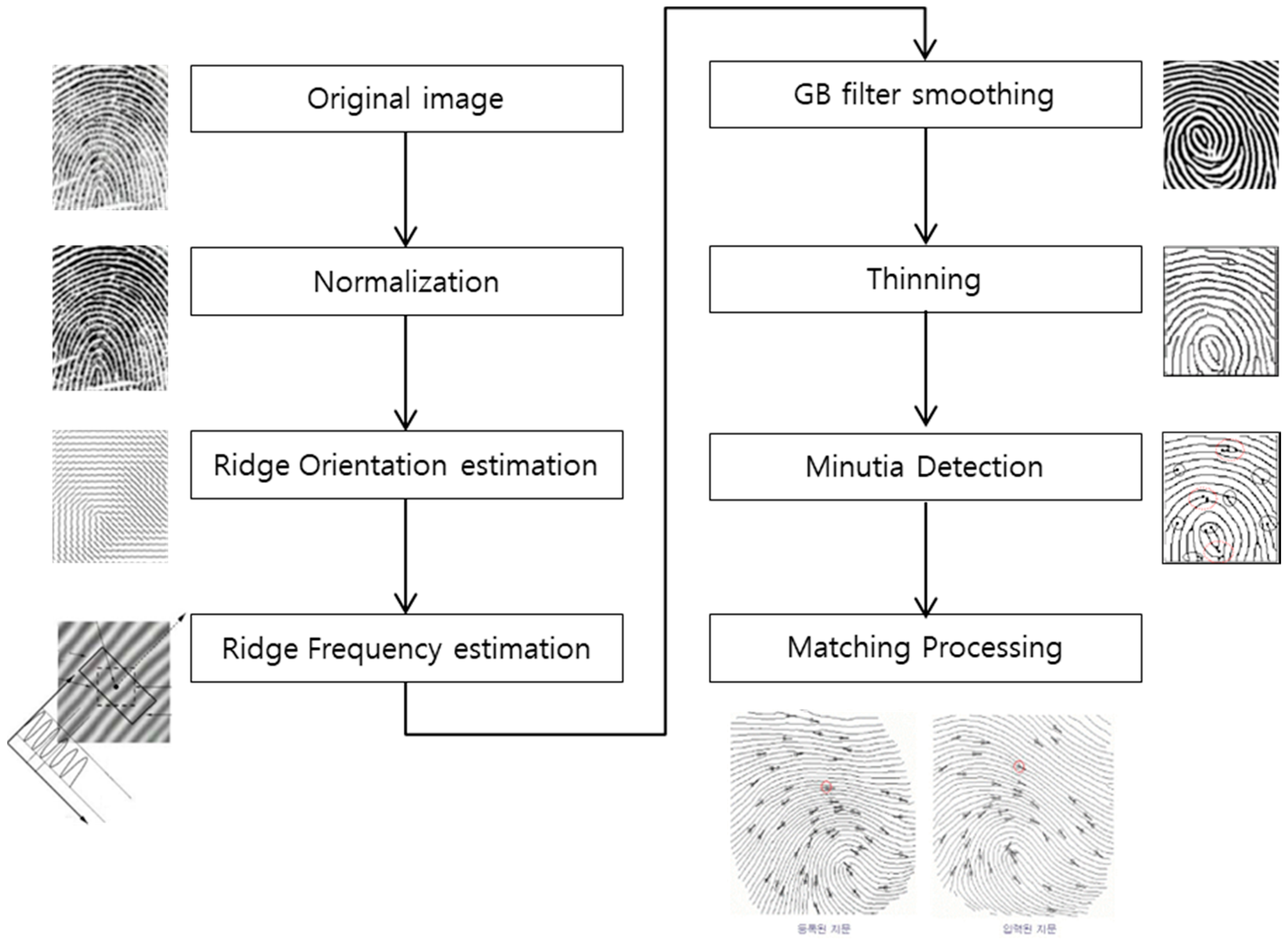
3. Analysis of Fingerprint Algorithm
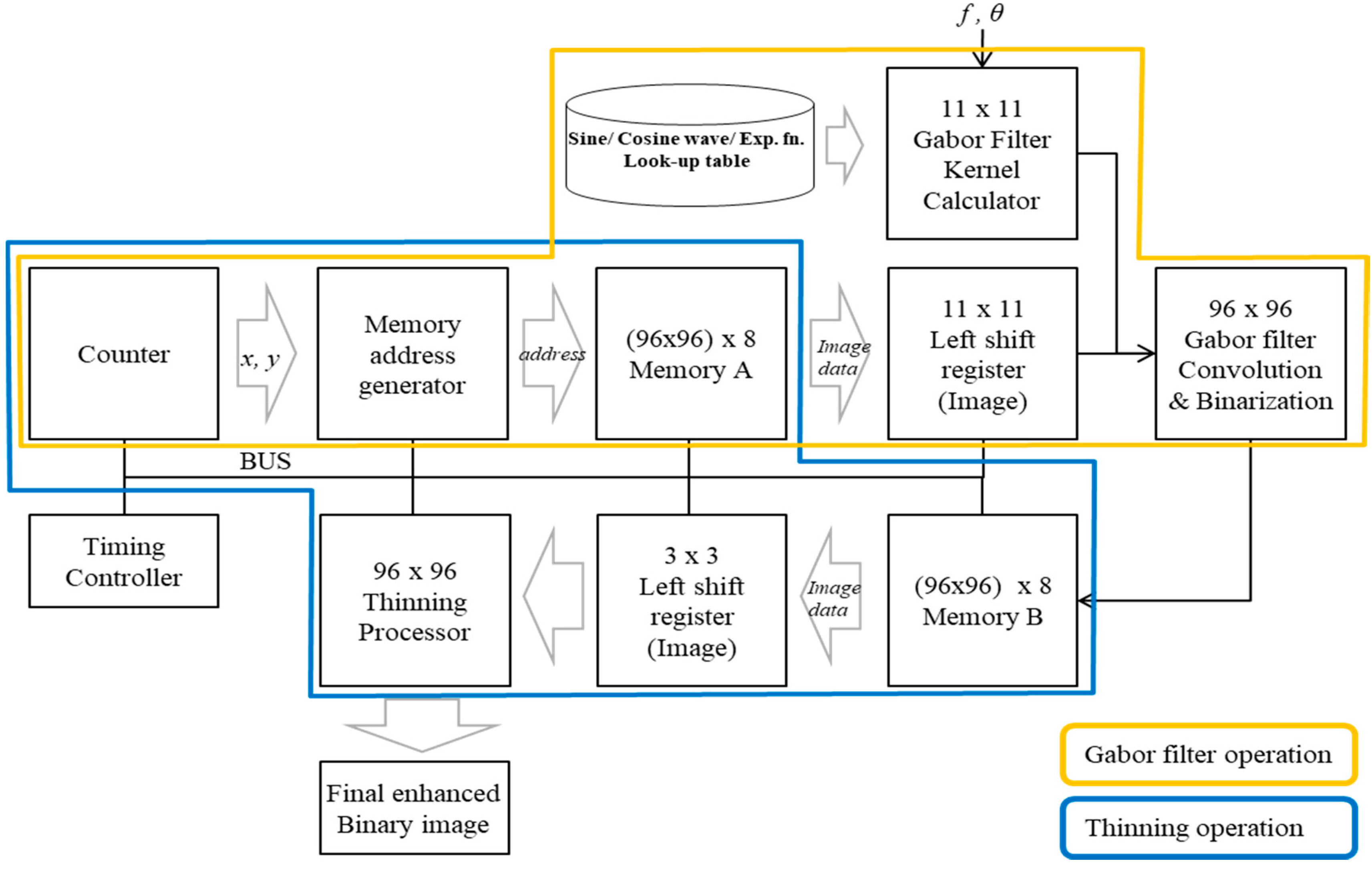
4. Algorithm Processor and MCU Design
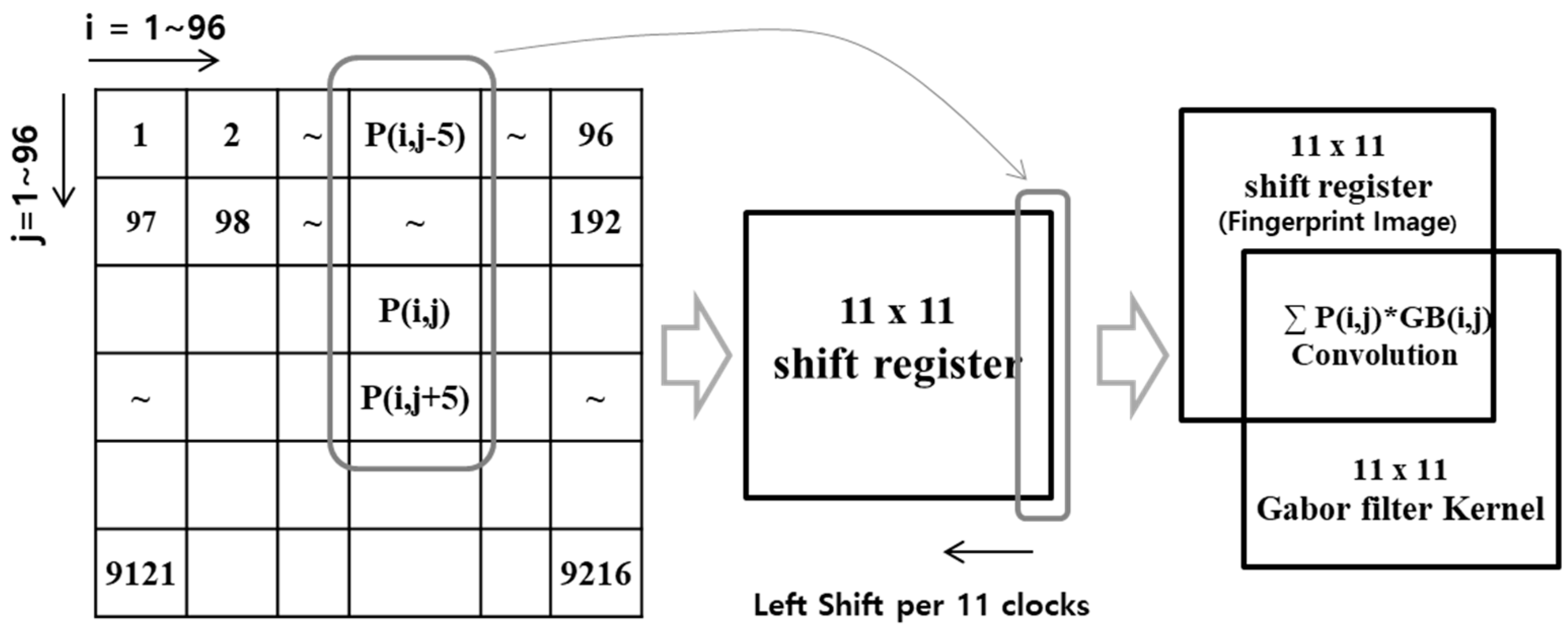
4.1. Gabor Filter Design
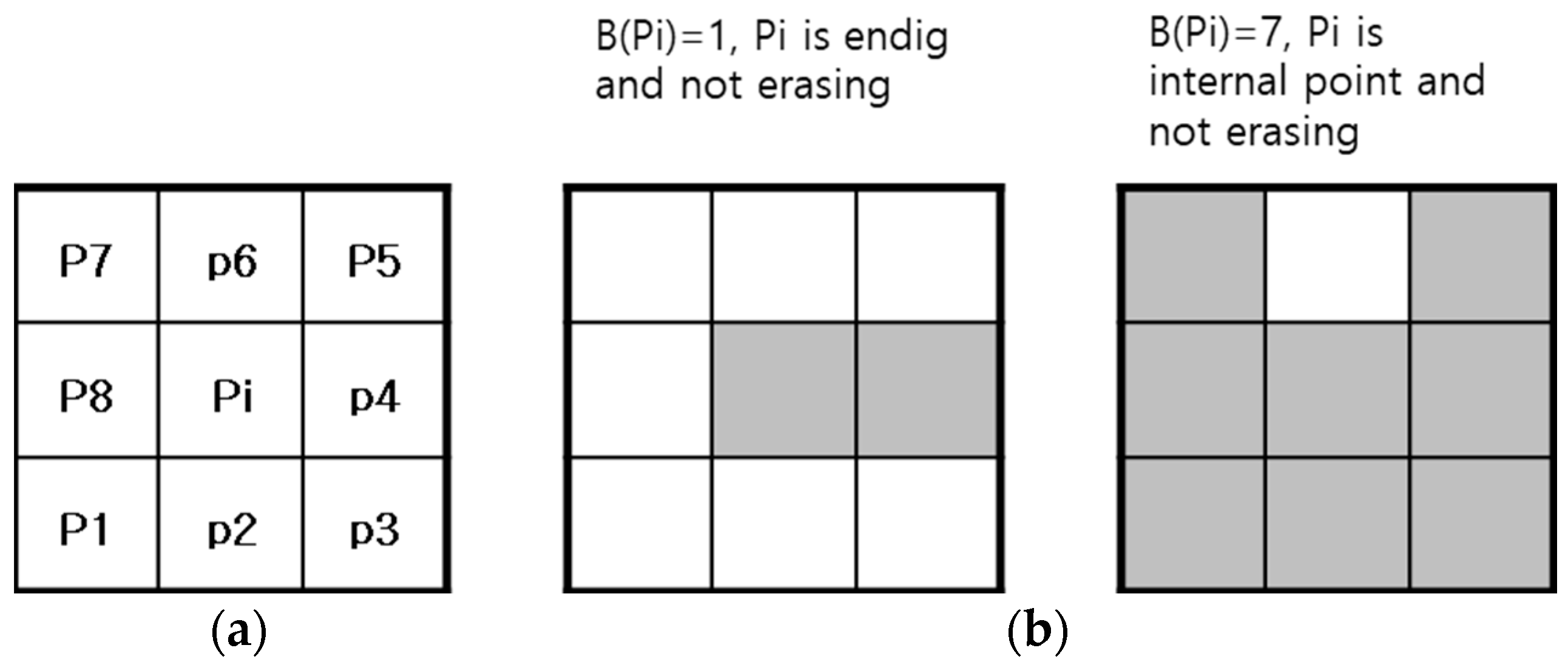
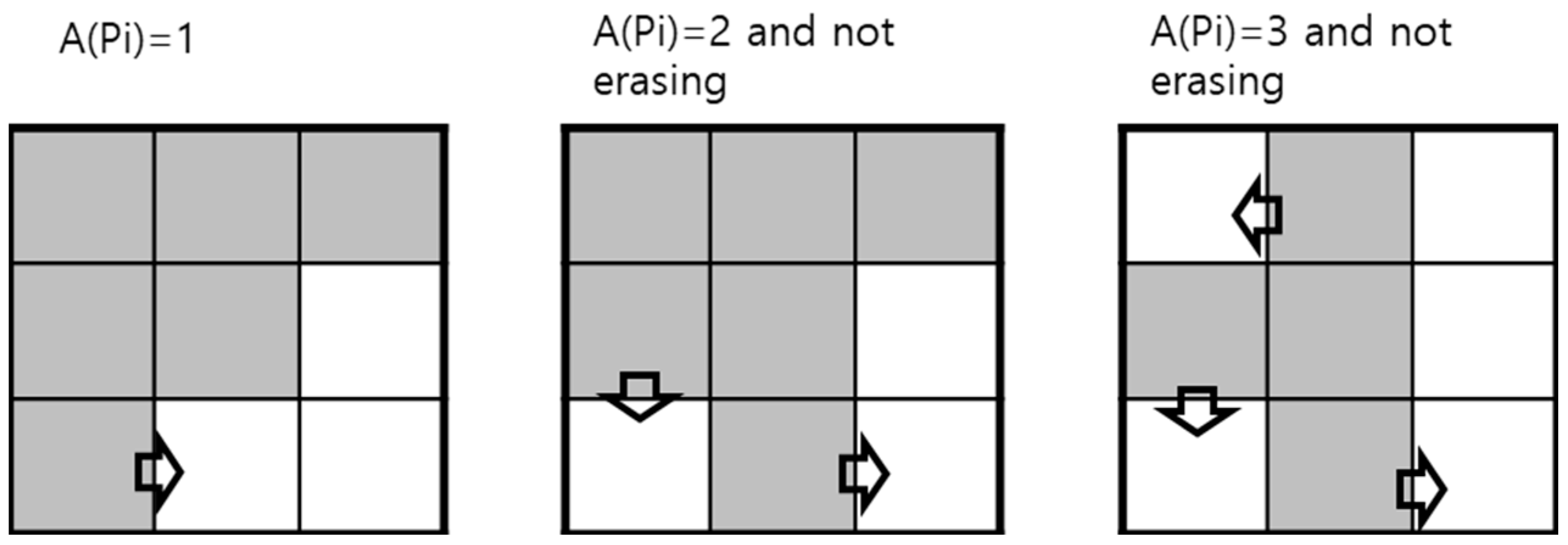
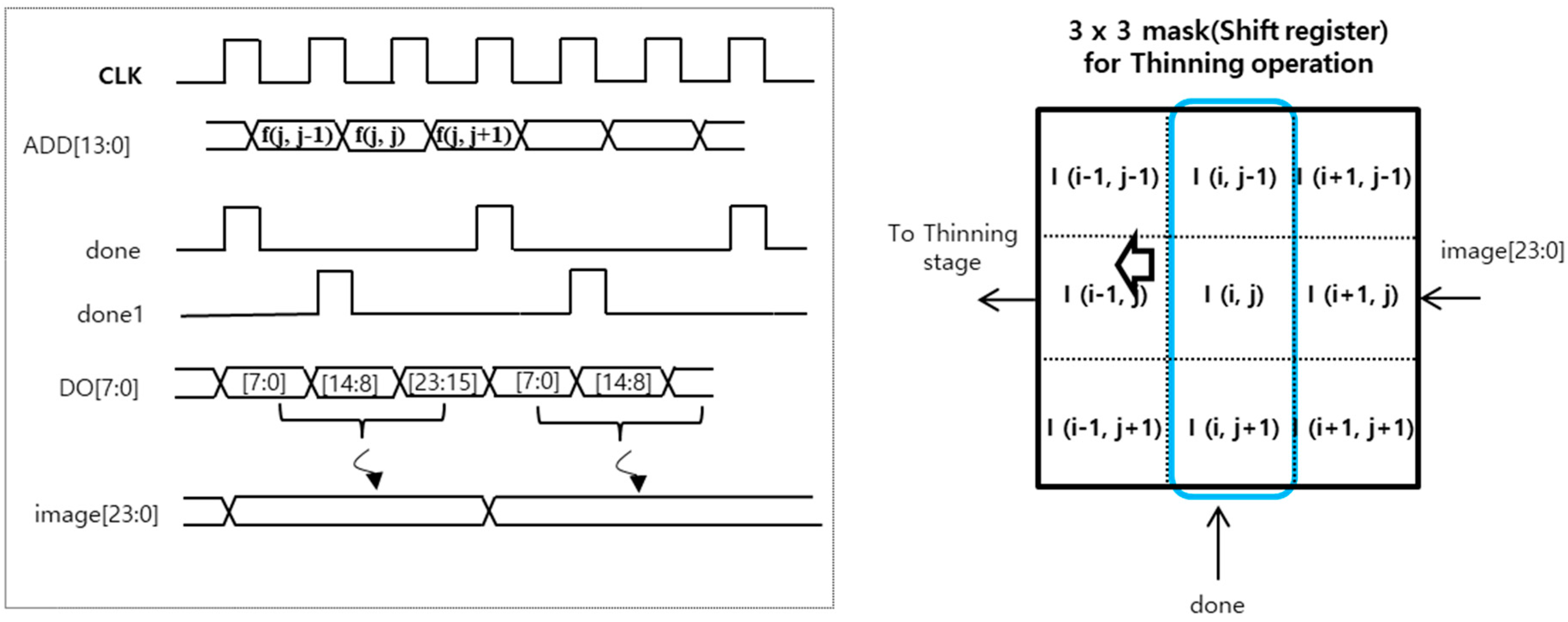
4.2. Thinning Algorithm Design
- (i)
- P(i) is a value between 2 and 6;
- (ii)
- A (Pi) = 1;
- (iii)
- At least one of P2 and P6 and P8 is 0;
- (iv)
- At least one of P4 and P6 and P8 is 0.
- (v)
- At least one of P2 and P4 and P8 is 0;
- (vi)
- At least one of P2 and P4 and P6 is 0.
4.3. Algorithm Processor Design
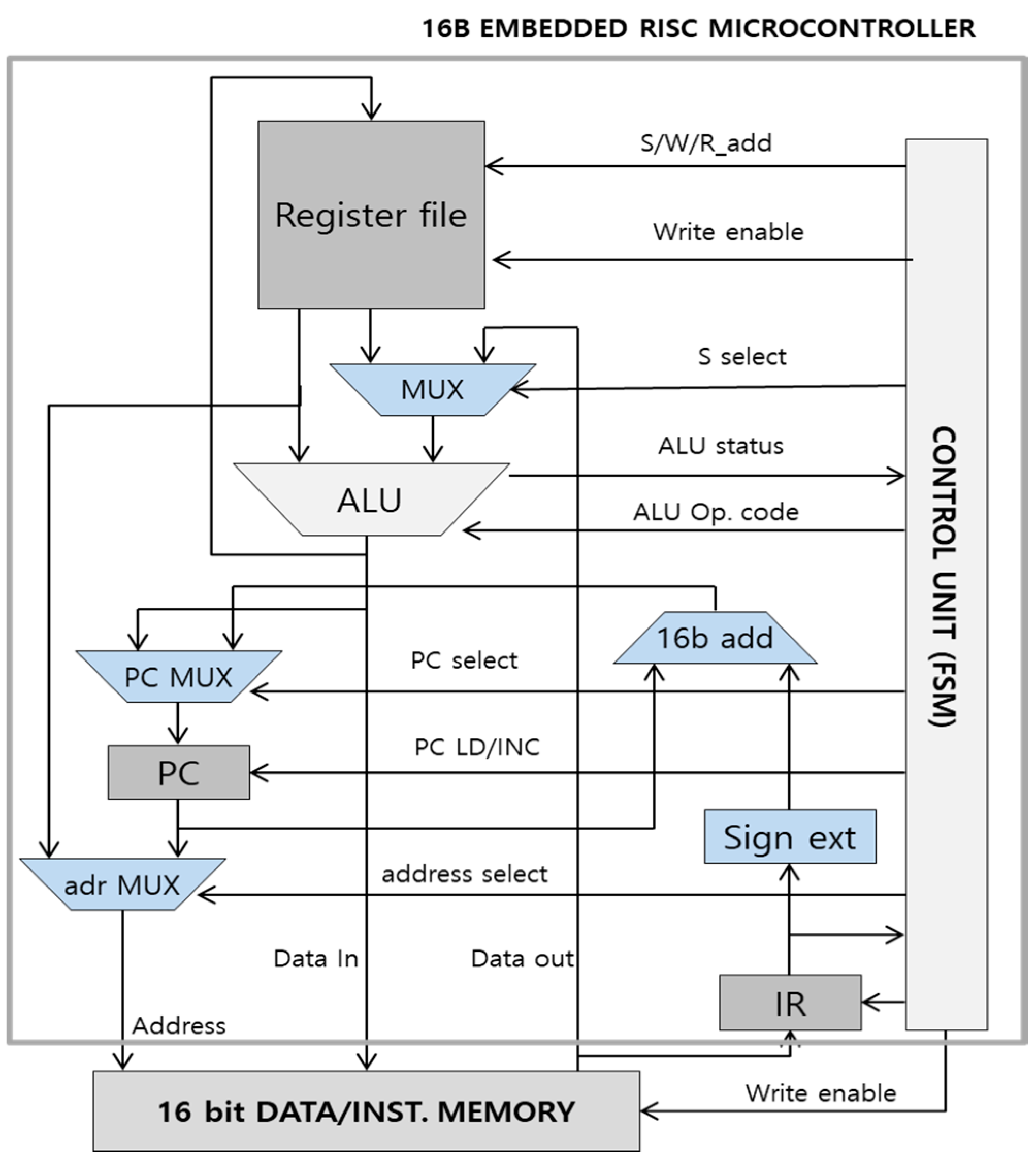
4.4. 16-Bit Risc MCU Design
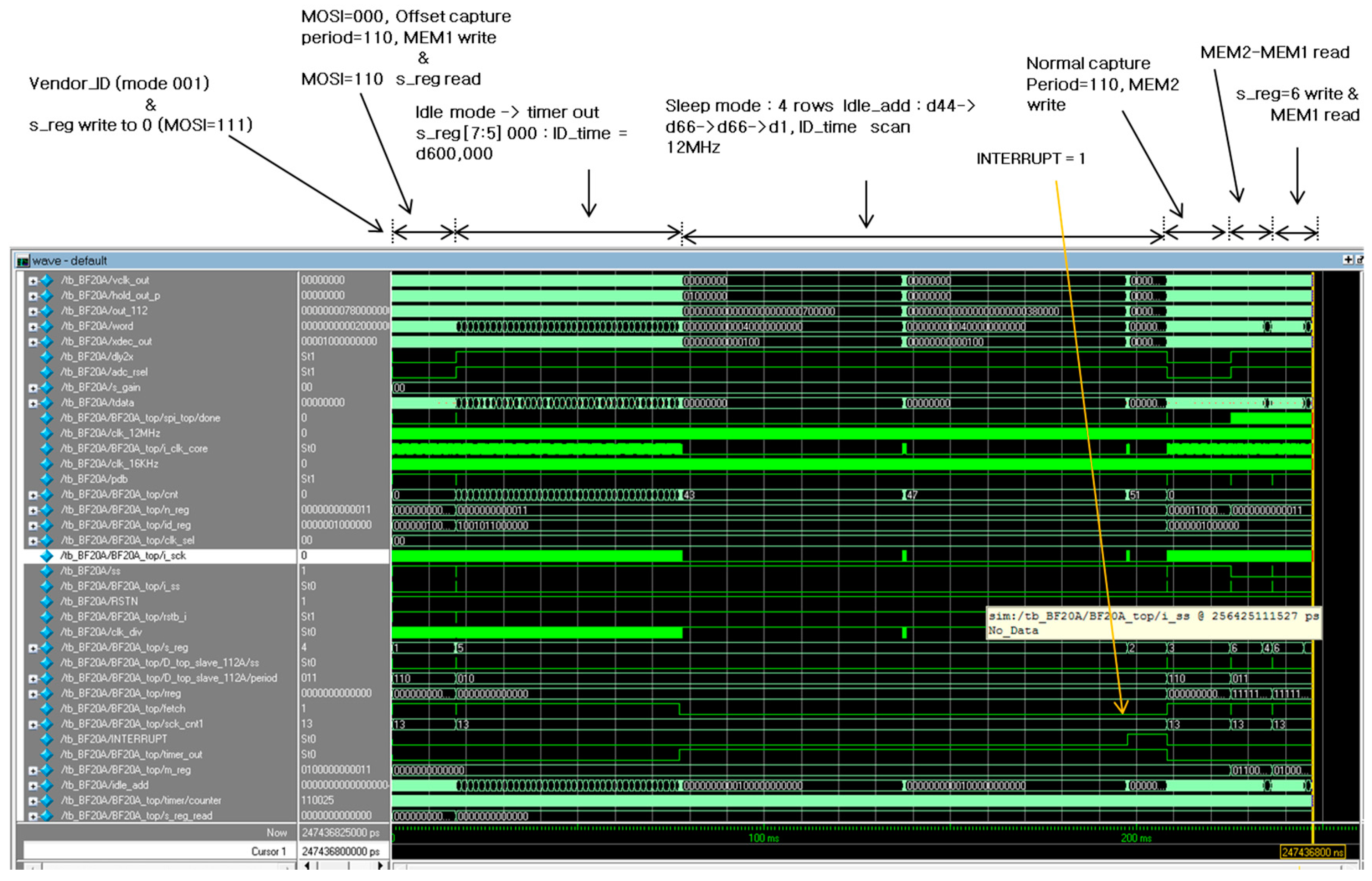
5. Full Chip Integration
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Chugh, T.; Cao, K.; Jain, A.K. Fingerprint spoof buster: Use of minutiae-centered patches. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2190–2202. [Google Scholar] [CrossRef]
- Tolosana, R.; Gomez-Barrero, M.; Busch, C.; Ortega-Garcia, J. Biometric presentation attack detection: Beyond the visible spectrum. IEEE Trans. Inf. Forensics Secur. 2019, 15, 1261–1275. [Google Scholar] [CrossRef]
- Jung, S.-M.; Nam, J.-M.; Yang, D.-H.; Lee, M.-K. A CMOS integrated capacitive fingerprint sensor with 32-bit RISC microcontroller. IEEE J. Solid-State Circuits 2005, 40, 1745–1750. [Google Scholar] [CrossRef]
- Alibeigi, E.; Samavi, S.; Shirani, S.; Rahmani, Z. Real time ridge orientation estimation for fingerprint images. Computer Vision and Pattern Recognition. arXiv 2017, arXiv:1710.05027. [Google Scholar]
- Gayathri, S.; Sridhar, V. Design and simulation of Gabor filter using verilog HDL. Int. J. Latest Trends Eng. Technol. 2013, 2, 77–83. [Google Scholar]
- Chen, W.; Sui, L.; Xu, Z.; Lang, Y. Improved Zhang-Suen thinning algorithm in binary line drawing applications. In Proceedings of the 2012 International Conference on Systems and Informatics (ICSAI2012), Yantai, China, 19–20 May 2012; pp. 1947–1950. [Google Scholar]
- Voß, N.; Mertsching, B. Design and Implementation of an Accelerated Gabor Filter Bank Using Parallel Hardware. In International Conference on Field Programmable Logic and Applications; Springer: Berlin/Heidelberg, Germany, 2001; pp. 451–460. [Google Scholar]
- Spinei, A.; Pellelin, D.; Fernandes, D.; Heraults, J. Fast Hardware Implementation of Gabor Filter Based Motion Estimation. Integr. Comput. Eng. 2000, 7, 67–77. [Google Scholar] [CrossRef]
- Painkras, E.; Charoensak, C. A VLSI architecture for Gabor filtering in face processing applications. In Proceedings of the 2005 International Symposium on Intelligent Signal Processing and Communication Systems, Hong Kong, China, 13–16 December 2005. [Google Scholar]
- Jothi, S.A.; Dhatchayani, K.; Devi, G.G.R.; Raja, M.R. VLSI Implementation of Gabor Filter in Image Detection–Research Direction. Int. J. Circuit Theory Appl. 2017, 10, 133–138. [Google Scholar]
- Kheiri, F.; Samavi, S.; Karimi, N. Hardware design for binarization and thinning of fingerprint images. arXiv 2017, arXiv:1710.05749. [Google Scholar]
- Das, R.K.; De, A.; Pal, C.; Chakrabarti, A. DSP hardware design for fingerprint binarization and thinning on FPGA. In Proceedings of the 2014 International Conference on Control, Instrumentation, Energy and Communication (CIEC), Calcutta, India, 31 January–2 February 2014. [Google Scholar]
- Wakil, Y.; Tariq, S.G.; Humayun, A.; Abbas, N. An FPGA based Minutiae Extraction System for Fingerprint Recognition. Int. J. Comput. Appl. 2015, 111, 31–35. [Google Scholar] [CrossRef]
- Hermanto, L.; Sudiro, S.A.; Wibowo, E.P. Hardware implementation of fingerprint image thinning algorithm in FPGA device. In Proceedings of the 2010 International Conference on Networking and Information Technology, Manila, Philippines, 11–12 June 2010. [Google Scholar]
- SUPREMA. Available online: https://www.supremainc.com/embedded-modules/en/main.asp (accessed on 28 August 2020).
- Jung, S. Implementation of 144 × 64 Pixel Array Bezel-Less CMOS Fingerprint Sensor. Int. J. Smart Sens. Intell. Syst. 2018, 11, 1–5. [Google Scholar] [CrossRef]
- Jung, S. A Modified Architecture for Fingerprint Sensor of Switched Capacitive Integrator Scheme. Int. J. Bio-Sci. Bio-Technol. 2016, 8, 139–144. [Google Scholar] [CrossRef]
- Yeo, H. Analysis and Performance Comparison of Charge Transfer Circuits for Capacitive Sensing. J. Next Gener. Inf. Technol. 2014, 5, 16–26. [Google Scholar]
- Hyeopgoo, Y. A New Fingerprint Sensor based on Signal Integration Scheme using Charge Transfer Circuit. Int. J. Bio-Sci. Bio-Technol. 2015, 7, 29–38. [Google Scholar] [CrossRef]
- Yeo, H. Touch fingerprint sensor based on sensor cell isolation technique with pseudo direct signalling. Int. J. Smart Sens. Intell. Syst. 2019, 12, 1–9. [Google Scholar]
- Hong, L.; Wan, Y.; Jain, A. Fingerprint Image Enhancement: Algorithm and Performance Evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 777–789. [Google Scholar] [CrossRef]
- Molaei, S.; Abadi, M.E.S.A. Maintaining filter structure: A Gabor-based convolutional neural network for image analysis. Appl. Soft Comput. 2020. [Google Scholar] [CrossRef]
- Jung, S. Design of low power and high speed CMOS fingerprint sensor Design of low power and high speed CMOS fingerprint sensor. Int. J. Bio-Sci. Bio-Technol. 2013, 5, 1–16. [Google Scholar]





| Process Step | Instruction Cycle | ||||
|---|---|---|---|---|---|
| S-cycle | N-cycle | I-cycle | Total | % | |
| Normalization | 25,168 | 6292 | 3146 | 34,606 | 0.75% |
| Orientation Estimation | 176,023 | 47,705 | 47,520 | 271,248 | 5.84% |
| Frequency Estimation | 307,424 | 88,577 | 50,706 | 446,706 | 9.62% |
| Gabor Filtering | 1,314,689 | 329,066 | 230,502 | 1,874,257 | 40.37% |
| Thinning | 983,279 | 577,092 | 265,939 | 1,826,310 | 39.34% |
| Minutiae Detection | 118,453 | 40,741 | 17,642 | 176,836 | 3.81% |
| Matching Processing | 11,540 | 389 | 816 | 12,746 | 0.27% |
| Total Clock | 2,936,577 | 1,089,862 | 616,271 | 4,642,709 | 100% |
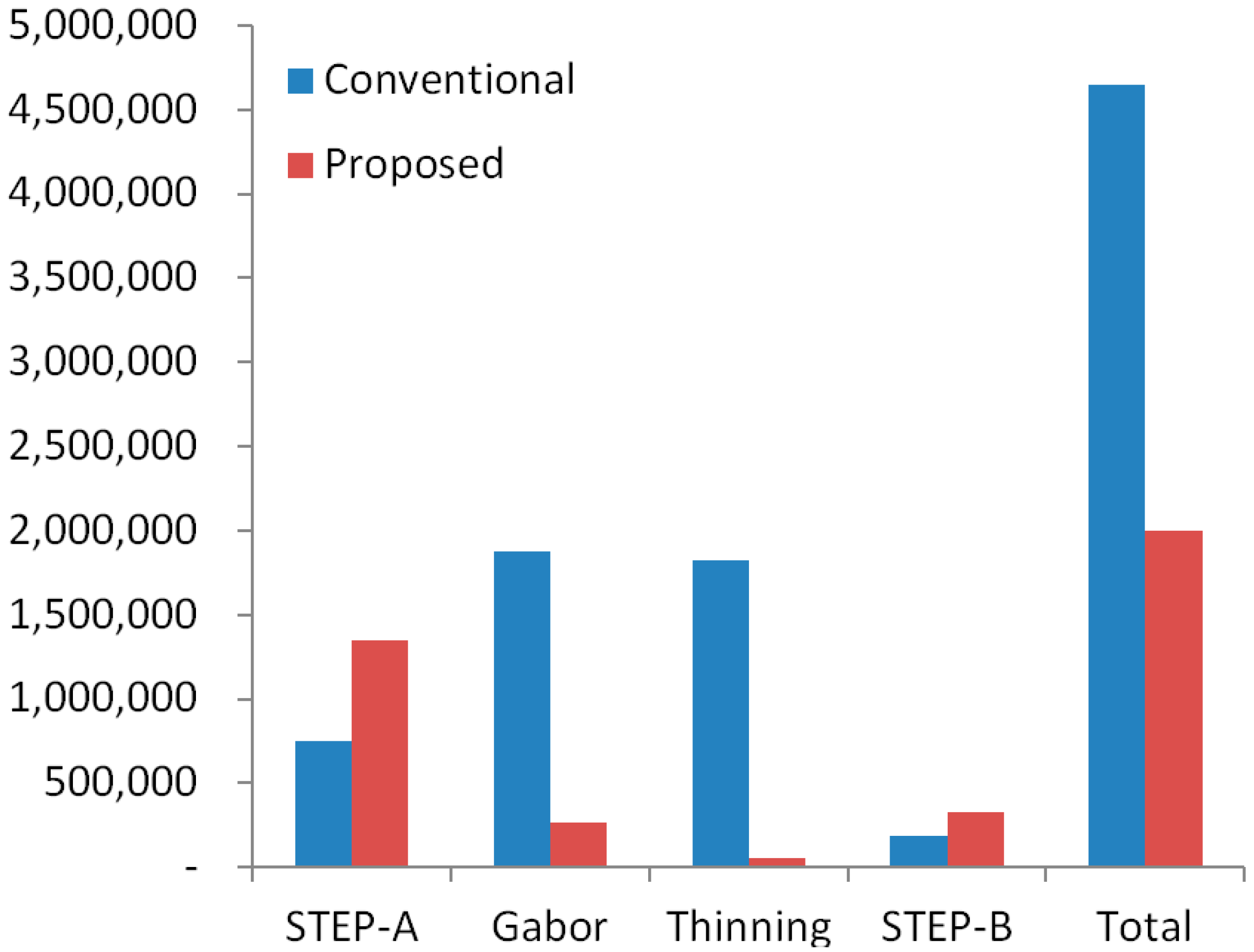
| STEP-A | Gabor | Thinning | STEP-B | Total | |
|---|---|---|---|---|---|
| Conventional | 752,560 | 1,874,257 | 1,826,310 | 189,582 | 4,642,709 |
| Proposed | 1,346,420 | 266,439 | 55,303 | 330,477 | 1,998,639 |
| Conventional Architecture (SW only) | Proposed Architecture ((SW+HW+MCU)) | Improvement (%) | Remarks | |
|---|---|---|---|---|
| Total CPU Cycle | 4,642,709 | 1,998,639 | 57 | |
| Chip Area (mm2) with 2 SRAM | 27.14 | 28.61 | −5.4 | 96 × 96 pixels area full chip |
| Power Consumption | - | 5.25 mW | - | 20 MHz, 1.8 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S. Image Processor and RISC MCU Embedded Single Chip Fingerprint Sensor. J. Sens. Actuator Netw. 2020, 9, 51. https://doi.org/10.3390/jsan9040051
Jung S. Image Processor and RISC MCU Embedded Single Chip Fingerprint Sensor. Journal of Sensor and Actuator Networks. 2020; 9(4):51. https://doi.org/10.3390/jsan9040051
Chicago/Turabian StyleJung, Seungmin. 2020. "Image Processor and RISC MCU Embedded Single Chip Fingerprint Sensor" Journal of Sensor and Actuator Networks 9, no. 4: 51. https://doi.org/10.3390/jsan9040051
APA StyleJung, S. (2020). Image Processor and RISC MCU Embedded Single Chip Fingerprint Sensor. Journal of Sensor and Actuator Networks, 9(4), 51. https://doi.org/10.3390/jsan9040051




