Detecting System Fault/Cyberattack within a Photovoltaic System Connected to the Grid: A Neural Network-Based Solution
Abstract
1. Introduction
1.1. Distributed Energy Resources (DERs)
1.2. The Need for Anomaly Detection and Aim of the Paper
2. State of The Art
2.1. Anomaly Detection in Industrial Control Systems (ICS)
2.2. DERs Anomaly Detection
3. Proposed Method
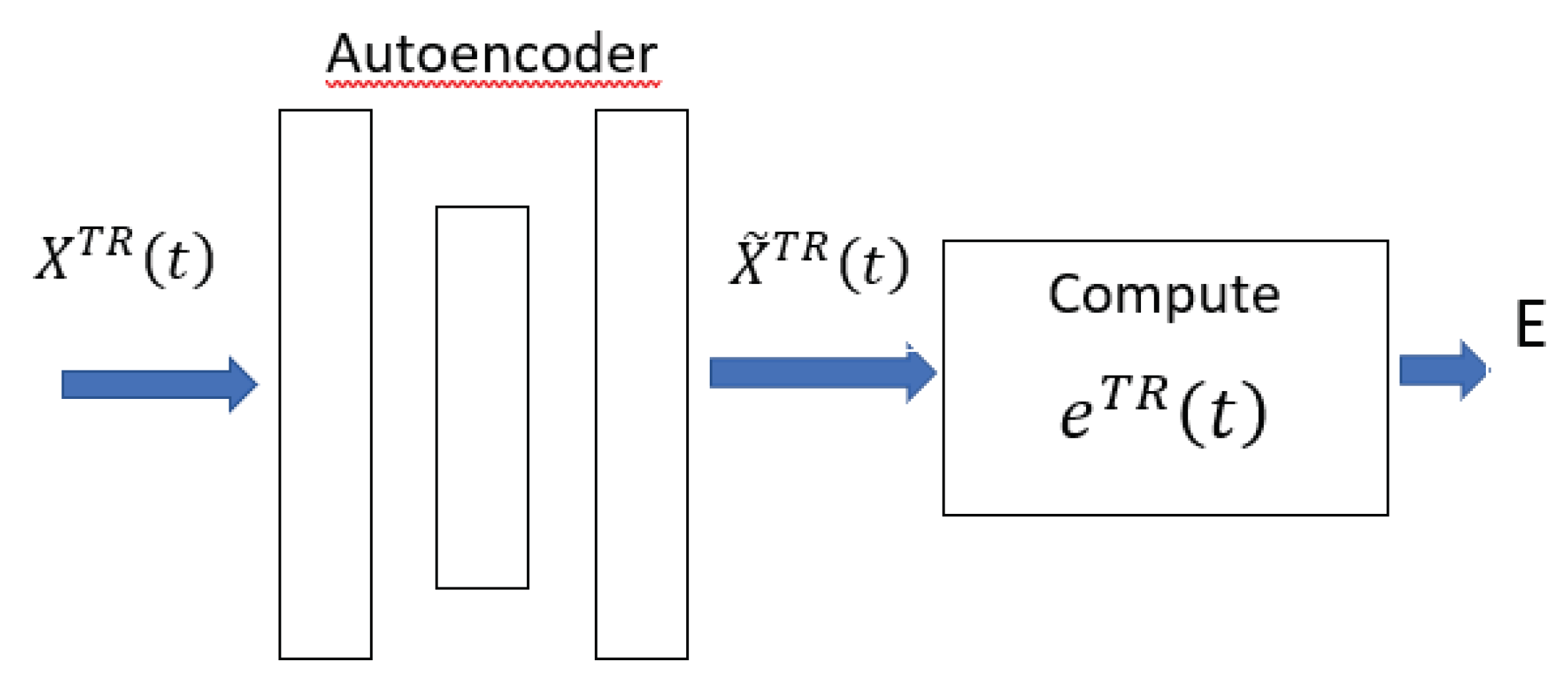
3.1. Preprocessing
3.2. Training Phase
3.3. Test Phase
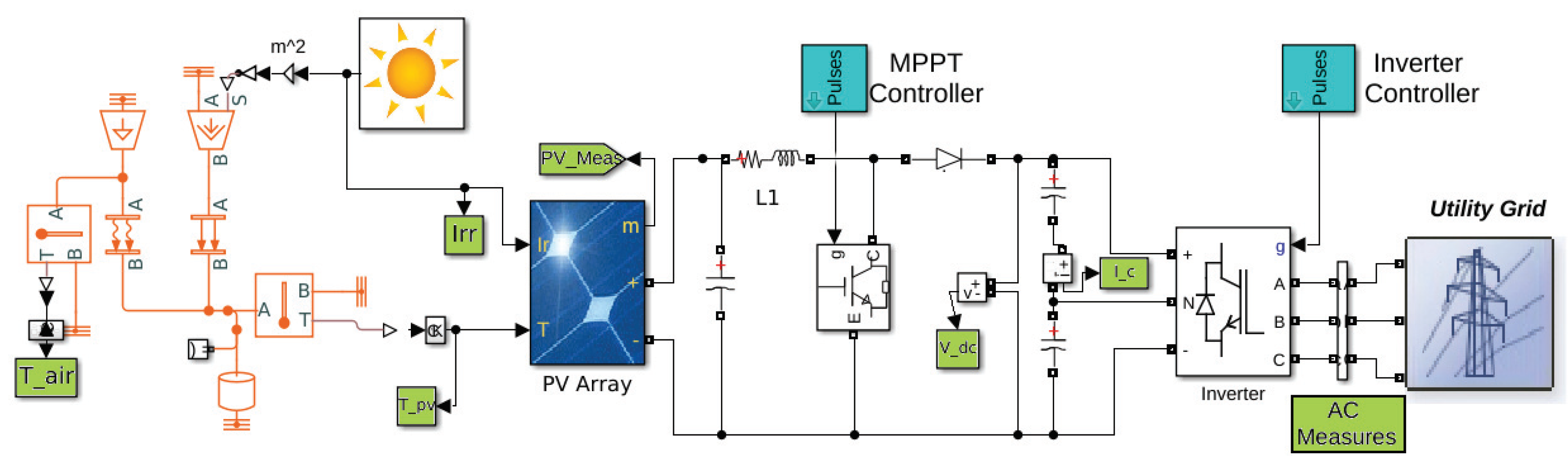
4. Materials and Methods
- Alternating Current (AC) side electrical information: active and reactive power, voltages (Root Mean Square, RMS), currents (RMS), frequencies, total harmonic distortion (THD)
- Direct-Current (DC) side electrical information: voltages and currents
- PV information: voltage, current, temperature of the cells
- Environmental information: irradiance, temperature of the air
- Electronic information: maximum power point, dc/dc converter duty cycle
- Reduction of active power injection
- Short circuit of some cells of the solar panel
- Bad data injection
- Batch size
- Epochs
5. Results
5.1. General Description
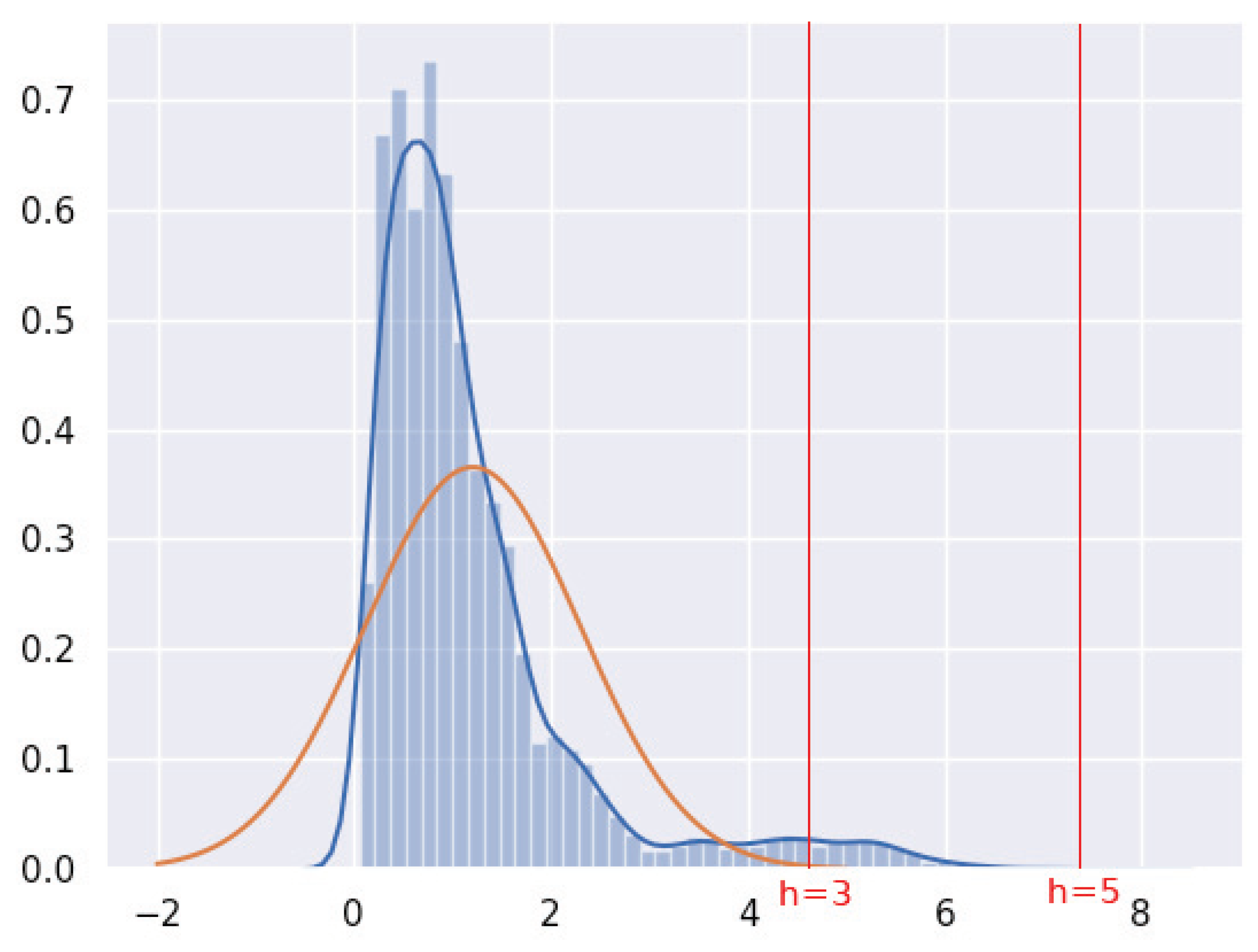
5.2. Threshold E
5.3. Autoencoder Architecture
5.4. Training Parameters
6. Discussion and Future Research Issues
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DER | Distributed Energy Resources |
| DL | Deep Learning |
| ICS | Industrial Control System |
| IDS | Intrusion Detection System |
| ML | Machine Learning |
| NN | Neural Network |
| RES | Renewable Energy Sources |
| SCADA | Supervisory Control and Data Acquisition |
References
- Chandola, V.; Arindam, B.; Vipin, K. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 15. [Google Scholar] [CrossRef]
- Markou, M.; Sameer, S. Novelty detection: A review—Part 1: Statistical approaches. Signal Process. 2003, 83, 2481–2497. [Google Scholar] [CrossRef]
- Markou, M.; Sameer, S. Novelty detection: A Review—part 2: Neural network based approaches. Signal Process. 2003, 83, 2499–2521. [Google Scholar] [CrossRef]
- Amarbayasgalan, T.; Bilguun, J.; Keun, R. Unsupervised novelty detection using deep autoencoders with density based clustering. Appl. Sci. 2018, 8, 1468. [Google Scholar] [CrossRef]
- Chen, J.; Sathe, S.; Aggarwal, C.; Turaga, D. Outlier detection with autoencoder ensembles. In Proceedings of the SIAM International Conference on Data Mining, Houston, TX, USA, 27–29 April 2017; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Chalapathy, R.; Aditya, K.M.; Sanjay, C. Anomaly detection using one-class neural networks. arXiv 2018, arXiv:1802.06360. [Google Scholar]
- Zhu, B.; Shankar, S. SCADA-specific intrusion detection/prevention systems: A survey and taxonomy. In Proceedings of the 1st Workshop on Secure Control Systems (SCS), Stockholm, Sweden, 12 April 2010; Volume 11. [Google Scholar]
- Radoglou-Grammatikis, P.I.; Panagiotis, G.S. Securing the smart grid: A comprehensive compilation of intrusion detection and prevention systems. IEEE Access 2019, 7, 46595–46620. [Google Scholar] [CrossRef]
- Xu, Y.; Yi, Y.; Tianran, L.; Jiaqi, J.; Qi, W.; Jiaqi, J.; Qi, W. Review on cyber vulnerabilities of communication protocols in industrial control systems. In Proceedings of the IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017. [Google Scholar]
- Gao, W.; Morris, T.; Reaves, B.; Richey, D. On SCADA control system command and response injection and intrusion detection. In Proceedings of the IEEE eCrime Researchers Summit, Dallas, TX, USA, 18–20 October 2010. [Google Scholar]
- Fovino, I.N.; Coletta, A.; Carcano, A.; Masera, M. Critical state-based filtering system for securing SCADA network protocols. IEEE Trans. Ind. Electron. 2011, 59, 3943–3950. [Google Scholar] [CrossRef]
- Zhao, J.; Gomez-Exposito, A.; Netto, M.; Mili, M.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power system dynamic state estimation: Motivations, definitions, methodologies, and future work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Hu, Q.; Fooladivanda, D.; Chang, Y.H.; Tomlin, C.J. Secure state estimation and control for cyber security of the nonlinear power systems. IEEE Trans. Control. Netw. Syst. 2017, 5, 1310–1321. [Google Scholar] [CrossRef]
- Li, Y.; Zhi, L.; Liang, C. Dynamic State Estimation of Generators Under Cyber Attacks. IEEE Access 2019, 7, 125253–125267. [Google Scholar] [CrossRef]
- Harrou, F.; Bilal, T.; Ying, S. Improved k NN-Based Monitoring Schemes for Detecting Faults in PV Systems. IEEE J. Photovolt. 2019, 9, 811–821. [Google Scholar] [CrossRef]
- Costamagna, P.; De Giorgi, A.; Magistri, L.; Moser, G.; Pellaco, L.; Trucco, A. A classification approach for model-based fault diagnosis in power generation systems based on solid oxide fuel cells. IEEE Trans. Energy Convers. 2015, 31, 676–687. [Google Scholar] [CrossRef]
- Kosek, A.M. Contextual anomaly detection for cyber-physical security in Smart Grids based on an artificial neural network model. In Proceedings of the IEEE Joint Workshop on Cyber-Physical Security and Resilience in Smart Grids (CPSR-SG), Vienna, Austria, 11–14 April 2016. [Google Scholar]
- Kosek, A.M.; Gehrke, O. Ensemble regression model-based anomaly detection for cyber-physical intrusion detection in smart grids. In Proceedings of the IEEE Electrical Power and Energy Conference (EPEC), Ottawa, ON, Canada, 12–14 October 2016. [Google Scholar]
- Principi, E.; Rossetti, D.; Squartini, S.; Piazza, F. Unsupervised electric motor fault detection by using deep autoencoders. IEEE/Caa J. Autom. Sin. 2019, 6, 441–451. [Google Scholar] [CrossRef]
- Pillai, D.S.; Blaabjerg, F.; Rajasekar, N. A comparative evaluation of advanced fault detection approaches for PV systems. IEEE J. Photovolt. 2019, 9, 513–527. [Google Scholar] [CrossRef]
- AbdulMawjood, K.; Shady, S.R.; Walid, G.M. Detection and prediction of faults in photovoltaic arrays: A review. In Proceedings of the IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 28 February 2020).
Sample Availability: Samples of the compounds are available from the authors. |


| Feature | Symbol | Description |
|---|---|---|
| Irr | the solar irradiance hitting the panel | |
| the temperature of the environment | ||
| the temperature of the PV’s cells | ||
| the voltage measured at the terminals of the panel | ||
| the current emitted by the panel | ||
| the voltage measured at the DC link | ||
| the average current in the DC capacitor | ||
| the dutycycle of the DC/DC converter | ||
| the voltage of phase a (AC side) | ||
| the voltage of phase b (AC side) | ||
| the voltage of phase c (AC side) | ||
| the current of phase a | ||
| the current of phase b | ||
| the current of phase c | ||
| the frequency of phase a | ||
| the frequency of phase b | ||
| the frequency of phase c | ||
| the total harmonic distortion of the voltage on phase a | ||
| the total harmonic distortion of the voltage on phase b | ||
| the total harmonic distortion of the voltage on phase c | ||
| Q | the reactive power emitted by the inverter | |
| P | the active power emitted by the inverter |
| Power Reduction | Short Circuited Cells | Bad Data Injection | |
|---|---|---|---|
| h = 3 | Accuracy: 0.729 TN: 221 FN: 0 FP: 216 TP: 361 | Accuracy: 0.772 TN: 243 FN: 1 FP: 183 TP: 379 | Accuracy: 0.497 TN: 125 FN: 15 FP: 339 TP: 225 |
| h = 4 | Accuracy: 0.948 TN: 396 FN: 0 FP: 41 TP: 361 | Accuracy: 0.842 TN: 412 FN: 113 FP: 14 TP: 267 | Accuracy: 0.714 TN: 314 FN: 51 FP: 150 TP: 189 |
| h = 5 | Accuracy: 0.995 TN: 433 FN: 0 FP: 4 TP: 361 | Accuracy: 0.68 TN: 424 FN: 230 FP: 2 TP: 130 | Accuracy: 0.839 TN: 440 FN: 89 FP: 24 TP: 151 |
| h = 6 | Accuracy: 1 TN: 437 FN: 0 FP: 0 TP: 361 | Accuracy: 0.547 TN: 426 FN: 365 FP: 0 TP: 15 | Accuracy: 0.839 TN: 456 FN: 105 FP: 8 TP: 135 |
| h = 7 | Accuracy: 1 TN: 437 FN: 0 FP: 0 TP: 361 | Accuracy: 0.536 TN: 426 FN: 374 FP: 0 TP: 6 | Accuracy: 0.841 TN: 463 FN: 111 FP: 1 TP: 129 |
| Power Reduction | Short Circuited Cells | Bad Data Injection | |
|---|---|---|---|
| 22-18-22 | 0.994 | 0.660 | 0.820 |
| 22-15-22 | 0.995 | 0.687 | 0.839 |
| 22-10-22 | 0.995 | 0.680 | 0.824 |
| 22-15-10-15-22 | 0.995 | 0.612 | 0.825 |
| 22-18-15-18-22 | 0.995 | 0.661 | 0.830 |
| 22-21-(...)-13-(...)-22 | 0.995 | 0.659 | 0.830 |
| Power Reduction | Short Circuited Cells | Bad Data Injection | Mean Accuracy | |
|---|---|---|---|---|
| Batch size: 256 | 0.995 | 0.650 | 0.837 | 0.827 |
| Batch size = 64 | 0.993 | 0.702 | 0.820 | 0.838 |
| Batch size = 32 | 0.992 | 0.789 | 0.825 | 0.869 |
| Batch size = 16 | 0.992 | 0.819 | 0.801 | 0.870 |
| Batch size = 1 | 0.992 | 0.801 | 0.801 | 0.864 |
| Power Reduction | Short Circuited Cells | Bad Data Injection | Mean Accuracy | |
|---|---|---|---|---|
| Epochs = 10 | 0.992 | 0.789 | 0.825 | 0.868 |
| Epochs = 50 | 0.992 | 0.814 | 0.809 | 0.872 |
| Epochs = 100 | 0.992 | 0.840 | 0.808 | 0.880 |
| Epochs = 200 | 0.992 | 0.834 | 0.788 | 0.871 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaggero, G.B.; Rossi, M.; Girdinio, P.; Marchese, M. Detecting System Fault/Cyberattack within a Photovoltaic System Connected to the Grid: A Neural Network-Based Solution. J. Sens. Actuator Netw. 2020, 9, 20. https://doi.org/10.3390/jsan9020020
Gaggero GB, Rossi M, Girdinio P, Marchese M. Detecting System Fault/Cyberattack within a Photovoltaic System Connected to the Grid: A Neural Network-Based Solution. Journal of Sensor and Actuator Networks. 2020; 9(2):20. https://doi.org/10.3390/jsan9020020
Chicago/Turabian StyleGaggero, Giovanni Battista, Mansueto Rossi, Paola Girdinio, and Mario Marchese. 2020. "Detecting System Fault/Cyberattack within a Photovoltaic System Connected to the Grid: A Neural Network-Based Solution" Journal of Sensor and Actuator Networks 9, no. 2: 20. https://doi.org/10.3390/jsan9020020
APA StyleGaggero, G. B., Rossi, M., Girdinio, P., & Marchese, M. (2020). Detecting System Fault/Cyberattack within a Photovoltaic System Connected to the Grid: A Neural Network-Based Solution. Journal of Sensor and Actuator Networks, 9(2), 20. https://doi.org/10.3390/jsan9020020







