Scalable Edge Computing Deployment for Reliable Service Provisioning in Vehicular Networks
Abstract
1. Introduction
2. Background
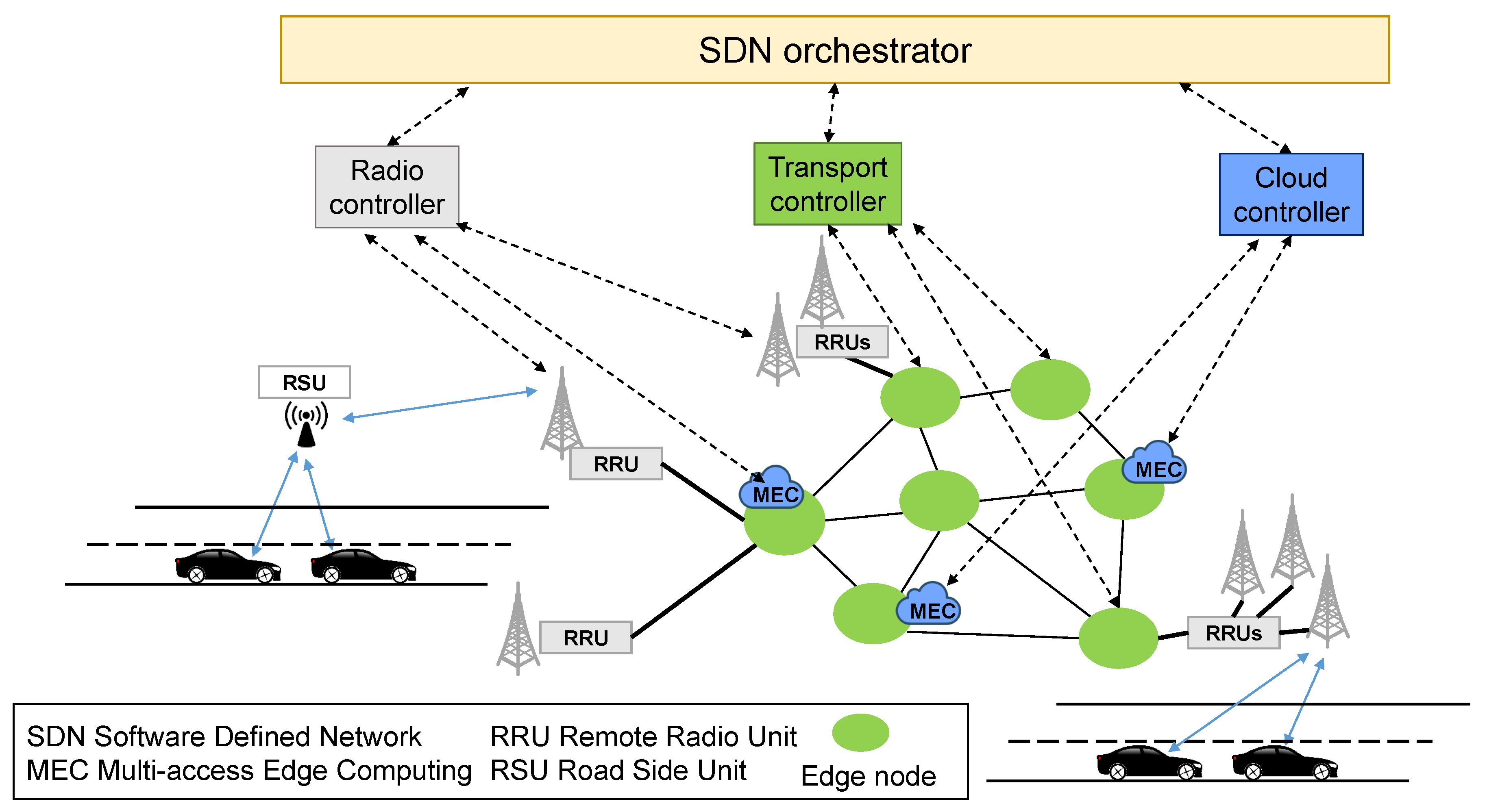
3. Architectural Solution and Problem Formulation
- Given a set of RRUs to be connected to active edge nodes, a set of edge nodes (candidates to host BBU and edge processing resources), and a set of links connecting edge nodes.
- Find active edge nodes and suitable optical resource assignment such that (i) the number of active nodes and (ii) total wavelengths are minimized.
- Ensure that each RRU is connected to two active edge nodes (one for primary and one for backup purposes) and that the maximum available wavelengths per link and maximum allowed distance to provide target service are not exceeded.
4. ILP-Based Optimization
Objective Function
5. Two-Phases Hybrid Approach
- H matrix: This is an matrix, where each row represents a node of the network; the first column indicates which is the primary edge node chosen by the node on that row, while the second column indicates which is the backup node.
- W matrix: This is an matrix which keeps track of the use of the links between nodes. In W, there is one row for each source edge node (where the RRUs are physically connected). W has one column for each edge node, that is, the possible locations for the edge server performing baseband and services for the specific RRUs. This matrix is needed to provide a feasible solution at the end of phase 1 but is not used in phase 2.
| Algorithm 1 C-RAN reliable coverage (phase 1). |
|
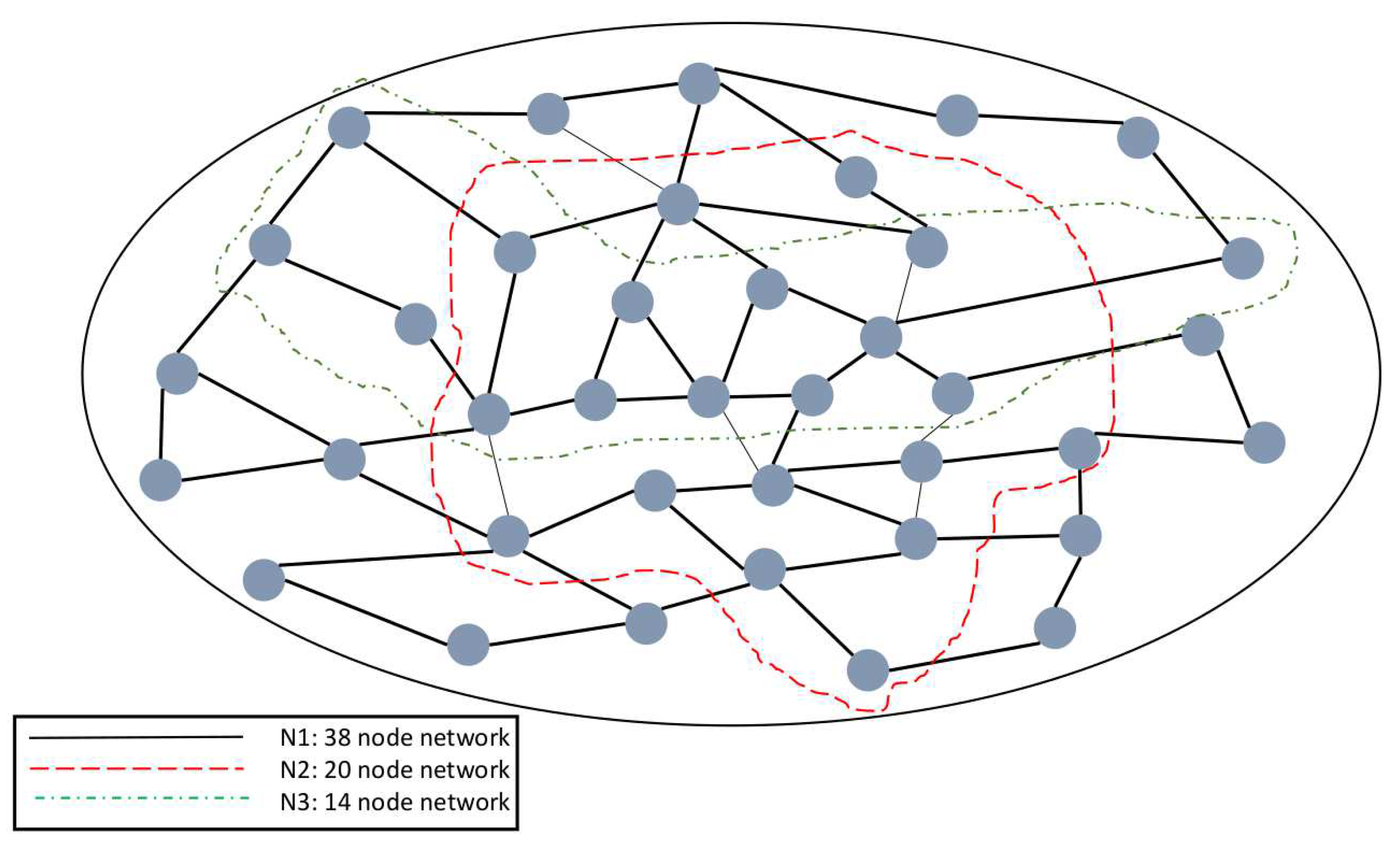
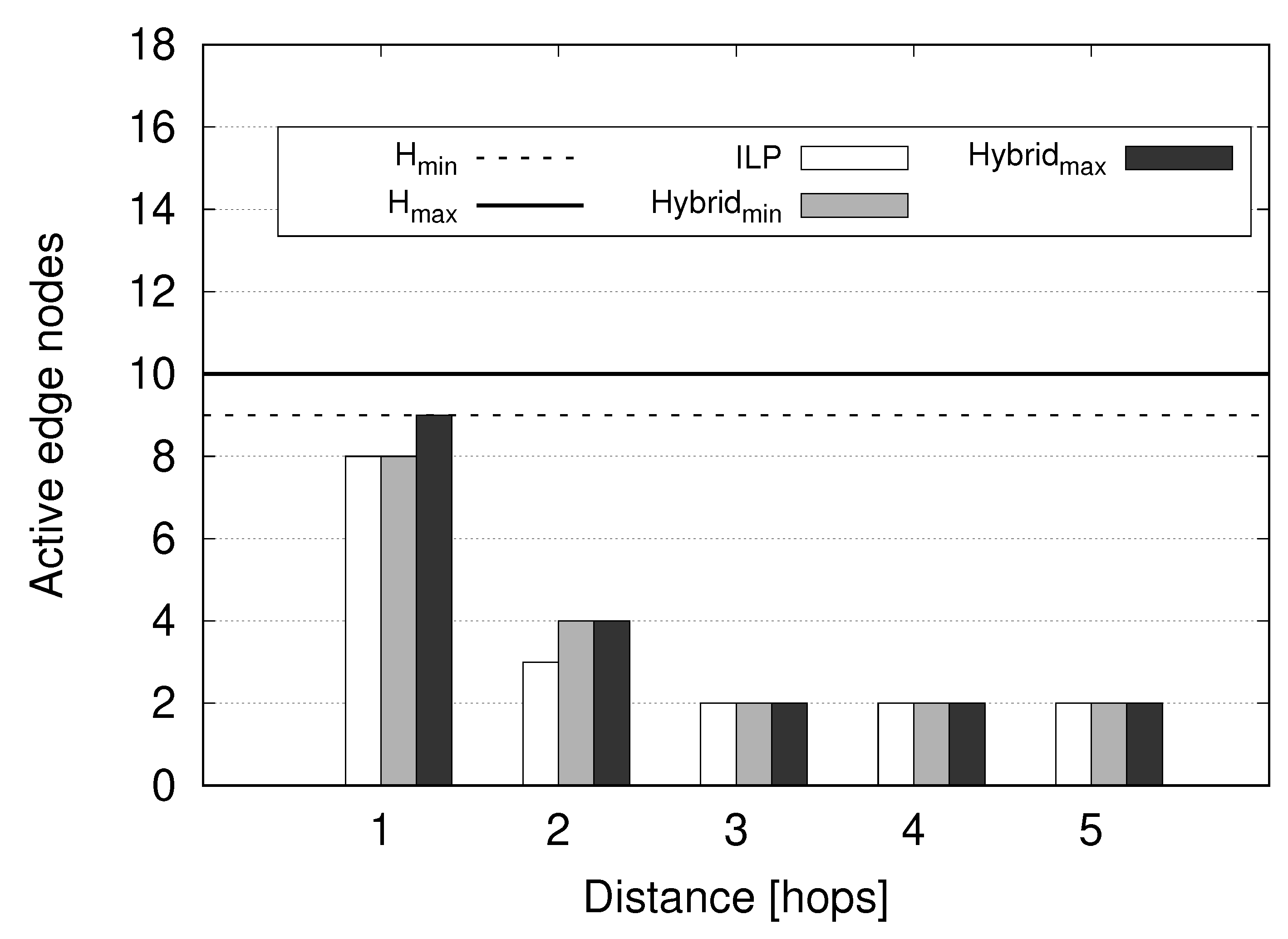
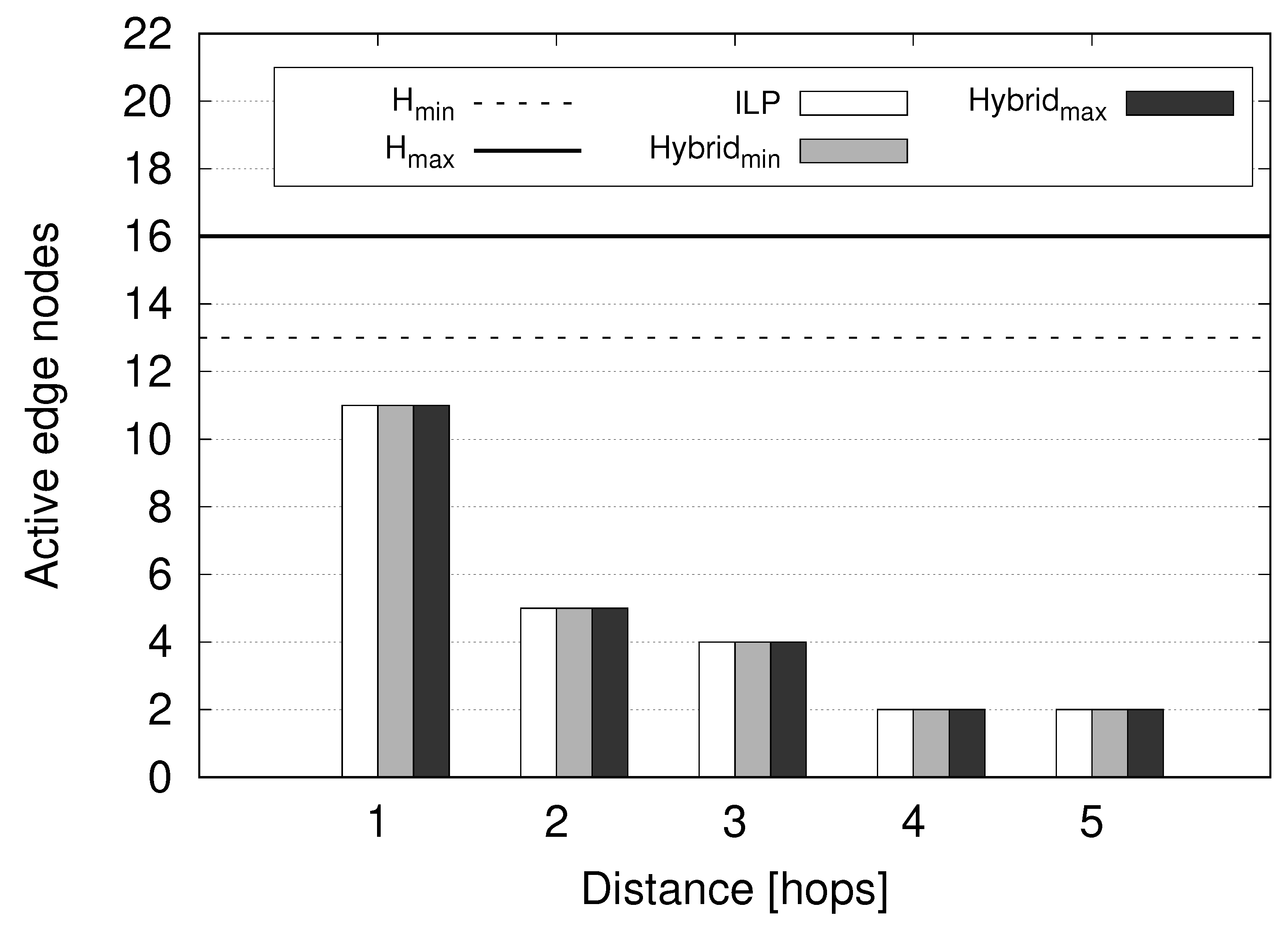
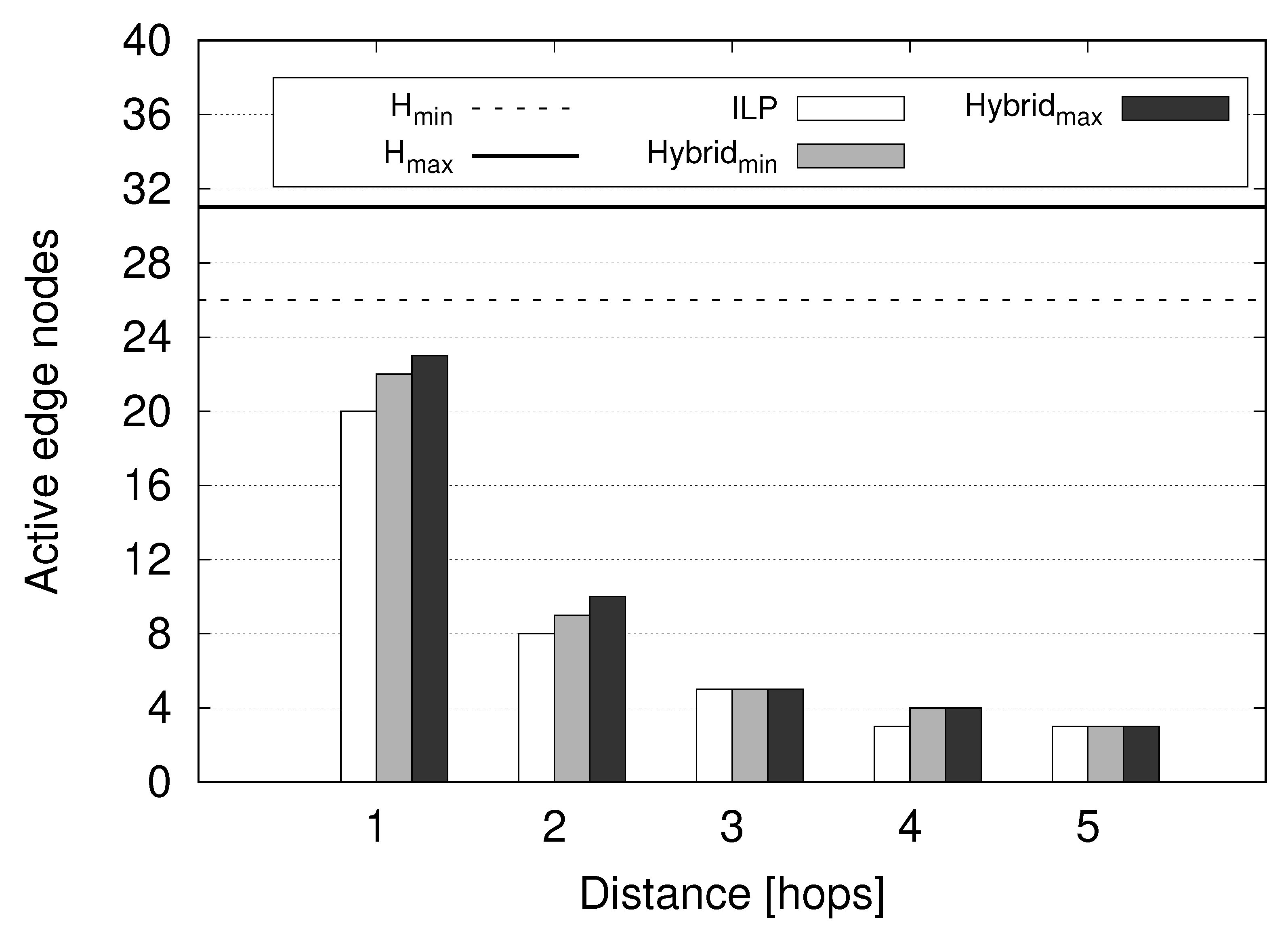
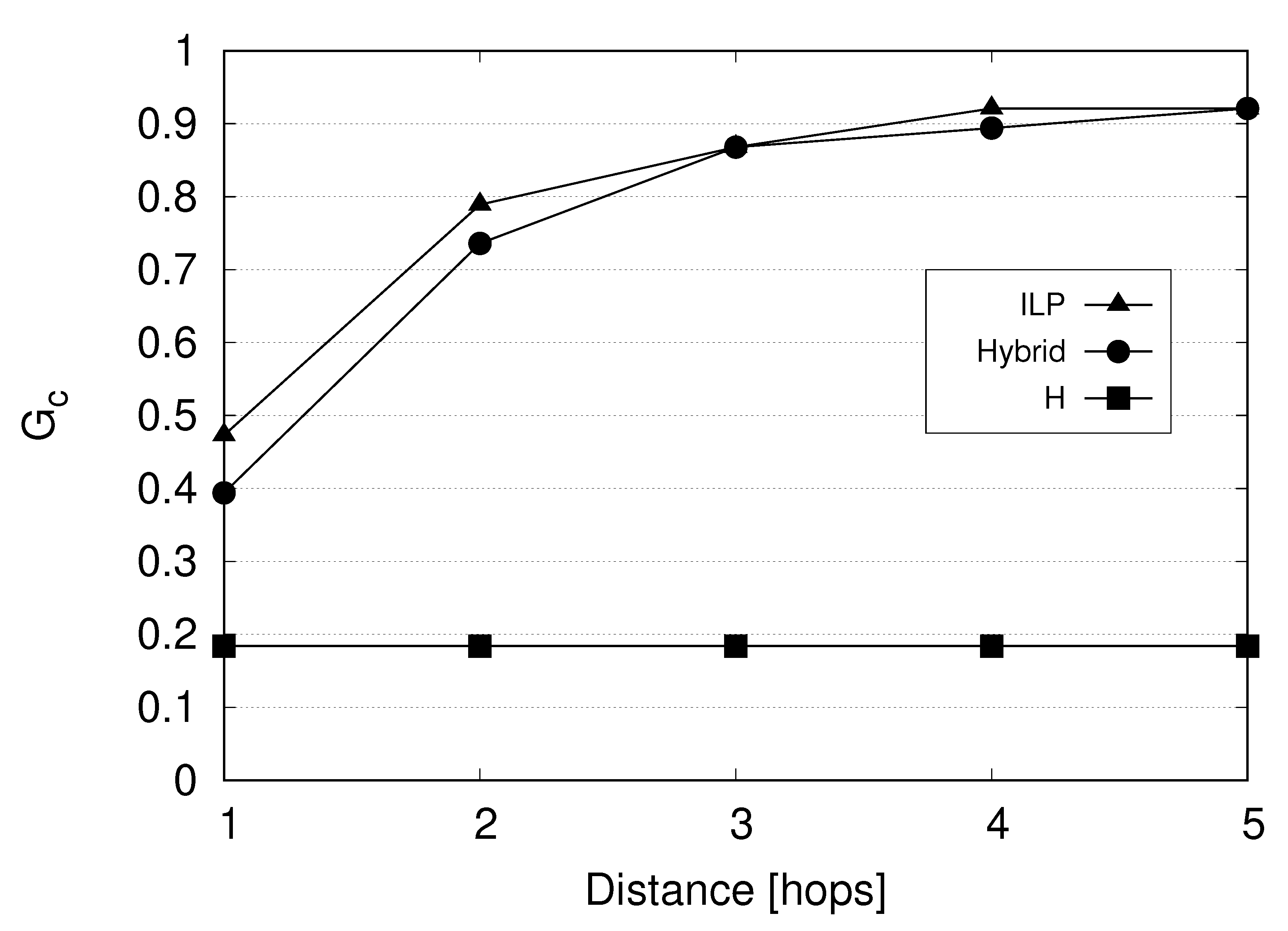
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Global Status Report on Road Safety 2018; Technical Report; WHO: Geneva, Switzerland, 2018. [Google Scholar]
- GSMA. Connecting Vehicles Today and in the 5G Era with C-V2X; White Paper; GSMA: London, UK, 2019. [Google Scholar]
- Mueck, M.; Karls, I. Networking Vehicles to Everything: Evolving Automotive Solutions; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- 5G-TRANSFORMER Initial System Design–Project Grant No. 761536. Deliverable D1.2, H2020; 5G-TRANSFORMER. Available online: http://5g-transformer.eu/index.php/deliverables/ (accessed on 1 October 2018).
- Checko, A.; Christiansen, H.L.; Yan, Y.; Scolari, L.; Kardaras, G.; Berger, M.S.; Dittmann, L. Cloud RAN for mobile networks A technology overview. IEEE Commun. Surv. Tutor. 2015, 17, 405–426. [Google Scholar] [CrossRef]
- Van Lingen, F.; Yannuzzi, M.; Jain, A.; Irons-Mclean, R.; Lluch, O.; Carrera, D.; Perez, J.L.; Gutierrez, A.; Montero, D.; Marti, J.; et al. The Unavoidable Convergence of NFV, 5G, and Fog: A Model-Driven Approach to Bridge Cloud and Edge. IEEE Commun. Mag. 2017, 55, 28–35. [Google Scholar] [CrossRef]
- Öhlén, P.; Skubic, B.; Rostami, A.; Fiorani, M.; Monti, P.; Ghebretensaé, Z.; Mårtensson, J.; Wang, K.; Wosinska, L. Data plane and control architectures for 5G transport networks. J. Light. Technol. 2016, 34, 1501–1508. [Google Scholar] [CrossRef]
- Nobre, J.C.; de Souza, A.M.; Rosário, D.; Both, C.; Villas, L.A.; Cerqueira, E.; Braun, T.; Gerla, M. Vehicular software-defined networking and fog computing: Integration and design principles. Ad Hoc Netw. 2019, 82, 172–181. [Google Scholar] [CrossRef]
- European Telecommunications Standards Institute. Cloud RAN and MEC: A Perfect Pairing; White Paper; ETSI: Sophia Antipolis, France, 2018. [Google Scholar]
- Khorsandi, B.M.; Tonini, F.; Raffaelli, C. Design methodologies and algorithms for survivable C-RAN. In Proceedings of the 2018 International Conference on Optical Network Design and Modeling (ONDM), Dublin, Ireland, 14–17 May 2018; pp. 106–111. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Pei, Q.; Maharjan, S.; Zhang, Y. Vehicular Edge Computing and Networking: A Survey. arXiv 2019, arXiv:1908.06849. [Google Scholar]
- 3GPP. 3rd Generation Partnership Project; Technical Specification Group Services and System Aspects; Summary of Rel-14 Work Items; White Paper; 3GPP: Sophia Antipolis, France, 2018. [Google Scholar]
- European Telecommunications Standards Institute. Intelligent Transport Systems (ITS); Access Layer Specification for Intelligent Transport Systems Operating in The 5 GHz Frequency Band; White Paper; ETSI: Sophia Antipolis, France, 2012. [Google Scholar]
- Ning, Z.; Wang, X.; Huang, J. Mobile Edge Computing-Enabled 5G Vehicular Networks: Toward the Integration of Communication and Computing. IEEE Veh. Technol. Mag. 2019, 14, 54–61. [Google Scholar] [CrossRef]
- Fiorani, M.; Skubic, B.; Mårtensson, J.; Valcarenghi, L.; Castoldi, P.; Wosinska, L.; Monti, P. On the design of 5G transport networks. Photonic Netw. Commun. 2015, 30, 403–415. [Google Scholar] [CrossRef]
- Larsen, L.M.P.; Checko, A.; Christiansen, H.L. A Survey of the Functional Splits Proposed for 5G Mobile Crosshaul Networks. IEEE Commun. Surv. Tutor. 2019, 21, 146–172. [Google Scholar] [CrossRef]
- Pfeiffer, T. Next generation mobile fronthaul and midhaul architectures. J. Opt. Commun. Netw. 2015, 7, B38–B45. [Google Scholar] [CrossRef]
- 3GPP. TR38.801—Radio Access Architecture and Interfaces; Technical Report; 3GPP: Sophia Antipolis, France, 2017. [Google Scholar]
- eCPRI V2.0 Specification. 2019. Available online: http://www.cpri.info/spec.html (accessed on 10 May 2019).
- Shah, S.A.A.; Ahmed, E.; Imran, M.; Zeadally, S. 5G for Vehicular Communications. IEEE Commun. Mag. 2018, 56, 111–117. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, W.; Li, Y.; Colman Meixner, C.; Tornatore, M.; Zhang, J. Edge Computing and Networking: A Survey on Infrastructures and Applications. IEEE Access 2019, 7, 101213–101230. [Google Scholar] [CrossRef]
- Leyva-Pupo, I.; Santoyo-González, A.; Cervelló-Pastor, C. A Framework for the Joint Placement of Edge Service Infrastructure and User Plane Functions for 5G. Sensors 2019, 19, 3975. [Google Scholar] [CrossRef] [PubMed]
- Santoyo-González, A.; Cervelló-Pastor, C. Latency-aware cost optimization of the service infrastructure placement in 5G networks. J. Netw. Comput. Appl. 2018, 114, 29–37. [Google Scholar] [CrossRef]
- Musumeci, F.; Bellanzon, C.; Carapellese, N.; Tornatore, M.; Pattavina, A.; Gosselin, S. Optimal BBU placement for 5G C-RAN deployment over WDM aggregation networks. J. Light. Technol. 2016, 34, 1963–1970. [Google Scholar] [CrossRef]
- Raffaelli, C.; Khorsandi, B.M.; Tonini, F. Distributed Location Algorithms for Flexible BBU Hotel Placement in C-RAN. In Proceedings of the 2018 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Khorsandi, B.M.; Tonini, F.; Raffaelli, C. Centralized vs. distributed algorithms for resilient 5G access networks. Photonic Netw. Commun. 2019, 37, 376–387. [Google Scholar] [CrossRef]
- Shehata, M.; Musumeci, F.; Tornatore, M. Resilient BBU placement in 5G C-RAN over optical aggregation networks. Photonic Netw. Commun. 2019, 37, 388–398. [Google Scholar] [CrossRef]
- Khan, A.A.; Abolhasan, M.; Ni, W. 5G next generation VANETs using SDN and fog computing framework. In Proceedings of the 2018 15th IEEE Annual Consumer Communications Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Xu, J.; Yuan, J.; Hsu, C.H. Edge server placement in mobile edge computing. J. Parallel Distrib. Comput. 2019, 127, 160–168. [Google Scholar] [CrossRef]
- Tinini, R.I.; Batista, D.M.; Figueiredo, G.B.; Tornatore, M.; Mukherjee, B. Low-latency and energy-efficient BBU placement and VPON formation in virtualized cloud-fog RAN. IEEE/OSA J. Opt. Commun. Netw. 2019, 11, B37–B48. [Google Scholar] [CrossRef]
- Fiorani, M.; Rostami, A.; Wosinska, L.; Monti, P. Abstraction models for optical 5G transport networks. IEEE/OSA J. Opt. Commun. Netw. 2016, 8, 656–665. [Google Scholar] [CrossRef]
- European Telecommunications Standards Institute. MEC in 5G Networks; White Paper; ETSI: Sophia Antipolis, France, 2018. [Google Scholar]
- IBM. IBM ILOG CPLEX Optimization Studio V12.6.3. 2018. Available online: https://www.ibm.com/support/pages/downloading-ibm-ilog-cplex-optimization-studio-v1263 (accessed on 1 October 2018).
| Parameter | Definition |
|---|---|
| N | set of edge nodes in the network, . |
| number of sources (RRUs) directly connected to . | |
| C | matrix. if node i is directly connected to node j, 0 otherwise. |
| binary variable, equal to 1 if edge node acts as primary for RRUs at node (cell site) ; 0 otherwise. | |
| binary variable, equal to 1 if edge node acts as backup for RRUs at node (cell site) ; 0 otherwise. | |
| binary variable equal to 1 if edge node is active, 0 otherwise. | |
| binary variable, equal to 1 if the path to connect RRUs at node and primary edge node is using physical link ; 0 otherwise. | |
| binary variable, equal to 1 if the path to connect RRUs at node and backup edge node is using physical link ; 0 otherwise. | |
| max. available wavelengths in each link. | |
| max. allowed distance between RRUs and edge nodes. | |
| tuning parameters for the objective function. | |
| a large number (e.g., ). |
| Dist. | Hybrid | ILP | ||||
|---|---|---|---|---|---|---|
| Active | Max | Total | Active | Max | Total | |
| 1 | 45 | 10 | 530 | 48 | 10 | 560 |
| 2 | 51 | 40 | 950 | 50 | 40 | 1040 |
| 3 | 49 | 70 | 1370 | 51 | 60 | 1350 |
| 4 | 52 | 70 | 1530 | 48 | 80 | 1830 |
| 5 | 51 | 80 | 1790 | 52 | 80 | 1780 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tonini, F.; Khorsandi, B.M.; Amato, E.; Raffaelli, C. Scalable Edge Computing Deployment for Reliable Service Provisioning in Vehicular Networks. J. Sens. Actuator Netw. 2019, 8, 51. https://doi.org/10.3390/jsan8040051
Tonini F, Khorsandi BM, Amato E, Raffaelli C. Scalable Edge Computing Deployment for Reliable Service Provisioning in Vehicular Networks. Journal of Sensor and Actuator Networks. 2019; 8(4):51. https://doi.org/10.3390/jsan8040051
Chicago/Turabian StyleTonini, Federico, Bahare M. Khorsandi, Elisabetta Amato, and Carla Raffaelli. 2019. "Scalable Edge Computing Deployment for Reliable Service Provisioning in Vehicular Networks" Journal of Sensor and Actuator Networks 8, no. 4: 51. https://doi.org/10.3390/jsan8040051
APA StyleTonini, F., Khorsandi, B. M., Amato, E., & Raffaelli, C. (2019). Scalable Edge Computing Deployment for Reliable Service Provisioning in Vehicular Networks. Journal of Sensor and Actuator Networks, 8(4), 51. https://doi.org/10.3390/jsan8040051






