Hybrid TOA/RSS Range-Based Localization with Self-Calibration in Asynchronous Wireless Networks
Abstract
1. Introduction
- a first calibration phase carried out by the different nodes in the network to estimate all the unknown RSS and TOA model parameters, including the synchronization offsets;
- a second localization step that leverages the combination of hybrid TOA/RSS ranging and iterative least squares (ILS) approach to estimate the unknown target position.
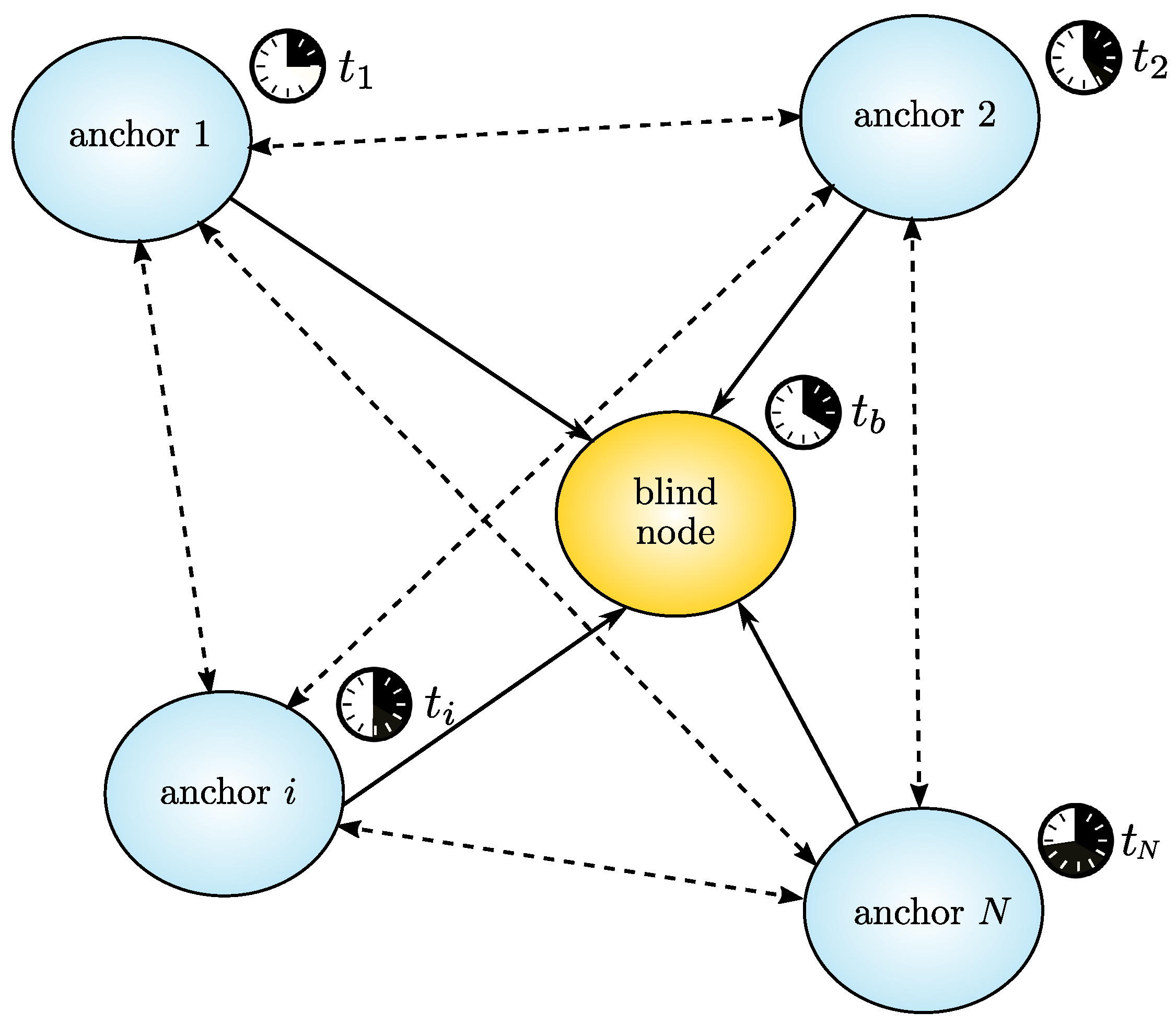
2. Hybrid TOA/RSS Localization: Formulation and Resolution Approaches
2.1. RSS Model
2.2. TOA Model
2.3. Joint Maximum Likelihood Position Estimation
2.4. Resolution Approaches
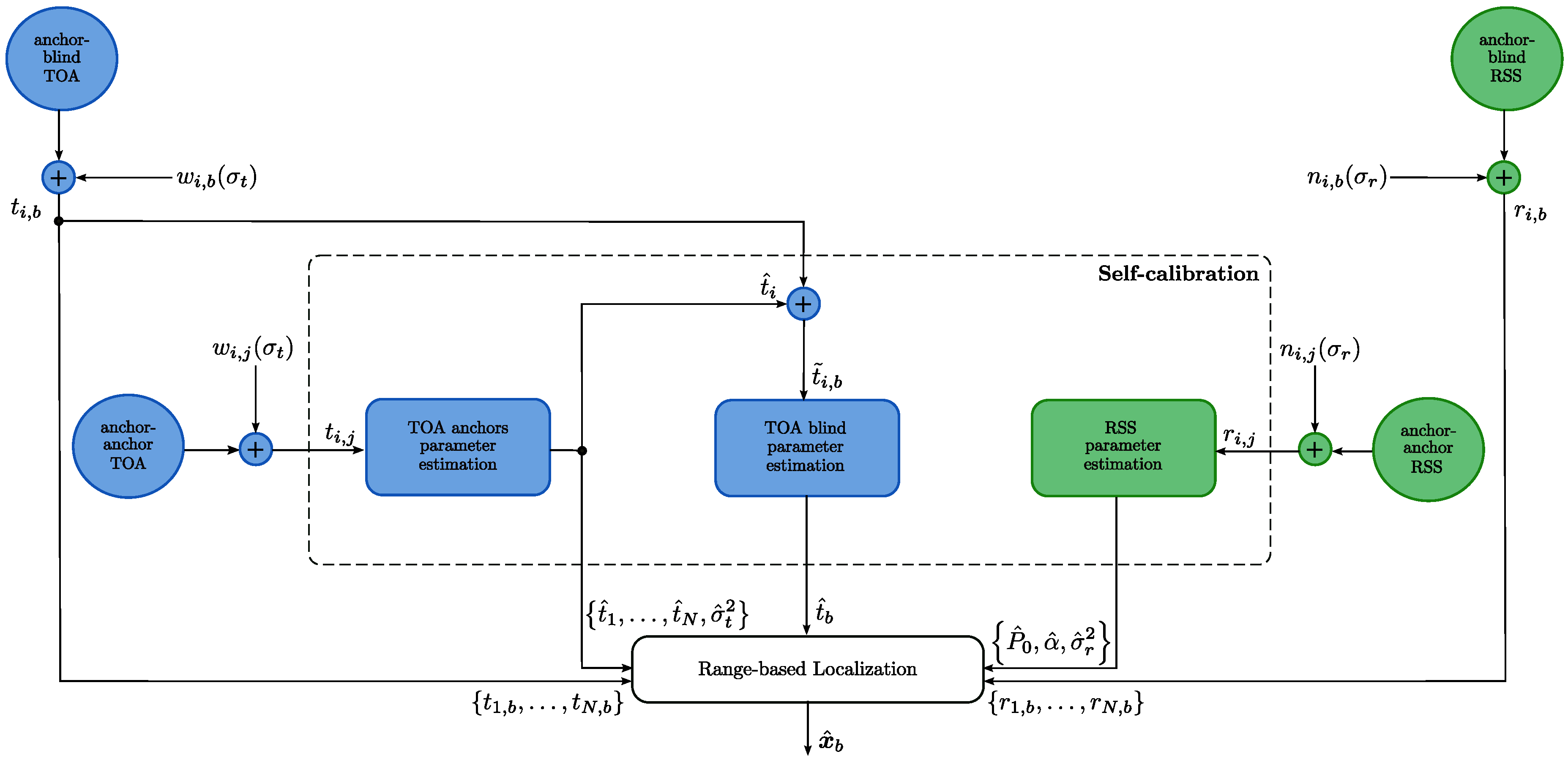
3. Proposed Localization Algorithm with Self-Calibration
3.1. TOA/RSS Parameters Estimation Using Self-Calibration
3.2. Hybrid TOA/RSS Range-Based Localization
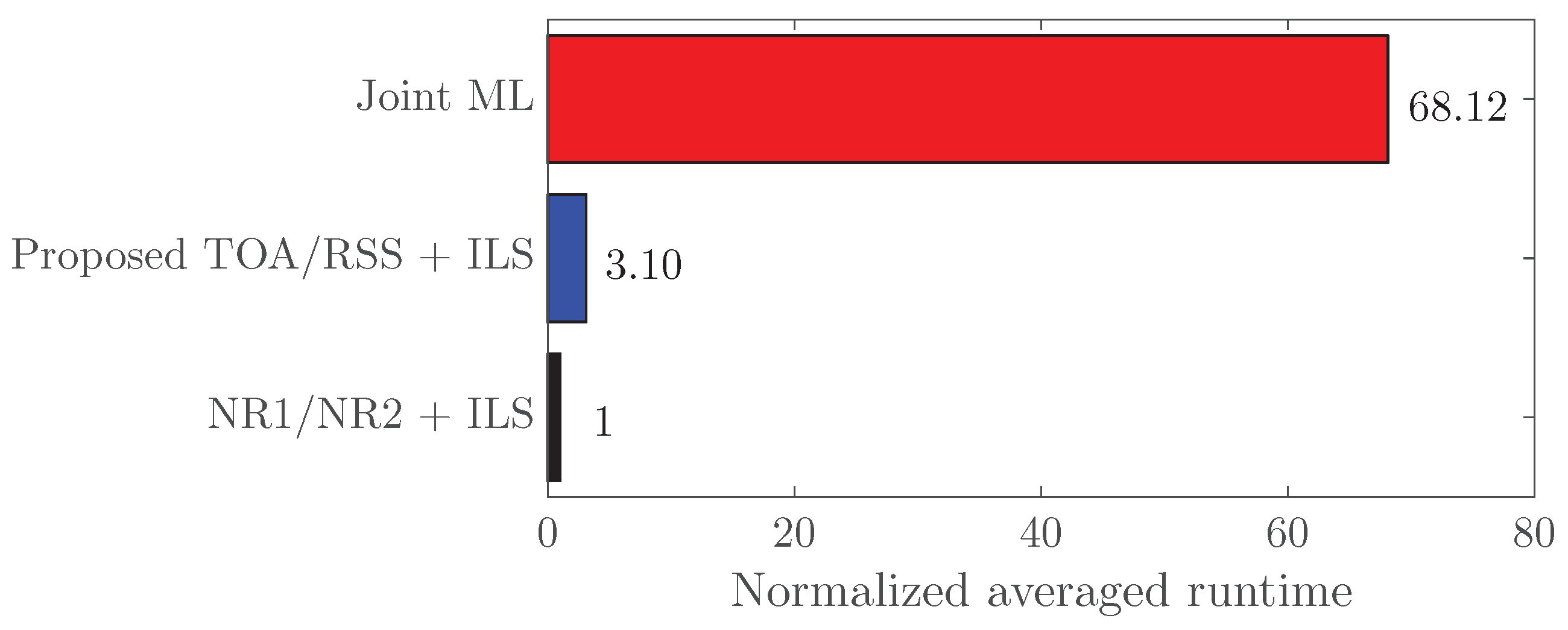
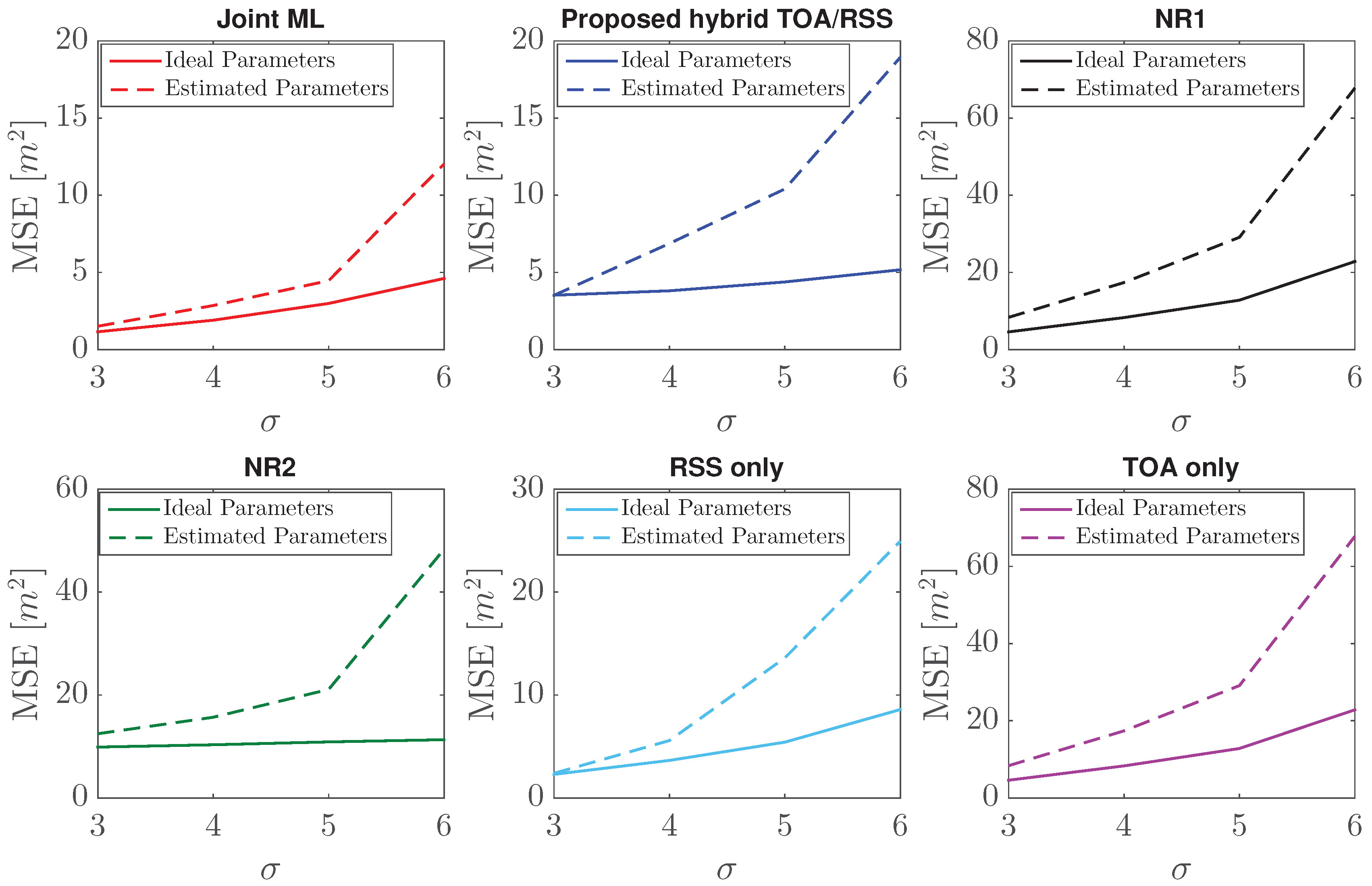
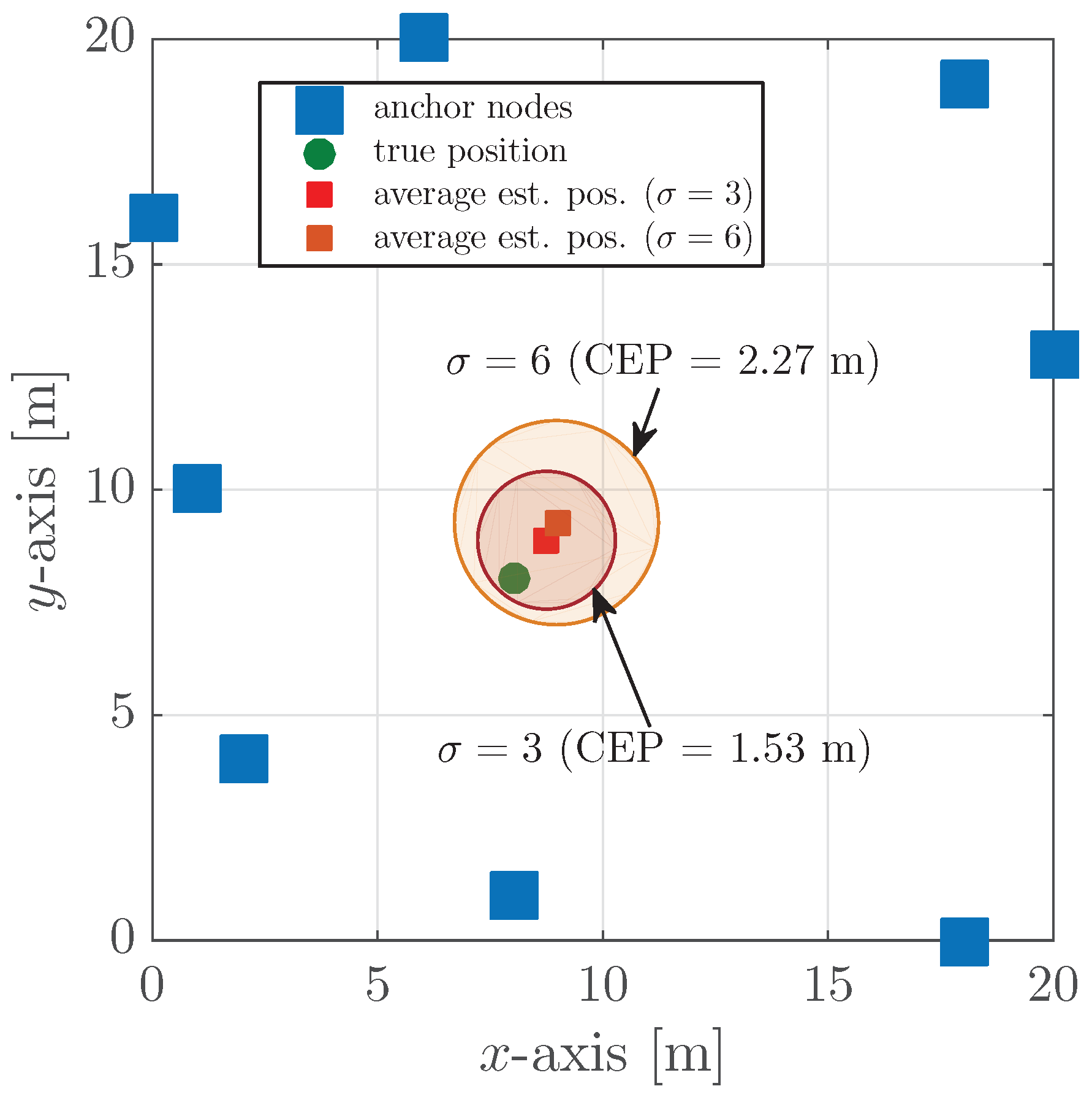
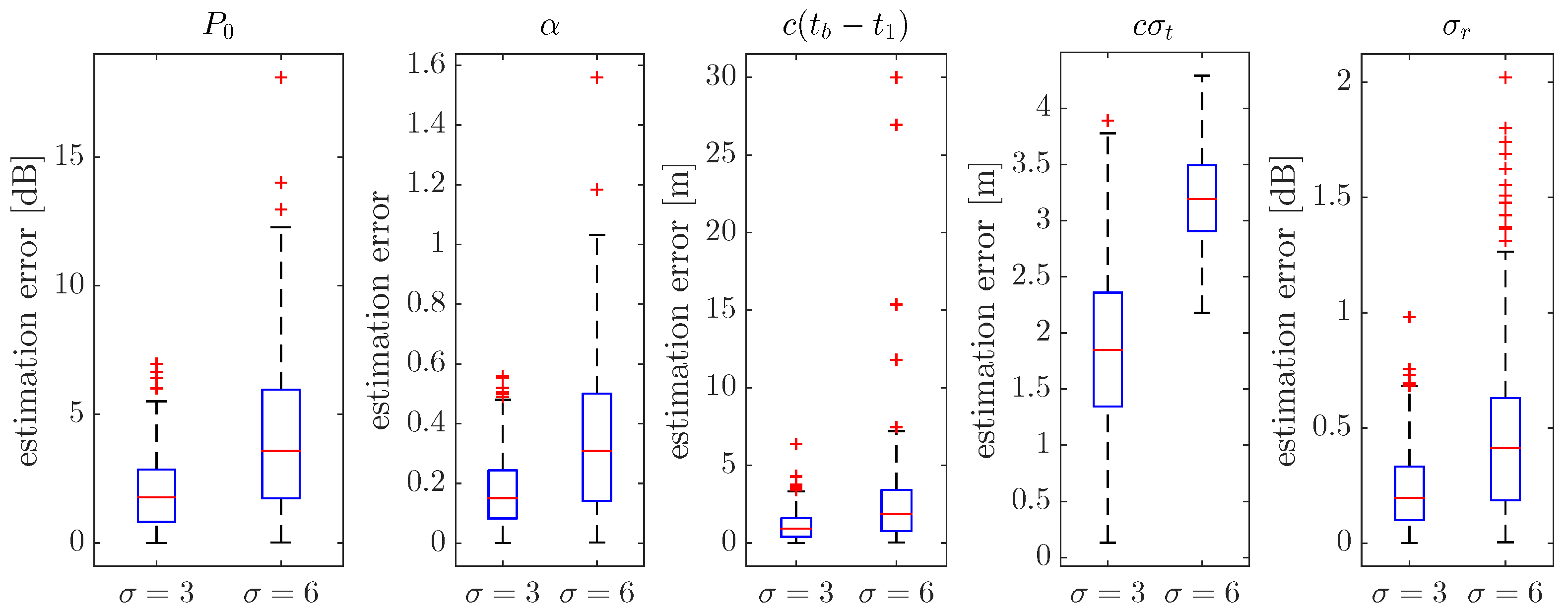
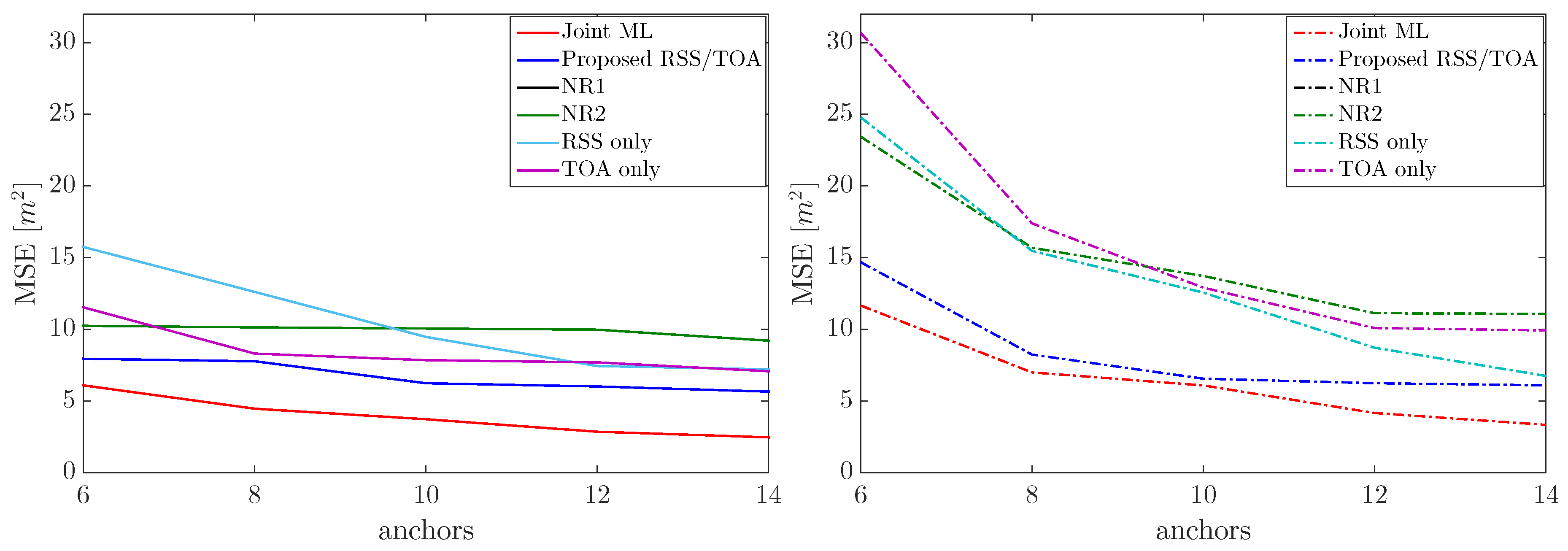
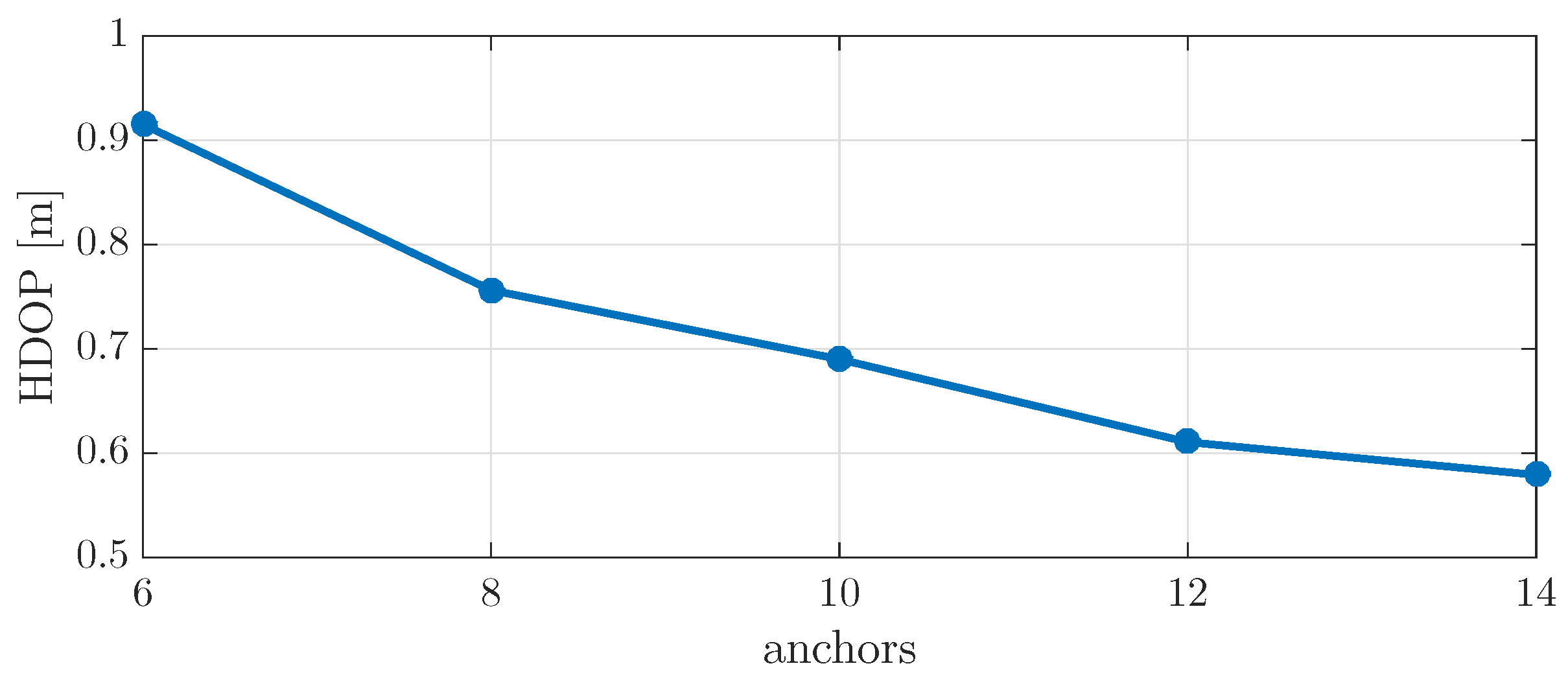
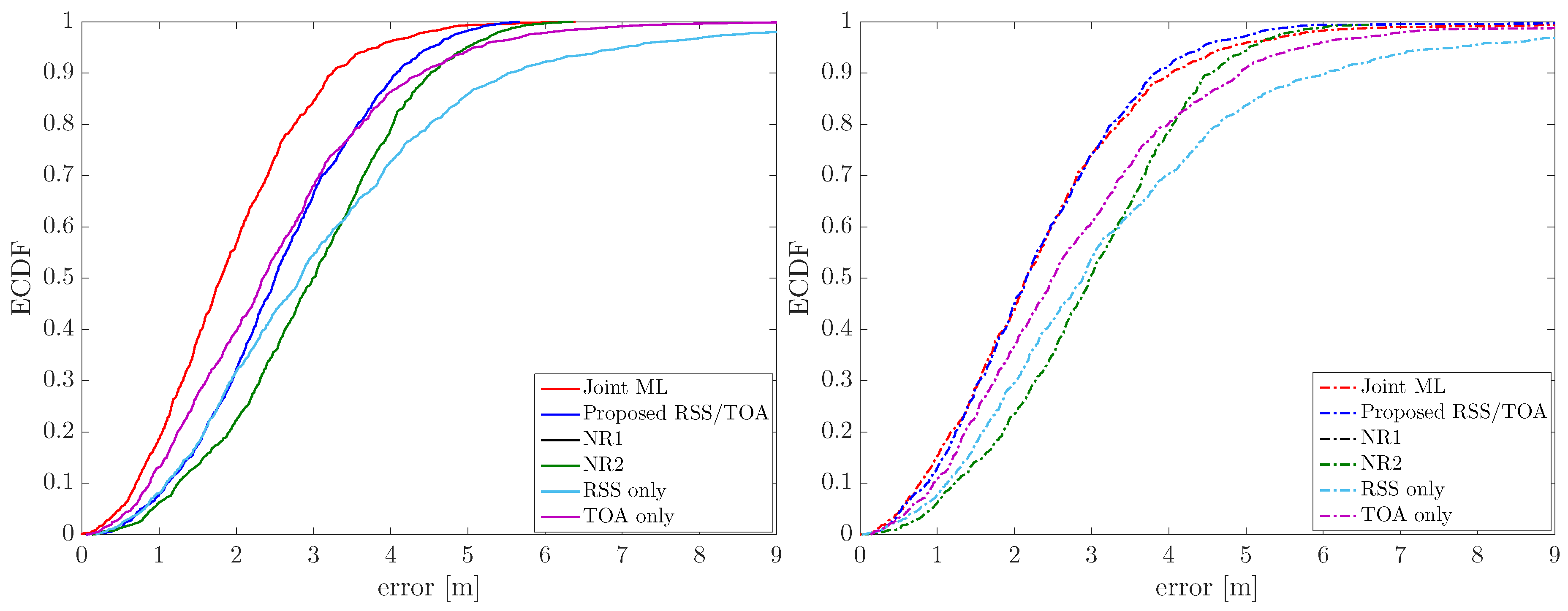
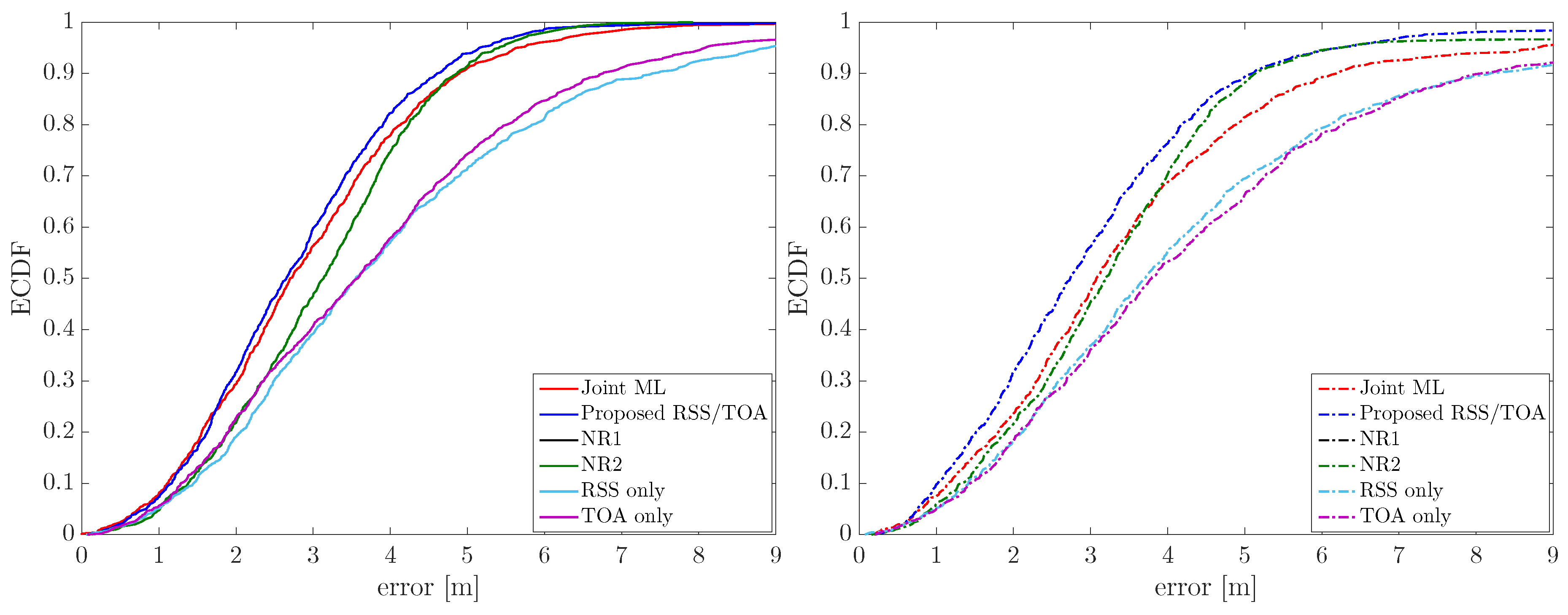
4. Performance Assessment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gezici, S. A survey on wireless position estimation. Wirel. Pers. Commun. 2008, 44, 263–282. [Google Scholar] [CrossRef]
- Win, M.Z.; Conti, A.; Mazuelas, S.; Shen, Y.; Gifford, W.M.; Dardari, D.; Chiani, M. Network localization and navigation via cooperation. IEEE Commun. Mag. 2011, 49, 56–62. [Google Scholar] [CrossRef]
- Coluccia, A.; Fascista, A. A Review of Advanced Localization Techniques for Crowdsensing Wireless Sensor Networks. Sensors 2019, 19, 988. [Google Scholar] [CrossRef] [PubMed]
- Sayed, A.H.; Tarighat, A.; Khajehnouri, N. Network-based wireless location: Challenges faced in developing techniques for accurate wireless location information. IEEE Signal Process. Mag. 2005, 22, 24–40. [Google Scholar] [CrossRef]
- Dai, W.; Shen, Y.; Win, M.Z. Energy-efficient network navigation algorithms. IEEE J. Sel. Areas Commun. 2015, 33, 1418–1430. [Google Scholar] [CrossRef]
- Coluccia, A.; Ricciato, F.; Ricci, G. Positioning based on signals of opportunity. IEEE Commun. Lett. 2014, 18, 356–359. [Google Scholar] [CrossRef]
- Waadt, A.E.; Kocks, C.; Wang, S.; Bruck, G.H.; Jung, P. Maximum likelihood localization estimation based on received signal strength. In Proceedings of the 2010 3rd International Symposium on Applied Sciences in Biomedical and Communication Technologies (ISABEL), Rome, Italy, 7–10 November 2010; pp. 1–5. [Google Scholar]
- Coluccia, A.; Ricciato, F. RSS-based localization via Bayesian ranging and Iterative Least Squares positioning. IEEE Commun. Lett. 2014, 18, 873–876. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. Distributed RSS-Based Localization in Wireless Sensor Networks Based on Second-Order Cone Programming. Sensors 2014, 14, 18410–18432. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. RSS-based Localization in Wireless Sensor Networks Using Convex Relaxation: Noncooperative and Cooperative Schemes. IEEE Trans. Veh. Technol. 2015, 64, 2037–2050. [Google Scholar] [CrossRef]
- Patwari, N.; Hero, A.O., III; Perkins, M.; Correal, N.S.; O’Dea, R.J. Relative Location Estimation in Wireless Sensor Networks. IEEE Trans. Signal Proc. 2003, 51, 2137–2148. [Google Scholar] [CrossRef]
- Mao, G.; Fidan, B.; Anderson, B.D.O. Wireless Sensor Network Localization Techniques. Comput. Netw. 2007, 51, 2529–2553. [Google Scholar] [CrossRef]
- Wang, G.; Yang, K. A New Approach to Sensor Node Localization Using RSS Measurements in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2011, 10, 1389–1395. [Google Scholar] [CrossRef]
- Coluccia, A.; Ricciato, F. On ML estimation for automatic RSS-based indoor localization. In Proceedings of the IEEE 5th International Symposium on Wireless Pervasive Computing, Modena, Italy, 5–7 May 2010. [Google Scholar]
- Salari, S.; Shahbazpanahi, S.; Ozdemir, K. Mobility-Aided Wireless Sensor Network Localization via Semidefinite Programming. IEEE Trans. Wirel. Commun. 2013, 12, 5966–5978. [Google Scholar] [CrossRef]
- Weiss, A.J. On the Accuracy of a Cellular Location System Based on RSS Measurements. IEEE Trans. Veh. Technol. 2003, 52, 1508–1518. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H.; Li, Y.; Ansari, N. NLOS Error Mitigation for TOA-Based Localization via Convex Relaxation. IEEE Trans. Wirel. Commun. 2014, 13, 4119–4131. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, S.; Wang, G.; Li, Y. Robust NLOS Error Mitigation Method for TOA-Based Localization via Second-Order Cone Relaxation. IEEE Commun. Lett. 2015, 19, 2210–2213. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M. Exact Robust Solution to TW-ToA-Based Target Localization Problem with Clock Imperfections. IEEE Signal Process. Lett. 2018, 25, 531–535. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. A Robust Bisection-Based Estimator for TOA-Based Target Localization in NLOS Environments. IEEE Commun. Lett. 2017, 21, 2488–2491. [Google Scholar] [CrossRef]
- Patwari, N.; Ash, J.; Kyperountas, S.; Hero, A.O., III; Moses, R.; Correal, N. Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal Proc. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Rong, P.; Sichitiu, M.L. Angle of Arrival Localization for Wireless Sensor Networks. In Proceedings of the 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks, Reston, VA, USA, 28 September 2006; pp. 374–382. [Google Scholar]
- Fascista, A.; Ciccarese, G.; Coluccia, A.; Ricci, G. A Localization Algorithm Based on V2I Communications and AOA Estimation. IEEE Signal Process. Lett. 2017, 24, 136–140. [Google Scholar] [CrossRef]
- Fascista, A.; Ciccarese, G.; Coluccia, A.; Ricci, G. Angle-of-Arrival based Cooperative Positioning for Smart Vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2880–2892. [Google Scholar] [CrossRef]
- Fascista, A.; Ciccarese, G.; Coluccia, A.; Ricci, G. A change-detection approach to mobile node localization in bounded domains. In Proceedings of the 52nd IEEE Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 21–23 March 2018; pp. 1–6. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. Distributed Algorithm for Target Localization in Wireless Sensor Networks Using RSS and AoA Measurements. Pervasive Mob. Comput. 2017, 37, 63–77. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. A Closed-form Solution for RSS/AoA Target Localization by Spherical Coordinates Conversion. IEEE Wirel. Commun. Lett. 2016, 5, 680–683. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Gomes, J.P. Target Tracking with Sensor Navigation Using Coupled RSS and AoA Measurements. Sensors 2017, 17, 2690. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. 3-D Target Localization in Wireless Sensor Networks Using RSS and AoA Measurements. IEEE Trans. Veh. Technol. 2017, 66, 3197–3210. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Tuba, M.; Bacanin, N. Bayesian Methodology for Target Tracking Using RSS and AoA Measurements. Phys. Commun. 2017, 25, 158–166. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Tuba, M. A Linear Estimator for Network Localization Using Integrated RSS and AOA Measurements. IEEE Signal Process. Lett. 2019, 26, 405–409. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Bernardo, L. On Target Localization Using Combined RSS and AoA Measurements. Sensors 2018, 18, 1266. [Google Scholar] [CrossRef]
- Catovic, A.; Sahinoglu, Z. The Cramer-Rao Bounds of Hybrid TOA/RSS and TDOA/RSS Location Estimation Schemes. IEEE Commun. Lett. 2004, 8, 626–628. [Google Scholar] [CrossRef]
- Tiwari, S.; Wang, D.; Fattouche, M.; Ghannouchi, F. A Hybrid TOA/RSS Method for 3D Positioning in an Indoor Environment. ISRN Signal Proc. 2012, 2012. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Tuba, M.; Correia, V.M.F. Target Localization in NLOS Environments Using RSS and TOA Measurements. IEEE Wirel. Commun. Lett. 2018, 7, 1062–1065. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M. A Robust NLOS Bias Mitigation Technique for RSS-TOA-Based Target Localization. IEEE Signal Process. Lett. 2019, 26, 64–68. [Google Scholar] [CrossRef]
- McGuire, M.; Plataniotis, K.N.; Venetsanopoulos, A.N. Data Fusion of Power and Time Measurements for Mobile Terminal Location. IEEE Trans. Mob. Comput. 2005, 4, 142–153. [Google Scholar] [CrossRef]
- Prieto, J.; Mazuelas, S.; Bahillo, A.; Fernández, P.; Lorenzo, R.M.; Abril, E.J. Adaptive Data Fusion for Wireless Localization in Harsh Environments. IEEE Trans. Signal Process. 2012, 60, 1585–1596. [Google Scholar] [CrossRef]
- Sahinoglu, Z.; Catovic, A. A Hybrid Location Estimation Scheme (H-LES) for Partially Synchronized Wireless Sensor Networks. In Proceedings of the 2004 IEEE International Conference on Communications (ICC), Paris, France, 20–24 June 2004. [Google Scholar]
- Bahillo, A.; Mazuelas, S.; Prieto, J.; Fernandez, P.; Lorenzo, R.M.; Abril, E.J. Hybrid RSS-RTT Localization Scheme for Wireless Networks. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Zurich, Switzerland, 15–17 September 2010. [Google Scholar]
- Laaraiedh, M.; Avrillon, S.; Uguen, B. Hybrid Data Fusion Techniques for Localization in UWB Networks. In Proceedings of the 2009 6th Workshop on Positioning, Navigation and Communication (WPNC), Hannover, Germany, 19 March 2009. [Google Scholar]
- Laaraiedh, M.; Yu, L.; Avrillon, S.; Uguen, B. Comparison of Hybrid Localization Schemes using RSSI, TOA, and TDOA. In Proceedings of the 17th European Wireless 2011—Sustainable Wireless Technologies, Vienna, Austria, 27–29 April 2011. [Google Scholar]
- Coluccia, A. Reduced-Bias ML-Based Estimators with Low Complexity for Self-Calibrating RSS Ranging. IEEE Trans. Wirel. Commun. 2013, 12, 1220–1230. [Google Scholar] [CrossRef]
- Coluccia, A.; Fascista, A. On the Hybrid TOA/RSS Range Estimation in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2018, 17, 361–371. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Zanca, G.; Zorzi, F.; Zanella, A.; Zorzi, M. Experimental comparison of RSSI-based localization algorithms for indoor wireless sensor networks. In Proceedings of the ACM Workshop on Real-World Wireless Sensor Networks, Glasgow, UK, 1 April 2008. [Google Scholar]
- Lim, H.; Kung, L.C.; Hou, J.C.; Luo, H. Zero-Configuration, Robust Indoor Localization: Theory and Experimentation. In Proceedings of the IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006. [Google Scholar]
- Coluccia, A.; Ricciato, F. A Software-Defined Radio tool for experimenting with RSS measurements in IEEE 802.15.4: Implementation and applications. In Proceedings of the 2012 21st International Conference on Computer Communications and Networks, Munich, Germany, 30 July–2 August 2013. [Google Scholar]
- Bernhardt, R.C. Macroscopic Diversity in Frequency Reuse Radio Systems. IEEE J. Sel. Areas Commun. 1987, 5, 862–870. [Google Scholar] [CrossRef]
- Babich, F.; Lombardi, G. Statistical Analysis and Characterization of the Indoor Propagation Channel. IEEE Trans. Commun. 2000, 48, 455–464. [Google Scholar] [CrossRef]
- Andersen, J.B.; Rappaport, T.S.; Yoshida, S. Propagation Measurements and Models for Wireless Communications Channels. IEEE Commun. Mag. 1995, 33, 42–49. [Google Scholar] [CrossRef]
- Macii, D.; Colombo, A.; Pivato, P.; Fontanelli, D. A Data Fusion Technique for Wireless Ranging Performance Improvement. IEEE Trans. Instrum. Meas. 2013, 62, 27–37. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, L.; Wang, Y.; Hu, L. Measurement-based indoor NLoS ToA/RSS range error modelling. Electron. Lett. 2016, 52, 165–167. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Tsui, J.B.-Y. Fundamentals of Global Positioning System Receivers: A Software Approach; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- He, Y.; Martin, R.; Bilgic, A.M. Approximate iterative Least Squares algorithms for GPS positioning. In Proceedings of the 10th IEEE International Symposium on Signal Processing and Information Technology, Luxor, Egypt, 15–18 December 2010; pp. 231–236. [Google Scholar]
- Yan, J.; Tiberius, C.C.J.M.; Teunissen, P.J.G.; Bellusci, G.; Janssen, G.J.M. A Framework for Low Complexity Least-Squares Localization with High Accuracy. IEEE Trans. Signal Process. 2010, 58, 4836–4847. [Google Scholar]
- Coluccia, A.; Ricciato, F. Maximum Likelihood trajectory estimation of a mobile node from RSS measurements. In Proceedings of the 9th Annual Conference on Wireless on-Demand Network Systems and Services (WONS), Courmayeur, Italy, 9–11 January 2012; pp. 151–158. [Google Scholar]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W Function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coluccia, A.; Fascista, A. Hybrid TOA/RSS Range-Based Localization with Self-Calibration in Asynchronous Wireless Networks. J. Sens. Actuator Netw. 2019, 8, 31. https://doi.org/10.3390/jsan8020031
Coluccia A, Fascista A. Hybrid TOA/RSS Range-Based Localization with Self-Calibration in Asynchronous Wireless Networks. Journal of Sensor and Actuator Networks. 2019; 8(2):31. https://doi.org/10.3390/jsan8020031
Chicago/Turabian StyleColuccia, Angelo, and Alessio Fascista. 2019. "Hybrid TOA/RSS Range-Based Localization with Self-Calibration in Asynchronous Wireless Networks" Journal of Sensor and Actuator Networks 8, no. 2: 31. https://doi.org/10.3390/jsan8020031
APA StyleColuccia, A., & Fascista, A. (2019). Hybrid TOA/RSS Range-Based Localization with Self-Calibration in Asynchronous Wireless Networks. Journal of Sensor and Actuator Networks, 8(2), 31. https://doi.org/10.3390/jsan8020031





