Experimental Study of Lidar System for a Static Object in Adverse Weather Conditions

Abstract

Thanks to light detection and ranging (LiDAR), unmanned ground vehicles (UGVs) are able to detect different objects in their environment and measure the distance between them. This device gives the ability to see its surroundings in real time. However, the accuracy of LiDAR can be reduced, especially in rainy weather, fog, urban smog and the like. These factors can have disastrous consequences as they increase the errors in the vehicle’s control computer. The aim of this research was to determine the most appropriate LiDAR frequency for static objects, depending on the distance to them and the scanning frequency in different weather conditions; therefore, it is based on empiric data obtained by using the RoboPeak A1M8 LiDAR. The results obtained in rainy conditions are compared with the same ones in clear weather, using stochastic methods. A direct influence of both the frequencies used and the rain on the accuracy of the LiDAR measurements was found. The range measurement errors increase in rainy weather; as the scanning frequency increases, the results become more accurate but capture a smaller number of object points. The higher frequencies lead to about five times less error at the farthest distances compared to the lower frequencies.

1. Introduction

UGVs are one of the most rapidly developing areas of transport, where the latest technologies and achievements in sensors, artificial intelligence and information technologies are concentrated [1,2,3]. It is expected that the latest technologies in this field and the development of new driving functions will have a positive impact on the economic, natural and social environment [4,5,6,7], according to the work of large scientific teams, experienced engineers as well as students and even junior researchers.

The systems of UGVs need to detect various objects in the environment and at the same time evaluate distances, usually using a laser range finder (hereafter referred to as LiDAR) [8,9]. This device is considered one of the most important because it gives the ability to see its surroundings in real time.

The accuracy of modern LiDAR distance measurements is relatively low. Ongoing work in this area will correct this drawback and, according to the authors of [10,11,12], this improvement in LiDAR will allow it to be used in even more applications.

There are six factors that generally affect the return signal and adversely affect the results, and they can be divided into the following groups: false detection of various objects (cars, pedestrians or other infrastructure), noise in the optical unit or detector amplifier, electromagnetic interference, too high signal level in the receiver circuit, ground relief reflections and false detections in changing weather conditions [13,14]. Additional factors (such as driving parameters and the type of surface being scanned) also affect the accuracy of LiDAR readings.

To date, there has been little research evaluating the accuracy of LiDAR performance in autonomous vehicles. Most of it focuses on LiDAR applications for unmanned aerial vehicles (UAVs). However, some conclusions on LiDAR accuracy can be drawn from the analysis of such studies.

For example, refs. [15,16,17,18] state that LiDAR research data cannot replace traditional distance measurements when centimeter or even millimeter accuracy is required. Similarly, ref. [19] found that the accuracy of an LiDAR mounted on a UAV reached 10 cm or more when the LiDAR was 50 m away from the object.

Various LiDAR result processing algorithms [20], such as iterative closed point (ICP) algorithms, generalized ICP algorithms and normal distributions transform (NDT) algorithms, have been proposed to improve measurement accuracy [13,21,22,23]. However, the use of such algorithms requires a large number of points, which are not always available.

One of the few studies on the accuracy of LiDAR in cars is presented in [24], where the Pro-SiVIC LiDAR was investigated by simulating normal weather conditions and using a laser beam with the following parameters: wavelength λ = 905 nm, pulse energy 1.6 μJ, pulse duration 16 ns, and divergence 0.07°. The results obtained show how the signal-to-noise ratio (SNR) changes as a function of the distance between the sensor and the car. It can be seen that the SNR values are higher when the car body reflects the signal. This is due to the nature of the metal material, which can reflect more than plastic or semi-transparent objects such as glass. Signal intensity decreases with distance according to Lambert’s law of light absorption. The LiDAR receiver can also detect the return signal from objects with strong reflective properties (e.g., metal surfaces) at long range (190 m). The detection range can be extended by increasing the laser power or reducing the beam divergence.

In summary, reflective objects with flat metal surfaces such as trucks, cars and road signs can be detected at a distance of more than 100 m under normal weather conditions: For motorcycles and pedestrians, the maximum detection distance is lower because there are fewer or no metal surfaces. The signal decays exponentially as the distance between the LiDAR and the vehicle increases. With a dense distribution of water particles in the atmosphere (rain, fog), the signal amplitude decreases rapidly, and the range of detectable distance decreases many times. As a result, it can be difficult to maintain a safe distance between vehicles in poor visibility [25], and it would be difficult to control the situation if, for example, an oncoming vehicle suddenly brakes [10,15,19,21,22,24].

The application of LiDAR in adverse weather conditions is discussed in [26,27,28,29]. Issues such as the availability of suitable data, processing and noise reduction in raw point clouds, reliable perception algorithms and sensor fusion to mitigate the shortcomings caused by adverse weather conditions are discussed in [26]. The latter study discusses as many as 80 sources related to the application of LiDAR in adverse weather conditions. In addition, the most relevant insights are presented, and promising research directions are indicated. A similar review of 106 references was carried out in [27], which pays significant attention to the processing of the obtained LiDAR results (pixels) in complex weather conditions. The performance of LiDAR in artificially created fog is studied in [28], where the results of a video camera and LiDAR are compared. It is shown that in severe artificial fog, in some cases, an insufficient number of points are recorded even at a distance of 4.4 m. Unfortunately, this article does not make it clear what constitutes “moderate” and “heavy” fog.

Analysis of the above research revealed their incompleteness. Most studies were conducted in good weather conditions. A smaller part of them studied the performance of LiDAR in one of the bad weather conditions, and very few studies have studied both good and bad weather conditions. This limits both the field of science and the development of UGVs. In the field of science, data standardization is impossible due to the lack of data, i.e., there are currently no universal benchmarks for LiDAR performance in bad weather conditions, so it is difficult to compare the results of different studies. In the field of UGV development, the lack of such data hinders the development of reliable LiDAR-based autonomous driving systems. Therefore, to assess the influence of LiDAR scanning frequency on the accuracy of the distance to the static obstacle and its shape, to conduct the same experiment in good weather and rainy conditions and perform a stochastic analysis of these data. This is the main aim of this research.

2. Influence of Weather Conditions on Data Analysis

Both rain and fog consist of tiny water droplets that scatter the energy of the laser beam. The backscattering in a single water droplet can be modelled as the scattering of an electromagnetic wave by a dielectric sphere of diameter D and refractive index n, which depends on the wavelength. A statistical distribution of water droplets with different diameters D can be used to model rain and fog. The probability of a laser transmitter hitting a droplet of diameter D is assumed to be N(D). It is assumed that there is only inelastic dissipation, i.e., light scattered by water droplets is not scattered by another droplet and no energy is converted to another wavelength. In this case, the attenuation of the signal in the atmosphere, i.e., the extinction coefficient α and the backscatter coefficient β:

$$\alpha ={\displaystyle \frac{\pi }{8}}·{\int }_{D=0}^{\infty }{D}^2{Q}_{EXT}\left(D\right)·N\left(D\right)dD,$$

(1)

$$\beta ={\displaystyle \frac{\pi }{8}}·{\int }_{D=0}^{\infty }{D}^2{Q}_B\left(D\right)·N\left(D\right)dD,$$

(2)

where D is the droplet diameter [mm] and N(D) is the probability of hitting a water drop with a diameter of D.

An experimental computer simulation [24] showed that the accuracy of the results obtained in the case of the Velodyne VLP-16 LiDAR in an environment with different obstacles and different rain intensities is affected by factors such as the reflection coefficient of body surfaces. The simulation used the obstacle detection and avoidance (ODOA) algorithms, which are used in the safety functions of today’s advanced driver assistance systems (ADASs). This safe driving system automates the vehicle, ensuring safety and minimizing driver error. It is also shown that as the rain intensity increases, the number of points scanned after a scan cycle decreases. At the same time, the resulting point cloud map is severely degraded.

At a rain intensity of less than 17 mm/h (i.e., heavy to moderate rain [26]), there was no strong effect on the obstacle detection distance. As the rain intensity increases, the maximum detectable distance decreases by 5–6 m.

It is obvious that as the rate of rain increases, the number of possible readable points decrease and the environmental point cloud is affected.

The data obtained from the experiments must be evaluated by statistical analysis, as this allows for the evaluation of such factors as data reliability (errors), correlation, etc. One of these is root mean square error (RMS), which is used as a measure of the difference between the true (or expected) values and the obtained values:

$$RMS=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\left({\widehat{x}}_i-x_i\right)}^2}{n}}},$$

(3)

where ${\widehat{x}}_i$ is the expected value; $x_i$ is the obtained value; and n is the number of measurements.

Another parameter, which is used for statistical empiric data analysis, is the correlation coefficient ρ, which shows the strength and direction of the relationship between variables, i.e., how similar are the measurements of two or more variables. This analysis helps to optimize the data set and is expressed through the following:

$$R{\rho }_{xy}={\displaystyle \frac{Cov\left(x,y\right)}{{\sigma }_x{\sigma }_y}},$$

(4)

where $R{\rho }_{xy}$ is the Pearson correlation coefficient; $Co\vartheta (x,y)$ is the covariance of quantities x and y; and ${\sigma }_x$ and ${\sigma }_y$ are standard deviations (variance):

$$\sigma =\sqrt{{\displaystyle \frac{\sum {\left(x_i-\mu \right)}^2}{n-1}}},$$

(5)

$$\mu ={\displaystyle \frac{\sum x_i}{n}},$$

(6)

where $x_i-\mu$ is the deviation in the individual result from the arithmetic mean.

The normal distribution, also known as Gaussian distribution, is a type of probability distribution for a real-valued random variable, where small deviations occur more frequently than large ones. A probability density function (PDF) is used to find the probability that a value of a random variable will occur within a given range of values:

$$f_{PDF}\left(x\right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}}.$$

(7)

The cumulative distribution function (CDF) is used to calculate the cumulative probability, and it means that a random variable will acquire a value less than or equal to it:

$$f_{CDF}\left(x\right)=\Phi \left({\displaystyle \frac{x}{\sigma }}\right),$$

(8)

where Φ is the cumulative distribution function of the normal distribution. In this paper, CDF is used for the graphical evaluation of the experimental results.

3. Methodology of the Experiments

The RoboPeak A1M8 laser rangefinder from Slamtec Co., Ltd. was selected for the experimental research [30]. The system of this device can perform 360-degree environmental scanning at a range of up to 12 m, with a standard rotation of range finder module (laser spot onto the target); the reflected light falls on the receiver element at an angle depending on the distance. 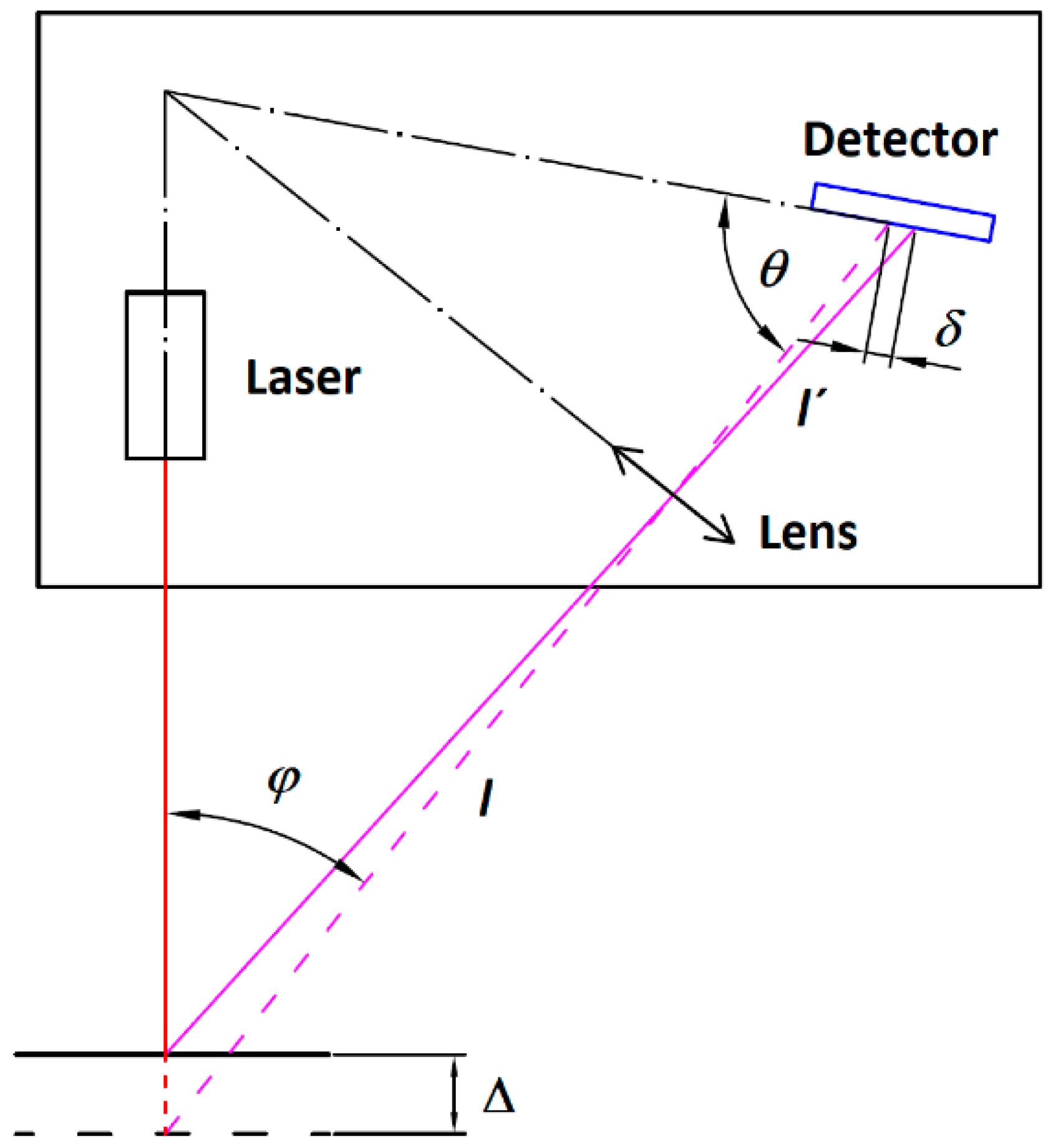The principle of the laser triangulation sensor is presented in Figure 1 [31]. Δ is the geometric relationship between the two laser spot positions (initial and shifted due to the object displacement) and the corresponding image displacement in the detector δ. The device has the following optical characteristics: wavelength λ = 795 nm, laser power is 5 mW, and pulse duration 300 μs [32]. I and I″ are the optical paths from the object to the receiver before and after object shift, whereas angle φ is the angle between the laser beam and the receiver imaging optics axis.

The light source is a low-power (<5 mW) infrared laser controlled by modulated pulses. In addition, this model has integrated high-speed environmental image acquisition and processing hardware. The system can take 2000 measurements per second and process the measurement data to create a two-dimensional point map. The resolution of RoboPeak A1M8 can reach up to 1% of the actual measuring distance. A belt attached to the electric motor pulley drives the unit that scans the environment.

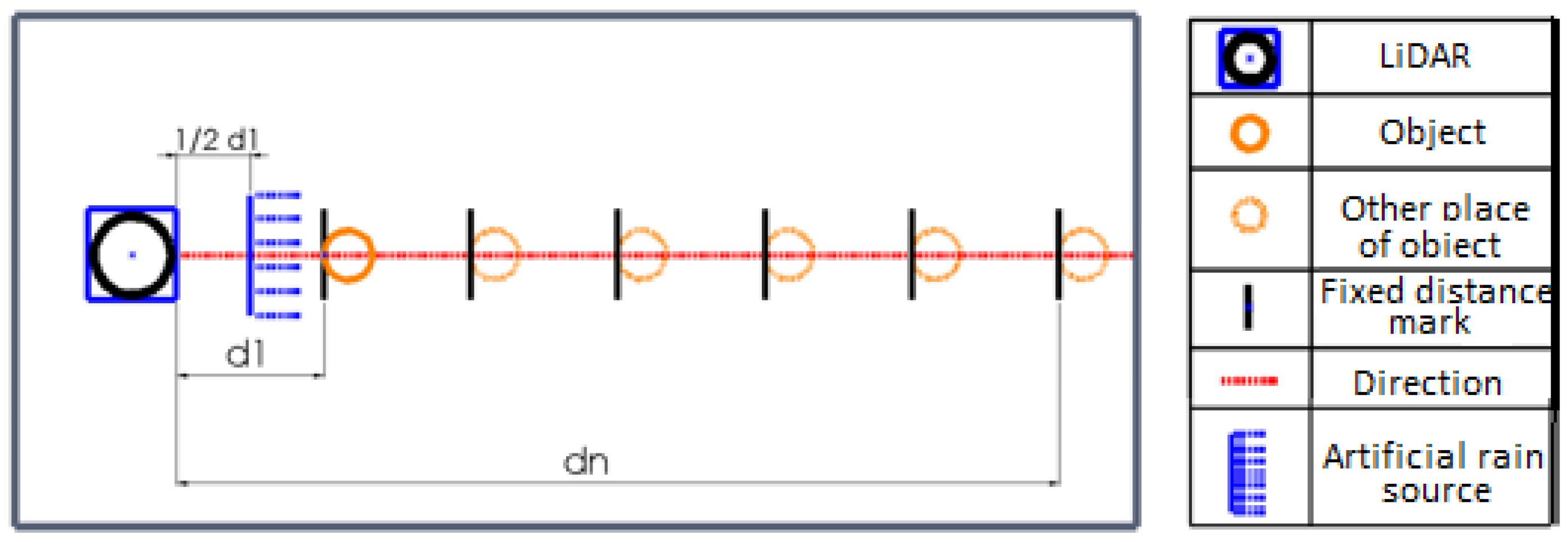
Experiments are carried out in both clear (no rain) and rainy conditions by scanning a reference object (target, stationary sphere of 135 mm diameter) at different frequencies and storing the surrounding map data on the computer using the RP-LiDAR frame grabber software program (v1.12.0).

After scanning at a distance d, the target is moved, and the measurements are repeated at the next position. By repeating this process 6 times, measurements are taken in a distance range of 1 to 6 m. In this way, measurements are taken every 1 m up to the limit distance d_n, at which the measured object is just fuzzily recognized.

3.1. Test in Clear Weather Conditions

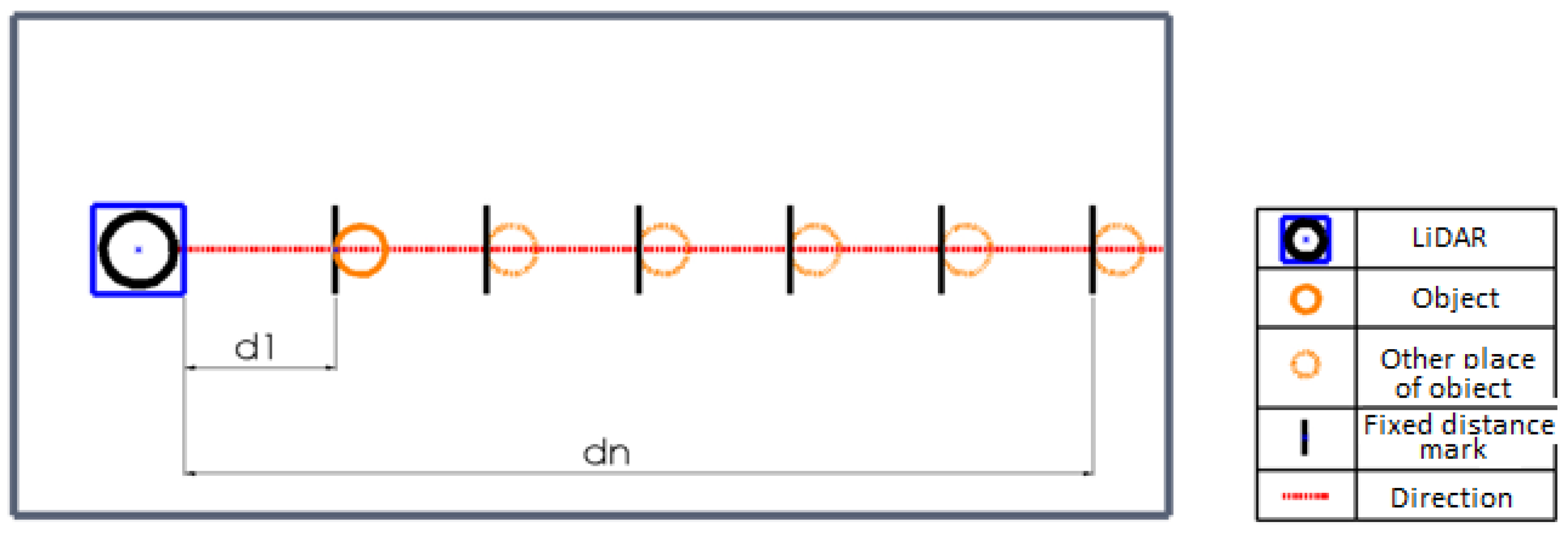
The setup used for the experimental evaluation of the LiDAR sensor performance in clear weather conditions is shown in Figure 2. The legend in the right part of the figure explains the symbols used for detailed understanding.

The measurement data, collected in this configuration, are shown as statistics in

Table 1. The results of the experiment in clear weather conditions and at a distance d of 1 m.

d, m	f, Hz	i, Number of Points	di = 1 mat, m	${\mathbf{R}\mathbf{M}\mathbf{S}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm	${\mathsf{\sigma }}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm
1	2	49	0.944	44.467	7.837
	2.6	29	0.971	23.097	5.946
	3.5	21	0.975	20.081	6.671
	4,3	17	0.987	8.564	3.796
	5.5	13	0.998	4.809	4.393
	7	10	0.996	4.589	2.886

for the distance set as d = 1 m and in

Table 2. The results of the experiment in clear conditions and at a distance d of 6 m.

d, m	f, Hz	I, Number of Points	di = 1 mat, m	${\mathbf{R}\mathbf{M}\mathbf{S}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm	${\mathsf{\sigma }}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm
6	2	10	5.885	82.033	36.745
	2.6	4	5.901	82.820	14.879
	3.5	3	5.923	80.886	3.402
	4.3	2	5.924	80.662	6.442
	5.5	1	5.982	20.227	-
	7	1	5.946	54.173	-

for the set distance of d_i of 6 m, which is mentioned also in the first column of both tables as distance d [m] to the object under investigation.

In addition, f is the scanning frequency [Hz], i is the number of the captured shape points of the object, d is the distance [m] actually measured to the closest point of the target (which is considered as an obstacle in real use, so shortest distance is the critical one), ${RMS}_{vid}$ is the mean square error of measurements and ${ \sigma }_{vid}$ is the dispersion of measurements.

Calculations of the RMS (Formula (3)) have revealed that the highest distance errors occurred when using a scanning frequency of 2 Hz, while the lowest ones were obtained at 5.5 or 7 Hz (RMS at 2 Hz was almost 10 times higher than at 7 Hz). It means that RMS has an opposite pattern with increasing frequency (Table 1). Although at the closest distance (1 m) a scanning frequency of 5.5 or 7 Hz cause about 9 times smaller errors compared to the errors recorded at the longest distance (6 m); also, here the errors are still 6 times smaller using high scanning frequencies compared to the case of just 2 Hz. This test has revealed a clear dependence of the distance variation on the scanning frequency; the distances are most accurate in the range of higher frequencies of 5.5 and 7 Hz (Table 1, Figure 3).

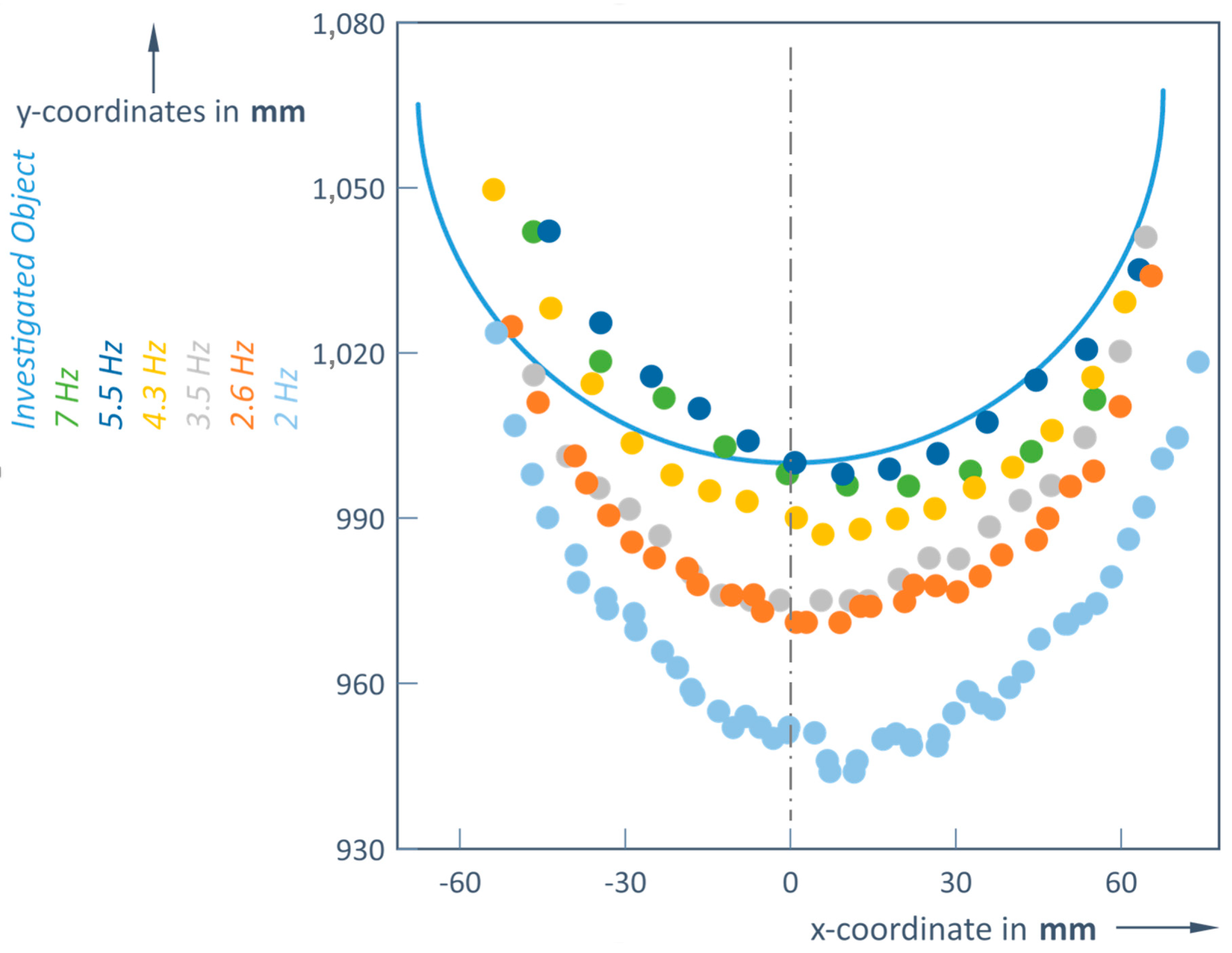
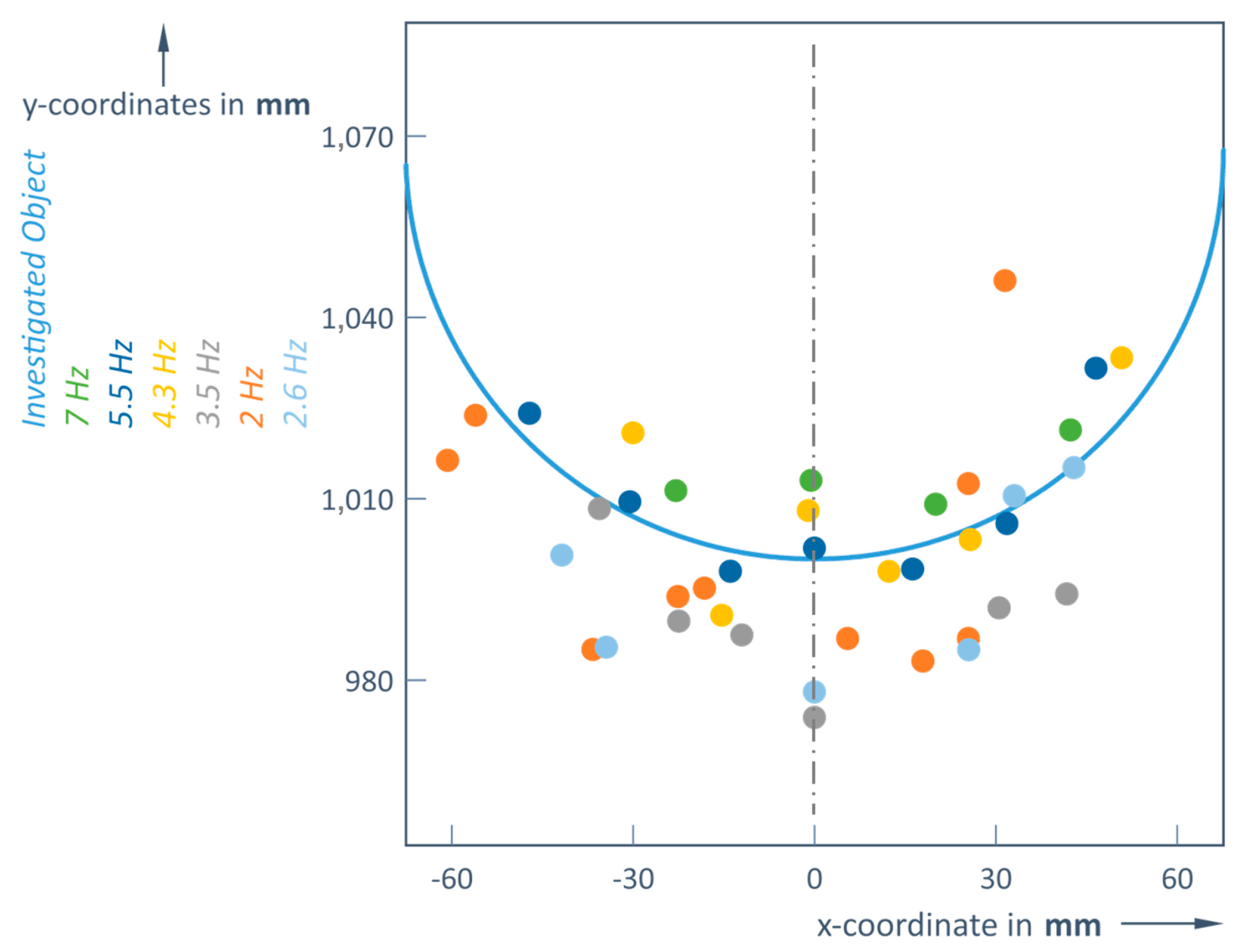
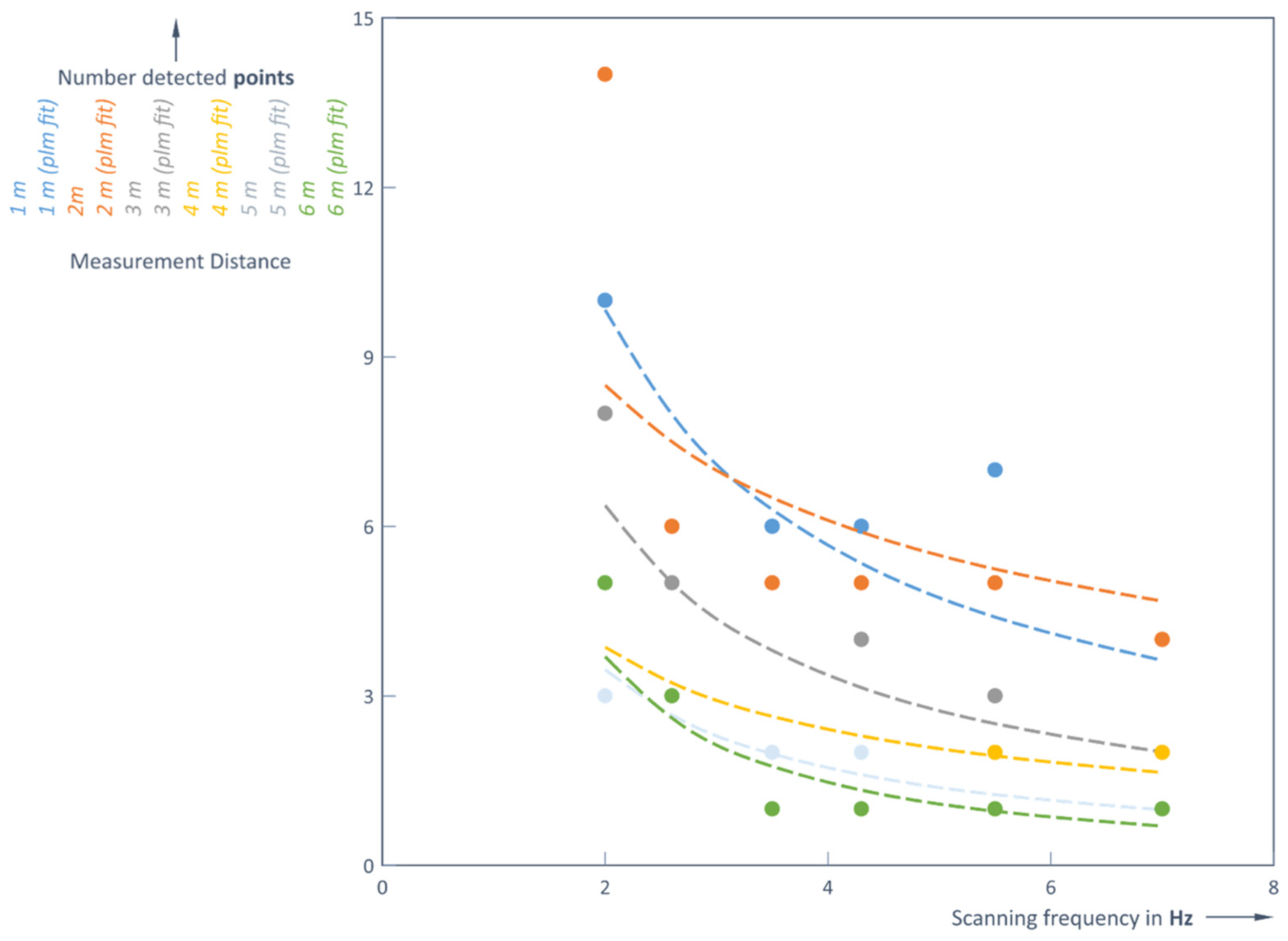
The number of points that the LiDAR receiver can detect determines the accuracy of the shape of the object. This number strongly depends on both the distance to the object and the scanning frequency of the LiDAR (Figure 4). Here, in a first example, the silhouette of a person is depicted in a red frame (magnification right to the complete picture). It can be seen very clear that in the case of rain at the given distance (5 m), the silhouette of a person is difficult to recognize. Although most points of the object have been registered at lower frequencies (2 and 2.6 Hz), these frequencies resulted in a bigger loss of distance accuracy (Table 1); when the real distance was 1 m, the LiDAR captured distances of 0.944 m and 0.971 m.

The upper and lower images show the situation without rain and with rain, respectively. A scanning frequency of 7 Hz was used, with measurements taken at a distance of 5 m. Rain intensity is 9.84 mm per hour. Rain fell on the person and between them and the LiDAR. The tree was unaffected by the rain.

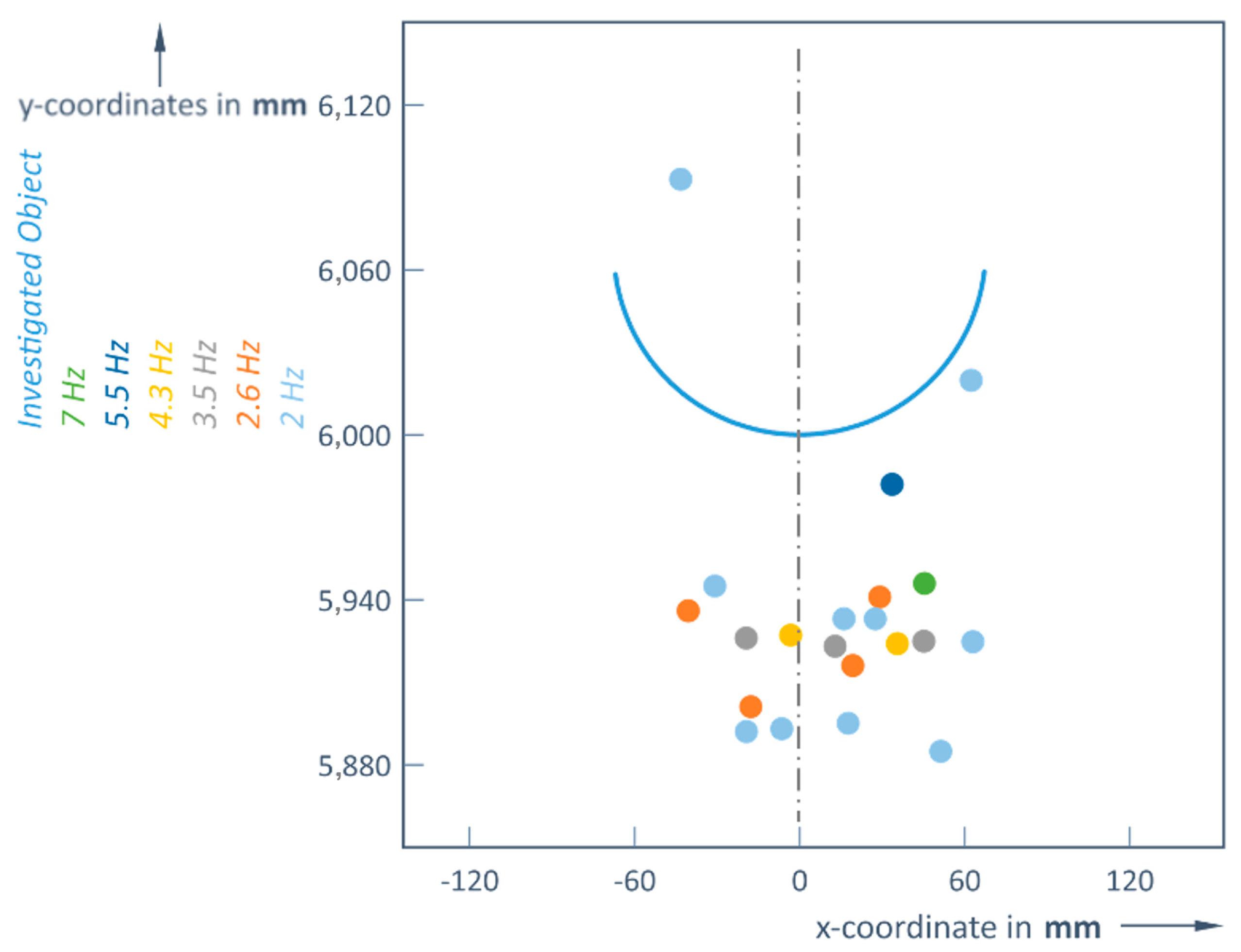
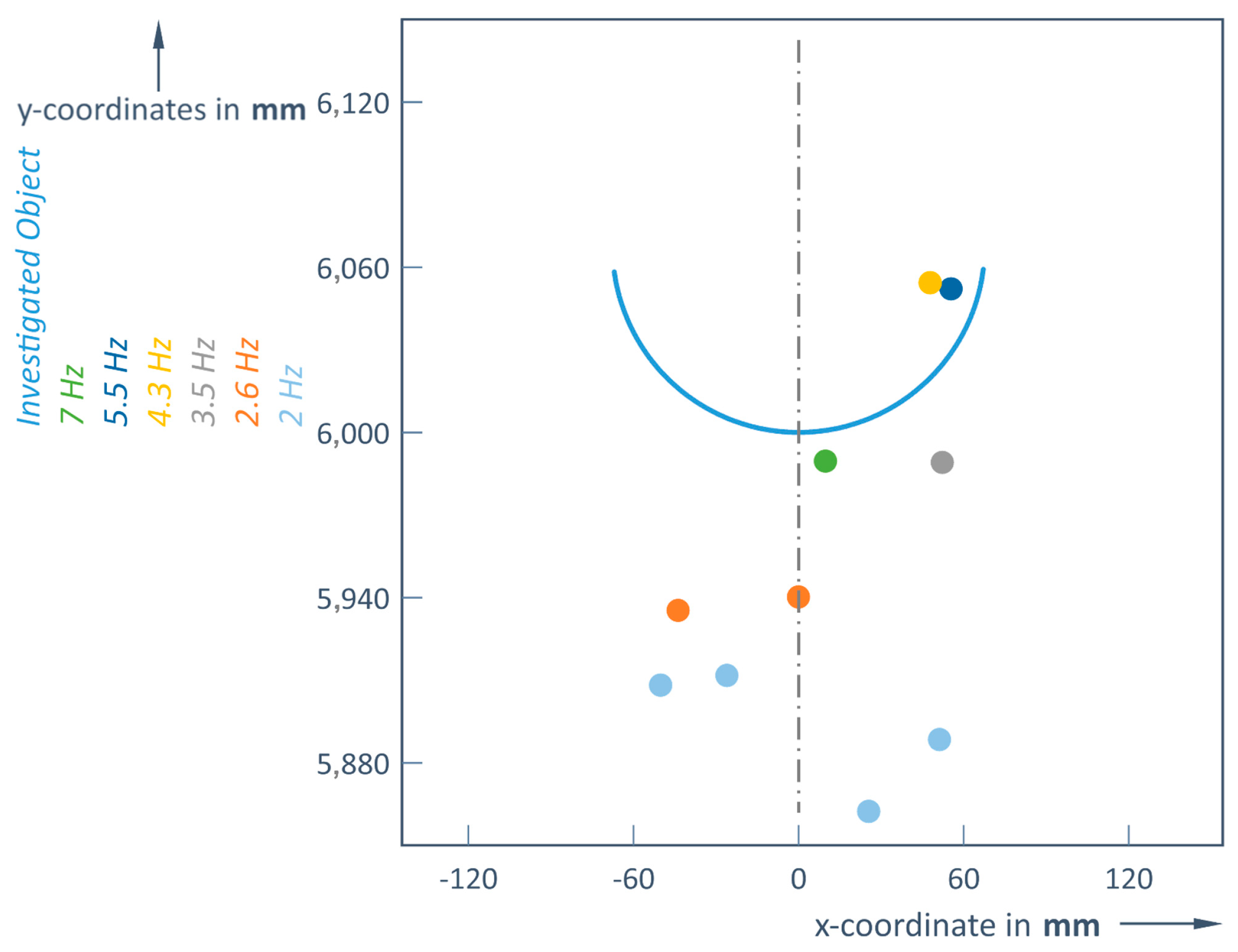
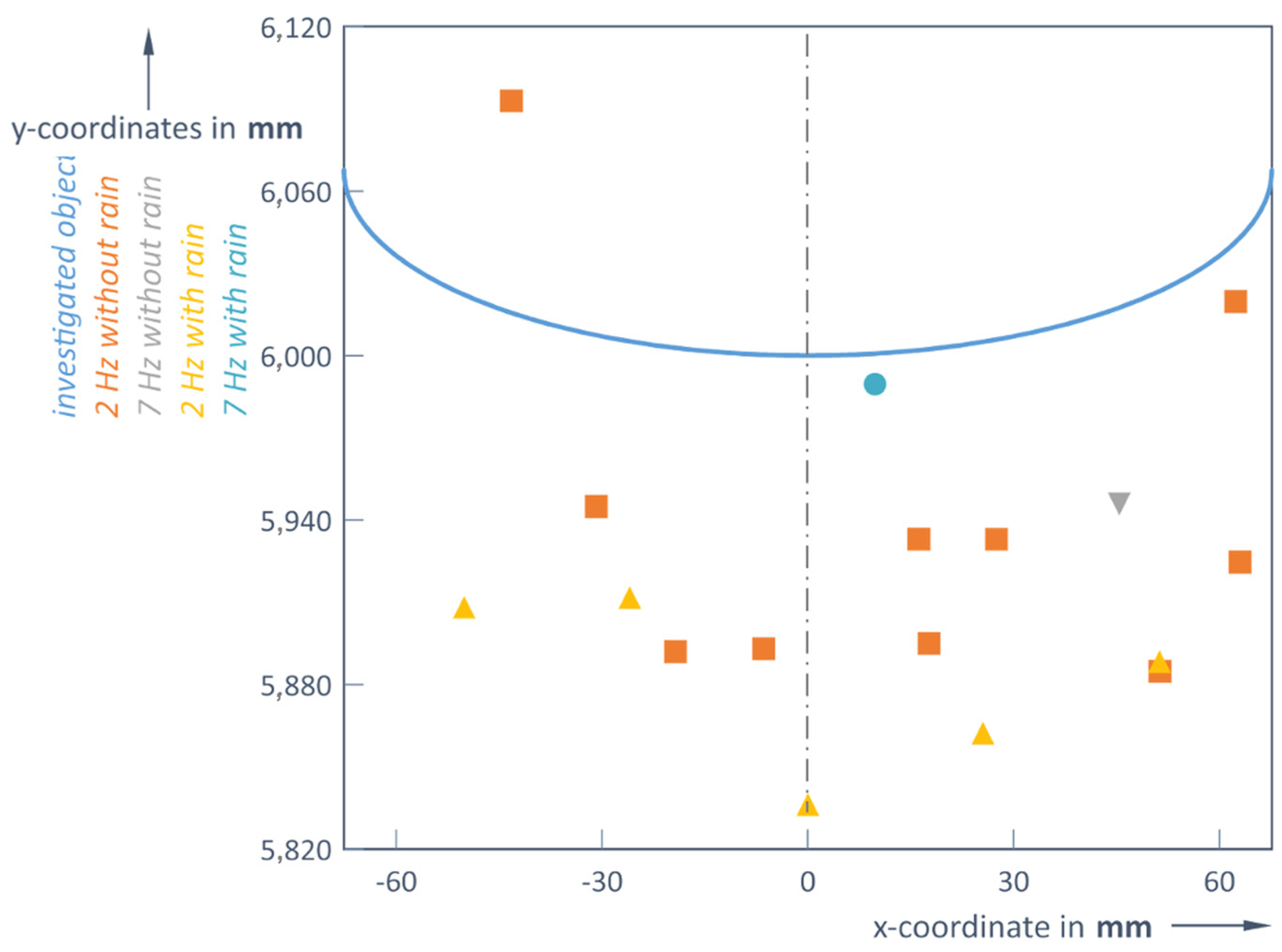
Therefore, it is important to determine an optimal scanning frequency depending on the distance to the object. For an object at a distance of 6 m, the detector can only pick up more than one reflected signal from that object if a frequency of 4.3 Hz or less is used. This means that at higher scanning frequencies (5.5 or 7 Hz), the object (again a ball of 135 mm diameter) becomes practically invisible at this 6 m distance limit; the Slamtec RoboPeak A1M8 LiDAR could only detect 1 point (Table 2, Figure 5).

From this, it can be concluded that there must be an object at the measured distance. This information is still useful for rough obstacle detection, but no longer for control routines, as the shape and size information of the object is lost.

3.2. Test in Rainy Weather Conditions

This experiment scenario is similar to clear weather conditions, but it is carried out by causing artificial rain between the LiDAR transmitter and the object (Figure 6). The artificial rain was placed next to the sensor, between the sensor and the object.

The object was again placed at distances from 1 to 6 m. The frequencies were selected based on the specifications of the LiDAR device used [30]. Technical characteristics: sampling—7 Hz, 6 m measurement range, 360-degree scan.

To determine the direct influence on the determination of distance to the obstacle and its shape, for the purity of the experiment, it was chosen to perform it in contrasting weather conditions: clear weather and heavy rain. As for the measurement duration, the measurements are performed instantaneously for discrete frequencies; and the controlled variables are the distance to the object in meters, which is measured to the closest point of the target, and captured shape points of the object. The results at distances (d) of 1 m and 6 m are shown in

Table 3. The results with rain at a distance of d = 1 m.

d, m	f, Hz	I, Number of Points	di = 1 mat, m	${\mathbf{R}\mathbf{M}\mathbf{S}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm	${\mathsf{\sigma }}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm
1	2	10	0.983	16.739	10.104
	2.6	6	0.978	13.658	10.359
	3.5	6	0.974	16.735	8.589
	4.3	6	0.991	8.050	4.656
	5.5	7	0.998	4.418	3.925
	7	4	1.009	8.178	3.256

and

Table 4. The results for rain at a distance of d = 6 m.

d, m	f, Hz	I, Number of Points	di = 1 mat, m	${\mathbf{R}\mathbf{M}\mathbf{S}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm	${\mathsf{\sigma }}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$, mm
6	2	5	5.836	129.825	26.977
	2.6	3	5.823	110.360	70.211
	3.5	1	5.989	35.633	-
	4.3	1	6.054	34.449	-
	5.5	1	6.052	23.182	-
	7	1	5.989	11.225	-

, respectively.

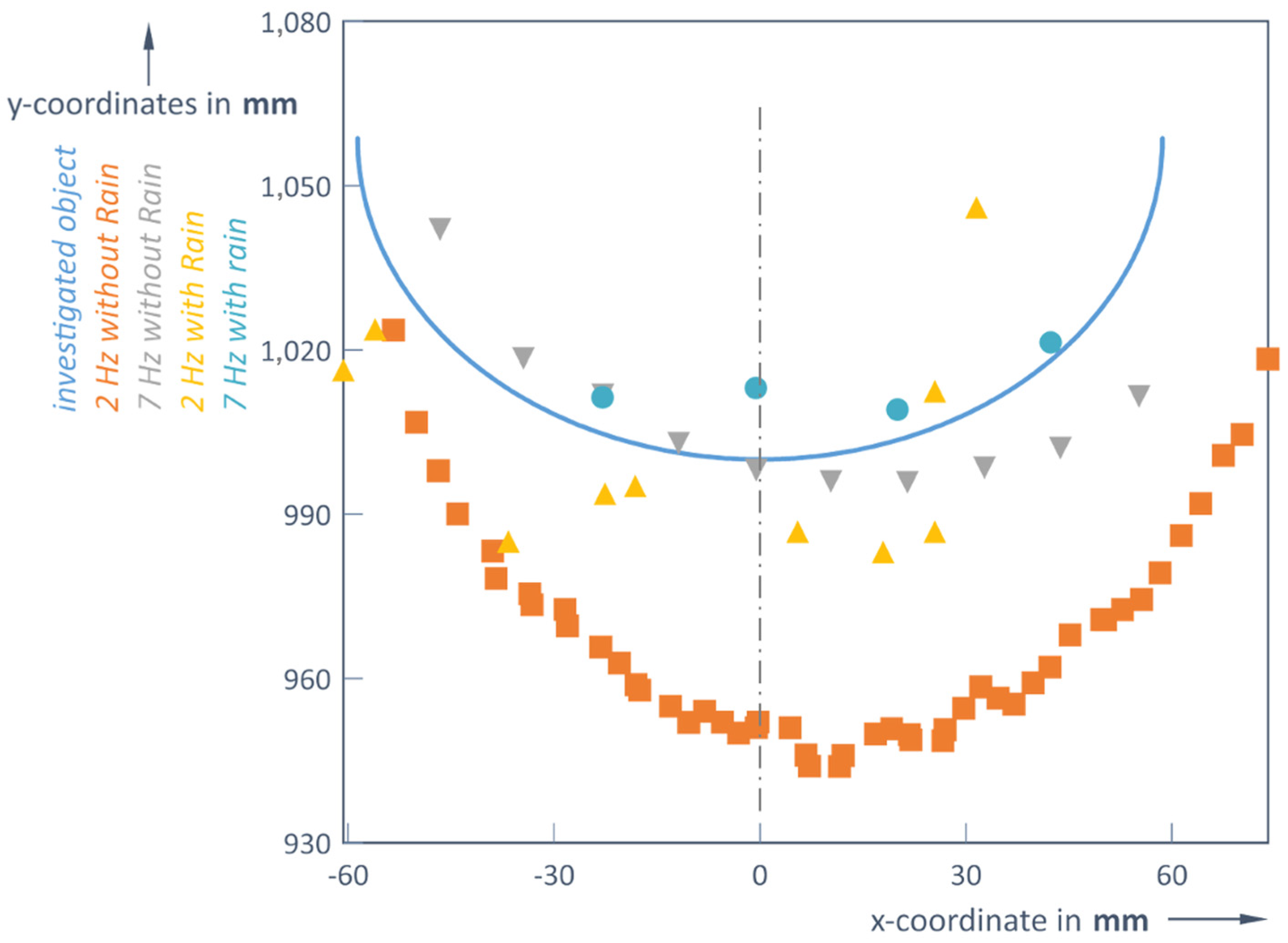
Rainy weather data (Table 3) revealed that measuring at 1 m, the distance is determined quite accurately using higher frequencies (5.5 and 7 Hz), which is very similar to the clear weather experiment (1 m reference distance was measured as 0.998 m and 1.009 m). The object becomes invisible at a distance of 6 m when the scanning frequency is 3.5 Hz (or higher), while at a frequency lower than 2.6 Hz, this object is detected but its shape is lost (Table 4). Thus, with increasing distance, the dispersion of points recorded from the object increases as well (Figure 7 and Figure 8). However, using a 2 Hz LiDAR scan rate, the RMS at 1 m is 5 times smaller than the one under good weather conditions. This could be explained by the self-compensation effect on multiple paths due to heavy rain.

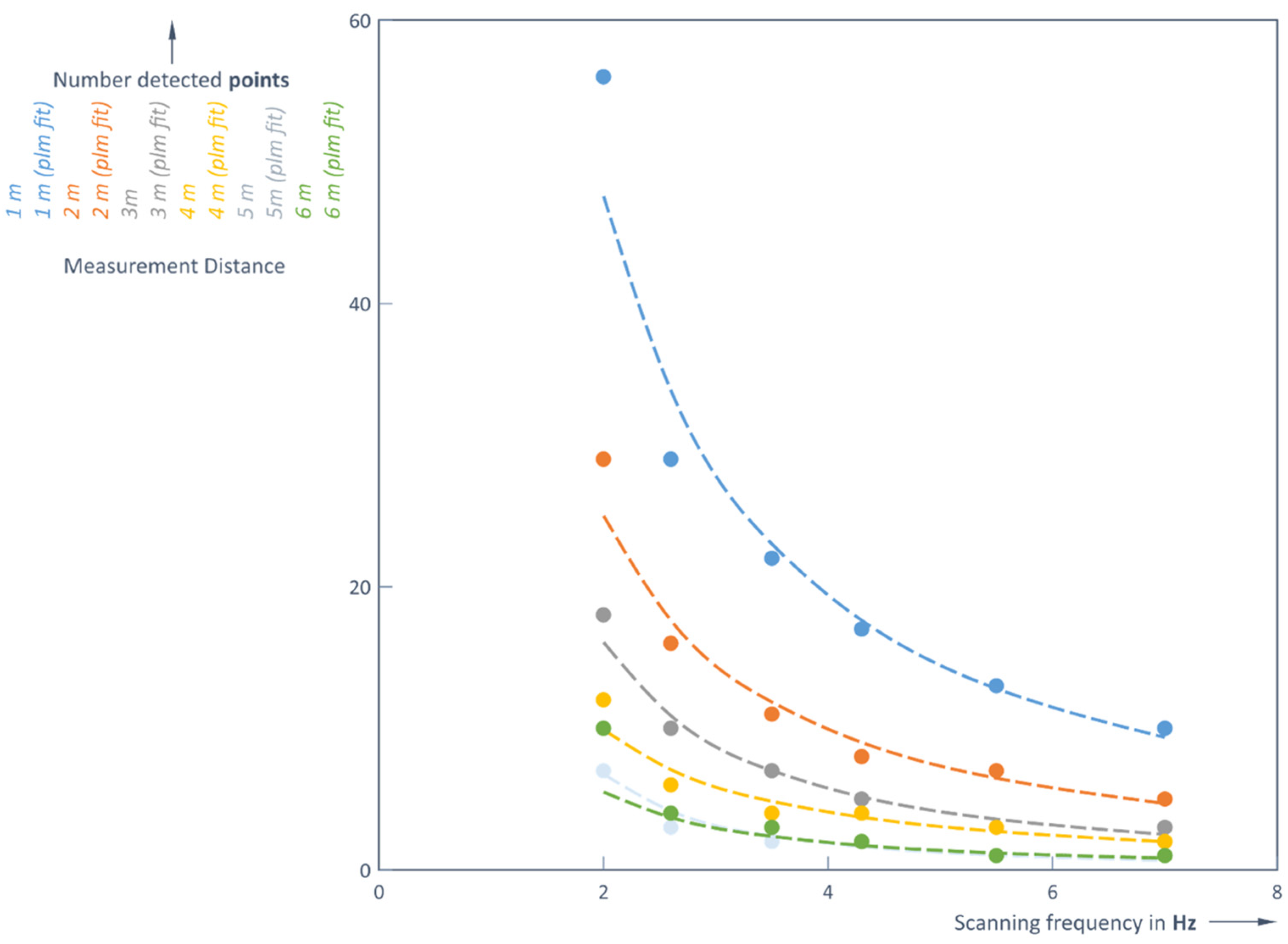
It can be clearly seen that the number of points of the detected object decreases, since the field increases with the increasing distance at a constant angle of view, resulting in fewer points being detected for more distant objects (Table 1, Table 2, Table 3, Table 4 and Figure 3, Figure 5, Figure 7 and Figure 8, correspondingly). This inverse dependence is seen in Figure 9 and Figure 10 for both weather conditions.

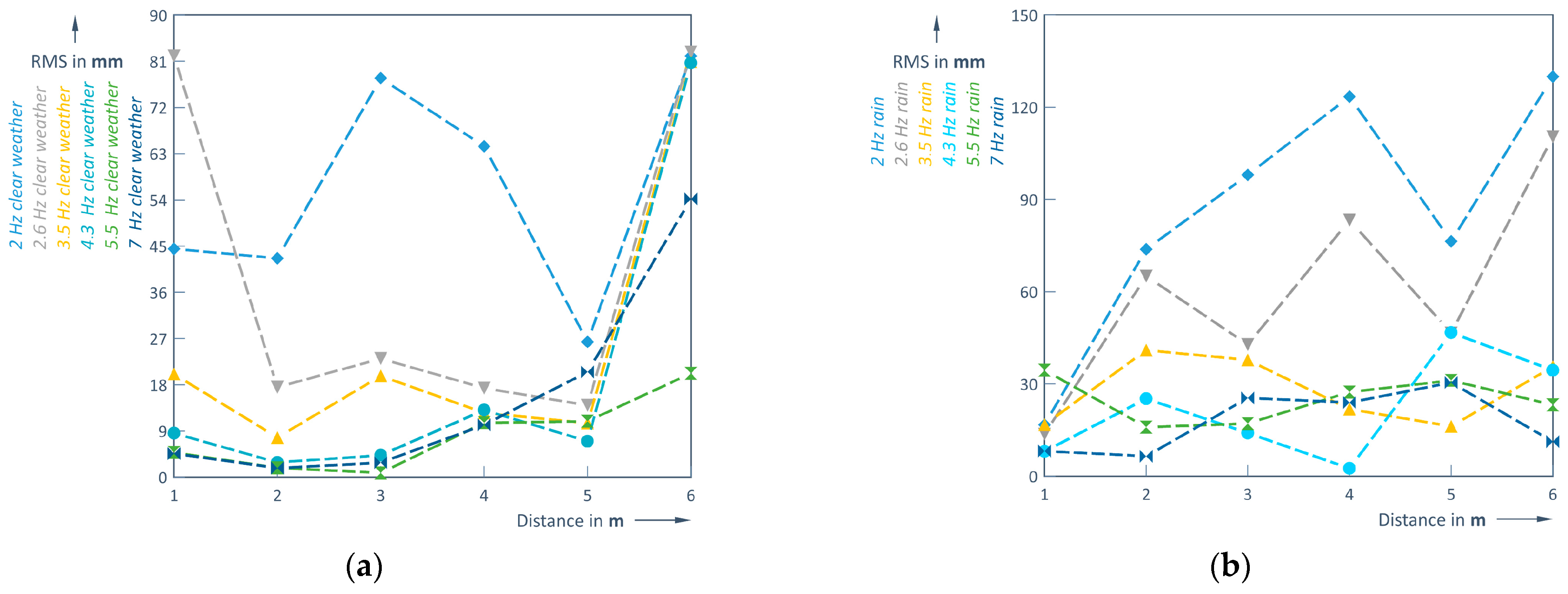
Heavy rain increases the errors in detecting a precise distance to the object and its shape, compared with clear weather (Figure 11 and Figure 12). It provides less points of the object shape, and this is especially visible when measuring at a distance of 1 m (Figure 11).

When measuring at 6 m, an object is poorly detected in clear conditions and heavy rain, and the frequency used does not play a significant role (Figure 12).

When the distance increases, the number of points of the detected object decreases significantly. At a number of detected points per object below five, just the presence of the object and distance to it is detected, but not its shape and size. The same trend occurs at all scanning frequencies, as also shown in the following two diagrams.

Such dependencies of the number of points can be approximated very well by these corresponding equations: without rain (9) and with rain (10):

$$n=120.25d^{-1.006}{f}^{-\left(1.169+0.085d\right)},$$

(9)

$$n_r=14.674d^{-0.353}{f}^{-\left(0.414+0.139d\right)},$$

(10)

where n and n_r are the number of detected points without rain and in rainy conditions; d is the distance from the LiDAR to the object in meters (m); and f is the scanning frequency in hertz (Hz) of the LiDAR sensor.

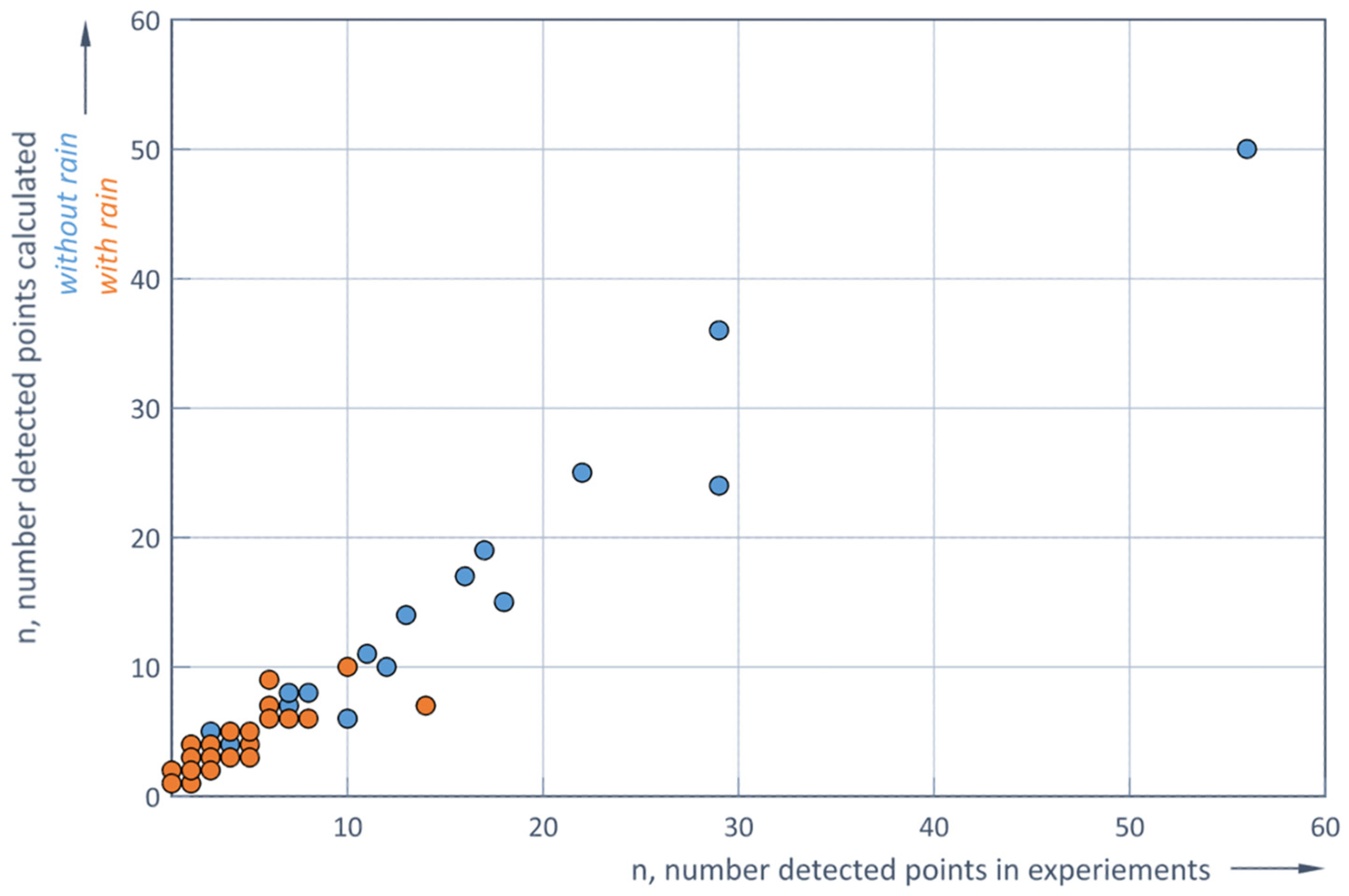
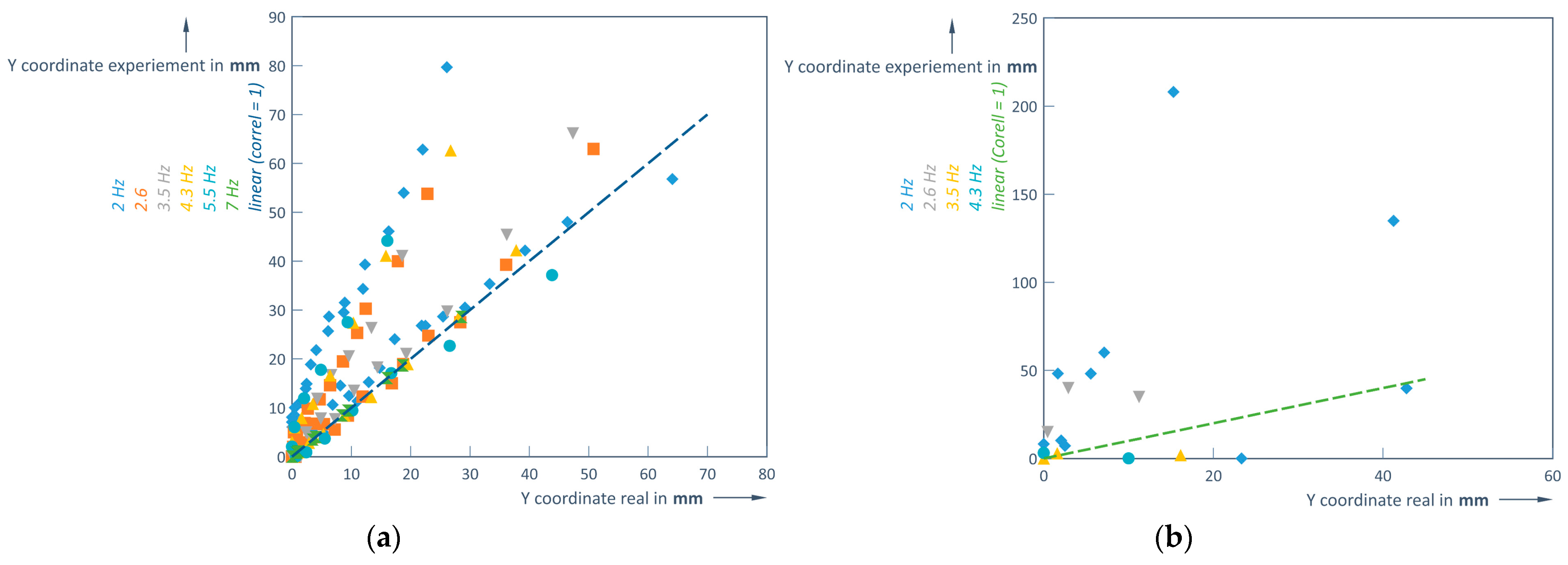
Figure 13 shows the correlation between the experimentally detected number of points and the number of points calculated using the two Formulas (9) and (10) for conditions with and without rain. The correlation coefficients are 0.98 without rain and 0.83 with rain. These strong correlations confirm the adequacy of both models, Formulas (9) and (10), with respect to the experimental results (Figure 13).

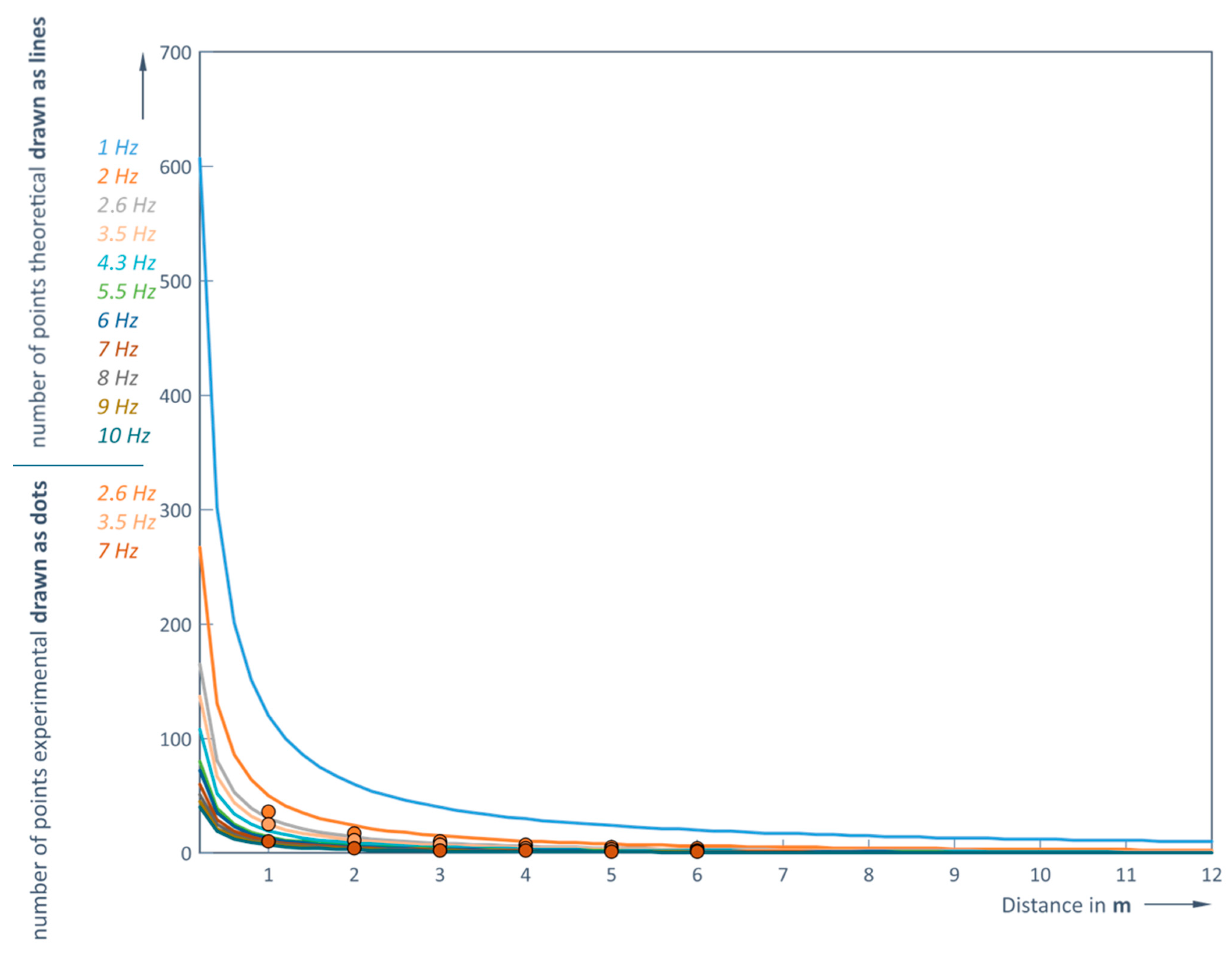
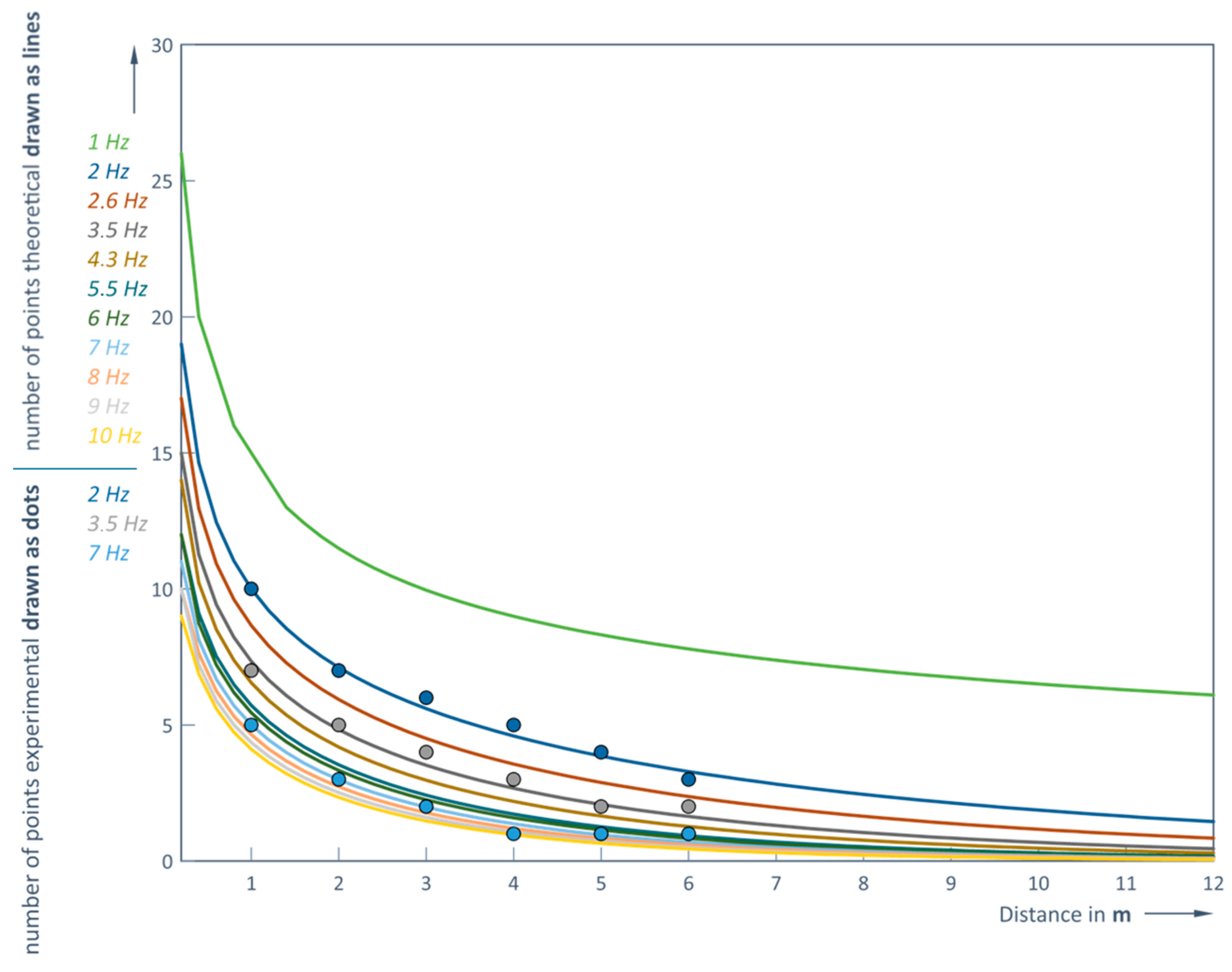
Thus, it is possible to predict the number of captured points that the sensor under study can detect depending on the distance and the LiDAR operating frequency without rain. The results of this prediction and the comparison with the experimental data are shown in Figure 14 (for the clear weather conditions) and in Figure 15 (for the rainy conditions).

It can be concluded that the modeled dependencies and experimental results correspond very well (Figure 14 and Figure 15). At an LiDAR operating frequency of 1 Hz (in clear weather conditions) the number of points recorded at the minimum distance of 0.2 m between the sensor and the obstacle are more than 600, and at the maximum distance of 12 m, this number is reduced to 10 (Figure 14). However, at the maximum LiDAR operating frequency of 10 Hz, it is possible to capture a sufficient number of points (at least one) at a distance of no more than 5 m (

Table 5. Predicted number of recorded points as a function of distance d [m] and scanning frequency f [Hz] in clear weather conditions (regarding Figure 14).

d [m]	n @ 2 Hz	N @ 3.5 Hz	N @ 7 Hz
1	56	22	10
2	29	11	5
3	18	7	3
4	12	4	2
5	7	2	1
6	10	3	1

and

Table 6. Predictive number of recorded points depending on distance d [m] and scanning frequency f [Hz] in rainy weather conditions (regarding Figure 15).

d [m]	n @ 2 Hz	N @ 3.5 Hz	N @ 7 Hz
1	10	6	4
2	14	5	4
3	8	2	2
4	5	2	2
5	3	2	1
6	5	1	1

).

The object points should no longer be recorded from 3.8 m in rainy weather and when the LiDAR operating frequency is 10 Hz (Figure 15). The actual values of the measured distance at 1 and 6 m are 0.983 m (clear weather) and 0.978 m (rainy weather) and 5.836 m and 5.823 m. The influence of the rain is therefore quite small in these measurement conditions. The smallest measurement errors are obtained with 5.5 or 7 Hz. For example, RMS at 1 m and 5.5 Hz is 4.42 mm, RMS at 1 m and 7 Hz is 8.18 mm, RMS at 6 m and 5.5 Hz is 27.35 mm and RMS at 6 m and 7 Hz is 23.93 mm. Thus, in rainy weather conditions, when the measured object is 6 m away, the scanning frequency of 5.5 Hz ensures about 5–6 times bigger errors (RMS) compared to the case when 2 Hz is used. So, both the distance to the object and its shape are determined much more accurately in higher frequencies.

The obtained measured distance values after simulating in this case at a distance of 1 m are strongly linearly correlated, as the calculated Pearson correlation coefficient is equal to 0.81 (Formula (4)). An obtained correlation coefficient is 0.49 at a distance of 6 m, so it is assumed that the existing correlation between the measurements is moderately strong. In this case, the evaluation of the results includes measurements only at 2 and 2.6 Hz.

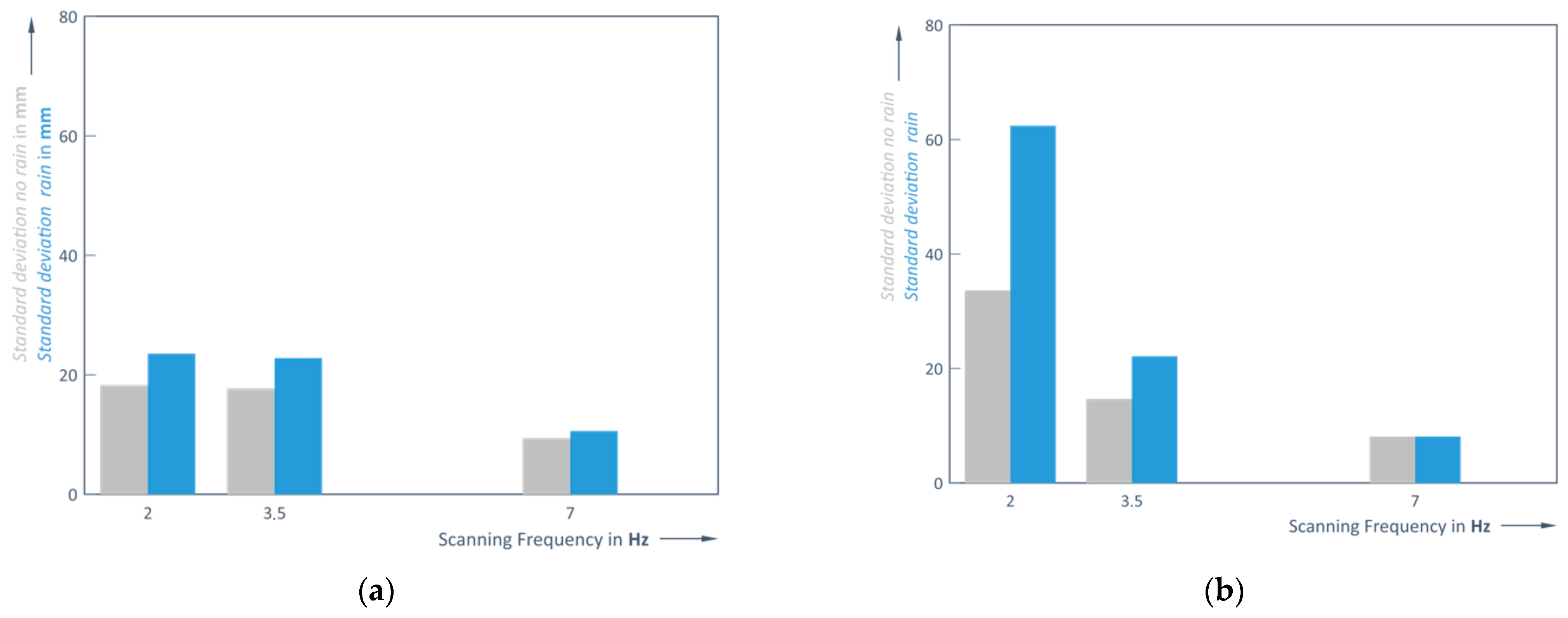
It is worthwhile depicting the dependence of the RMS variation on distance d [m] at different LiDAR operating frequencies f [Hz]. A quite large dispersion of empiric results is observed in Figure 16a,b:

Calculation of the RMS shows that the largest error occurs at a scanning frequency of 2 Hz (RMS at 1 m measuring distance is 16.74 mm and at 4 m 123.43 mm). In this case, the correlation coefficients are 0.61 in clear weather and 0.73 in rain. In the last case (Formula (12)), the correlation coefficient is strong compared to the case without rain (Formula (11)) where the correlation is only moderate. Furthermore, when assessing the correlation at different frequencies, a strong correlation only occurs at higher LiDAR operating frequencies (>5 Hz) (Figure 16).

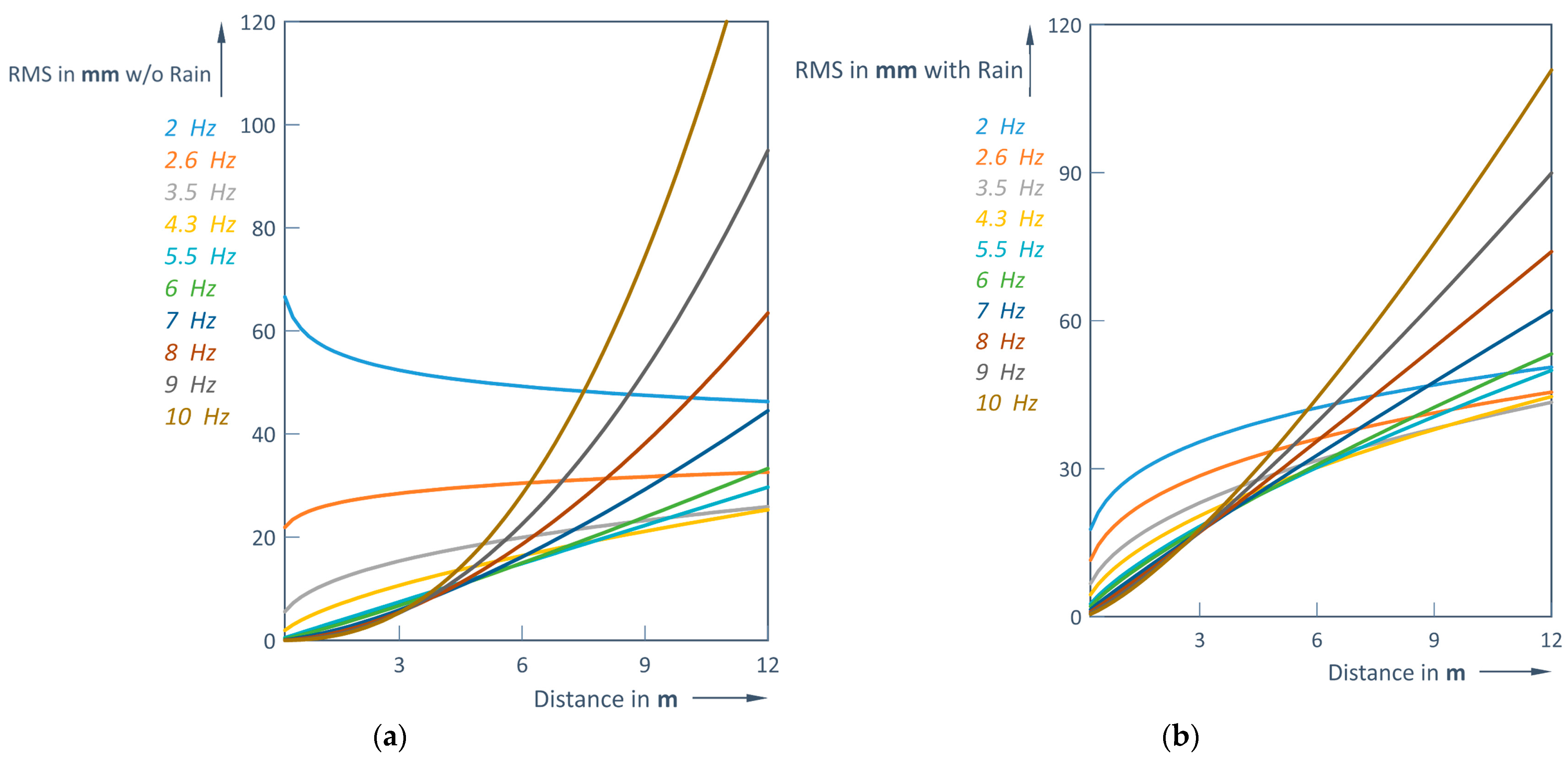
Approximate Formulas (11) and (12) are used to depict the RMS forecast under clear and rainy weather conditions (Figure 17a,b):

$$RMS=495.17f^{-3.101}{d}^{\left(0.310f-0.708\right)}$$

(11)

$${RMS}_r=59.681f^{-1.159}{d}^{\left(0.133f-0.01\right)}$$

(12)

An interesting trend about the different nature of the RMS depending on the frequency range can be seen in Figure 17. As long as the frequencies are <6 Hz, the RMS variation with increasing distance d varies significantly up to a distance of 3 m, but as the distance increases further, the RMS increase is already smaller (stabilization behavior). Meanwhile, at higher frequencies (f > 6 Hz), the RMS increase is almost linear with gradients; the higher the frequency, the higher the gradient. This particular behavior results in a lower RMS for distances up to about 6 m when using higher frequencies (6 Hz and above), while at longer distances lower scanning frequencies (below 6 Hz) provide a lower RMS. This should be considered when taking practical measurements.

4. Stochastic Analysis of Experimental Data

Correlation analysis reveals the correspondence between the measured and real values. At a measurement distance of 1 m, the actual values for the spherical shape have a linear dependence (values from the LiDAR sensor and geometric values), as shown in Figure 16a, since the calculated Pearson correlation coefficient is equal to 0.97. The evaluation of the results is performed at a distance of 6 m (Figure 18b), but the data at 5.5 and 7 Hz are not included, since only one point of the observed object is recorded at these frequencies. Again, for the evaluated frequencies a linear correlation was found.

Obviously, the LiDAR scan frequency and distance to the object directly determine the measurement accuracy. The correlation coefficient is calculated based on the average value of the measurements using different scan rates; 0.84 is obtained at a distance of 6 m, which is lower compared to a distance of 1 m, but the correlation is still quite high (Figure 19).

As can be seen in Figure 19a,b, the lower the scanning frequency, the larger the errors (RMS). The largest data discrepancy occurs when using a 2 Hz scanning frequency, which is very pronounced at a distance of 2 m (Figure 19b). Except for the case where the object is 1 m away and 7 Hz is used for scanning, the influence of rain causes greater measurement errors than in clear weather conditions (Figure 19); this tendency is particularly evident at lower frequencies and as the distance from the measured object increases. In addition, the 3.5 Hz measurements in clear weather conditions are only slightly more accurate than the 2 Hz case. This trend is clearly observed when scanning at higher frequencies, with the results approaching the steeper shape of the theoretical CDF curve (Figure 20).

This means that when scanning at a frequency of 7 Hz, the dispersion of measurements becomes minimal, and the measurement results are more reliable (Figure 20). It was found that when scanning a sphere with a diameter of 135 mm or less at a distance of more than 5 m, only one point is recorded due to limited visibility (rain). The beam emitted by the LiDAR is refracted when it passes through a water droplet; it changes direction, and the sensor cannot receive it. This leads to sampling errors. During this study, it was observed that the refraction increases with the increasing distance between the LiDAR and the scanned object because in this case, more raindrops refract the laser beam and effectively separate the LiDAR from the scanned object.

5. Discussions

Based on this research with a commercially available LiDAR sensor, important conclusions can be drawn about the most appropriate use of the sensor in various weather conditions when measuring the distance to an object.

As for the performance of the actual RoboPeak A1M8 LiDAR sensor, the following can be summarized: the most accurate readings at a 1 m distance in clear weather conditions are obtained using the higher scan frequencies of 5.5 and 7 Hz. At a 135 mm diameter sphere test object, respective distances of 0.998 m and 0.996 m are measured. Although more object points are collected at lower frequencies (2 and 2.6 Hz), the distance accuracy is reduced (distances of 0.944 m and 0.971 m are obtained). The scanning frequencies of 5.5 or 7 Hz allow about 9 times smaller errors to be obtained compared to 2 Hz. When measuring the same object at a distance of 6–7 m, the errors also increase for the higher scan frequencies, but they are still 6 times smaller compared to the 2 Hz frequency already mentioned. Therefore, it is recommended to use the highest possible scanning frequency for object identification in clear weather conditions.

When measuring the 1 meter distance with higher frequencies (5.5 and 7 Hz) in rainy conditions, the readings were still quite accurate (0.998 m and 1.009 m, respectively). However, as the distance to the object increases, the scattering of the measurement points increases significantly, as the raindrops changes the normal environmental conditions and introduce errors due to the refraction phenomenon described above. It has been found that the test object becomes invisible at larger distances when scanning frequencies of 3.5 Hz and higher are used. Using frequencies lower than 2.6 Hz, even at longer distances, the test object can still be detected, but shape recognition is lost.

Comparing the results in clear and rainy conditions shows the same qualitative behavior, which can be generalized for LiDAR sensors: increasing the scan frequency results in more accurate distance data, but in this case, a smaller number of object points are recorded, and shape recognition is reduced or even lost. The direct influence of rain on reducing the accuracy of LiDAR readings is also evident in the data, which can be explained by the reflection of laser light. Based on this, in clear weather it would be worthwhile to use higher frequencies for detecting of moving objects, and once they are detected, a lower frequency should be used for shape estimation. Talking about rainy weather, it is recommended to use only lower frequencies for detecting of moving objects, and for its shape detection as well.

Based on the results collected and discussed in this article, the authors suggest that the LiDAR frequency can be selected dynamically (adaptively), depending on weather conditions (see the paragraph above) and the speed and distance of the object; however, this still needs to be investigated.

The authors understand that the experiments were conducted with static spherical objects at a certain distance and this differs from the real-world conditions of using LiDAR for autonomous driving. Given that real-world targets often change speed, orientation and are obstructed, the authors recommend conducting studies of the feasibility of using LiDAR, taking these factors into account, i.e., it would be worthwhile conducting research into the detection of a moving object with rapidly changing coordinates. To study the influence of different LiDAR models on the validity of the results, as well as the long-term influence of weather conditions on the calibration of sensors, are also of high importance.

It is appropriate also to conduct research in complicated weather conditions (e.g., fog, mist or snow). The latter is very important to improve the reliability and safety of UGVs, especially in regions that experience frequent rain. This would lead to the development of more robust perception systems, improved sensor fusion strategies and consistent performance, which would ultimately accelerate the deployment of UGVs in diverse and complex environments.

Integrating LiDAR with other sensors (cameras, radars, ultrasonic sensors), applying weather models and artificial intelligence could dynamically control UGVs in different weather conditions.

These are precisely the directions of further research.