A Two-Stage Strategy Integrating Gaussian Processes and TD3 for Leader–Follower Coordination in Multi-Agent Systems
Abstract
1. Introduction
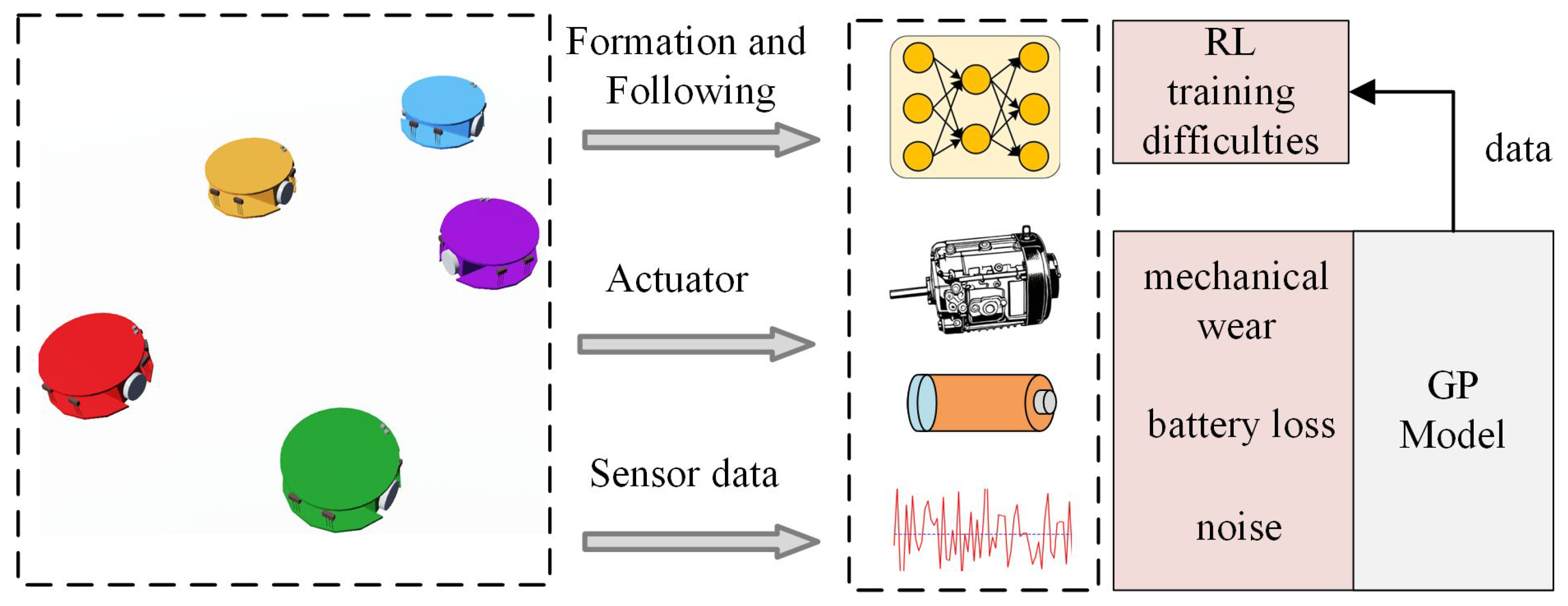
- We leverage GPs to model agent dynamics in a virtual environment, thereby reducing physical training risks and avoiding actuator constraints like voltage limits and mechanical wear. This virtual GP model supports initial control policy learning with TD3, leveraging GPs’ probabilistic nature to filter sensor noise via measuring the uncertainty modeled through its covariance kernel.
- The proposed method uses a two-stage training process inspired by [26,27]. The first stage focuses on individual agent control, simplifying training by tackling smaller subproblems. The second stage adds a compensation TD3 network to improve convergence in multi-agent training, resulting in more stable and efficient learning.
- Furthermore, a dual-layer reward mechanism is designed to optimize multiple objectives simultaneously. Unlike existing methods [9,12], our approach implements a phased reward mechanism with decoupled position and attitude reinforcement stages. It provides a smoother learning process for the leader–follower control strategy.
2. Related Work
2.1. Traditional Control Strategy
2.2. RL Control Method
3. Problem Formulation
3.1. Agent Model
3.2. Leader–Follower Formation Description
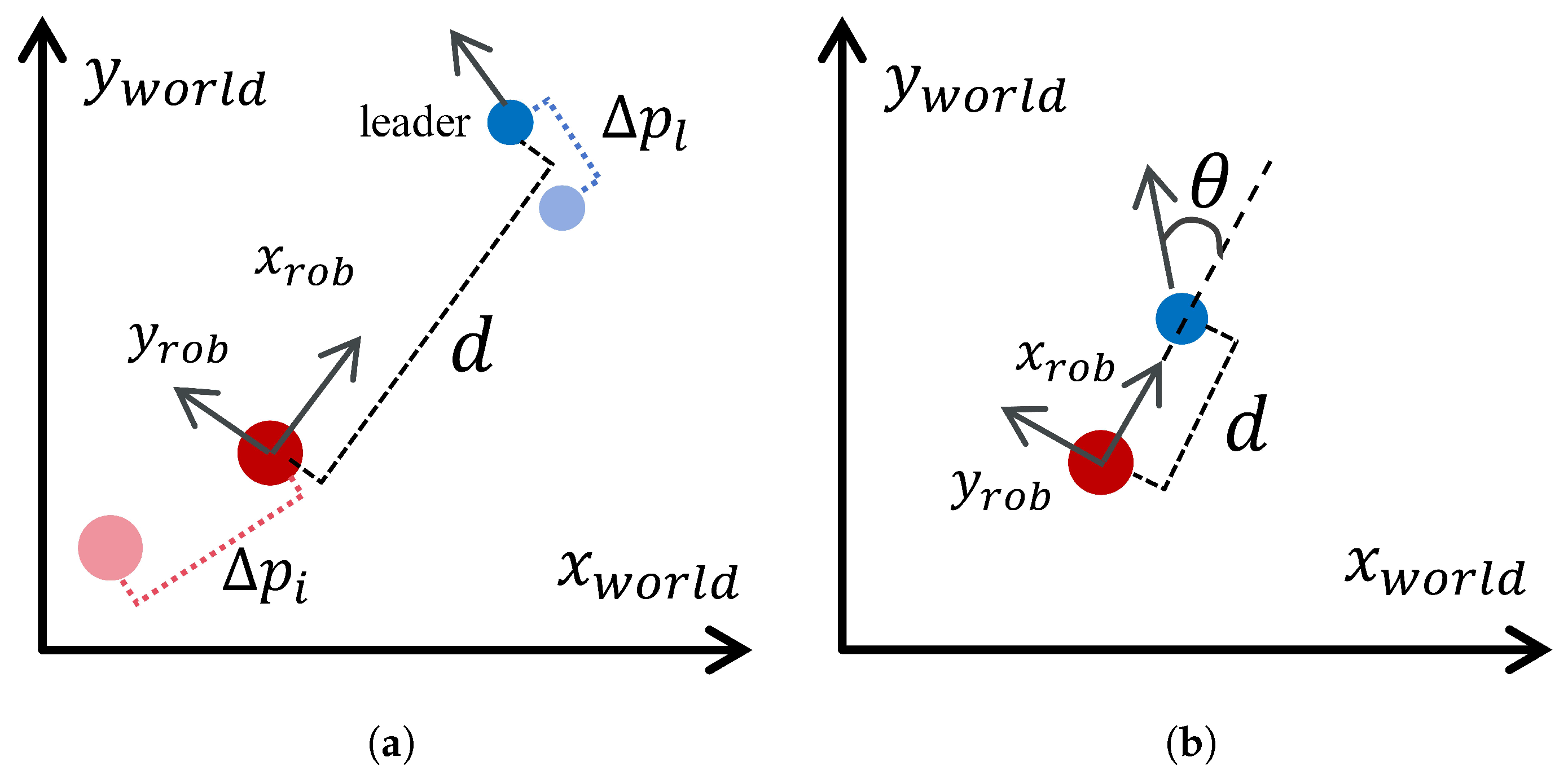
- Leader-centric formation: In Figure 2, the blue formation connecting lines are defined from the perspective of the leader’s local coordinate system. Each follower agent is required to track a predefined position within this coordinate system. This is the traditional leader–follower control paradigm in which followers adjust their positions to maintain a specific geometric relationship with the leader. The formation control problem can be formulated as follows:where denote the position of the leader agent, and denote the position of the i-th follower agent. represents the desired position of the i-th follower agent relative to the leader’s position .
- Follower-centric formation: In Figure 2, the orange formation connecting lines are defined from the perspective of each follower’s local coordinate system. Even when followers have not yet reached their desired positions in relation to the leader, they must maintain a specific formation among themselves. This means that each follower agent must track its own local formation position while also adjusting its position relative to the leader. This can be formulated as follows:where represents the desired relative position of the i-th follower agent with respect to another follower agent j.
4. Leader–Follower Formation Control Based on GPTD3
4.1. MOGP Design
4.2. Single-Agent Following TD3_1 Design
- State errors in the agent’s own coordinate system: These errors represent the deviations of the current state (position, velocity, heading angle, etc.) from the desired target state. Specifically, the errors in the x and y directions are used to quantify the difference between the agent’s current position and the target position. These errors are essential for guiding the agent toward the target.
- Cumulative state errors in the agent’s own coordinate system: By incorporating the cumulative errors in the x and y directions, the network can capture historical information about the agent’s performance. This helps the network to better understand the dynamic characteristics of the unknown system and adjust its policy accordingly. The cumulative errors provide a long-term perspective on the agent’s trajectory, which is crucial for learning stable and effective control policies.
- Changes in state errors in the agent’s own coordinate system: These reflect the trends of the errors over time. By considering the changes in the x and y direction errors, the network can predict future state evolution and make more informed decisions to correct the agent’s trajectory. The error changes provide insight into the system’s dynamics and help the network adapt to varying conditions.
4.3. Multi Agent Collaborative TD3_2 Design
- Neighbor positions relative to Agent i: The positions of neighboring agents within the local coordinate system of agent i.
- First-stage policy TD3_1 output: The output from the first-stage policy serves as an input to the compensation network, enabling it to refine and optimize the existing strategy further.
| Algorithm 1 GPTD3 algorithm for leader–follower formation control |
|
5. Results
5.1. Experimental Environment and Training Setting
5.2. MOGP Results
5.3. TD3_1 Results
5.4. TD3_2 Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Proskurnikov, A.; Cao, M. Consensus in Multi-Agent Systems. In Wiley Encyclopedia of Electrical and Electronics Engineering; Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, H.; Luo, Y.; Xiao, G. Data-Driven Optimal Consensus Control for Discrete-Time Multi-Agent Systems with Unknown Dynamics Using Reinforcement Learning Method. IEEE Trans. Ind. Electron. 2017, 64, 4091–4100. [Google Scholar] [CrossRef]
- Xu, Y.; Yuan, Y.; Liu, H. Event-driven MPC for leader-follower nonlinear multi-agent systems. In Proceedings of the 2018 3rd International Conference on Advanced Robotics and Mechatronics (ICARM), Singapore, 18–20 July 2018; pp. 526–531. [Google Scholar] [CrossRef]
- Bai, W.; Cao, L.; Dong, G.; Li, H. Adaptive Reinforcement Learning Tracking Control for Second-Order Multi-Agent Systems. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; pp. 202–207. [Google Scholar] [CrossRef]
- Tan, X. Distributed Adaptive Control for Second-order Leader-following Multi-agent Systems. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.A.; Yogamani, S.; Pérez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Wen, G.; Chen, C.L.P.; Li, B. Optimized Formation Control Using Simplified Reinforcement Learning for a Class of Multiagent Systems with Unknown Dynamics. IEEE Trans. Ind. Electron. 2020, 67, 7879–7888. [Google Scholar] [CrossRef]
- Mahdavi Golmisheh, F.; Shamaghdari, S. Optimal Robust Formation of Multi-Agent Systems as Adversarial Graphical Apprentice Games with Inverse Reinforcement Learning. IEEE Trans. Autom. Sci. Eng. 2025, 22, 4867–4880. [Google Scholar] [CrossRef]
- AlMania, Z.; Sheltami, T.; Ahmed, G.; Mahmoud, A.; Barnawi, A. Energy-Efficient Online Path Planning for Internet of Drones Using Reinforcement Learning. J. Sens. Actuator Netw. 2024, 13, 50. [Google Scholar] [CrossRef]
- Liu, H.; Feng, Z.; Tian, X.; Mai, Q. Adaptive predefined-time specific performance control for underactuated multi-AUVs: An edge computing-based optimized RL method. Ocean. Eng. 2025, 318, 120048. [Google Scholar] [CrossRef]
- Peng, H.; Shen, X. Multi-Agent Reinforcement Learning Based Resource Management in MEC- and UAV-Assisted Vehicular Networks. IEEE J. Sel. Areas Commun. 2021, 39, 131–141. [Google Scholar] [CrossRef]
- Xie, J.; Zhou, R.; Liu, Y.; Luo, J.; Xie, S.; Peng, Y.; Pu, H. Reinforcement-Learning-Based Asynchronous Formation Control Scheme for Multiple Unmanned Surface Vehicles. Appl. Sci. 2021, 11, 546. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Li, S.; Ye, Q.; Wang, C.; Xie, G. Decentralized Circle Formation Control for Fish-like Robots in the Real-world via Reinforcement Learning. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8814–8820. [Google Scholar] [CrossRef]
- Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement Learning for Selective Key Applications in Power Systems: Recent Advances and Future Challenges. IEEE Trans. Smart Grid 2022, 13, 2935–2958. [Google Scholar] [CrossRef]
- Chang, G.N.; Fu, W.X.; Cui, T.; Song, L.Y.; Dong, P. Distributed Consensus Multi-Distribution Filter for Heavy-Tailed Noise. J. Sens. Actuator Netw. 2024, 13, 38. [Google Scholar] [CrossRef]
- Umlauft, J.; Hirche, S. Feedback Linearization Based on Gaussian Processes with Event-Triggered Online Learning. IEEE Trans. Autom. Control 2020, 65, 4154–4169. [Google Scholar] [CrossRef]
- Berkenkamp, F.; Schoellig, A.P. Safe and robust learning control with Gaussian processes. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2496–2501. [Google Scholar] [CrossRef]
- Beckers, T.; Hirche, S.; Colombo, L. Online Learning-based Formation Control of Multi-Agent Systems with Gaussian Processes. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 13–17 December 2021; pp. 2197–2202. [Google Scholar] [CrossRef]
- Lederer, A.; Yang, Z.; Jiao, J.; Hirche, S. Cooperative Control of Uncertain Multiagent Systems via Distributed Gaussian Processes. IEEE Trans. Autom. Control 2023, 68, 3091–3098. [Google Scholar] [CrossRef]
- Dong, Z.; Shao, H.; Huang, H. Variable Impedance Control for Force Tracking Based on PILCO in Uncertain Environment. In Proceedings of the 2023 IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 6–9 August 2023; pp. 439–444. [Google Scholar] [CrossRef]
- Jendoubi, I.; Bouffard, F. Multi-agent hierarchical reinforcement learning for energy management. Appl. Energy 2023, 332, 120500. [Google Scholar] [CrossRef]
- Shi, Y.; Hua, Y.; Yu, J.; Dong, X.; Lü, J.; Ren, Z. Cooperative Fault-Tolerant Formation Tracking Control for Heterogeneous Air–Ground Systems Using a Learning-Based Method. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1505–1518. [Google Scholar] [CrossRef]
- Dong, X.; Shi, Y.; Hua, Y.; Yu, J.; Ren, Z. Robust Formation Tracking Control for Multi-Agent Systems Using Reinforcement Learning Methods. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2025. [Google Scholar] [CrossRef]
- Liu, S.; Wen, L.; Cui, J.; Yang, X.; Cao, J.; Liu, Y. Moving Forward in Formation: A Decentralized Hierarchical Learning Approach to Multi-Agent Moving Together. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4777–4784. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Y.Y. Formation Tracking of Spatiotemporal Multiagent Systems: A Decentralized Reinforcement Learning Approach. IEEE Syst. Man Cybern. Mag. 2024, 10, 52–60. [Google Scholar] [CrossRef]
- DeepSeek-AI. DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. arXiv 2025, arXiv:2501.12948. [Google Scholar]
- Andrychowicz, M.; Raichuk, A.; Stańczyk, P.; Orsini, M.; Girgin, S.; Marinier, R.; Hussenot, L.; Geist, M.; Pietquin, O.; Michalski, M.; et al. What Matters In On-Policy Reinforcement Learning? A Large-Scale Empirical Study. arXiv 2020, arXiv:2006.05990. [Google Scholar]
- Panteleev, A.; Karane, M. Application of a Novel Multi-Agent Optimization Algorithm Based on PID Controllers in Stochastic Control Problems. Mathematics 2023, 11, 2903. [Google Scholar] [CrossRef]
- Esfahani, H.N.; Velni, J.M. Cooperative Multi-Agent Q-Learning Using Distributed MPC. IEEE Control Syst. Lett. 2024, 8, 2193–2198. [Google Scholar] [CrossRef]
- Zhou, C.; Li, J.; Shi, Y.; Lin, Z. Research on Multi-Robot Formation Control Based on MATD3 Algorithm. Appl. Sci. 2023, 13, 1874. [Google Scholar] [CrossRef]
- Garcia, G.; Eskandarian, A.; Fabregas, E.; Vargas, H.; Farias, G. Cooperative Formation Control of a Multi-Agent Khepera IV Mobile Robots System Using Deep Reinforcement Learning. Appl. Sci. 2025, 15, 1777. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, X.; Jiang, Y.; Xu, X.; Liu, J. Leader-Follower Formation Control For Indoor Wheeled Robots Via Dual Heuristic Programming. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 600–605. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, H.; Lewis, F.L. Robust Formation Control for Cooperative Underactuated Quadrotors via Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4577–4587. [Google Scholar] [CrossRef] [PubMed]







| Abbreviation | Full Form | Description |
|---|---|---|
| AC | Actor–Critic | Algorithm |
| DDPG | Deep Deterministic Policy Gradient | Algorithm |
| GPs | Gaussian Processes | Statistical Model |
| GPTD3 | Gaussian Processes and TD3 | Algorithm |
| MAS | Multi-Agent System | System |
| MOGPs | Multi-Output Gaussian Processes | Statistical Model |
| MPC | Model Predictive Control | Control Strategy |
| MSE | Mean Squared Error | Metric |
| PID | Proportional Integral Differential | Control Strategy |
| PILCO | Probabilistic Inference for Learning Control | Algorithm |
| RBF | Radial Basis Function | Function |
| RL | Reinforcement Learning | Learning Paradigm |
| TD3 | Twin Delayed Deep Deterministic Policy Gradient | Algorithm |
| TD3_1 | Single-Agent Learning Network in GPTD3 | Algorithm |
| TD3_2 | Multi-Agent Compensation Network in GPTD3 | Algorithm |
| Method | Model Dependency | Adaptability | Convergence Speed | Robustness |
|---|---|---|---|---|
| PID | High | Poor | Moderate | Moderate |
| MPC | High | Moderate | Moderate | Moderate |
| AC | Low | Moderate | Moderate | Moderate |
| DDPG | Low | Good | Slow | Moderate |
| TD3 | Low | Good | Moderate | High |
| GPTD3 | Low | Good | Good | High |
| MOGP Mean | Linear Velocity (v) | Angular Velocity () |
|---|---|---|
| MSE | 0.00168 | 0.00197 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Jiang, B.; Deng, F.; Zhao, M. A Two-Stage Strategy Integrating Gaussian Processes and TD3 for Leader–Follower Coordination in Multi-Agent Systems. J. Sens. Actuator Netw. 2025, 14, 51. https://doi.org/10.3390/jsan14030051
Zhang X, Jiang B, Deng F, Zhao M. A Two-Stage Strategy Integrating Gaussian Processes and TD3 for Leader–Follower Coordination in Multi-Agent Systems. Journal of Sensor and Actuator Networks. 2025; 14(3):51. https://doi.org/10.3390/jsan14030051
Chicago/Turabian StyleZhang, Xicheng, Bingchun Jiang, Fuqin Deng, and Min Zhao. 2025. "A Two-Stage Strategy Integrating Gaussian Processes and TD3 for Leader–Follower Coordination in Multi-Agent Systems" Journal of Sensor and Actuator Networks 14, no. 3: 51. https://doi.org/10.3390/jsan14030051
APA StyleZhang, X., Jiang, B., Deng, F., & Zhao, M. (2025). A Two-Stage Strategy Integrating Gaussian Processes and TD3 for Leader–Follower Coordination in Multi-Agent Systems. Journal of Sensor and Actuator Networks, 14(3), 51. https://doi.org/10.3390/jsan14030051






