Enhancing Mental Fatigue Detection through Physiological Signals and Machine Learning Using Contextual Insights and Efficient Modelling
Abstract
1. Introduction
- How can context awareness be integrated into a traditional ML modeling process when implementing a cognitive fatigue detection system?
- How can we account for the time-related feature variability associated with mental fatigue in the ML modeling process?
- How can we attain high performance while utilizing ML algorithms and working with a small dataset?
2. Related Work
- The correct choice of input data features in ML predictive models is critical and should be controlled efficiently. Therefore, we integrate a feature selection process that combines both numerical and contextual analysis. It is noteworthy that most literature studies do not take into account contextual information when selecting features to train their ML models. They rely on the correlation between the features and the model’s target output or simply integrate the maximum number of features to achieve a high accuracy. However, we highlight that a high accuracy does not necessarily guarantee a relevant model output. Indeed, some features may be influenced by the context of the study, and their use in an ML model may be questionable;
- The ML models used to capture time-related variations associated with mental fatigue often rely on complex models, such as RNN and LSTM. While these models excel in learning feature characteristics and their temporal variability, integrating them into real-time applications using wearable devices with limited processing capacity is challenging. To address this constraint, we employ a feature sequencing and set compression technique to prepare time-series “like” data for presentation to ML algorithms that are not specialized in processing sequential data. We demonstrate that this technique enhances the model accuracy. Notably, our model was used to detect mental fatigue using physiological signals from [30] and achieved a maximum accuracy of 98%.
3. Materials and Methods
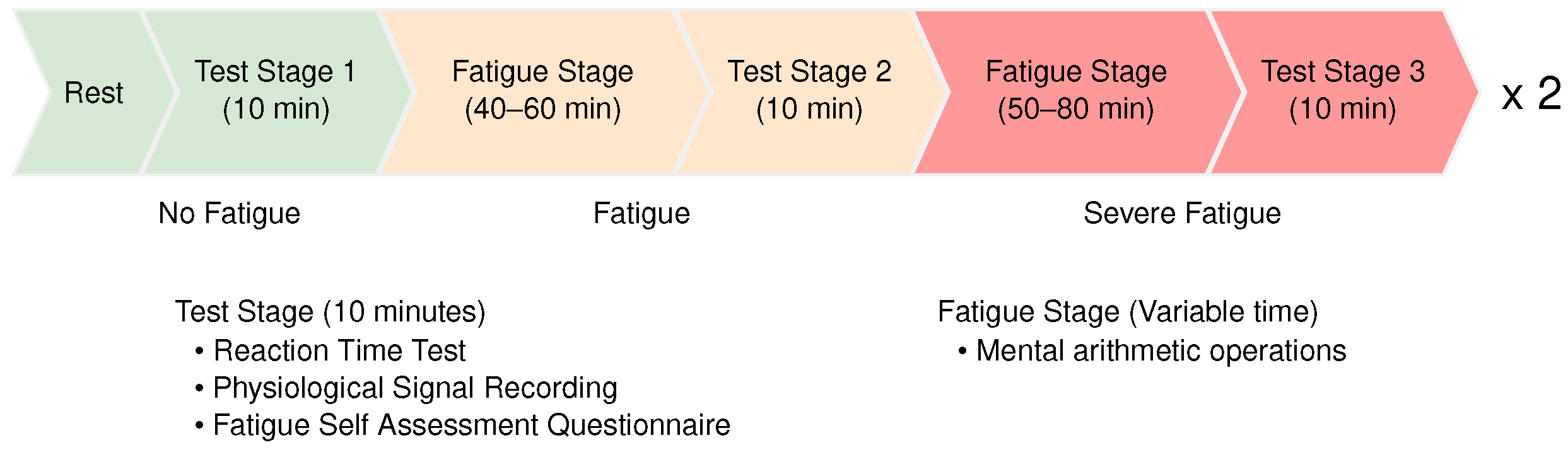
3.1. Data Description
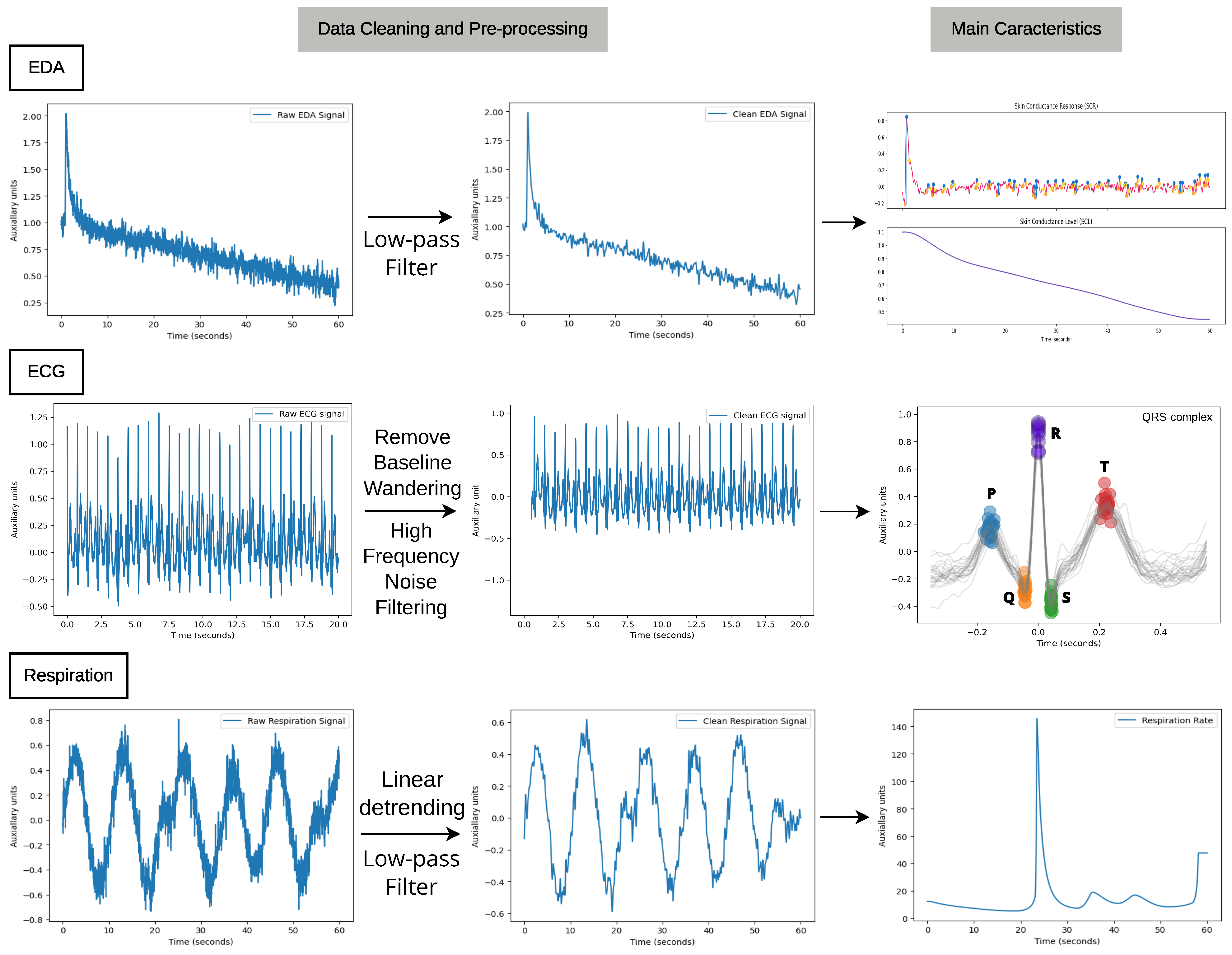
3.2. Data Cleaning
3.2.1. Electrodermal Activity (EDA)
3.2.2. Electrocardiogram (ECG)
3.2.3. Respiration
3.3. Feature Engineering
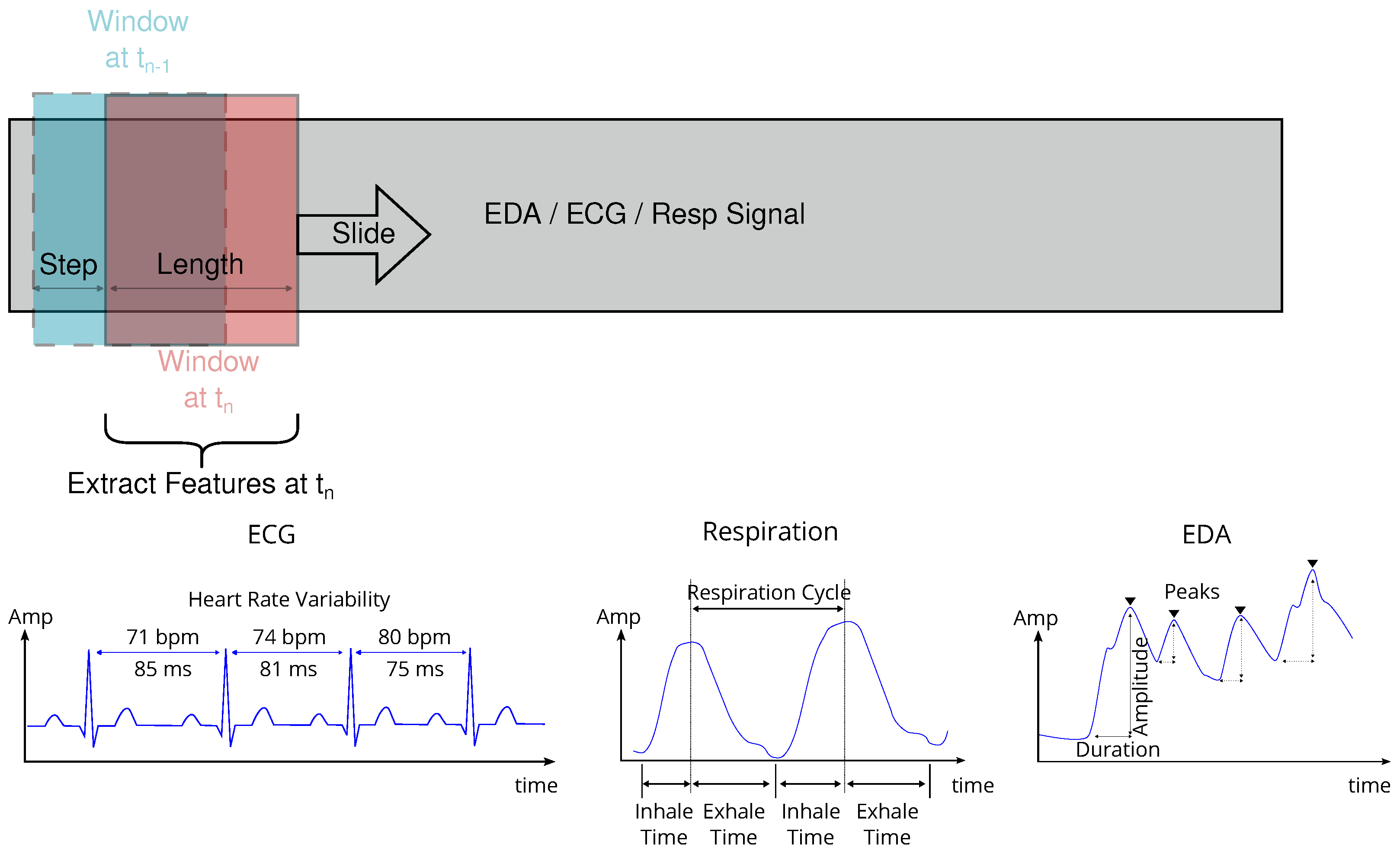
3.3.1. Windowing
3.3.2. Feature Extraction
3.3.3. Features Selection
4. Modeling
5. Results and Discussion
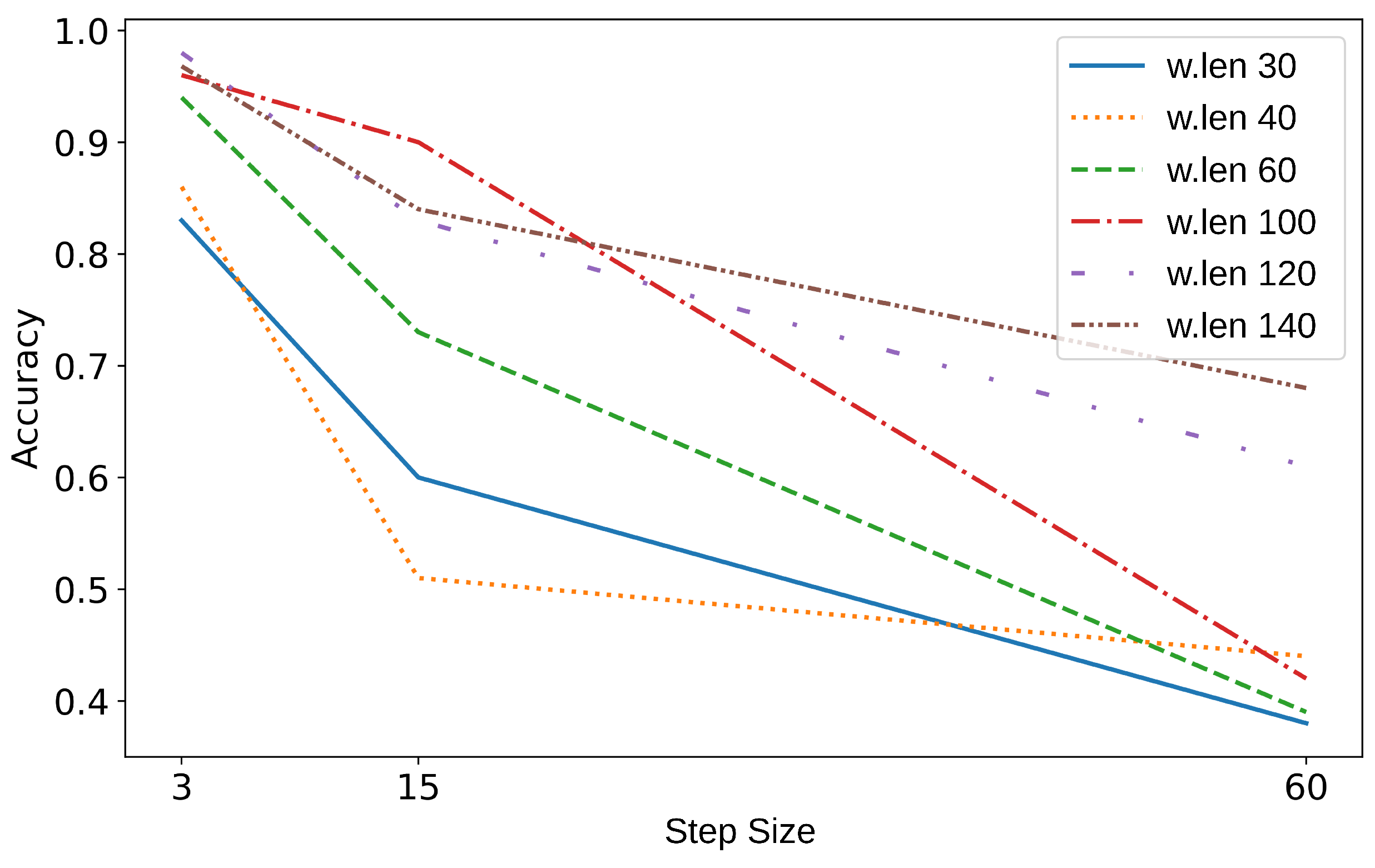
5.1. Windowing Analysis
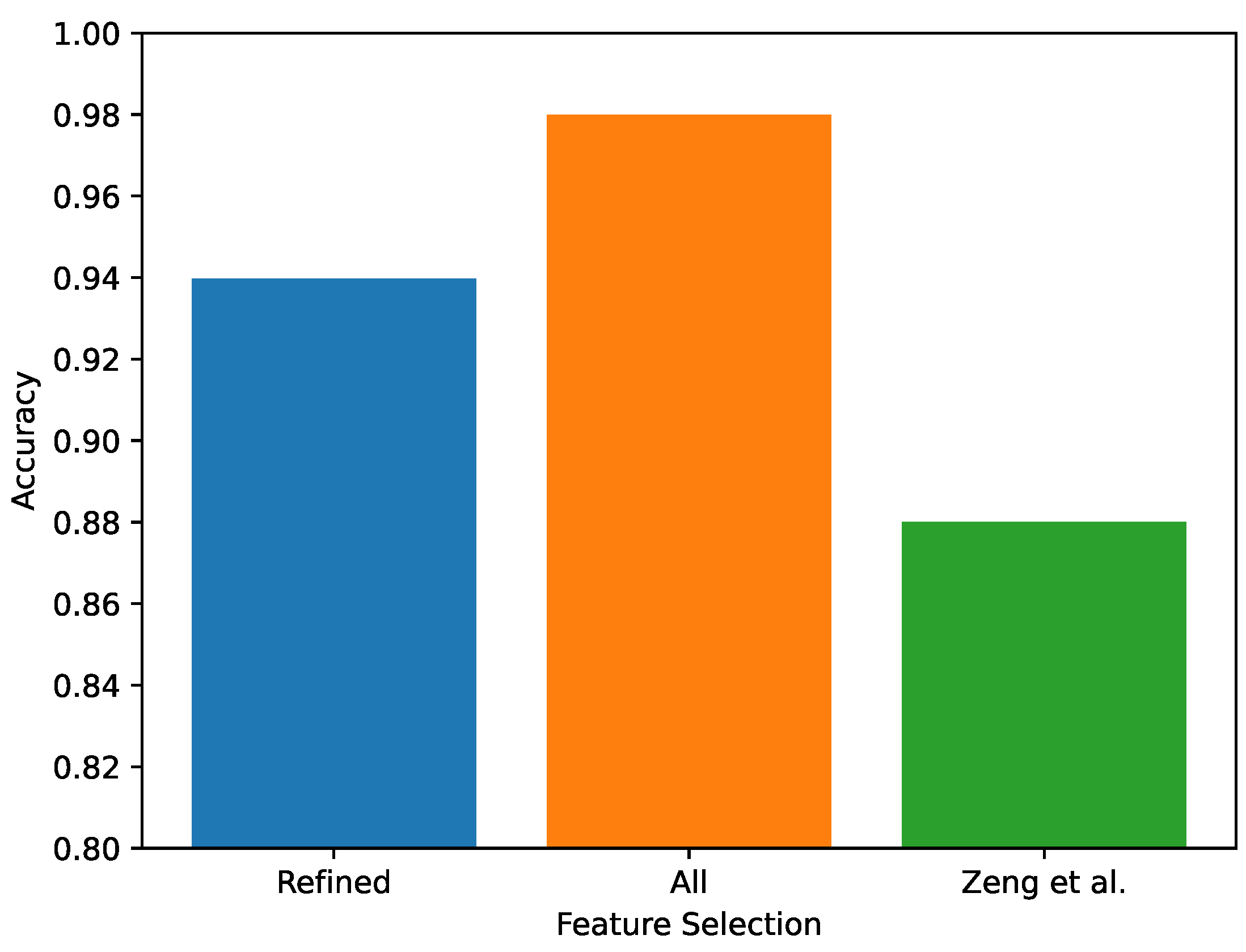
5.2. Feature Selection Analysis
- Refined features (our selected features): SCR.mean.amp, SCR.mean.dur, mHR, HRV.-MeanNN, HRV.SDNN, and RSP.rate;
- Zeng et al.’s features (i.e., the features used in [30]): SCR.peak.rate, SCR.amp.sum, SCR.dur.sum, mHR, HRV.SDNN, and RSP.rate;
- All features from Table 2: the commonly used features in the literature, including our selected features and those of Zeng et al.
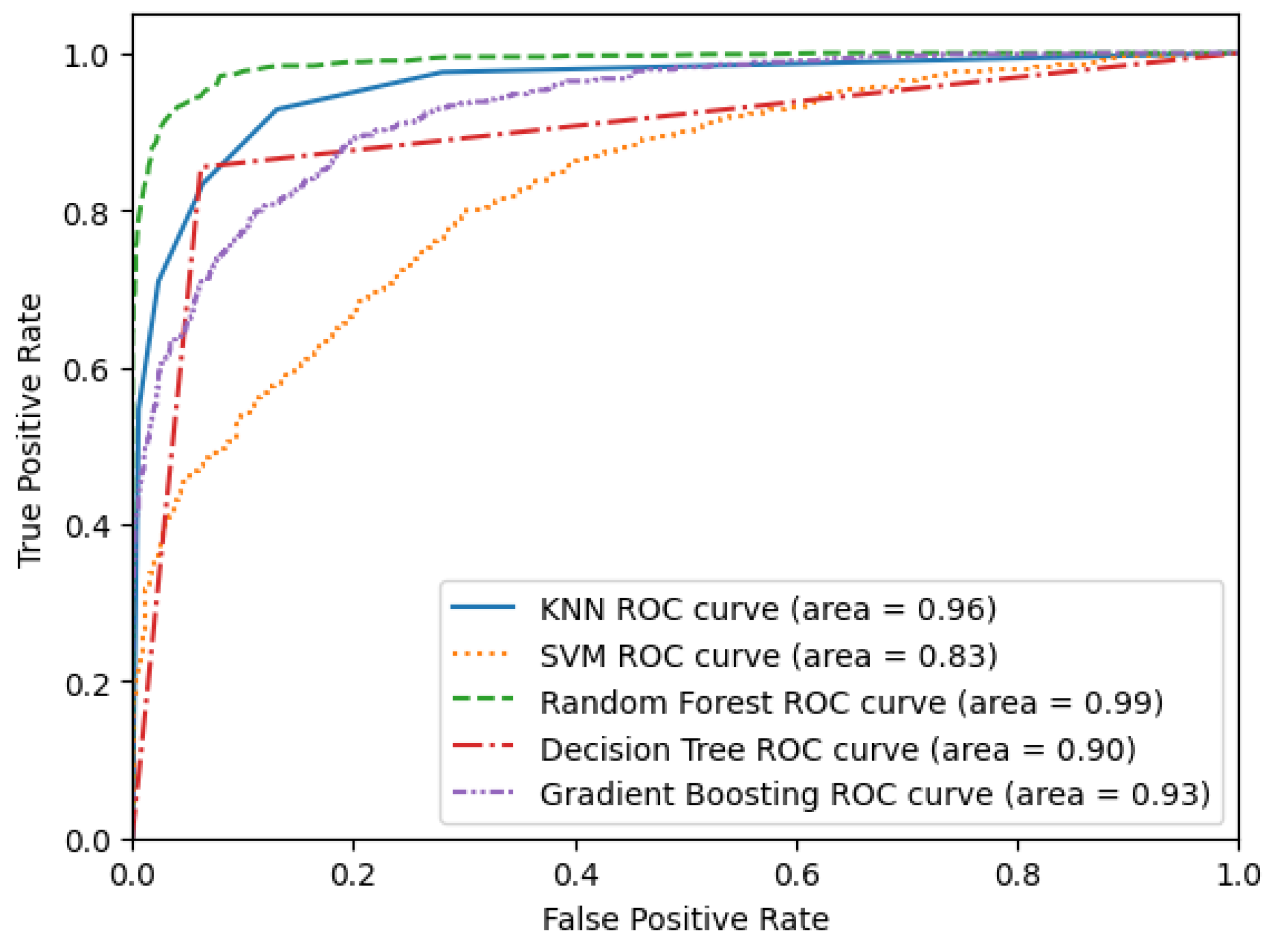
5.3. Classification Algorithm Analysis
5.4. Cross-Validation Analysis
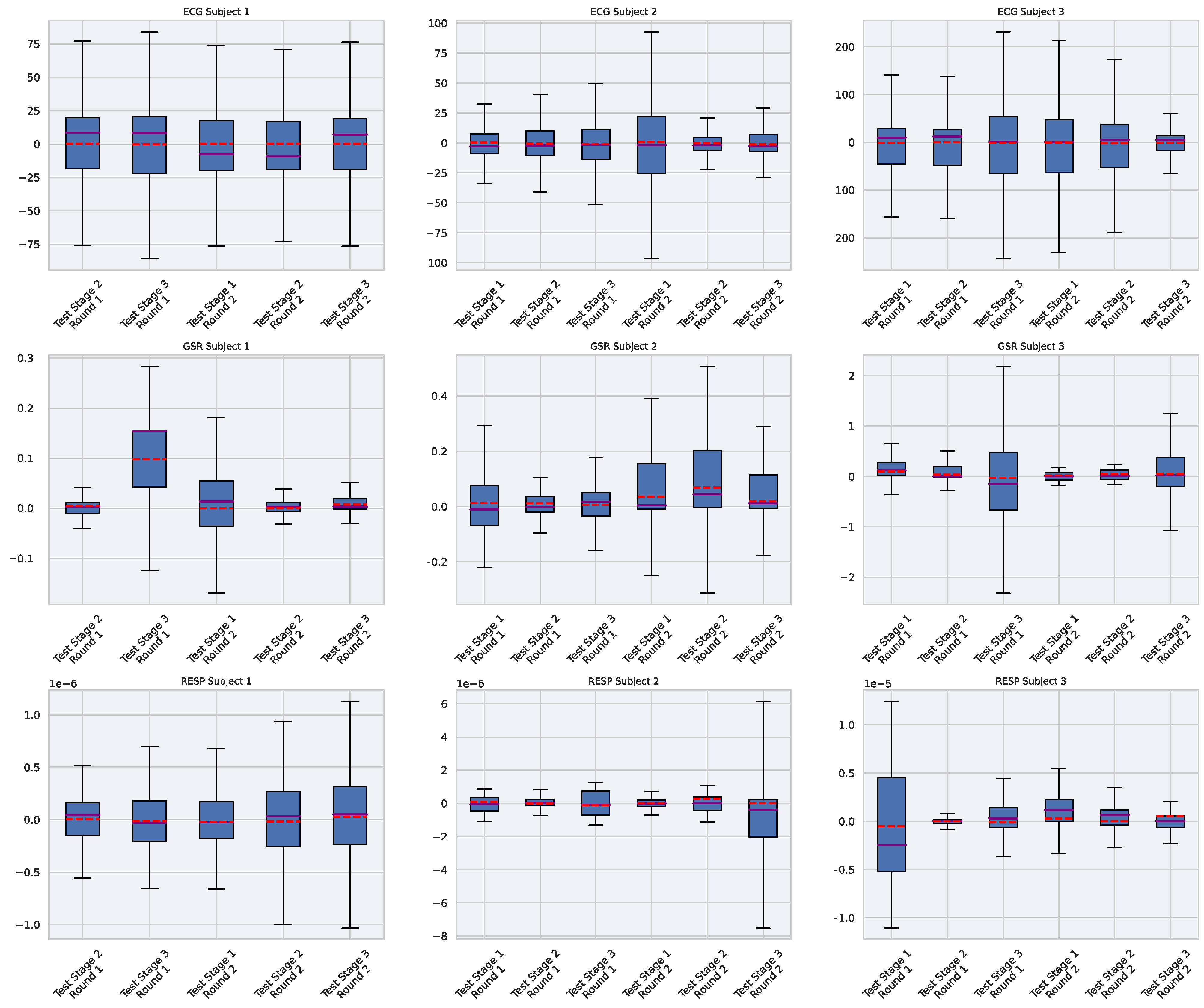
5.5. Per Subject Variability Analysis
6. Conclusions and Perspective
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECG | Electrocardiogram |
| EDA | Electrodermal Activity |
| SDNN | Standard Deviation of all NN intervals |
| KNN | K-nearest neighbor |
| DT | Decision Tree |
| HRV | Heart Rate Variability |
| SVM | Support vector machines |
| GB | Gradient Boosting |
| ROC | Receiver Operating Characteristic |
| AUC | The area under the ROC curve |
| SCL | Skin Conductance Level |
| PSD | Power Spectral Density |
References
- Wang, Q.; Yang, J.; Ren, M.; Zheng, Y. Driver Fatigue Detection: A Survey. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 2, pp. 8587–8591. [Google Scholar] [CrossRef]
- Wang, X.; Xu, C. Driver drowsiness detection based on non-intrusive metrics considering individual specifics. Accid. Anal. Prev. 2016, 95, 350–357. [Google Scholar] [CrossRef] [PubMed]
- Brown, I.D. Driver Fatigue. Hum. Factors 1994, 36, 298–314. [Google Scholar] [CrossRef] [PubMed]
- Brookhuis, K.A.; de Waard, D. Monitoring drivers’ mental workload in driving simulators using physiological measures. Accid. Anal. Prev. 2010, 42, 898–903. [Google Scholar] [CrossRef]
- Dingus, T.A. Development of Models for Detection of Automobile Driver Impairment. Ph.D. Thesis, Faculty of Virginia Polytechnic Institute, Blacksburg, VA, USA, 1985. [Google Scholar]
- Thiffault, P.; Bergeron, J. Monotony of Road Environment and Driver Fatigue: A Simulator Study. Accid. Anal. Prev. 2003, 35, 381–391. [Google Scholar] [CrossRef] [PubMed]
- Weng, C.H.; Lai, Y.H.; Lai, S.H. Driver Drowsiness Detection via a Hierarchical Temporal Deep Belief Network. In Proceedings of the Computer Vision—ACCV 2016 Workshops, Taipei, Taiwan, 20–24 November 2016; Chen, C.S., Lu, J., Ma, K.K., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2017; pp. 117–133. [Google Scholar] [CrossRef]
- Benzo, R.M.; Farag, A.; Whitaker, K.M.; Xiao, Q.; Carr, L.J. Examining the Impact of 12-Hour Day and Night Shifts on Nurses’ Fatigue: A Prospective Cohort Study. Int. J. Nurs. Stud. Adv. 2022, 4, 100076. [Google Scholar] [CrossRef]
- Givi, Z.; Jaber, M.; Neumann, W. Modelling Worker Reliability with Learning and Fatigue. Appl. Math. Model. 2015, 39, 5186–5199. [Google Scholar] [CrossRef]
- Bentall, R.P.; Wood, G.C.; Marrinan, T.; Deans, C.; Edwards, R.H.T. A Brief Mental Fatigue Questionnaire. Br. J. Clin. Psychol. 1993, 32, 375–377. [Google Scholar] [CrossRef]
- Shahid, A.; Wilkinson, K.; Marcu, S.; Shapiro, C.M. Visual Analogue Scale to Evaluate Fatigue Severity (VAS-F). In STOP, THAT and One Hundred Other Sleep Scales; Shahid, A., Wilkinson, K., Marcu, S., Shapiro, C.M., Eds.; Springer: New York, NY, USA, 2011; pp. 399–402. [Google Scholar] [CrossRef]
- Lee, I.S.; Bardwell, W.A.; Ancoli-Israel, S.; Dimsdale, J.E. Number of Lapses during the Psychomotor Vigilance Task as an Objective Measure of Fatigue. J. Clin. Sleep Med. 2010, 6, 163–168. [Google Scholar] [CrossRef]
- Stancin, I.; Cifrek, M.; Jovic, A. A Review of EEG Signal Features and Their Application in Driver Drowsiness Detection Systems. Sensors 2021, 21, 3786. [Google Scholar] [CrossRef]
- Hasan, M.M.; Watling, C.N.; Larue, G.S. Physiological signal-based drowsiness detection using machine learning: Singular and hybrid signal approaches. J. Saf. Res. 2022, 80, 215–225. [Google Scholar] [CrossRef]
- Heaton, K.J.; Williamson, J.R.; Lammert, A.C.; Finkelstein, K.R.; Haven, C.C.; Sturim, D.; Smalt, C.J.; Quatieri, T.F. Predicting changes in performance due to cognitive fatigue: A multimodal approach based on speech motor coordination and electrodermal activity. Clin. Neuropsychol. 2020, 34, 1190–1214. [Google Scholar] [CrossRef] [PubMed]
- Adão Martins, N.R.; Annaheim, S.; Spengler, C.M.; Rossi, R.M. Fatigue Monitoring Through Wearables: A State-of-the-Art Review. Front. Physiol. 2021, 12, 2285. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Li, P.; Lin, H.; Rohani, E.; Choi, G.; Shao, B.; Wang, Q. Support Vector Machine Based Detection of Drowsiness Using Minimum EEG Features. In Proceedings of the 2013 International Conference on Social Computing, Alexandria, VA, USA, 8–14 September 2013; pp. 827–835. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Kodagoda, S.; Lal, S.; Dissanayake, G. Driver Drowsiness Classification Using Fuzzy Wavelet-Packet-Based Feature-Extraction Algorithm. IEEE Trans. Biomed. Eng. 2011, 58, 121–131. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Li, W.; Fan, X.; Fei, Z. Driver fatigue evaluation model with integration of multi-indicators based on dynamic Bayesian network. IET Intell. Transp. Syst. 2015, 9, 547–554. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, R.; Zhang, K.; Pan, Y.; Wu, J. The Impairing Effect of Mental Fatigue on Visual Sustained Attention under Monotonous Multi-Object Visual Attention Task in Long Durations: An Event-Related Potential Based Study. PLoS ONE 2016, 11, e0163360. [Google Scholar] [CrossRef] [PubMed]
- McNaboe, R.; Beardslee, L.; Kong, Y.; Smith, B.N.; Chen, I.P.; Posada-Quintero, H.F.; Chon, K.H. Design and Validation of a Multimodal Wearable Device for Simultaneous Collection of Electrocardiogram, Electromyogram, and Electrodermal Activity. Sensors 2022, 22, 8851. [Google Scholar] [CrossRef]
- Matuz, A.; Van Der Linden, D.; Kisander, Z.; Hernádi, I.; Kázmér, K.; Csathó, Á. Enhanced Cardiac Vagal Tone in Mental Fatigue: Analysis of Heart Rate Variability in Time-on-Task, Recovery, and Reactivity. PLoS ONE 2021, 16, e0238670. [Google Scholar] [CrossRef]
- Egelund, N. Spectral analysis of heart rate variability as an indicator of driver fatigue. Ergonomics 1982, 25, 663–672. [Google Scholar] [CrossRef]
- Abdul Rahim, H.; Dalimi, A.; Jaafar, H. Detecting Drowsy Driver Using Pulse Sensor. J. Teknol. 2015, 73, 5–8. [Google Scholar] [CrossRef][Green Version]
- Patel, M.; Lal, S.; Kavanagh, D.; Rossiter, P. Applying neural network analysis on heart rate variability data to assess driver fatigue. Expert Syst. Appl. 2011, 38, 7235–7242. [Google Scholar] [CrossRef]
- Abbas, Q.; Ibrahim, M.E.; Khan, S.; Baig, A.R. Hypo-Driver: A Multiview Driver Fatigue and Distraction Level Detection System. Comput. Mater. Contin. 2022, 71, 1999–2007. [Google Scholar] [CrossRef]
- Wang, D.; Shen, P.; Wang, T.; Xiao, Z. Fatigue Detection of Vehicular Driver through Skin Conductance, Pulse Oximetry and Respiration: A Random Forest Classifier. In Proceedings of the 2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), Guangzhou, China, 6–8 May 2017; pp. 1162–1166. [Google Scholar] [CrossRef]
- Malathi, D.; Dorathi Jayaseeli, J.; Madhuri, S.; Senthilkumar, K. Electrodermal Activity Based Wearable Device for Drowsy Drivers. J. Phys. Conf. Ser. 2018, 1000, 012048. [Google Scholar] [CrossRef]
- Williamson, J.R.; Heaton, K.J.; Lammert, A.; Finkelstein, K.; Sturim, D.; Smalt, C.; Ciccarelli, G.; Quatieri, T.F. Audio, Visual, and Electrodermal Arousal Signals as Predictors of Mental Fatigue Following Sustained Cognitive Work. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 832–836. [Google Scholar] [CrossRef]
- Zeng, Z.; Huang, Z.; Leng, K.; Han, W.; Niu, H.; Yu, Y.; Ling, Q.; Liu, J.; Wu, Z.; Zang, J. Nonintrusive Monitoring of Mental Fatigue Status Using Epidermal Electronic Systems and Machine-Learning Algorithms. ACS Sens. 2020, 5, 1305–1313. [Google Scholar] [CrossRef]
- Makowski, D.; Pham, T.; Lau, Z.J.; Brammer, J.C.; Lespinasse, F.; Pham, H.; Schölzel, C.; Chen, S.H.A. NeuroKit2: A Python toolbox for neurophysiological signal processing. Behav. Res. Methods 2021, 53, 1689–1696. [Google Scholar] [CrossRef]
- Braithwaite, J.J.; Watson, D.G.; Jones, R.; Rowe, M. A guide for analysing electrodermal activity (EDA) & skin conductance responses (SCRs) for psychological experiments. Psychophysiology 2013, 49, 1017–1034. [Google Scholar]
- Chavan, M.S.; Agarwala, R.; Uplane, M. Suppression of baseline wander and power line interference in ECG using digital IIR filter. Int. J. Circuits Syst. Signal Process. 2008, 2, 356–365. [Google Scholar]
- Bui, N.T.; Byun, G.s. The Comparison Features of ECG Signal with Different Sampling Frequencies and Filter Methods for Real-Time Measurement. Symmetry 2021, 13, 1461. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, BME-32, 230–236. [Google Scholar] [CrossRef]
- Khodadad, D.; Nordebo, S.; Müller, B.; Waldmann, A.; Yerworth, R.; Becher, T.; Frerichs, I.; Sophocleous, L.; Van Kaam, A.; Miedema, M.; et al. Optimized breath detection algorithm in electrical impedance tomography. Physiol. Meas. 2018, 39, 094001. [Google Scholar] [CrossRef]
- Lambert, A.; Soni, A.; Soukane, A.; Cherif, A.; Rabat, A. Artificial Intelligence Modelling Human Mental Fatigue: A Comprehensive Survey. Neurocomputing 2023. accepted. [Google Scholar] [CrossRef]
- Bonaccorso, G. Machine Learning Algorithms: A Reference Guide to Popular Algorithms for Data Science and Machine Learning; Packt Publishing: Birmingham, UK, 2017. [Google Scholar]
- SAYKRS, B. Analysis of Heart Rate Variability. Ergonomics 1973, 16, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Malik, M.; Bigger, J.T.; Camm, A.J.; Kleiger, R.E.; Malliani, A.; Moss, A.J.; Schwartz, P.J. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Eur. Heart J. 1996, 17, 354–381. [Google Scholar] [CrossRef]
- Karrer, K.; Vöhringer-Kuhnt, T.; Baumgarten, T.; Briest, S. The role of individual differences in driver fatigue prediction. In Proceedings of the Third International Conference on Traffic and Transport Psychology, Nottingham, UK; 2004; pp. 5–9. [Google Scholar]



| Signal | Sampling Interval (ms) | Sampling Frequency (Hz) | Full Length of the Analysed Signal |
|---|---|---|---|
| ECG | 5 | 200 | 120,000 |
| EDA | 100 | 10 | 6000 |
| Respiration | 120 | 8.33 | 5000 |
| Signal | Feature | Description | Var. | Corr. f.stage | Sel |
|---|---|---|---|---|---|
| EDA | SCR.peak.rate | Number of SCR peaks. | 0.042 | 0.31 | |
| SCR.amp.sum | Sum of SCR peak amplitudes. | 0.019 | 0.15 | ||
| SCR.dur.sum | Sum of SCR peak durations. | 0.033 | 0.26 | ||
| SCR.mean.amp | Mean amplitude of SCR peaks. | 0.037 | 0.26 | ✓ | |
| SCR.mean.dur | Mean duration of SCR peaks. | 0.0085 | 0.24 | ✓ | |
| mean.SCL | Mean value of tonic activity. | 0.029 | 0.14 | ||
| SCL.SD | Standard deviation of tonic activity. | 0.027 | 0.1 | ||
| ECG | mHR | Mean heart rate. | 0.041 | 0.17 | ✓ |
| HRV.MeanNN | Mean of the RR intervals. | 0.044 | 0.18 | ✓ | |
| HRV.SDNN | Standard deviation of the RR intervals. | 0.038 | 0.1 | ✓ | |
| HRV.VLF | Very low frequency (0.0033–0.04 Hz) spectral power. | 0 | 0 | ||
| HRV.LF | Low frequency (0.04–0.15 Hz) spectral power. | 0.060 | 0.09 | ||
| HRV.HF | High frequency (0.15–0.4 Hz) spectral power. | 0.046 | 0.12 | ||
| HRV.VHF | Very high-frequency (0.4–0.5 Hz) spectral power. | 0.025 | 0.11 | ||
| HRV.LFHF | Ratio of low-frequency power to high-frequency power. | 0.018 | 0.12 | ||
| Respiration | RSP.rate | Mean breathing rate. | 0.038 | 0.31 | ✓ |
| Feature | Score | p |
|---|---|---|
| SCR.mean.amp | 67.30 | |
| SCR.mean.dur | 73.16 | |
| mHR | 14.43 | |
| HRV.MeanNN | 14.86 | |
| HRV.SDNN | 83.39 | |
| RSP.rate | 120.99 |
| Model | Accuracy without TS Feature Set Conversion | F1-Score without TS Feature Set Conversion | Accuracy with 2 Windows | F1-Score with 2 Windows | Accuracy with 3 Windows | F1-Score with 3 Windows | Accuracy with 5 Windows | F1-Score with 5 Windows |
|---|---|---|---|---|---|---|---|---|
| SVM | 0.66 | 0.66 | 0.64 | 0.64 | 0.65 | 0.64 | 0.7 | 0.7 |
| KNN | 0.87 | 0.87 | 0.85 | 0.85 | 0.85 | 0.85 | 0.88 | 0.88 |
| DT | 0.85 | 0.85 | 0.83 | 0.83 | 0.81 | 0.81 | 0.8 | 0.8 |
| GB | 0.83 | 0.84 | 0.82 | 0.83 | 0.8 | 0.8 | 0.82 | 0.82 |
| RF | 0.94 | 0.94 | 0.96 | 0.96 | 0.96 | 0.96 | 0.98 | 0.98 |
| K-Fold | Accuracy | F1-Score |
|---|---|---|
| 1 | 0.98 | 0.98 |
| 2 | 0.95 | 0.95 |
| 3 | 0.96 | 0.96 |
| 4 | 0.96 | 0.96 |
| 5 | 0.95 | 0.95 |
| Average | 0.96 | 0.96 |
| Train | Re-Train | Test | Accuracy on Test without Re-Training | F1-Score on Test without Re-Training | Accuracy on Test (80%) with Re-Training (20%) | F1-Score on Test (80%) with Re-Training (20%) |
|---|---|---|---|---|---|---|
| Subject 1 and 2 | Subject 3 | Subject 3 | 0.68 | 0.68 | 0.88 | 0.88 |
| Subject 2 and 3 | Subject 1 | Subject 1 | 0.7 | 0.69 | 0.93 | 0.93 |
| Subject 3 and 1 | Subject 2 | Subject 2 | 0.7 | 0.6 | 0.88 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cos, C.-A.; Lambert, A.; Soni, A.; Jeridi, H.; Thieulin, C.; Jaouadi, A. Enhancing Mental Fatigue Detection through Physiological Signals and Machine Learning Using Contextual Insights and Efficient Modelling. J. Sens. Actuator Netw. 2023, 12, 77. https://doi.org/10.3390/jsan12060077
Cos C-A, Lambert A, Soni A, Jeridi H, Thieulin C, Jaouadi A. Enhancing Mental Fatigue Detection through Physiological Signals and Machine Learning Using Contextual Insights and Efficient Modelling. Journal of Sensor and Actuator Networks. 2023; 12(6):77. https://doi.org/10.3390/jsan12060077
Chicago/Turabian StyleCos, Carole-Anne, Alexandre Lambert, Aakash Soni, Haifa Jeridi, Coralie Thieulin, and Amine Jaouadi. 2023. "Enhancing Mental Fatigue Detection through Physiological Signals and Machine Learning Using Contextual Insights and Efficient Modelling" Journal of Sensor and Actuator Networks 12, no. 6: 77. https://doi.org/10.3390/jsan12060077
APA StyleCos, C.-A., Lambert, A., Soni, A., Jeridi, H., Thieulin, C., & Jaouadi, A. (2023). Enhancing Mental Fatigue Detection through Physiological Signals and Machine Learning Using Contextual Insights and Efficient Modelling. Journal of Sensor and Actuator Networks, 12(6), 77. https://doi.org/10.3390/jsan12060077






