Genomic Predictions Using Low-Density SNP Markers, Pedigree and GWAS Information: A Case Study with the Non-Model Species Eucalyptus cladocalyx
Abstract
:1. Introduction
2. Results
2.1. SNP Data and Comparison of Genomic Prediction Models
2.2. Heritability Estimates
3. Discussion
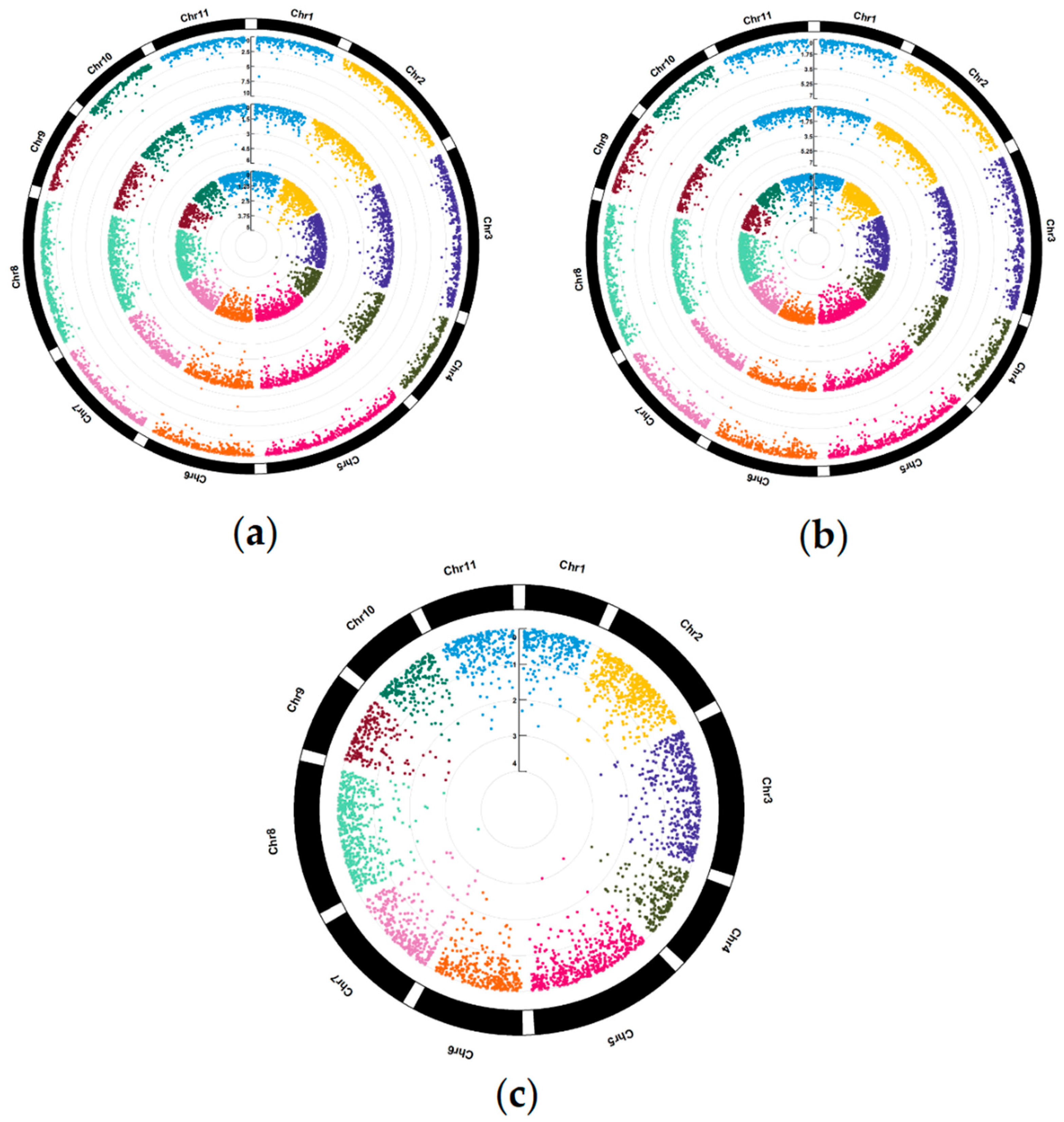
3.1. Marker-Trait Associations for All Studied Traits
3.2. Comparison between Genomic Prediction Models
3.3. Heritability Estimates
4. Materials and Methods
4.1. Plant Material and Phenotypic Evaluation
4.2. DNA Extraction and Tree Genotyping
4.3. Genomic Prediction Models
4.4. Heritability Estimates
4.5. Comparison between Genomic Prediction Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Viana, J.; Pereira, H.D.; Mundim, G.B.; Piepho, H.-P.; Fonseca e Silva, F. Efficiency of genomic prediction of non-assessed single crosses. Heredity 2018, 120, 283–295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, D.; Wang, X.; Kumar, U.; Gao, L.; Noor, M.; Imtiaz, M.; Singh, R.P.; Poland, J. High-throughput phenotyping enabled genetic dissection of crop lodging in wheat. Front. Plant Sci. 2019, 10, 394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Contreras-Soto, R.I.; Mora, F.; De Oliveira, M.A.R.; Higashi, W.; Scapim, C.A.; Schuster, I. A genome-wide association study for agronomic traits in soybean using SNP markers and SNP-based haplotype analysis. PLoS ONE 2017, 12, e0171105. [Google Scholar] [CrossRef]
- Maldonado, C.; Mora, F.; Scapim, C.A.; Coan, M. Genome-wide haplotype-based association analysis of key traits of plant lodging and architecture of maize identifies major determinants for leaf angle: hapLA4. PLoS ONE 2019, 14, e0212925. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senhorinho, H.J.C.; Coan, M.M.D.; Marino, T.P.; Kuki, M.C.; Barth-Pinto, R.S.; Scapim, C.A.; Holland, J.B. Genomic-Wide Association Study of Popping Expansion in Tropical Popcorn and Field Corn Germplasm. Crop Sci. 2019, 59, 2007–2019. [Google Scholar] [CrossRef] [Green Version]
- Mafra, G.S.; Do Amaral Júnior, A.T.; Almeida, F.J.E.D.; Vivas, M.; Araújo Diniz-Santos, P.H.; Saltires-Santos, J.; Ferreira-Pena, G.; De Lima, V.J.; Kamphorst, S.H.; De Oliveira, F.T.; et al. SNP-based mixed model association of growth-and yield-related traits in popcorn. PLoS ONE 2019, 14, e0218552. [Google Scholar] [CrossRef]
- Silva-Junior, O.B.; Faria, D.A.; Grattapaglia, D. A flexible multi-species genome-wide 60K SNP chip developed from pooled resequencing of 240 Eucalyptus tree genomes across 12 species. New Phytol. 2015, 206, 1527–1540. [Google Scholar] [CrossRef] [Green Version]
- Torres-Dini, D.; Nunes, A.C.P.; Aguiar, A.; Nikichuk, N.; Centurión, C.; Cabrera, M.; Moraes, M.L.T.; Resende, M.D.V.; Sebbenn, A.M. Clonal selection of Eucalyptus grandis x Eucalyptus globulus for productivity, adaptability, and stability, using SNP markers. Silvae Genet 2016, 65, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Klápště, J.; Suontama, M.; Telfer, E.; Graham, N.; Low, C.; Stovold, T.; McKinley, R.; Dumgey, H. Exploration of genetic architecture through sib-ship reconstruction in advanced breeding population of Eucalyptus nitens. PLoS ONE 2017, 12, e0185137. [Google Scholar] [CrossRef] [Green Version]
- Durán, R.; Isik, F.; Zapata-Valenzuela, J.; Balocchi, C.; Valenzuela, S. Genomic predictions of breeding values in a cloned Eucalyptus globulus population in Chile. Tree Genet Genomes 2017, 13, 74. [Google Scholar] [CrossRef]
- Suontama, M.; Klápště, J.; Telfer, E.; Graham, N.; Stovold, T.; Low, C.; McKinley, R.; Dungey, H. Efficiency of genomic prediction across two Eucalyptus nitens seed orchards with different selection histories. Heredity 2019, 122, 370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ballesta, P.; Maldonado, C.; Pérez-Rodríguez, P.; Mora, F. SNP and Haplotype-Based Genomic Selection of Quantitative Traits in Eucalyptus globulus. Plants 2019, 8, 331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aguirre, N.C.; Filippi, C.V.; Zaina, G.; Rivas, J.G.; Acuña, C.V.; Villalba, P.V.; García, M.N.; González, S.; Rivarola, M.; Maetínez, M.C. Optimizing ddRADseq in non-model species: A case study in Eucalyptus dunnii Maiden. Agronomy 2019, 9, 484. [Google Scholar] [CrossRef] [Green Version]
- Pryce, J.E.; Johnston, J.; Hayes, B.J.; Sahana, G.; Weigel, K.A.; McParland, S.; Spurlock, D.; Krattenmacher, N.; Spelman, R.J.; Wall, E.; et al. Imputation of genotypes from low density (50,000 markers) to high density (700,000 markers) of cows from research herds in Europe, North America, and Australasia using 2 reference populations. J. Dairy Sci. 2014, 97, 1799–1811. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Müller, B.S.; Neves, L.G.; De Almeida, F.J.E.; Resende, M.F.R., Jr.; Muñoz, P.R.; Dos Santos, P.E.T.; Paludzyszyn Filho, E.; Kirst, M.; Grattapaglia, D. Genomic prediction in contrast to a genome-wide association study in explaining heritable variation of complex growth traits in breeding populations of Eucalyptus. BMC Genomes 2017, 18, 524. [Google Scholar]
- Porto-Neto, L.R.; Kijas, J.W.; Reverter, A. The extent of linkage disequilibrium in beef cattle breeds using high-density SNP genotypes. Genet. Sel. Evol. 2014, 46, 22. [Google Scholar] [CrossRef] [Green Version]
- Bolormaa, S.; Gore, K.; van der Werf, J.H.J.; Hayes, B.J.; Daetwyler, H.D. Design of a low-density SNP chip for the main Australian sheep breeds and its effect on imputation and genomic prediction accuracy. Anim. Genet. 2015, 46, 544–556. [Google Scholar] [CrossRef]
- Wu, X.-L.; Xu, J.; Feng, G.; Wiggans, G.R.; Taylor, J.F.; He, J.; Qian, C.; Qiu, J.; Simpson, B.; Walker, J.; et al. Optimal Design of Low-Density SNP Arrays for Genomic Prediction: Algorithm and Applications. PLoS ONE 2016, 11, e0161719. [Google Scholar] [CrossRef]
- Silva, F.F.; Jerez, E.A.Z.; De Resende, M.D.V.; Soriano-Viana, M.; Ferreira-Azevedo, C.; Lopes, P.S.; Nascimento, M.; Oliveira de Lima, R.; Facioni-Guimaraes, S.E. Bayesian model combining linkage and linkage disequilibrium analysis for low density-based genomic selection in animal breeding. J. Appl. Anim. Res. 2018, 46, 873–878. [Google Scholar] [CrossRef] [Green Version]
- Rice, B.; Lipka, A.E. Evaluation of RR-BLUP genomic selection models that incorporate peak genome-wide association study signals in maize and sorghum. Plant Genome 2019, 12. [Google Scholar] [CrossRef] [Green Version]
- Bernardo, R. Genomewide selection when major genes are known. Crop Sci. 2014, 54, 68–75. [Google Scholar] [CrossRef]
- Brooker, M.I.H. A new classification of the genus Eucalyptus L’Her. (Myrtaceae). Aust. Syst. Bot. 2000, 13, 79–148. [Google Scholar] [CrossRef]
- McDonald, M.W.; Rawlins, M.; Butchet, P.A.; Bell, C. Regional divergence and inbreeding in Eucalyptus cladocalyx (Myrtaceae). Aust. J. Bot. 2003, 51, 393–403. [Google Scholar] [CrossRef]
- Mora, F.; Arriagada, O.; Ballesta, P.; Ruiz, E. Genetic diversity and population structure of a drought-tolerant species of Eucalyptus, using microsatellite markers. J. Plant Biochem. Biotechnol. 2017, 26, 274–281. [Google Scholar] [CrossRef]
- Ballesta, P.; Mora, F.; Contreras-Soto, R.I.; Ruiz, E.; Perret, S. Analysis of the genetic diversity of Eucalyptus cladocalyx (sugar gum) using ISSR markers. Acta Sci. Agron. 2015, 37, 133–140. [Google Scholar] [CrossRef] [Green Version]
- Arriagada, O.; Do Amaral Junior, A.T.; Mora, F. Thirteen years under arid conditions: Exploring marker-trait associations in Eucalyptus cladocalyx for complex traits related to flowering, stem form and growth. Breed. Sci. 2018, 68, 367–374. [Google Scholar] [CrossRef] [Green Version]
- Maldonado, C.; Contreras-Soto, R.I.; Gerhardt, I.F.S.; Do Amaral Júnior, A.T.; Mora, F. Stable marker-trait associations for growth across different ages in Eucalyptus cladocalyx through the use of microsatellites. Sci. For. 2018, 46, 367–376. [Google Scholar] [CrossRef]
- Valenzuela, C.E.; Ballesta, P.; Maldonado, C.; Baettig, R.; Arriagada, O.; Mafra, G.S.; Mora, F. Bayesian Mapping Reveals Large-Effect Pleiotropic QTLs for Wood Density and Slenderness Index in 17-Year-Old Trees of Eucalyptus cladocalyx. Forests 2019, 10, 241. [Google Scholar] [CrossRef] [Green Version]
- Cané-Retamales, C.; Mora, F.; Vargas-Reeve, F.; Perret, S.; Contreras-Soto, R. Bayesian threshold analysis of breeding values, genetic correlation and heritability of flowering intensity in Eucalyptus cladocalyx under arid conditions. Euphytica 2011, 178, 177–183. [Google Scholar] [CrossRef]
- De Lange, W.J.; Veldtman, R.; Allsopp, M.H. Valuation of pollinator forage services provided by Eucalyptus cladocalyx. J. Environ. Manag. 2013, 125, 12–18. [Google Scholar] [CrossRef]
- Missiaggia, A.A.; Piacezzi, A.L.; Grattapaglia, D. Genetic mapping of Eef1, a major effect QTL for early flowering in Eucalyptus grandis. Tree Genet. Genomes 2005, 1, 79. [Google Scholar] [CrossRef] [Green Version]
- Contreras-Soto, R.; Ballesta, P.; Ruiz, E.; Mora, F. Identification of ISSR markers linked to flowering traits in a representative sample of Eucalyptus cladocalyx. J. For. Res. 2016, 27, 239–245. [Google Scholar] [CrossRef]
- Ratcliffe, B.; El-Dien, O.G.; Klápště, J.; Porth, I.; Chen, C.; Jaquish, B.; El-Kasaby, Y.A. A comparison of genomic selection models across time in interior spruce (Picea engelmannii × glauca) using unordered SNP imputation methods. Heredity 2015, 115, 547–555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gamal-Dien, O.; Ratcliffe, B.; Klápště, J.; Chen, C.; Porth, I.; El-Kasaby, Y.A. Prediction accuracies for growth and wood attributes of interior spruce in space using genotyping-by-sequencing. BMC Genom. 2015, 16, 370. [Google Scholar]
- Lenz, P.R.; Beaulieu, J.; Mansfield, S.D.; Clément, S.; Desponts, M.; Bousquet, J. Factors affecting the accuracy of genomic selection for growth and wood quality traits in an advanced-breeding population of black spruce (Picea mariana). BMC Genom. 2017, 18, 335. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Baison, J.; Pan, J.; Karlsson, B.; Andersson, B.; Westin, J.; García-Gil, M.R.; Wu, H.X. Accuracy of genomic selection for growth and wood quality traits in two control-pollinated progeny trials using exome capture as the genotyping platform in Norway spruce. BMC Genom. 2018, 19, 946. [Google Scholar] [CrossRef] [Green Version]
- Bush, D.; Thumma, B. Characterising a Eucalyptus cladocalyx breeding population using SNP markers. Tree Genet. Genomes 2013, 9, 741–752. [Google Scholar] [CrossRef]
- Ballesta, P.; Serra, N.; Guerra, F.; Hasbún, R.; Mora, F. Genomic prediction of growth and stem quality traits in Eucalyptus globulus Labill at its southernmost distribution limit in Chile. Forests 2018, 9, 779. [Google Scholar] [CrossRef] [Green Version]
- De los Campos, G.; Hickey, J.M.; Pong-Wong, R.; Daetwyler, H.D.; Calus, M.P.L. Whole-Genome regression and prediction methods applied to plant and animal breeding. Genetics 2013, 193, 327–345. [Google Scholar] [CrossRef] [Green Version]
- González-Recio, O.; Rosa, G.J.; Gianola, D. Machine learning methods and predictive ability metrics for genome-wide prediction of complex traits. Livest. Sci. 2014, 166, 217–231. [Google Scholar] [CrossRef]
- Solberg, T.R.; Sonesson, A.K.; Woolliams, J.A.; Meuwissen, T.H.E. Reducing dimensionality for prediction of genome-wide breeding values. Genet. Sel. Evol. 2009, 41, 29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, C.; Wei, J.; Wang, S.; Jia, Z. Genomic selection using principal component regression. Heredity 2018, 121, 12–23. [Google Scholar] [CrossRef] [PubMed]
- Habier, D.; Fernando, R.L.; Dekkers, J.C. The impact of genetic relationship information on genome-assisted breeding values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macciotta, N.P.; Gaspa, G.; Steri, R.; Pieramati, C.; Carnier, P.; Dimauro, C. Pre-selection of most significant SNPS for the estimation of genomic breeding values. BMC Proc. 2009, 3, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arojju, S.K.; Conaghan, P.; Barth, S.; Milbourne, D.; Casler, M.D.; Hodkinson, T.R.; Michel, T.; Byrne, S.L. Genomic prediction of crown rust resistance in Lolium perenne. BMC Genet. 2018, 19, 35. [Google Scholar] [CrossRef]
- Resende, M.F., Jr.; Muñoz, P.; Resende, M.D.; Garrick, D.J.; Fernando, R.L.; Davis, M.J.; Jokela, E.J.; Martin, T.A.; Peter, G.F.; Kirst, M. Accuracy of genomic selection methods in a standard data set of loblolly pine (Pinus taeda L.). Genetics 2012, 190, 1503–1510. [Google Scholar] [CrossRef] [Green Version]
- Beaulieu, J.; Doerksen, T.K.; MacKay, J.; Rainville, A.; Bousquet, J. Genomic selection accuracies within and between environments and small breeding groups in white spruce. BMC Genom. 2014, 15, 1048. [Google Scholar] [CrossRef] [Green Version]
- Thistlethwaite, F.R.; Ratcliffe, B.; Klápště, J.; Porth, I.; Chen, C.; Stoehr, M.U.; El-Kassaby, Y.A. Genomic prediction accuracies in space and time for height and wood density of Douglas-fir using exome capture as the genotyping platform. BMC Genom. 2017, 18, 930. [Google Scholar] [CrossRef] [Green Version]
- Wolfe, M.D.; Del Carpio, D.P.; Alabi, O.; Ezenwaka, L.C.; Ikeogu, U.N.; Kayondo, I.S.; Lozano, R.; Okeke, U.G.; Ozimati, A.A.; Williams, E.; et al. Prospects for genomic selection in cassava breeding. Plant Genome 2017, 10, 1–9. [Google Scholar] [CrossRef] [Green Version]
- De los Campos, G.; Sorensen, D.; Gianola, D. Genomic heritability: What is it? PLoS Genet. 2015, 11, e1005048. [Google Scholar] [CrossRef] [Green Version]
- Mora, F.; Gleadow, R.; Perret, S.; Scapim, C.A. Genetic variation for early flowering, survival and growth in sugar gum (Eucalyptus cladocalyx F. Muell) in southern Atacama Desert. Euphytica 2009, 169, 335–344. [Google Scholar] [CrossRef]
- Bush, D.; McCarthy, K.; Meder, R. Genetic variation of natural durability traits in Eucalyptus cladocalyx (sugar gum). Ann. For. Sci. 2011, 68, 1057. [Google Scholar] [CrossRef]
- Vargas-Reeve, F.; Mora, F.; Perret, S.; Scapim, C.A. Heritability of stem straightness and genetic correlations in Eucalyptus cladocalyx in the semi-arid region of Chile. Crop Breed. Appl. Biotechnol. 2013, 13, 107–112. [Google Scholar] [CrossRef] [Green Version]
- Bush, D.; Kain, D.; Kanowski, P.; Matheson, C. Genetic parameter estimates informed by a marker-based pedigree: A case study with Eucalyptus cladocalyx in southern Australia. Tree Genet. Genomes 2015, 11, 798. [Google Scholar] [CrossRef]
- Hall, D.; Hallingbäck, H.R.; Wu, H.X. Estimation of number and size of QTL effects in forest tree traits. Tree Genet. Genomes 2016, 12, 110. [Google Scholar] [CrossRef] [Green Version]
- Porebski, S.; Bailey, L.G.; Baum, B.R. Modification of a CTAB DNA extraction protocol for plants containing high polysaccharide and polyphenol components. Plant Mol. Biol. Rep. 1997, 15, 8–15. [Google Scholar] [CrossRef]
- Doyle, J.J.; Doyle, J.L. Isolation of plant DNA from fresh tissue. Focus 1990, 12, 13–15. [Google Scholar]
- Bradbury, P.J.; Zhang, Z.; Kroon, D.E.; Casstevens, T.M.; Ramdoss, Y.; Buckler, E.S. TASSEL: Software for association mapping of complex traits in diverse samples. Bioinformatics 2007, 23, 2633–2635. [Google Scholar] [CrossRef]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar]
- Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the Bayesian alphabet for genomic selection. BMC Bioinform. 2011, 12, 186. [Google Scholar] [CrossRef] [Green Version]
- Gianola, D. Priors in whole-genome regression: The Bayesian alphabet returns. Genetics 2013, 194, 573–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asoro, F.G.; Newell, M.A.; Beavis, W.D.; Scott, M.P.; Jannink, J.-L. Accuracy and training population design for genomic selection on quantitative traits in elite North American oats. Plant Genome 2011, 4, 132–144. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, A.J.; Smith, K.P.; Jannink, J.L. Potential and optimization of genomic selection for Fusarium head blight resistance in six-row barley. Crop Sci. 2012, 52, 1609–1621. [Google Scholar] [CrossRef]
- Pérez, P.; De Los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, K.; Iwata, H.; Moriguchi, Y.; Ujino-Ihara, T.; Ueno, S.; Taguchi, Y.; Tsuboruma, M.; Mishima, K.; Iki, T.; Watanabe, A.; et al. Demonstration of genome-wide association studies for identifying markers for wood property and male strobili traits in Cryptomeria japonica. PLoS ONE 2013, 8, e79866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Endelman, J.B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 2011, 4, 250–255. [Google Scholar] [CrossRef] [Green Version]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar]
- Peakall, R.O.D.; Smouse, P.E. GENALEX 6: Genetic analysis in Excel. Population genetic software for teaching and research. Mol. Ecol. Notes 2006, 6, 288–295. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. 2002, 64, 583–639. [Google Scholar] [CrossRef] [Green Version]
| Trait/Model | Bayes A | Bayes B | Bayes C | BRR b |
|---|---|---|---|---|
| Tree height | ||||
| GS | 1968.9 | 1959.5 | 1968.6 | 1965.4 |
| GSq | 1951.2 | 1971.3 | 1941.3 | 1941.2 |
| ΔDIC a | 17.7 ** | 11.8 ** | 27.3 ** | 24.2 ** |
| Diameter at breast height | ||||
| GS | 2556.5 | 2544.7 | 2539.8 | 2538.2 |
| GSq | 2490.4 | 2480.7 | 2480.2 | 2473.3 |
| ΔDIC | 66.1 ** | 64.0 ** | 59.6 ** | 64.9 ** |
| Stem straightness | ||||
| GS | 947.7 | 941.4 | 932.7 | 935.3 |
| GSq | 947.0 | 944.7 | 947.2 | 946.2 |
| ΔDIC | 0.7 | 3.3 | 14.5 ** | 10.8 ** |
| Slenderness index | ||||
| GS | 4302.5 | 4299.5 | 4294.3 | 4290.5 |
| GSq | 4268.1 | 4268.5 | 4264.3 | 4261.3 |
| ΔDIC | 34.4 ** | 31.0 ** | 30.0 ** | 29.2 ** |
| Wood density | ||||
| GS | 2094.3 | 2082.4 | 2101.8 | 2042.0 |
| GSq | 2067.1 | 2075.9 | 2067.6 | 2070.3 |
| ΔDIC | 27.2 ** | 6.5 * | 34.3 ** | 28.4 ** |
| Flowering intensity | ||||
| GS | 1293.9 | 1301.2 | 1282.3 | 1285.9 |
| GSq | 1306.0 | 1309.7 | 1301.3 | 1295.2 |
| ΔDIC | 12.1 ** | 8.4 * | 19.0 ** | 9.4 * |
| First bifurcation height | ||||
| GS | 1491.9 | 1490.6 | 1487.3 | 1485.8 |
| GSq | 1426.6 | 1424.9 | 1424.9 | 1423.5 |
| ΔDIC | 65.3 ** | 65.7 ** | 62.4 ** | 62.3 ** |
| Trait/Model | Bayes A | Bayes B | Bayes C | BRR a | |
|---|---|---|---|---|---|
| Tree height | |||||
| GS | 0.33 | 0.32 | 0.33 | 0.34 | 0.33 |
| GSq | 0.45 | 0.44 | 0.44 | 0.45 | 0.44 |
| Diameter at breast height | |||||
| GS | 0.21 | 0.23 | 0.22 | 0.22 | 0.22 |
| GSq | 0.41 | 0.41 | 0.41 | 0.42 | 0.41 |
| Stem straightness | |||||
| GS | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 |
| GSq | 0.40 | 0.40 | 0.40 | 0.39 | 0.40 |
| Slenderness index | |||||
| GS | 0.20 | 0.20 | 0.21 | 0.21 | 0.21 |
| GSq | 0.32 | 0.32 | 0.31 | 0.31 | 0.32 |
| Wood density | |||||
| GS | 0.27 | 0.27 | 0.27 | 0.28 | 0.27 |
| GSq | 0.43 | 0.43 | 0.43 | 0.43 | 0.43 |
| Flowering intensity | |||||
| GS | 0.25 | 0.25 | 0.24 | 0.23 | 0.24 |
| GSq | 0.25 | 0.25 | 0.25 | 0.24 | 0.25 |
| First bifurcation height | |||||
| GS | 0.19 | 0.20 | 0.20 | 0.19 | 0.19 |
| GSq | 0.38 | 0.38 | 0.39 | 0.39 | 0.38 |
| Trait/Model | Bayes A | Bayes B | Bayes C | BRR a | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tree height | ||||||||||||
| GS | 0.28 | 0.24 | - | 0.21 | 0.45 | - | 0.22 | 0.40 | - | 0.29 | 0.24 | - |
| GSq | 0.16 | 0.14 | 0.32 | 0.18 | 0.12 | 0.29 | 0.13 | 0.27 | 0.29 | 0.14 | 0.17 | 0.34 |
| Diameter at breast height | ||||||||||||
| GS | 0.20 | 0.14 | - | 0.15 | 0.37 | - | 0.15 | 0.39 | - | 0.19 | 0.24 | - |
| GSq | 0.11 | 0.05 | 0.44 | 0.09 | 0.15 | 0.42 | 0.09 | 0.17 | 0.40 | 0.10 | 0.11 | 0.45 |
| Stem straightness | ||||||||||||
| GS | 0.23 | 0.32 | - | 0.18 | 0.31 | - | 0.16 | 0.30 | - | 0.21 | 0.30 | - |
| GSq | 0.18 | 0.18 | 0.01 | 0.14 | 0.37 | 0.01 | 0.14 | 0.32 | 0.01 | 0.18 | 0.19 | 0.013 |
| Slenderness index | ||||||||||||
| GS | 0.19 | 0.12 | - | 0.16 | 0.27 | - | 0.15 | 0.33 | - | 0.18 | 0.21 | - |
| GSq | 0.09 | 0.02 | 0.39 | 0.08 | 0.05 | 0.36 | 0.08 | 0.17 | 0.33 | 0.09 | 0.10 | 0.35 |
| Wood density | ||||||||||||
| GS | 0.25 | 0.28 | - | 0.18 | 0.50 | - | 0.19 | 0.45 | - | 0.21 | 0.42 | - |
| GSq | 0.17 | 0.13 | 0.31 | 0.17 | 0.18 | 0.27 | 0.14 | 0.24 | 0.27 | 0.17 | 0.12 | 0.31 |
| Flowering intensity | ||||||||||||
| GS | 0.34 | 0.07 | - | 0.32 | 0.10 | - | 0.27 | 0.29 | - | 0.33 | 0.13 | - |
| GSq | 0.30 | 0.06 | 0.00 | 0.29 | 0.06 | 0.00 | 0.27 | 0.20 | 0.00 | 0.31 | 0.10 | 0.002 |
| First bifurcation height | ||||||||||||
| GS | 0.20 | 0.05 | - | 0.19 | 0.12 | - | 0.16 | 0.27 | - | 0.19 | 0.14 | - |
| GSq | 0.08 | 0.04 | 0.44 | 0.08 | 0.11 | 0.42 | 0.08 | 0.13 | 0.41 | 0.08 | 0.06 | 0.45 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballesta, P.; Bush, D.; Silva, F.F.; Mora, F. Genomic Predictions Using Low-Density SNP Markers, Pedigree and GWAS Information: A Case Study with the Non-Model Species Eucalyptus cladocalyx. Plants 2020, 9, 99. https://doi.org/10.3390/plants9010099
Ballesta P, Bush D, Silva FF, Mora F. Genomic Predictions Using Low-Density SNP Markers, Pedigree and GWAS Information: A Case Study with the Non-Model Species Eucalyptus cladocalyx. Plants. 2020; 9(1):99. https://doi.org/10.3390/plants9010099
Chicago/Turabian StyleBallesta, Paulina, David Bush, Fabyano Fonseca Silva, and Freddy Mora. 2020. "Genomic Predictions Using Low-Density SNP Markers, Pedigree and GWAS Information: A Case Study with the Non-Model Species Eucalyptus cladocalyx" Plants 9, no. 1: 99. https://doi.org/10.3390/plants9010099
APA StyleBallesta, P., Bush, D., Silva, F. F., & Mora, F. (2020). Genomic Predictions Using Low-Density SNP Markers, Pedigree and GWAS Information: A Case Study with the Non-Model Species Eucalyptus cladocalyx. Plants, 9(1), 99. https://doi.org/10.3390/plants9010099







