Non-Destructive Estimation of Leaf Size and Shape Characteristics in Advanced Progenies of Coffea arabica L. from Intraspecific and Interspecific Crossing
Abstract
1. Introduction
2. Results
2.1. Fit of Models M1 and M2 for Estimating LS and Research Hypotheses
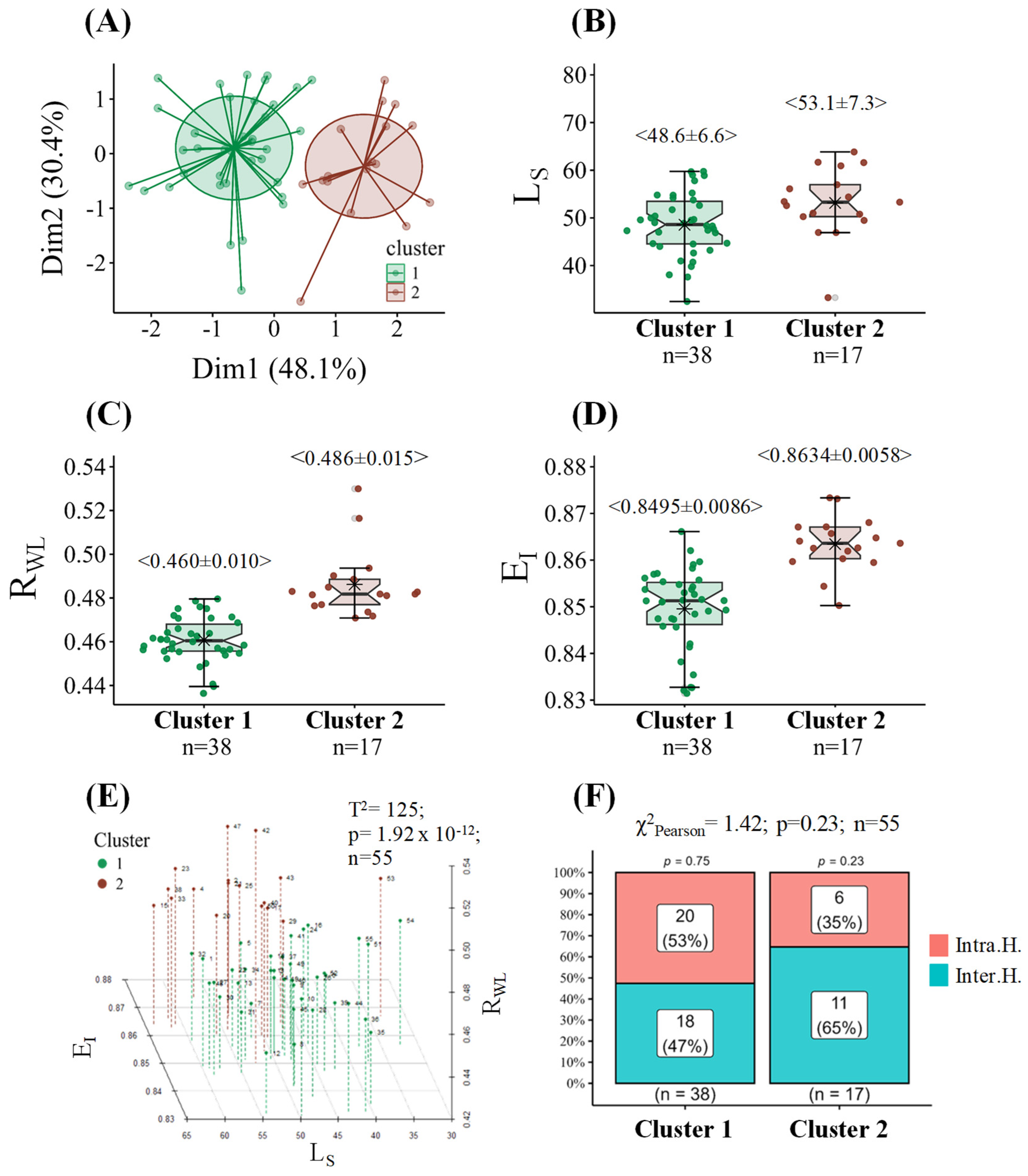
2.2. Leaf Shape Characteristics Related to Leaf Size
3. Discussion
4. Materials and Methods
4.1. Location and Plant Material
4.2. Leaf Image Processing
4.3. Parameter Estimation and Hypothesis Testing
4.4. Analysis of LS and Sh
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Verwijst, T.; Wen, D.-Z. Leaf Allometry of Salix Viminalis during the First Growing Season. Tree Physiol. 1996, 16, 655–660. [Google Scholar] [CrossRef]
- Westoby, M.; Falster, D.S.; Moles, A.T.; Vesk, P.A.; Wright, I.J. Plant Ecological Strategies: Some Leading Dimensions of Variation Between Species. Annu. Rev. Ecol. Syst. 2002, 33, 125–159. [Google Scholar] [CrossRef]
- Wright, I.J.; Dong, N.; Maire, V.; Prentice, I.C.; Westoby, M.; Díaz, S.; Gallagher, R.V.; Jacobs, B.F.; Kooyman, R.; Law, E.A.; et al. Global Climatic Drivers of Leaf Size. Science 2017, 357, 917–921. [Google Scholar] [CrossRef]
- Baird, A.S.; Taylor, S.H.; Pasquet-Kok, J.; Vuong, C.; Zhang, Y.; Watcharamongkol, T.; Scoffoni, C.; Edwards, E.J.; Christin, P.-A.; Osborne, C.P.; et al. Developmental and Biophysical Determinants of Grass Leaf Size Worldwide. Nature 2021, 592, 242–247. [Google Scholar] [CrossRef] [PubMed]
- Falster, D.S.; Westoby, M. Leaf Size and Angle Vary Widely across Species: What Consequences for Light Interception? New Phytol. 2003, 158, 509–525. [Google Scholar] [CrossRef]
- Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.C.; Diemer, M.; et al. The Worldwide Leaf Economics Spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
- Lambers, H.; Chapin, F.S.; Pons, T.L. Plant Physiological Ecology; Springer: New York, NY, USA, 2008; ISBN 978-0-387-78340-6. [Google Scholar]
- Leigh, A.; Sevanto, S.; Close, J.D.; Nicotra, A.B. The Influence of Leaf Size and Shape on Leaf Thermal Dynamics: Does Theory Hold up under Natural Conditions? Plant Cell Environ. 2017, 40, 237–248. [Google Scholar] [CrossRef]
- Yu, X.; Shi, P.; Schrader, J.; Niklas, K.J. Nondestructive Estimation of Leaf Area for 15 Species of Vines with Different Leaf Shapes. Am. J. Bot. 2020, 107, 1481–1490. [Google Scholar] [CrossRef]
- Mielke, M.S.; Santos, G.O.; Lopes, E.C.S.; Schilling, A.C.; dos Santos, M.S.; Pérez-Molina, J.P. Allometric Models to Estimate the Individual Leaf Area of Arabica Coffee: An Approach from Frequentist and Bayesian Statistics. Acta Physiol. Plant. 2023, 45, 39. [Google Scholar] [CrossRef]
- Fallovo, C.; Cristofori, V.; Mendoza de-Gyves, E.; Rivera, C.M.; Rea, R.; Fanasca, S.; Bignami, C.; Sassine, Y.; Rouphael, Y. Leaf Area Estimation Model for Small Fruits from Linear Measurements. HortScience 2008, 43, 2263–2267. [Google Scholar] [CrossRef]
- Schrader, J.; Pillar, G.; Kreft, H. Leaf-IT: An Android Application for Measuring Leaf Area. Ecol. Evol. 2017, 7, 9731–9738. [Google Scholar] [CrossRef]
- Olivoto, T. Lights, Camera, Pliman! An R Package for Plant Image Analysis. Methods Ecol. Evol. 2022, 13, 789–798. [Google Scholar] [CrossRef]
- Unigarro, C.A.; Hernández, J.D.; Montoya, E.C.; Medina, R.D.; Ibarra, L.N.; Carmona, C.Y.; Flórez, C.P. Estimation of Leaf Area in Coffee Leaves (Coffea arabica L.) of the Castillo Variety. Bragantia 2015, 74, 412–416. [Google Scholar] [CrossRef]
- Antunes, W.C.; Pompelli, M.; Carretero, D.M.; DaMatta, F.M. Allometric Models for Non-Destructive Leaf Area Estimation in Coffee (Coffea arabica and Coffea canephora). Ann. Appl. Biol. 2008, 153, 33–40. [Google Scholar] [CrossRef]
- Shi, P.; Liu, M.; Ratkowsky, D.A.; Gielis, J.; Su, J.; Yu, X.; Wang, P.; Zhang, L.; Lin, Z.; Schrader, J. Leaf Area–Length Allometry and Its Implications in Leaf Shape Evolution. Trees 2019, 33, 1073–1085. [Google Scholar] [CrossRef]
- Shi, P.; Zhao, L.; Ratkowsky, D.A.; Niklas, K.J.; Huang, W.; Lin, S.; Ding, Y.; Hui, C.; Li, B.-L. Influence of the Physical Dimension of Leaf Size Measures on the Goodness of Fit for Taylor’s Power Law Using 101 Bamboo Taxa. Glob. Ecol. Conserv. 2019, 19, e00657. [Google Scholar] [CrossRef]
- Schrader, J.; Shi, P.; Royer, D.L.; Peppe, D.J.; Gallagher, R.V.; Li, Y.; Wang, R.; Wright, I.J. Leaf Size Estimation Based on Leaf Length, Width and Shape. Ann. Bot. 2021, 128, 395–406. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form; Bonner, J.T., Ed.; Canto; Cambridge University Press: Cambridge, UK, 1992; ISBN 978-1-107-32585-2. [Google Scholar]
- Montgomery, E.G. Correlation Studies in Corn. In Annual Report of Nebraska Agricultural Experimental Station; Scientific Research: Lincoln, NB, USA, 1911. [Google Scholar]
- Li, Y.; Quinn, B.K.; Niinemets, Ü.; Schrader, J.; Gielis, J.; Liu, M.; Shi, P. Ellipticalness Index—A Simple Measure of the Complexity of Oval Leaf Shape. Pak. J. Bot. 2022, 54, 2233–2240. [Google Scholar] [CrossRef] [PubMed]
- Cain, S.A.; de Oliveira Castro, G.M. Life Form and Leaf Size. In Manual of Vegetation Analyses; Harper and Brothers: New York, NY, USA, 1959; pp. 255–319. [Google Scholar]
- Dolph, G.E. The Effect of Different Calculational Techniques on the Estimation of Leaf Area and the Construction of Leaf Size Distributions. Bull. Torrey Bot. Club 1977, 104, 264–269. [Google Scholar] [CrossRef]
- Ma, J.; Niklas, K.J.; Liu, L.; Fang, Z.; Li, Y.; Shi, P. Tree Size Influences Leaf Shape but Does Not Affect the Proportional Relationship Between Leaf Area and the Product of Length and Width. Front. Plant Sci. 2022, 13, 850203. [Google Scholar] [CrossRef] [PubMed]
- Sicard, A.; Thamm, A.; Marona, C.; Lee, Y.W.; Wahl, V.; Stinchcombe, J.R.; Wright, S.I.; Kappel, C.; Lenhard, M. Repeated Evolutionary Changes of Leaf Morphology Caused by Mutations to a Homeobox Gene. Curr. Biol. 2014, 24, 1880–1886. [Google Scholar] [CrossRef]
- Tsukaya, H. Leaf Shape: Genetic Controls and Environmental Factors. Int. J. Dev. Biol. 2005, 49, 547–555. [Google Scholar] [CrossRef]
- Nicotra, A.B.; Cosgrove, M.J.; Cowling, A.; Schlichting, C.D.; Jones, C.S. Leaf Shape Linked to Photosynthetic Rates and Temperature Optima in South African Pelargonium Species. Oecologia 2008, 154, 625–635. [Google Scholar] [CrossRef]
- Nicotra, A.B.; Leigh, A.; Boyce, C.K.; Jones, C.S.; Niklas, K.J.; Royer, D.L.; Tsukaya, H. The Evolution and Functional Significance of Leaf Shape in the Angiosperms. Funct. Plant Biol. 2011, 38, 535–552. [Google Scholar] [CrossRef]
- Sun, J.; Fan, R.; Niklas, K.J.; Zhong, Q.; Yang, F.; Li, M.; Chen, X.; Sun, M.; Cheng, D. “Diminishing Returns” in the Scaling of Leaf Area vs. Dry Mass in Wuyi Mountain Bamboos, Southeast China. Am. J. Bot. 2017, 104, 993–998. [Google Scholar] [CrossRef]
- Niinemets, Ü.; Portsmuth, A.; Tobias, M. Leaf Shape and Venation Pattern Alter the Support Investments within Leaf Lamina in Temperate Species: A Neglected Source of Leaf Physiological Differentiation? Funct. Ecol. 2007, 21, 28–40. [Google Scholar] [CrossRef]
- Lin, S.; Niklas, K.J.; Wan, Y.; Hölscher, D.; Hui, C.; Ding, Y.; Shi, P. Leaf Shape Influences the Scaling of Leaf Dry Mass vs. Area: A Test Case Using Bamboos. Ann. For. Sci. 2020, 77, 11. [Google Scholar] [CrossRef]
- Shi, P.; Yu, K.; Niinemets, Ü.; Gielis, J. Can Leaf Shape Be Represented by the Ratio of Leaf Width to Length? Evidence from Nine Species of Magnolia and Michelia (Magnoliaceae). Forests 2021, 12, 41. [Google Scholar] [CrossRef]
- Sachs, J.D.; Cordes, K.Y.; Rising, J.; Toledano, P.; Maennling, N. Ensuring Economic Viability and Sustainability of Coffee Production; Columbia Center on Sustainable Investment: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Arcila, J.; Buhr, L.; Bleiholder, H.; Hack, H.; Meier, U.; Wicke, H. Application of the Extended BBCH Scale for the Description of the Growth Stages of Coffee (Coffea spp.). Ann. Appl. Biol. 2002, 141, 19–27. [Google Scholar] [CrossRef]
- Rakočević, M. Coffee Plant Architecture. In Advances in Botanical Research; Academic Press: Cambridge, MA, USA, 2024. [Google Scholar]
- Ellis, B.; Daly, D.; Hickey, L.; Johnson, K.; Mitchell, J.; Peter, W.; Scott, W. Manual of Leaf Architecture; Cornell University Press: Ithaca, NY, USA, 2009; ISBN 978-0-8014-7518-4. [Google Scholar]
- Unigarro, C.A.; Medina, R.D.; Flórez, C.P. Relación entre producción y las características fenotípicas en Coffea arabica L. Rev. Cenicafé 2017, 68, 62–72. [Google Scholar]
- Barros, R.S.; Maestri, M.; Vieira, M.; Bragafilho, L.J. Determinação de área de folhas do café (Coffea arabica L. cv. “Bourbon Amarelo”). Rev. Ceres 1973, 20, 44–52. [Google Scholar]
- Partelli, F.L.; Vieira, H.D.; Detmann, E.; Campostrini, E. Estimativa da área foliar do cafeeiro conilon a partir do comprimento da folha. Rev. Ceres 2006, 53, 204–210. [Google Scholar]
- Flumignan, D.L.; Adami, M.; de Faria, R.T. Área foliar de folhas íntegras e danificadas de cafeeiro determinada por dimensões foliares e imagem digital. Coffee Sci. 2008, 3, 1–6. [Google Scholar]
- Taugourdeau, S.; Le Maire, G.; Avelino, J.; Jones, J.R.; Ramirez, L.G.; Jara Quesada, M.; Charbonnier, F.; Gómez-Delgado, F.; Harmand, J.-M.; Rapidel, B.; et al. Leaf Area Index as an Indicator of Ecosystem Services and Management Practices: An Application for Coffee Agroforestry. Agric. Ecosyst. Environ. 2014, 192, 19–37. [Google Scholar] [CrossRef]
- Brinate, S.V.B.; Rodrigues, W.N.; Martins, L.D.; Colodetti, T.V.; Tomaz, M.A.; Amaral, J.F.T.D. Applicability of the Method of Linear Dimensions to Estimate Leaf Area in Improved Genotypes of Coffea arabica and Coffea canephora. Am. J. Plant Sci. 2015, 6, 651–658. [Google Scholar] [CrossRef]
- Schmildt, E.R.; Amaral, J.A.T.D.; Santos, J.S.; Schmildt, O. Allometric Model for Estimating Leaf Area in Clonal Varieties of Coffee (Coffea canephora). Rev. Ciência Agronômica 2015, 46, 740–748. [Google Scholar] [CrossRef]
- Misgana, Z.; Daba, G.; Debela, A. Modeling Leaf Area Estimation for Arabica Coffee (Coffea Arabica L.) Grown at Different Altitudes of Mana District, Jimma Zone. Am. J. Plant Sci. 2018, 9, 1292–1307. [Google Scholar] [CrossRef]
- Adem, A. Determination of Linear Model for Coffee Leaf Area Measurement. J. Genet. Genom. Plant Breed. 2020, 4, 141–146. [Google Scholar]
- Cavallaro, R.J.; Uber-Bucek, E.; Delalibera, J.R. Mathematical Model for Determining the Coffee Leaf Area. Am. Sci. Res. J. Eng. Technol. Sci. 2020, 71, 11–19. [Google Scholar]
- Pereira, D.R.; Ferreira, A.D.; Bono, J.A.M.; Pedrinho, D.R.; Nascimento, L.S.D. Comparação entre métodos não destrutivos de estimativa da área foliar em café arábica. Br. J. Anaesth. 2020, 3, 2819–2828. [Google Scholar] [CrossRef]
- Arcila, J.; Chaves, B. Desarrollo foliar del cafeto en tres densidades de siembra. Rev. Cenicafé 1995, 46, 5–20. [Google Scholar]
- Castillo, E.; Arcila, J.; Jaramillo, A.; Sanabria, R.J. Estructura Del Dosel e Interceptación de La Radiación Solar En Café Coffea arabica L., Var. Colombia. Rev. Cenicafé 1996, 47, 4–15. [Google Scholar]
- León-Burgos, A.F.; Rendón, J.R.; Imbachi, L.C.; Toro-Herrera, M.A.; Unigarro, C.A.; Osorio, V.; Balaguera-López, H.E. Increased Fruit Load Influences Vegetative Growth, Dry Mass Partitioning, and Bean Quality Attributes in Full-Sun Coffee Cultivation. Front. Sustain. Food Syst. 2024, 8, 1379207. [Google Scholar] [CrossRef]
- León-Burgos, A.F.; Unigarro, C.A.; Balaguera-López, H.E. Soil Waterlogging Conditions Affect Growth, Water Status, and Chlorophyll “a” Fluorescence in Coffee Plants (Coffea arabica L.). Agronomy 2022, 12, 1270. [Google Scholar] [CrossRef]
- Lince Salazar, L.A.; Sadeghian-Khalajabadi, S.; Sarmiento Herrera, N.G. Evaluación de parámetros relacionados con el crecimiento de plantas de café (Coffea arabica L.) en respuesta al déficit hídrico del suelo. Rev. Investig. Agrar. Ambient. 2024, 15, 11–34. [Google Scholar] [CrossRef]
- Montoya, E.C.; Hernández, J.D.; Unigarro, C.A.; Flórez, C.P. Estimación del área foliar en café variedad Castillo® a libre exposición y su relación con la producción. Rev. Cenicafé 2017, 68, 55–61. [Google Scholar] [CrossRef]
- Shi, P.; Liu, M.; Yu, X.; Gielis, J.; Ratkowsky, D. Proportional Relationship between Leaf Area and the Product of Leaf Length and Width of Four Types of Special Leaf Shapes. Forests 2019, 10, 178. [Google Scholar] [CrossRef]
- Complementary Strategies for Ex Situ Conservation of Coffee (Coffea arabica L.) Genetic Ressources: A Case Study in CATIE, Costa Rica; Engelmann, F., Dulloo, M.E., Astorga, C., Dussert, S., Anthony, F., Eds.; Topical reviews in Agricultural Biodiverstity; Bioversity International: Rome, Italy, 2007; ISBN 978-92-9043-752-9. [Google Scholar]
- Lin, S.; Shao, L.; Hui, C.; Song, Y.; Reddy, G.V.P.; Gielis, J.; Li, F.; Ding, Y.; Wei, Q.; Shi, P. Why Does Not the Leaf Weight-Area Allometry of Bamboos Follow the 3/2-Power Law? Front. Plant Sci. 2018, 9, 583. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Niklas, K.J.; Gielis, J.; Niinemets, Ü.; Schrader, J.; Wang, R.; Shi, P. An Elliptical Blade Is Not a True Ellipse, but a Superellipse–Evidence from Two Michelia Species. J. For. Res. 2022, 33, 1341–1348. [Google Scholar] [CrossRef]
- Unigarro, C.A.; Trejos Pinzón, J.F.; Acuña-Zornosa, J.R. Estructura y distribución lumínica en el dosel de dos progenies de café con ángulos foliares diferentes. Rev. Cenicafé 2021, 72, e72104. [Google Scholar] [CrossRef]
- Cannell, M.G.R. Effects of Fruiting, Defoliation and Ring-Barking on the Accumulation and Distribution of Dry Matter in Branches of Coffea arabica L. in Kenya. Exp. Agric. 1971, 7, 63–74. [Google Scholar] [CrossRef]
- Okoma, P.; Akaffou, S.; De Reffye, P.; Hamon, P.; Hamon, S.; Konan, O.; Kouassi, K.H.; Legnate, H.; Letort, V.; Sabatier, S. Estimation of Stem and Leaf Dry Biomass Using a Non-Destructive Method Applied to African Coffea Species. Agrofor. Syst. 2018, 92, 667–675. [Google Scholar] [CrossRef]
- FNC (Federación Nacional de Cafeteros de Colombia). Atlas Cafetero de Colombia; Imprenta Nacional de Colombia: Bogota, Colombia, 2017; ISBN 978-958-8323-89-3. [Google Scholar]
- Sadeghian, S. Manejo integrado de nutrientes para una caficultura sostenible. Suelos Ecuat. 2014, 44, 74–89. [Google Scholar]
- Centro Nacional de Investigaciones de Café. Guía Más Agronomia, Más Productividad, Más Calidad, 3rd ed.; Centro Nacional de Investigaciones de Café: Bogotá, Colombia, 2021; ISBN 978-958-8490-49-6. [Google Scholar]
- Su, J.; Niklas, K.J.; Huang, W.; Yu, X.; Yang, Y.; Shi, P. Lamina Shape Does Not Correlate with Lamina Surface Area: An Analysis Based on the Simplified Gielis Equation. Glob. Ecol. Conserv. 2019, 19, e00666. [Google Scholar] [CrossRef]
- Shi, P.; Gielis, J.; Quinn, B.K.; Niklas, K.J.; Ratkowsky, D.A.; Schrader, J.; Ruan, H.; Wang, L.; Niinemets, Ü. ‘Biogeom’: An R Package for Simulating and Fitting Natural Shapes. Ann. N. Y. Acad. Sci. 2022, 1516, 123–134. [Google Scholar] [CrossRef]
- Elzhov, T.V.; Mullen, K.M.; Spiess, A.-N.; Bolker, B. Minpack.Lm: R Interface to the Levenberg-Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds, version 1.2-4; Comprehensive R Archive Network: Vienna, Austria, 2023.
- Fox, J.; Weisberg, S.; Price, B.; Adler, D.; Bates, D.; Baud-Bovy, G.; Bolker, B.; Ellison, S.; Firth, D.; Friendly, M.; et al. Car: Companion to Applied Regression; BibBase: Menlo Park, CA, USA, 2021. [Google Scholar]
- Rousselet, G.A.; Pernet, C.R.; Wilcox, R.R. The Percentile Bootstrap: A Primer With Step-by-Step Instructions in R. Adv. Methods Pract. Psychol. Sci. 2021, 4, 2515245920911881. [Google Scholar] [CrossRef]
- Walther, B.A.; Moore, J.L. The Concepts of Bias, Precision and Accuracy, and Their Use in Testing the Performance of Species Richness Estimators, with a Literature Review of Estimator Performance. Ecography 2005, 28, 815–829. [Google Scholar] [CrossRef]
- Hamner, B.; Frasco, M.; LeDell, E. Metrics: Evaluation Metrics for Machine Learning, version 0.1.4; R-Universe: Middlesex, UK, 2018.
- Niknafs, A.; Boiteau, V.; Ghazzali, N.; Charrad, M. NbClust: Determining the Best Number of Clusters in a Data Set, version 3.0.1; Comprehensive R Archive Network: Vienna, Austria, 2022.
- Hennig, C. Fpc: Flexible Procedures for Clustering, version 2.2-13; Comprehensive R Archive Network: Vienna, Austria, 2024.
- Bulut, H. MVTests: Multivariate Hypothesis Tests, version 2.3.1; Comprehensive R Archive Network: Vienna, Austria, 2025.
- Korkmaz, S.; Goksuluk, D.; Zararsiz, G. MVN: Multivariate Normality Tests, version 6.1; Comprehensive R Archive Network: Vienna, Austria, 2025.
- Da Silva, A.R. Biotools: Tools for Biometry and Applied Statistics in Agricultural Science, version 4.3; Comprehensive R Archive Network: Vienna, Austria, 2025.
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hube, M.; Hornik, K.; Studer, M.; Roudier, P.; Gonzalez, J.; Kozlowski, K.; Schubert, E.; et al. Cluster: “Finding Groups in Data”: Cluster Analysis Extended Rousseeuw et al. version 2.1.8.1; Comprehensive R Archive Network: Vienna, Austria, 2025.
- Kassambara, A.; Mundt, F. Factoextra: Extract and Visualize the Results of Multivariate Data Analyses, version 1.0.7; GESIS: Mannheim, Germany, 2020.
- Patil, I.; Powell, C. ggstatsplot: “ggplot2” Based Plots with Statistical Details, version 0.13.2; Comprehensive R Archive Network: Vienna, Austria, 2025.
- Makowski, D.; Wiernik, B.M.; Patil, I.; Lüdecke, D.; Ben-Shachar, M.S.; White, M.; Rabe, M.M. Correlation: Methods for Correlation Analysis, version 0.8.8; Comprehensive R Archive Network: Vienna, Austria, 2020.
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis, 2nd ed.; Springer International Publishing: Houston, TX, USA, 2016; ISBN 978-3-319-24275-0. [Google Scholar]
- Ligges, U.; Maechler, M.; Schnackenberg, S. Scatterplot3d: 3D Scatter Plot, version 0.3-44; Comprehensive R Archive Network: Vienna, Austria, 2023.
- R Core Team. R: A Language and Environment for Statistical Computing—Reference Index; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]

| {#} | H | Pd | M1: LS = α LW + ɛ | |||||
|---|---|---|---|---|---|---|
| α (LCI–UCI) | H1 | H2 | H3 | H4 | RMSE | |
| {1} | 0.66686 (0.66368–0.67003) | ∈ | ∈ | ∈ | ∉ | 1.955 |
| {2} | 0.68176 (0.67830–0.68516) | ∈ | ∈ | ∈ | ∈ | 1.839 |
| {3} | 0.67095 (0.66769–0.67421) | ∉ | ∈ | ∈ | ∈ | 1.576 |
| {4} | 0.68592 (0.68267–0.68910) | ∈ | ∈ | ∈ | ∈ | 1.834 |
| {5} | 0.67704 (0.67380–0.68028) | ∈ | ∈ | ∈ | ∈ | 1.781 |
| {6} | 0.68024 (0.67701–0.68353) | ∈ | ∈ | ∈ | ∈ | 1.329 |
| {7} | 0.67469 (0.67150–0.67782) | ∈ | ∈ | ∈ | ∈ | 1.745 |
| {8} | 0.66135 (0.65833–0.66430) | ∈ | ∈ | ∈ | ∈ | 1.573 |
| {9} | 0.66838 (0.66541–0.67126) | ∉ | ∈ | ∈ | ∉ | 1.554 |
| {10} | 0.65302 (0.65010–0.65602) | ∈ | ∈ | ∈ | ∈ | 1.590 |
| {11} | 0.67051 (0.66716–0.67392) | ∉ | ∈ | ∈ | ∈ | 1.838 |
| {12} | 0.65352 (0.65024–0.65669) | ∈ | ∈ | ∈ | ∈ | 1.799 |
| {13} | 0.66858 (0.66576–0.67137) | ∉ | ∈ | ∈ | ∉ | 1.652 |
| {14} | 0.67051 (0.66766–0.67329) | ∉ | ∈ | ∈ | ∈ | 1.443 |
| {15} | 0.67828 (0.67573–0.68081) | ∈ | ∈ | ∈ | ∈ | 1.736 |
| {16} | 0.67320 (0.67022–0.67618) | ∉ | ∈ | ∈ | ∈ | 1.380 |
| {17} | 0.67504 (0.67140–0.67858) | ∈ | ∈ | ∈ | ∈ | 1.858 |
| {18} | 0.66882 (0.66631–0.67135) | ∉ | ∈ | ∈ | ∉ | 1.326 |
| {19} | 0.66967 (0.66646–0.67303) | ∉ | ∈ | ∈ | ∉ | 1.567 |
| {49} | 0.67306 (0.66935–0.67665) | ∉ | ∈ | ∈ | ∈ | 1.542 |
| {50} | 0.67520 (0.67175–0.67865) | ∈ | ∈ | ∈ | ∈ | 1.664 |
| {51} | 0.66842 (0.66542–0.67139) | ∉ | ∈ | ∈ | ∉ | 1.207 |
| {52} | 0.66561 (0.66214–0.66900) | ∈ | ∈ | ∈ | ∉ | 1.489 |
| {53} | 0.68104 (0.67774–0.68429) | ∈ | ∈ | ∈ | ∈ | 1.126 |
| {54} | 0.67241 (0.66861–0.67621) | ∉ | ∈ | ∈ | ∈ | 1.300 |
| {55} | 0.67180 (0.66802–0.67559) | ∉ | ∈ | ∈ | ∈ | 1.438 |
| Intra.H. [n = 5928] | 0.67118 (0.67049–0.67187) | ∉ | ∈ | ∈ | ∈ | 1.718 |
| {20} | 0.67568 (0.67261–0.67865) | ∈ | ∈ | ∈ | ∈ | 1.828 |
| {21} | 0.68101 (0.67761–0.68445) | ∈ | ∈ | ∈ | ∈ | 1.845 |
| {22} | 0.67209 (0.66874–0.67548) | ∉ | ∈ | ∈ | ∈ | 1.855 |
| {23} | 0.67863 (0.67525–0.68202) | ∈ | ∈ | ∈ | ∈ | 2.064 |
| {24} | 0.67517 (0.67130–0.67910) | ∈ | ∈ | ∈ | ∈ | 1.711 |
| {25} | 0.68576 (0.68222–0.68931) | ∈ | ∈ | ∈ | ∈ | 1.819 |
| {26} | 0.66703 (0.66277–0.67126) | ∉ | ∈ | ∈ | ∉ | 1.948 |
| {27} | 0.66431 (0.66119–0.66739) | ∈ | ∈ | ∈ | ∉ | 1.989 |
| {28} | 0.65832 (0.65432–0.66221) | ∈ | ∈ | ∈ | ∈ | 1.809 |
| {29} | 0.67744 (0.67367–0.68121) | ∈ | ∈ | ∈ | ∈ | 1.748 |
| {30} | 0.66558 (0.66251–0.66869) | ∈ | ∈ | ∈ | ∉ | 1.801 |
| {31} | 0.66418 (0.66126–0.66703) | ∈ | ∈ | ∈ | ∉ | 1.708 |
| {32} | 0.67406 (0.67072–0.67732) | ∉ | ∈ | ∈ | ∈ | 1.848 |
| {33} | 0.67750 (0.67442–0.68058) | ∈ | ∈ | ∈ | ∈ | 1.999 |
| {34} | 0.66868 (0.66539–0.67199) | ∉ | ∈ | ∈ | ∉ | 1.856 |
| {35} | 0.65613 (0.65126–0.66010) | ∈ | ∈ | ∈ | ∈ | 1.772 |
| {36} | 0.65404 (0.65088–0.65720) | ∈ | ∈ | ∈ | ∈ | 1.376 |
| {37} | 0.67133 (0.66724–0.67545) | ∉ | ∈ | ∈ | ∈ | 1.912 |
| {38} | 0.67992 (0.67723–0.68262) | ∈ | ∈ | ∈ | ∈ | 1.767 |
| {39} | 0.66546 (0.66108–0.67012) | ∈ | ∈ | ∈ | ∉ | 1.764 |
| {40} | 0.67104 (0.66791–0.67413) | ∉ | ∈ | ∈ | ∈ | 1.550 |
| {41} | 0.66863 (0.66574–0.67140) | ∉ | ∈ | ∈ | ∉ | 1.456 |
| {42} | 0.66780 (0.66504–0.67057) | ∈ | ∈ | ∈ | ∉ | 1.568 |
| {43} | 0.67918 (0.67662–0.68180) | ∈ | ∈ | ∈ | ∈ | 1.195 |
| {44} | 0.65397 (0.65086–0.65700) | ∈ | ∈ | ∈ | ∈ | 1.398 |
| {45} | 0.66081 (0.65760–0.66402) | ∈ | ∈ | ∈ | ∈ | 1.629 |
| {46} | 0.66996 (0.66704–0.67289) | ∉ | ∈ | ∈ | ∈ | 1.428 |
| {47} | 0.67696 (0.67418–0.67983) | ∈ | ∈ | ∈ | ∈ | 1.652 |
| {48} | 0.66636 (0.66347–0.66915) | ∈ | ∈ | ∈ | ∉ | 1.802 |
| Inter.H. [n = 6612] | 0.67066 (0.66998–0.67130) | ∉ | ∈ | ∈ | ∈ | 1.860 |
| Pd [n = 12,540] | 0.67089 (0.67041–0.67136) | ∉ | ∈ | ∈ | ∈ | 1.795 |
| {#} | H | Pd | M2: LS = α Lβ + ɛ | |||
|---|---|---|---|---|
| α (LCI–UCI) | β (LCI–UCI) | H5 | RMSE | |
| {1} | 0.25877 (0.22601–0.29345) | 2.07500 (2.02716–2.12488) | ∈ | 4.199 |
| {2} | 0.36990 (0.29479–0.45083) | 1.96047 (1.88175–2.04577) | ∉ | 5.715 |
| {3} | 0.31694 (0.26548–0.37583) | 1.99277 (1.92571–2.05904) | ∉ | 4.804 |
| {4} | 0.38739 (0.28614–0.50618) | 1.93773 (1.83103–2.05025) | ∉ | 7.083 |
| {5} | 0.35360 (0.28476–0.43064) | 1.95203 (1.87291–2.03416) | ∉ | 5.989 |
| {6} | 0.34285 (0.26477–0.42618) | 1.94735 (1.85676–2.04846) | ∉ | 4.573 |
| {7} | 0.27203 (0.22436–0.32807) | 2.03317 (1.95950–2.10516) | ∉ | 5.156 |
| {8} | 0.31192 (0.24560–0.38438) | 1.97482 (1.89293–2.06343) | ∉ | 5.511 |
| {9} | 0.22642 (0.19681–0.26117) | 2.11907 (2.06329–2.17123) | ∈ | 3.882 |
| {10} | 0.24628 (0.20807–0.28729) | 2.09340 (2.03287–2.15745) | ∈ | 4.245 |
| {11} | 0.31048 (0.25957–0.36374) | 2.00134 (1.93963–2.06942) | ∉ | 5.064 |
| {12} | 0.30810 (0.25019–0.37304) | 1.98809 (1.91314–2.06586) | ∉ | 4.751 |
| {13} | 0.25891 (0.21686–0.30564) | 2.06643 (2.00088–2.13351) | ∈ | 4.723 |
| {14} | 0.27174 (0.22945–0.31864) | 2.05013 (1.98827–2.11394) | ∉ | 4.409 |
| {15} | 0.28537 (0.24248–0.33555) | 2.05120 (1.98998–2.11073) | ∉ | 5.305 |
| {16} | 0.28925 (0.24669–0.33575) | 2.04323 (1.98315–2.10506) | ∉ | 3.989 |
| {17} | 0.28314 (0.23382–0.33765) | 2.05854 (1.98845–2.13224) | ∉ | 4.963 |
| {18} | 0.28766 (0.24146–0.33643) | 2.03916 (1.97773–2.10566) | ∉ | 4.324 |
| {19} | 0.20524 (0.17186–0.24022) | 2.16050 (2.09827–2.22836) | ∈ | 4.015 |
| {49} | 0.28495 (0.21925–0.35683) | 2.03631 (1.94577–2.13661) | ∉ | 4.932 |
| {50} | 0.24479 (0.21155–0.28038) | 2.11315 (2.05973–2.16877) | ∈ | 3.994 |
| {51} | 0.22530 (0.19806–0.25448) | 2.14276 (2.09190–2.19486) | ∈ | 2.948 |
| {52} | 0.28975 (0.24273–0.34120) | 2.02721 (1.96067–2.09671) | ∉ | 4.171 |
| {53} | 0.22691 (0.18636–0.27136) | 2.16317 (2.08460–2.24513) | ∈ | 3.214 |
| {54} | 0.24731 (0.20467–0.29337) | 2.11482 (2.04146–2.19285) | ∈ | 3.152 |
| {55} | 0.21637 (0.17793–0.25872) | 2.16075 (2.08509–2.23968) | ∈ | 3.468 |
| Intra.H. [n = 5928] | 0.30201 (0.29032–0.31374) | 2.01444 (1.99948–2.02970) | ∉ | 5.090 |
| {20} | 0.24093 (0.19998–0.28392) | 2.11504 (2.05074–2.18478) | ∈ | 5.139 |
| {21} | 0.27413 (0.22135–0.33404) | 2.07572 (1.99774–2.15567) | ∉ | 5.166 |
| {22} | 0.30906 (0.25770–0.36612) | 2.00135 (1.93558–2.06985) | ∉ | 5.467 |
| {23} | 0.28115 (0.23273–0.33223) | 2.07134 (2.00753–2.14122) | ∈ | 5.353 |
| {24} | 0.29412 (0.25208–0.33994) | 2.03489 (1.97629–2.09582) | ∉ | 4.258 |
| {25} | 0.34505 (0.27538–0.42378) | 1.98475 (1.90178–2.07040) | ∉ | 5.396 |
| {26} | 0.27678 (0.22209–0.33890) | 2.04462 (1.96343–2.12882) | ∉ | 5.651 |
| {27} | 0.25509 (0.20864–0.30927) | 2.07474 (2.00025–2.14887) | ∈ | 5.866 |
| {28} | 0.22551 (0.18432–0.27515) | 2.12108 (2.04049–2.19718) | ∈ | 4.900 |
| {29} | 0.28506 (0.23698–0.33491) | 2.05095 (1.98608–2.12277) | ∉ | 5.063 |
| {30} | 0.28951 (0.23539–0.35113) | 2.02048 (1.94664–2.09670) | ∉ | 5.953 |
| {31} | 0.22457 (0.19007–0.26139) | 2.11258 (2.05475–2.17429) | ∈ | 5.050 |
| {32} | 0.30869 (0.26549–0.35446) | 2.00993 (1.95822–2.06454) | ∉ | 5.213 |
| {33} | 0.22501 (0.19468–0.25797) | 2.14477 (2.09394–2.19643) | ∈ | 5.339 |
| {34} | 0.18521 (0.14555–0.22895) | 2.20373 (2.12046–2.29300) | ∈ | 5.111 |
| {35} | 0.21729 (0.17268–0.26875) | 2.13535 (2.04595–2.22539) | ∈ | 3.794 |
| {36} | 0.27029 (0.22599–0.31829) | 2.05141 (1.98538–2.12233) | ∉ | 3.793 |
| {37} | 0.18678 (0.15636–0.22212) | 2.20481 (2.13550–2.27293) | ∈ | 4.874 |
| {38} | 0.28646 (0.24083–0.33785) | 2.05624 (1.99237–2.12073) | ∉ | 5.345 |
| {39} | 0.21582 (0.17874–0.25908) | 2.13592 (2.06139–2.20890) | ∈ | 4.531 |
| {40} | 0.40067 (0.31984–0.48698) | 1.92734 (1.84768–2.01528) | ∉ | 4.984 |
| {41} | 0.30507 (0.26861–0.34154) | 2.02238 (1.97772–2.07172) | ∉ | 3.462 |
| {42} | 0.36245 (0.30029–0.43098) | 1.99611 (1.92690–2.06835) | ∉ | 4.917 |
| {43} | 0.35200 (0.30674–0.40401) | 1.98069 (1.92476–2.03393) | ∉ | 3.677 |
| {44} | 0.29143 (0.25033–0.33579) | 2.02361 (1.96545–2.08349) | ∉ | 3.642 |
| {45} | 0.26744 (0.22596–0.31237) | 2.05124 (1.99168–2.11369) | ∉ | 5.206 |
| {46} | 0.28228 (0.24817–0.31667) | 2.03401 (1.99003–2.08263) | ∉ | 3.939 |
| {47} | 0.26209 (0.21597–0.31384) | 2.11646 (2.04455–2.19042) | ∈ | 5.032 |
| {48} | 0.24343 (0.20059–0.29256) | 2.08918 (2.01817–2.15936) | ∈ | 5.378 |
| Inter.H. [n = 6612] | 0.28027 (0.26962–0.29070) | 2.05001 (2.03580–2.06499) | ∈ | 5.573 |
| Pd [n = 12,540] | 0.28729 (0.27967–0.29518) | 2.03737 (2.02691–2.04776) | ∈ | 5.383 |
| Intra.H. | Inter.H. | Pd | ||||
|---|---|---|---|---|---|---|
| M1 | M2 | M1 | M2 | M1 | M2 | |
| Estimation of LS to progenies | Yes | Yes | Yes | Yes | - | - |
| Estimation of LS for the group | Yes | Yes | Yes | Not | Yes | Not |
| Accuracy | High | Low | High | Low | High | Low |
| Leaf dimensions in the measure | L and W | L | L and W | L | L and W | L |
| Speed of measure in the field | Slow | Fast | Slow | Fast | Slow | Fast |
| Hybridization | Progeny | {#} | Crossing | F |
|---|---|---|---|
| Intra.H. | |||
| MEG105003(2017-1) #251 | {6} | (Caturra × Timor hybrid) × Etiopía | F5 |
| MEG102014(2017-2) #295 | {1} | Etiopía × (Caturra × Timor hybrid) | F5 |
| MEG102014(2017-2) #721 | {2} | Etiopía × (Caturra × Timor hybrid) | F5 |
| MEG102004(2010-6) #150 | {5} | (Caturra × Timor hybrid) × Timor hybrid | F5 |
| MEG102004(2010-6) #47 | {4} | Timor hybrid × (Caturra × Timor hybrid) | F5 |
| MEG105001(LIBANO 7 × 7) #1359 | {19} | Caturra × Timor hybrid | F8 |
| MEG105001(LIBANO 7 × 7) #1472 | {14} | Caturra × Timor hybrid | F7 |
| MEG105001(LIBANO 8 × 8) #195 | {18} | Caturra × Timor hybrid | F8 |
| MEG105001(LIBANO 8 × 8) #433 | {17} | Caturra × Timor hybrid | F8 |
| MEG102014(2017-2) #1949 | {3} | Caturra × Timor hybrid | F7 |
| MEG105001(2013-2) #48 | {15} | Caturra × Timor hybrid | F8 |
| MEG105001(2013-2) #706 | {16} | Caturra × Timor hybrid | F8 |
| MEG105001(LIBANO 8 × 8) #304 | {7} | [Caturra × (Caturra × C. Canephora)] × [Catuaí × (Caturra × Borbón)] | F5 |
| MEG105001(LIBANO 8 × 8) #326 | {12} | [(Caturra × Timor hybrid) × (Caturra × Timor hybrid)] × [Catuaí × (Caturra × Borbón)] | F5 |
| MEG105001(LIBANO 8 × 8) #349 | {10} | [Caturra × (Caturra × C. Canephora)] × Etiopia | F5 |
| MEG105001(LIBANO 8 × 8) #380 | {9} | [Caturra × (Caturra × C. Canephora)] × [Catuaí × (Caturra × Borbón)] | F5 |
| MEG105001(LIBANO 8 × 8) #407 | {8} | [(Caturra × Timor hybrid) × (Caturra × Timor hybrid)] × (Sudán Rume × Catuaí) | F5 |
| MEG105001(LIBANO 8 × 8) #568 | {11} | (Caturra × Timor hybrid) × Dalecho | F5 |
| MEG105001(LIBANO 8 × 8) #571 | {13} | [(Caturra × Timor hybrid) × (Caturra × Timor hybrid)] × Etiopia | F5 |
| CU1819 | {53} | Caturra × Timor hybrid | F5 |
| CU1825 | {54} | Caturra × Timor hybrid | F5 |
| CU1849 | {55} | Caturra × Timor hybrid | F5 |
| CU1953 | {50} | Caturra × Timor hybrid | F5 |
| CU2021 | {51} | Caturra × Timor hybrid | F5 |
| CU2034 | {52} | Caturra × Timor hybrid | F5 |
| CX2866 | {49} | Caturra × Timor hybrid | F5 |
| Inter.H. | |||
| MEG105001 BLONAY #170,173 | {30} | (Caturra × C. canephora) × Caturra | F6 |
| MEG105001(LIBANO 8 × 8) #123 | {21} | Caturra × [(Caturra × C. canephora) × Caturra] | F5 |
| MEG105001(LIBANO 8 × 8) #139 | {22} | (Caturra × C. canephora) × Caturra | F7 |
| MEG105001(LIBANO 8 × 8) #159 | {24} | (Caturra × C. canephora) × Caturra | F7 |
| MEG105001(LIBANO 8 × 8) #290 | {26} | (Caturra × C. canephora) × Caturra | F7 |
| MEG105001(LIBANO 8 × 8) #365 | {25} | (Caturra × C. canephora) × Caturra | F7 |
| MEG105001(LIBANO 8 × 8) #469 | {27} | (Caturra × C. canephora) × Caturra | F7 |
| MEG105001(LIBANO 8 × 8) #601 | {20} | Caturra × [(Caturra × C. canephora) × Caturra] | F5 |
| MEG105001(LIBANO 8 × 8) #615 | {23} | (Caturra × C. canephora) × Caturra | F7 |
| MEG105001(2013-2) #102 | {33} | (Caturra × C. canephora) × Caturra | F6 |
| MEG102003(2009-17) #109 | {43} | (Caturra × C. canephora) × Caturra | F5 |
| MEG102003(2009-17) #13 | {46} | (Caturra × C. canephora) × Caturra | F5 |
| MEG105001(2013-3) #1511 | {39} | (Caturra × C. canephora) × Caturra | F6 |
| MEG105001(2013-2) #165 | {31} | (Caturra × C. canephora) × Caturra | F6 |
| MEG102003(2009-17) #250 | {40} | (Caturra × C. canephora) × Caturra | F5 |
| MEG105001(2013-2) #289 | {35} | (Caturra × C. canephora) × Caturra | F6 |
| MEG102003(2009-17) #300 | {42} | (Caturra × C. canephora) × Caturra | F5 |
| MEG105001(2013-2) #552 | {36} | (Caturra × C. canephora) × Caturra | F6 |
| MEG102003(2009-17) #561 | {48} | (Caturra × C. canephora) × Caturra | F5 |
| MEG102003(2009-17) #572 | {41} | (Caturra × C. canephora) × Caturra | F5 |
| MEG102003(2009-17) #583 | {47} | (Caturra × C. canephora) × Caturra | F5 |
| MEG102003(2009-17) #601 | {44} | (Caturra × C. canephora) × Caturra | F5 |
| MEG105001(2013-2) #679 | {38} | (Caturra × C. canephora) × Caturra | F6 |
| MEG105001(2013-2) #698 | {29} | (Caturra × C. canephora) × Caturra | F6 |
| MEG105001(2013-2) # 718 | {34} | (Caturra × C. canephora) × Caturra | F6 |
| MEG105001(2013-2) #84 | {32} | (Caturra × C. canephora) × Caturra | F6 |
| MEG102003(2009-17) #86 | {45} | (Caturra × C. canephora) × Caturra | F5 |
| MEG105001(2013-2) #98 | {37} | (Caturra × C. canephora) × Caturra | F6 |
| MEG105001(2013-2) #305,493 | {28} | (Caturra × C. canephora) × Caturra | F6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unigarro, C.A.; Darghan, A.E.; Cayón Salinas, D.G.; Flórez-Ramos, C.P. Non-Destructive Estimation of Leaf Size and Shape Characteristics in Advanced Progenies of Coffea arabica L. from Intraspecific and Interspecific Crossing. Plants 2025, 14, 2985. https://doi.org/10.3390/plants14192985
Unigarro CA, Darghan AE, Cayón Salinas DG, Flórez-Ramos CP. Non-Destructive Estimation of Leaf Size and Shape Characteristics in Advanced Progenies of Coffea arabica L. from Intraspecific and Interspecific Crossing. Plants. 2025; 14(19):2985. https://doi.org/10.3390/plants14192985
Chicago/Turabian StyleUnigarro, Carlos Andres, Aquiles Enrique Darghan, Daniel Gerardo Cayón Salinas, and Claudia Patricia Flórez-Ramos. 2025. "Non-Destructive Estimation of Leaf Size and Shape Characteristics in Advanced Progenies of Coffea arabica L. from Intraspecific and Interspecific Crossing" Plants 14, no. 19: 2985. https://doi.org/10.3390/plants14192985
APA StyleUnigarro, C. A., Darghan, A. E., Cayón Salinas, D. G., & Flórez-Ramos, C. P. (2025). Non-Destructive Estimation of Leaf Size and Shape Characteristics in Advanced Progenies of Coffea arabica L. from Intraspecific and Interspecific Crossing. Plants, 14(19), 2985. https://doi.org/10.3390/plants14192985







