Estimating Soil Moisture Content in Winter Wheat in Southern Xinjiang by Fusing UAV Texture Feature with Novel Three-Dimensional Texture Indexes
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Area and Experimental Design
2.2. Data Acquisition and Preprocessing
2.2.1. Multispectral Data Acquisition and Processing
2.2.2. Soil Moisture Measurement
2.3. Modeling Approach
2.4. Dataset Partitioning and Model Evaluation
3. Results and Analysis
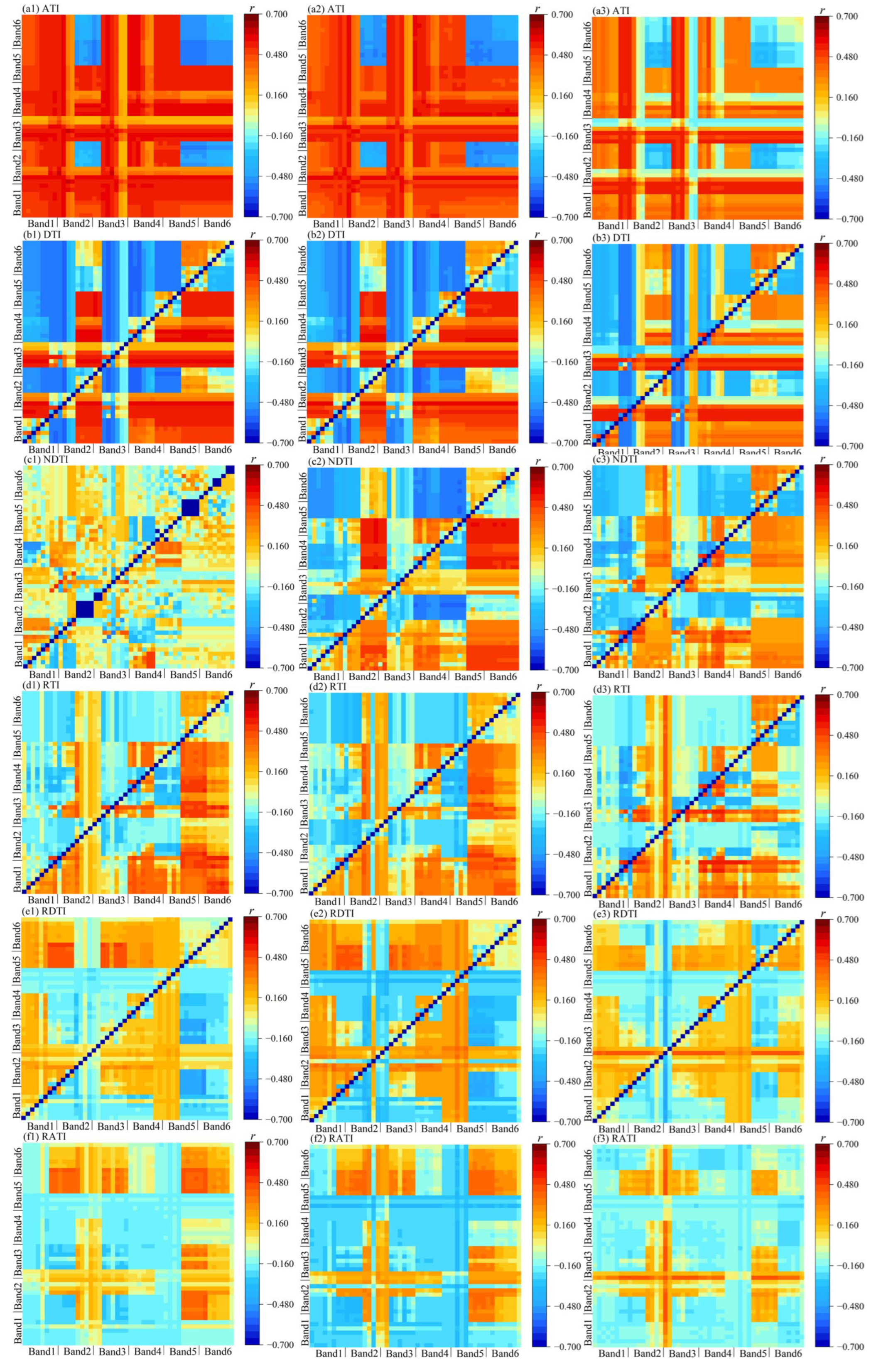
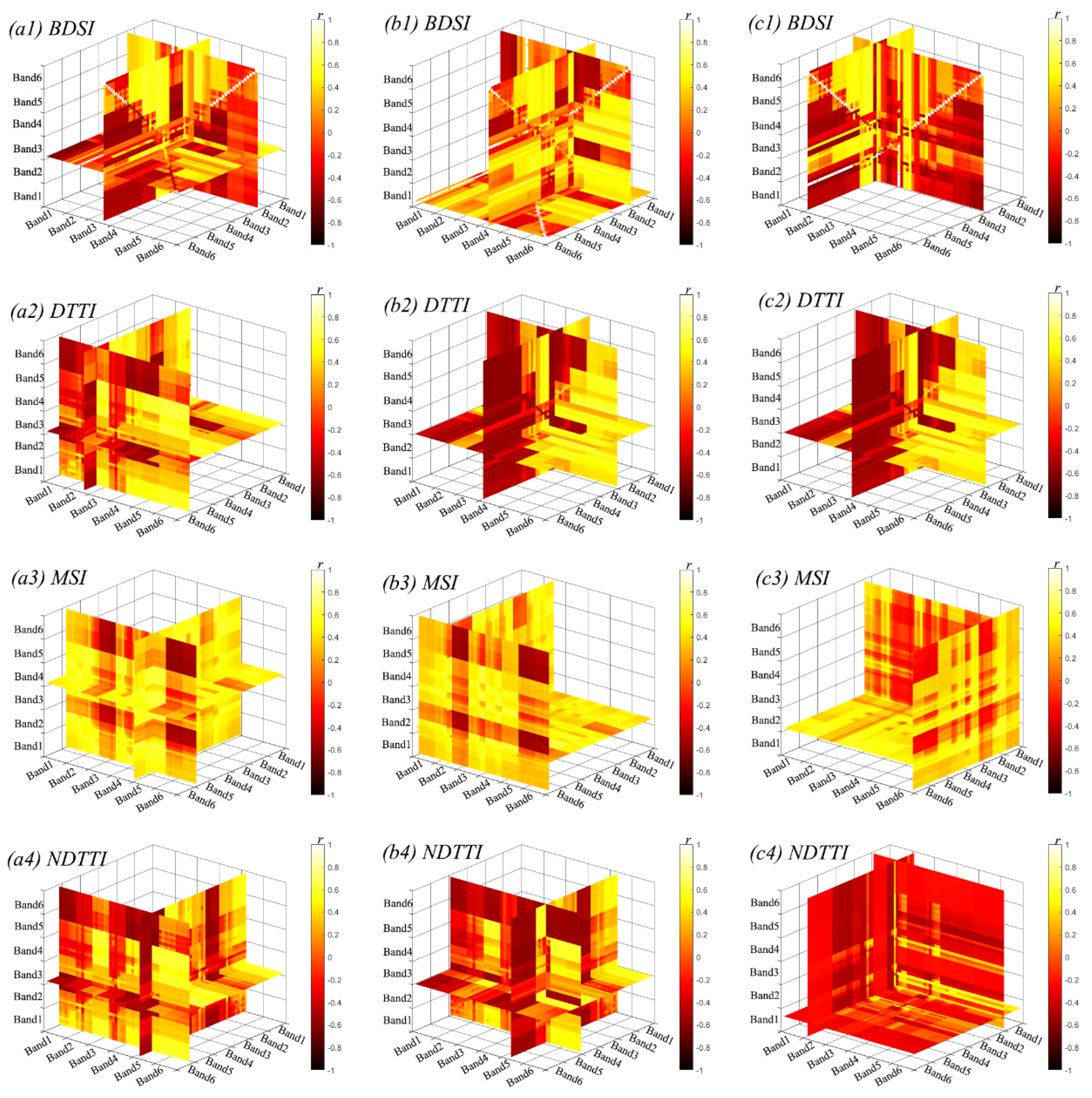
3.1. Correlation Between Multispectral Texture Parameters and Soil Moisture Content in Winter Wheat
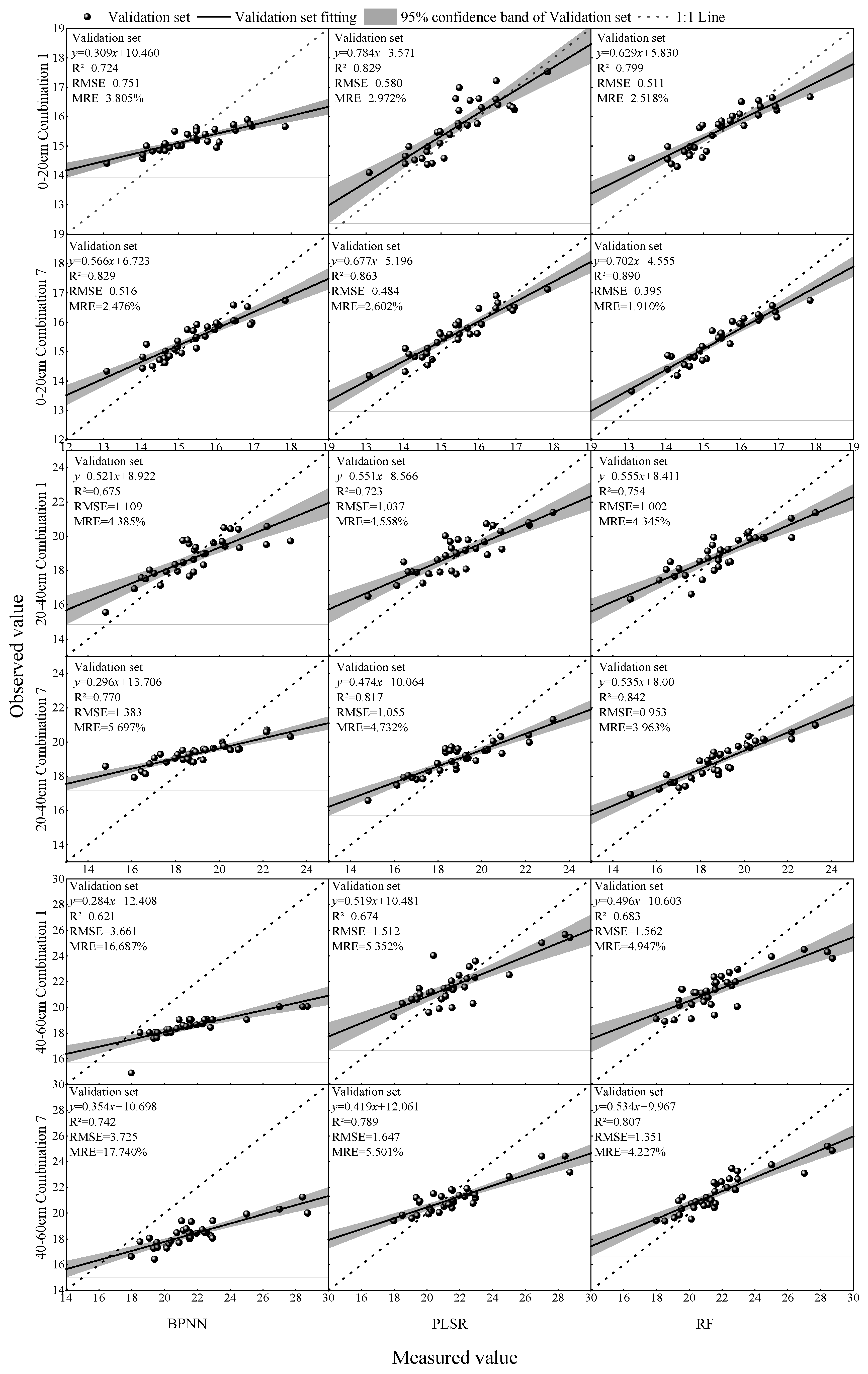
3.2. Model Construction for SMC at Different Depths
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lei, Q.; Tao, W.; Lin, S.; Su, L.; Deng, M.; Wang, Q.; Yang, F.; Zhu, T.; Ma, L. The synergistic production effect of water and nitrogen on winter wheat in southern Xinjiang. Plants 2024, 13, 1391. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Wang, X.; Zhu, X.; Li, Y. Prediction of soil organic matter content in winter wheat jointing stage based on UAV multispectral and machine learning. Measurement 2025, 256, 118508. [Google Scholar] [CrossRef]
- Tang, Z.; Lu, J.; Xiang, Y.; Shi, H.; Sun, T.; Zhang, W.; Wang, H.; Zhang, X.; Li, Z.; Zhang, F. Farmland mulching and optimized irrigation increase water productivity and seed yield by regulating functional parameters of soybean (Glycine max L.) Leaves. Agric. Water Manag. 2024, 298, 108875. [Google Scholar] [CrossRef]
- Cheng, M.; Lu, X.; Liu, Z.; Yang, G.; Zhang, L.; Sun, B.; Wang, Z.; Zhang, Z.; Shang, M.; Sun, C. Accurate characterization of soil moisture in wheat fields with an improved drought index from unmanned aerial vehicle observations. Agronomy 2024, 14, 1783. [Google Scholar] [CrossRef]
- Tang, Y.; Ma, J.; Xu, J.; Wu, W.; Wang, Y.; Guo, H. Assessing the impacts of tidal creeks on the spatial patterns of coastal salt marsh vegetation and its aboveground biomass. Remote Sens. 2022, 14, 1839. [Google Scholar] [CrossRef]
- Aït-Kaddour, A.; Loudiyi, M.; Boukria, O.; Safarov, J.; Sultanova, S.; Andueza, D.; Listrat, A.; Cahyana, Y. Beef muscle discrimination based on two-trace two-dimensional correlation spectroscopy (2t2d COS) combined with snapshot visible-near infrared multispectral imaging. Meat Sci. 2024, 214, 109533. [Google Scholar] [CrossRef]
- Orlando, S.; Minacapilli, M.; Sarno, M.; Carrubba, A.; Motisi, A. A low-cost multispectral imaging system for the characterisation of soil and small vegetation properties using visible and near-infrared reflectance. Comput. Electron. Agric. 2022, 202, 107359. [Google Scholar] [CrossRef]
- Amaro, R.P.; Todoroff, P.; Christina, M.; Garbellini Duft, D.; Dos Santos Luciano, A.C. Performance evaluation of sentinel-2 imagery, agronomic and climatic data for sugarcane yield estimation. Comput. Electron. Agric. 2025, 237, 110522. [Google Scholar] [CrossRef]
- Eid, A.N.M.; Olatubara, C.O.; Ewemoje, T.A.; El-Hennawy, M.T.; Farouk, H. Inland wetland time-series digital change detection based on SAVI and NDWI indecies: Wadi el-rayan lakes, Egypt. Remote Sens. Appl. Soc. Environ. 2020, 19, 100347. [Google Scholar] [CrossRef]
- Wójtowicz, A.; Piekarczyk, J.; Czernecki, B.; Ratajkiewicz, H. A random forest model for the classification of wheat and rye leaf rust symptoms based on pure spectra at leaf scale. J. Photochem. Photobiol. B Biol. 2021, 223, 112278. [Google Scholar] [CrossRef]
- Bonsoms, J.; Boulet, G. Ensemble machine learning outperforms empirical equations for the ground heat flux estimation with remote sensing data. Remote Sens. 2022, 14, 1788. [Google Scholar] [CrossRef]
- Tang, Z.; Lu, J.; Abdelghany, A.E.; Su, P.; Jin, M.; Li, S.; Sun, T.; Xiang, Y.; Li, Z.; Zhang, F. Winter oilseed rape LAI inversion via multi-source UAV fusion: A three-dimensional texture and machine learning approach. Plants 2025, 14, 1245. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, X.; Zhang, Y.; Shi, L.; Wang, L.; Yang, Y.; Shen, J.; Zhu, J.; Zhang, D.; Qu, Z. Assimilating UAV observations and crop model simulations for dynamic estimation of crop water stress. Agric. Water Manag. 2025, 318, 109688. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Zhang, J.; Guo, Y.; Yang, X.; Yu, G.; Bai, X.; Chen, J.; Chen, Y.; Shi, L.; et al. Improving estimation of maize leaf area index by combining of UAV-based multispectral and thermal infrared data: The potential of new texture index. Comput. Electron. Agric. 2023, 214, 108294. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.; Chen, G.; Cui, S.; Wu, Y.; Liu, X.; Meng, W.; Liu, Y.; He, J.; Liu, D.; et al. Soybean (glycine max l.) Leaf moisture estimation based on multisource unmanned aerial vehicle image feature fusion. Plants 2024, 13, 1498. [Google Scholar] [CrossRef]
- Pei, S.; Dai, Y.; Bai, Z.; Li, Z.; Zhang, F.; Yin, F.; Fan, J. Improved estimation of canopy water status in cotton using vegetation indices along with textural information from UAV-based multispectral images. Comput. Electron. Agric. 2024, 224, 109176. [Google Scholar] [CrossRef]
- Geng, J.; Lv, J.; Pei, J.; Liao, C.; Tan, Q.; Wang, T.; Fang, H.; Wang, L. Prediction of soil organic carbon in black soil based on a synergistic scheme from hyperspectral data: Combining fractional-order derivatives and three-dimensional spectral indices. Comput. Electron. Agric. 2024, 220, 108905. [Google Scholar] [CrossRef]
- Wang, H.; Dai, Y.; Yao, Q.; Ma, L.; Zhang, Z.; Lv, X. Multi-task learning model driven by climate and remote sensing data collaboration for mid-season cotton yield prediction. Field Crops Res. 2025, 333, 110070. [Google Scholar] [CrossRef]
- Zhai, J.; Wang, N.; Hu, B.; Han, J.; Feng, C.; Peng, J.; Luo, D.; Shi, Z. Estimation of soil salinity by combining spectral and texture information from UAV multispectral images in the tarim river basin, China. Remote Sens. 2024, 16, 3671. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, H.; Yang, X.; Jiang, Y.; Wu, Y.; Shui, J.; Liu, Y.; Guo, M.; Li, L. Spatial downscaling of SMAP soil moisture to high resolution using machine learning over China’s loess plateau. Catena 2024, 247, 108492. [Google Scholar] [CrossRef]
- Chen, P.; Chen, C.; Kang, C.; Liu, J.; Li, Y. Soil water content prediction across seasons using random forest based on precipitation-related data. Comput. Electron. Agric. 2025, 230, 109802. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Z.; Huo, Y.; Xu, J.; Gu, X.; Cai, H. Optimization of irrigation-nitrogen-straw management measures for summer maize under future climate conditions in the Guanzhong plain of China. Field Crops Res. 2025, 328, 109945. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative remote sensing at ultra-high resolution with UAV spectroscopy: A review of sensor technology, measurement procedures, and data correction workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Shi, H.; Liu, Z.; Li, S.; Jin, M.; Tang, Z.; Sun, T.; Liu, X.; Li, Z.; Zhang, F.; Xiang, Y. Monitoring soybean soil moisture content based on UAV multispectral and thermal-infrared remote-sensing information fusion. Plants 2024, 13, 2417. [Google Scholar] [CrossRef]
- Yue, J.; Li, T.; Feng, H.; Fu, Y.; Liu, Y.; Tian, J.; Yang, H.; Yang, G. Enhancing field soil moisture content monitoring using laboratory-based soil spectral measurements and radiative transfer models. Agric. Commun. 2024, 2, 100060. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, X.; Liu, Y.; Shao, M.; Yu, X.; Bai, Y.; Wang, Z.; Wang, S.; Tuohuti, N.; Liu, S.; et al. Estimation of soil moisture content under high maize canopy coverage from UAV multimodal data and machine learning. Agric. Water Manag. 2022, 264, 107530. [Google Scholar] [CrossRef]
- Sharma, J.; Prasad, R.; Srivastava, P.K.; Singh, S.K.; Yadav, S.A.; Pandey, D.K. Improved radar vegetation water content integration for SMAP soil moisture retrieval. Remote Sens. Appl. Soc. Environ. 2025, 37, 101443. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, Z.; Cui, N.; Zheng, S.; Zhu, S.; Jiang, S.; Wang, Z.; Gong, D.; Wang, Y.; Zhao, L. Soil moisture content estimation of drip-irrigated citrus orchard based on UAV images and machine learning algorithm in southwest China. Agric. Water Manag. 2024, 303, 109069. [Google Scholar] [CrossRef]
- Meng, Q.; Kecskeméthy, A. Determination of maximum virtual coefficients in motion-force interaction performance indices for parallel mechanisms. Mech. Mach. Theory 2025, 214, 106111. [Google Scholar] [CrossRef]
- Reiter, S.; Werner, S.W.R. Interpolatory model reduction of dynamical systems with root mean squared error. IFAC-PapersOnLine 2025, 59, 385–390. [Google Scholar] [CrossRef]
- Pulighe, G.; Belocchi, A.; Tani, A.C.; Lupia, F. Impacts of agricultural management practices on water cycle, soil erosion and crop yields in a mediterranean agroecosystem. Sci. Total Environ. 2025, 995, 180111. [Google Scholar] [CrossRef]
- Yuan, L.; Yu, Q.; Xiang, L.; Zeng, F.; Dong, J.; Xu, O.; Zhang, J. Integrating UAV and high-resolution satellite remote sensing for multi-scale rice disease monitoring. Comput. Electron. Agric. 2025, 234, 110287. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, X.; Yan, C.; Li, R.; Li, B. Unveiling seaward expansion pattern in mangrove forests using UAV remote sensing and deep learning. Ecol. Indic. 2025, 178, 114054. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, N.; Zhang, W.; Yang, Y.; Gong, D.; Liu, Q.; Zhao, L.; Xing, L.; He, Q.; Zhu, S.; et al. Estimation of soil moisture in drip-irrigated citrus orchards using multi-modal UAV remote sensing. Agric. Water Manag. 2024, 302, 108972. [Google Scholar] [CrossRef]
- Yin, L.; Yan, S.; Li, M.; Liu, W.; Zhang, S.; Xie, X.; Wang, X.; Wang, W.; Chang, S.; Hou, F. Enhancing soil moisture estimation in alfalfa root-zone using UAV-based multimodal remote sensing and deep learning. Eur. J. Agron. 2024, 161, 127366. [Google Scholar] [CrossRef]
- Li, H.; Liu, N.; Shao, L.; Liu, X.; Sun, H.; Chen, S.; Zhang, X. Changes in root growth and water uptake contribute to the yield and water productivity improvement in winter wheat during the past three decades: A case study in the north China plain. Agric. Water Manag. 2025, 313, 109482. [Google Scholar] [CrossRef]
- Lopez, G.; Hadir, S.; Mouratidis, S.D.; Shuva, M.A.; Hüging, H.; Bauke, S.L.; Gaiser, T.; Schaaf, G.; Seidel, S.J. Winter wheat shoot and root phenotypic plasticity under fertilized and nutrient-deficient field conditions. Eur. J. Agron. 2025, 168, 127634. [Google Scholar] [CrossRef]
- Gu, H.; Wang, Y.; Peruzzo, L.; Li, B.; Lu, Y.; Liu, X. Linking winter wheat (Triticum aestivum L) root traits and root water uptake with electrical resistivity tomography. Agric. Water Manag. 2025, 307, 109247. [Google Scholar] [CrossRef]
- Liao, Z.; Dai, Y.; Wang, H.; Ketterings, Q.M.; Lu, J.; Zhang, F.; Li, Z.; Fan, J. A double-layer model for improving the estimation of wheat canopy nitrogen content from unmanned aerial vehicle multispectral imagery. J. Integr. Agric. 2023, 22, 2248–2270. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, J.; Guo, J.; Hui, X.; Wang, Y.; Cai, D.; Yan, H. Detecting water stress in winter wheat based on multifeature fusion from UAV remote sensing and stacking ensemble learning method. Remote Sens. 2024, 16, 4100. [Google Scholar] [CrossRef]
- Schleich, A.; Vega, C.; Renaud, J.; Bouriaud, O.; Durrieu, S. KNN-Bagging NFI, GEDI, sentinel-2 and sentinel-1 data to produce estimates of forest volumes. For. Ecol. Manag. 2025, 595, 122964. [Google Scholar] [CrossRef]
- Badrakh, M.; Tserendash, N.; Choindonjamts, E.; Albert, G. Potential of random forest machine learning algorithm for geological mapping using PALSAR and sentinel-2a remote sensing data: A case study of Tsagaan-uul area, southern Mongolia. J. Asian Earth Sci. X 2025, 14, 100204. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.; Xiao, H.; Fang, Y.; Wang, T.; Liu, N.; Wang, M.; Feng, Z. An InSAR DEMs refinement framework integrating random forest with multi-source remote sensing datasets. Adv. Space Res. 2025, 76, 4125–4144. [Google Scholar] [CrossRef]
- Virtriana, R.; Ihsan, K.T.N.; Anggraini, T.S.; Deliar, A.; Harto, A.B.; Riqqi, A.; Sakti, A.D. Development of location suitability prediction for health facilities using random forest machine learning in 2030 integrating remote sensing and GIS in west java, Indonesia. Environ. Adv. 2025, 19, 100604. [Google Scholar] [CrossRef]
- He, W.; Yao, Y.; Li, Y.; Yu, L.; Ni, L.; Fu, B.; Huang, J.; Li, D. Accurately estimating and revealing the patterns of leaf c:n:p stoichiometry with remote sensing and neural network methods in a karst area. Comput. Electron. Agric. 2025, 231, 110006. [Google Scholar] [CrossRef]
- Xu, H.; Li, P.; Wang, J.; Liang, W. A study on black screen fault detection of single-phase smart energy meter based on random forest binary classifier. Measurement 2025, 242, 116245. [Google Scholar] [CrossRef]
- Ghahramani, E.; Hoerig, C.; Wallace, K.; Wu, M.; Mamou, J. Random forest-based detection of metastases in clinically scanned lymph nodes using quantitative ultrasound imaging. Ultrasound Med. Biol. 2025, 51, 1439–1446. [Google Scholar] [CrossRef]
- Marques Filho, P.C. Confidence intervals for the random forest generalization error. Pattern Recognit. Lett. 2022, 158, 171–175. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, T.; Wu, Z.; Lin, T.; Huang, H. A study on dynamic cleaning of charging pile electric energy metering data based on improved random forest algorithm. Measurement 2025, 256, 118114. [Google Scholar] [CrossRef]
- Qiu, Y.; Liao, Y.; Feng, A.; Wang, Y.; Yin, H.; Tian, H.; Deng, A.; Li, Y. Enhanced rice chlorophyll detection: A novel PLSR-RF and BOSS integration framework with dual spectral analysis. Measurement 2025, 255, 117883. [Google Scholar] [CrossRef]
- Lesnoff, M. Averaging a local PLSR pipeline to predict chemical compositions and nutritive values of forages and feed from spectral near infrared data. Chemom. Intell. Lab. Syst. 2024, 244, 105031. [Google Scholar] [CrossRef]
- Feng, H.; Zhou, Y.; Zeng, W.; Guo, W. A physics-based PSO-BPNN model for civil aircraft noise assessment. Appl. Acoust. 2024, 221, 109992. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, Q.; Wang, J.; Han, L.; Zhou, R.; He, Y.; Li, K. Predictive control modeling of ADS’s MEBT using BPNN to reduce the impact of noise on the control system. Ann. Nucl. Energy 2019, 132, 576–583. [Google Scholar] [CrossRef]
- Sangeetha, V.; Agilandeeswari, L. Artificial intelligence enabled spectral-spatial feature extraction techniques for land use and land cover classification using hyperspectral images—An inclusive review. Egypt. J. Remote Sens. Space Sci. 2025, 28, 455–467. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Wang, S.; Song, L. Spatial-spectral adaptive generalization driven high-precision BRDF modeling for extensible areas using UAV-borne remote sensing. ISPRS J. Photogramm. Remote Sens. 2025, 227, 12–30. [Google Scholar] [CrossRef]
- Chávez-Martínez, O.; Monjardin-Armenta, S.A.; Rangel-Peraza, J.G.; Mora-Felix, Z.D.; Sanhouse-García, A.J. Dataset of aerial photographs acquired with UAV using a multispectral (green, red and near-infrared) camera for cherry tomato (Solanum lycopersicum var. cerasiforme) monitoring. Data Brief 2025, 58, 111256. [Google Scholar] [CrossRef]
- Viaña-Borja, S.P.; Heredia, S.; Navarro, G.; Santamarta-Benito, X.; Araujo-Suarez, N.; Caballero, I. Comparative assessment of bathymetric methods using unmanned aerial vehicle (UAV) high-resolution multispectral imaging. Coast. Eng. 2025, 202, 104854. [Google Scholar] [CrossRef]
- Trevisan, L.; Shokry, A.; Montini, M.; Moulines, E.; Zio, E. A hybrid approach for steady-state production optimization of a real oil and gas platform: Integrating physics-based models, machine learning techniques, and field monitoring signals. Comput. Chem. Eng. 2025, 203, 109320. [Google Scholar] [CrossRef]
- Merino-Olagüe, M.; Iriarte, X.; Castellano-Aldave, C.; Plaza, A. Hybrid modelling and identification of mechanical systems using physics-enhanced machine learning. Eng. Appl. Artif. Intell. 2025, 159, 111762. [Google Scholar] [CrossRef]
- Yan, C.; Yang, G.; Liang, Z.; Cheng, H.; Wu, G.; Srivastava, A.K.; Yu, Q.; Zhao, G. CO-ResNetRS50-SSL: Enhanced convolution and semi-supervised learning for accurate rice growth stage recognition in complex field conditions. Eur. J. Agron. 2025, 168, 127631. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Dong, X.; Li, J.; Liu, H.; Cai, X.; Xu, J.; Wang, G.; Lyu, H.; Li, J. Distribution of emergent aquatic vegetation leaf inclination angle and its simulation. Aquat. Bot. 2023, 189, 103703. [Google Scholar] [CrossRef]
- Ali, A.; Zhao, T.; Feng, C.; Zhao, X.; Li, L.; Wu, R.; Liu, H.; Huang, Q.; Lin, J.; Wang, J. Decoding the hormonal, genetic, and environmental signals regulating leaf angle in plants. Plant Stress 2025, 17, 100918. [Google Scholar] [CrossRef]
- Sellan, G.; Thompson, J.; Robert, R.; Brearley, F.Q. Nutrient addition to a white sand tropical forest results in greater growth of saplings of canopy tree species than understorey specialist tree species. For. Ecol. Manag. 2025, 589, 122755. [Google Scholar] [CrossRef]
- Cheng, F.; Zhao, X.; Luo, Y.; Tian, J.; Sun, Y.; Wang, H.; Wang, Q.; Zhu, J.; Yang, C.; He, H.; et al. Effects of thinning on canopy structure, forest productivity, and productivity stability in mixed conifer-broadleaf forest: Insights from a LiDAR survey. J. Environ. Manag. 2025, 385, 125707. [Google Scholar] [CrossRef]


| Texture Indices | Formula | References |
|---|---|---|
| ATI | ATI = | [12] |
| DTI | DTI = | [12] |
| NDTI | NDTI = | [12] |
| RTI | RTI = | [15] |
| RDTI | RDTI = ( | [15] |
| RATI | RATI = | [15] |
| Texture Indices | Formula |
|---|---|
| BDSI | BDSI = |
| DTTI | DTTI = |
| MSI | MSI = |
| NDTTI | NDTTI = |
| Soil Depth | Texture Feature | Correlation Coefficient (p < 0.05) | |||||
|---|---|---|---|---|---|---|---|
| Band 1 | Band 2 | Band 3 | Band 4 | Band 5 | Band 6 | ||
| 0–20 cm | MEA | 0.485 * | 0.478 * | 0.481 * | 0.493 * | 0.539 * | 0.543 * |
| VAR | 0.568 * | 0.585 * | 0.558 * | 0.609 * | 0.371 * | 0.304 * | |
| HOM | 0.350 * | 0.267 * | 0.311 * | 0.316 * | 0.442 * | 0.421 * | |
| CON | 0.585 * | 0.601 * | 0.567 * | 0.498 * | 0.211 * | 0.173 | |
| DIS | 0.622 * | 0.593 * | 0.619 * | 0.488 * | 0.336 * | 0.306 * | |
| ENT | 0.574 * | 0.581 * | 0.572 * | 0.583 * | 0.577 * | 0.578 * | |
| SEC | 0.559 * | 0.571 * | 0.563 * | 0.563 * | 0.565 * | 0.577 * | |
| COR | 0.377 * | 0.388 * | 0.377 * | 0.363 * | 0.317 * | 0.320 * | |
| 20–40 cm | MEA | 0.421 * | 0.413 * | 0.407 * | 0.434 * | 0.479 * | 0.489 * |
| VAR | 0.517 * | 0.539 * | 0.483 * | 0.612 * | 0.414 * | 0.353 * | |
| HOM | 0.396 * | 0.335 * | 0.356 * | 0.417 * | 0.404 * | 0.456 * | |
| CON | 0.538 * | 0.571 * | 0.492 * | 0.548 * | 0.279 * | 0.242 * | |
| DIS | 0.593 * | 0.584 * | 0.562 * | 0.521 * | 0.387 * | 0.358 * | |
| ENT | 0.533 * | 0.532 * | 0.525 * | 0.535 * | 0.534 * | 0.537 * | |
| SEC | 0.527 * | 0.536 * | 0.542 * | 0.534 * | 0.523 * | 0.532 * | |
| COR | 0.439 * | 0.423 * | 0.440 * | 0.385 * | 0.382 * | 0.372 * | |
| 40–60 cm | MEA | 0.389 * | 0.362 * | 0.403 * | 0.338 * | 0.288 * | 0.272 * |
| VAR | 0.570 * | 0.537 * | 0.576 * | 0.424 * | 0.009 | 0.077 | |
| HOM | 0.297 * | 0.243 * | 0.248 * | 0.248 * | 0.426 * | 0.305 * | |
| CON | 0.554 * | 0.488 * | 0.569 * | 0.211 * | 0.159 | 0.193 | |
| DIS | 0.405 * | 0.319 * | 0.481 * | 0.132 | 0.063 | 0.093 * | |
| ENT | 0.328 * | 0.328 * | 0.327 * | 0.332 * | 0.329 * | 0.330 * | |
| SEC | 0.300 * | 0.336 * | 0.316 * | 0.325 * | 0.289 * | 0.326 * | |
| COR | 0.073 | 0.079 | 0.074 | 0.071 | 0.000 | 0.008 | |
| Index | 0–20 cm | 20–40 cm | 40–60 cm | |||
|---|---|---|---|---|---|---|
| Correlation Coefficient | Position | Correlation Coefficient | Position | Correlation Coefficient | Position | |
| ATI | 0.643 * | (HOM2, MEA2) | 0.615 * | (HOM2, MEA2) | 0.576 * | (HOM2, MEA2) |
| DTI | 0.636 * | (MEA3, MEA4) | 0.614 * | (MEA3, MEA4) | 0.583 * | (MEA3, MEA4) |
| NDTI | 0.537 * | (MEA2, DIS3) | 0.598 * | (MEA2, DIS3) | 0.559 * | (MEA2, DIS3) |
| RTI | 0.575 * | (CON6, MEA2) | 0.520 * | (CON6, MEA2) | 0.578 * | (CON6, MEA2) |
| RDTI | 0.496 * | (HOM3, VAR6) | 0.467 * | (HOM3, VAR6) | 0.472 * | (HOM3, VAR6) |
| RATI | 0.470 * | (VAR6, VAR6) | 0.419 * | (VAR6, VAR6) | 0.459 * | (VAR6, VAR6) |
| Index | 0–20 cm | 20–40 cm | 40–60 cm | |||
|---|---|---|---|---|---|---|
| R | Position | R | Position | R | Position | |
| BDSI | 0.617 | (HOM5, CON3, VAR6) | 0.598 | (VAR4, DIS3, VAR6) | 0.584 | (HOM5, VAR3, COR6) |
| DTTI | 0.644 | (HOM5, HOM2, SEC6) | 0.621 | (HOM4, DIS1, HOM4) | 0.621 | (HOM4, DIS1, HOM4) |
| MSI | 0.637 | (SEC3, ENT2, DIS1) | 0.632 | (COR4, VAR6, VAR4) | 0.592 | (COR5, VAR6, VAR3) |
| NDTTI | 0.622 | (SEC6, ENT4, HOM5) | 0.612 | (ENT2, ENT5, HOM4) | 0.567 | (VAR2, VAR3, MEA5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Li, Z.; Tang, Z.; Zhang, W.; Li, W.; Liu, Z.; Wu, J.; Liu, S.; Xiang, Y.; Zhang, F. Estimating Soil Moisture Content in Winter Wheat in Southern Xinjiang by Fusing UAV Texture Feature with Novel Three-Dimensional Texture Indexes. Plants 2025, 14, 2948. https://doi.org/10.3390/plants14192948
Sun T, Li Z, Tang Z, Zhang W, Li W, Liu Z, Wu J, Liu S, Xiang Y, Zhang F. Estimating Soil Moisture Content in Winter Wheat in Southern Xinjiang by Fusing UAV Texture Feature with Novel Three-Dimensional Texture Indexes. Plants. 2025; 14(19):2948. https://doi.org/10.3390/plants14192948
Chicago/Turabian StyleSun, Tao, Zhijun Li, Zijun Tang, Wei Zhang, Wangyang Li, Zhiying Liu, Jinqi Wu, Shiqi Liu, Youzhen Xiang, and Fucang Zhang. 2025. "Estimating Soil Moisture Content in Winter Wheat in Southern Xinjiang by Fusing UAV Texture Feature with Novel Three-Dimensional Texture Indexes" Plants 14, no. 19: 2948. https://doi.org/10.3390/plants14192948
APA StyleSun, T., Li, Z., Tang, Z., Zhang, W., Li, W., Liu, Z., Wu, J., Liu, S., Xiang, Y., & Zhang, F. (2025). Estimating Soil Moisture Content in Winter Wheat in Southern Xinjiang by Fusing UAV Texture Feature with Novel Three-Dimensional Texture Indexes. Plants, 14(19), 2948. https://doi.org/10.3390/plants14192948








