A Bottom-Up Multi-Feature Fusion Algorithm for Individual Tree Segmentation in Dense Rubber Tree Plantations Using Unmanned Aerial Vehicle–Light Detecting and Ranging
Abstract
1. Introduction
2. Results
2.1. Parameter Sensitivity Analysis
2.2. Comparison with Existing Methods
2.3. Accuracy Assessment of Individual Tree Parameter Extraction
3. Discussion
4. Materials and Methods
4.1. Data Acquisition
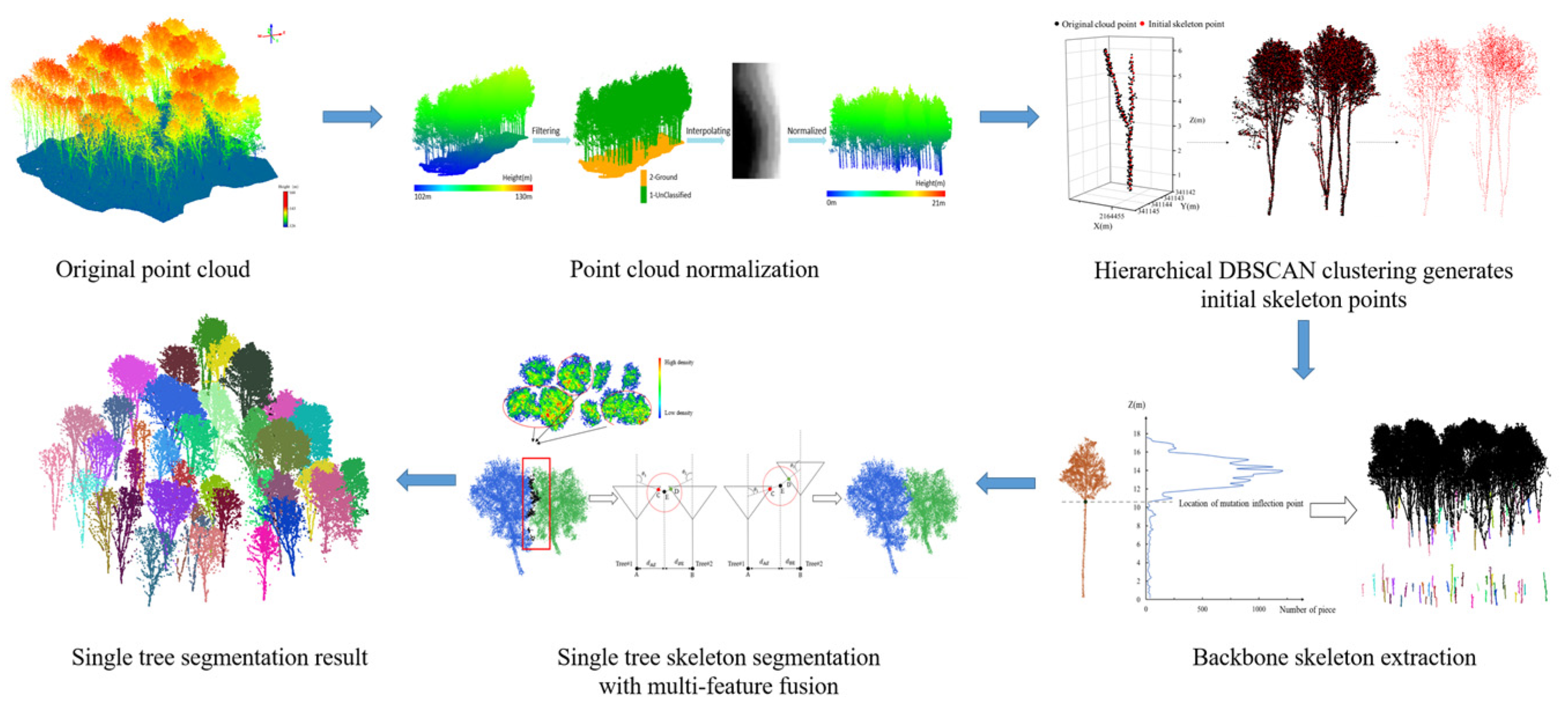
4.2. Data Preprocessing
4.3. Bottom-Up Multi-Feature Fusion Algorithm for ITS
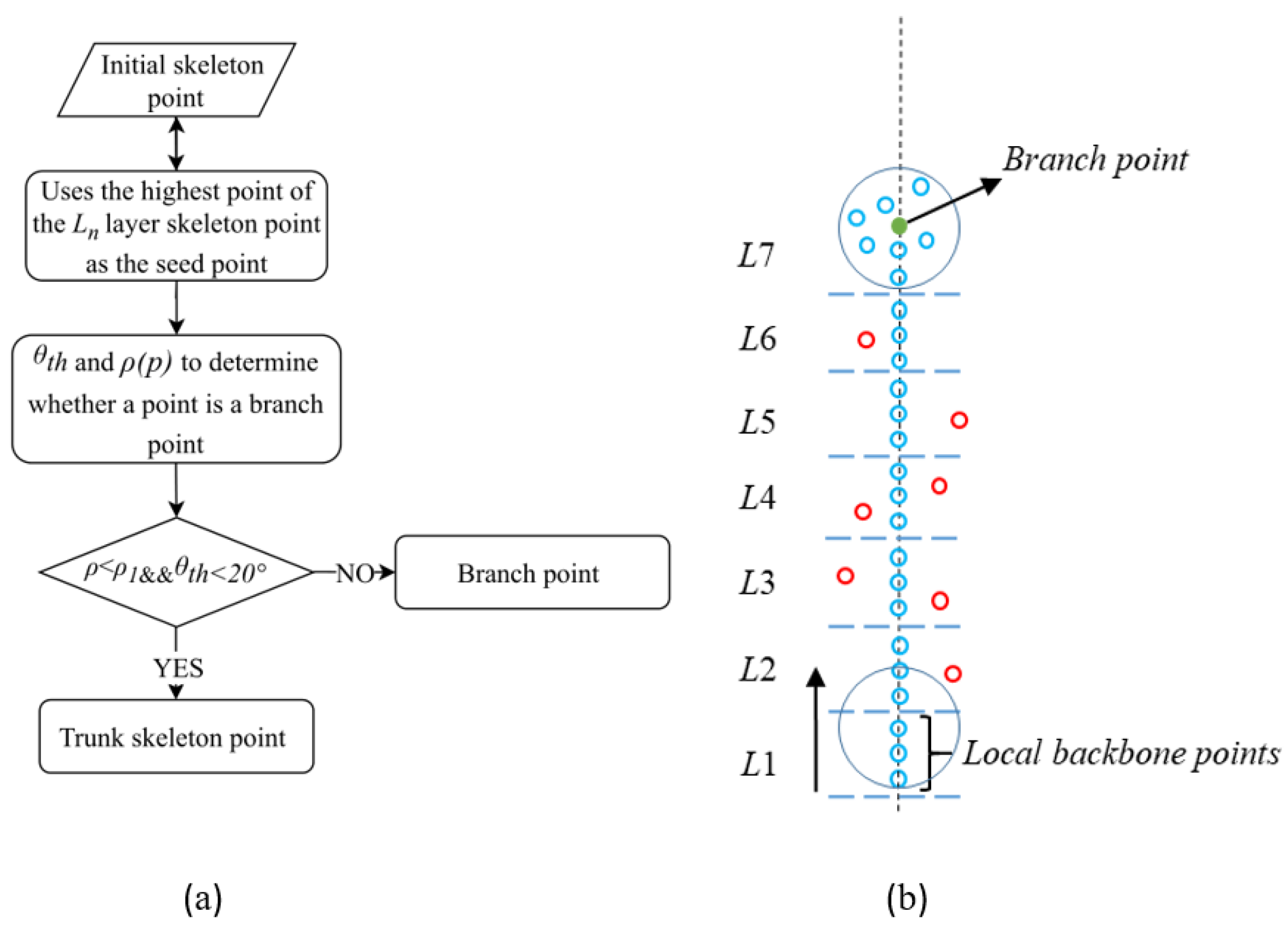
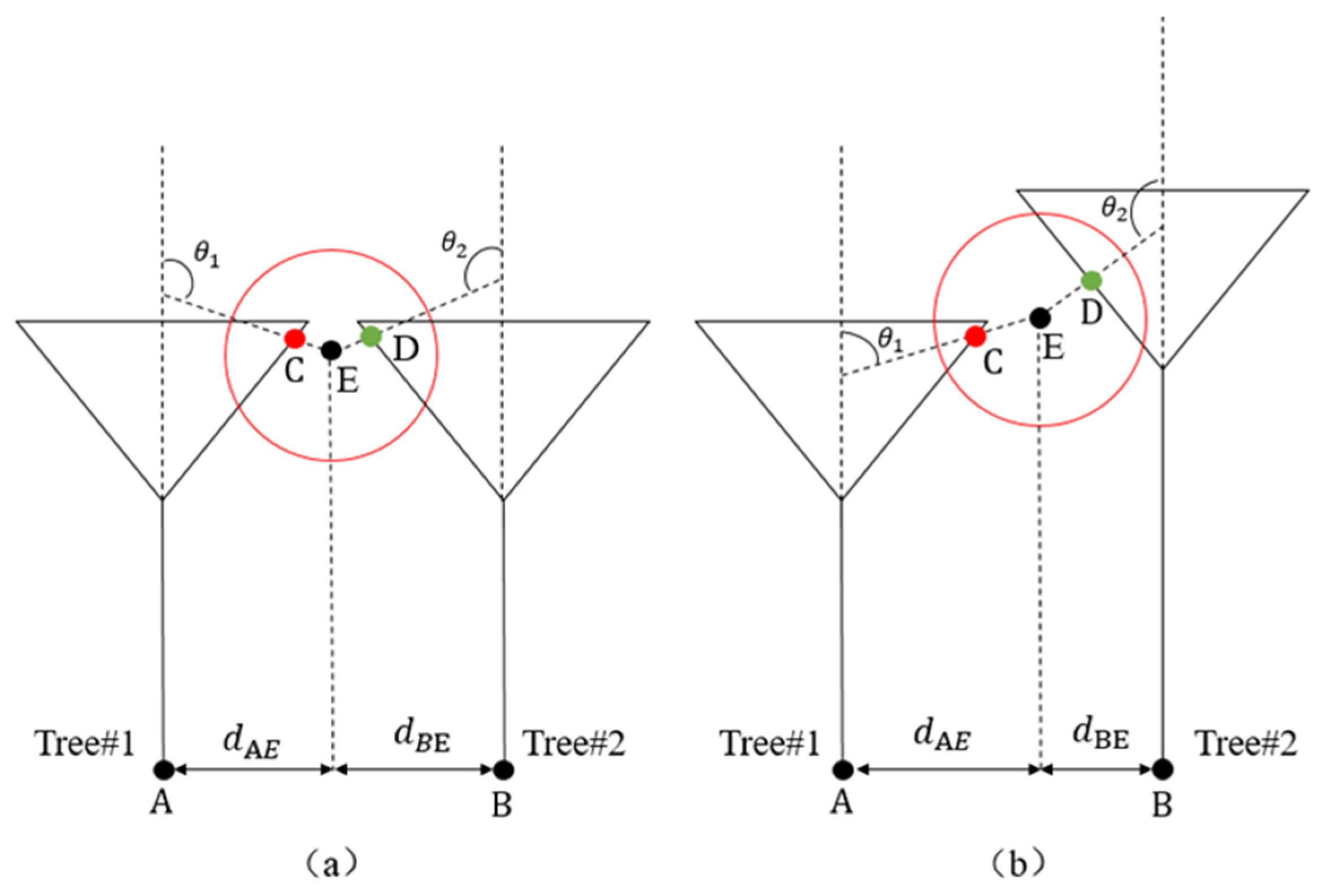
4.3.1. Generation of Initial Skeleton Points
4.3.2. Extraction of the Skeleton of Individual Tree Main Trunks
4.3.3. Multi-Feature Fusion-Based Extraction of the Canopy
| Algorithm 1 Multi-Feature Fusion Canopy Extraction |
| Input: Skeleton points S, Branch points B, Thresholds: THD1, THD2, ρ2, ρ3, θth Output: Classified labels L(s) ∈ {TreeID, unclassified} 1: Initialize all s ∈ S with L(s) = unclassified 2: Core Crown Point Identification for each branch point b_j∈B do 3: S_candidates = {s ∈ S | dist(s, b_j) ≤ THD1} 4: for each point s∈S_candidate do 5: if ρ(s) ≥ ρ3 then 6: l(s) ← j // Mark as core point of tree j 7: end if 8: end for 9: end for 10: Boundary and Disputed Point Classification for each unclassified point s∈S do 11: Compute distance to nearest branch point d = min(dist(s, b_j)) 13: if THD1 < d ≤ THD2 then 14: if ρ(s) < ρ2 then 15: l(s) ← TreeID of nearest classified point // Boundary point 16: else if ρ(s) < ρ3 then 17: l(s) ← resolve_directional_conflict(s) // Handle disputed point 18: else 19: l(s) ← treeID of nearest branch point // High-density peripheral point 20: end if 21: end if 22: end for |
4.3.4. Accuracy Assessment of ITS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hanssen, F.; Barton, D.N.; Venter, Z.S.; Nowell, M.S.; Cimburova, Z. Utilizing LiDAR data to map tree canopy for urban ecosystem extent and condition accounts in Oslo. Ecol. Indic. 2021, 130, 108007. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Cao, L.; An, F.; Chen, B.; Xue, L.; Yun, T. Individual rubber tree segmentation based on ground-based LiDAR data and faster R-CNN of deep learning. Forests 2019, 10, 793. [Google Scholar] [CrossRef]
- Zhao, Y.; Im, J.; Zhen, Z.; Zhao, Y. Towards accurate individual tree parameters estimation in dense forest: Optimized coarse-to-fine algorithms for registering UAV and terrestrial LiDAR data. GIScience Remote Sens. 2023, 60, 2197281. [Google Scholar] [CrossRef]
- Liang, Y.; Sun, Y.; Kou, W.; Xu, W.; Wang, J.; Wang, Q.; Wang, H.; Lu, N. Rubber Tree Recognition Based on UAV RGB Multi-Angle Imagery and Deep Learning. Drones 2023, 7, 547. [Google Scholar] [CrossRef]
- Burt, A.; Disney, M.; Calders, K. Extracting individual trees from lidar point clouds using treeseg. Methods Ecol. Evol. 2019, 10, 438–445. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Chen, C.; Guo, J.; Wu, H.; Li, Y.; Shi, B. Performance comparison of filtering algorithms for high-density airborne LiDAR point clouds over complex landscapes. Remote Sens. 2021, 13, 2663. [Google Scholar] [CrossRef]
- Jakubowski, M.K.; Li, W.; Guo, Q.; Kelly, M. Delineating individual trees from LiDAR data: A comparison of vector- and raster-based segmentation approaches. Remote Sens. 2013, 5, 4163–4186. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Qiu, F. Individual tree segmentation from LiDAR point clouds for urban forest inventory. Remote Sens. 2015, 7, 7892–7913. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. arXiv 2017, arXiv:1706.02413. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. arXiv 2020, arXiv:1911.11236. [Google Scholar] [CrossRef]
- Lassalle, G.; Ferreira, M.P.; La Rosa, L.E.C.; Filho, C.R.d.S. Deep learning-based individual tree crown delineation in mangrove forests using very-high-resolution satellite imagery. ISPRS J. Photogramm. Remote Sens. 2022, 189, 220–235. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, Y.; Qi, C.R.; Gong, B.; Su, H.; Anguelov, D. LESS: Label-Efficient Semantic Segmentation for LiDAR Point Clouds. In Computer Vision—ECCV 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Lecture Notes in Computer Science; Springer Nature: Cham, Switzerland, 2022; pp. 70–89. [Google Scholar]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2016, 38, 2392–2410. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Noland, T.; Li, J. An individual tree crown delineation method based on multi-scale segmentation of imagery. ISPRS J. Photogramm. Remote Sens. 2012, 70, 88–98. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2012, 85, 27–40. [Google Scholar] [CrossRef]
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]
- Li, W.K.; Guo, Q.H.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the LiDAR point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Ayrey, E.; Fraver, S.; Kershaw, J.A.; Kenefic, L.S.; Hayes, D.; Weiskittel, A.R.; Roth, B.E. Layer stacking: A novel algorithm for individual forest tree segmentation from LiDAR point clouds. Can. J. Remote Sens. 2017, 43, 16–27. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Reitberger, J.; Krzystek, P.; Stilla, U. Benefit of airborne full waveform lidar for 3D segmentation and classification of single trees. In Proceedings of the ASPRS 2009 Annual Conference, Baltimore, MD, USA, 9–13 March 2009. [Google Scholar]
- Trochta, J.; Krůček, M.; Vrška, T.; Král, K. 3D Forest: An application for descriptions of three-dimensional forest structures using terrestrial LiDAR. PLoS ONE 2017, 12, e176871. [Google Scholar] [CrossRef] [PubMed]
- Shendryk, I.; Broich, M.; Tulbure, M.G.; Alexandrov, S.V. Bottom-up delineation of individual trees from full-waveform airborne laser scans in a structurally complex eucalypt forest. Remote Sens. Environ. 2016, 173, 69–83. [Google Scholar] [CrossRef]
- Jaskierniak, D.; Lucieer, A.; Kuczera, G.; Turner, D.; Lane, P.; Benyon, R.; Haydon, S. Individual tree detection and crown delineation from Unmanned Aircraft System (UAS) LiDAR in structurally complex mixed species eucalypt forests. ISPRS J. Photogramm. Remote Sens. 2021, 171, 171–187. [Google Scholar] [CrossRef]
- Xiang, B.; Wielgosz, M.; Kontogianni, T.; Peters, T.; Puliti, S.; Astrup, R.; Schindler, K. Automated forest inventory: Analysis of high-density airborne LiDAR point clouds with 3D deep learning. Remote Sens. Environ. 2024, 305, 114078. [Google Scholar] [CrossRef]
- Wielgosz, M.; Puliti, S.; Xiang, B.; Schindler, K.; Astrup, R. SegmentAnyTree: A sensor and platform agnostic deep learning model for tree segmentation using laser scanning data. Remote Sens. Environ. 2024, 313, 114367. [Google Scholar] [CrossRef]
- Kim, D.-H.; Ko, C.-U.; Kim, D.-G.; Kang, J.T.; Park, J.M.; Cho, H.J. Automated Segmentation of Individual Tree Structures Using Deep Learning over LiDAR Point Cloud Data. Forests 2023, 14, 1159. [Google Scholar] [CrossRef]
- Puliti, S.; Fischer, C.; Astrup, R. BranchPoseNet: Characterizing tree branching with a deep learning-based pose estimation approach. arXiv 2024, arXiv:2409.14755. [Google Scholar] [CrossRef]
- Amini, A.; Saboohi, H.; Ying Wah, T.; Herawan, T. A fast density-based clustering algorithm for real-time internet of things stream. Sci. World J. 2014, 2014, 926020. [Google Scholar] [CrossRef]
- Wang, G.; Li, Q.; Yang, X.; Wang, C. Real Scene Modeling of Forest Based on Airborne LiDAR Data. J. Beijing Inst. Civ. Eng. Archit. 2021, 37, 39–46. [Google Scholar]
- Waleed, M.; Um, T.; Khan, A.; Khan, U. Automatic detection system of olive trees using improved K-means algorithm. Remote Sens. 2020, 12, 760. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An individual tree segmentation method based on watershed algorithm and three-dimensional spatial distribution analysis from airborne LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Lan, G.; Wang, J.; Wu, Z.; Xie, G. Species composition and community characteristics of rubber forest in Danzhou, Hainan island. J. Southwest For. Univ. 2014, 34, 8–13. [Google Scholar]
- Wu, J.; Xiang, L.; You, H.; Tang, L.; Gai, J. Plant-Denoising-Net (PDN): A plant point cloud denoising network based on density gradient field learning. ISPRS J. Photogramm. Remote Sens. 2024, 210, 282–299. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Z.; Fei, J.; Chen, L.; Wei, W. ATSGPN: Adaptive threshold instance segmentation network in 3D point cloud. In MIPPR 2019: Pattern Recognition and Computer Vision; SPIE: Bellingham, WA, USA, 2020. [Google Scholar]
- Ye, L.; Li, J.; Wang, J. An Adaptive Threshold Method for Ground Segmentation. In International Conference on Autonomous Unmanned Systems; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Dai, M.; Li, G. Soft segmentation and reconstruction of tree crown from laser scanning data. Electronics 2023, 12, 2300. [Google Scholar] [CrossRef]
- Paris, C.; Kelbe, D.; Van Aardt, J.; Bruzzone, L. A novel automatic method for the fusion of ALS and TLS LiDAR data for robust assessment of tree crown structure. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3679–3693. [Google Scholar] [CrossRef]
- Aubry-Kientz, M.; Laybros, A.; Weinstein, B.; Ball, J.G.; Jackson, T.; Coomes, D.; Vincent, G. Multisensor data fusion for improved segmentation of individual tree crowns in dense tropical forests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3927–3936. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Nelson, R. Lidar remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å. Identifying species of individual trees using airborne laser scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Bortolot, Z.J.; Wynne, R.H. Estimating forest biomass using small footprint LiDAR data: An individual tree-based approach that incorporates training data. ISPRS J. Photogramm. Remote Sens. 2005, 59, 342–360. [Google Scholar] [CrossRef]
- Edson, C.; Wing, M.G. Airborne light detection and ranging (LiDAR) for individual tree stem location, height, and biomass measurements. Remote Sens. 2011, 3, 2494–2528. [Google Scholar] [CrossRef]
- Regaya, Y.; Fadli, F.; Amira, A. Point-Denoise: Unsupervised outlier detection for 3D point clouds enhancement. Multimed. Tools Appl. 2021, 80, 28161–28177. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Wang, Y.; Weinacker, H.; Koch, B. A lidar point cloud based procedure for vertical canopy structure analysis and 3D single tree modelling in forest. Sensors 2008, 8, 3938–3951. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, KDD’96, Portland, Oregon, 2–4 August 1996; AAAI Press: Washington, DC, USA, 1996; pp. 226–231. [Google Scholar]
- Fan, W.; Yang, B.; Dong, Z.; Liang, F.; Xiao, J.; Li, F. Confidence-guided roadside individual tree extraction for ecological benefit estimation. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102368. [Google Scholar] [CrossRef]
- Moreira, A.; Santos, M.Y. Concave hull: A k-nearest neighbours approach for the computation of the region occupied by a set of points. In Proceedings of the Second International Conference on Computer Graphics Theory and Applications VISIGRAPP, Barcelona, Spain, 8–11 March 2007. [Google Scholar]
- Yan, Z.; Liu, R.; Cheng, L.; Zhou, X.; Ruan, X.; Xiao, Y. A concave hull methodology for calculating the crown volume of individual trees based on vehicle-borne LiDAR data. Remote Sens. 2019, 11, 623. [Google Scholar] [CrossRef]
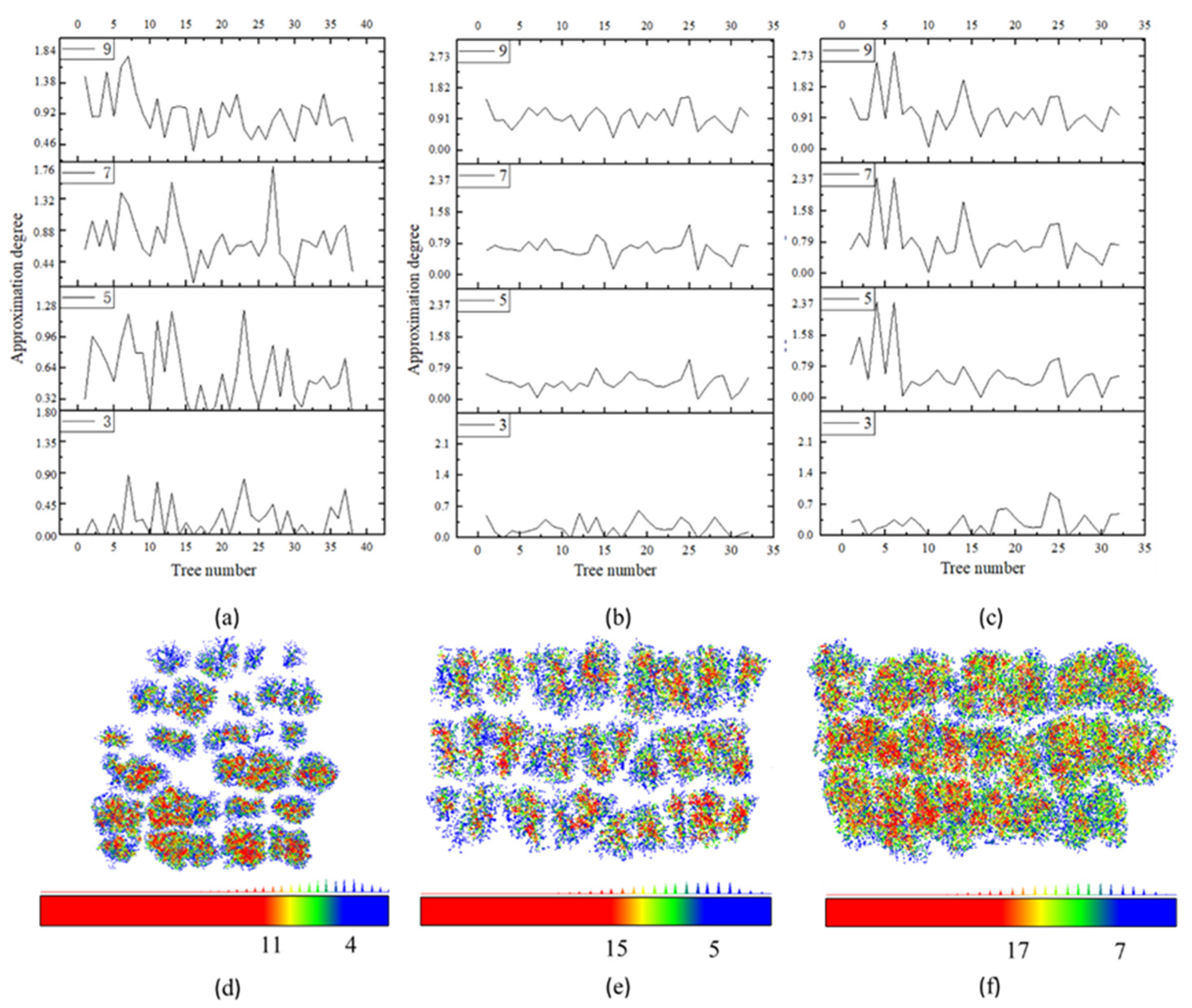


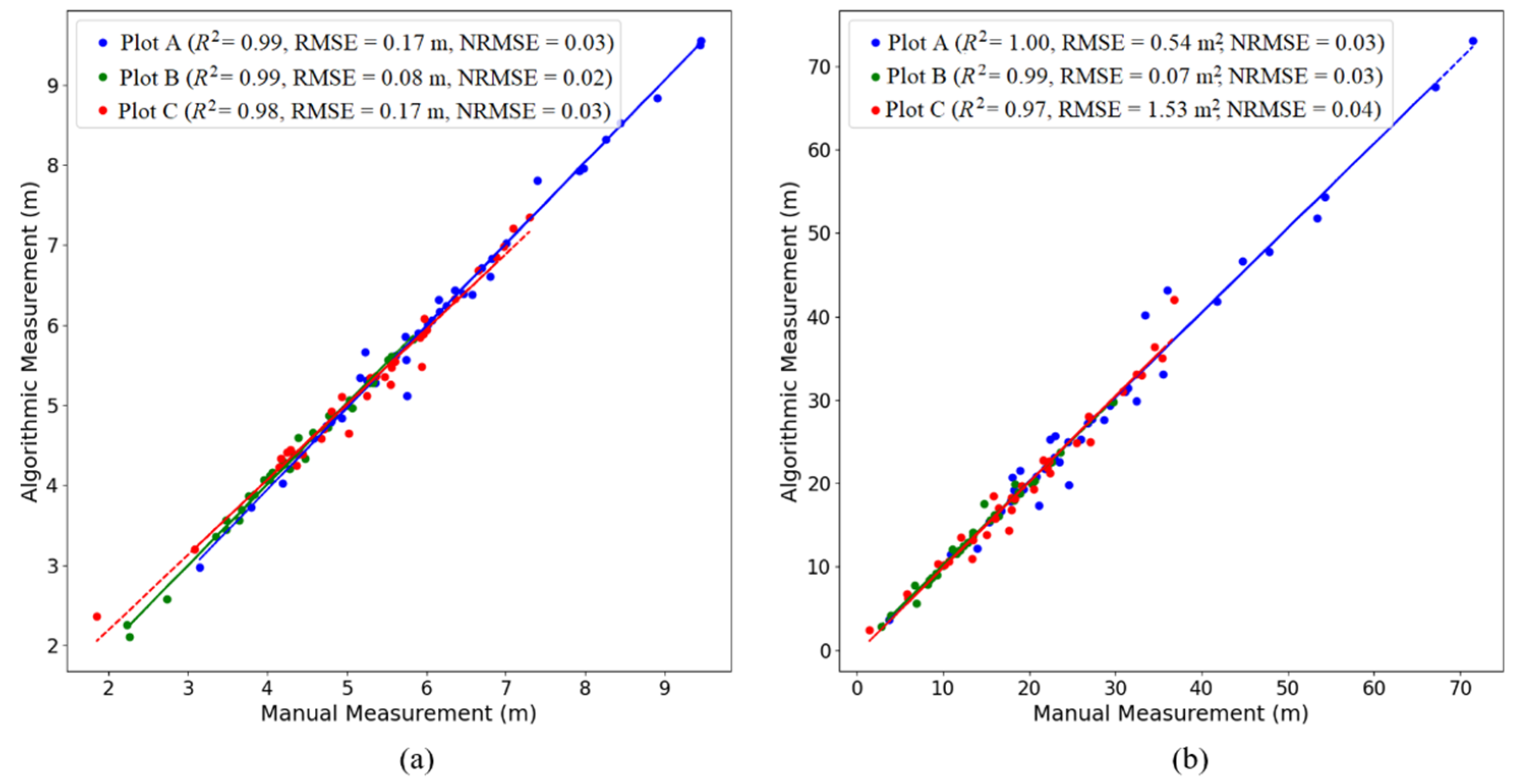

| Study Area | Method | Ground Truth of Total Tree Count | TP | FN | FP | R | P | F |
|---|---|---|---|---|---|---|---|---|
| Plot A | Proposed approach | 38 | 36 | 1 | 1 | 0.97 | 0.97 | 0.97 |
| DBSCAN | 38 | 31 | 5 | 2 | 0.86 | 0.94 | 0.90 | |
| PCS | 38 | 28 | 7 | 3 | 0.80 | 0.90 | 0.85 | |
| Layer stacking | 38 | 23 | 8 | 7 | 0.74 | 0.77 | 0.75 | |
| K-means | 38 | 18 | 10 | 10 | 0.64 | 0.64 | 0.64 | |
| ForAINet | 38 | 13 | 10 | 15 | 0.56 | 0.46 | 0.55 | |
| Watershed | 38 | 11 | 17 | 10 | 0.39 | 0.52 | 0.45 | |
| Plot B | Proposed approach | 32 | 31 | 1 | 0 | 0.97 | 1.00 | 0.98 |
| DBSCAN | 32 | 22 | 5 | 5 | 0.81 | 0.81 | 0.81 | |
| PCS | 32 | 19 | 7 | 6 | 0.73 | 0.76 | 0.75 | |
| ForAINet | 32 | 18 | 2 | 12 | 0.90 | 0.60 | 0.72 | |
| Layer stacking | 32 | 10 | 12 | 10 | 0.45 | 0.50 | 0.48 | |
| K-means | 32 | 8 | 13 | 11 | 0.38 | 0.42 | 0.40 | |
| Watershed | 32 | 2 | 18 | 12 | 0.10 | 0.14 | 0.12 | |
| Plot C | Proposed approach | 32 | 29 | 2 | 1 | 0.94 | 0.97 | 0.95 |
| DBSCAN | 32 | 15 | 10 | 7 | 0.60 | 0.68 | 0.64 | |
| ForAINet | 32 | 7 | 10 | 15 | 0.41 | 0.32 | 0.36 | |
| PCS | 32 | 6 | 14 | 12 | 0.30 | 0.33 | 0.32 | |
| Layer stacking | 32 | 5 | 16 | 11 | 0.24 | 0.31 | 0.27 | |
| K-means | 32 | 3 | 18 | 11 | 0.14 | 0.21 | 0.17 | |
| Watershed | 32 | 1 | 22 | 9 | 0.04 | 0.10 | 0.06 |
| Study Area | Area (m2) | Canopy Closure Level | Canopy Closure (%) | Total Tree Number | LiDAR Point Density (pt/m2) | Total LiDAR Points (×10,000) |
|---|---|---|---|---|---|---|
| Plot A | 1189.9 | Low | 41.5 | 38 | 2114 | 70.8 |
| Plot B | 376.323 | Medium | 68.9 | 32 | 1384 | 46.6 |
| Plot C | 404.212 | High | 89.3 | 32 | 3110 | 97.3 |
| Criteria of the Percentage of Points | Segmentation Category |
|---|---|
| ρalgorithm/reference > 105% | Correctly segmented |
| 105% ≥ ρalgorithm/reference ≥ 95% | Over-segmented |
| ρalgorithm/reference < 95% | Under-segmented |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Miao, J.; Huang, X.; Chen, P.; Zhou, P.; Tan, J.; Wang, X. A Bottom-Up Multi-Feature Fusion Algorithm for Individual Tree Segmentation in Dense Rubber Tree Plantations Using Unmanned Aerial Vehicle–Light Detecting and Ranging. Plants 2025, 14, 1640. https://doi.org/10.3390/plants14111640
Zeng Z, Miao J, Huang X, Chen P, Zhou P, Tan J, Wang X. A Bottom-Up Multi-Feature Fusion Algorithm for Individual Tree Segmentation in Dense Rubber Tree Plantations Using Unmanned Aerial Vehicle–Light Detecting and Ranging. Plants. 2025; 14(11):1640. https://doi.org/10.3390/plants14111640
Chicago/Turabian StyleZeng, Zhipeng, Junpeng Miao, Xiao Huang, Peng Chen, Ping Zhou, Junxiang Tan, and Xiangjun Wang. 2025. "A Bottom-Up Multi-Feature Fusion Algorithm for Individual Tree Segmentation in Dense Rubber Tree Plantations Using Unmanned Aerial Vehicle–Light Detecting and Ranging" Plants 14, no. 11: 1640. https://doi.org/10.3390/plants14111640
APA StyleZeng, Z., Miao, J., Huang, X., Chen, P., Zhou, P., Tan, J., & Wang, X. (2025). A Bottom-Up Multi-Feature Fusion Algorithm for Individual Tree Segmentation in Dense Rubber Tree Plantations Using Unmanned Aerial Vehicle–Light Detecting and Ranging. Plants, 14(11), 1640. https://doi.org/10.3390/plants14111640






