Towards a Stochastic Model to Simulate Grapevine Architecture: A Case Study on Digitized Riesling Vines Considering Effects of Elevated CO2
Abstract
:1. Introduction
1.1. Modeling Phenology
1.2. Plant Growth Modeling
1.3. Bayesian Model Calibration
2. Materials and Methods
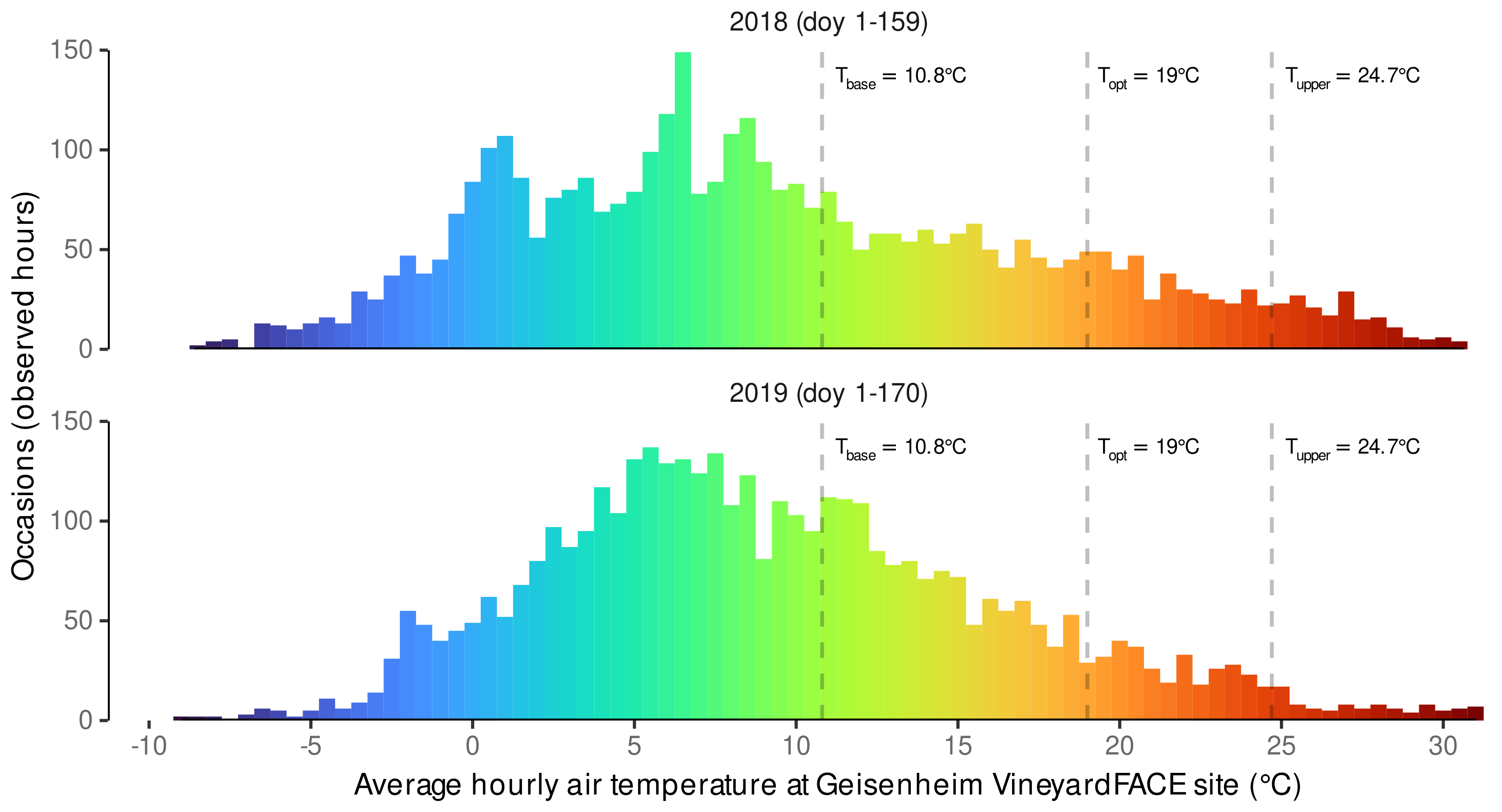
2.1. Experimental Site
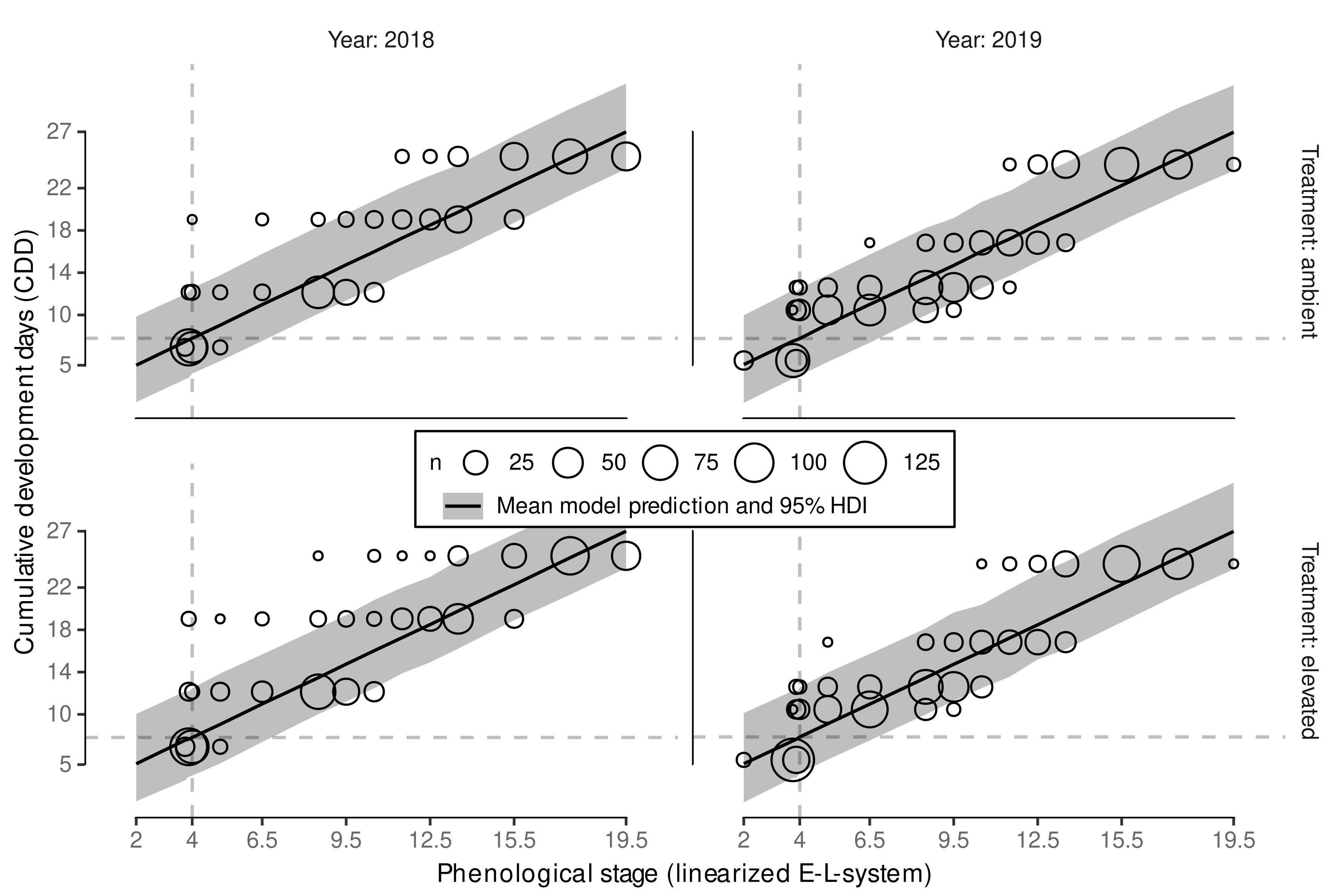
2.2. Cumulative Development Days Model
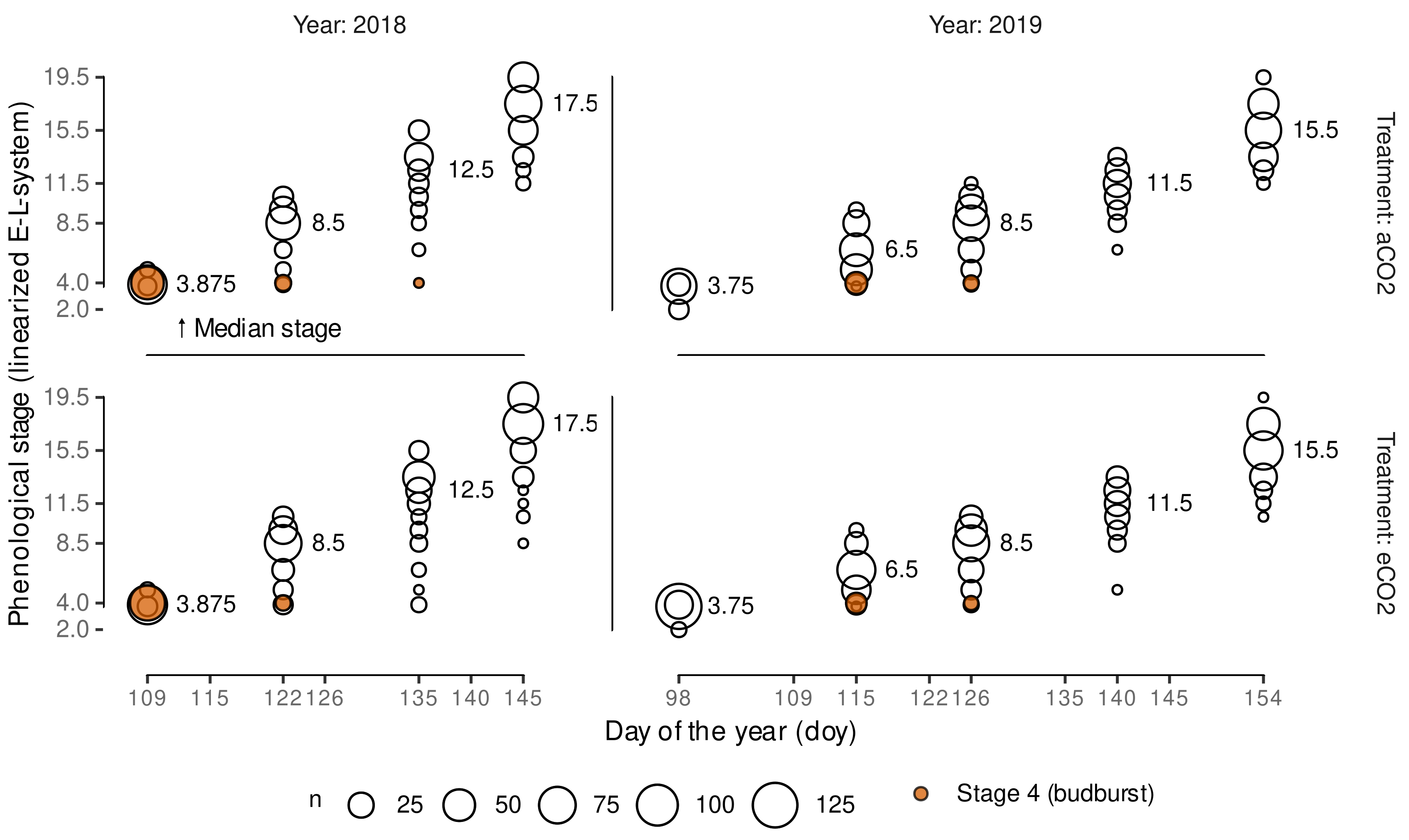
2.3. Grapevine Phenology Assessment
2.4. Grapevine Phenology Linearization
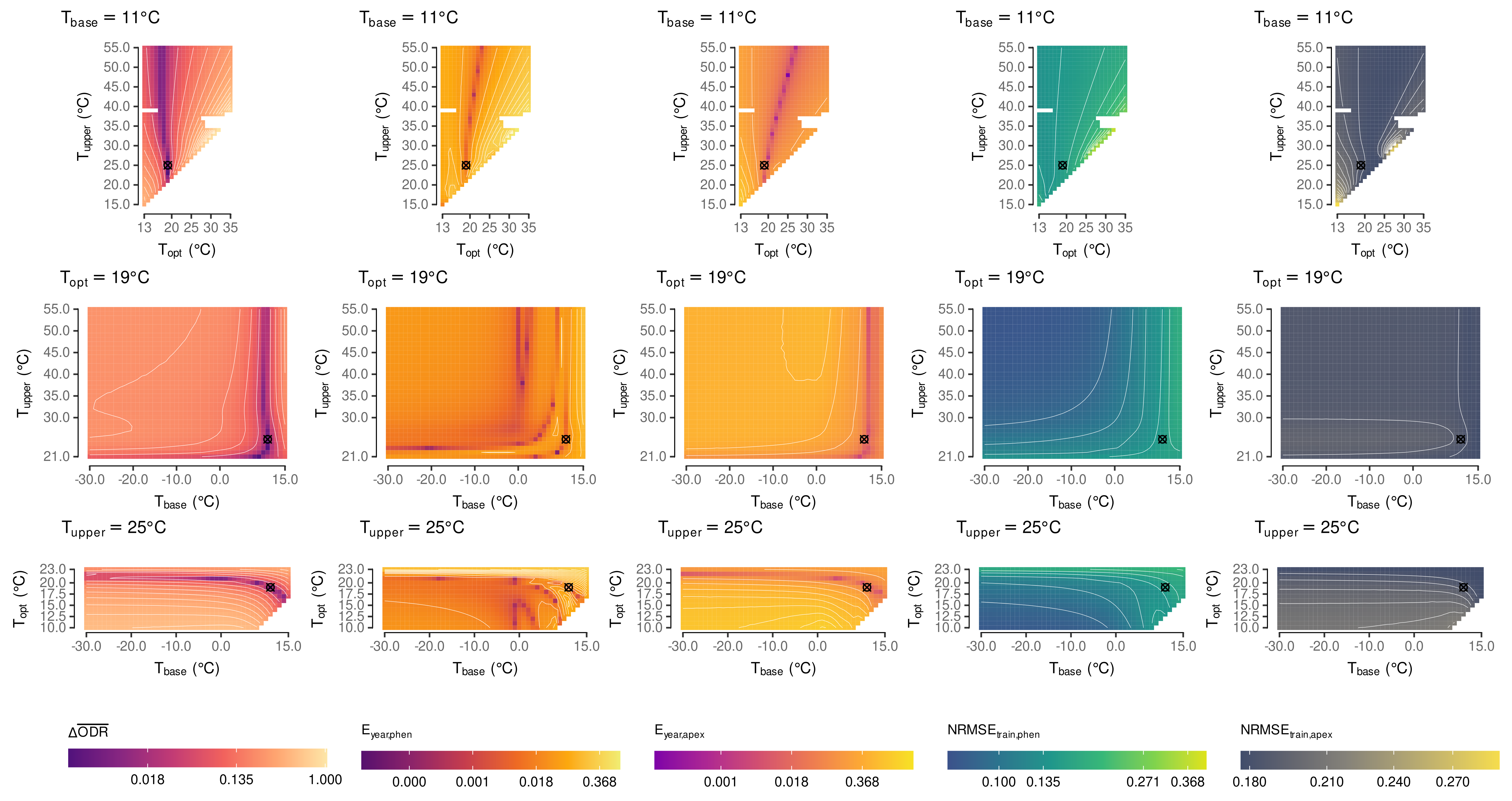
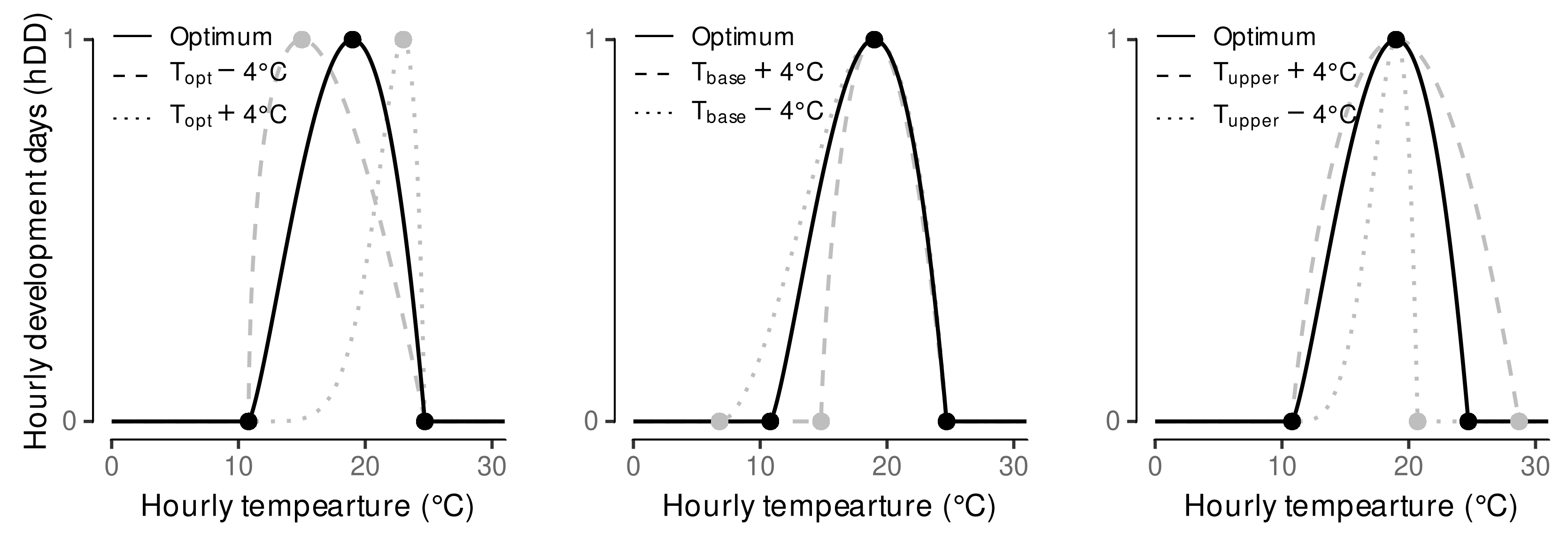
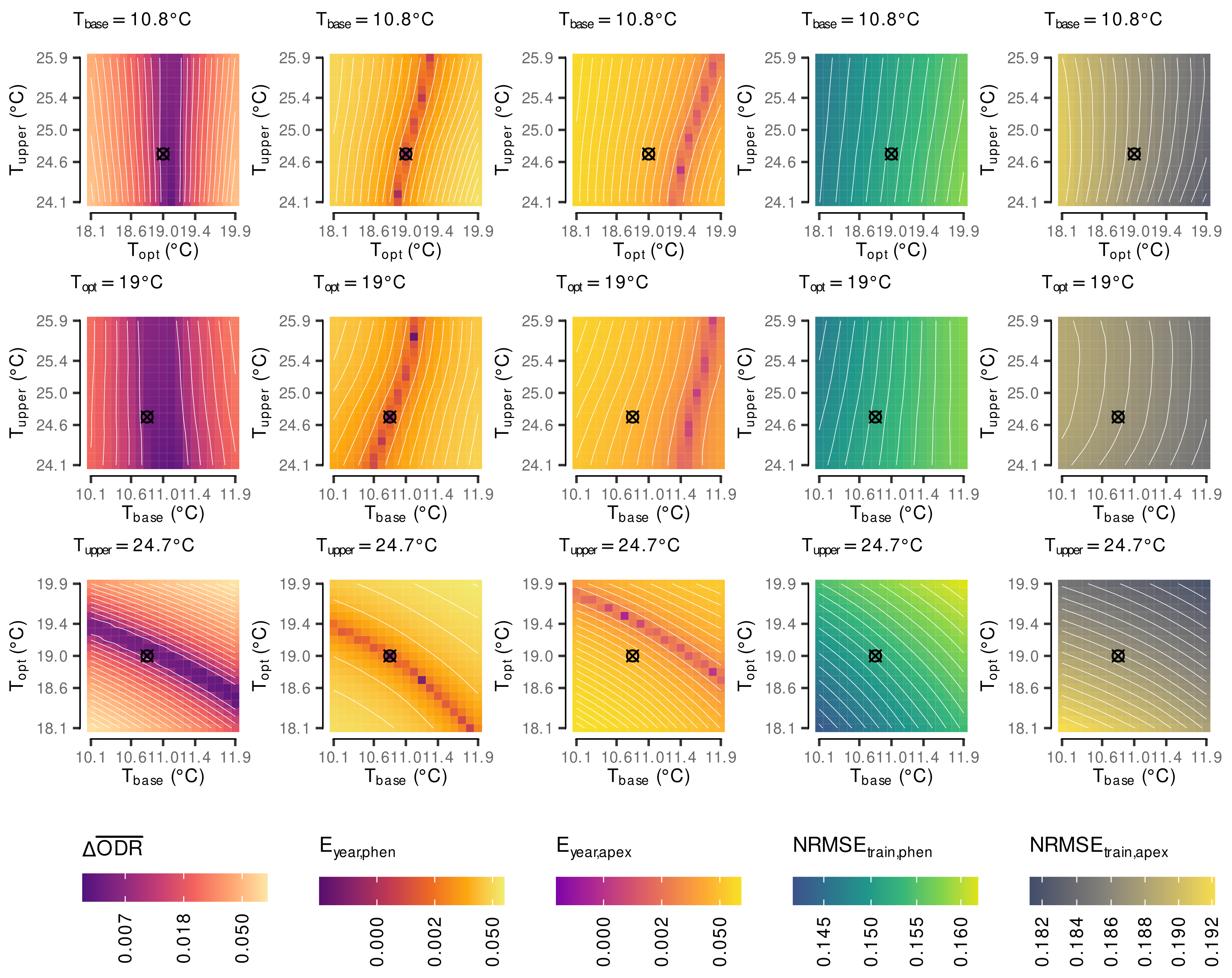
2.5. Estimation of Cardinal Temperatures by Multi-Objective Optimization
- -
- treatment-averaged normalized absolute difference between the organ development rates ()
- -
- absolute effect of year in both models (,)
2.6. Modeling Budburst Variability
2.7. Modeling Internode Development
2.8. Internode Length Model
2.9. Model Implementation and Diagnostics
2.10. Model Validation
2.10.1. Phenology Prediction
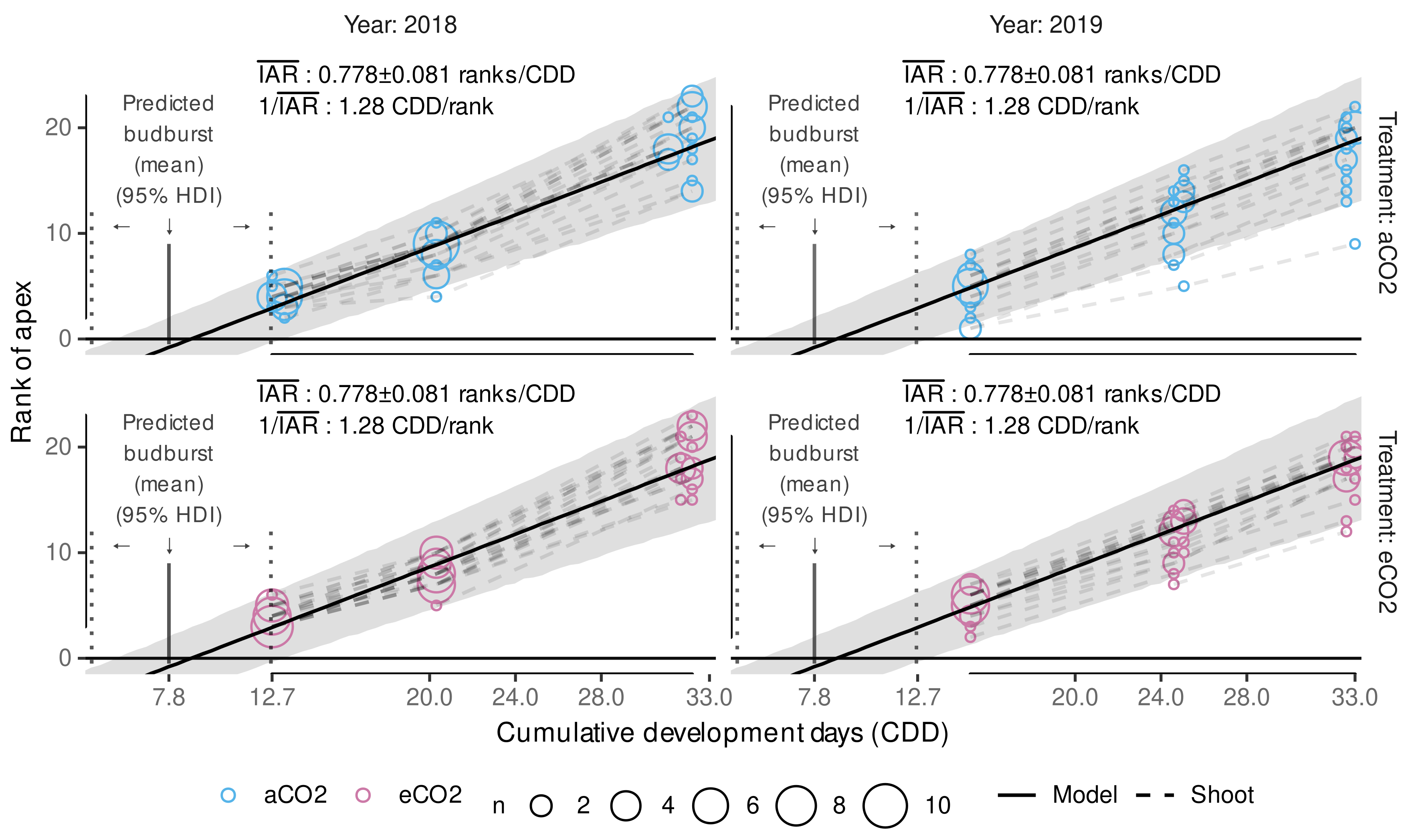
2.10.2. Predicting the Apex Rank
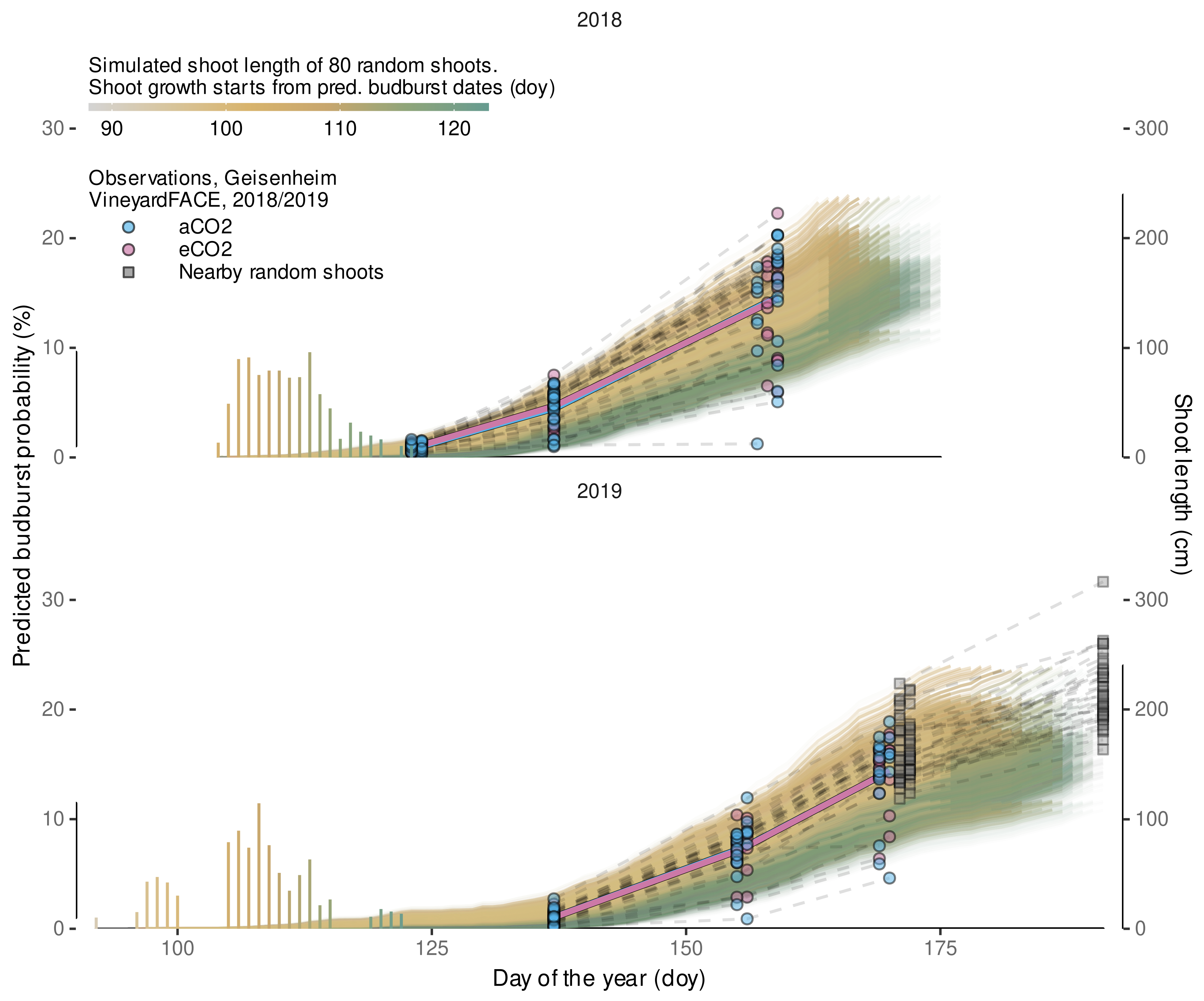
2.10.3. Shoot Length Predictions
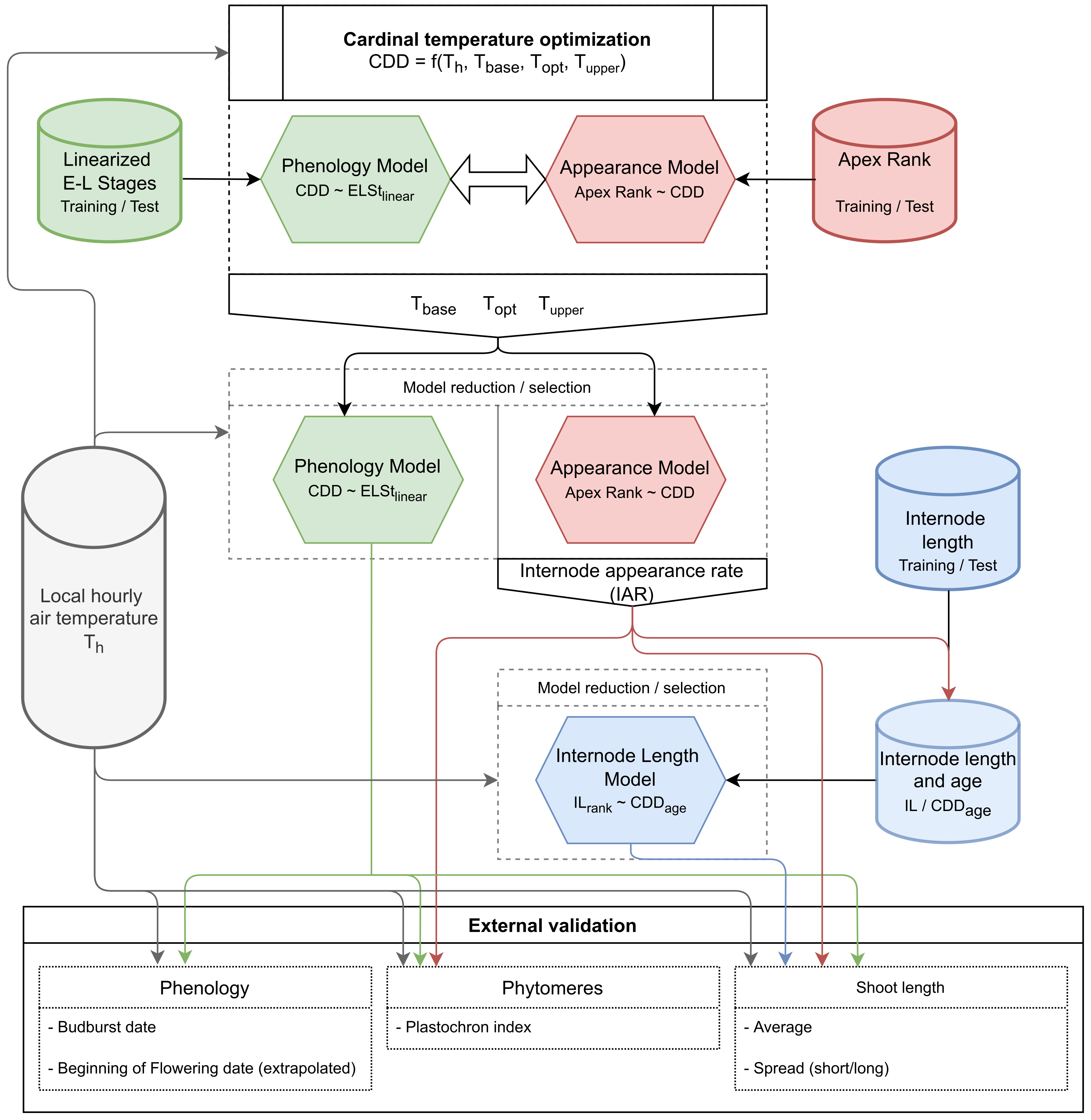
2.11. Flowchart of the Model Development and Validation Progress
3. Results and Discussion
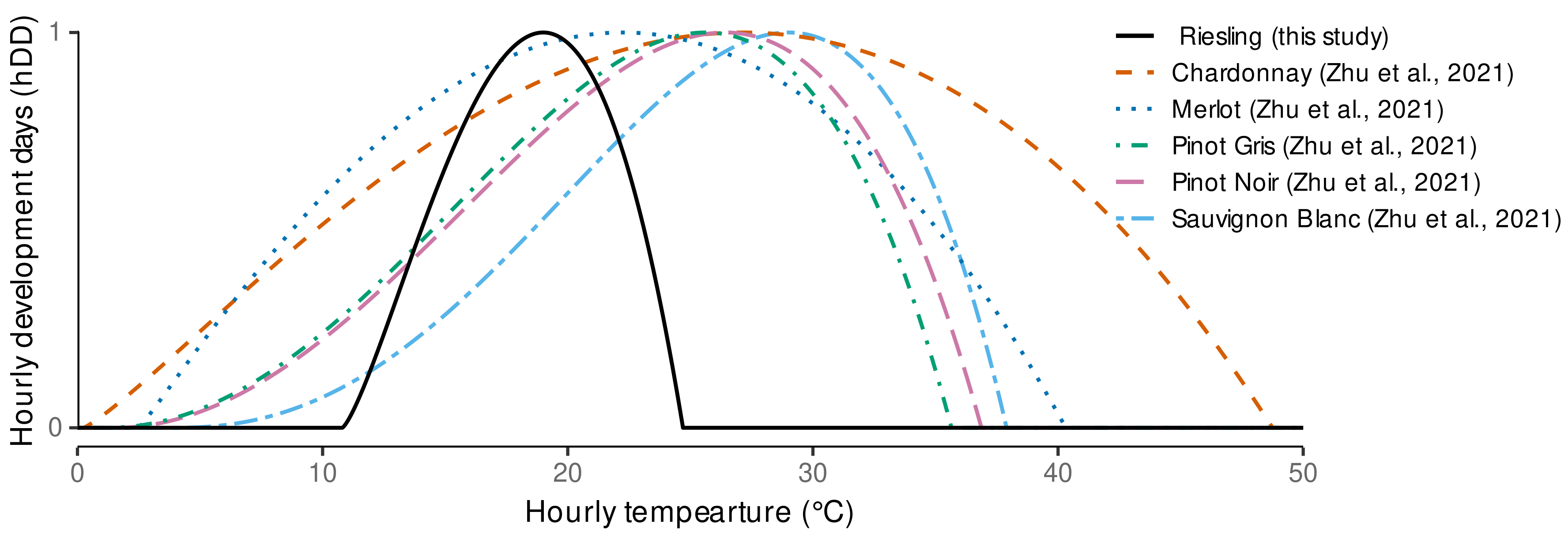
3.1. Estimated Cardinal Temperatures for Riesling Development
3.2. Phenology Prediction
3.2.1. Model Reduction
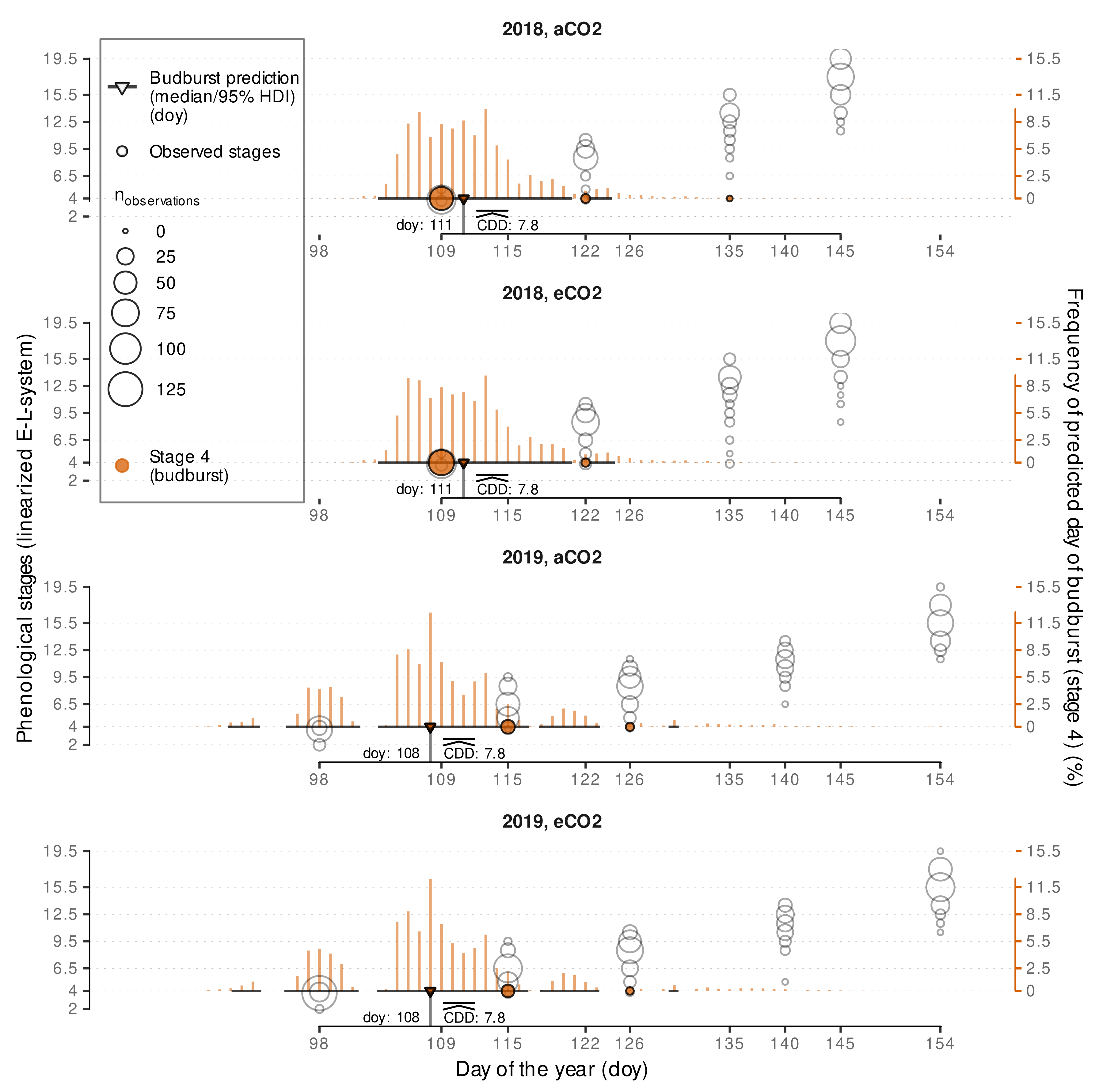
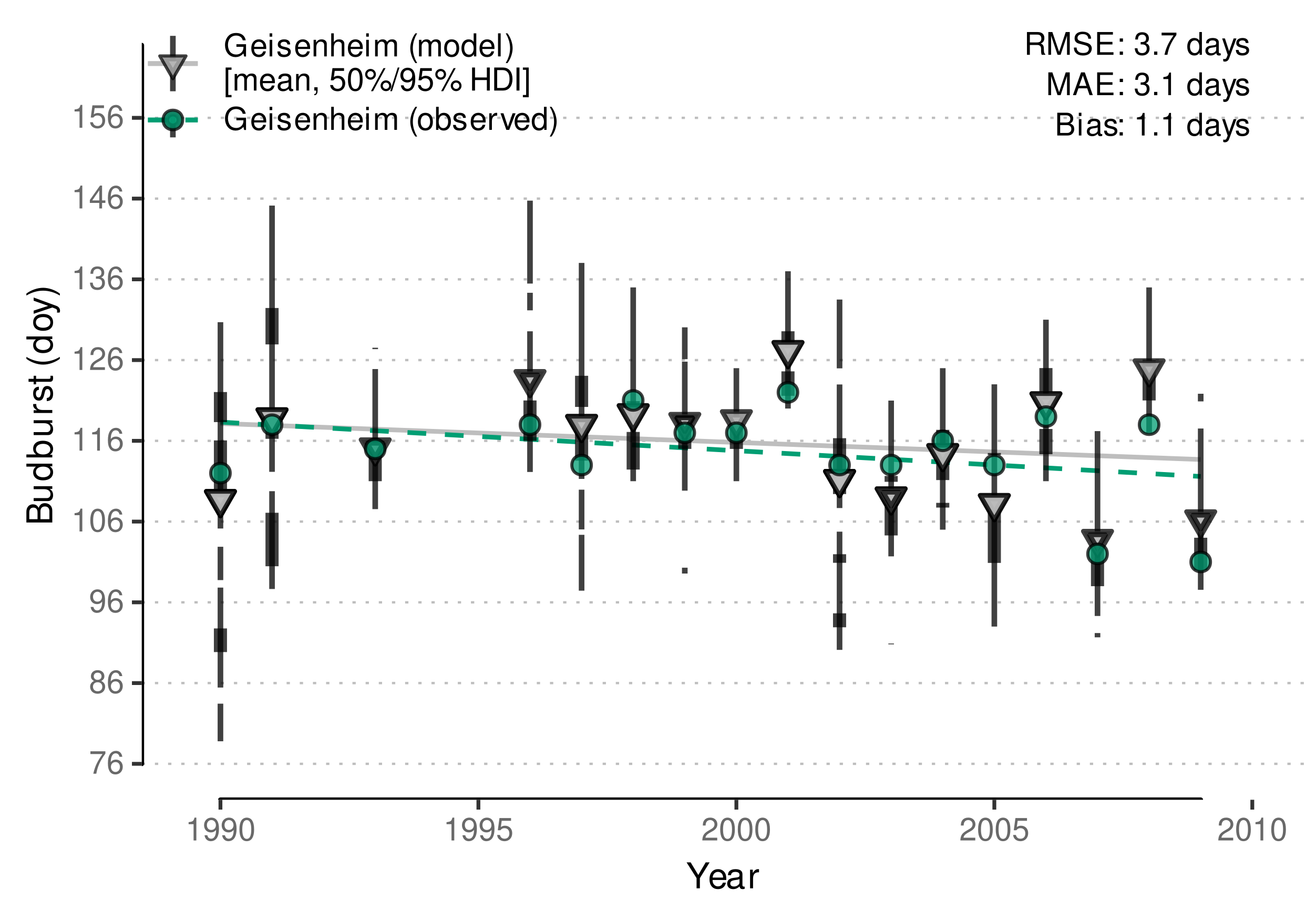
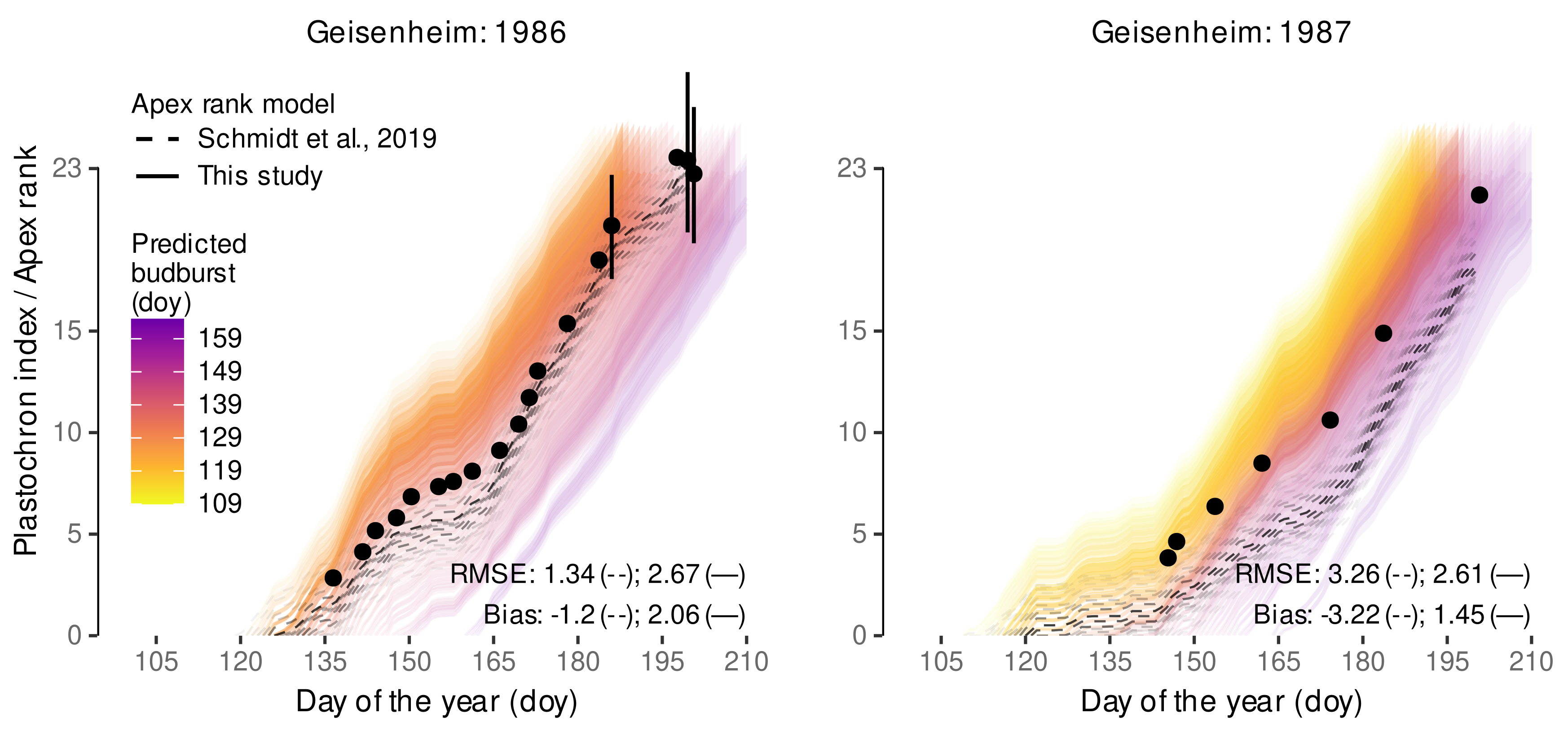
3.2.2. External Validation of Budburst Data Predictions
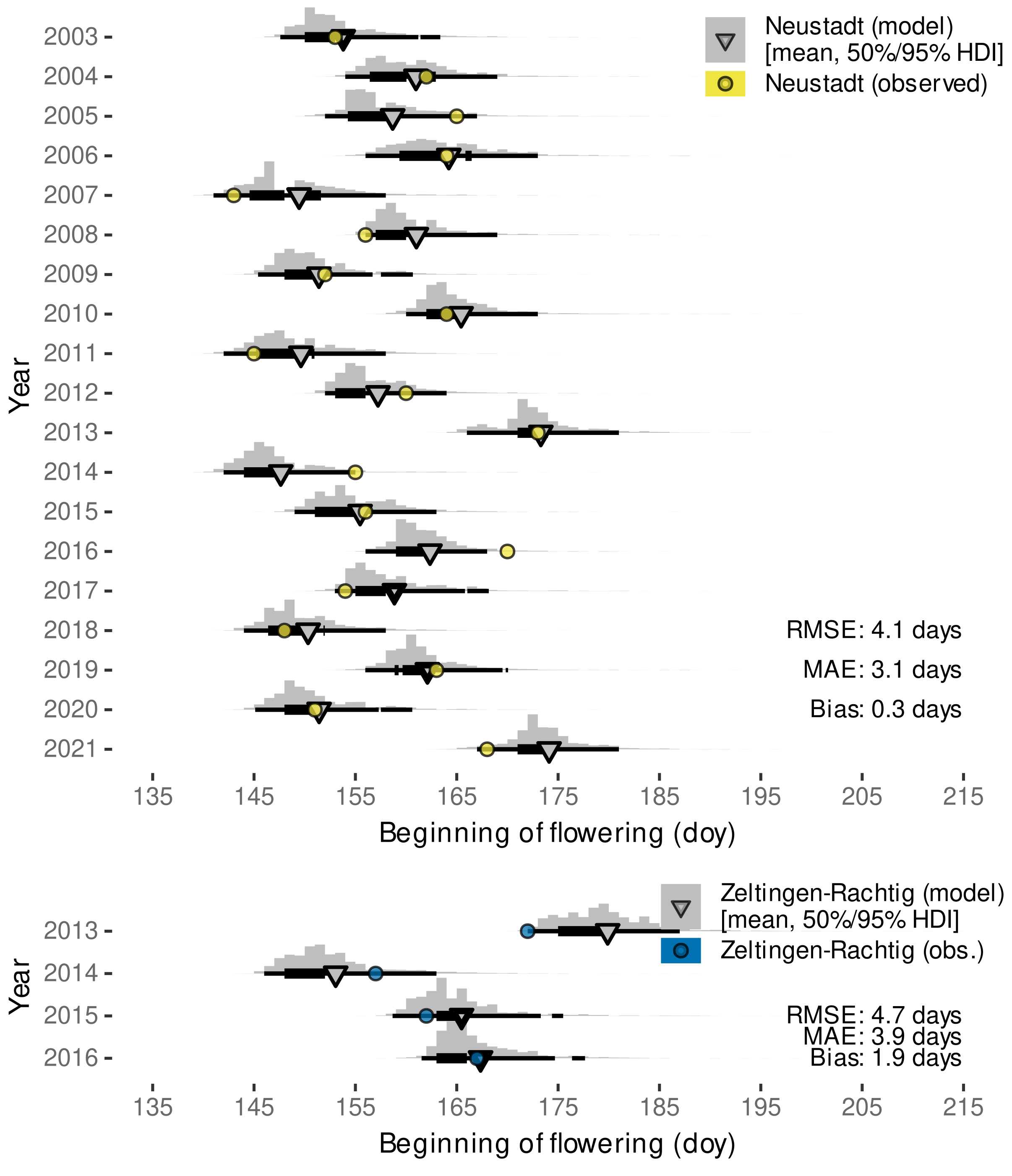
3.2.3. External Validation by Projections of Beginning of Flowering Date
3.3. Primary Shoot Internode Appearance
3.3.1. Model Reduction
3.3.2. External Validation of Appearance Rate
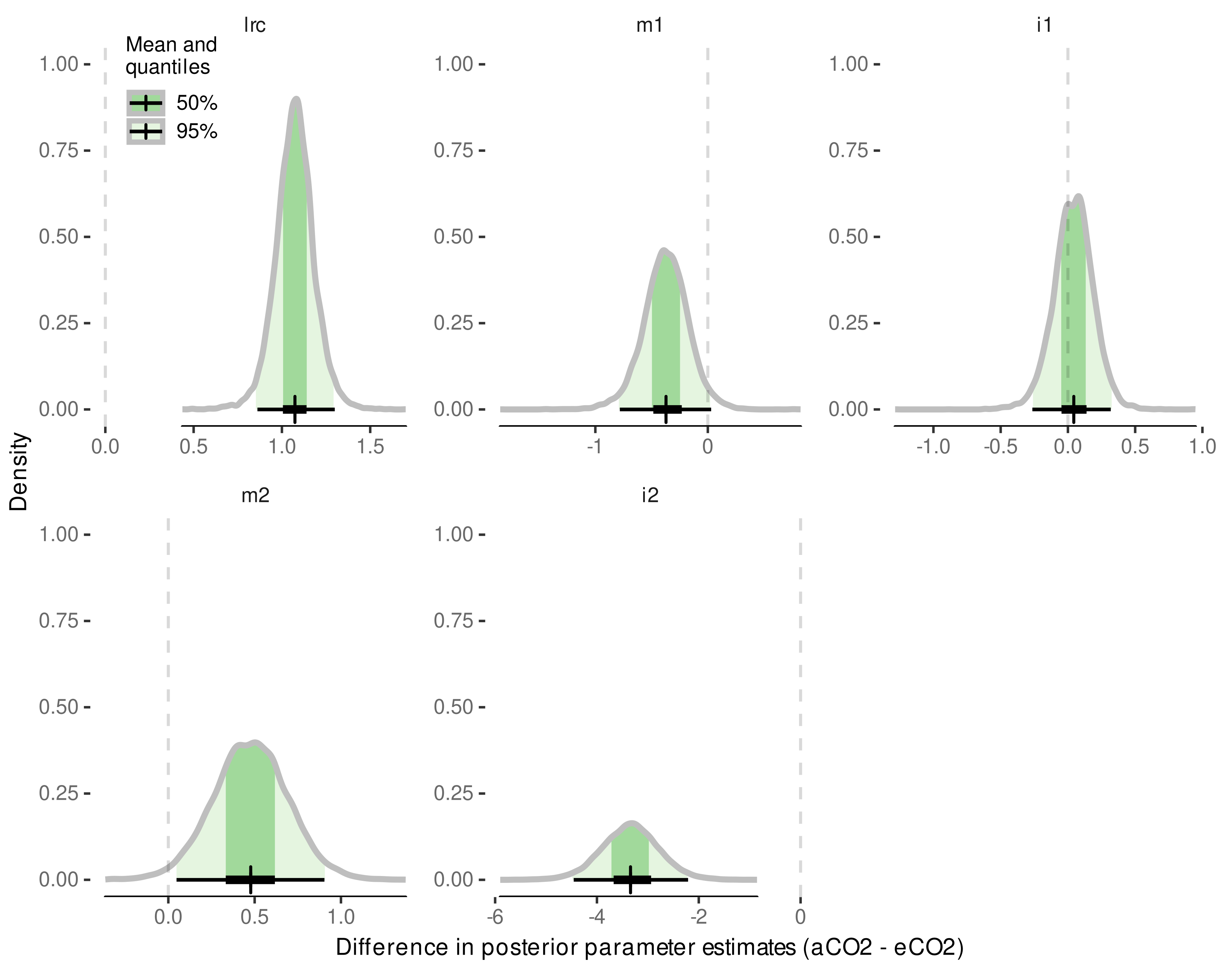
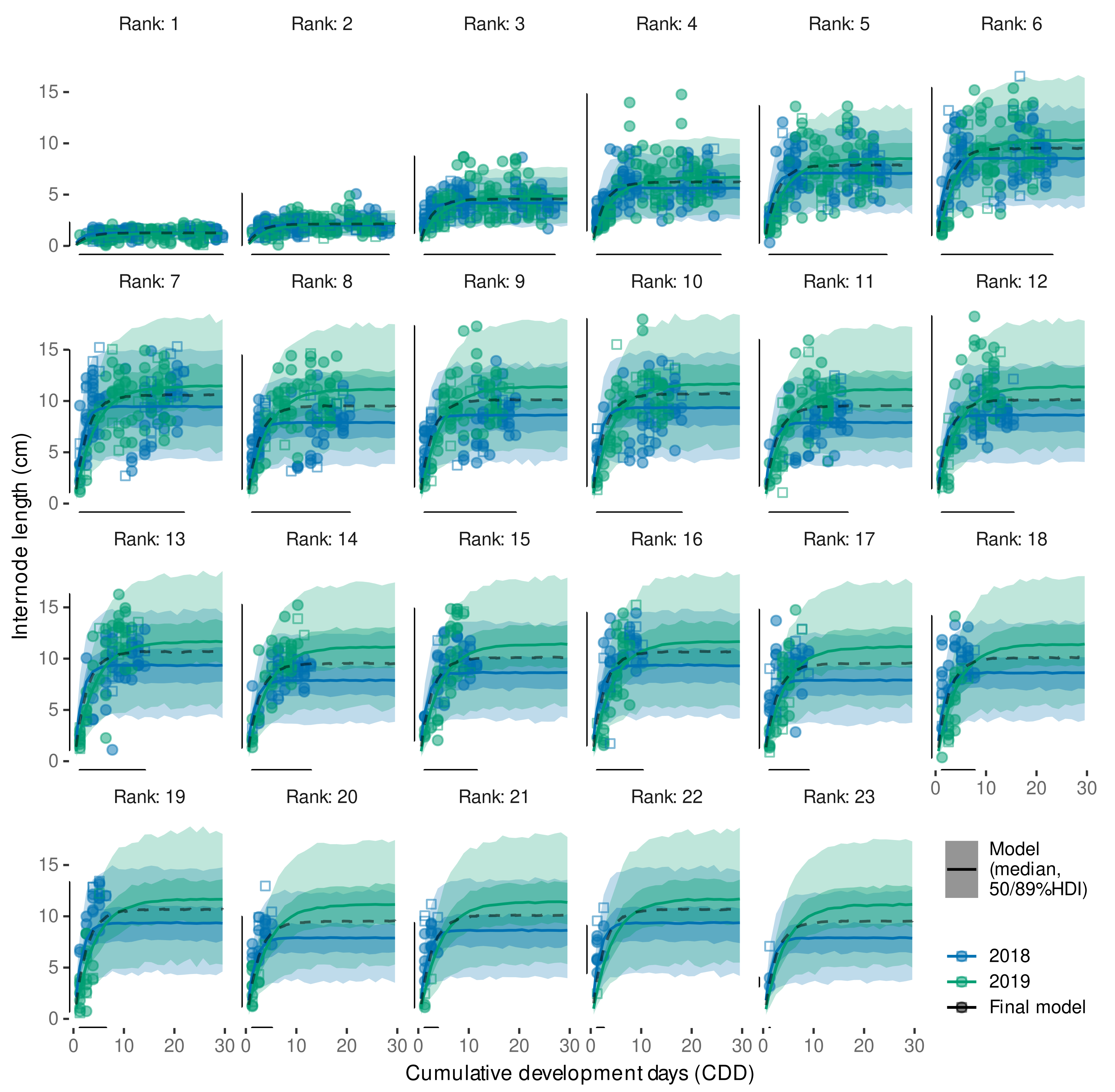
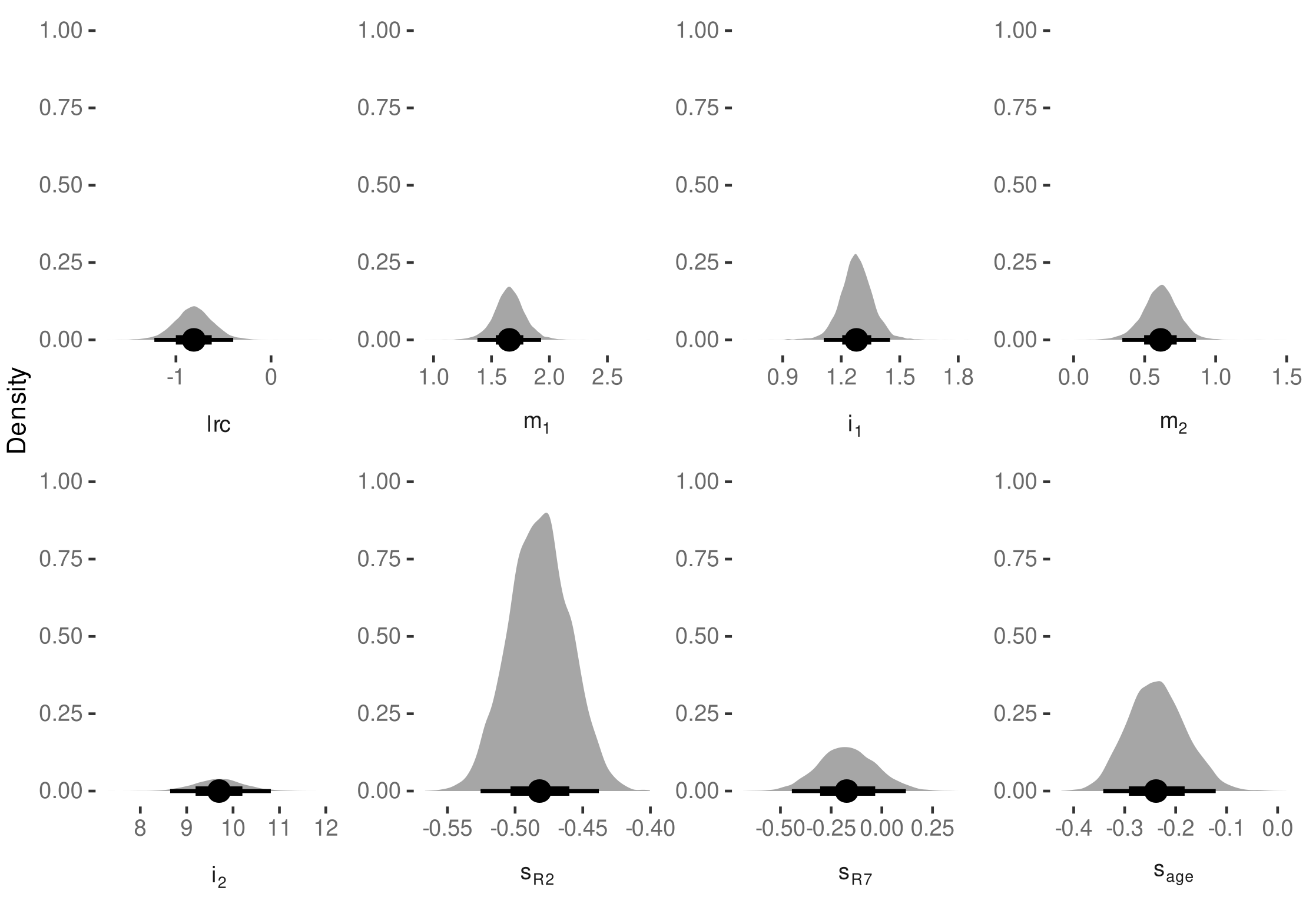
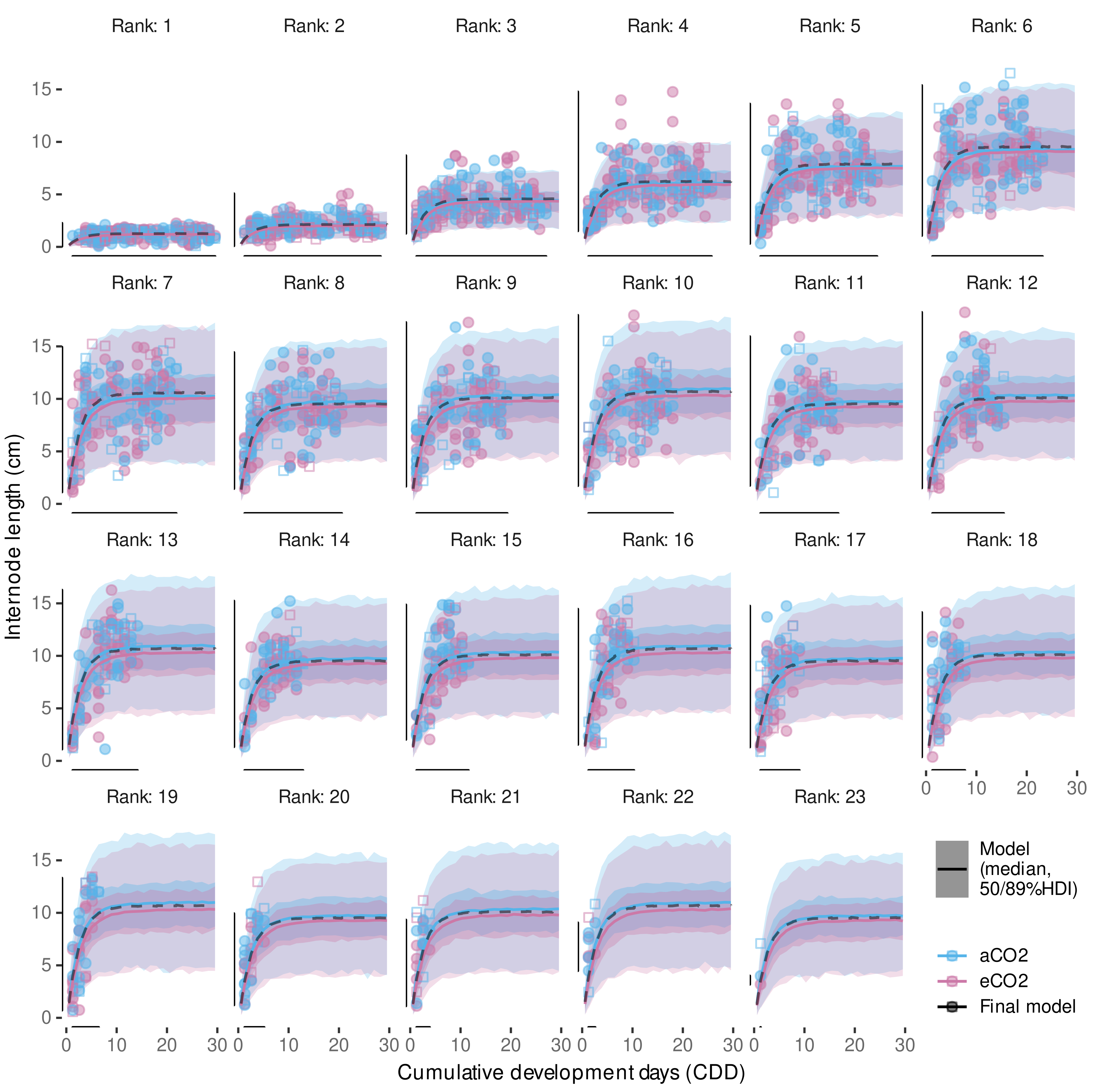
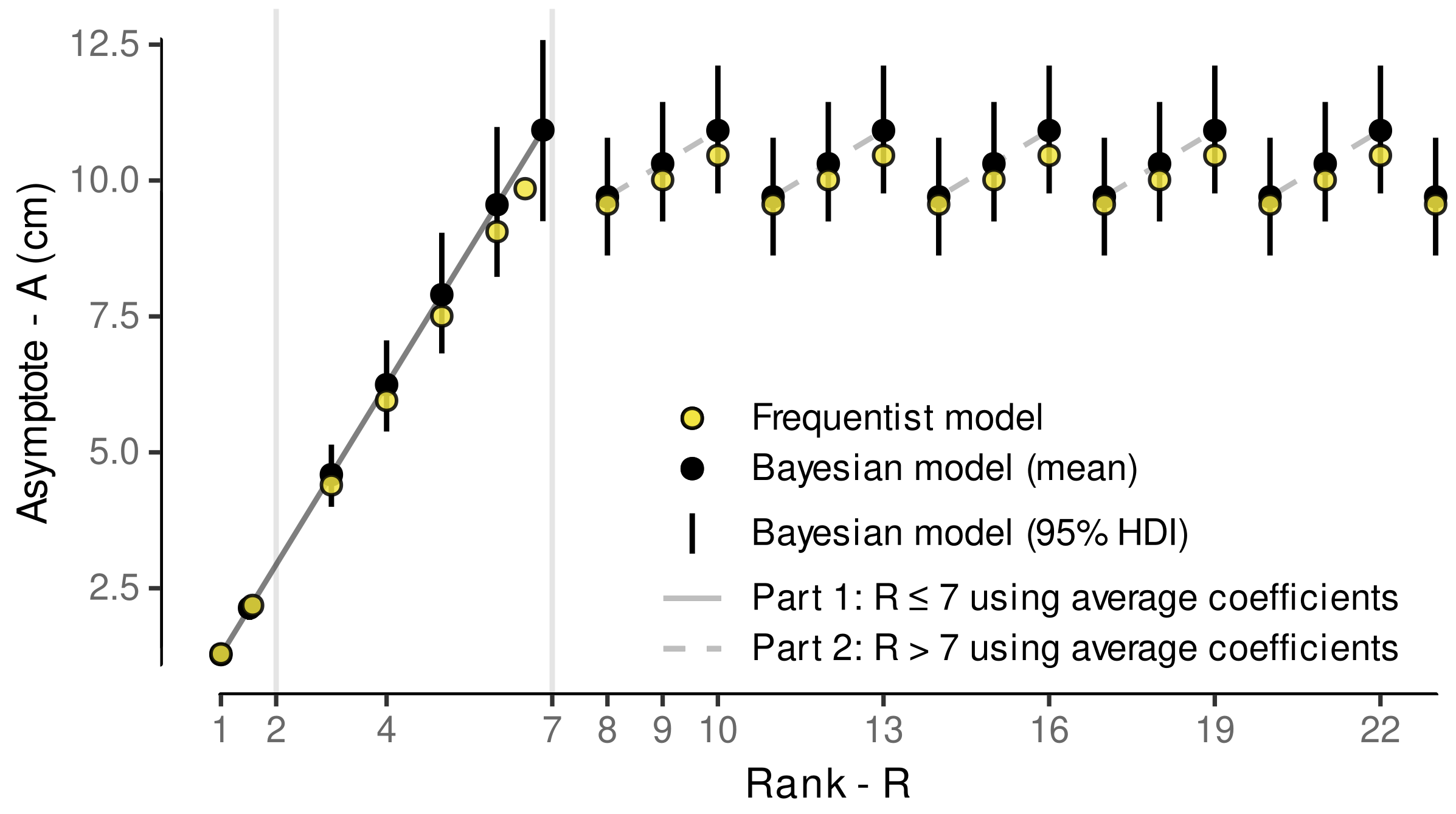
3.4. Internode Length Model
3.4.1. Model Selection
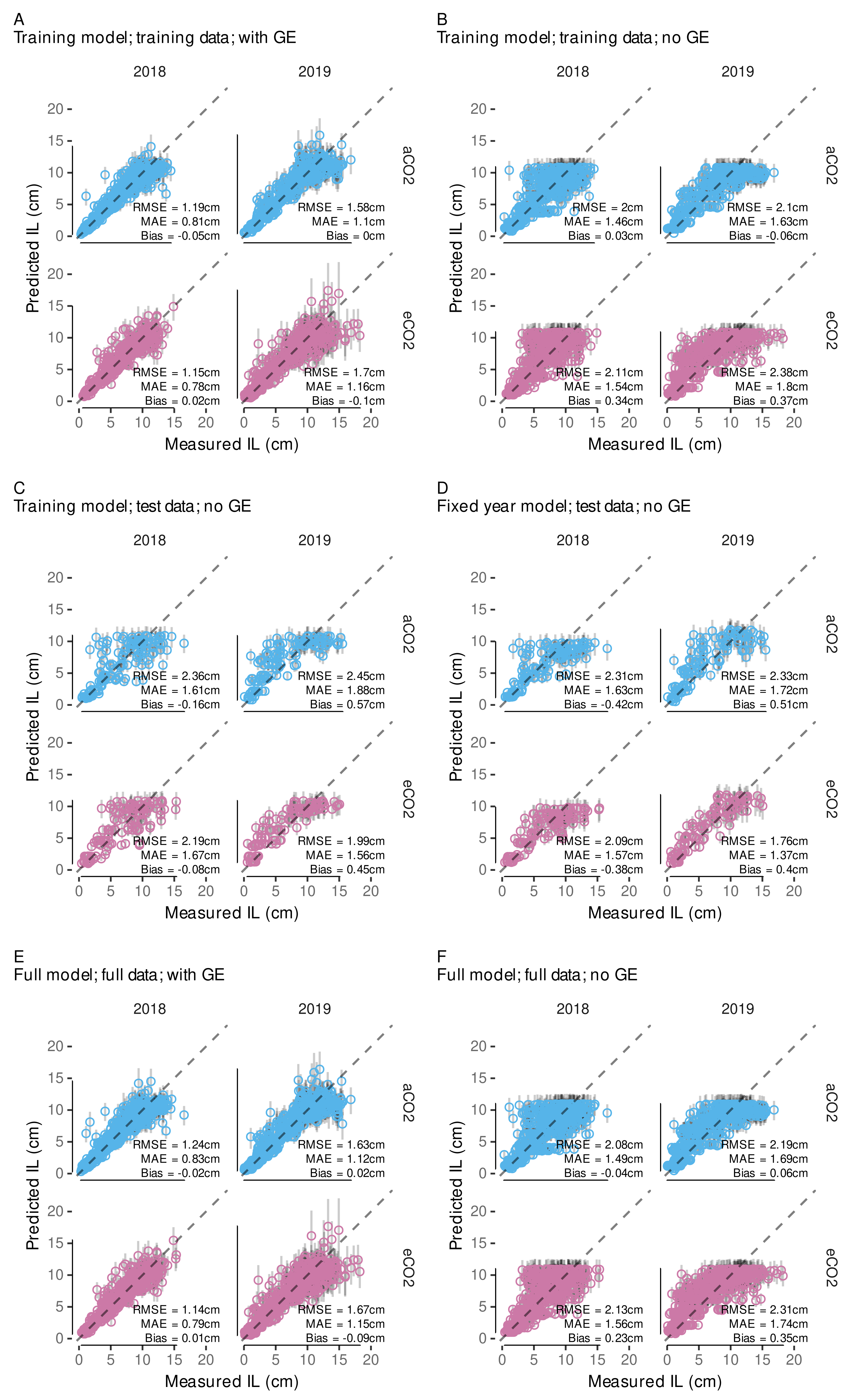
3.4.2. Model Predictive Performance
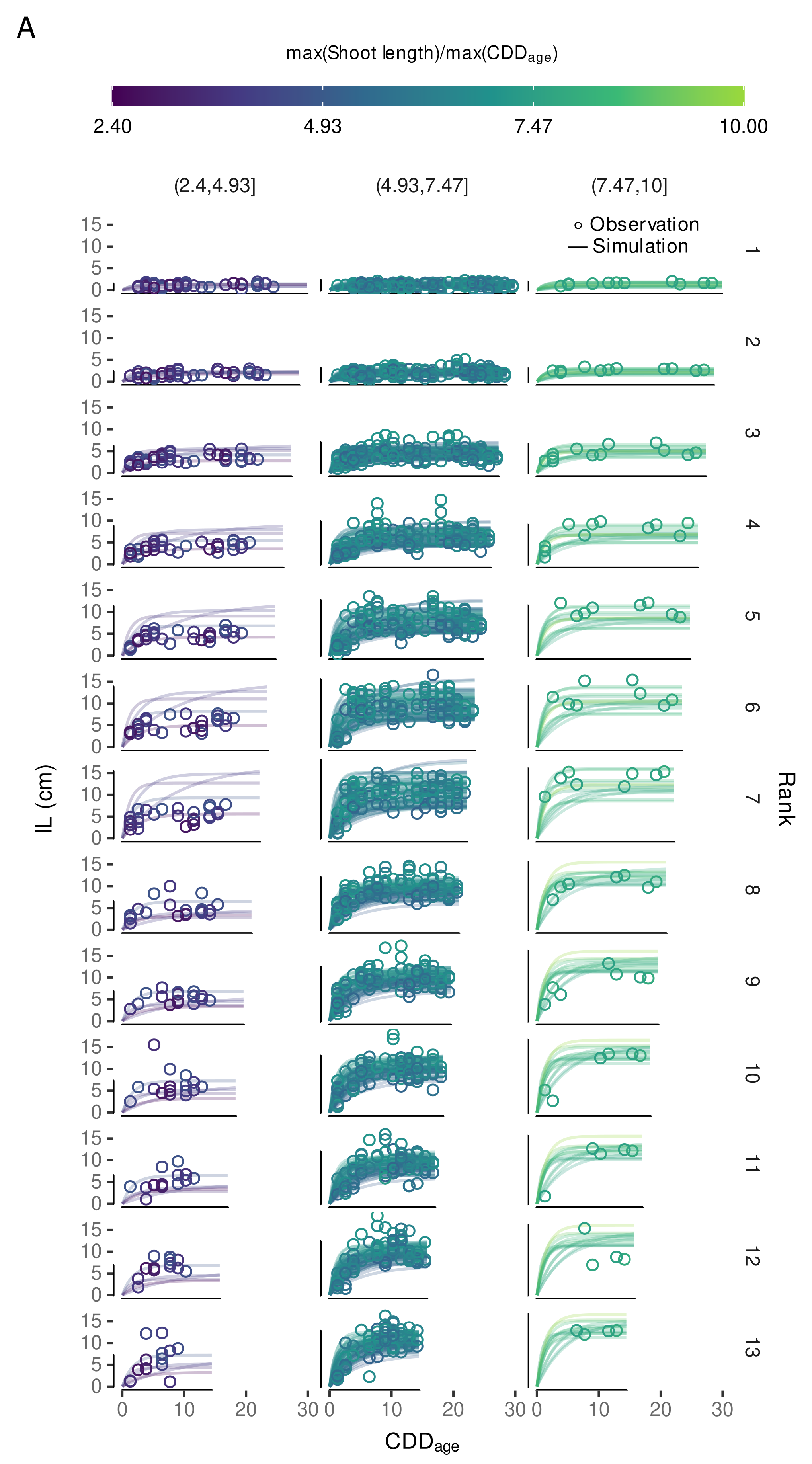
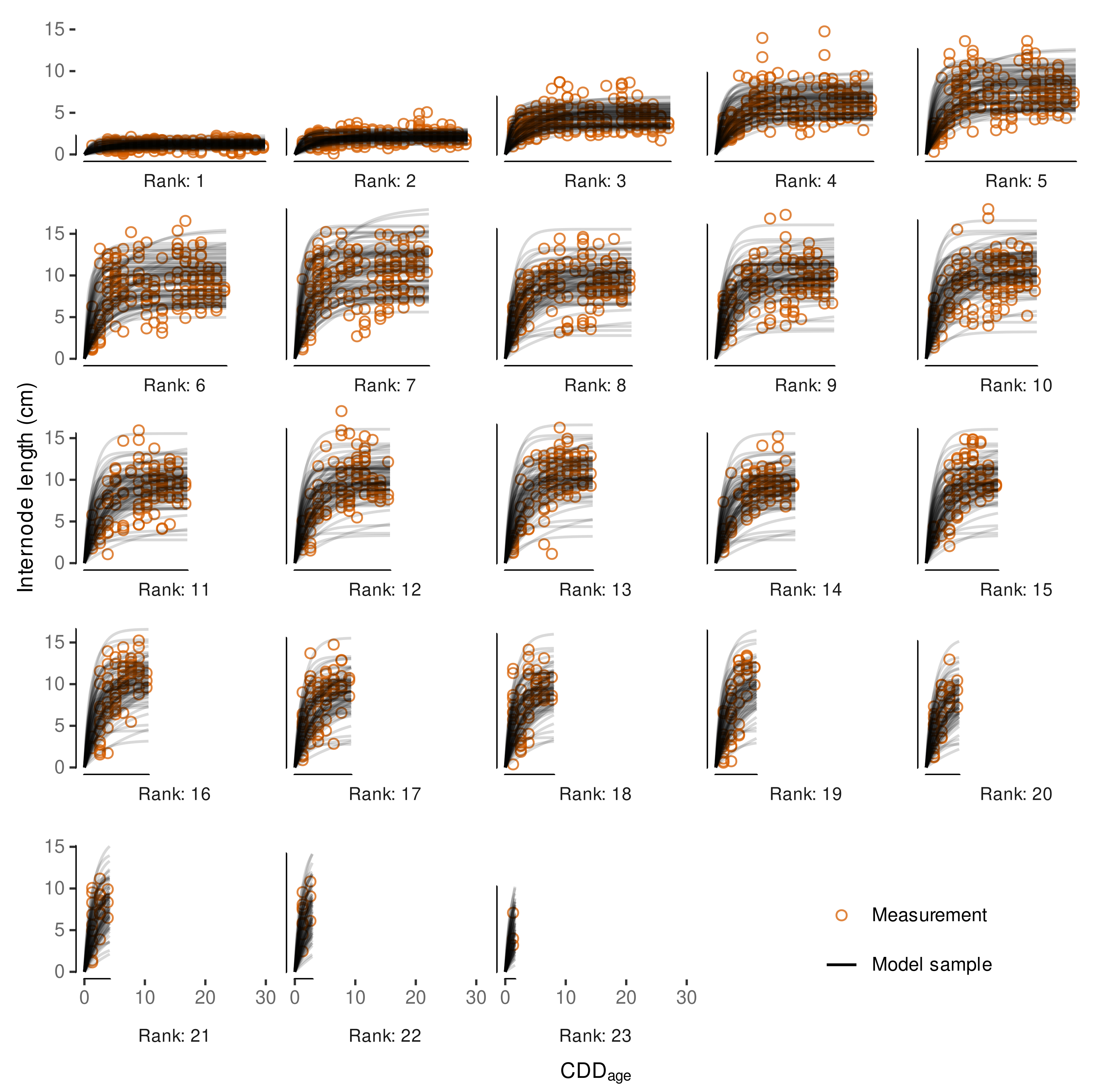
3.4.3. Variability in Internode Length Simulations
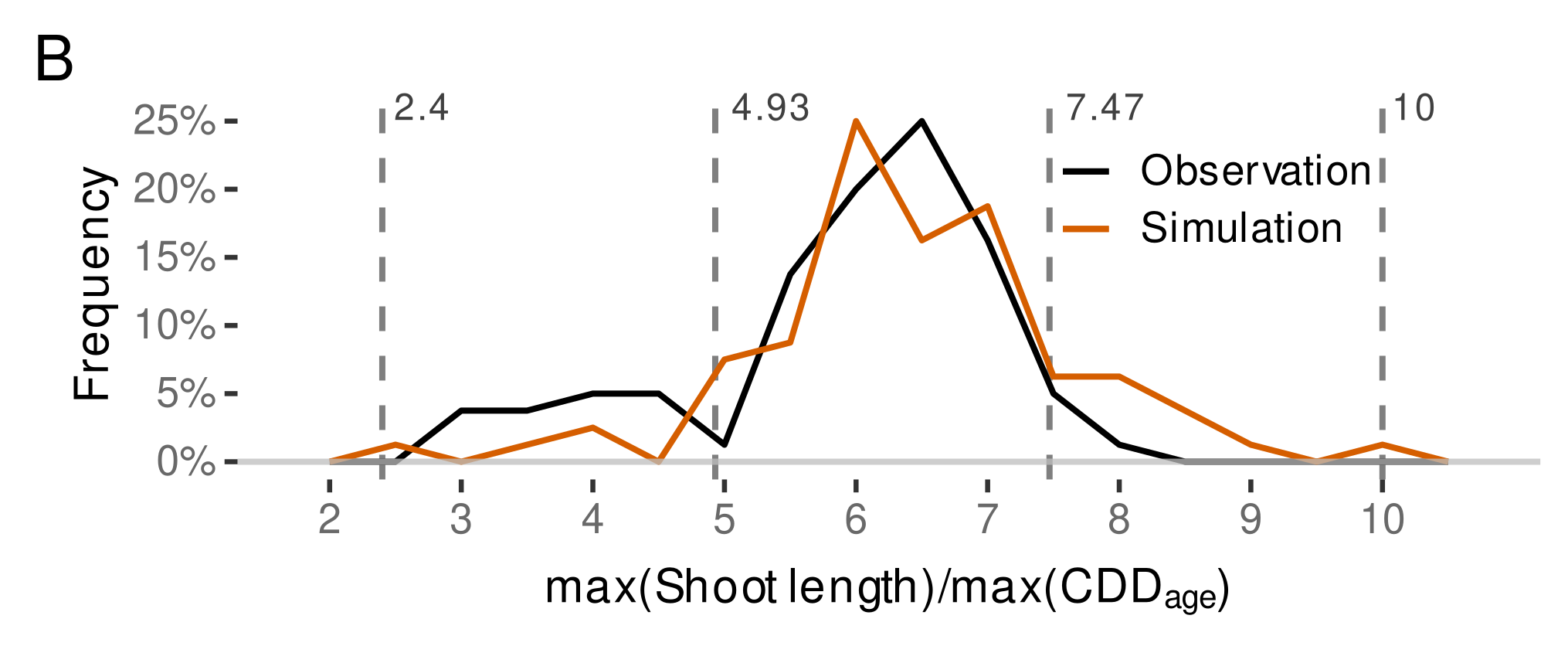
3.4.4. External Validation Based on Shoot Length Ranges
3.4.5. Local, Independent Validation Using Shoot Length Data from 2020 Season
3.5. Future Work and Perspective Use Cases
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| aCO | ambient carbon dioxide |
| CO | carbon dioxide |
| CDD | cumulative development days |
| doy | day of the year |
| eCO | elevated carbon dioxide |
| ELPD | expected log predictive densit |
| FACE | free air carbon dioxide enrichment |
| FE | fixed effect |
| FSP model | functional-structural plant model |
| GE | group-level effect |
| HDI | highest density interval |
| LOOIC | leave-one-out cross-validation information criterion |
| MAE | mean absolute error |
| q | quantile |
| RMSE | root mean squared error |
Appendix A
Appendix A.1. More on Phenology Modeling
Appendix A.2. More on Bayesian Model Calibration
| Day of the Year (Doy) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Year | Ring | 98 | 109 | 115 | 122 | 126 | 135 | 140 | 145 | 154 |
| 2018 | aCO[1] | 60 | 60 | 48 | 60 | |||||
| 2018 | aCO[2] | 40 | 60 | 44 | 60 | |||||
| 2018 | aCO[3] | 51 | 52 | |||||||
| 2018 | eCO[1] | 60 | 56 | 38 | 60 | |||||
| 2018 | eCO[2] | 49 | 60 | 51 | 60 | |||||
| 2018 | eCO[3] | 60 | 46 | 37 | 60 | |||||
| 2019 | aCO[1] | 60 | 60 | 60 | 29 | 60 | ||||
| 2019 | aCO[2] | 12 | 55 | 60 | 36 | 60 | ||||
| 2019 | aCO[3] | 24 | 49 | 60 | 39 | 45 | ||||
| 2019 | eCO[1] | 60 | 60 | 60 | 35 | 60 | ||||
| 2019 | eCO[2] | 60 | 53 | 60 | 36 | 60 | ||||
| 2019 | eCO[3] | 48 | 53 | 60 | 37 | 60 | ||||
| Listing A1. Codeblock of brms-formula for the final internode length model. |
 |
| Year 2018 | Year 2019 | |||||||
|---|---|---|---|---|---|---|---|---|
| Training | Test | Training | Test | |||||
| Rank | n | n | n | n | ||||
| 1 | 108 | 1.25 | 27 | 1.21 | 84 | 1.06 | 21 | 1.12 |
| 2 | 108 | 2.03 | 27 | 1.92 | 83 | 2.01 | 21 | 1.73 |
| 3 | 107 | 3.96 | 27 | 3.83 | 82 | 4.35 | 20 | 3.84 |
| 4 | 97 | 5.34 | 24 | 5.32 | 81 | 5.71 | 19 | 5.11 |
| 5 | 82 | 6.60 | 20 | 7.06 | 77 | 6.43 | 19 | 5.72 |
| 6 | 72 | 8.53 | 19 | 8.32 | 66 | 8.39 | 18 | 6.92 |
| 7 | 69 | 8.86 | 17 | 10.10 | 59 | 9.70 | 15 | 8.89 |
| 8 | 64 | 6.92 | 15 | 8.05 | 56 | 9.49 | 14 | 8.83 |
| 9 | 54 | 7.46 | 14 | 7.92 | 53 | 9.17 | 13 | 9.90 |
| 10 | 41 | 8.44 | 12 | 8.63 | 52 | 9.16 | 13 | 9.79 |
| 11 | 37 | 7.61 | 9 | 8.42 | 49 | 8.66 | 12 | 8.02 |
| 12 | 36 | 8.67 | 9 | 8.54 | 46 | 9.04 | 12 | 8.34 |
| 13 | 36 | 9.18 | 9 | 9.65 | 41 | 8.88 | 10 | 8.91 |
| 14 | 36 | 8.23 | 9 | 8.28 | 34 | 8.31 | 7 | 10.66 |
| 15 | 35 | 9.18 | 8 | 9.32 | 28 | 8.98 | 7 | 9.49 |
| 16 | 32 | 10.13 | 8 | 9.77 | 25 | 7.84 | 7 | 8.69 |
| 17 | 32 | 8.62 | 8 | 9.20 | 24 | 6.67 | 6 | 5.98 |
| 18 | 27 | 9.63 | 7 | 8.03 | 19 | 5.59 | 5 | 6.02 |
| 19 | 20 | 10.18 | 4 | 12.78 | 17 | 3.87 | 5 | 4.42 |
| 20 | 18 | 7.75 | 4 | 10.59 | 10 | 3.35 | 3 | 4.41 |
| 21 | 14 | 7.20 | 4 | 10.17 | 2 | 1.25 | 2 | 3.18 |
| 22 | 9 | 6.70 | 2 | 10.20 | 1 | 2.45 | ||
| 23 | 2 | 3.59 | 1 | 7.08 | ||||

| Model | AICc | RMSE | RMSE (Test) | Parameter | Estimate |
|---|---|---|---|---|---|
| trt | 8125.19 | 2.19 | 2.34 | ||
| no trt | 8115.96 | 2.19 | 2.30 | ||
| no trt; heteroscedasticity (fitted values) | 7551.48 | 2.17 | 2.27 | ||
| no trt; heteroscedasticity (per rank) | 7327.16 | 2.17 | 2.29 | ||
| trt; heteroscedasticity (fitted values and per rank) | 7272.82 | 2.15 | 2.30 | ||
| no trt; heteroscedasticity (fitted values and per rank) | 7263.05 | 2.16 | 2.28 | 1.55 | |
| 1.29 | |||||
| 0.45 | |||||
| 9.56 | |||||
| lrc | −0.56 | ||||
| −0.56 | |||||
| −0.43 | |||||
| −0.49 |

| Prior | Class |
|---|---|
| student_t(10, 0, 1) | FE |
| student_t(3, 12.6, 8.4) | Intercept |
| normal(0, 1) | GE |
| normal(0, 1) | GE |
| student_t(3, 0, 8.4) | sigma |
| Prior | Class |
|---|---|
| student_t(10, 0, 1) | FE |
| student_t(3, 9.5, 6.7) | Intercept |
| student_t(3, 0, 1) | GE |
| student_t(3, 0, 6.7) | sigma |
| Prior | Class | Dpar | Nlpar | Bound |
|---|---|---|---|---|
| normal(0.6, 0.3) | FE | sage | ||
| normal(1, 1) | FE | i1 | <lower = 0> | |
| normal(10, 2) | FE | i2 | <lower = 0> | |
| normal(−1, 1) | FE | lrc | ||
| normal(1.5, 1) | FE | m1 | <lower = 0> | |
| normal(0.7, 0.5) | FE | m2 | ||
| normal(0, 0.5) | FE | sR2 | ||
| normal(0, 0.5) | FE | sR7 | ||
| student_t(3, 0, 2.5) | GE | shape | ||
| student_t(3, 0, 2.5) | GE | sage | ||
| normal(0, 1) | GE | i1 | ||
| normal(0, 1) | GE | i2 | ||
| normal(0, 0.5) | GE | lrc | ||
| normal(0, 0.5) | GE | m1 | ||
| normal(0, 0.5) | GE | m2 | ||
| student_t(3, 0, 2.5) | GE | shape |

References
- Chen, Y. Bayesian Inference in Plant Growth Models for Prediction and Uncertainty Assessment. Ph.D. Thesis, Ecole Centrale Paris, Châtenay-Malabry, France, 2014. [Google Scholar]
- Oijen, M.V.; Rougier, J.; Smith, R. Bayesian calibration of process-based forest models: Bridging the gap between models and data. Tree Physiol. 2005, 25, 915–927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ogle, K. Hierarchical Bayesian statistics: Merging experimental and modeling approaches in ecology. Ecol. Appl. 2009, 19, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Little, R. Calibrated Bayes, for statistics in general, and missing data in particular. Stat. Sci. 2011, 26, 162–174. [Google Scholar] [CrossRef]
- Ogle, K.; Barber, J.J. Bayesian Data—Model Integration in Plant Physiological and Ecosystem Ecology. In Progress in Botany; Springer: Berlin/Heidelberg, Germany, 2008; pp. 281–311. [Google Scholar] [CrossRef]
- Ogle, K.; Peltier, D.; Fell, M.; Guo, J.; Kropp, H.; Barber, J. Should we be concerned about multiple comparisons in hierarchical Bayesian models? Methods Ecol. Evol. 2019, 10, 553–564. [Google Scholar] [CrossRef]
- Jiao, Y.; Rogers-Bennett, L.; Taniguchi, I.; Butler, J.; Crone, P. Incorporating temporal variation in the growth of red abalone (Haliotis rufescens) using hierarchical Bayesian growth models. Can. J. Fish. Aquat. Sci. 2010, 67, 730–742. [Google Scholar] [CrossRef] [Green Version]
- Senf, C.; Pflugmacher, D.; Heurich, M.; Krueger, T. A Bayesian hierarchical model for estimating spatial and temporal variation in vegetation phenology from Landsat time series. Remote Sens. Environ. 2017, 194, 155–160. [Google Scholar] [CrossRef]
- Shirley, R.; Pope, E.; Bartlett, M.; Oliver, S.; Quadrianto, N.; Hurley, P.; Duivenvoorden, S.; Rooney, P.; Barrett, A.B.; Kent, C.; et al. An empirical, Bayesian approach to modelling crop yield: Maize in USA. Environ. Res. Commun. 2020, 2, 025002. [Google Scholar] [CrossRef]
- Tanno, K. Analysis of changes in topdressing application effect on rice by NDVI using hierarchical Bayesian model. Agron. J. 2021, 113, 3434–3443. [Google Scholar] [CrossRef]
- Ellis, R.; Moltchanova, E.; Gerhard, D.; Trought, M.; Yang, L. Using Bayesian growth models to predict grape yield. OENO One 2020, 54, 443–453. [Google Scholar] [CrossRef]
- Schmidt, D.; Bahr, C.; Friedel, M.; Kahlen, K. Modelling Approach for Predicting the Impact of Changing Temperature Conditions on Grapevine Canopy Architectures. Agronomy 2019, 9, 426. [Google Scholar] [CrossRef] [Green Version]
- Duchêne, E.; Huard, F.; Dumas, V.; Schneider, C.; Merdinoglu, D. The challenge of adapting grapevine varieties to climate change. Clim. Res. 2010, 41, 193–204. [Google Scholar] [CrossRef] [Green Version]
- Stoll, M.; Lafontaine, M.; Schultz, H.R. Possibilities to reduce the velocity of berry maturation through various leaf area to fruit ratio modifications in Vitis vinifera L. Riesling. Progrès Agric. Vitic. 2010, 127, 68–71. [Google Scholar]
- Pope, K.S.; Dose, V.; Da Silva, D.; Brown, P.H.; Leslie, C.A.; DeJong, T.M. Detecting nonlinear response of spring phenology to climate change by Bayesian analysis. Glob. Change Biol. 2013, 19, 1518–1525. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Li, X.; Zhou, X.; Geng, X.; Guo, Y.; Zhang, Y. Progress in plant phenology modeling under global climate change. Sci. China Earth Sci. 2020, 63, 1237–1247. [Google Scholar] [CrossRef]
- Piao, S.; Liu, Q.; Chen, A.; Janssens, I.A.; Fu, Y.; Dai, J.; Liu, L.; Lian, X.; Shen, M.; Zhu, X. Plant phenology and global climate change: Current progresses and challenges. Glob. Change Biol. 2019, 25, 1922–1940. [Google Scholar] [CrossRef]
- Parker, A.K.; de Cortázar-Atauri, I.G.; Trought, M.C.; Destrac, A.; Agnew, R.; Sturman, A.; Leeuwen, C.V. Adaptation to climate change by determining grapevine cultivar differences using temperature-based phenology models. OENO One 2020, 54, 955–974. [Google Scholar] [CrossRef]
- Molitor, D.; Junk, J.; Evers, D.; Hoffmann, L.; Beyer, M. A High-Resolution Cumulative Degree Day-Based Model to Simulate Phenological Development of Grapevine. Am. J. Enol. Vitic. 2013, 65, 72–80. [Google Scholar] [CrossRef]
- Jones, G.V.; Davis, R.E. Climate influences on grapevine phenology, grape composition, and wine production and quality for Bordeaux, France. Am. J. Enol. Vitic. 2000, 51, 249–261. [Google Scholar]
- Nendel, C. Grapevine bud break prediction for cool winter climates. Int. J. Biometeorol. 2009, 54, 231–241. [Google Scholar] [CrossRef]
- Zapata, D.; Salazar-Gutierrez, M.; Chaves, B.; Keller, M.; Hoogenboom, G. Predicting Key Phenological Stages for 17 Grapevine Cultivars (Vitis vinifera L.). Am. J. Enol. Vitic. 2016, 68, 60–72. [Google Scholar] [CrossRef]
- Parker, A.; de Cortázar-Atauri, I.G.; Chuine, I.; Barbeau, G.; Bois, B.; Boursiquot, J.M.; Cahurel, J.Y.; Claverie, M.; Dufourcq, T.; Gény, L.; et al. Classification of varieties for their timing of flowering and veraison using a modelling approach: A case study for the grapevine species Vitis vinifera L. Agric. For. Meteorol. 2013, 180, 249–264. [Google Scholar] [CrossRef]
- Molitor, D.; Fraga, H.; Junk, J. UniPhen—A unified high resolution model approach to simulate the phenological development of a broad range of grape cultivars as well as a potential new bioclimatic indicator. Agric. For. Meteorol. 2020, 291, 108024. [Google Scholar] [CrossRef]
- Leolini, L.; Costafreda-Aumedes, S.; Santos, J.A.; Menz, C.; Fraga, H.; Molitor, D.; Merante, P.; Junk, J.; Kartschall, T.; Destrac-Irvine, A.; et al. Phenological Model Intercomparison for Estimating Grapevine Budbreak Date (Vitis vinifera L.) in Europe. Appl. Sci. 2020, 10, 3800. [Google Scholar] [CrossRef]
- Piña-Rey, A.; Ribeiro, H.; Fernández-González, M.; Abreu, I.; Rodríguez-Rajo, F.J. Phenological Model to Predict Budbreak and Flowering Dates of Four Vitis vinifera L. Cultivars Cultivated in DO. Ribeiro (North-West Spain). Plants 2021, 10, 502. [Google Scholar] [CrossRef]
- Prats-Llinàs, M.T.; Nieto, H.; DeJong, T.M.; Girona, J.; Marsal, J. Using forced regrowth to manipulate Chardonnay grapevine (Vitis vinifera L.) development to evaluate phenological stage responses to temperature. Sci. Hortic. 2020, 262, 109065. [Google Scholar] [CrossRef]
- Zhu, J.; Parker, A.; Gou, F.; Agnew, R.; Yang, L.; Greven, M.; Raw, V.; Neal, S.; Martin, D.; Trought, M.C.T.; et al. Developing perennial fruit crop models in APSIM Next Generation using grapevine as an example. In Silico Plants 2021, 3, diab021. [Google Scholar] [CrossRef]
- Wang, E.; Engel, T. Simulation of phenological development of wheat crops. Agric. Syst. 1998, 58, 1–24. [Google Scholar] [CrossRef]
- Goudriaan, J.; Van Laar, H. Modelling Potential Crop Growth Processes: Textbook with Exercises; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 2. [Google Scholar]
- Zhou, G.; Wang, Q. A new nonlinear method for calculating growing degree days. Sci. Rep. 2018, 8, 10149. [Google Scholar] [CrossRef]
- de Cortázar-Atauri, I.G.; Brisson, N.; Gaudillere, J.P. Performance of several models for predicting budburst date of grapevine (Vitis vinifera L.). Int. J. Biometeorol. 2009, 53, 317–326. [Google Scholar] [CrossRef]
- de Cortázar-Atauri, I.G.; Daux, V.; Garnier, E.; Yiou, P.; Viovy, N.; Seguin, B.; Boursiquot, J.; Parker, A.; van Leeuwen, C.; Chuine, I. Climate reconstructions from grape harvest dates: Methodology and uncertainties. Holocene 2010, 20, 599–608. [Google Scholar] [CrossRef]
- Coombe, B.; Dry, P. Viticulture Volume 1-Resources, 2nd ed.; Winetitles Pty Ltd.: Broadview, SA, Australia, 2004. [Google Scholar]
- Coombe, B. Growth stages of the grapevine: Adoption of a system for identifying grapevine growth stages. Aust. J. Grape Wine Res. 1995, 1, 104–110. [Google Scholar] [CrossRef]
- Estes, L.D.; Bradley, B.A.; Beukes, H.; Hole, D.G.; Lau, M.; Oppenheimer, M.G.; Schulze, R.; Tadross, M.A.; Turner, W.R. Comparing mechanistic and empirical model projections of crop suitability and productivity: Implications for ecological forecasting. Glob. Ecol. Biogeogr. 2013, 22, 1007–1018. [Google Scholar] [CrossRef]
- Villordon, A.; Clark, C.; Ferrin, D.; LaBonte, D. Using Growing Degree Days, Agrometeorological Variables, Linear Regression, and Data Mining Methods to Help Improve Prediction of Sweetpotato Harvest Date in Louisiana. Horttechnol. Hortte 2009, 19, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model stics. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Holzworth, D.P.; Huth, N.I.; deVoil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM—Evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Schlenker, W.; Roberts, M.J. Nonlinear temperature effects indicate severe damages to US crop yields under climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef] [Green Version]
- Della Noce, A.; Letort, V.; Hansart, A.; Baey, C.; Viaud, G.; Barot, S.; Lata, J.C.; Raynaud, X.; Cournède, P.H.; Gignoux, J. Modeling the inter-individual variability of single-stemmed plant development. In Proceedings of the 2016 IEEE International Conference on Functional-Structural Plant Growth Modeling, Simulation, Visualization and Applications (FSPMA), Qingdao, China, 7–11 November 2016; pp. 44–51. [Google Scholar] [CrossRef]
- Schultz, H.R. An empirical model for the simulation of leaf appearance and leaf area development of primary shoots of several grapevine (Vitis vinifera L.) canopy-systems. Sci. Hortic. 1992, 52, 179–200. [Google Scholar] [CrossRef]
- Migault, V.; Pallas, B.; Costes, E. Combining Genome-Wide Information with a Functional Structural Plant Model to Simulate 1-Year-Old Apple Tree Architecture. Front. Plant Sci. 2017, 7, 2065. [Google Scholar] [CrossRef] [Green Version]
- Fournier, C.; Andrieu, B.; Ljutovac, S.; Saint-Jean, S. ADEL-Wheat: A 3D Architectural Model of wheat development. In Plant Growth Modeling and Applications; Hu, B.-G., Jaeger, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 54–63. [Google Scholar]
- de León, M.A.P.; Bailey, B.N. A 3D model for simulating spatial and temporal fluctuations in grape berry temperature. Agric. For. Meteorol. 2021, 306, 108431. [Google Scholar] [CrossRef]
- Bahr, C.; Schmidt, D.; Friedel, M.; Kahlen, K. Leaf removal effects on light absorption in virtual Riesling canopies (Vitis vinifera). In Silico Plants 2021, 3, diab027. [Google Scholar] [CrossRef]
- Schmidt, D.; Kahlen, K. Towards More Realistic Leaf Shapes in Functional-Structural Plant Models. Symmetry 2018, 10, 278. [Google Scholar] [CrossRef] [Green Version]
- Kahlen, K.; Wiechers, D.; Stützel, H. Modelling leaf phototropism in a cucumber canopy. Funct. Plant Biol. 2008, 35, 876–884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vermeiren, J.; Villers, S.L.Y.; Wittemans, L.; Vanlommel, W.; van Roy, J.; Marien, H.; Coussement, J.R.; Steppe, K. Quantifying the importance of a realistic tomato (Solanum lycopersicum) leaflet shape for 3-D light modelling. Ann. Bot. 2019, 126, 661–670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barillot, R.; Combes, D.; Huynh, P.; Gutierrez, A.E. Analysing light competition in cereal/legume intercropping systems through Functional Structural Plant Models. In Proceedings of the 6th International Workshop on Functional-Structural Plant Models, Davis, CA, USA, 12–17 September 2010; p. 307. [Google Scholar]
- Bongers, F.J. Functional-structural plant models to boost understanding of complementarity in light capture and use in mixed-species forests. Basic Appl. Ecol. 2020, 48, 92–101. [Google Scholar] [CrossRef]
- DeJong, T.M.; Da Silva, D.; Vos, J.; Escobar-Gutiérrez, A.J. Using functional-structural plant models to study, understand and integrate plant development and ecophysiology. Ann. Bot. 2011, 108, 987–989. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kahlen, K.; Stützel, H. Modelling photo-modulated internode elongation in growing glasshouse cucumber canopies. New Phytol. 2011, 190, 697–708. [Google Scholar] [CrossRef]
- Bailey, B.N. Helios: A Scalable 3D Plant and Environmental Biophysical Modeling Framework. Front. Plant Sci. 2019, 10, 1185. [Google Scholar] [CrossRef]
- Louarn, G.; Lecoeur, J.; Lebon, E. A Three-dimensional Statistical Reconstruction Model of Grapevine (Vitis vinifera) Simulating Canopy Structure Variability within and between Cultivar/Training System Pairs. Ann. Bot. 2007, 101, 1167–1184. [Google Scholar] [CrossRef] [Green Version]
- Torregrosa, L.; Carbonneau, A.; Kelner, J.J. The shoot system architecture of Vitis vinifera ssp. sativa. Sci. Hortic. 2021, 288, 110404. [Google Scholar] [CrossRef]
- Moravie, M.A.; Davison, A.; Pasquier, D.; Charmillot, P.J. Bayesian forecasting of grape moth emergence. Ecol. Model. 2006, 197, 478–489. [Google Scholar] [CrossRef]
- Paine, C.E.T.; Marthews, T.R.; Vogt, D.R.; Purves, D.; Rees, M.; Hector, A.; Turnbull, L.A. How to fit nonlinear plant growth models and calculate growth rates: An update for ecologists. Methods Ecol. Evol. 2011, 3, 245–256. [Google Scholar] [CrossRef]
- Gelman, A. Multilevel (hierarchical) modeling: What it can and cannot do. Technometrics 2006, 48, 432–435. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, H. Multilevel Statistical Models, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Colegrave, N.; Ruxton, G.D. Using Biological Insight and Pragmatism When Thinking about Pseudoreplication. Trends Ecol. Evol. 2018, 33, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Malakoff, D. Bayes Offers a ‘New’ Way to Make Sense of Numbers. Science 1999, 286, 1460–1464. [Google Scholar] [CrossRef] [Green Version]
- Wallach, D.; Buis, S.; Lecharpentier, P.; Bourges, J.; Clastre, P.; Launay, M.; Bergez, J.E.; Guerif, M.; Soudais, J.; Justes, E. A package of parameter estimation methods and implementation for the STICS crop-soil model. Environ. Model. Softw. 2011, 26, 386–394. [Google Scholar] [CrossRef]
- Jansen, M.J.; Hagenaars, T. Calibration in a Bayesian modelling framwork. In Proceedings of the Frontis Workshop on Bayesian Statistics and Quality Modelling in the Agro-Food Production Chain, Wageningen, The Netherlands, 1–14 May 2004; pp. 47–55. [Google Scholar]
- Makowski, D.; Hillier, J.; Wallach, D.; Andrieu, B.; Jeuffroy, M. Parameter estimation for crop models. In Working with Dynamic Crop Models; Wallach, D., Makowski, D., Jones James, W., Brun, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 101–149. [Google Scholar]
- Hartig, F.; Calabrese, J.M.; Reineking, B.; Wiegand, T.; Huth, A. Statistical inference for stochastic simulation models—Theory and application. Ecol. Lett. 2011, 14, 816–827. [Google Scholar] [CrossRef]
- Stan Development Team. RStan: The R Interface to Stan. R Package Version 2.21.2. 2020. Available online: http://mc-stan.org/ (accessed on 7 February 2022).
- Goodrich, B.; Gabry, J.; Ali, I.; Brilleman, S. rstanarm: Bayesian Applied Regression Modeling via Stan. Package Version 2.21.1. 2020. Available online: https://mc-stan.org/rstanarm (accessed on 7 February 2022).
- Bürkner, P.C. brms: An R Package for Bayesian Multilevel Models Using Stan. J. Stat. Softw. 2017, 80, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Bürkner, P.C. Advanced Bayesian Multilevel Modeling with the R Package brms. R J. 2018, 10, 395–411. [Google Scholar] [CrossRef]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef] [Green Version]
- Capretto, T.; Piho, C.; Kumar, R.; Westfall, J.; Yarkoni, T.; Martin, O.A. Bambi: A simple interface for fitting Bayesian linear models in Python. arXiv 2020, arXiv:stat.CO/2012.10754. [Google Scholar]
- McElreath, R. Statistical Rethinking; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar] [CrossRef]
- Kruschke, J. Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Upreti, D.; Pignatti, S.; Pascucci, S.; Tolomio, M.; Huang, W.; Casa, R. Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data. Remote Sens. 2020, 12, 2666. [Google Scholar] [CrossRef]
- Wallach, D.; Keussayan, N.; Brun, F.; Lacroix, B.; Bergez, J.E. Assessing the Uncertainty when Using a Model to Compare Irrigation Strategies. Agron. J. 2012, 104, 1274–1283. [Google Scholar] [CrossRef]
- Gouache, D.; Bensadoun, A.; Brun, F.; Pagé, C.; Makowski, D.; Wallach, D. Modelling climate change impact on Septoria tritici blotch (STB) in France: Accounting for climate model and disease model uncertainty. Agric. For. Meteorol. 2013, 170, 242–252. [Google Scholar] [CrossRef]
- Ceglar, A.; Črepinšek, Z.; Kajfež-Bogataj, L.; Pogačar, T. The simulation of phenological development in dynamic crop model: The Bayesian comparison of different methods. Agric. For. Meteorol. 2011, 151, 101–115. [Google Scholar] [CrossRef]
- Logothetis, D.; Malefaki, S.; Trevezas, S.; Cournède, P.H. Bayesian Estimation for the GreenLab Plant Growth Model with Deterministic Organogenesis. J. Agric. Biol. Environ. Stat. 2021. [Google Scholar] [CrossRef]
- Sexton, J.; Everingham, Y.; Inman-Bamber, G. A theoretical and real world evaluation of two Bayesian techniques for the calibration of variety parameters in a sugarcane crop model. Environ. Model. Softw. 2016, 83, 126–142. [Google Scholar] [CrossRef]
- Tan, J.; Cao, J.; Cui, Y.; Duan, Q.; Gong, W. Comparison of the Generalized Likelihood Uncertainty Estimation and Markov Chain Monte Carlo Methods for Uncertainty Analysis of the ORYZA_V3 Model. Agron. J. 2019, 111, 555–564. [Google Scholar] [CrossRef]
- Gao, Y.; Wallach, D.; Liu, B.; Dingkuhn, M.; Boote, K.J.; Singh, U.; Asseng, S.; Kahveci, T.; He, J.; Zhang, R.; et al. Comparison of three calibration methods for modeling rice phenology. Agric. For. Meteorol. 2020, 280, 107785. [Google Scholar] [CrossRef]
- Wallach, D.; Palosuo, T.; Thorburn, P.; Hochman, Z.; Gourdain, E.; Andrianasolo, F.; Asseng, S.; Basso, B.; Buis, S.; Crout, N.; et al. The chaos in calibrating crop models: Lessons learned from a multi-model calibration exercise. Environ. Model. Softw. 2021, 145, 105206. [Google Scholar] [CrossRef]
- Seidel, S.; Palosuo, T.; Thorburn, P.; Wallach, D. Towards improved calibration of crop models—Where are we now and where should we go? Eur. J. Agron. 2018, 94, 25–35. [Google Scholar] [CrossRef]
- Parker, A.K.; Fourie, J.; Trought, M.C.T.; Phalawatta, K.; Meenken, E.; Eyharts, A.; Moltchanova, E. Evaluating sources of variability in inflorescence number, flower number and the progression of flowering in Sauvignon blanc using a Bayesian modelling framework. OENO One 2022, 56, 1–15. [Google Scholar] [CrossRef]
- Spitters, C. Crop growth models: Their usefulness and limitations. Acta Hortic. 1990, 267, 349–368. [Google Scholar] [CrossRef]
- Wohlfahrt, Y.; Smith, J.; Tittmann, S.; Honermeier, B.; Stoll, M. Primary productivity and physiological responses of Vitis vinifera L. cvs. under Free Air Carbon dioxide Enrichment (FACE). Eur. J. Agron. 2018, 101, 149–162. [Google Scholar] [CrossRef]
- Parent, B.; Tardieu, F. Temperature responses of developmental processes have not been affected by breeding in different ecological areas for 17 crop species. New Phytol. 2012, 194, 760–774. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Yang, X.S. Multi-Objective Optimization. In Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014; pp. 197–211. [Google Scholar] [CrossRef]
- Kochenderfer, M.J.; Wheeler, T.A. Algorithms for Optimization; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Makowski, D.; Ben-Shachar, M.S.; Chen, S.H.A.; Lüdecke, D. Indices of Effect Existence and Significance in the Bayesian Framework. Front. Psychol. 2019, 10, 2767. [Google Scholar] [CrossRef]
- Vehtari, A.; Lampinen, J. Bayesian Model Assessment and Comparison Using Cross-Validation Predictive Densities. Neural Comput. 2002, 14, 2439–2468. [Google Scholar] [CrossRef]
- Vehtari, A.; Gelman, A.; Gabry, J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 2016, 27, 1413–1432. [Google Scholar] [CrossRef] [Green Version]
- Bartoń, K. MuMIn: Multi-Model Inference. R Package Version 1.43.1. 2020. Available online: https://CRAN.R-project.org/package=MuMIn (accessed on 7 February 2022).
- Bürkner, P.C. Bayesian Item Response Modeling in R with brms and Stan. J. Stat. Softw. 2021, 100, 1–54. [Google Scholar] [CrossRef]
- Schultz, H.R.; Matthews, M.A. Vegetative growth distribution during water deficits in Vitis vinifera L. Funct. Plant Biol. 1988, 15, 641–656. [Google Scholar] [CrossRef]
- Louarn, G.; Guedon, Y.; Lecoeur, J.; Lebon, E. Quantitative Analysis of the Phenotypic Variability of Shoot Architecture in Two Grapevine (Vitis vinifera) Cultivars. Ann. Bot. 2007, 99, 425–437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-152. 2021. Available online: https://CRAN.R-project.org/package=nlme (accessed on 7 February 2022).
- Gabry, J.; Simpson, D.; Vehtari, A.; Betancourt, M.; Gelman, A. Visualization in Bayesian workflow. J. R. Stat. Soc. Ser. (Stat. Soc.) 2019, 182, 389–402. [Google Scholar] [CrossRef] [Green Version]
- Coleman, M.C.; Block, D.E. Bayesian parameter estimation with informative priors for nonlinear systems. AIChE J. 2006, 52, 651–667. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Vehtari, A.; Gelman, A.; Simpson, D.; Carpenter, B.; Bürkner, P.C. Rank-Normalization, Folding, and Localization: An Improved Rˆ for Assessing Convergence of MCMC (with Discussion). Bayesian Anal. 2021, 16, 667–718. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.; Stern, H.; Dunson, D.; Vehtari, A.; Rubin, D. Bayesian Data Analysis, 3rd ed.; Chapman and Hall/CRC: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Gelman, A.; Goodrich, B.; Gabry, J.; Vehtari, A. R-squared for Bayesian Regression Models. Am. Stat. 2019, 73, 307–309. [Google Scholar] [CrossRef]
- Makowski, D.; Ben-Shachar, M.S.; Lüdecke, D. bayestestR: Describing Effects and their Uncertainty, Existence and Significance within the Bayesian Framework. J. Open Source Softw. 2019, 4, 1541. [Google Scholar] [CrossRef]
- Dowle, M.; Srinivasan, A. data.table: Extension of ‘data.frame’. R Package Version 1.14.0. 2021. Available online: https://CRAN.R-project.org/package=data.table (accessed on 7 February 2022).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Lorenz, D.; Eichhorn, K.; Bleiholder, H.; Klose, R.; Meier, U.; Weber, E. Growth Stages of the Grapevine: Phenological growth stages of the grapevine (Vitis vinifera L. ssp. vinifera)—Codes and descriptions according to the extended BBCH scale. Aust. J. Grape Wine Res. 1995, 1, 100–103. [Google Scholar] [CrossRef]
- Molitor, D.; Biewers, B.; Junglen, M.; Schultz, M.; Clementi, P.; Permesang, G.; Regnery, D.; Porten, M.; Herzog, K.; Hoffmann, L.; et al. Multi-annual comparisons demonstrate differences in the bunch rot susceptibility of nine Vitis vinifera L.‘Riesling’clones. Vitis 2018, 57, 17–25. [Google Scholar]
- Molitor, D.; Keller, M. Yield of Müller-Thurgau and Riesling grapevines is altered by meteorological conditions in the current and previous growing seasons. OENO One 2017, 50, 245–258. [Google Scholar] [CrossRef] [Green Version]
- Meicenheimer, R.D. The plastochron index: Still useful after nearly six decades. Am. J. Bot. 2014, 101, 1821–1835. [Google Scholar] [CrossRef] [Green Version]
- Rohatgi, A. Webplotdigitizer: Version 4.5. 2021. Available online: https://automeris.io/WebPlotDigitizer/ (accessed on 7 February 2022).
- Pagay, V.; Zufferey, V.; Lakso, A.N. The influence of water stress on grapevine (Vitis vinifera L.) shoots in a cool, humid climate: Growth, gas exchange and hydraulics. Funct. Plant Biol. 2016, 43, 827–837. [Google Scholar] [CrossRef] [PubMed]
- Fichtl, L. Untersuchung des Triebwachstums von Riesling in Abhängigkeit verschiedener Laubschnittzeitpunkte. Bachelor’s Thesis, Hochschule Geisenheim University, Geisenheim, Germany, 2020. [Google Scholar]
- Molitor, D.; Baus, O.; Hoffmann, L.; Beyer, M. Meteorological conditions determine the thermal-temporal position of the annual Botrytis bunch rot epidemic on Vitis vinifera L. cv. Riesling grapes. Oeno One 2016, 50, 231–244. [Google Scholar] [CrossRef] [Green Version]
- Buttrose, M.; Hale, C. Effect of temperature on development of the grapevine inflorescence after bud burst. Am. J. Enol. Vitic. 1973, 24, 14–16. [Google Scholar]
- Williams, D.; L E, W.; Barnett, W.; Kelley, K.M.; McKenry, M. Validation of a model for the growth and development of the Thompson Seedless grapevine. I. Vegetative growth and fruit yield. Am. J. Enol. Vitic. 1985, 36, 275–282. [Google Scholar]
- Van Leeuwen, C.; Garnier, C.; Agut, C.; Baculat, B.; Barbeau, G.; Besnard, E.; Bois, B.; Boursiquot, J.M.; Chuine, I.; Dessup, T.; et al. Heat requirements for grapevine varieties is essential information to adapt plant material in a changing climate. In Proceedings of the 7th Congrès International des Terroirs Viticoles, Agroscope Changins-Wädenswil Research Station ACW, Nyon, Switzerland, 19–23 May 2008. [Google Scholar]
- Gu, S. Growing degree hours—A simple, accurate, and precise protocol to approximate growing heat summation for grapevines. Int. J. Biometeorol. 2015, 60, 1123–1134. [Google Scholar] [CrossRef]
- Martínez-Lüscher, J.; Kizildeniz, T.; Vučetić, V.; Dai, Z.; Luedeling, E.; van Leeuwen, C.; Gomès, E.; Pascual, I.; Irigoyen, J.J.; Morales, F.; et al. Sensitivity of Grapevine Phenology to Water Availability, Temperature and CO2 Concentration. Front. Environ. Sci. 2016, 4, 48. [Google Scholar] [CrossRef]
- Cameron, W.; Petrie, P.R.; Barlow, E.; Howell, K.; Jarvis, C.; Fuentes, S. A comparison of the effect of temperature on grapevine phenology between vineyards. OENO One 2021, 55, 301–320. [Google Scholar] [CrossRef]
- Dinu, D.G.; Ricciardi, V.; Demarco, C.; Zingarofalo, G.; Lorenzis, G.D.; Buccolieri, R.; Cola, G.; Rustioni, L. Climate Change Impacts on Plant Phenology: Grapevine (Vitis vinifera) Bud Break in Wintertime in Southern Italy. Foods 2021, 10, 2769. [Google Scholar] [CrossRef]
- Bahr, C.; Schmidt, D.; Kahlen, K. Missing Links in Predicting Berry Sunburn in Future Vineyards. Front. Plant Sci. 2021, 12, 1–8. [Google Scholar] [CrossRef]
- Sivula, T.; Magnusson, M.; Vehtari, A. Uncertainty in Bayesian Leave-One-Out Cross-Validation Based Model Comparison. arXiv 2020, arXiv:stat.ME/2008.10296. [Google Scholar]
- Greer, D.H.; Weston, C. Effects of fruiting on vegetative growth and development dynamics of grapevines (Vitis vinifera cv. Semillon) can be traced back to events at or before budbreak. Funct. Plant Biol. 2010, 37, 756. [Google Scholar] [CrossRef]
- Pellegrino, A.; Lebon, E.; Simonneau, T.; Wery, J. Towards a simple indicator of water stress in grapevine (Vitis vinifera L.) based on the differential sensitivities of vegetative growth components. Aust. J. Grape Wine Res. 2005, 11, 306–315. [Google Scholar] [CrossRef]
- Keller, M.; Tarara, J.M. Warm spring temperatures induce persistent season-long changes in shoot development in grapevines. Ann. Bot. 2010, 106, 131–141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelman, A.; Hill, J.; Yajima, M. Why We (Usually) Don’t Have to Worry About Multiple Comparisons. J. Res. Educ. Eff. 2012, 5, 189–211. [Google Scholar] [CrossRef] [Green Version]
- Sofaer, H.R.; Chapman, P.L.; Sillett, T.S.; Ghalambor, C.K. Advantages of nonlinear mixed models for fitting avian growth curves. J. Avian Biol. 2013, 44, 469–478. [Google Scholar] [CrossRef]
- Rives, M. Vigour, pruning, cropping in the grapevine (Vitis vinifera L.). I. A literature review. Agronomy 2000, 20, 79–91. [Google Scholar] [CrossRef] [Green Version]
- Bonada, M.; Catania, A.; Gambetta, J.; Petrie, P. Soil water availability during spring modulates canopy growth and impacts the chemical and sensory composition of Shiraz fruit and wine. Aust. J. Grape Wine Res. 2021, 27, 491–507. [Google Scholar] [CrossRef]
- Gambetta, J.M.; Holzapfel, B.P.; Stoll, M.; Friedel, M. Sunburn in Grapes: A Review. Front. Plant Sci. 2021, 11, 1–21. [Google Scholar] [CrossRef]
- Patenaude, G.; Milne, R.; Oijen, M.V.; Rowland, C.S.; Hill, R.A. Integrating remote sensing datasets into ecological modelling: A Bayesian approach. Int. J. Remote Sens. 2008, 29, 1295–1315. [Google Scholar] [CrossRef] [Green Version]
- van Oijen, M.; Reyer, C.; Bohn, F.; Cameron, D.; Deckmyn, G.; Flechsig, M.; Härkönen, S.; Hartig, F.; Huth, A.; Kiviste, A.; et al. Bayesian calibration, comparison and averaging of six forest models, using data from Scots pine stands across Europe. For. Ecol. Manag. 2013, 289, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Ovalle-Rivera, O.; Van Oijen, M.; Läderach, P.; Roupsard, O.; de Melo Virginio Filho, E.; Barrios, M.; Rapidel, B. Assessing the accuracy and robustness of a process-based model for coffee agroforestry systems in Central America. Agrofor. Syst. 2020, 94, 2033–2051. [Google Scholar] [CrossRef]
- Hurley, P.D.; Oliver, S.; Betancourt, M.; Clarke, C.; Cowley, W.I.; Duivenvoorden, S.; Farrah, D.; Griffin, M.; Lacey, C.; Le Floc’h, E.; et al. HELP: Xid+, the probabilistic de-blender for Herschel SPIRE maps. Mon. Not. R. Astron. Soc. 2016, 464, 885–896. [Google Scholar] [CrossRef] [Green Version]
- Ben Touhami, H.; Bellocchi, G. Bayesian calibration of the Pasture Simulation model (PaSim) to simulate European grasslands under water stress. Ecol. Informatics 2015, 30, 356–364. [Google Scholar] [CrossRef]
- Blanc, E.; Enjalbert, J.; Barbillon, P. Automatic calibration of a functional-structural wheat model using an adaptive design and a metamodelling approach. bioRxiv 2021, 1–27. [Google Scholar] [CrossRef]
- Byrne, M. How many times should a stochastic model be run? An approach based on confidence intervals. In Proceedings of the 12th International Conference on Cognitive Modeling, Ottawa, ON, Canada, 11–14 July 2013; pp. 445–450. [Google Scholar]

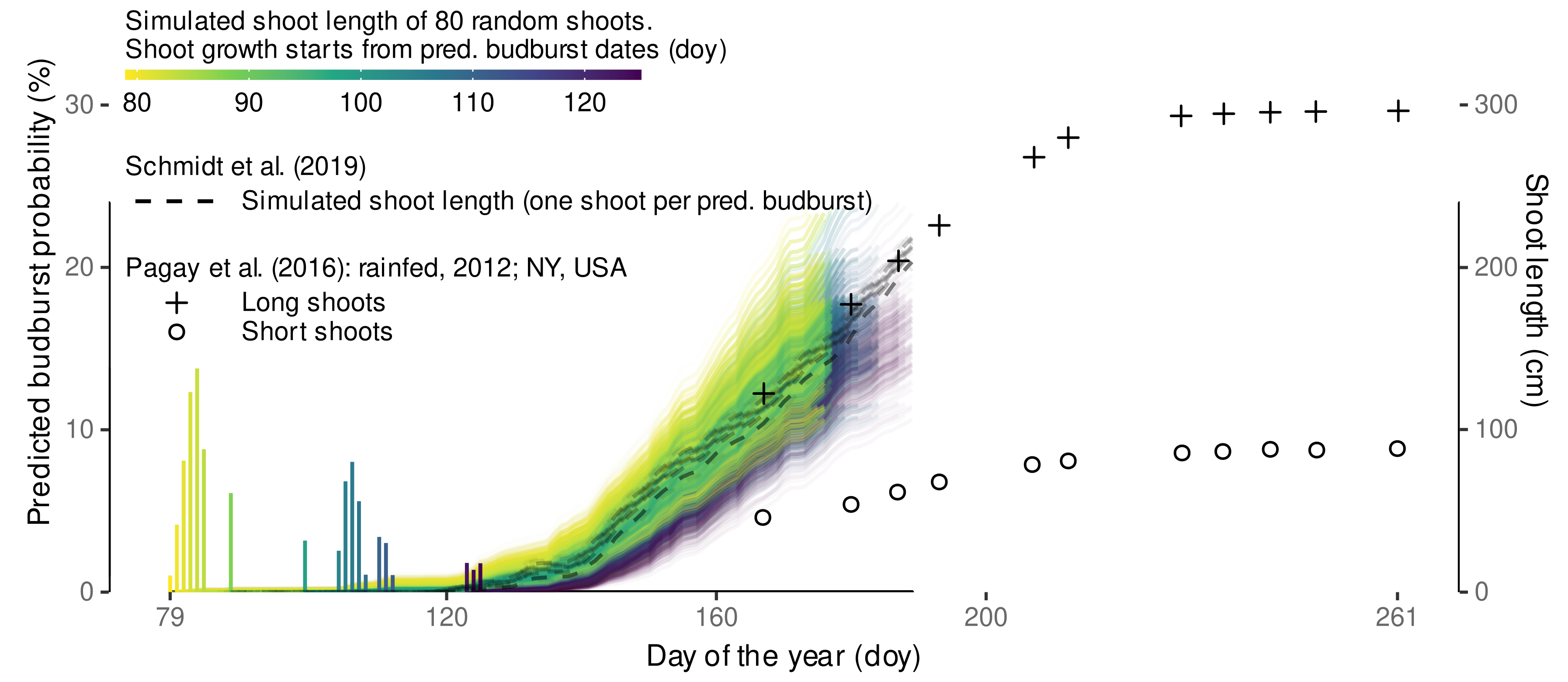
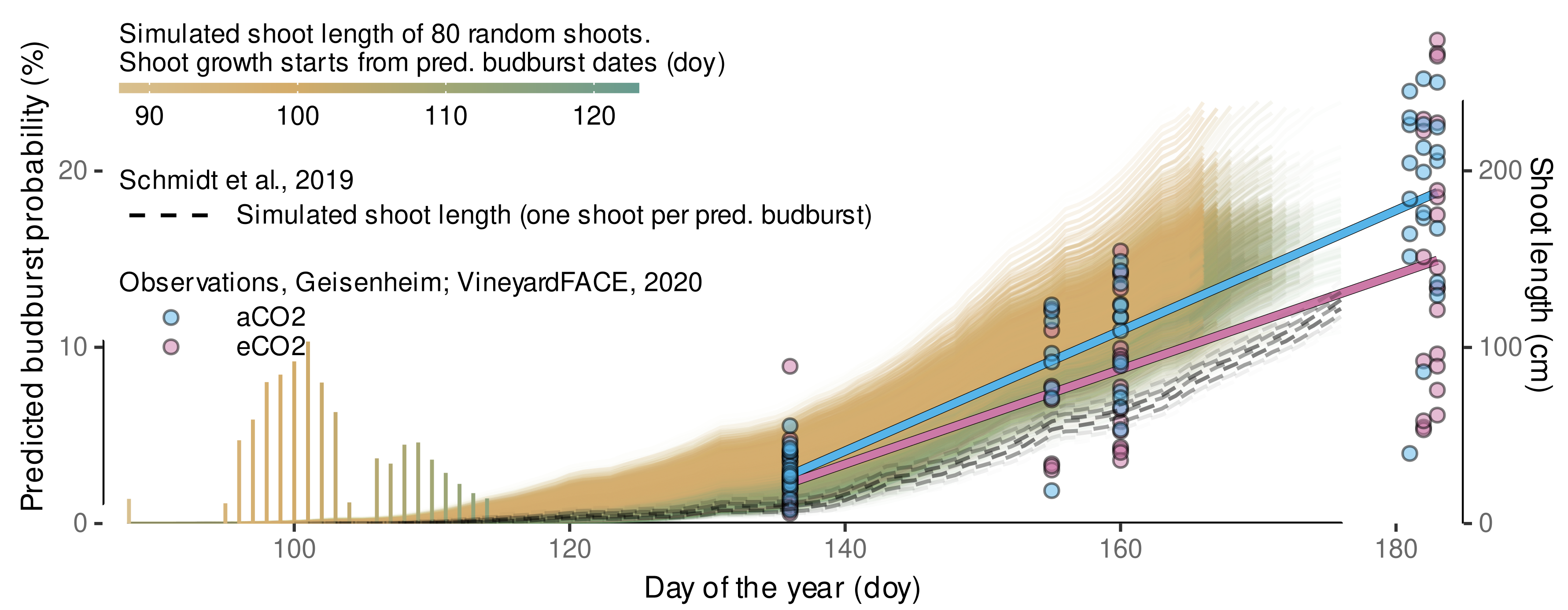
| 1 | (2-)3 | 4 | 5 | 6 | 7 | 8 | 10 | 12 | 14 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ELSt | 1 | 2 | 3 | 4 | 5 | 7 | 9 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| ELSt | 2.00 | 3.75 | 3.875 | 4.00 | 5.00 | 6.50 | 8.50 | 9.50 | 10.50 | 11.50 | 12.50 | 13.50 | 15.50 | 17.50 | 19.50 |
| Location | Season | Stage | Source |
|---|---|---|---|
| Neustadt an der Weinstraße, Germany | 2003–2021 | ’Austrieb’ (budburst), ‘Blühbeginn’ (beginning of flowering) | https://www.dlr-rheinpfalz.rlp.de/Internet/global/themen.nsf/2eca2af4a2290c7fc1256e8b005161c9/8096dedb652c43cbc12571b00048fe49?OpenDocument (accessed on 27 August 2021) |
| Zeltingen-Rachtig, Germany | 2013–2016 | budburst (BBCH 09 [110]), beginning of flowering | Molitor et al. [111], Suppl. Mat: https://ojs.openagrar.de/index.php/VITIS/article/view/8462/8625 (accessed on 7 February 2022) |
| Remich, Luxembourg | 1993–2015 | budburst (BBCH 09 [110]) | Molitor and Keller (Table 2 [112]) |
| Geisenheim, Germany | 1990–2009 | budburst | Stoll et al. (Figure 1 [14]) |
| Iteration 1 | Iteration 2 | ||||||
|---|---|---|---|---|---|---|---|
| 11 | 19 | 25 | 67 | 10.8 | 19.0 | 24.7 | 49 |
| 9 | 19 | 21 | 37 | 11.8 | 18.7 | 24.1 | 30 |
| 12 | 16 | 35 | 28 | 10.9 | 19.1 | 25.3 | 19 |
| 15 | 17 | 22 | 24 | 11.8 | 18.8 | 24.1 | 15 |
| 11 | 19 | 24 | 23 | 10.6 | 19.3 | 25.3 | 14 |
| −8 | 21 | 24 | 15 | 11.5 | 18.7 | 24.2 | 13 |
| −38 | 22 | 25 | 9 | 10.6 | 19.8 | 25.4 | 8 |
| 12 | 15 | 50 | 4 | 11.3 | 19.1 | 24.4 | 6 |
| −11 | 20 | 22 | 4 | 10.5 | 19.5 | 25.0 | 5 |
| 15 | 17 | 21 | 2 | 11.9 | 18.7 | 24.3 | 5 |
| 8 | 20 | 24 | 2 | 11.9 | 18.7 | 24.2 | 5 |
| 11 | 19 | 23 | 2 | 11.6 | 18.9 | 24.2 | 4 |
| 9 | 19 | 22 | 1 | ||||
| 4 | 21 | 25 | 1 | ||||
| Model | LOOIC [SE] | RMSE [95% HDI] | RMSE (test) [95% HDI] | R2 [95% HDI] | Parameter | Estimate [Q2.5, Q97.5] | pd (%) |
|---|---|---|---|---|---|---|---|
| full | 9234.46 [95.41] | 3.188 [3.0925, 3.2912] | 3.0593 [2.8977, 3.2232] | 0.8893 [0.8856, 0.8929] | ELStlinear | 1.2892 [1.259, 1.3203] | 100.00 |
| full | Intercept | 2.5436 [1.9893, 3.082] | 100.00 | ||||
| full | trteCO2 | −0.0481 [−0.708, 0.6182] | 56.43 | ||||
| full | trteCO2:ELStlinear | −4 [−0.0402, 0.0406] | 50.50 | ||||
| full | year2019 | −0.0237 [−0.4223, 0.3781] | 54.86 | ||||
| no interaction | 9233.05 [95.37] | 3.1866 [3.0892, 3.2842] | 3.0593 [2.9053, 3.2345] | 0.8893 [0.8857, 0.8931] | ELStlinear | 1.289 [1.2682, 1.3099] | 100.00 |
| no interaction | Intercept | 2.5352 [2.0315, 3.0276] | 100.00 | ||||
| no interaction | trteCO2 | −0.0479 [−0.6024, 0.5175] | 58.26 | ||||
| no interaction | year2019 | −0.0178 [−0.4036, 0.3833] | 54.05 | ||||
| no year | 9232.04 [95.39] | 3.1856 [3.0897, 3.2842] | 3.0576 [2.8999, 3.2182] | 0.8893 [0.886, 0.8933] | ELStlinear | 1.2891 [1.2685, 1.3101] | 100.00 |
| no year | Intercept | 2.5262 [2.0715, 2.983] | 100.00 | ||||
| no year | trteCO2 | −0.0518 [−0.5796, 0.4729] | 59.39 | ||||
| final | 9232.64 [95.39] | 3.1817 [3.0891, 3.2836] | 3.0553 [2.8938, 3.2123] | 0.8893 [0.8857, 0.8928] | ELStlinear | 1.2893 [1.269, 1.3092] | 100.00 |
| final | Intercept | 2.5006 [2.1734, 2.8311] | 100.00 | ||||
| final (exGaussian) | 8775.62 [79.81] | 3.2624 [3.1183, 3.3996] | 3.1466 [2.9118, 3.3836] | 0.8789 [0.875, 0.8829] | ELStlinear | 1.2539 [1.2345, 1.2736] | 100.00 |
| final (exGaussian) | Intercept | 2.8502 [2.5594, 3.1455] | 100.00 | ||||
| final (exG., full data) | 11,288.56 [90.97] | 3.1998 [3.0805, 3.3182] | — | 0.8887 [0.8853, 0.8919] | ELStlinear | 1.2577 [1.241, 1.2741] | 100.00 |
| final (exG., full data) | Intercept | 2.7789 [2.4794, 3.0868] | 100.00 |
| Model | LOOIC [SE] | RMSE [95% HDI] | RMSE (Test) [95% HDI] | R2 [95% HDI] | Parameter | Estimate [Q2.5, Q97.5] | pd (%) |
|---|---|---|---|---|---|---|---|
| full | 642.61 [17.97] | 2.3803 [2.1842, 2.5924] | 2.5867 [2.279, 2.8805] | 0.9751 [0.9707, 0.9791] | Intercept | −6.7827 [−7.8887, −5.7296] | 100.00 |
| full | CDD | 0.7747 [0.7372, 0.8118] | 100.00 | ||||
| full | CDD:trt | 0.0087 [−0.0418, 0.0593] | 63.65 | ||||
| full | trt | −0.0139 [−1.1569, 1.1765] | 51.11 | ||||
| full | year | −0.268 [−1.2436, 0.7435] | 71.44 | ||||
| rm trt interaction | 639.82 [17.89] | 2.3721 [2.178, 2.567] | 2.574 [2.2815, 2.873] | 0.9752 [0.9708, 0.9792] | Intercept | −6.8255 [−7.8867, −5.7655] | 100.00 |
| rm trt interaction | CDD | 0.7792 [0.7533, 0.8041] | 100.00 | ||||
| rm trt interaction | trt | 0.0582 [−1.0514, 1.1574] | 54.84 | ||||
| rm trt interaction | year | −0.2694 [−1.2459, 0.7285] | 71.25 | ||||
| rm year | 638.34 [17.53] | 2.3748 [2.1999, 2.5562] | 2.5915 [2.3077, 2.8755] | 0.9753 [0.9711, 0.9793] | Intercept | −6.9295 [−7.8836, −6.023] | 100.00 |
| rm year | CDD | 0.7794 [0.7537, 0.8054] | 100.00 | ||||
| rm year | trt | 0.0427 [−1.0245, 1.124] | 53.00 | ||||
| rm trt | 638.99 [17.8] | 2.3521 [2.1713, 2.5334] | 2.5572 [2.2669, 2.8495] | 0.9752 [0.9709, 0.9792] | Intercept | −6.7851 [−7.6507, −5.9236] | 100.00 |
| rm trt | CDD | 0.7797 [0.7541, 0.8059] | 100.00 | ||||
| rm trt | year | −0.2686 [−1.2425, 0.7031] | 71.39 | ||||
| add year GE | 640.27 [17.92] | 2.4214 [2.1622, 2.7362] | 2.6286 [2.2688, 3.0283] | 0.9752 [0.9712, 0.9793] | Intercept | −6.9483 [−8.3861, −5.6148] | 100.00 |
| add year GE | CDD | 0.7798 [0.7539, 0.8051] | 100.00 | ||||
| final | 640.12 [17.99] | 2.3589 [2.2037, 2.5365] | 2.5789 [2.3162, 2.8699] | 0.9753 [0.9712, 0.9793] | Intercept | −6.9059 [−7.6626, −6.1822] | 100.00 |
| final | CDD | 0.7789 [0.7533, 0.8051] | 100.00 | ||||
| final (full data) | 832.6 [20.89] | 2.4104 [2.2682, 2.5492] | −−− | 0.9745 [0.9707, 0.978] | Intercept | −6.921 [−7.5665, −6.2985] | 100.00 |
| final (full data) | CDD | 0.7784 [0.7547, 0.8018] | 100.00 |
| Model | LOOIC [SE] | RMSE [95% HDI] | RMSE (Test) [95% HDI] | R2 [95% HDI] | Parameter | Estimate [Q2.5, Q97.5] | pd (%) |
|---|---|---|---|---|---|---|---|
| fixed trt | 6731.24 [101.24] | 3.8366 [2.1598, 7.2981] | 3.9045 [2.2945, 7.3602] | 0.8466 [0.8396, 0.8536] | −0.2172 [−0.3351, −0.0854] | 99.92 | |
| fixed trt | −0.48 [−0.5296, −0.4313] | 100.00 | |||||
| fixed trt | −0.3748 [−0.6671, −0.0708] | 99.11 | |||||
| fixed trt | 1.2515 [0.537, 1.8146] | 100.00 | |||||
| fixed trt | 1.2428 [0.5443, 1.8105] | 100.00 | |||||
| fixed trt | 10.0877 [8.2055, 11.9674] | 100.00 | |||||
| fixed trt | 9.6182 [7.7617, 11.5094] | 100.00 | |||||
| fixed trt | lrc | −0.797 [−1.6328, −0.0273] | 97.77 | ||||
| fixed trt | lrc | −0.9274 [−1.7598, −0.1525] | 99.00 | ||||
| fixed trt | 1.6845 [1.0109, 2.3235] | 100.00 | |||||
| fixed trt | 1.647 [0.9916, 2.2534] | 100.00 | |||||
| fixed trt | 0.6347 [0.1027, 1.1799] | 98.89 | |||||
| fixed trt | 0.5439 [0.0166, 1.0948] | 97.78 | |||||
| fixed year | 6731.92 [101.6] | 3.5725 [2.0063, 6.9003] | 3.6335 [2.1216, 6.9794] | 0.8467 [0.8395, 0.8536] | −0.2178 [−0.3378, −0.0841] | 99.92 | |
| fixed year | −0.4795 [−0.529, −0.4287] | 100.00 | |||||
| fixed year | −0.3763 [−0.6666, −0.0714] | 99.15 | |||||
| fixed year | 1.3029 [1.0787, 1.5259] | 100.00 | |||||
| fixed year | 1.2628 [1.0168, 1.5155] | 100.00 | |||||
| fixed year | 8.1287 [7.3206, 8.9449] | 100.00 | |||||
| fixed year | 11.4742 [10.5318, 12.4614] | 100.00 | |||||
| fixed year | lrc | −0.283 [−0.5315, −0.0391] | 98.65 | ||||
| fixed year | lrc | −1.3557 [−1.5916, −1.1194] | 100.00 | ||||
| fixed year | 1.5069 [1.1818, 1.8159] | 100.00 | |||||
| fixed year | 1.8811 [1.5457, 2.2236] | 100.00 | |||||
| fixed year | 0.7489 [0.4476, 1.062] | 100.00 | |||||
| fixed year | 0.2729 [−0.1296, 0.6765] | 91.47 | |||||
| no fixed | 6737.69 [101.75] | 3.8481 [2.1888, 7.2349] | 3.8924 [2.2786, 7.2188] | 0.8465 [0.8395, 0.8538] | −0.2179 [−0.3402, −0.086] | 99.88 | |
| no fixed | −0.4796 [−0.5293, −0.4297] | 100.00 | |||||
| no fixed | −0.3766 [−0.6703, −0.0737] | 99.26 | |||||
| no fixed | 1.2663 [0.5514, 1.8706] | 100.00 | |||||
| no fixed | 9.8205 [7.844, 11.8148] | 100.00 | |||||
| no fixed | lrc | −0.8415 [−1.7012, −4e−04] | 97.50 | ||||
| no fixed | 1.6856 [1.1053, 2.2669] | 100.00 | |||||
| no fixed | 0.5593 [0.0307, 1.0996] | 97.91 | |||||
| no year = final | 6736.88 [101.64] | 2.7603 [2.4947, 3.0985] | 2.8545 [2.5506, 3.1883] | 0.8462 [0.8389, 0.8533] | −0.2185 [−0.3383, −0.0863] | 99.85 | |
| no year = final | −0.4779 [−0.528, −0.4284] | 100.00 | |||||
| no year = final | −0.3627 [−0.6528, −0.0528] | 98.81 | |||||
| no year = final | 1.2905 [1.1, 1.4792] | 100.00 | |||||
| no year = final | 9.7018 [8.5788, 10.8534] | 100.00 | |||||
| no year = final | lrc | −0.8119 [−1.2259, −0.3988] | 99.96 | ||||
| no year = final | 1.6843 [1.4069, 1.9595] | 100.00 | |||||
| no year = final | 0.5879 [0.2818, 0.8683] | 99.89 | |||||
| final (full data) | 8436.07 [112.44] | 2.7954 [2.5169, 3.1104] | 2.7953 [2.5242, 3.1178] | 0.8473 [0.8412, 0.8535] | −0.2368 [−0.342, −0.1215] | 99.98 | |
| final (full data) | −0.482 [−0.5255, −0.4381] | 100.00 | |||||
| final (full data) | −0.1699 [−0.4437, 0.1185] | 88.13 | |||||
| final (full data) | 1.2795 [1.1104, 1.4503] | 100.00 | |||||
| final (full data) | 9.6989 [8.6432, 10.8139] | 100.00 | |||||
| final (full data) | lrc | −0.812 [−1.227, −0.3979] | 99.87 | ||||
| final (full data) | 1.6552 [1.3787, 1.9278] | 100.00 | |||||
| final (full data) | 0.6104 [0.3429, 0.8614] | 99.98 |
| Observation | Schmidt et al., 2019 | This Study | ||||
|---|---|---|---|---|---|---|
| Doy | Treatment | () | () | () | () | () |
| 136 | eCO | 25.2 | 10.0 | −15.1 | 32.1 | 6.9 |
| 136 | aCO | 29.5 | 10.0 | −19.5 | 32.1 | 2.6 |
| 155 | eCO | 68.0 | 56.3 | −11.7 | 101.1 | 33.1 |
| 155 | aCO | 89.3 | 56.3 | −33.0 | 101.1 | 11.8 |
| 160 | eCO | 84.9 | 63.3 | −21.6 | 119.2 | 34.3 |
| 160 | aCO | 104.8 | 63.3 | −41.4 | 119.2 | 14.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, D.; Kahlen, K.; Bahr, C.; Friedel, M. Towards a Stochastic Model to Simulate Grapevine Architecture: A Case Study on Digitized Riesling Vines Considering Effects of Elevated CO2. Plants 2022, 11, 801. https://doi.org/10.3390/plants11060801
Schmidt D, Kahlen K, Bahr C, Friedel M. Towards a Stochastic Model to Simulate Grapevine Architecture: A Case Study on Digitized Riesling Vines Considering Effects of Elevated CO2. Plants. 2022; 11(6):801. https://doi.org/10.3390/plants11060801
Chicago/Turabian StyleSchmidt, Dominik, Katrin Kahlen, Christopher Bahr, and Matthias Friedel. 2022. "Towards a Stochastic Model to Simulate Grapevine Architecture: A Case Study on Digitized Riesling Vines Considering Effects of Elevated CO2" Plants 11, no. 6: 801. https://doi.org/10.3390/plants11060801
APA StyleSchmidt, D., Kahlen, K., Bahr, C., & Friedel, M. (2022). Towards a Stochastic Model to Simulate Grapevine Architecture: A Case Study on Digitized Riesling Vines Considering Effects of Elevated CO2. Plants, 11(6), 801. https://doi.org/10.3390/plants11060801