1. Introduction
Many economists have recently emphasized space and spatial effects in their research [
1,
2]. More than before, it is important to improve the implementation of geographic information science (GIScience) and understanding of the related methods. This paper shows the results of one of the most studied socioeconomic phenomena in social sciences and economy, namely, unemployment, interpreted through GIS and spatial methods. Due to its high complexity and accessibility at a microscale [
3,
4,
5], unemployment is an important topic across disciplines, and GIS can offer many insights [
6,
7].
Unemployment studies have received a lot of attention from sociologists, economists, and geographers. In this study, we focused on the spatial dimension of unemployment, which is connected with regional unemployment and regional disparities in general. The spatial aspects of unemployment have been studied by many authors, such as [
7,
8,
9]. Authors who have studied unemployment have all found quite stable regional patterns that oscillate around national unemployment means yet often have some specific outliers, as shown in [
8,
10,
11,
12,
13] as well as [
14], which specifically studied Czechia. This has consistently been found on an international level as well [
15,
16,
17,
18]. Even though the explanations behind the high inertia of spatial patterns of unemployment differ by author, the relative stability of these patterns is generally agreed upon.
Another consensus can be found when decomposing unemployment into differences between countries and differences between regions within those countries. Empirical works have shown that the differences tend to transfer from between countries to within countries [
19,
20,
21,
22]. Similar effects can be found on a regional level, with the importance of within-region differences rising compared to the between-region component of the overall differentiation. However, there are significant differences (outliers) in specific regions undergoing dramatic social and/or economic transformation. Central/Eastern Europe (in this paper, specifically Czechia) is one of the regions where recent spatial patterns have been shaped by this development. The spatial patterns stabilized relatively quickly and have recently been changing very slowly. Yet, we can still observe some significant tendencies in spatial patterns of unemployment. In Czechia, there is a vast amount of literature focusing on unemployment and its changes over time, such as [
23,
24,
25,
26]. The majority of authors agree that microdifferentiation has been increasing over time, although the process has been very steady. Despite an abundance of research on this topic, there are many unanswered questions. Above all, the majority of hypotheses have not been tested on a longer time series with data on detailed levels (such as municipalities).
We studied the spatial dimension of unemployment in Czechia in a unique, long-term series based on yearly data from 2002 to 2019. We examined unemployment using municipal data, namely, 6250 units of approximately 12.6 square kilometers. This detailed spatial level enabled us to use more sophisticated methods, such as spatial autocorrelation and entropy decomposition. When analyzing municipal data with spatial statistics methods, the spatial weights are often considered an important methodological issue, although we have shown in our previous paper [
23] that the role of spatial weights is slightly exaggerated. When studying general patterns, there is one important, valid issue, i.e., the difference between the spatial weights based on Euclidean distances and spatial weights based on network distances as a time function (time accessibility, distance decay) [
27,
28,
29]. Network distances are more suitable when studying social processes (including unemployment). Moreover, within the context of unemployment, which is largely dependent on commuting, it is useful to understand distances as a time function (travel time between municipalities) [
30]. Therefore, in addition to Euclidean distances, we also used network distances (based on the Czech road network) and their time representation as a proxy (the modelled travel time in space). The importance of spatial weight differences has not been studied on such a dataset. Specifically, network spatial weights based on real-time accessibility are often mentioned as a potential bias, but there is no empirical evidence for this hypothesis.
This study had two main goals. The first goal was to identify long-term trends in the spatial distribution of unemployment (spatial dimension of unemployment) at the municipal level in Czechia. An extensive, long-term empirical analysis of this territorial detail is still missing. This would bring new insights regarding evolutionary tendencies of unemployment in space and time. The second goal was to examine the significance of time when analyzing spatial dimension of unemployment in Czechia. We compared the results of spatial analyses based on Euclidean distances and distances as a time function (time accessibility), which is important from a methodological point of view. As we have studied an important social variable, the results might have policy implications. Examining policy implications was out of the scope of this study, although some suggestions on how to address relevant policies may be found in [
31,
32].
This paper is empirically oriented, while some more complex methodological issues are discussed to improve the comprehensibility of the paper for readers. Based on the typology of Pászto et al. [
33], we not only worked with spatial statistics (level 3) and a combination of analytical methods (level 4) but also with spatial modelling, labelled as level 5. Specifically, we studied the spatial dimension of socioeconomic disparities (for more theoretical discussion and methodological detail, see [
23,
34,
35]). Besides the spatial dimension, it is important to take the time dimension into account. Regarding the time dimension, we not only studied the phenomena in time but also worked to understand spatial distances as time functions, i.e., the distance between two cities measured as time to get from one city to another city.
The main added value of this extensive empirical study is the use of complex GIS methods and modelling. The research done in Czechia may be replicated in other countries. As a result, it may be implemented internationally as one important added value of the methodology is its low sensitivity to differences in spatial structures in two or more rather different systems (such as countries). Specifically, in this context, we paid a lot of attention to spatial weights by testing their significance according to the results of spatial analyses. We not only used the traditional distance-based spatial weights but also used the network spatial weights based on real-time accessibility, which is not common in current studies. It is especially uncommon due to the unavailability of data on microlevels, where traditional distance may be distinguished differently than travel distance (due to physical barriers, borders etc.). On regional levels, the travel distance is based on the average value from the whole region, which may lead to less accurate results. Still, there are some empirical examples of such research [
12].
This paper is structured into four sections: (1) Introduction outlining theoretical concepts and the empirical context in Czechia; (2) Methodology with special attention given to novel approaches, such as network spatial weights based on real-time accessibility; (3) Results as derived from a space-time analysis of unemployment using real-time accessibility; and (4) Conclusions noting the main outcomes of this study.
2. Methodology
In regional unemployment research, only aggregated regional data are often used, such as basic regions for the application of regional policies in the European Union, NUTS 2 regions. However, to study the within-region component of differentiation and spatial aspects in their full scope, more detailed data are needed. We studied unemployment in Czechia. In all analyses, we used municipal data in an extended time series (2002–2019). We used statistics from labor offices in Czechia, which report the number of unemployed. In this study, unemployment is defined as the share of unemployed persons within the economically active population (15–64 age group). Data on the economically active population are available from the Czech Statistical Office on the 31st of December each year. Unfortunately, data from 2012 and 2013 were not available as data in those years were not collected on a municipal level. Importantly, regions in the whole time series were readjusted to the regional structure in 2019 to control for structural changes.
We used methods of spatial autocorrelation and entropy decomposition to study spatial aspects of unemployment [
23]. The spatial autocorrelation was represented by Moran’s
I [
36,
37] and the entropy decomposition by the Theil index [
38]. These two methods are closely methodologically related (for details, see [
23]). The Theil index decomposition enabled us to quantify the share of a selected regional level on the overall variability (between municipalities in this case). We could thus study shift of variability between regional levels. We studied shifts in variability between areas of municipalities with extended powers (AMEP) and NUTS 3 regions to variability between municipalities within these regions. Spatial autocorrelation added information about overall level of clustering of unemployment (global spatial autocorrelation, Moran’s
I) and its spatial representation in the form of local clusters (local indicators of spatial association (LISA) cluster maps). The formulas for both methods (Moran’s
I and Theil index decomposition) can be written as follows:
where
n = number of units,
i = index for individual units,
j = index for regions,
k = number of regions,
y = unemployment mean,
wij = spatial weight matrix. In addition, for
T (overall Theil index),
TB = between-region component of the Theil index and
TW = within-region component of the Theil index. The decomposition, the share of the between-region component on the overall Theil index, can be written as T
B/T. In the Theil decomposition, we used two regional levels: 14 NUTS 3 regions and 206 AMEPs.
To understand the change of spatial autocorrelation over time, we used bivariate spatial autocorrelation [
39]. Bivariate spatial autocorrelation measures correlations of Moran’s
I in time. Specifically, bivariate Moran’s
I was calculated as a regular Moran’s
I, but values from a selected year in each spatial unit (municipalities) were correlated with mean values in the neighborhood in a reference year (spatial lag). Usually, the bivariate Moran’s
I is used for correlation between one variable and the spatial leg of another variable. However, this might overestimate the spatial aspect of the correlation, which is often due to the in-place correlation [
40].
One of the often discussed issues connected with the use of spatial autocorrelation is the representation of space, i.e., spatial weight matrix (
wij). This matrix operationalizes the position and proximity of spatial units [
36,
41]. The selection of the spatial weight matrix is not crucial when general patterns are studied [
23,
42]. However, when studying unemployment, which is strongly influenced by commuting, applying network distances can significantly influence not only the absolute levels of Moran’s
I but also its spatial patterns. Network spatial weights were used in [
43,
44]. In order to generate network spatial weights, we needed to associate each municipality with a point feature class representing both origin and feature destination. To create network spatial weights, we used the travel distance (as a time function) to calculate the weight between all pairs of the municipality. For a more in-depth discussion on geographical spatial weight matrices, see [
45].
In this study, we used distance-based spatial weights and network spatial weights based on real-time distances between municipalities. A point representing each municipality was positioned into a specifically selected location, which was representative of the municipality (compared to often used centroids). These locations were available from the Czech Statistical Office; thus, we were not forced to use centroids. Time accessibility was based on the Czech road network from 2011, and accessibility times were constructed from [
46,
47]. The use of network spatial weights is quite rare in unemployment research. The reason is that, for the construction of network spatial weights, one needs point data, and unemployment studies are usually associated with regional data. However, the use of network spatial weights in unemployment research can be found in [
12]. The comparison of spatial weights based on Euclidean distances and network spatial weights in the Czech regional system is presented in
Table 1. Even though there was a strong correlation between the two methods in all three selected characteristics (percentage of spatial connectivity, average number of neighbors, and maximum number of neighbors), there were still significant differences, specifically, the maximum number of neighbors (along highways). It is important to bear in mind that this similarity is caused by a relatively homogenous Czech road network. The situation may be quite different in countries with less homogenous road networks.
The biggest differences between Euclidean distances and time-based network distances (accessibility distances) were observed in individual cases. An example of a region of neighboring units delimited using both types of spatial weights is depicted in
Figure 1, where the neighboring units using Euclidean distances are compared with those based on time accessibility. The map clearly shows a significant difference between the distance-based spatial weights working with Euclidean distances and network spatial weights based on time accessibility in a real network. For time accessibility delimitation for the whole of Czechia, see [
48]. The network spatial weights affected regional delimitation mostly along important highways and roads, where the average speed is much higher compared to others. Therefore, the neighboring units were stretched along these roads. Network spatial weights can help to mitigate the often-stated bias of Euclidean distance spatial weights.
3. Empirical Evidence in Czechia
In this section, all empirical results are presented. There are two main parts. First, we show results of the Theil index decomposition and spatial autocorrelation (Moran’s I) with a distance-based spatial weight matrix with a threshold distance of 10 km. The significance of differences over time is shown by bivariate spatial autocorrelation. Second, we present spatial autocorrelation using network spatial weights. All results are presented in the time series.
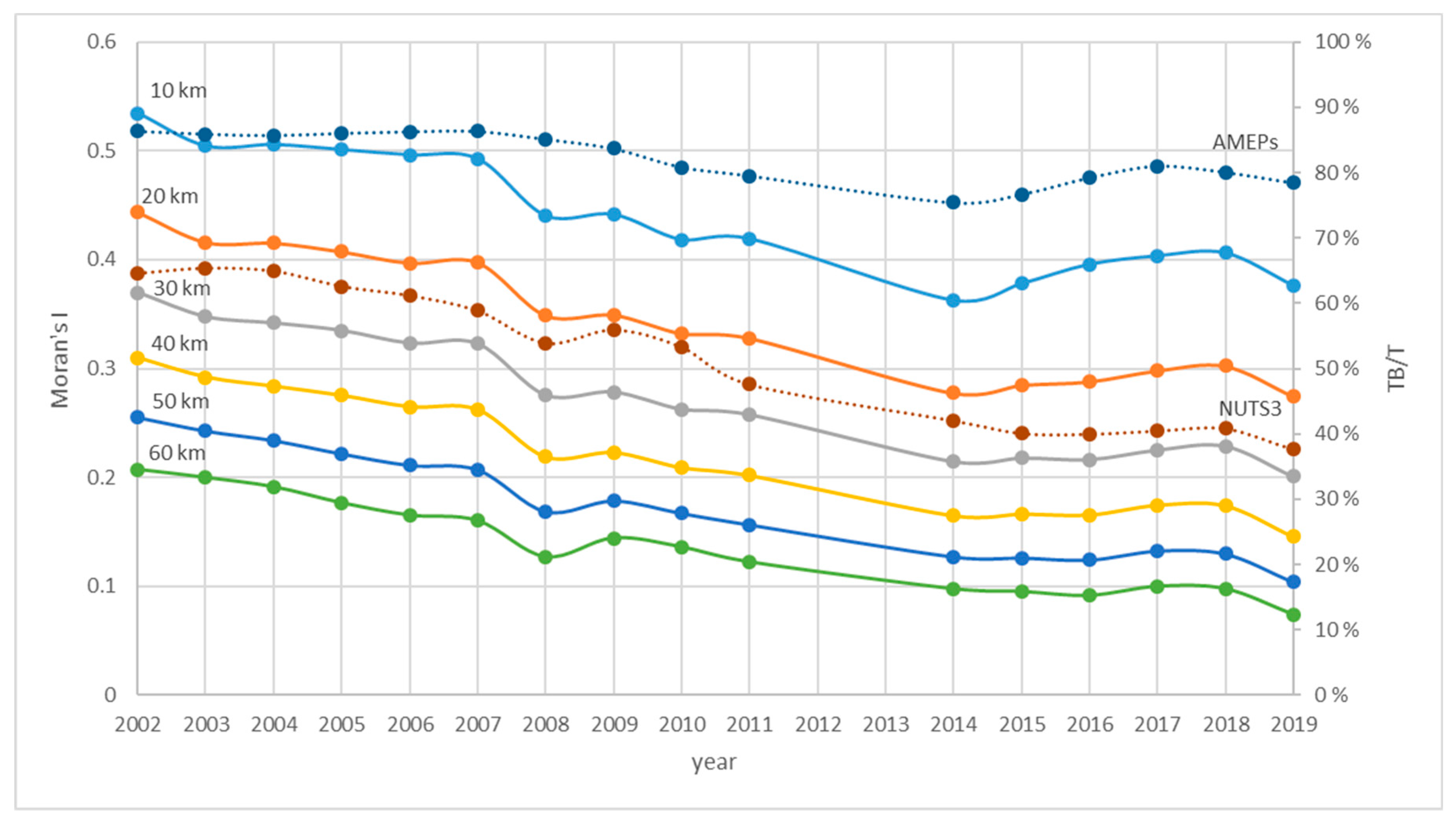
Figure 2 shows the results of the Theil index decomposition on the AMEP and NUTS 3 levels and values of Moran’s
I for spatial weight matrices with threshold distances of 10, 20, 30, 40, 50, and 60 km. From all values, it is evident that both the share of regions on overall disparities (Theil decomposition) and the spatial autocorrelation decreased over time. It also confirms the fact that the Theil index decomposition and spatial autocorrelation are closely related [
23]. Importantly, the decreasing, between-region component of the Theil index (
TB/T) indicates that disparities shifted from between regions to within regions, shifting to lower geographical levels. While the share of between-region variability on the AMEP level decreased steadily by 8 percentage points (from 86% to 78%) in the studied period, it decreased by 27 percentage points (from 65% to 38%) in the case of the bigger NUTS 3 regions. This can be interpreted as a significant increase in the share of the within-region component of variability (differences between municipalities within regions). The tendencies of Moran’s
I confirm this finding because the overall level of clustering, i.e., concentration of similar values in space, decreased.
Besides steadily decreasing values of both Theil index decomposition and Moran’s
I, there is another important observation. The data do not reflect rather dramatic social and economic changes during this period, specifically the economic crisis. However, some changes in the crisis years (2008–2010 in Czechia) can be observed. As overall unemployment rose during this period, we could observe convergence in misery (decreasing regional disparities due to overall bad conditions) [
5]. Nevertheless, even though the absolute levels of unemployment did change during these times, the overall spatial patterns remained stable with only small changes. This finding supports the conclusions of other authors that unemployment is a very stable variable with a high level of inertia [
3,
10,
49,
50].
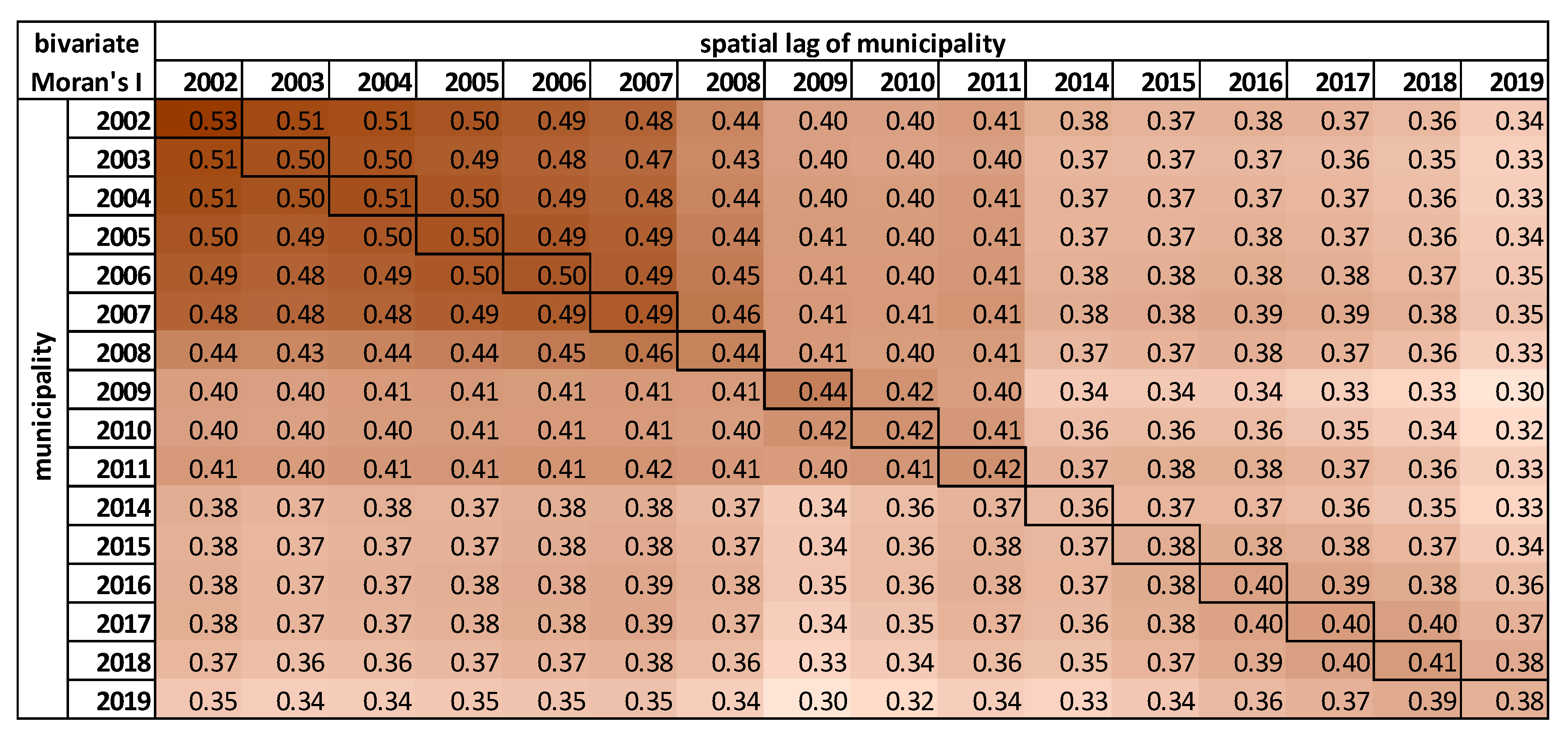
To systematically test the Moran’s
I change over time, we calculated bivariate Moran’s
I. The bivariate spatial autocorrelation helps to quantify the assumption of stability of spatial patterns over time. In
Figure 3, the diagonal values represent values of Moran’s
I in the presented years. Other values in the matrix represent the correlation of Moran’s
I in time. For example, the first value in the 2003 column (0.51) was calculated as the Moran’s
I for the unemployment in municipalities based on values from the year 2002 based on the spatial structure of the corresponding year from the matrix, in this case, 2003. The first value in the 2019 column (0.34) thus represents the Moran’s
I calculated from values in 2013 based on the spatial structure in 2019. When we compared this value with the actual value from 2019 (0.38), the difference was surprisingly low. The bivariate Moran’s
I supported the finding that unemployment spatial patterns have been relatively stable over time.
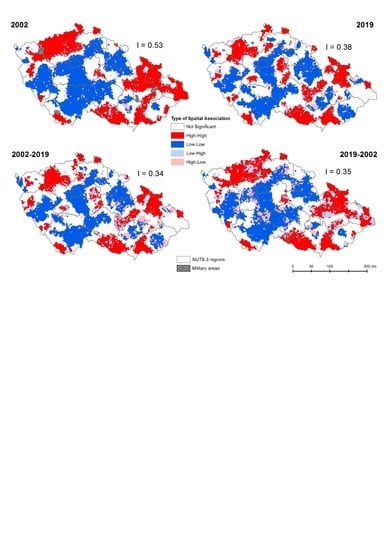
The bivariate Moran’s
I captured the general stability of spatial patterns over time on a global scale for all of Czechia. However, there might be some significant differences at local levels. Thus, we constructed local representation of Moran’s
I as LISA maps (see
Figure 4). LISA is a local representation of spatial clustering, while Moran’s
I quantifies spatial autocorrelation through a single value. LISA cluster maps reveal local spatial clusters and answer important questions, such as where these clusters can be found or what they look like [
35]. Areas with significant spatial clustering of municipalities with above mean (below mean) values of unemployment were visualized as high–high (low–low) clusters. Municipalities that differed in their level of unemployment from their neighborhood were high–low or low–high spatial outliers. We compared the beginning and the end of the studied period, i.e., years 2002 and 2019. The maps clearly documented the stability of not only the overall spatial autocorrelation but also the spatial patterns at the local level. The comparison showed which clusters remained stable over time and which areas had changed the most.
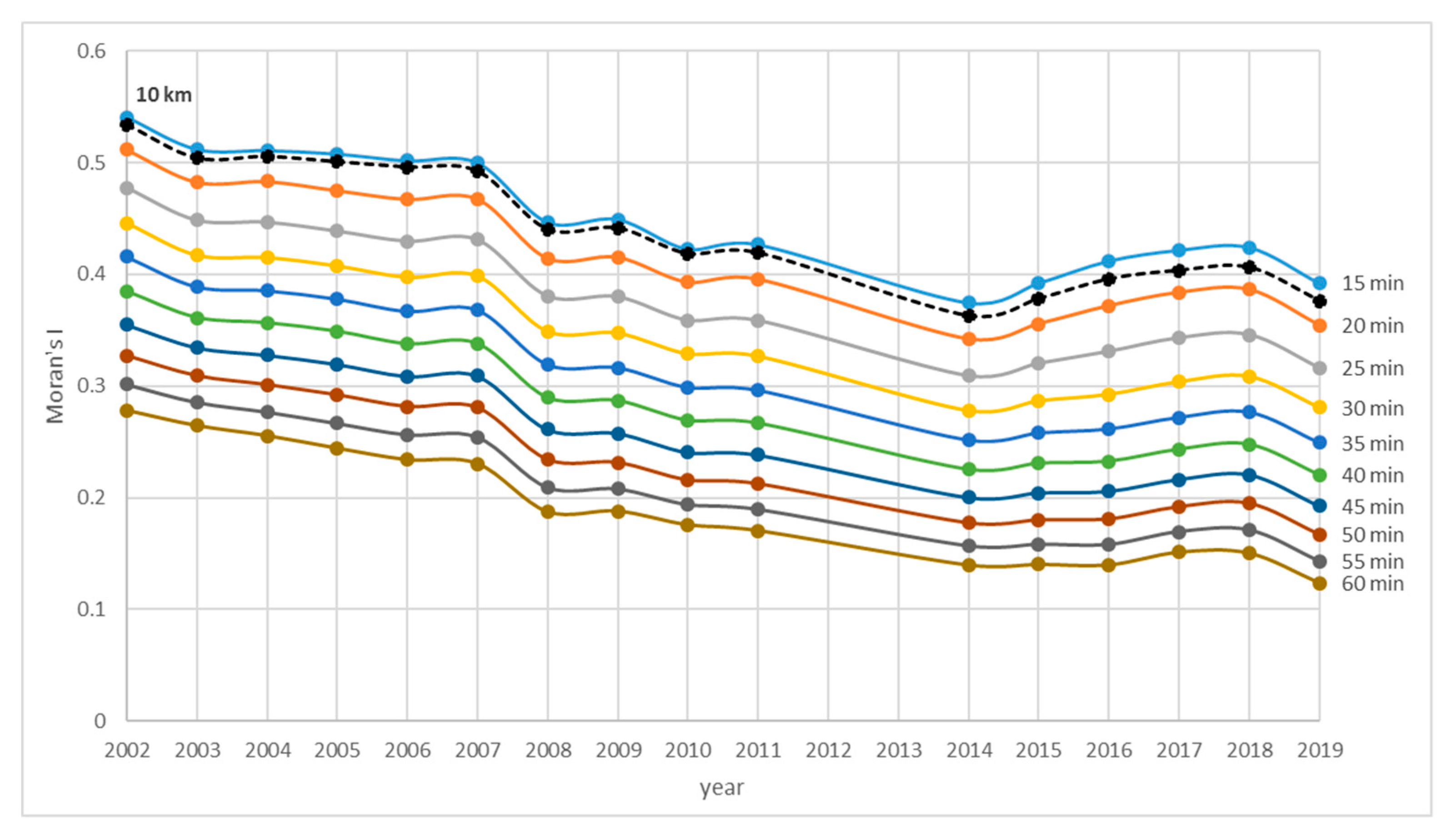
So far, all results were based on the Euclidean distance-based spatial weight matrices. In
Figure 5, the results with network spatial weights based on real-time accessibility are presented. The results were tested for different time accessibility thresholds in 5 min intervals from 15 to 60 min accessibility distances between municipalities. The behavior of Moran’s
I for each value of time accessibility had a very similar pattern to values of Moran’s
I increasing with a decreasing time threshold. This is not surprising as the neighborhood shrinks and more clusters can form with a decreasing time threshold.
However, it is a bit surprising that the values of Moran’s
I calculated using Euclidean distance spatial weights were very similar to Moran’s
I values calculated using network spatial weights (0.95 Spearman’s coefficient; 0.99 Pearson’s coefficient). The similarity is especially surprising given the geography of the neighborhood is quite different for these two spatial weights (see
Figure 1). The interpretation of this outcome is interesting nonetheless. Unemployment spatial patterns can be calculated using only Euclidean distance spatial weights, not taking time accessibility into account. This is important as time accessible data are usually not available. This finding supports the findings in [
51], where the difference between administrative and functional regions was only minimal. Yet, the similarity of results using these two methods has also been affected by the fact that there is quite a dense road network in Czechia. The assumption of similarity of these two spatial weights would have to be confirmed for different countries/regions.
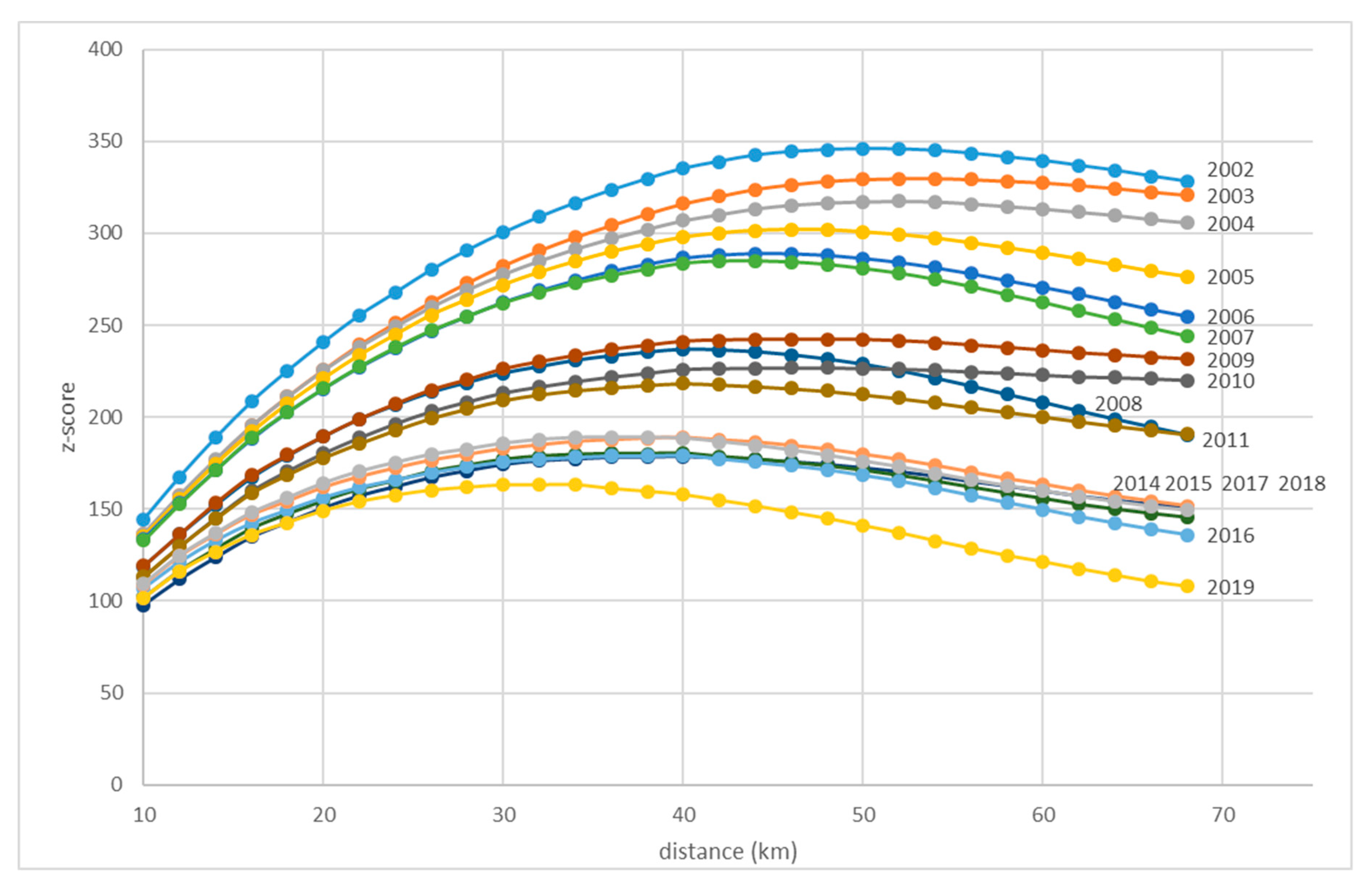
The similarity of results for different time accessibilities can be explained by calculating the z-score significance levels for the spatial autocorrelation. The z-score peaks in
Figure 6 show on which distance (Euclidean) the Moran’s
I was most significant in the studied years. In the case of Czechia, the most significant distances were quite big, even though they did decrease over time (50 km in 2002 vs. 35 km in 2019). When introducing time accessibility spatial weights, one should take the z-score into account. However, Czechia is rather small to use longer time accessibilities as the spatial clusters would be too big to allow for meaningful interpretation. However, using z-score and selecting the suitable time accessibility level may be important when different (larger) countries or regions are studied.
4. Conclusions
The main goals of the study were (i) to study long-term trends in spatial distribution on unemployment (spatial dimension of unemployment) and (ii) to study differences between Euclidean distances and distances as a time function (time accessibility, distance decay). In this section, we present key methodological and empirical findings with some discussion on their policy implications.
Although the use of network spatial weights, which were scarcely used in the empirical context of this study, significantly changed the definition of neighborhoods (which are closer to functional regions constructed using travel to work data), the resulting spatial pattern of unemployment was very similar. This suggests that when studying unemployment, Euclidean distances will suffice for calculating spatial clustering using spatial autocorrelation methods. This is an important finding as time accessibility data are usually not available, and this study has proven that they are not necessary for robust results in certain conditions. However, network spatial weight might be important in the case of differing variables or when studying different regions with less dense road networks. Using network spatial weights, the spatial patterns of unemployment support the hypothesis that, for unemployment in Czechia, the regional structure corresponds with the structure of functional regions. This was shown by comparison of a Theil index decomposition (which works with regions) and spatial autocorrelation (which works with municipalities in this case). This is in line with findings from other authors.
The unemployment spatial patterns proved to be very stable. They were not significantly affected by economic and political changes and shocks (such as economic crises or opening of borders within Schengen). Even when the absolute values of unemployment changed significantly over time, the spatial patterns remained relatively stable. However, a slow yet steady shift of differentiation from macrolevels (variability between AMEP and NUTS 3 regions) to microlevels (variability between municipalities within these regions) was observed. This was documented by the Theil index decomposition as well as measuring the z-scores of Moran’s I. All aforementioned outcomes (relative stability and shift of differentiation to microlevels) are in line with the conclusions of other authors.
The empirical findings may have substantial regional and national policy implications. The significant shift of variability from the between-region component to within-region component suggests that the schemes tackling unemployment should refocus from regional mitigation tools to locally specific tools within the regions. Moreover, regional authorities may be given more flexibility to address the differences between municipalities. The stability of unemployment spatial patterns and the decrease in regional disparities in crises (such as in 2008–2010) indicate that problematic regions do not have to be treated differently during these times, and the regional aspects of state support do not have to be given different priority.
In future research, policy implications deserve more attention. From a methodological point of view, network spatial weights should be tested on different variables as time accessibility can play a much more important role. This approach is especially useful in border studies as bordering regions typically have bigger differences between Euclidean distance and time accessibility distance due to less dense transport infrastructure along the borders, especially in the case of countries from either side of the Iron Curtain.