1. Introduction
Crime has an inherent geographical and temporal quality, because when a crime occurs it happens at a certain place and a certain time [
1]. Since geographic data have a close relationship to time, more and more Geographic Information System (GIS) applications also allow the analysis of spatio-temporal data [
2]. However, it should be noted that when spatio-temporal data are investigated, GIS, as well as other crime analysis tools, have mainly focused on analyzing the geographic component [
3]. As a result, fewer methods are available for temporal analysis as compared to spatial analysis. This is especially true for certain types of crime investigation, such as crime predictive analytics. The aim of this study is to discuss, compare, and evaluate eight different temporal approximation methods using burglary data from Vienna, Austria, in order to improve the quality of the temporal component.
Temporal analysis plays an important role in criminal investigations. An objective comparison of different temporal approximation methods was conducted by [
4]. Their main findings were that results vary based on the type of crime and that the aoristic and the novel aoristic
ext methods perform significantly better than three traditional estimation methods. The research proposed in the current study extends the [
4] approach and includes a larger sample of crime data and two additional novel temporal approximation methods. The main goal of this research is to identify the most accurate method for approximating offense times for apartment-, house-, and car burglaries in Vienna, which is the largest city and capital of Austria. The following eight methods, which are explained in detail below, are compared with each other: (1) start, (2) end, (3) average, (4) random, (5) aoristic, (6) aoristic
ext, (7) retrospective temporal approximation, and (8) extended retrospective temporal approximation. The latter two methods will be abbreviated as RTA and RTA
ext, respectively, in the remainder of this article. In contrast to existing methods, both novel methods (RTA and RTA
ext) include historical burglary crimes with accurately known time stamps in their temporal approximations. This is based on the simple concept that temporal distributions of burglaries stay more or less stable over time and that historical burglaries can be applied to estimate future crimes. The validity of this concept is supported by research on (1) repeat and near-repeat victimization and (2) the forecasting of burglary crimes. Research on repeat and near-repeat victimization has demonstrated that when a burglary occurs at one location, more burglaries than would be expected by chance, will occur at the same location in the near future (repeat victimization) [
5,
6] and/or close in space and time from the initial burglary location (near-repeat victimization) [
7,
8,
9,
10]. Similarly, the forecasting of burglary crimes takes advantage of the fact that burglaries are concentrated in a small number of places [
11] that seem to stay stable over time [
12]. For these reasons, historical burglary data can be used to identify where the highest risk of future victimization lies.
One reason for the slow development of temporal analysis could have been the challenge of presenting and analyzing temporal information in a GIS environment [
13]. Moreover, the limited understanding of the power of time in GIS software has shown the limitation of many GIS packages to cope with this kind of data [
14]. Two additional issues are the lack of appropriate statistics to analyze time patterns in a GIS and the low quality of temporal information for some reported crime data. When crimes are committed without any witnesses, crime data often contain uncertainties regarding time [
4]. This limits such data in the application of spatio-temporal analysis for accurately addressing certain research problems [
14]. Furthermore, the computational power of temporal approximation methods rapidly increases due to a large number of crimes, the temporal resolution (e.g., half an hour bins or shorter), and the complexity of the applied methodology. In the end, the overall outcome of temporal approximation models may not be valid for a long period of time (e.g., a whole year), because crime is a lively process [
15]. Therefore, different scenarios must be tested, to make appropriate predictions.
The main goal of this paper is to investigate which, of eight different temporal approximation methods, most accurately approximates the temporal distribution of a large sample of burglary data. Results are compared with known precise offense times under various scenarios. Evaluations are conducted with a one-hour temporal resolution. To achieve this goal, a key question is how the eight selected temporal approximation methods can be applied and evaluated objectively. This addresses not only the tools and implementation frameworks, but also the process for the implementation workflow (e.g., defining the test scenario, comparison criteria, and the evaluation process, etc.). To achieve this goal, a secondary task in this paper is to evaluate the prediction performance of selected approximation methods regarding offense times for different crime types, including house burglaries, car burglaries, and apartment burglaries. Finally, a third goal is to identify options for combining and/or extending any one of the presented approximation methods to achieve even more accurate temporal approximation methods.
2. Background
Since the late 1970s the spatial dimension of crime has begun to be more explored [
1]. The police, for example, has recognized the inherent geographical component of crime by sticking pins into maps, which are displayed on walls [
16]. This technique is identical to the principle of computer-based GIS applications, where each pin represents a point (e.g., crime location). From that time on, a series of new techniques have emerged. For instance, tools were created that identify spatial patterns and concentrations of crime, or relationships between crimes and the environment where crimes occur. Along with this development, the temporal aspect of crime pattern analysis has received less attention [
3]. Already in 1979, Cohen and Felson mentioned that criminologists traditionally concentrate on the spatial analysis of crime rates, and that they seldom consider the temporal component. As a consequence, [
17] introduced the Routine Activity Approach that describes space and time patterns of offenders, suitable targets, and the absence of capable guardians. This was an important research contribution that introduced a new way of analyzing crime rate trends and crime cycles. Routine activities explain crime patterns and their variations and convergence in space and in time [
17]. The two authors state that criminal acts require likely offenders, suitable targets, and the absence of capable guardians. Moreover, these requirements change in space and time. For example, certain crime types, such as property crimes (e.g., [
18]), show seasonal peaks. These seasonal variations in crime rates are a result of variations in people’s routines over the course of the year [
17,
19]. In addition, fluctuations of daily routines also have an impact on the accuracy of reported offense times. The Routine Activity Approach has continued to be used until today in order to explain temporal variations of crime at different temporal scales, such as the day, the week, the month, or the year (e.g., [
20,
21,
22]).
Reported crime events always have at least one spatial and one temporal characteristic. However, when an offense was committed without any witness, it may be difficult to obtain complete and precise spatial and temporal information [
4]. However, it is important for the police to have precise spatial and temporal properties for each reported crime. Precisely known spatio-temporal data allow law enforcement agencies to improve their understanding of crime patterns and to efficiently distribute their resources [
23]. The police cannot, however, always retrieve accurate spatio-temporal data, because crime events may possess some degree of uncertainty. For example, a supermarket looted at night shows exact spatial information (location of supermarket), but imprecise temporal information, since employees do not exactly know when the crime incident has happened. Because of that, crimes are often reported to not have occurred at a specific time stamp, but within some time interval. In this example, employees would report to the police the earliest and the latest possible times (end of late and beginning of morning shifts, respectively), when the looting could have occurred. Another example are apartment burglaries that are often daytime burglaries and occur when occupants are at work. The time window for apartment burglaries may span several hours. This may be one reason why many police officers seem to know more about where crime happens than when it happens [
24]. Only in cases where the perpetrator is interrupted by the apartment’s guardian during the crime event, an alarm is triggered, or the criminal is captured on tape, the exact time of the offense is known. In general, it is more likely than not that the actual offense time for burglaries is unknown. However, it is beneficial for crime analysts that the start and end times of burglaries, as reported by victims, are noted by the police. These recorded time intervals allow the application of temporal approximation methods. Another work that is related to our research was conducted by [
24]. They investigated 303 thefts of pedal cycles from railway stations with an unknown offense time. Based on the reported time span when offenses occurred and five different temporal approximation methods, the authors predicted the distribution of occurrence times and compared them with the distribution of crimes with known offense times. The results from this analysis provide the police with information about when to patrol the railway station.
Whenever events have an unknown time of occurrence, they have a degree of analytical complexity that makes the analysis of crime more difficult [
7,
14]. Information about when a crime was committed may help the police to figure out who has committed the crime. For this reason, the police apply different methods to approximate the most likely occurrence times of crime incidents with unknown time stamps. Which approximation method the police should select is important, since the choice of the method affects the estimated time stamp and the understanding of spatio-temporal crime patterns [
25].
As mentioned above, GIS analysis of spatial patterning has, in the past, received more attention than temporal analysis. Hollander and colleagues argue that “one reason for this may be the difficulty of representing and analyzing temporal data in a GIS environment” [
26]. For example, when calculating the average of a series of time stamps, circular statistics, instead of classical statistics, need to be applied [
26]. Felson and Poulsen used circular statistics to calculate the “median minute of crime” and the “crime’s daily timespan” [
27]. Three years earlier, Ratcliffe introduced an aoristic temporal weight to better approximate the occurrence times of crimes with unknown or inaccurate time stamps [
14]. This method is discussed together with the other seven approximation methods in more detail below.
3. Temporal Approximation Methods
The eight different temporal approximation methods, applied in this research, are discussed in detail next. The formulae for these eight methods are based on some of the following ten properties:
datestart: denotes the first date on which an offense could have occurred;
dateend: denotes the last date on which an offense could have occurred;
timestart (or tstart): denotes the first time an offense could have occurred on a certain date;
timeend (or tend): denotes the last time an offense could have occurred on a certain date
timeactual (or tactual): denotes crimes with a known occurrence time;
offensestart: denotes the first moment in time, measured in seconds, that an offense could have occurred; it is a combination of both a date and a time, expressed as {datestart, timestart};
offenseend: denotes the last moment in time that an offense could have occurred; it is a combination of both a date and a time, expressed as {dateend, timeend};
offenseduration (or trange): denotes the time duration during which an offense could have occurred, measured in seconds. It is calculated as:
The first approximation method is the start method. It is a naïve (trivial) method, as it simply regards the approximated occurrence time to be the same as
offensestart. In [
24], it is noted that when applying the start method, the analyst assumes that every crime occurred at
tstart and that the estimated time of each crime can be wrong by anything up to the value of
trange. A second quite similar method is the end method. It is another naïve method and works similarly to the start method, but instead regards the offense time to be
offenseend. The average method is the third naïve approximation method that is investigated in this research. It approximates the offense time to be in the middle of
offensestart and
offenseend, as expressed in Formula (2).
The last naïve method applied in this study is the random method. It randomly selects a moment in time within the time span bounded by offensestart and offenseend. Similar to the other three naïve methods, there is nothing that makes the moment in time selected by the random method more probable than any other moments within offenseduration. All four naïve methods usually predict different occurrence times due to their different formulae. In general, it can be expected that the performance of each method shows significant differences, especially if offenseduration covers a long time period. However, it is possible that, for example, the random method accidently selects the middle of offenseduration and thus predicts the same time as the average method. To better compare the results from each method, approximated times are often assigned to certain time slots. The length of the time slots is defined by the temporal resolution of the study and are often 30 or 60 min long. This means that the approximated offense time is assigned to one of 48 or 24 time slots, in the case of 30- or 60-min time slot lengths, respectively. For time slot lengths longer than one hour or, for offenseduration, less than one hour, the temporal approximation outcomes may not significantly differ between these four different naïve methods.
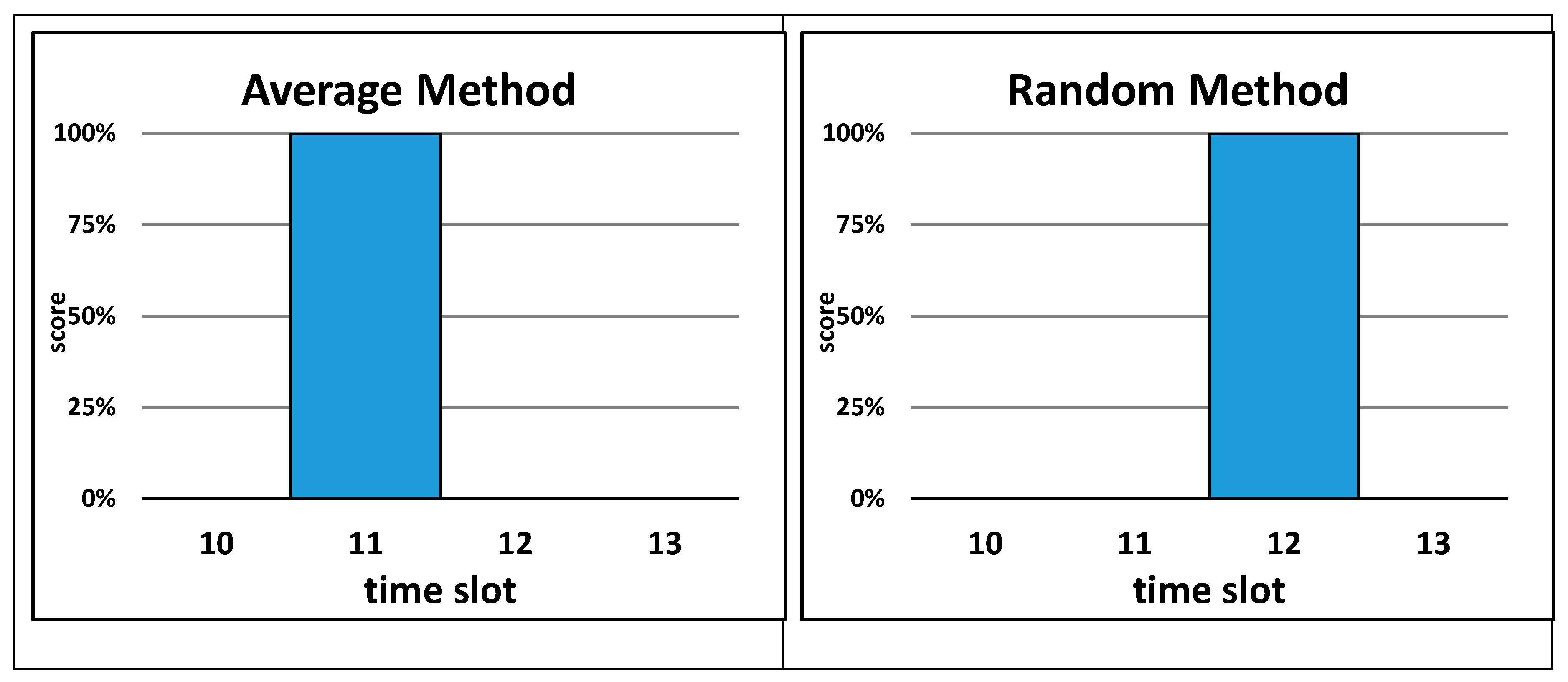
To further the understanding of the four naïve approximation methods, the following fictive example is provided. Assume that an apartment burglary was reported to have occurred sometime between 10:45 and 13:10. For this example, the start method defines 10:45 as the actual occurrence time, while the end method defines 13:10 as the real occurrence time for this crime event. For the average method, the approximated time is 11:57 and for the random method it is calculated to be 12:14. For this fictional example, the four naïve methods calculate four different approximated times. We now assign each approximated time to a temporal resolution of one-hour time slots. For the start method, the approximated time of 10:45 is assigned to the time slot 10, ranging from 10:00 to 10:59. For the end method, the approximated time falls into time slot 13, for the average method into time slot 11, and for the random method into time slot 12. Similar to the originally approximated times, the results of the four naïve methods are assigned to four different time slots (
Figure 1). If the approximated time falls into a specific time slot, then this slot receives the probability of 1 (or 100%), because it is approximated that the probability of this crime to happen in this time slot is 100%. All other time slots for the same approximation method receive a probability value of 0 (or 0%) (
Figure 1).
In addition to the four naïve approximation methods, two different aoristic temporal approximation methods are applied in this research. The standard form is called aoristic [
3] and the enhanced or extended form is called aoristic
ext [
4]. Their functionality is more complex than the naïve methods. The results from the two aoristic methods are probability (percentage) values associated with each time slot that are either 30 or 60 min long.
The aoristic method assigns each 30- or 60-min time slot of the
offenseduration (see Formula (1)) the same probability score. This value is calculated by dividing 1.0 by the total number of time slots (
n) (see Formula (3)). The same probability value is assigned to each time slot, whether slots are fully or partially covered by
offenseduration.
The aoristic
ext method is similar to the standard aoristic method, however it considers whether time slots are fully or only partially covered when calculating the probability value. The aoristic
ext method first calculates the
offenseduration in minutes (see Formula (1)). Next, the probability score for each (30 or 60 min) time slot is calculated by dividing the coverage of that time slot,
coverage(i) (0–30 or 0–60 min), with
offenseduration, as shown in Formula (4). The sum of the probability scores for all time slots must always be equal to 1.0 [
4].
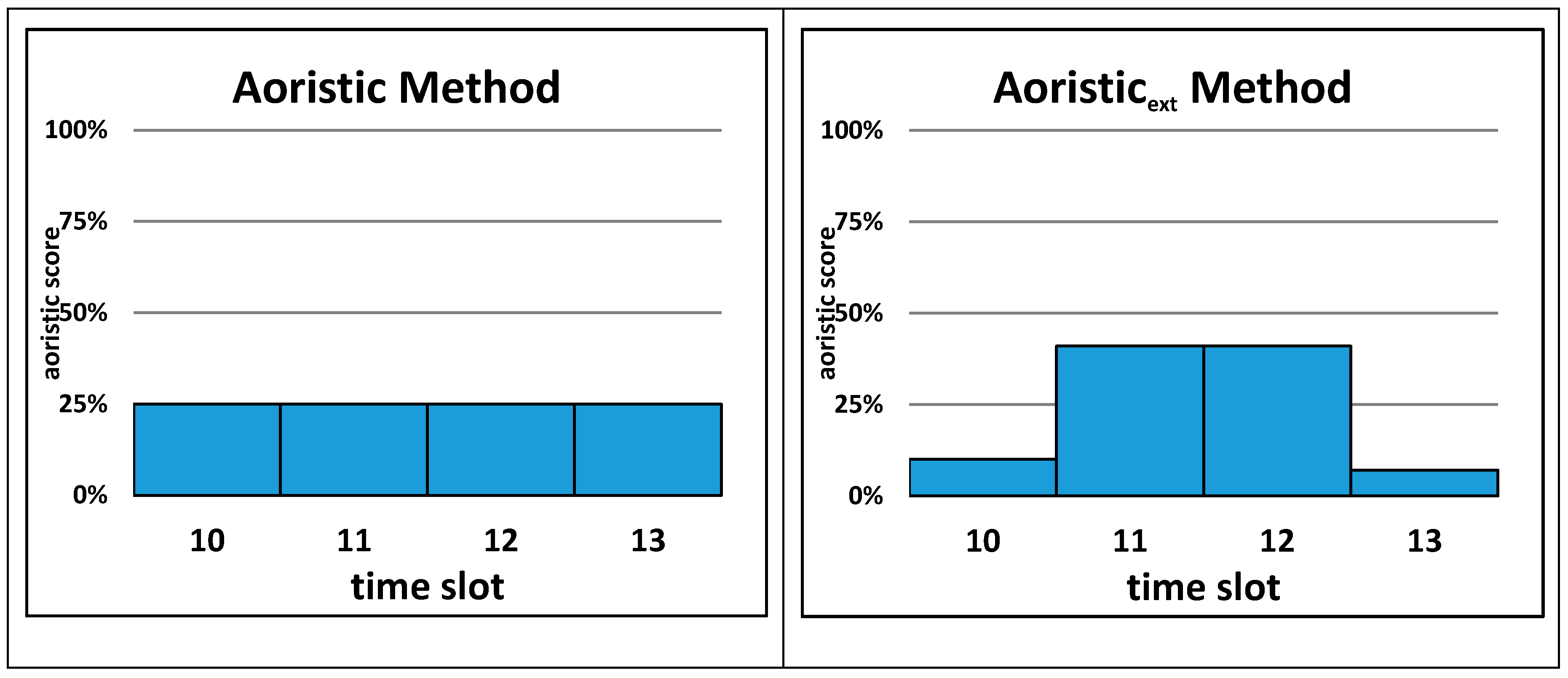
Similar to above, both aoristic methods are discussed with the same fictional example of an apartment burglary reported to have occurred sometime between 10:45 and 13:10. In the case of the aoristic method, the duration of the time when the burglary happened extends over four hours, when using one-hour time slots. The probability value assigned to each time slot is calculated as 1 divided by 4, which results in a probability value of 0.25 (25%) (Formula (3)). The same probability value of 0.25 (25%) is assigned to each of the four one-hour time slots. The aoristic
ext method uses the same four one-hour time slots, but these slots do not all receive the same probability score. First, the exact
offenseduration in minutes is calculated using Formula (1). This results in 145 min (15 + 60 + 60 + 10). In the next step, the probability score for each time slot is calculated as follows (see Formula (4)): probability score
1 = 15/145 = 0.1 (10%); probability score
2 = 60/145 = 0.41 (41%); probability score
3 = 0.41 (41%); probability score
4 = 10/145 = 0.07 (7%). To verify the result, the sum of all four probability scores should be equal to 1, which is true: 0.1 + 0.41 + 0.41 + 0.07 = 1.0.
Figure 2 shows the results of this fictional example for both aoristic methods (aoristic and aoristic
ext). The main difference of the two aoristic methods compared to the four naïve methods (
Figure 1) is that both aoristic methods can assign probability (percentage) scores to more than one time slot, while all naïve methods assign a score of 1 (or 100%) to only one time slot.
The first of the two novel approximation methods introduced in this research is the retrospective temporal approximation (RTA). While the main idea behind this research is to refine the time period (between the starting and ending time stamps) within which a crime has happened, the RTA method builds on the simple concept that temporal distributions of crimes stay more or less stable over time. This means that historical crimes with accurately known time stamps can be applied to estimate future crimes. The length of the retrospective period of historical crime data with known occurrence times may vary, but it makes sense to extend the length over several years and always include the most recent data. The length of the retrospective period should also be long enough to collect a large sample. In this research, the RTA method applies a four-year retrospective period (2009–2012) immediately preceding a three-year observation period (2013–2015). The calculation of the probability (percentage) scores for the RTA method is straightforward, as the exact same hourly probability scores from the retrospective period are applied to the observation period.
The last temporal approximation method is the extended retrospective temporal approximation (RTAext). It is a novel and hybrid approach that combines the RTA concept with the aoristicext method. First, a time series of historical crimes with exactly known time stamps is constructed. The relative frequency for each time slot (e.g., one hour) is used as the basis for the RTAext method. The main idea of the RTAext is to “refine” probabilities assigned to time slots from crimes with unknown occurrence times from the observation period with relative crime frequencies from a retrospective time period with precisely known occurrence times. It makes sense to select a retrospective time period that is equal in length or longer than the observation period. Obviously, different combinations of (1) calculating probability scores for the observation period (aoristic or aoristicext), (2) time slot lengths, and (3) lengths of the retrospective period, can been applied. In this research, the RTAext method (1) combines aoristicext probability scores with probability values derived from a retrospective time period that includes crimes with accurately known time stamps, (2) uses a one-hour time slot length, and, (3) similar to the RTA method, applies a four-year retrospective period (2009–2012) immediately preceding a three-year observation period (2013–2015). Since the RTAext method is novel, no reference or published criteria exists as how to determine the best combination of these three parameters. The best combination may also depend on the crime type and the study area.
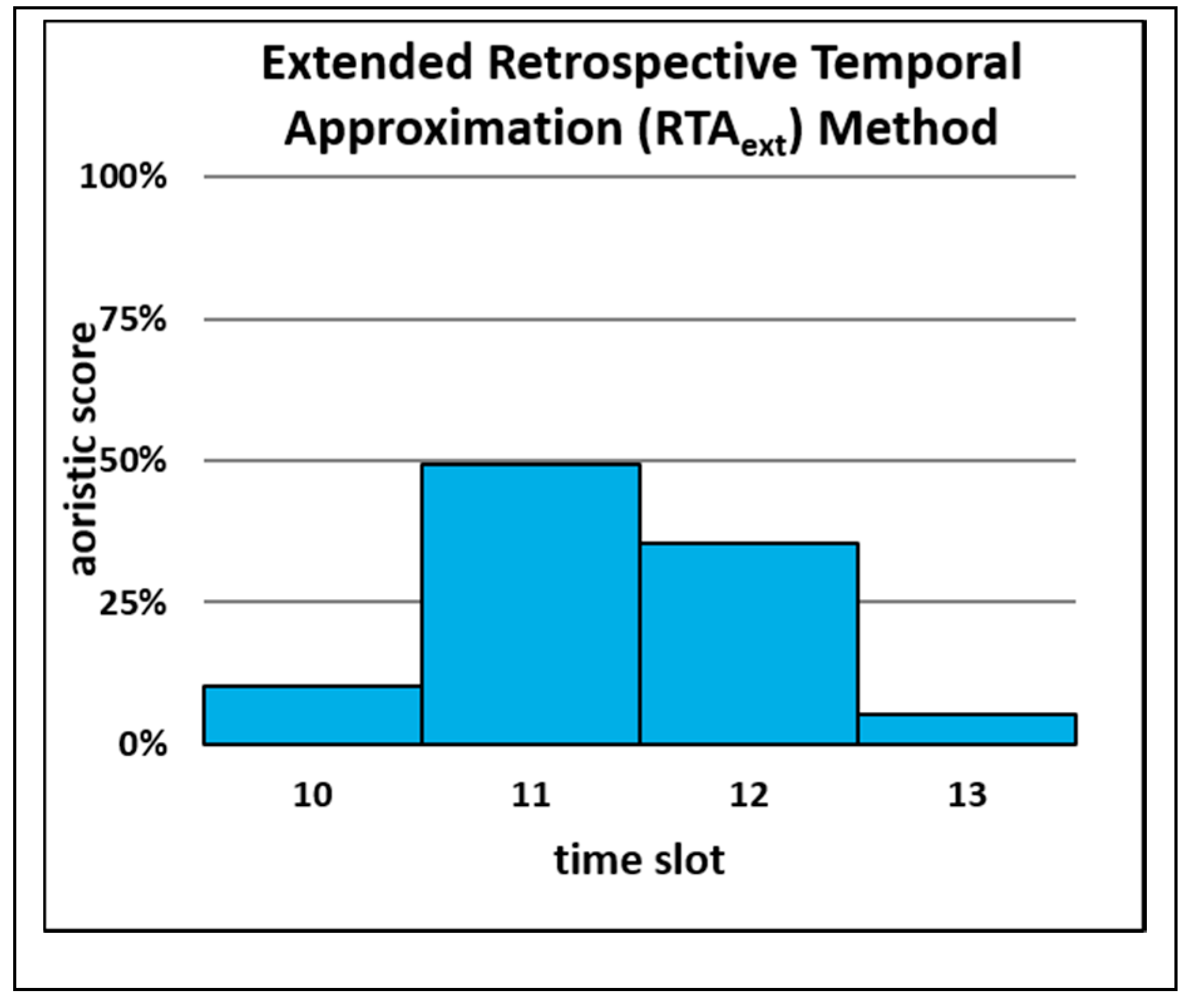
The calculation of probability (percentage) scores for the RTA
ext is demonstrated with the same fictional example of an apartment burglary reported to have occurred sometime between 10:45 and 13:10. Similar to the RTA method, apartment burglaries with precisely known temporal information from the last three years have been collected and are distributed as follows: time slot
10 (10:00 to 10:59): 7.02%; time slot
11 (11:00 to 11:59): 8.39%; time slot
12 (12:00 to 12:59): 5.98%; time slot
13 (13:00 to 13:59): 5.15%. These percentage values, in the form of probabilities, are used as weights and multiplied with aoristic
ext probability scores. The resulting products represent the new RTA
ext probability scores and are calculated as follows: probability score
1 = 0.1 × 0.0702 = 0.00702; probability score
2 = 0.41 × 0.0839 = 0.0344; probability score
3 = 0.41 × 0.0598 = 0.02452; probability score
4 = 0.07 × 0.0515 = 0.0036. After the multiplication, probability scores are standardized (probability score
(i) / sum of all probability scores), so that all probability scores sum up to 1. The final probability scores are: score
1 = 0.101, score
2 = 0.495, score
3 = 0.353, and score
4 = 0.052 (
Figure 3).
A visual comparison across the results of all eight temporal approximation methods (
Figure 1,
Figure 2 and
Figure 3) reveals that each method, introduced in this study, leads to a different result based on the one fictional example. The main goal in this research is to identify the most accurate of these eight approximation methods, applied to a large crime data set. The accuracy of each approximation method is evaluated by two different measures, both of which have been previously applied by [
4] in a similar study. The first evaluation measure is the Euclidean distance, which calculates the distance between two distributions, namely the estimated and the observed distributions. The calculation is based on all estimated and observed probability value pairs, each of one-hour length, over a 24-h period. In other words, estimated probability values for all 24 hourly time slots from 0:00 am (time slot 0) to 23:59 pm (time slot 23) are compared in a pairwise fashion with observed probability values for the same 24 hourly time slots (i.e., the estimated probability value for time slot 0 is paired with the observed probability value for time slot 0; the estimated probability value for time slot 1 is paired with the observed probability value for time slot 1, and so on) (Formula (5)).
where,
yest is the estimated probability from the approximation method and
yobs the observed probability of the reference data with accurately known time stamps. The lower the Euclidean distance, the more similar estimated and observed distributions are to each other, and vice versa.
The second evaluation measure is the Pearson’s chi-square (
Χ2) or goodness-of-fit statistic, which is used to investigate how well the estimated distribution correlates with the observed distribution [
28]. Similar to the Euclidean distance, the calculation of the
Χ2 statistic is based on all observed and estimated probability value pairs, each of one-hour length, over a 24-h period (Formula (6)):
where
yest is the estimated probability from the approximation method and
yobs the observed probability of the reference data with accurately known time stamps. The lower the
Χ2 statistic is, the more similar the estimated and observed distributions are to each other, and vice versa.
4. Study Area and Crime Data Set
The crime data set for this research was provided by the Criminal Intelligence Service Austria, which is the name for the Federal Police in Austria. It included all reported apartment, car, and house burglaries that were committed in the city of Vienna, Austria over a seven-year period (2009–2015). Vienna is the capital and the largest city in Austria. The crime data set was extracted from the Security Monitor database, in which all reported criminal cases in Austria are stored and which mostly serves as a basis for analysis for all law enforcement personnel in Austria [
29]. This database is used for preventing, tracking, and predicting criminal activities.
The complete data set included a total of 141,905 reported crimes. Upon further inspection, we identified 6161 crime records that were lacking information about the crime type and, for this reason, were excluded from further analysis. This reduced the data set to 135,744 crimes. Before proceeding with the analysis, the entire dataset was searched for missing information (e.g., no street name included in a crime record) or incorrect location (e.g., crime located outside of the study area). In addition, all crimes with an offenseduration longer than 24 h were also excluded from further analysis. This reduced the number of crimes further and resulted in a data set of 105,578 reported crimes. This total number of reported crimes included 37,474 apartment, 59,997 car, and 8107 house burglaries. The cleaning and preparation of the collected crime data set proceeded with MS Excel 2016 and the Spatial Analyst module in ArcGIS 10.4.
This crime data set is split into two parts, a “retrospective period” from 2009–2012 and an “observation period”, covering the remaining three years (2013–2015) (
Table 1). All eight temporal approximation methods are analyzed with crime data from the observation period. This period includes both crime events with precise and crime events with imprecise time stamps (
Table 1). Crimes with precisely known time stamps have an
offenseduration equal to 0, that is, the crime victim and the police know exactly when the crime has occurred. Crimes with imprecisely known time stamps are all crimes that have an
offenseduration greater than 0. All eight temporal approximation methods were applied to this latter data set to estimate the distribution of occurrence times. In contrast, the crime data set with precisely known time stamps for the three-year period from 2013–2015 is used for the evaluation of the results from all temporal approximation methods. From the retrospective period (2009–2012), only crimes with precisely known time stamps (
offenseduration equals to 0) are used either as the reference data for the RTA method, or as weights for the RTA
est method (
Table 1). For the other six approximation methods, crime data from the retrospective period are not used at all.
The final data set for both the retrospective and observation periods used in this analysis includes 45,789 burglaries. The crime type with the highest number of incidents is car burglaries (23,809), followed by apartment burglaries (17,871), and house burglaries (4105) (
Table 1). Interestingly, for the evaluation data (number of crimes with precisely known time stamps from the observation period), apartment burglaries have the highest number of incidents (2212), followed by car burglaries (1585), and house burglaries (712) (
Table 1). In the analysis that comes next, all eight temporal approximation methods are applied to each of the three crime types (apartment, car, and house burglaries) separately and estimated occurrence times are compared to observed occurrence times based on 60-min time slots.
5. Results
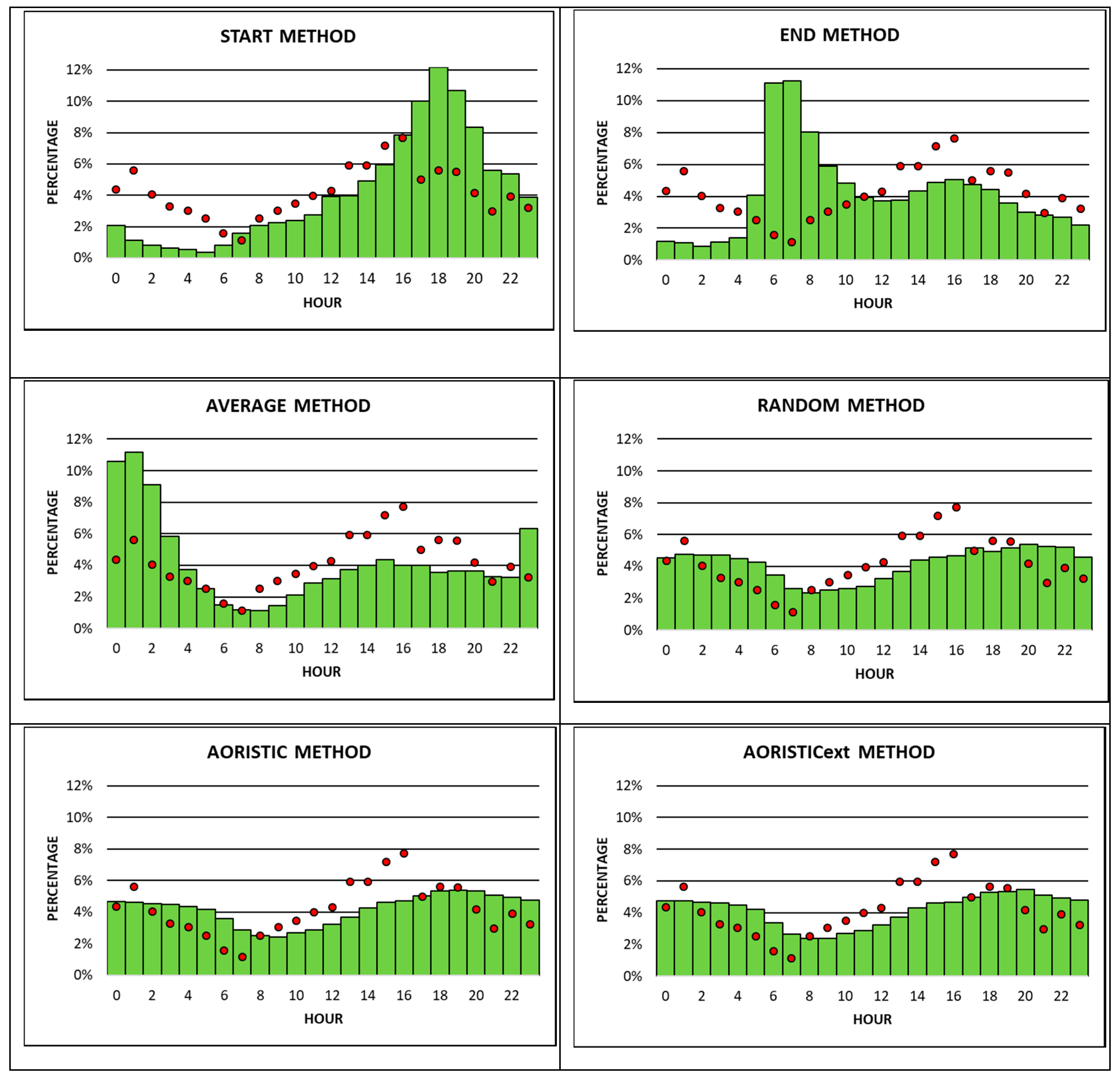
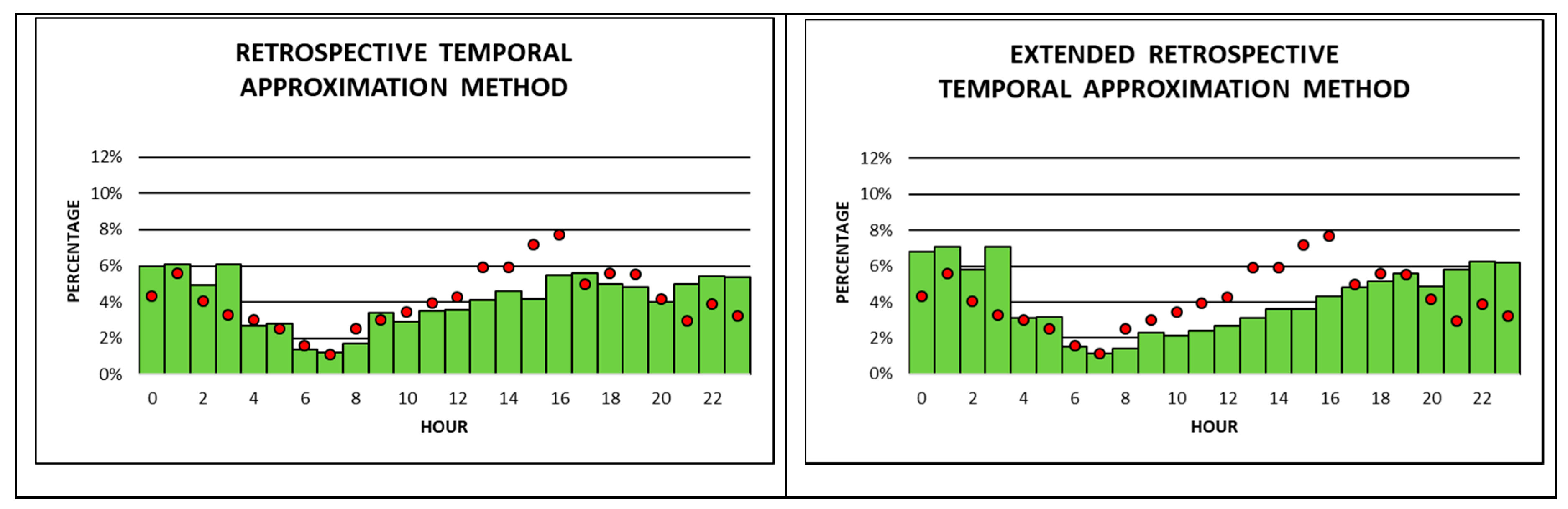
Results from the first set of analyses show occurrence times for each of the three burglary types estimated from the eight approximation methods for 60 min time slots across a 24-h time period. Included in the same results are the distributions from the three burglary types’ evaluation data sets (2013–2015), allowing the visual comparison of differences between the estimated and observed occurrence times (
Figure 4,
Figure 5 and
Figure 6).
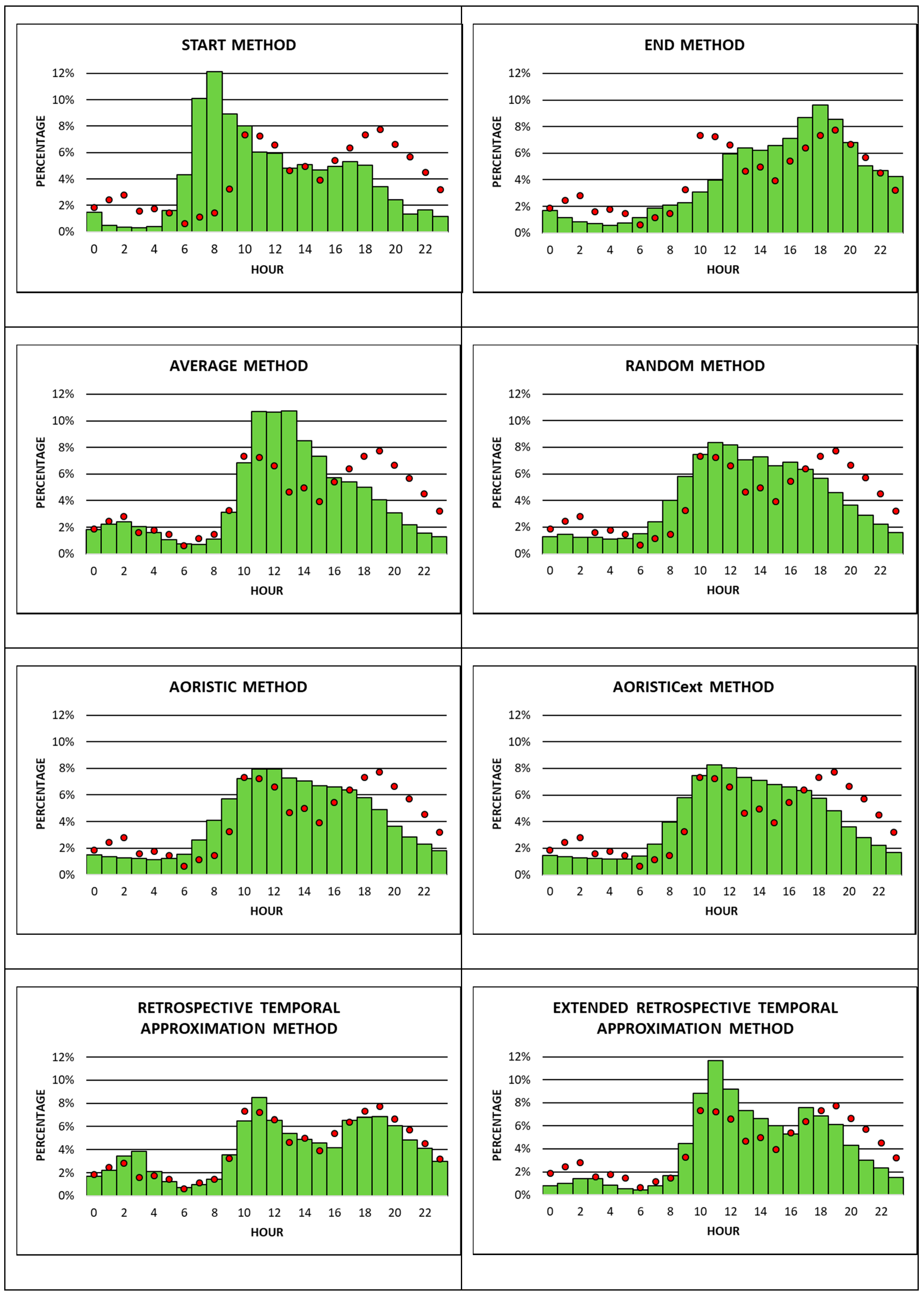
Figure 4 compares the occurrence times from two subsets of apartment burglaries with each other. The first are observed occurrence times based on apartment burglaries with known time stamps. The second are estimated occurrence times, derived from seven different approximation methods for apartment burglaries, with imprecisely known time stamps. The RTA method is the only exception, since it does not apply estimated occurrence times from an approximation method. Instead, it employs crimes with precisely known time stamps from the retrospective period (2009–2012) as the second apartment burglary subset that observed occurrence times from the observation period (2013–2015) are compared to.
Not surprisingly, observed apartment burglaries are lower during the night, with a minor peak between 2 am and 3 am, and higher during the day, between 10 am and 11 pm. The increase in the number of burglaries during the day shows two major peaks in the late morning from 10 am till 12 noon and in the late afternoon/early evening from 7 pm till 8 pm. Between 7% and 8% of all apartment burglaries during the entire 24-h time period happen in each of these three 60 min time slots. The peak in the late morning may be due to the fact that most apartments are empty and without guardians, since residents may be at work, school, or running errands. The peak in the late afternoon/ early evening is typical for spring and fall in Austria due to an increase in so-called “dusk burglaries”, which can be observed every year. During this time, inhabitants of apartments may still be at work, doing leisure activities, shopping, visiting friends, etc., so they cannot act as guardians of their own apartments. In addition, criminals may commit burglaries during this time of the day, because it is more difficult to identify them at dusk, however there is enough light to commit the crime. Finally, observed occurrence times show a minor peak at night between 2 am and 3 am (about 3% of burglaries), when inhabitants are at home and sleeping (
Figure 4).
All approximation methods do a reasonably good job in estimating low occurrence times for apartment burglaries during most of the night and high occurrence times during most of the day. However, the RTA and the RTAest are the only two approximation methods that pick up the two peaks in observed occurrence times during the day and late evening, and the minor peak between 2 am to 3 am. All of the other six approximation methods may correctly identify only one or two of these significant peaks. Overall, the RTA method seems to best match the observed with the estimated (in this case crimes with precisely known time stamps from the retrospective period) occurrence times of apartment burglaries.
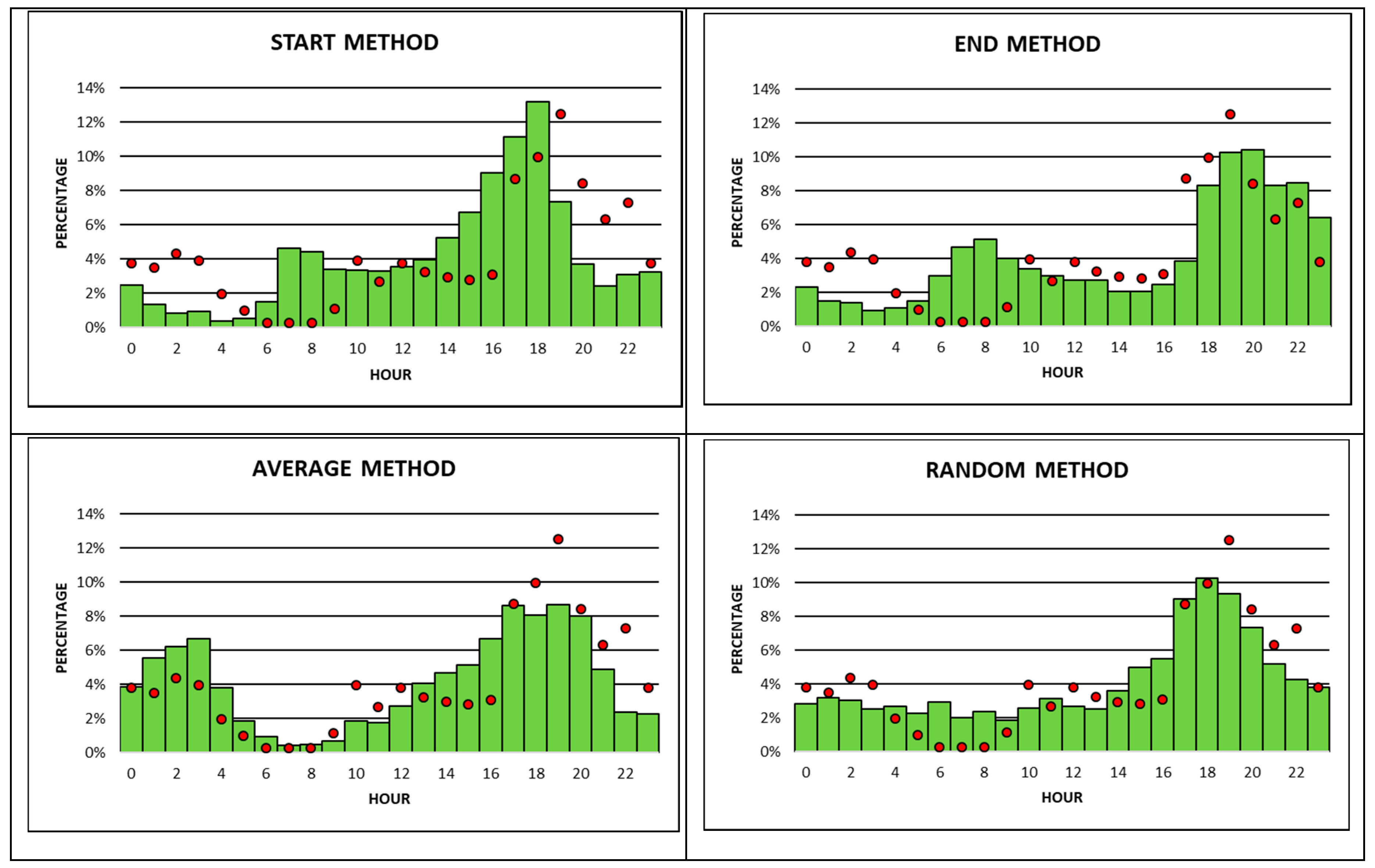
While observed occurrence times for apartment burglaries happen mostly during the day with two significant peaks shortly before noon and in the late afternoon/evening, observed car burglaries exhibit only one significant peak of almost 8% during the day in the late afternoon from 4 pm to 5 pm (
Figure 5). Compared to apartment burglaries, car burglaries also show higher percentages of observed occurrence times during the night, with a peak of almost 6% between 1 am and 2 am. Observed occurrence times for car burglaries are lowest from 7 am to 8 am at less than 1% (
Figure 5). With the possible exception of the RTA method, none of the other seven temporal approximation methods do a good job in approximating observed occurrence times, because neither of them detects the two significant peaks (4 pm to 5 pm and 1 am to 2 am) in the right place. The start, end, and average methods correlate the least with observed occurrence times. Similar to apartment burglaries, the RTA method seems to also be the best approximation method for car burglaries. However, the RTA
ext method does not perform much better than the random, aoristic, and aoristic
ext methods (
Figure 5). One possible reason may be that the number of apartment burglaries with accurately known time stamps is twice as high as the number of car burglaries with accurately known time stamps. This fact may lower the quality of weights calculated from retrospective car burglaries with accurately known time stamps applied to the RTA
ext method. In addition, the average
offenseduration for car burglaries is longer than for apartment burglaries. This may be the reason for the level of accuracy in approximating car burglaries (with the exception of the RTA method) being lower than for apartment burglaries.
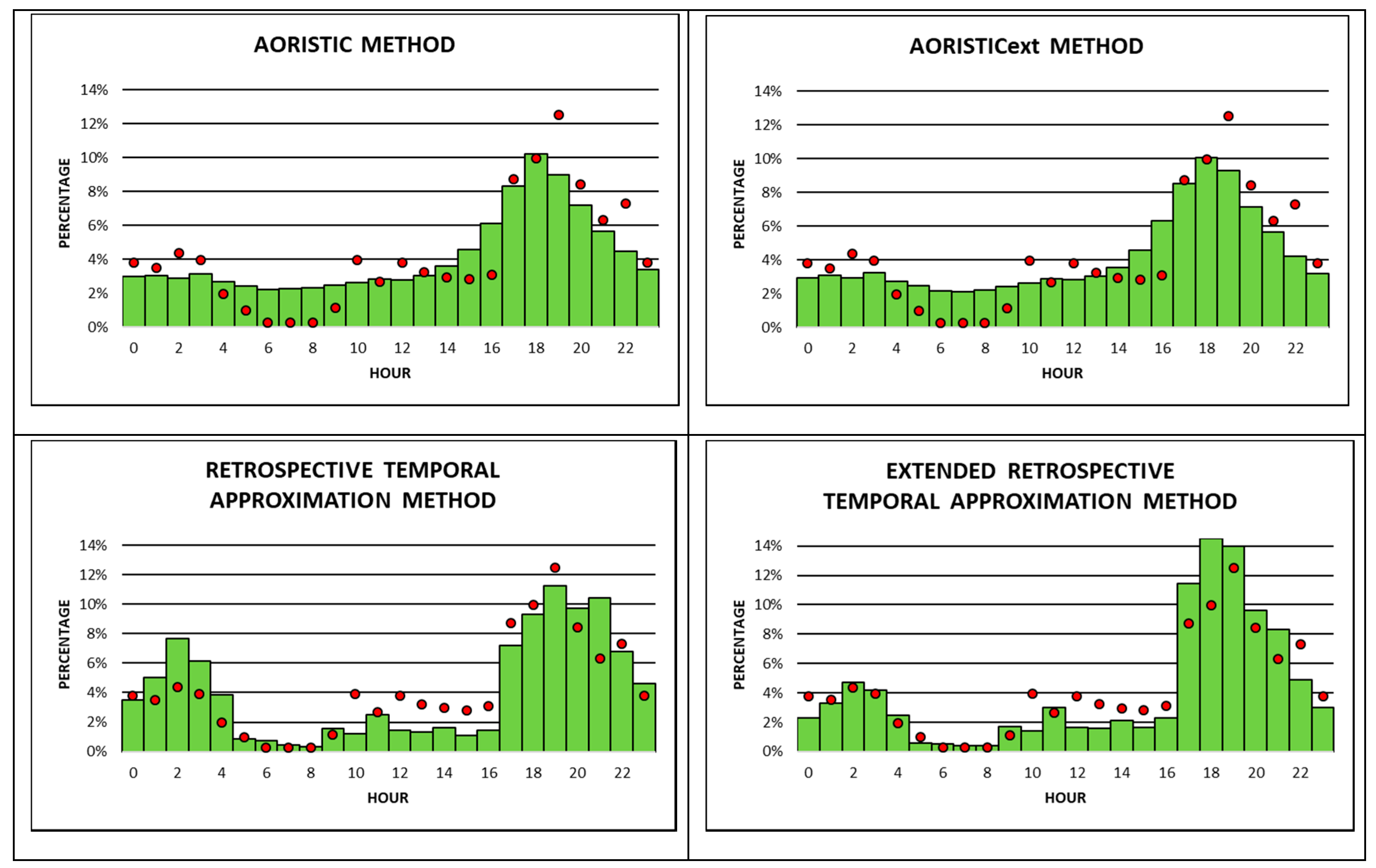
The final comparison between observed and estimated occurrence times is done for house burglaries (
Figure 6). This is by far the smallest of the three crime type data sets examined. Unexpectedly, differences in observed occurrence times between apartment and house burglaries can be detected. House burglaries show the highest percentage of observed occurrence times of more than 12% between 7 pm to 8 pm, which is most likely associated with the phenomenon of dusk burglaries during spring and fall. In contrast to apartment burglaries, house burglaries do not exhibit a peak in observed occurrence times between 10 am till 12 noon. However, house burglaries show a more accentuated peak (compared to apartment burglaries) between 2 am to 3 am, at more than 4%. The lowest likelihood for houses to be burglarized is between 6 am and 9 am, which is similar to apartment burglaries.
Overall, both the RTA and the RTAext methods correlate the closest among all eight approximation methods with observed occurrence times. Both methods do a good job in estimating the high percentages of occurrence times in the evening around 7 pm to 8 pm, and they also estimate highly accurately the lowest percentages of occurrence times between 6 am and 9 am. Only one other method, namely the average method, shows a similarly good fit between estimated and observed occurrence times during 6–9 am. The remaining five methods do not do a good job in estimating observed occurrence times for house burglaries.
The results of the evaluation of the eight different temporal approximation methods are included in
Table 2. In general, the novel RTA method outperforms all other approximation methods in the case of apartment and car burglaries, with (by far) the lowest Euclidean distances and
Χ2 values. The results are mixed for house burglaries with the aoristic
ext method showing the lowest Euclidean distance and the RTA
ext method the lowest
Χ2 statistic. The results for the RTA
ext method are not as good as for the simple RTA method, however they are similar to the best performing existing approximation methods across both evaluation measures and crime types. It seems that combining aoristic data from the observation period with historical burglaries with exactly known time stamps makes temporal approximations worse than solely using retrospective burglary crimes. Three of the four naïve methods (start, end, and average) perform the poorest, with one exception being the end method for apartment burglaries that, surprisingly, depicts the second lowest evaluation values just behind the RTA method. This result may have purely happened by chance. The results, in general, support the visual interpretation comparing observed with estimated occurrence times in
Figure 4,
Figure 5 and
Figure 6. Overall, the two evaluation statistics indicate that both novel RTA methods, especially the simple RTA, are at least equal or clearly superior to the other six existing temporal approximation methods (
Table 2).
6. Discussion and Future Research
While many applications in crime analysis require accurate temporal information, unfortunately, for many crime types such accurate temporal information is not always available. Contributing to research that attempts to derive more accurate temporal information from crime data that possesses inaccurate time stamps was the main motivation for writing this article. Using a data set of 105,578 crimes across three crime types from the city of Vienna, Austria, eight different temporal approximation methods were applied to more accurately calculate time stamps for crimes with inaccurate temporal information. Three different crime types, including apartment, car, and house burglaries, were analyzed. Of these, car burglaries possessed the least accurate and house burglaries the most accurate temporal information. Six of the eight temporal approximation methods were existing methods that included four naïve methods (start, end, average, and random), in addition to the aoristic and aoristicext methods. The other two were novel temporal approximation methods that were introduced in this research for the first time. They are referred to as retrospective temporal analysis (RTA) and extended retrospective temporal analysis (RTAext) methods. Both are based on the idea that temporal distributions of crimes stay more or less stable over time. In the context of this research, it meant that burglary crimes from the retrospective period with accurately known time stamps (2009–2012) possess a temporal distribution very similar to the distribution of the observed burglary crimes defined as the evaluation data (2013–2015). The RTA method directly applied this idea and used solely historical burglary crimes with accurately known time stamps to “estimate” future burglary crimes. The RTAext method, on the other hand, enhances the aoristicext method results with probability values derived from historical crime data with accurately known time stamps. Results from the eight temporal approximation methods are evaluated with the Euclidean distance and the Χ2 statistic. In general, both novel RTA methods, especially the simple RTA, are at least equal or clearly superior to the other six existing temporal approximation methods. This means that accurately known time stamps from historical burglary data may be able to estimate future time stamps for burglary crimes for which accurate temporal information is not available. Of course, more in-depth research needs to be conducted in order to find out whether this finding can be replicated in future studies.
In this study, it was assumed that burglary crimes which possess accurately known time stamps are a representative sample of the population of all burglary crimes (with and without accurately known time stamps). Similar approaches of using a subset of all offenses for evaluation purposes have been used in previous studies (e.g., [
4,
24]). For example, [
4] argues that the motivation behind this assumption is that the exact offense time is determined by external events, such as alarm records, witnesses or the plaintiffs being home during the offense. In general, a potential bias in the evaluation (sample) data in our research was reduced as much as possible by collecting large sample sizes that span a multi-year period (2013–2015). Sample sizes for apartment, car, or house burglaries with accurately known time stamps account for 15.19%, 7.34%, and 22.31%, respectively, of all apartment, car, or house burglaries. These sample sizes are higher than the 10% reported by [
4]. In addition, probability values were aggregated to one-hour time slots, further reducing the potential bias in the evaluation data. While the true temporal distribution for each of the three burglary types over a 24-h period will never be precisely known, it is believed that the evaluation (sample) data selected for this research represents, as accurately as possible, the true temporal distribution.
To the best knowledge of the authors of this research, no publicly available documentation or research exists about the temporal distribution of burglary crimes over a 24-h period in Vienna, Austria. The authors searched through all yearly crime statistics reports published on the website of the Austrian Federal Police (
https://bundeskriminalamt.at/501/start.aspx) from 2006 to the most recent one in 2018, but did not find this information. The work conducted in [
22] seems to be the only other existing research from Vienna that investigated the temporal distribution of a crime type over a 24-h period. In particular, [
22] researched whether near-repeat patterns of street robberies exist by weekdays and by time of day. Results from the research presented here seem to support the Routine Activity Approach [
17]. Burglary crimes are highest during the day and lowest during the night and thus reflect the fluctuations of the daily routines of occupants of apartments and houses. As such, occupants cannot serve as guardians during the day time, when they are at work and doing their leisure activities, shopping, and visiting friends afterwards. Similarly, the Routine Activity Approach [
17] can also be applied to the temporal distribution of car burglaries, which are highest at night, at around 1–2 am, and during the early afternoon, from approximately 1–4 pm, when many cars are parked (unoccupied) in front of homes or work places, respectively.
Future research can go into many different directions. First, the temporal resolution for observed and estimated occurrence times can be refined from one hour, as applied in this research, to one-half hour bins. This requires a large data set of crimes with accurately and inaccurately known time stamps for both the observation and retrospective periods. Second, crime data included in the retrospective and observation periods are four (2009–2012) and three (2013–2015) full years, respectively. However, the number of crimes and their occurrence times exhibit seasonal variations. For this reason, it may be worthwhile to replicate this study for different seasons of the year (e.g., several consecutive summers or winters) and explore the impact that a particular season has on the results of temporal approximation methods. Third, this study should be replicated with different crime types and in other study areas. Fourth, the impact that the length of the retrospective period has on the estimated time stamps of the both the RTA and RTAext methods should be investigated. It may be assumed that a longer retrospective period (more consecutive years) would yield more accurate estimations than a shorter retrospective period (fewer consecutive years). Finally, it should also be tested, whether crimes with accurately known time stamps from the retrospective period should all be equally weighted, as was done in this research, or that more recent time stamps should be weighted higher than older time stamps. All these future research efforts will ultimately lead to an increase in the temporal accuracy of crimes and to improved spatio-temporal models.