1. Introduction
Place and space are among the most fundamental concepts of geography [
1,
2]. Space is often considered to be points of locations represented by coordinates. Place, on the other hand, is an “experience-based dynamic construct” [
3]. Compared to space, the concept of place emphasizes on the meaning-making process that is complex, dynamic, and individualistic [
4]. In this paper, we study how different places are semantically similar, based on textual topics that appear in Volunteered Geographic Information (VGI) in these places. Our goal is to create a thematic similarity network that connects places of similar topics regardless of their physical distance. By applying a network clustering algorithm, we find groups of semantically similar places and analyze their topics and spatial autocorrelation qualitatively and quantitatively.
Analyzing and theorizing about places from a variety of perspectives, has a long history in geographical analysis—from social area analysis [
5,
6,
7,
8] to more recent geodemographic analysis that derives collective behaviors and characteristics from demographic data of geographic regions [
9,
10]. In the past decade, studies on place have taken advantage of a new data source, that of VGI [
11]. VGI comes in many different forms, from that of maps created by users to text from Wikipedia which has a geographic component (e.g., place names) [
12]. The research presented in this paper uses the textual form of VGI, specifically crowdsourced reviews from TripAdvisor and geolocated Twitter data (see
Section 3). Such platforms provide large amounts of textual data with either explicit or implicit geographic information contributed by users [
13,
14]. Leveraging this unstructured geographical information found in such texts allows us to comprehend the complexity of places at scale [
15,
16,
17].
Generally speaking, the most common method used by prior research to analyze geo-textual data is to structure the unstructured texts into themes (i.e., topics) through topic models (e.g., [
18]). This is then often followed by applying clustering algorithms (e.g., k-means) to expose the underlying patterns of sentiments, experiences, or activities captured in the text (e.g., [
12,
19,
20,
21,
22,
23,
24]). When places are clustered for further analysis, however, those in the same cluster are assumed to be carrying similar characteristics. Relationships between places are reduced to being either in-cluster or out-of-cluster. However, we would argue that the connectedness and relationships of places, in reality, are more complex. For instance, when connecting places in a network, places at the edge of their own clusters still have relatively weak out-of-cluster connections. The network approach presented in this paper, recognizes them as places with both in-cluster and out-of-cluster connections. Thus, this approach does not limit us to only perform network-level place clustering, but also to discover unique places based on their positions in the networks. To highlight this we use a case study to demonstrate the approach in the context of Manhattan, New York. In the remainder of the paper, we will first discuss related research pertaining to topic modeling and thematic similarity network analysis (
Section 2). This is followed by introducing the data (
Section 3) and the methodology (
Section 4) that we applied to our case study. The results are then presented in
Section 5 and finally, the implications and conclusions of our research are presented in
Section 6.
2. Related Work
The approach proposed in this paper involves two major steps, topic modeling using geo-textual data and thematic similarity network analysis. In what follows we review related work with respect to these steps. For step one, topic modeling is a widely used language model for understanding large amounts of unstructured textual data. Previous research has adopted generic topic modeling algorithms (e.g., [
18]) to ones that incorporate geographic information (e.g., [
25,
26]). Using these geographical topic models, studies have been able to derive the topics from travel blogs and Flickr tags to specific geographical units, such as states [
25,
26]. Other work has analyzed the relationships between topics and countries from online news articles and blogs [
27], or generated activity patterns from check-in data [
23]. In addition, topic modeling has been used to recommend travel destinations using travel blogs [
28,
29], create location related question-answering systems using Twitter and blogs [
30], and predict the future distribution of topics [
31]. Despite research on innovating geographic topic models, many researchers often chose to use generic topic models (such as Latent Dirichlet Allocation, LDA [
18]) to analyze geo-textual data. In such instances, the geolocational information in the text does not contribute to the results of the topic models but is used only after applying the model. For example, Adams et al. [
20] explored the temporal themes related to places using travel blogs and applied a similarity score between places based on the topics. Jenkins et al. [
32] compared themes of geographic areas from Twitter and Wikipedia whereas Xu et al. [
33] model the topics of restaurants of a city.
In addition, previous work has defined “place” at various levels of aggregation—countries, cities, neighborhoods, buildings, but such aggregations artificially split geographical areas. For example, at the neighborhood level, Cranshaw et al. [
34] detected boundaries of neighborhoods using check-in data and Foursquare venue descriptions in order to show that crowdsourced and official neighborhood definitions differed. At a more aggregated level, Preoţiuc-Pietro [
35] viewed cities as collections of Foursquare venues and clustered cities hierarchically using venue descriptions to show that similarities between cities can be captured through crowdsourced data. Since Foursquare venue data also provides venue categories, Noulas et al. [
36] clustered both geographic areas (in terms of
square meters) and users based on their visit history in order to enhance recommendation systems for different users. In another work, Crooks et al. [
12] proposed a multi-level (individual building, streets, and neighborhoods level) approach for discovering social functions through mining place topics. Clustering at different aggregations also allows us to find places where people share similar experiences [
20,
37] along with places with similar functions [
12]. When applying clustering, however, the relationship between places becomes binary, being similar or not similar, and thus the relationships between places in
different clusters are often ignored.
Turing to work pertaining to thematic similarity network analysis (i.e., the second step of our approach), previous studies have analyzed place similarities but rarely used a network approach in the context of geo-textual data. For example, Janowicz et al. [
38] used semantic similarity for developing geographic information retrieval applications. While Yan et al. [
39] trained word embeddings for place types that was then used for exploring similarity and relatedness between point-of-interests types. In terms of using a similarity network-based approach, Quercini and Samet [
40] created graph-based similarity measures to address spatial relatedness of a concept to a location using Wikipedia articles. In another work, Hu et al. [
41] placed cities into networks based on their semantic relatedness (i.e., number of news articles which contain the co-occurrences of the two cities). Similarity networks, however, have seen much wider applications in domains outside of geography, ranging from analyzing protein sequences and structures [
42], genome data [
43] to that of hospital patients [
44,
45]. Methodologically, such studies have demonstrated that one of the most important analysis for similarity networks is clustering (i.e., community detection), which captures groups of nodes that are most similar to each other. Although place clustering does not require connecting places in networks, one of the advantages of conducting network-based clustering is that it enables for downstream node level analysis in relation to clusters. For example, Valavanis et al. [
42] discovered structural similarities of protein folds and classes in the downstream analysis after carrying out network clustering. Similarly, in the case study presented throughout the rest of this paper, we will apply clustering to the similarity network as well as identifying special nodes (i.e., places) based on their positions in the network.
6. Conclusions
A place is a geographic location that has individuals’ experiences and meaning-making processes from it. As a place has different meanings to different individuals, it is difficult to summarize the collective sense of place (e.g., [
4,
13,
16]). As more and more textual data that describe people’s experiences of places are now available online via social media etc., it is possible to study places by crowdsourcing the online textual data from place reviews and geolocated social media. Furthermore, through the use of network science and natural language processing of crowdsourced experiences collected from individuals we can also study the connections between places which reveals not only richer information about the place itself and how places relate to each other.
To this end, in this paper we used TripAdvisor reviews and geolocated Twitter data to understand the characteristics and the connectedness of places. The complex relationships between places were modeled via thematic (i.e., topical) similarity networks. While previous research using crowdsourced data allowed for the clustering of places (e.g., [
32]), they do not explore the connections between places and clusters. The network approach developed in this paper enables us to perform clustering (i.e., network community detection) to discover the network and node level patterns of places. More specifically, the contributions of this research are as follows. First, similar to previous research with place clustering, the network approach of places also allow the performance of clustering on places using a network community detection algorithm. The case study in
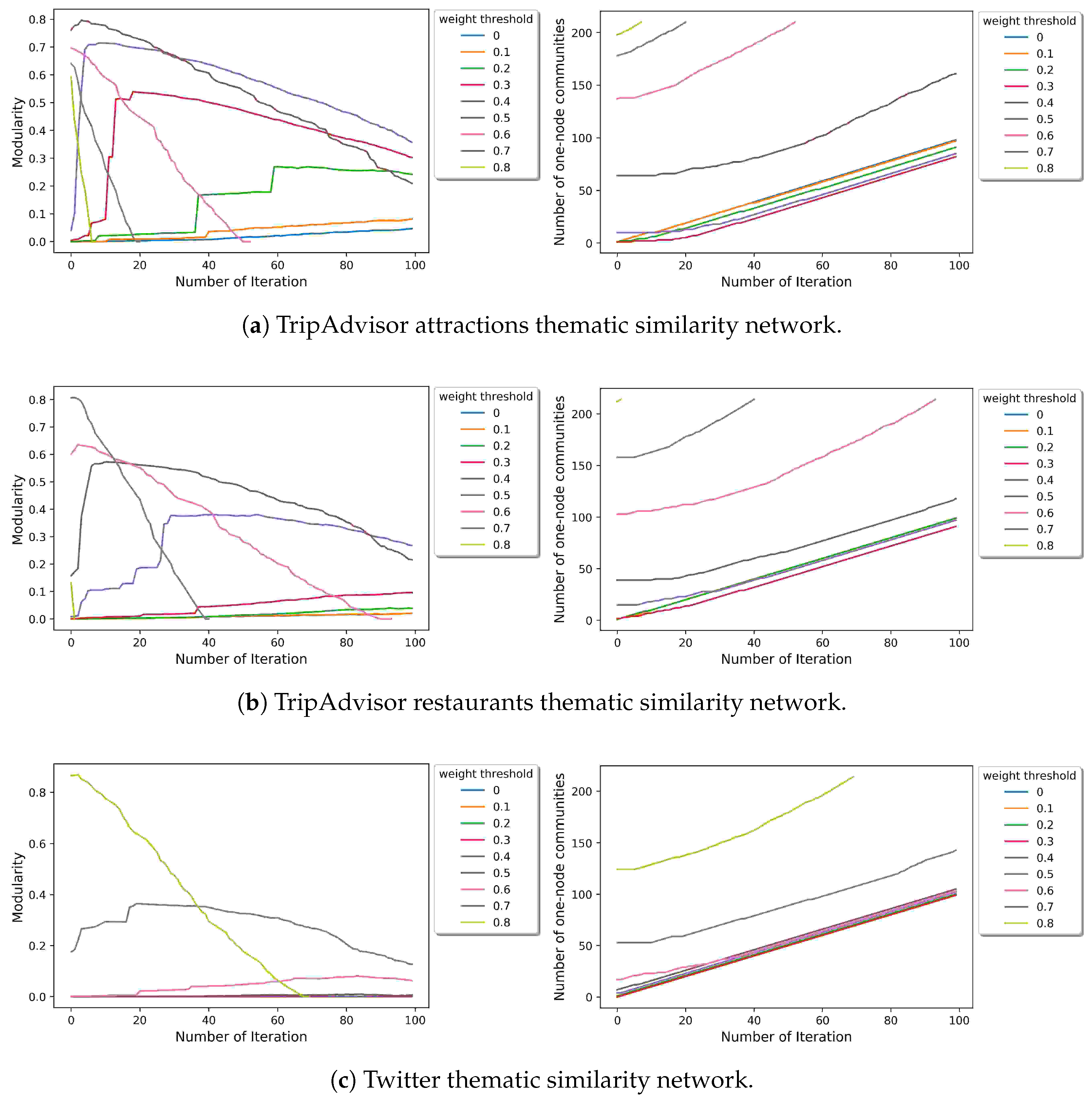
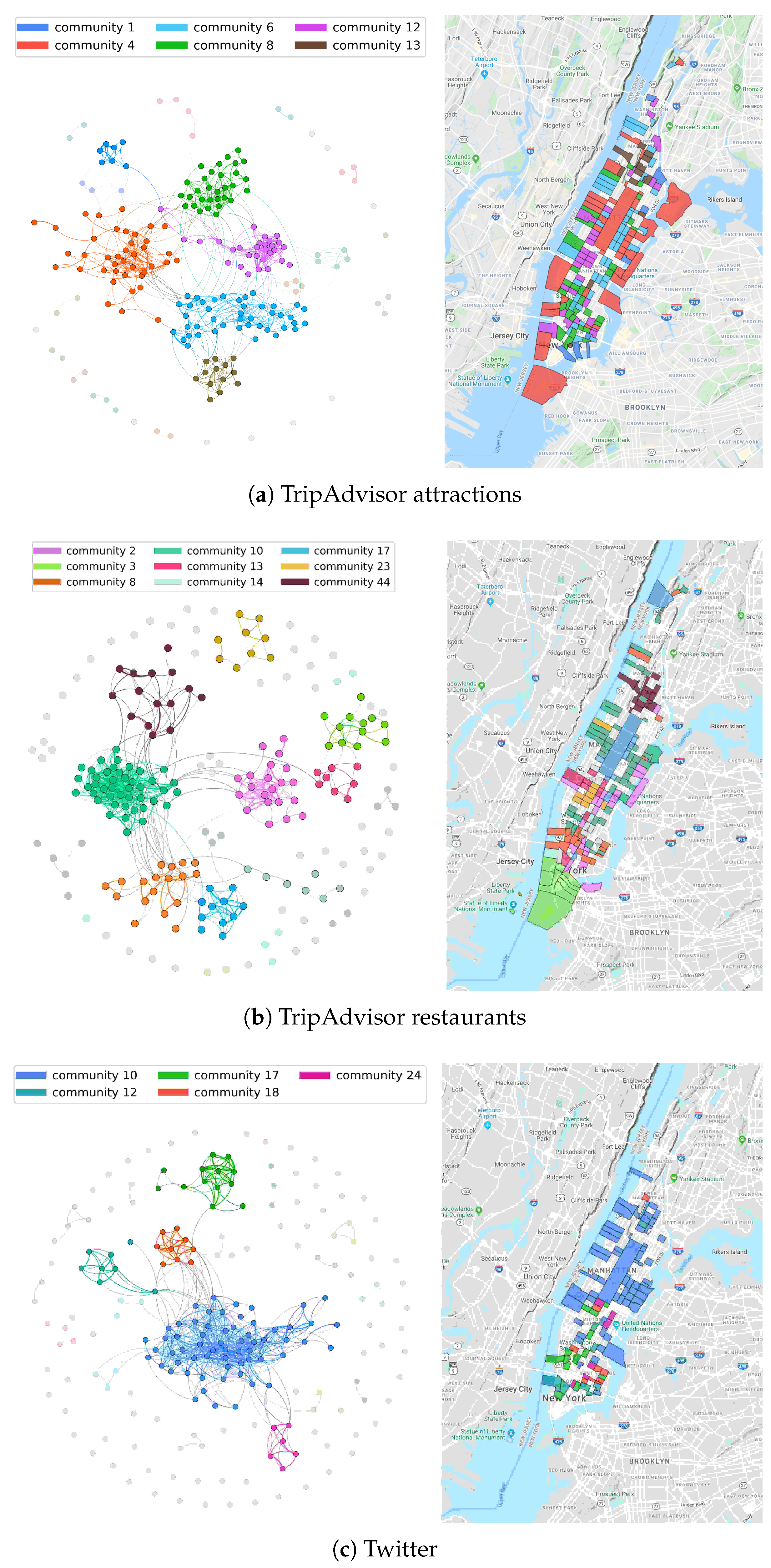
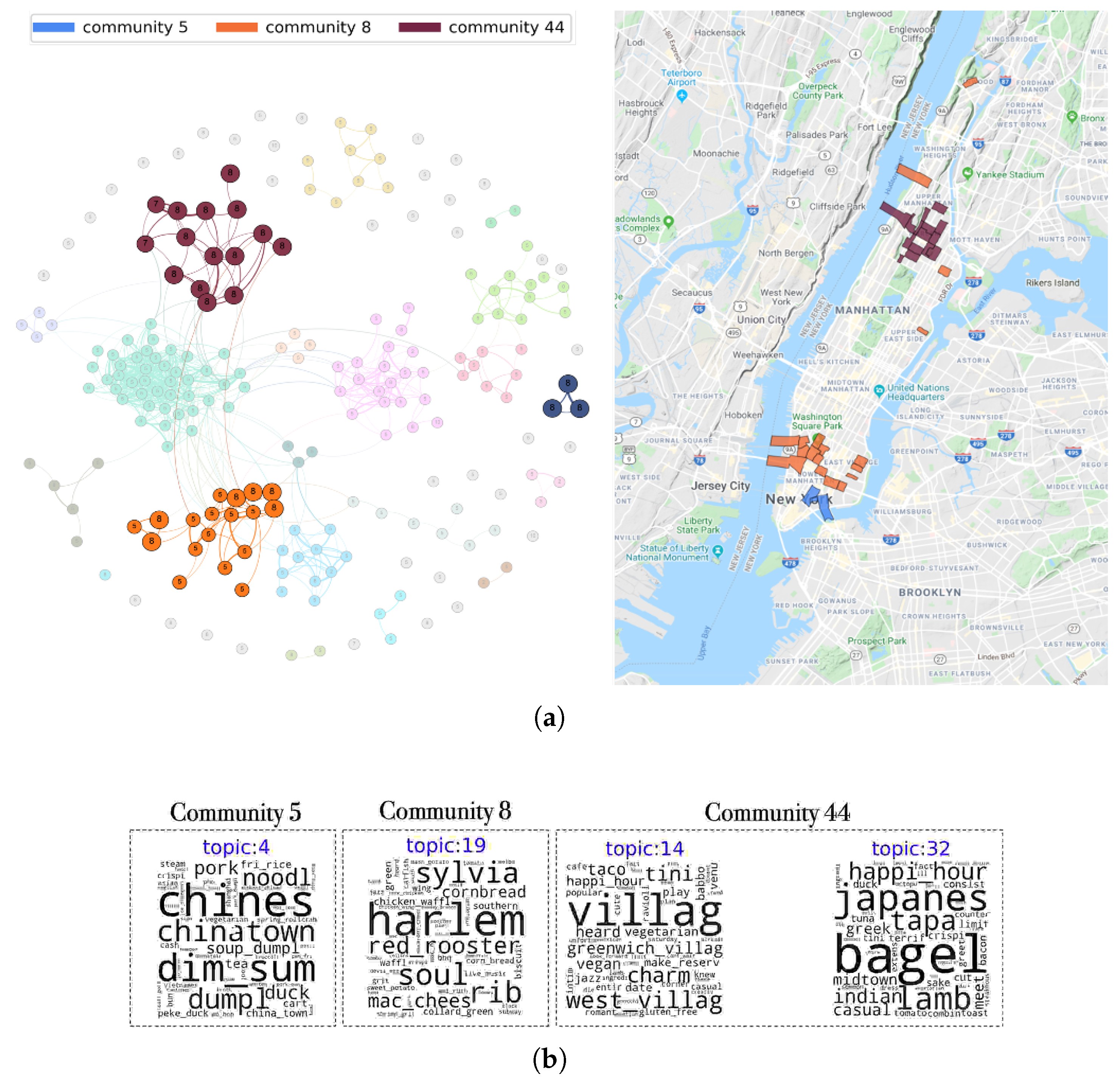
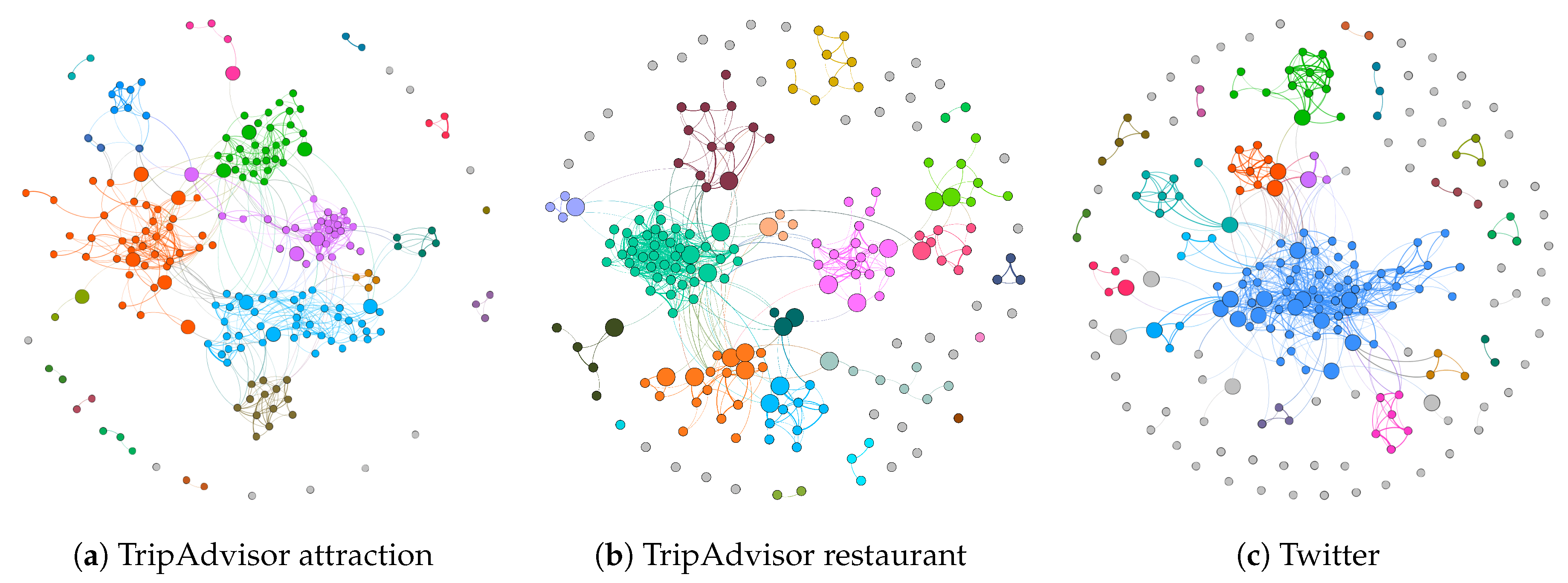
Section 5.1 show that community detected from the thematic similarity network from restaurant reviews tend to have higher Moran’s I value (i.e., geographical proximity) than that of attraction reviews and tweets. It suggests that certain geographical clusters correspond to certain restaurant culture in Manhattan (e.g., the bar and pub area at Downtown). Second, by using the network approach (as discussed in
Section 4), we can discover places of interest by exploiting the positions of the places in the network. In the case study shown in the paper, the places of interest are places of different levels of uniqueness (
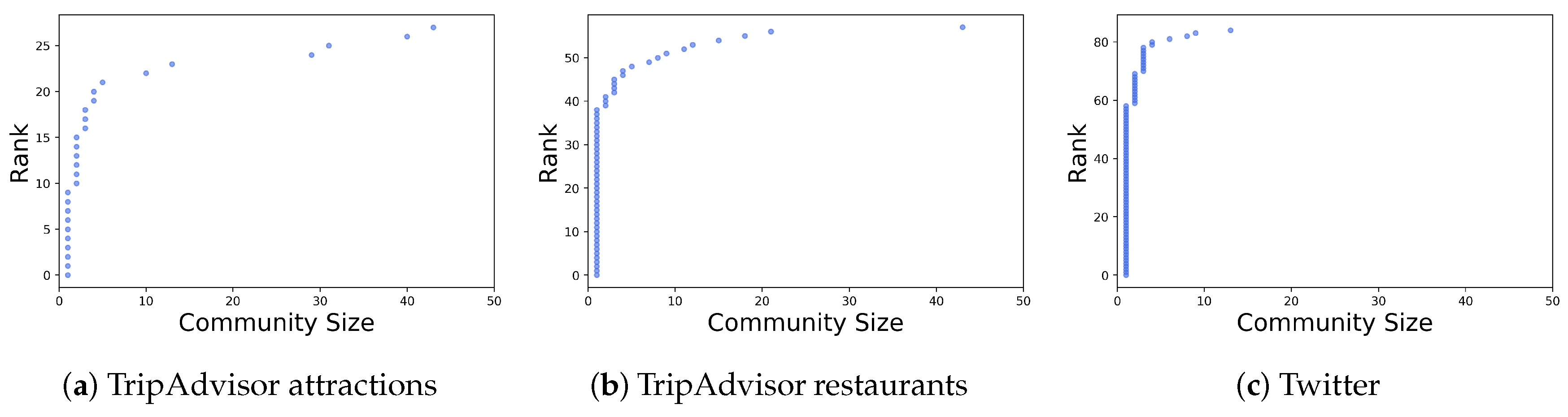
Section 5.3). Third, from the TripAdvisor restaurant network results, we found that even though most of the study area in Manhattan is high income, the low-income communities have a distinctive restaurant culture that the high-income areas do not have (
Section 5.2). Fourth, by comparing different datasets (i.e., Trip Advisor restaurants and attractions reviews and Twitter), we show implications of using such data for studying places (
Section 5.1). TripAdvisor review data represents experiences and perceptions people have directly about places, whereas geolocated Twitter data does not necessarily reflect places. However, as our case study shows, by using topic modeling one can overcome this challenge and filter out place-irrelevant topics, which do not require the time consuming hand labeling process as supervised learning (as shown in
Section 5.1.1).
While this study has shown how places are connected through individuals’ experiences and adds to the growing area of geographic data science [
62], there are several limitations to this research. First, although the clustering algorithm used in this study (i.e., the Girvan–Newman algorithm [
56]), produces deterministic results, it might not be an ideal choice when the networks become larger, say when expanding this research to larger areas. Therefore, researchers who expand this research might want to consider less computationally inexpensive algorithms such as Louvain community detection algorithm [
63] which use modularity optimization and has been shown to be scalable [
64]. Second, in this study, we define places as census tracts and further analysis is required to test whether some of the results still stand when places are defined otherwise (e.g., zip codes, city blocks etc.). Nonetheless, using census tracts in this research had the advantage of combining textual VGI data with Census data for further analysis (as shown in
Section 5.2). Turning to future work, other centrality measures (e.g., betweenness centrality, eigenvector centrality) could be explored to discover places of interest other than degree centrality and boundary nodes. Additionally, topic models could be trained by merging data from three datasets so that the topics are comparable across networks. As this work does not take tokens such as emojis into consideration, future work could explore topic models by incorporating them (e.g., [
65,
66]). The network can also constructed differently with edges representing similarities measured by methods other than topic similarity such as similarity based on users’ visit history, which has often been used in collaborative recommender systems [
67]. Even with these limitations and potential areas of further work, the research presented in this paper demonstrates a novel approach of studying places and their connections by combining textual VGI with network analysis.