An Approach for Filter Divergence Suppression in a Sequential Data Assimilation System and Its Application in Short-Term Traffic Flow Forecasting
Abstract
1. Introduction
2. Representation of Filter Divergence Phenomenon in Sequential Data Assimilation System for Short-Term Traffic Flow Forecasting
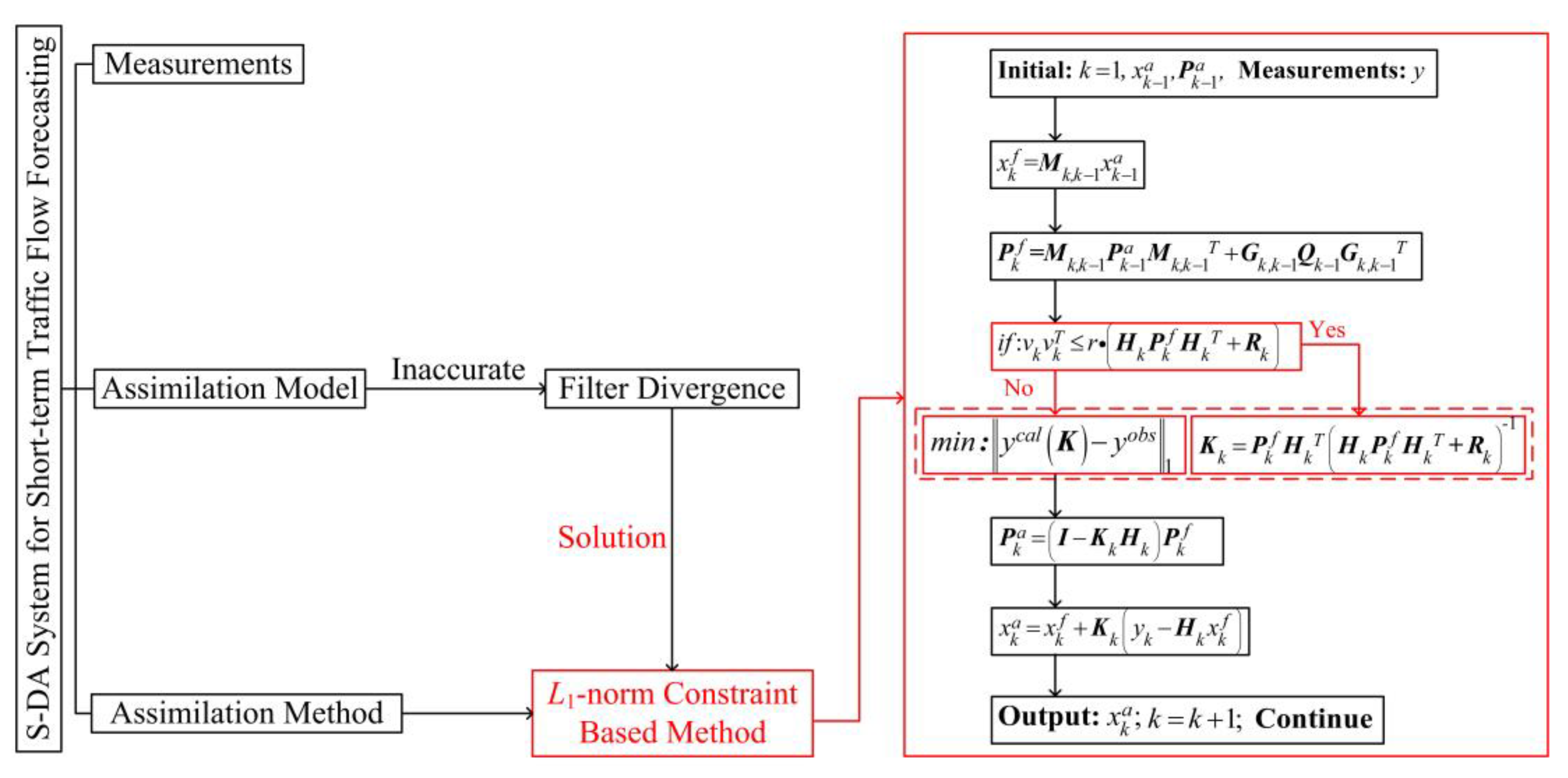
3. Methodology
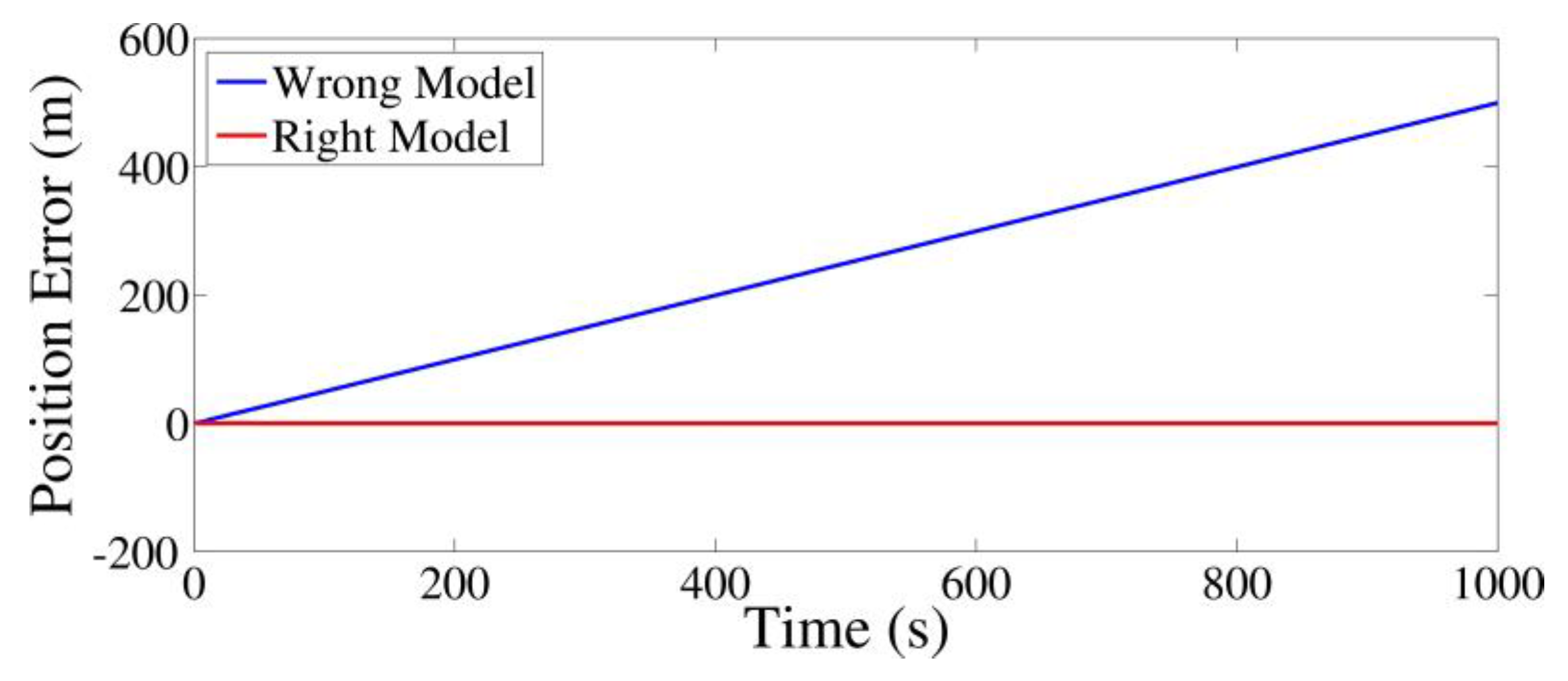
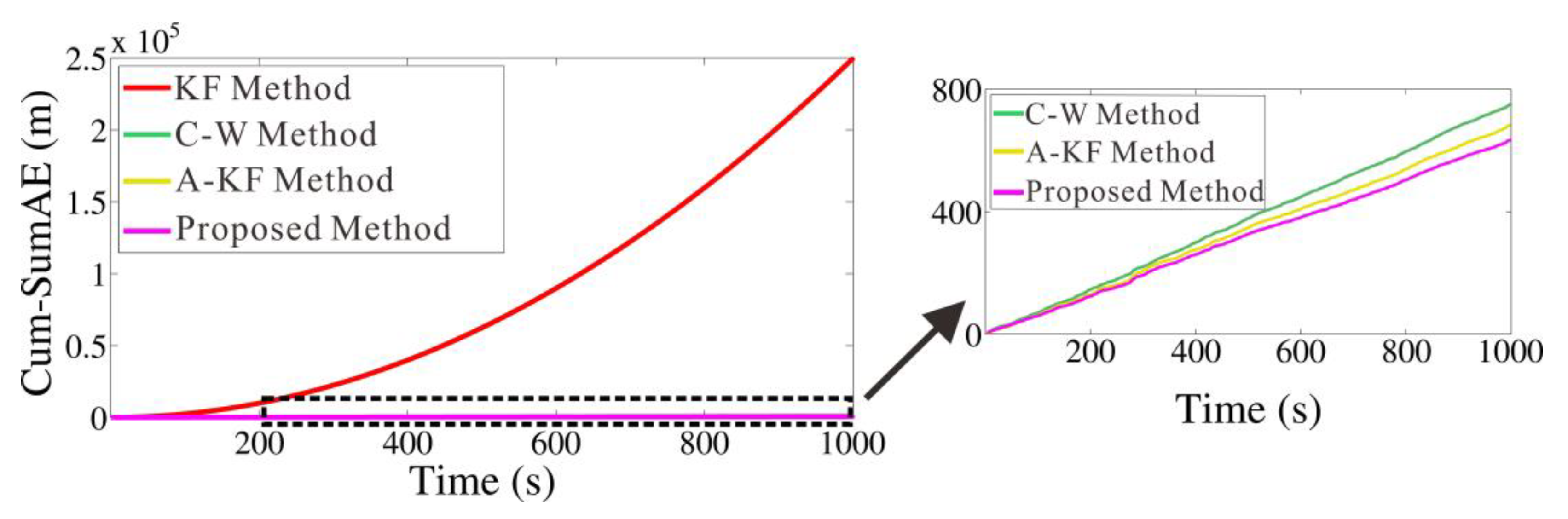
4. Numerical Study
5. Empirical Study
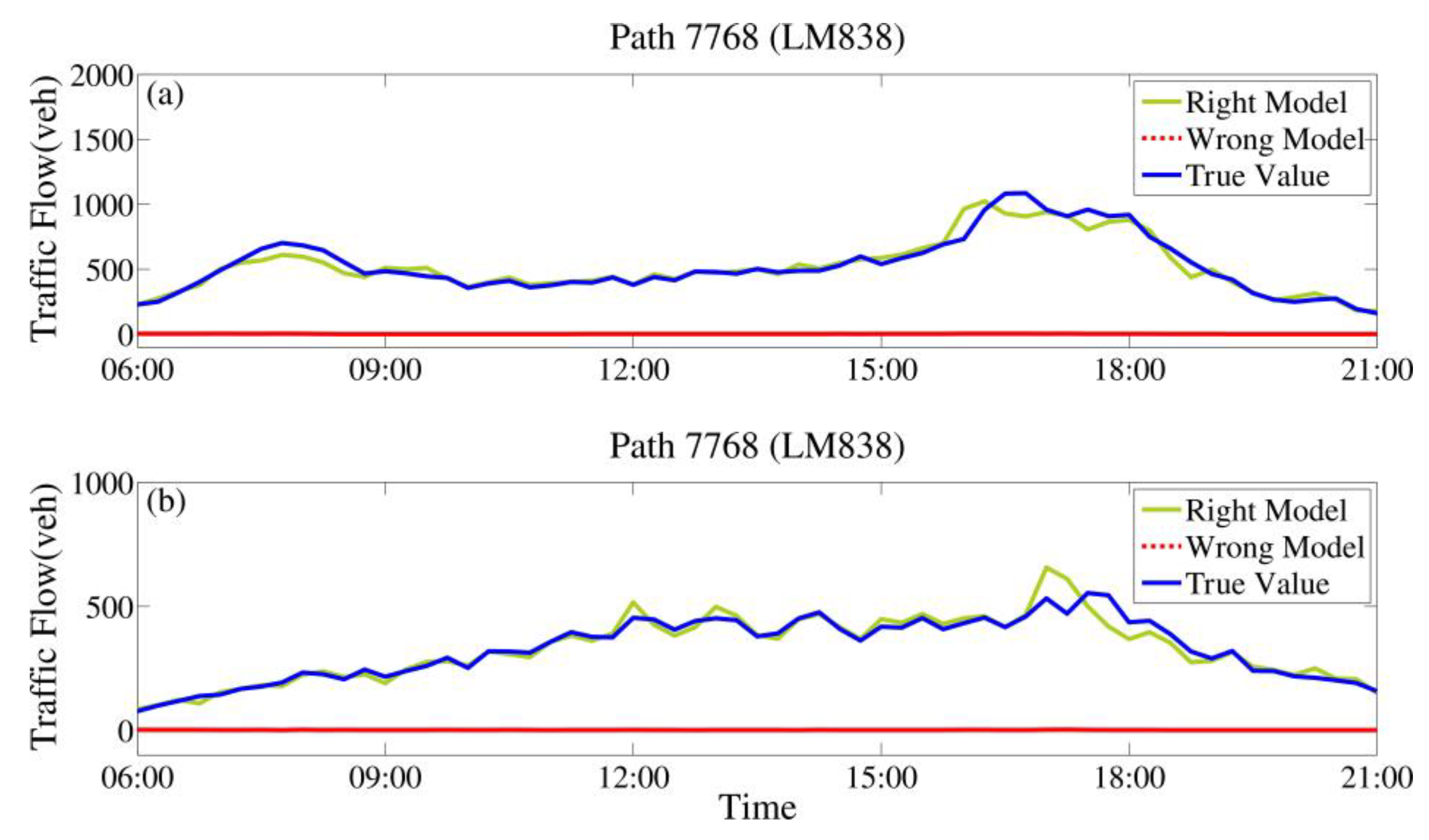
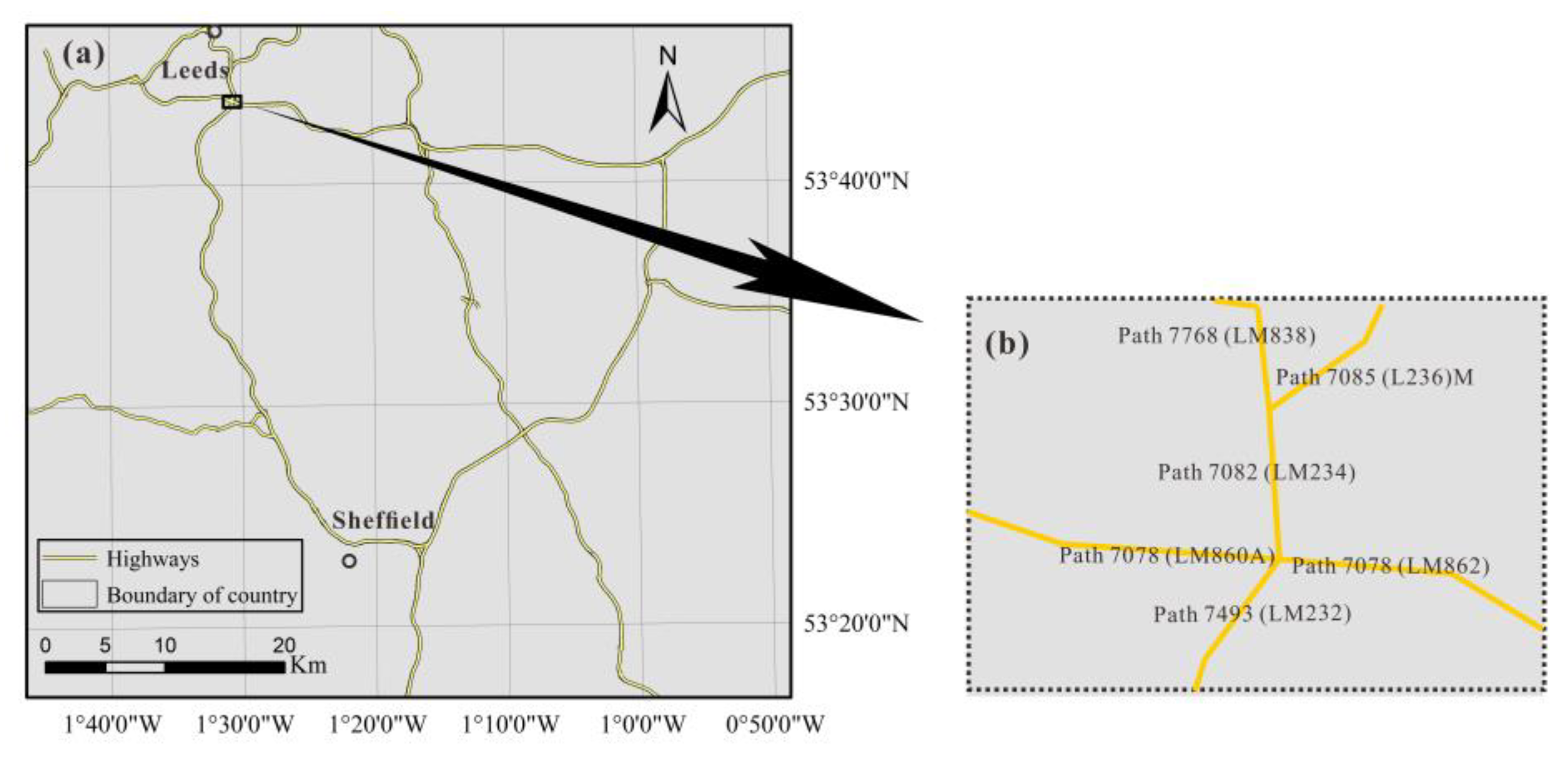
5.1. Study Area and Material Description
5.2. Test Design
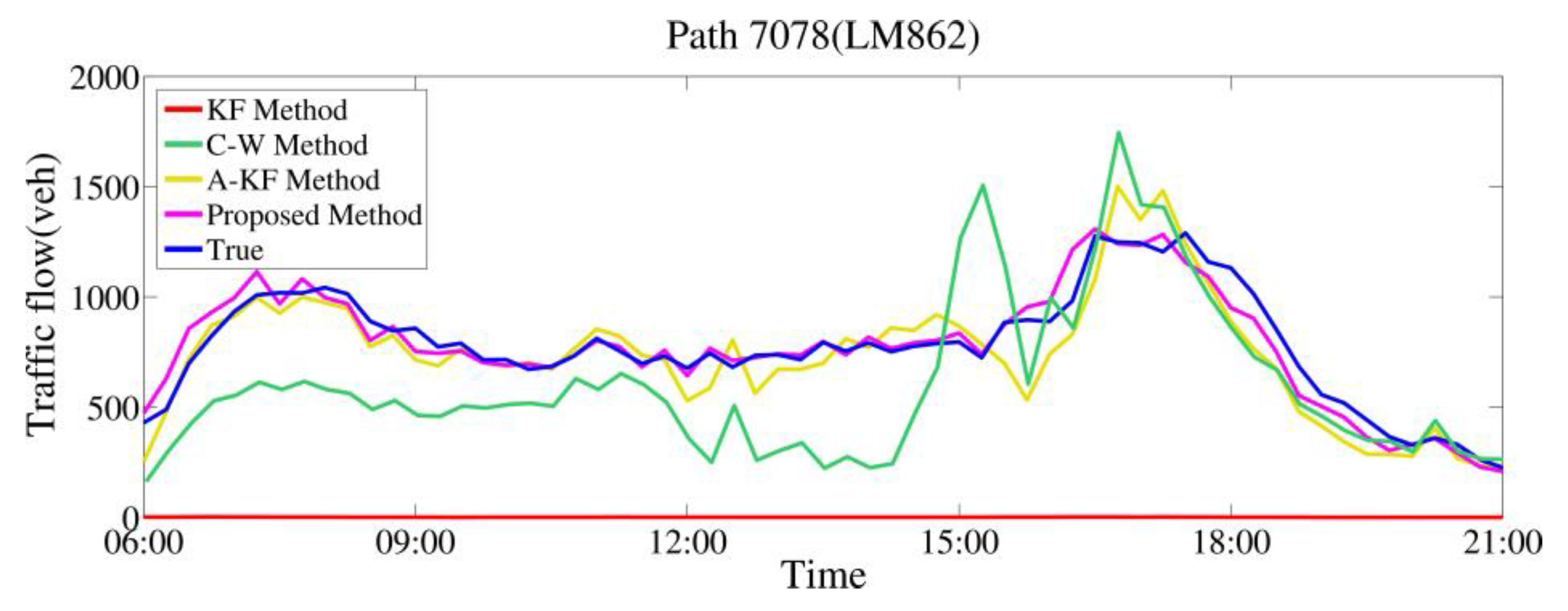
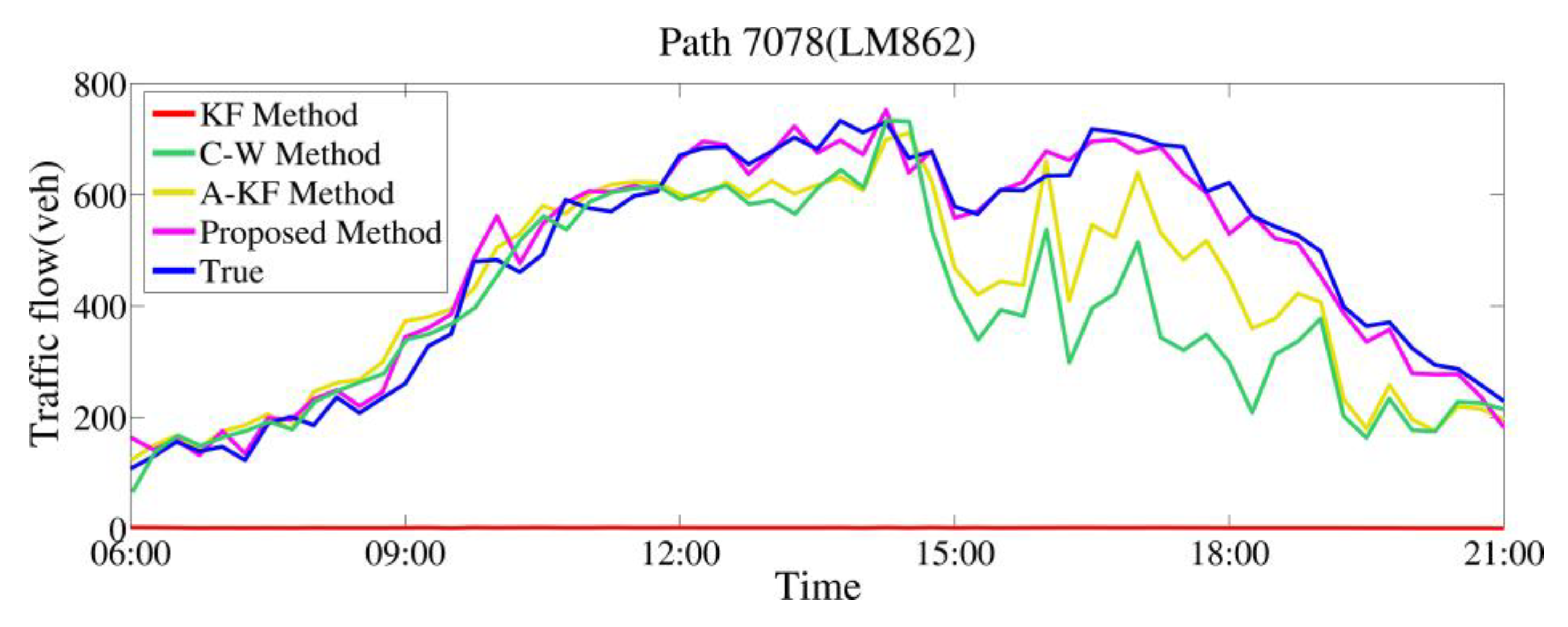
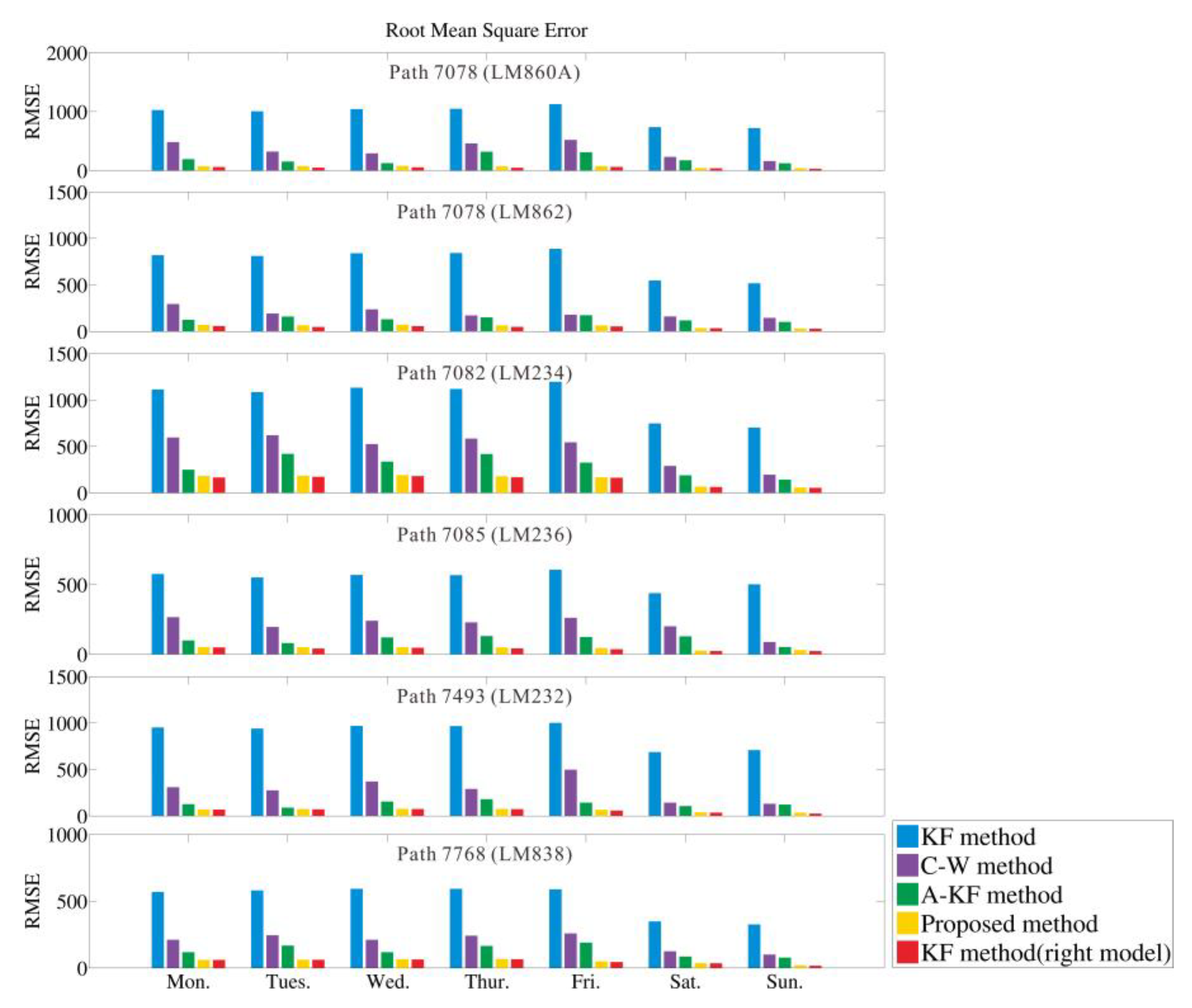
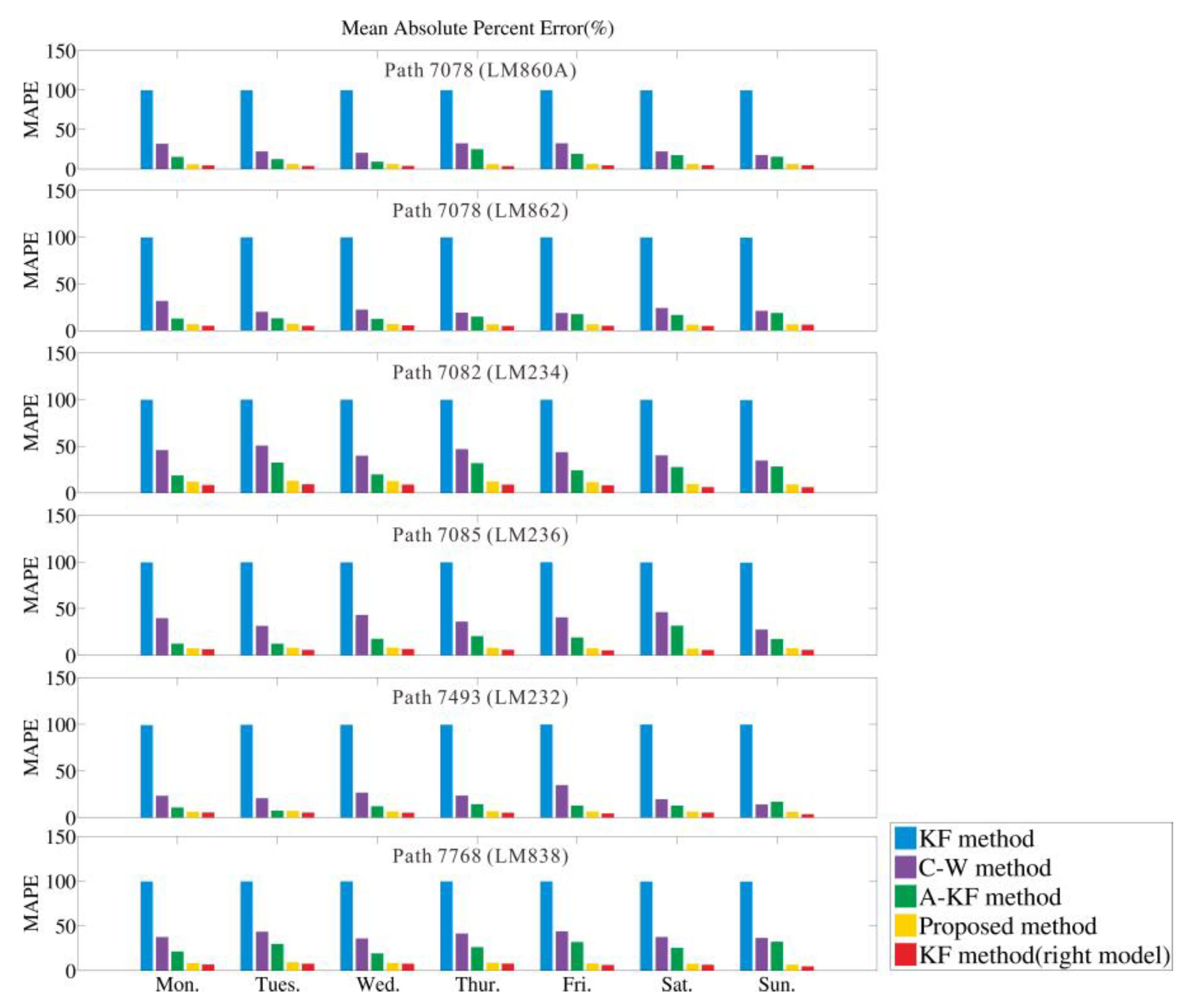
6. Results and Discussion
7. Conclusions
- The proposed approach based on the L1-norm constraint can suppress the filter-divergence phenomenon that occurs in the KF assimilation method of the S-DA system.
- The proposed approach based on the L1-norm constraint had a higher assimilation accuracy for suppressing filter divergence than the other two methods.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, H.B.; Grant-Muller, S. Use of sequential learning for short-term traffic flow forecasting. Transport. Res. C-Emer. 2001, 9, 319–336. [Google Scholar] [CrossRef]
- Hani, S.M. Traveler behavior and intelligent transportation systems. Transport. Res. C-emer. 1999, 7, 73–74. [Google Scholar]
- Li, Y.; Lin, Y.; Zhang, F. Research on geographic information system intelligent transportation systems. Chung-kuo Kung Lu Hsueh Pao China J. Highw. Transp. 2000, 13, 97–100. [Google Scholar]
- Zhang, Y.R.; Zhang, Y.L.; Haghani, A. A hybrid short-term traffic flow forecasting method based on spectral analysis and statistical volatility model. Transport. Res. C-Emer. 2014, 43, 65–78. [Google Scholar] [CrossRef]
- Lippi, M.; Bertini, M.; Frasconi, P. Short-Term Traffic Flow Forecasting: An Experimental Comparison of Time-Series Analysis and Supervised Learning. IEEE T Intell Transp. 2013, 14, 871–882. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Kong, Q.; Zhai, X.; Liu, Y. Urban traffic flow prediction: A spatio-temporal variable selection-based approach. J. Adv Transport. 2016, 50, 489–506. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, N.; Wang, R.; Malekian, R. A Method for Traffic Congestion Clustering Judgment Based on Grey Relational Analysis. ISPRS Int. J. Geo-Inf. 2016, 5, 71. [Google Scholar] [CrossRef]
- Guo, H.; Xiao, X.; Tang, Y. Short-Term Traffic Flow Forecasting Based on Grey Delay Model. In International Conference on Artificial Intelligence and Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Tchrakian, T.T.; Basu, B. Real time traffic flow forecasting and predictive ramp-metering using spectral analysis. In Proceedings of the IET Irish Signals and Systems Conference (ISSC 2009), Dublin, Ireland, 10–11 June 2009. [Google Scholar]
- Xu, J.; Li, X.; Shi, H. Short-term traffic flow forecasting model under missing data. J. Comput. Appl. 2010, 30, 1117–1120. [Google Scholar] [CrossRef]
- Jin, S.; Wang, D.; Xu, C.; Ma, D. Short-term traffic safety forecasting using Gaussian mixture model and Kalman filter. J. Zhejiang Univ-Sc A. 2013, 4, 3–15. [Google Scholar] [CrossRef]
- Okutani, I.; Stephanedes, Y.J. Dynamic prediction of traffic volume through Kalman filtering theory. Transport. Res. B-Meth. 1984, 18, 1–11. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Y.; Ye, Z. Short-Term Traffic Volume Forecasting Using Kalman Filter with Discrete Wavelet Decomposition. Comput-Aided Civ Inf. 2007, 22, 326–334. [Google Scholar] [CrossRef]
- Anderson, J.L. An Ensemble Adjustment Kalman Filter for Data Assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef]
- Georg, A. Gottwald. A mechanism for catastrophic filter divergence in data assimilation for sparse observation networks. Nonlinear Proc. Geoph. 2013, 20, 705–712. [Google Scholar]
- Law, K.J.H.; Stuart, A.M.; Zygalakis, K.C. Data Assimilation: A Mathematical Introduction. Revista Brasileira De Meteorologia. 2015, 26, 433–442. [Google Scholar]
- Bocquet, M.; Pires, C.A.; Wu, L. Beyond Gaussian Statistical Modeling in Geophysical Data Assimilation. Mon. Weather Rev. 2010, 138, 2997–3023. [Google Scholar] [CrossRef]
- Keith, B.; Jim, F. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 29. [Google Scholar]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transport. Res. C-Emer. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Smith, P.J.; Thornhill, G.; Dance, S.; Lawless, A.S.; Mason, D.C.; Nichols, N.K. Data assimilation for state and parameter estimation: Application to morphodynamic modelling. Q J. Roy. Meteor. Soc. 2013, 139, 314–327. [Google Scholar] [CrossRef]
- Narayan, A.; Marzouk, K.; Xiu, D. Sequential data assimilation with multiple models. J. Comput Phys. 2012, 231, 6401–6418. [Google Scholar] [CrossRef]
- Tanajura, C.A.S.; Belyaev, K. A sequential data assimilation method based on the properties of a diffusion-type process. Appl. Math. Model. 2012, 33, 2165–2174. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Bocher, M.; Coltice, N.; Fournier, A.; Tackley, P.J. A sequential data assimilation approach for the joint reconstruction of mantle convection and surface tectonics. Geophys J. Int. 2015, 204, 200–214. [Google Scholar] [CrossRef]
- Li, H.; Kalnay, E.; Miyoshi, T. Simultaneous estimation of covariance inflation and observation errors within an ensemble Kalman filter. Q J. Roy. Meteor. Soc. 2009, 135, 523–533. [Google Scholar] [CrossRef]
- Hou, E.; Lawrence, E.; Hero, A.O. Penalized Ensemble Kalman Filters for High Dimensional Non-linear Systems. 2018. Available online: https://arxiv.org/pdf/1610.00195.pdf (accessed on 16 December 2019).
- Deng, M.J.; Qu, S.R. Fuzzy State Transition and Kalman Filter Applied in Short-Term Traffic Flow Forecasting. Comput. Intel. Neurosc. 2015, 2015, 875243. [Google Scholar]
- Stathopoulos, A.; Karlaftis, M.G. A multivariate state space approach for urban traffic flow modeling and prediction. Transport. Res. C-Emer. 2003, 11, 121–135. [Google Scholar] [CrossRef]
- Pan, D.; Liu, H.; Li, Y. A wind speed forecasting optimization model for wind farms based on time series analysis and Kalman filter algorithm. Power Sys Thchno. 2008, 32, 82–86. [Google Scholar]
- Larry, M.; Takeo, K.; Richard, S. Kalman filter-based algorithms for estimating depth from image sequences. Int J. Comput Vision. 1989, 3, 209–238. [Google Scholar]
- Meinhold, R.J.; Singpurwalla, N.D. Understanding the Kalman Filter. Am. Stat. 1983, 37, 123–127. [Google Scholar]
- Wouter, D.H. Decay chain fitting with a Kalman filter. Nucl. Instrum. Methods Phys. Res. 2005, 552, 566–575. [Google Scholar]
- Esch, T.; Vary, P. Speech enhancement using a modified Kalman Filter based on complex linear prediction and supergaussian priors. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 4877–4880. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Price, C. An analysis of the divergence problem in the Kalman filter. IEEE T Automat. Contr. 1968, 13, 699–702. [Google Scholar] [CrossRef]
- Ma, R.P.; Wei, D.; Zhang, M.L. An Improved Self Adapting Kalman Filter and Application in Assembly Guidance. Inertia Technol. Trans. China 2006, 14, 37–40. (In Chinese) [Google Scholar]
- Deng, Z.L. Self-tuning α—β—γ tracking filter. JCD 1991, 6, 384–387. [Google Scholar]
- Grimble, M.J.; Jukes, K.A.; Goodall, D.P. Nonlinear Filters and Operators and the Constant-Gain Extended Kalman Filter. Ima J. Math. Control. I. 1984, 1, 359–386. [Google Scholar] [CrossRef]
- Kobayashi, T.; Simon, D.L.; Litt, J.S. Application of a constant gain extended Kalman filter for in-flight estimation of aircraft engine performance parameters. NASA Tech. Rep. Serv. (Ntrs) 2005, 1–12. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20050216398.pdf (accessed on 5 November 2019).
- Han, H.; Liu, R.P. A Limited Memory Kalman Filtering Equation with Dynamic Noise. Fire Control. Command Control. 2001, 26, 55–58. [Google Scholar]
- Xu, D.J.; He, R.; Shen, F.; Gai, M. Adaptive fading Kalman filter based on innovation covariance. J. Syst. Eng. Electron. 2011, 33, 2696–2699. [Google Scholar]
- Gao, J.; Leng, Z.; Zhang, B.; Liu, X.; Cai, G. The Application of Adaptive Kalman Filter in Traffic Flow Forecasting. Adv. Mater. Res. 2013, 680, 495–500. [Google Scholar] [CrossRef]
- Lu, P.; Zhao, L.; Chen, Z. Improved Sage-Husa adaptive filtering and its application. J. Syst. Simul. 2007, 19, 3503–3505. [Google Scholar]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filtering for INS/GPS. J. GEODESY. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, T. An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components. J. Navigation. 2003, 56, 231–240. [Google Scholar] [CrossRef]
- Huang, W.; Jia, W.; Guo, J.; Williams, B.M.; Shi, G.; Wei, Y.; Cao, J. Real-Time Prediction of Seasonal Heteroscedasticity in Vehicular Traffic Flow Series. IEEE T Intell Transp. 2017, 99, 1–11. [Google Scholar] [CrossRef]
- Yang, Y.X.; He, H.B.; Xu, T.H. Adaptive Robust Filtering for Kinematic GPS Positioning. Acta Geodaetica Et Cartogr. Sinica. 2001, 75, 109–116. [Google Scholar]
- Vlahogianni, E.; John, I.; Golias, C.; Karlaftis, M.G. Short-term traffic forecasting: Overview of objectives and methods. Transport. Reviews. 2004, 24, 533–557. [Google Scholar] [CrossRef]
- Chandra, S.R.; Al-Deek, H. Predictions of Freeway Traffic Speeds and Volumes Using Vector Autoregressive Models. J. Intell. Transport. Syst. Tech. Plann. Oper. 2014, 13, 53–72. [Google Scholar] [CrossRef]
- Shen, G.J.; Kong, X.J.; Chen, X. Short-term Traffic Flow Intelligent Hybrid Forecasting Model and Its Application. Control. Eng. Appl. Inf. 2011, 13, 65–73. [Google Scholar]
- Crase, E.; Pica, A.; Noble, M. Robust elastic nonlinear waveform inversion: Application to real data. Geophysics 1990, 55, 527–538. [Google Scholar] [CrossRef]
- Dai, Y.H.; Fletcher, R. Projected Barzilai-Borwein methods for large-scale box-constraint quadratic programming. Numer. Math. 2005, 100, 21–47. [Google Scholar] [CrossRef]
- Afonja, A.B. Use of the Generalized Variance and the Gradient Projection Method in Multivariate Stratified Sampling. Biometrics 1971, 7, 119–127. [Google Scholar]
- William, W.H.; Park, S. The Gradient Projection Method with Exact Line Search. J. Global Optim. 2004, 30, 103–118. [Google Scholar]
- Hager, W.W.; Zhang, H. A survey of nonlinear conjugate gradient methods. Pac. J. Optim. 2006, 2, 35–58. [Google Scholar]
- Faber, V.; Thomas, A.M. Necessary and Sufficient Conditions for the Existence of a Conjugate Gradient Method. SIAM J. Numer Anal. 1984, 21, 352–362. [Google Scholar] [CrossRef]
- Scales, J.A. Tomographic inversion via the conjugate gradient method. Geophysics 1987, 52, 179–185. [Google Scholar] [CrossRef]
- Sriyananda, H. A simple method for the control of divergence in Kalman-filter algorithms. Int. J. Control. 1972, 16, 1101–1106. [Google Scholar] [CrossRef]
- Wild, D. Short-term forecasting based on a transformation and classification of traffic volume time series. J. Forecasting. 1997, 13, 63–72. [Google Scholar] [CrossRef]
- Yin, H.; Wong, S.C.; Xu, J.; Wong, C.K. Urban traffic flow prediction using a fuzzy-neural approach. Transport. Res. C-emer. 2002, 10, 85–98. [Google Scholar] [CrossRef]
| Forecast | |
| Update | |
| RMSE | MAPE (%) | |
|---|---|---|
| KF method | 0.5647 | 31.81 |
| C-W method | 0.0368 | 0.16 |
| A-KF method | 0.0356 | 0.14 |
| Proposed method | 0.0340 | 0.12 |
| RMSE | |||||
|---|---|---|---|---|---|
| KF | C-W | A-KF | Proposed Method | KF (Correct Model) | |
| Monday | 842.65 | 394.20 | 152.55 | 85.37 | 77.38 |
| Tuesday | 829.18 | 340.98 | 178.67 | 85.69 | 74.59 |
| Wednesday | 857.94 | 346.18 | 164.94 | 88.85 | 80.74 |
| Thursday | 856.66 | 360.62 | 227.82 | 84.82 | 75.18 |
| Friday | 901.86 | 412.18 | 211.86 | 78.56 | 69.80 |
| Saturday | 584.92 | 210.12 | 134.08 | 41.29 | 39.22 |
| Sunday | 579.88 | 145.76 | 104.04 | 35.77 | 30.16 |
| MAPE (%) | |||||
|---|---|---|---|---|---|
| KF | C-W | A-KF | Proposed Method | KF (Correct Model) | |
| Monday | 99.56 | 39.67 | 15.31 | 7.23 | 6.76 |
| Tuesday | 99.71 | 35.72 | 17.99 | 7.91 | 6.82 |
| Wednesday | 99.70 | 34.62 | 15.15 | 7.58 | 7.00 |
| Thursday | 99.69 | 37.70 | 22.18 | 7.56 | 6.66 |
| Friday | 99.75 | 40.51 | 20.83 | 7.24 | 6.26 |
| Saturday | 99.65 | 35.94 | 22.05 | 6.70 | 6.15 |
| Sunday | 99.48 | 28.73 | 21.58 | 6.60 | 5.74 |
| RMSE | MAPE (%) | |||||
|---|---|---|---|---|---|---|
| C-W | A-KF | Proposed Method | C-W | A-KF | Proposed Method | |
| Monday | 316.82 | 75.17 | 7.99 | 32.91 | 8.55 | 0.47 |
| Tuesday | 266.39 | 104.08 | 11.10 | 28.90 | 11.17 | 1.09 |
| Wednesday | 265.44 | 84.20 | 8.11 | 27.62 | 8.15 | 0.58 |
| Thursday | 285.44 | 152.64 | 9.64 | 31.04 | 15.52 | 0.90 |
| Friday | 342.38 | 142.06 | 8.76 | 34.25 | 14.57 | 0.98 |
| Saturday | 170.90 | 94.86 | 2.07 | 29.79 | 15.90 | 0.55 |
| Sunday | 115.60 | 73.88 | 5.61 | 22.99 | 15.84 | 0.86 |
| RMSE | |||||
|---|---|---|---|---|---|
| KF | C-W | A-KF | Proposed Method | KF (Correct Model) | |
| Monday | 596.29 | 233.39 | 156.14 | 71.47 | 55.70 |
| Tuesday | 591.97 | 204.79 | 145.25 | 70.72 | 53.58 |
| Wednesday | 607.66 | 208.28 | 143.06 | 72.54 | 54.74 |
| Thursday | 606.60 | 213.69 | 161.17 | 95.87 | 52.45 |
| Friday | 649.17 | 252.80 | 222.20 | 68.37 | 50.28 |
| Saturday | 419.31 | 127.81 | 111.40 | 38.30 | 26.53 |
| Sunday | 414.71 | 102.03 | 96.47 | 36.77 | 23.62 |
| MAPE (%) | |||||
|---|---|---|---|---|---|
| KF | C-W | A-KF | Proposed Method | KF (Correct Model) | |
| Monday | 98.39 | 31.56 | 21.61 | 9.34 | 7.12 |
| Tuesday | 98.88 | 28.13 | 19.98 | 9.63 | 7.19 |
| Wednesday | 98.43 | 27.77 | 19.08 | 9.57 | 7.07 |
| Thursday | 97.99 | 28.91 | 21.59 | 10.06 | 6.87 |
| Friday | 98.15 | 32.42 | 25.47 | 8.90 | 6.55 |
| Saturday | 98.50 | 26.12 | 22.56 | 8.86 | 6.42 |
| Sunday | 97.94 | 25.80 | 24.11 | 9.23 | 6.71 |
| RMSE | MAPE (%) | |||||
|---|---|---|---|---|---|---|
| C-W | A-KF | Proposed Method | C-W | A-KF | Proposed Method | |
| Monday | 177.69 | 100.44 | 15.77 | 24.44 | 14.49 | 2.22 |
| Tuesday | 151.21 | 91.67 | 17.14 | 20.94 | 12.79 | 2.44 |
| Wednesday | 153.54 | 88.32 | 17.80 | 20.70 | 12.01 | 2.50 |
| Thursday | 161.24 | 108.72 | 43.42 | 22.04 | 14.72 | 3.19 |
| Friday | 202.52 | 171.92 | 18.09 | 25.87 | 18.92 | 2.35 |
| Saturday | 101.28 | 84.87 | 11.77 | 19.70 | 16.14 | 2.44 |
| Sunday | 78.41 | 72.85 | 13.15 | 19.09 | 17.40 | 2.52 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, X.; Wang, R.; Shi, W.; Li, Z. An Approach for Filter Divergence Suppression in a Sequential Data Assimilation System and Its Application in Short-Term Traffic Flow Forecasting. ISPRS Int. J. Geo-Inf. 2020, 9, 340. https://doi.org/10.3390/ijgi9060340
Tong X, Wang R, Shi W, Li Z. An Approach for Filter Divergence Suppression in a Sequential Data Assimilation System and Its Application in Short-Term Traffic Flow Forecasting. ISPRS International Journal of Geo-Information. 2020; 9(6):340. https://doi.org/10.3390/ijgi9060340
Chicago/Turabian StyleTong, Xiaohua, Runjie Wang, Wenzhong Shi, and Zhiyuan Li. 2020. "An Approach for Filter Divergence Suppression in a Sequential Data Assimilation System and Its Application in Short-Term Traffic Flow Forecasting" ISPRS International Journal of Geo-Information 9, no. 6: 340. https://doi.org/10.3390/ijgi9060340
APA StyleTong, X., Wang, R., Shi, W., & Li, Z. (2020). An Approach for Filter Divergence Suppression in a Sequential Data Assimilation System and Its Application in Short-Term Traffic Flow Forecasting. ISPRS International Journal of Geo-Information, 9(6), 340. https://doi.org/10.3390/ijgi9060340




