Exploring the Potential of Deep Learning Segmentation for Mountain Roads Generalisation
Abstract
1. Introduction
2. Related Work
3. Deep Learning Image Segmentation for Mountain Road Generalisation
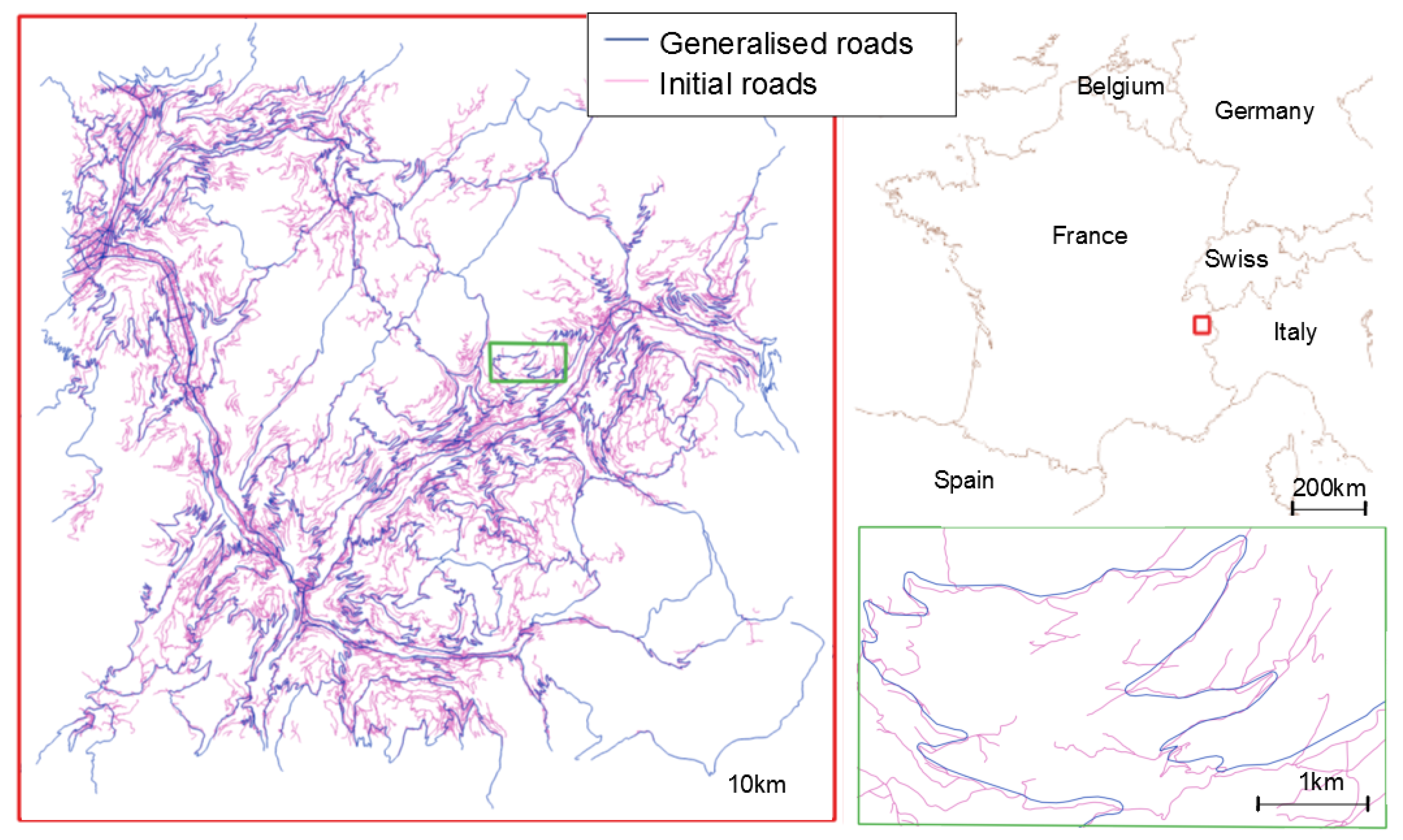
3.1. Use Case
3.2. Mountain Roads Generalisation as a Deep Learning Problem
- coalescence (there should be no symbol coalescence when the width of the road symbol is large enough for display scale);
- granularity (details of the line that are too small to be visible at display scale should be removed);
- position (the generalised road should be close to the initial road);
- smoothness (the generalised line should be smooth);
- general shape preservation (the generalised road should be similar to the initial road);
- sinuous bends and bend series preservation (the presence of sinuous bends or bend series should be preserved, at the risk of removing some of the bends in a series).
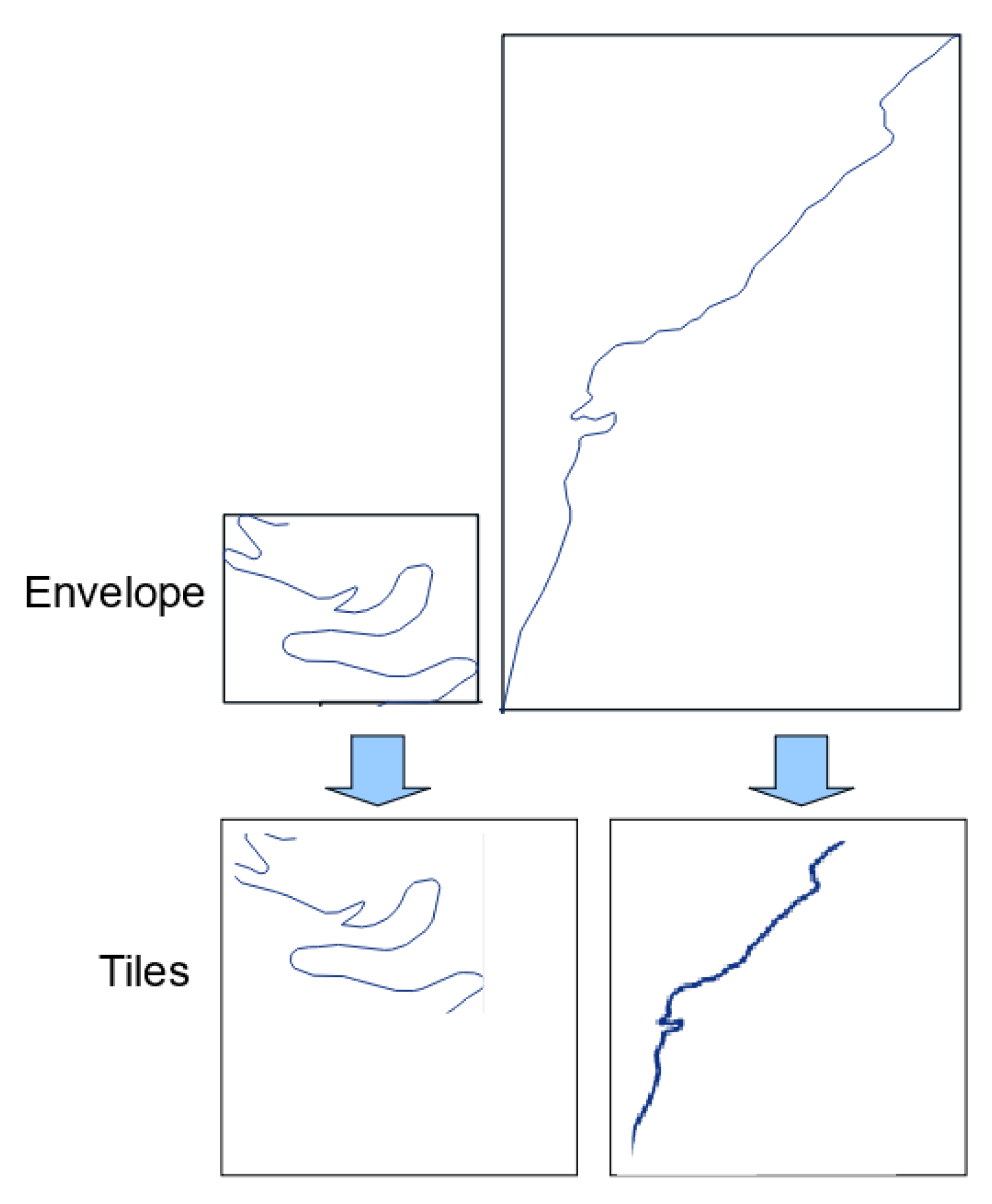
3.3. Creating an Adapted Learning Dataset
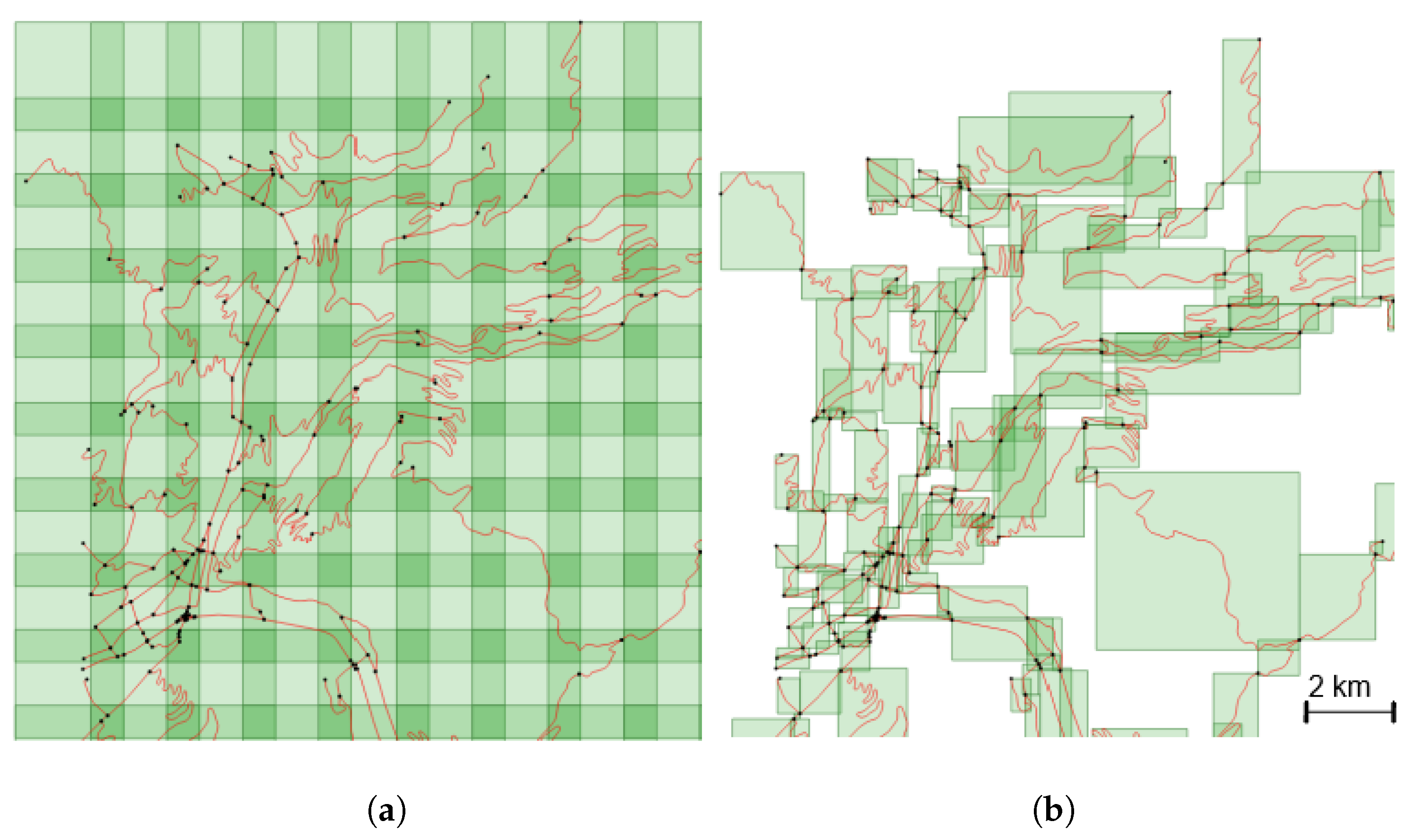
- to slide a fixed-size window over the study area. This method creates images with a fixed scale of the underlying data, but can generate irrelevant (only a very small portion of a road) or empty tiles.
- to overcome the problem of irrelevant tiles, we can use the road objects as a basis to guide tile creation. In this method, the whole geometry of a road is included in the tile, and as roads objects have varying lengths, and geometry extents, this process makes tiles that have different scales.
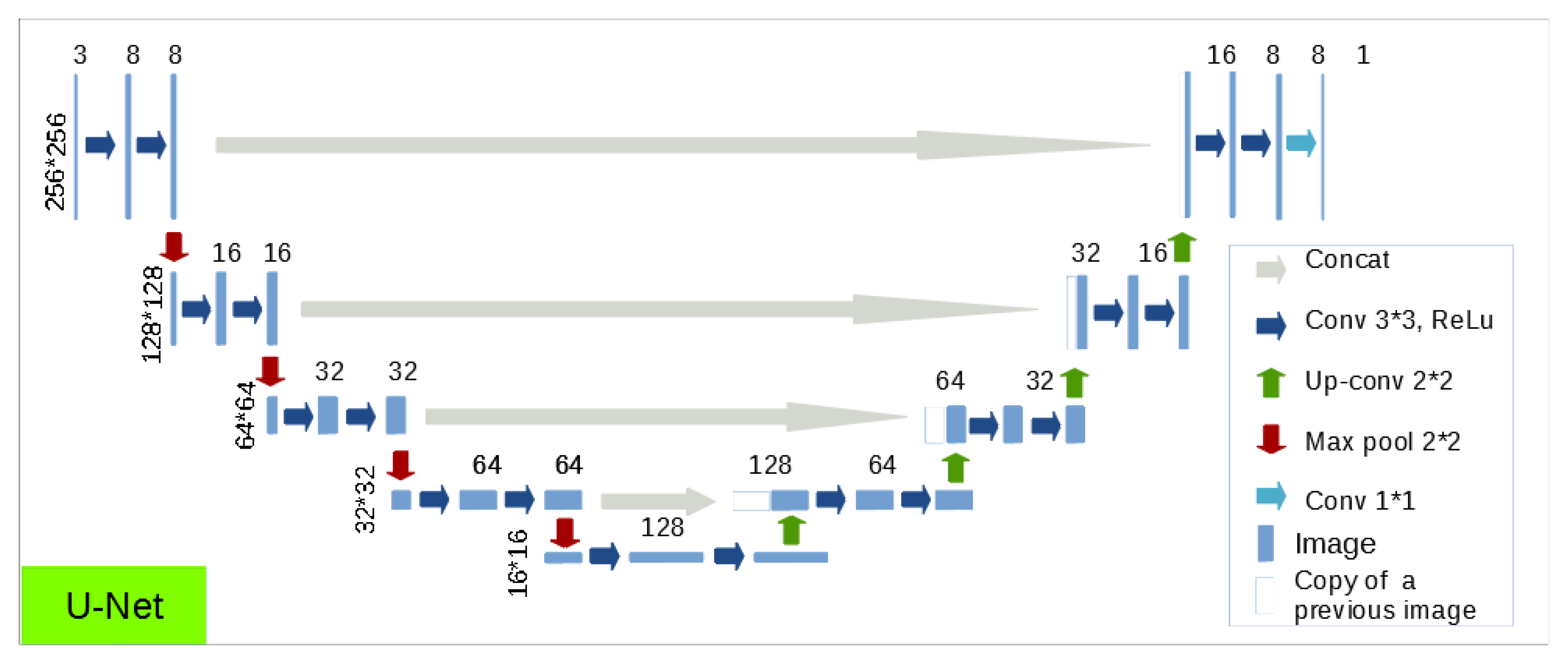
3.4. Choice of a Neural Network Architecture
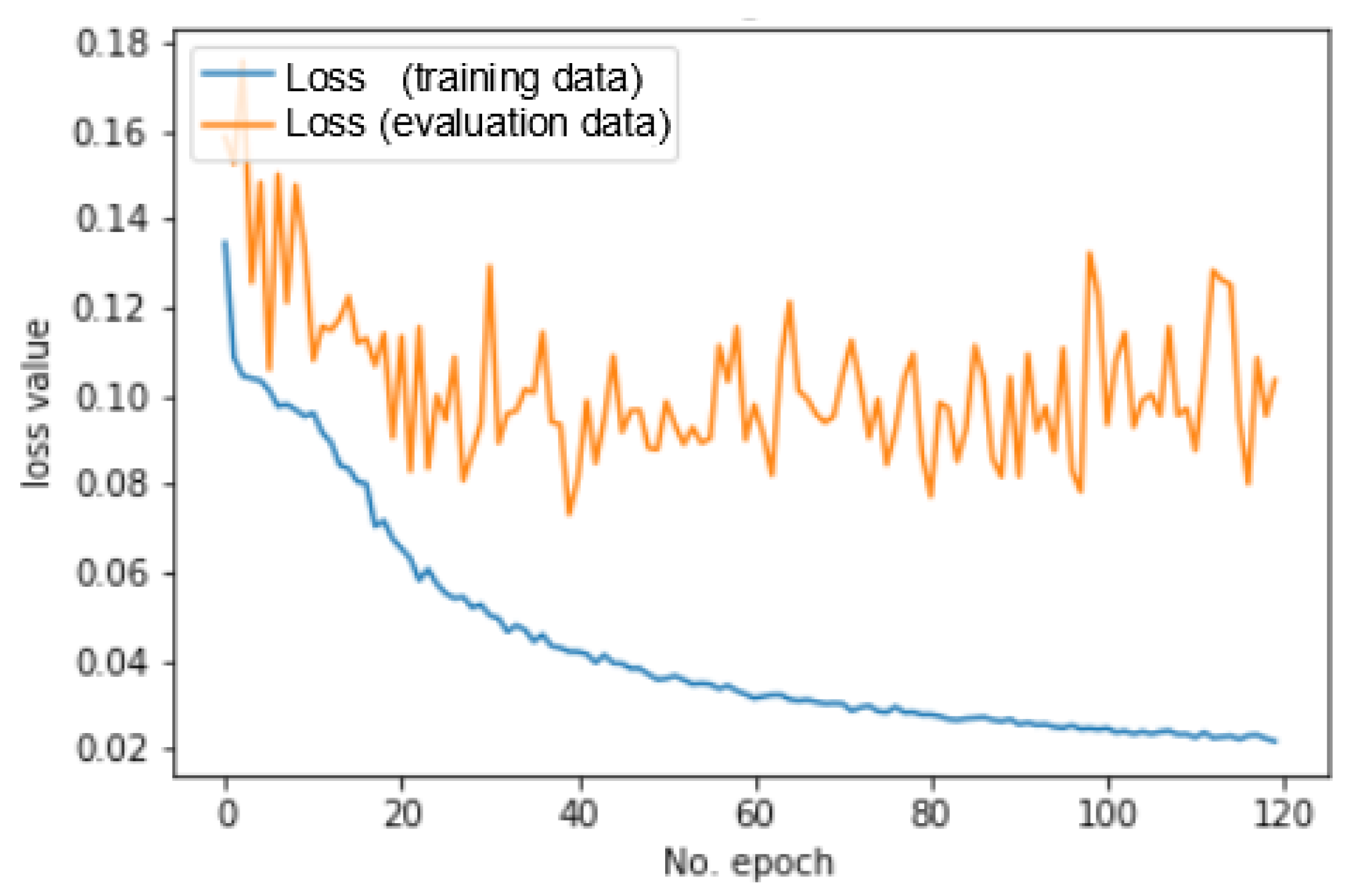
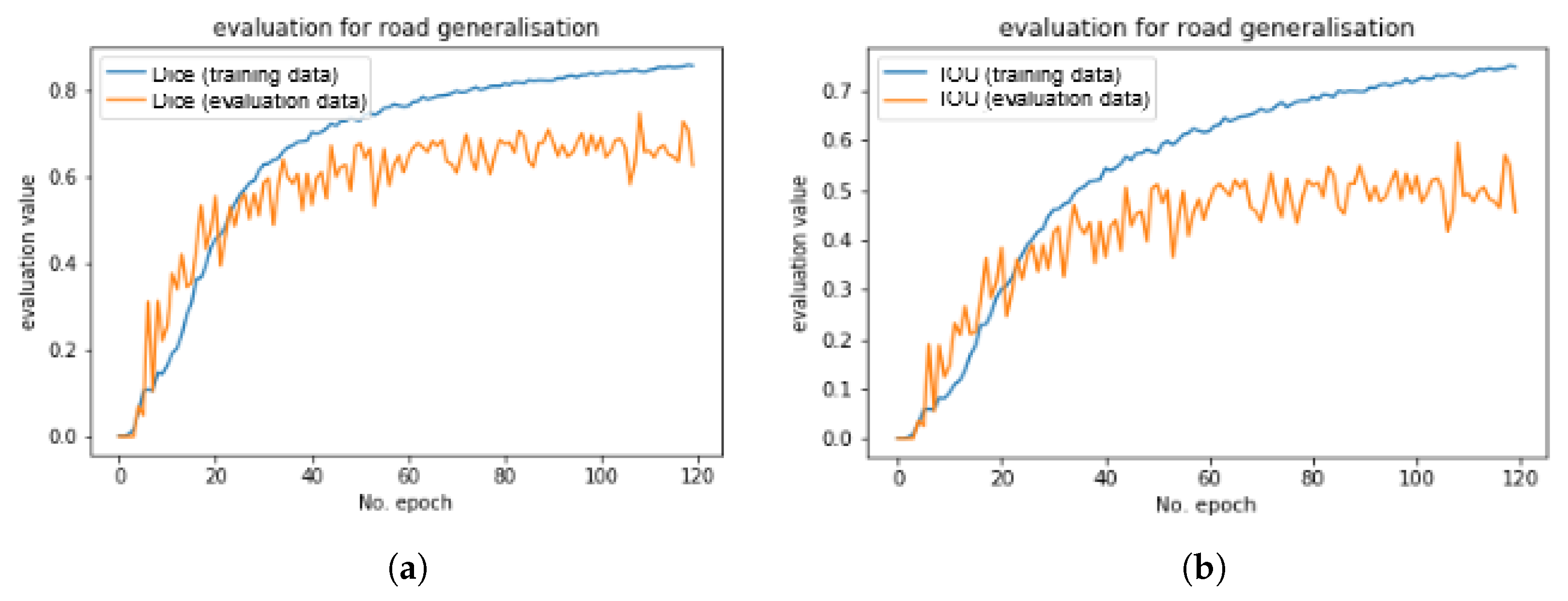
3.5. Evaluation and Loss
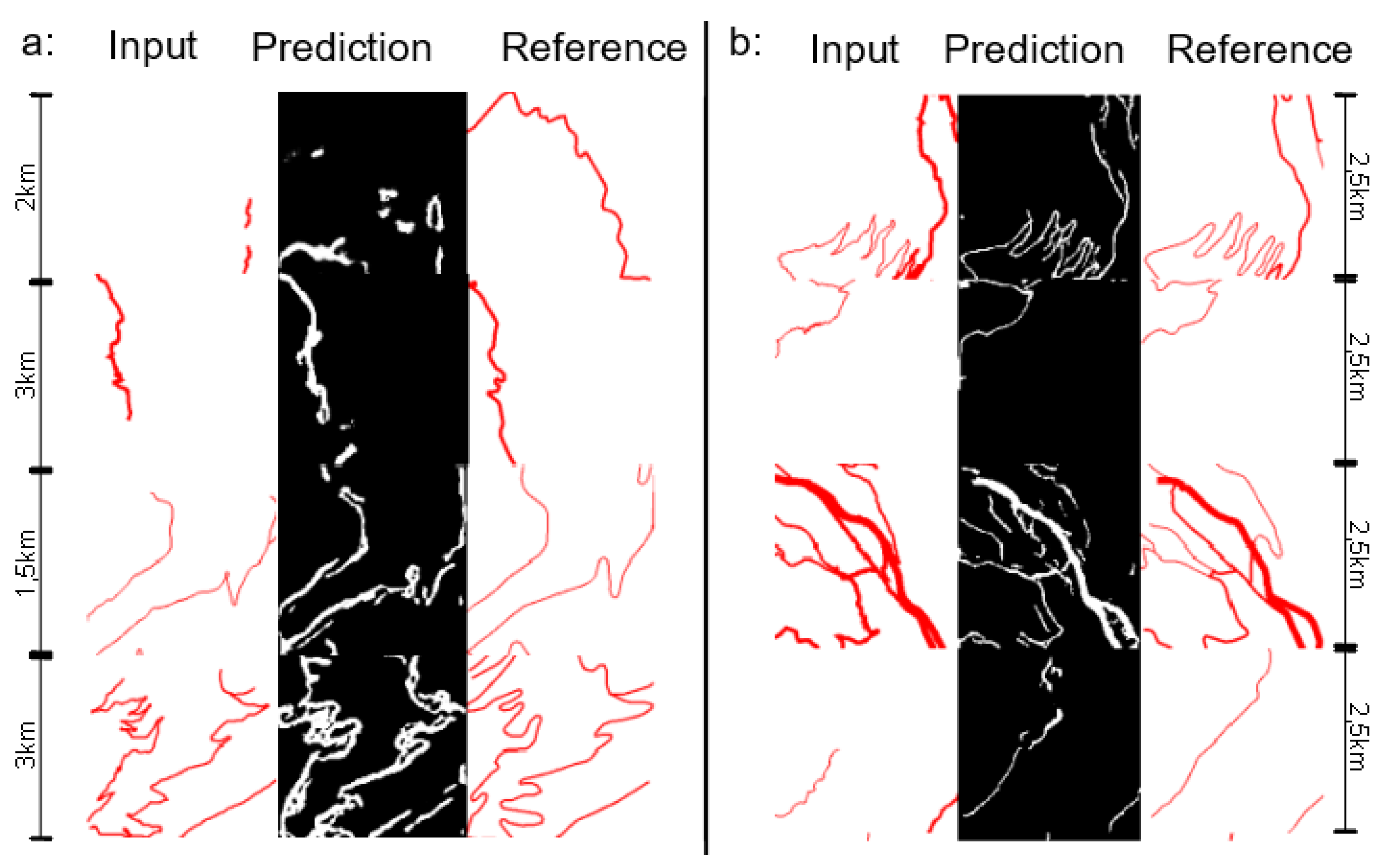
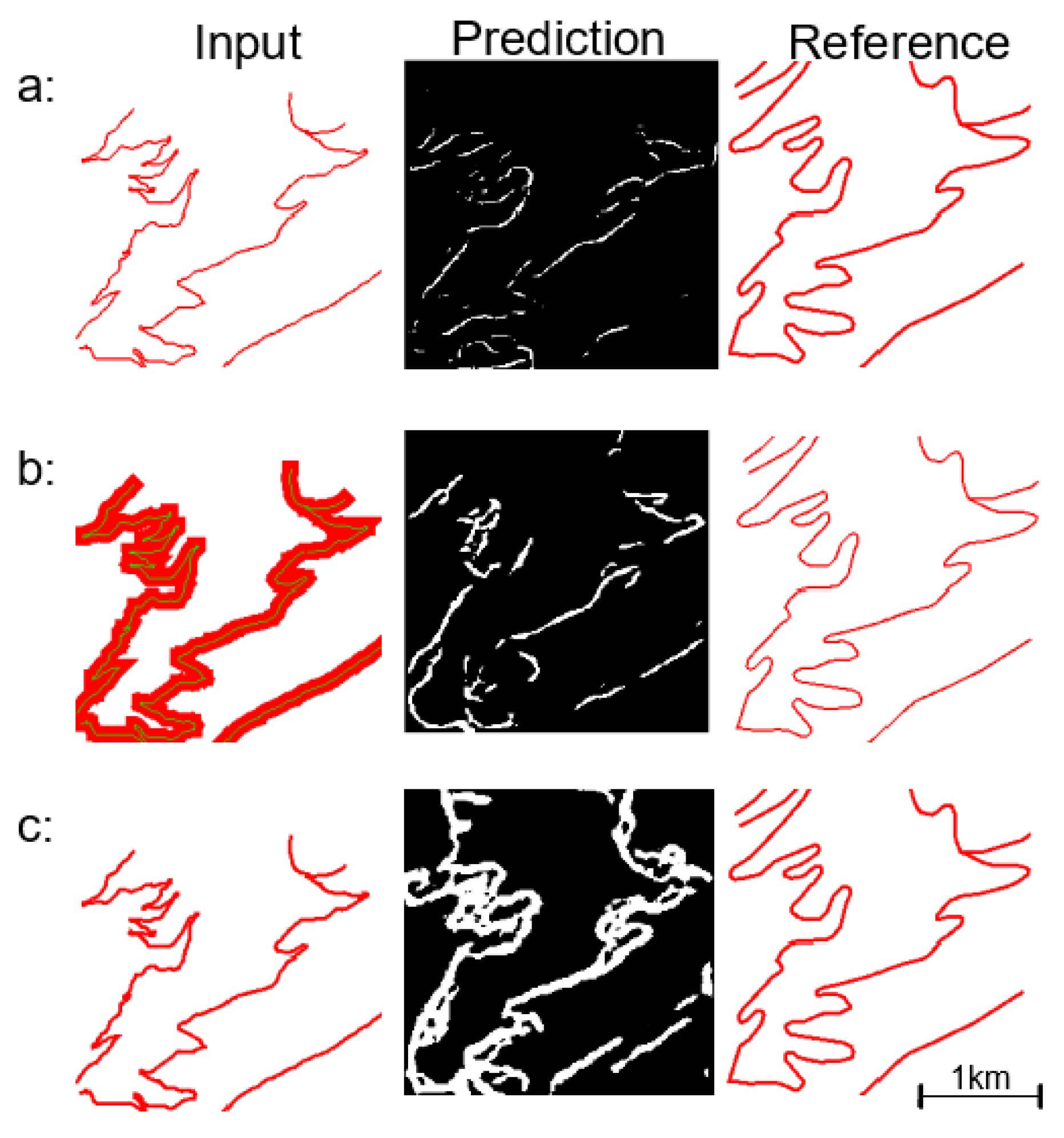
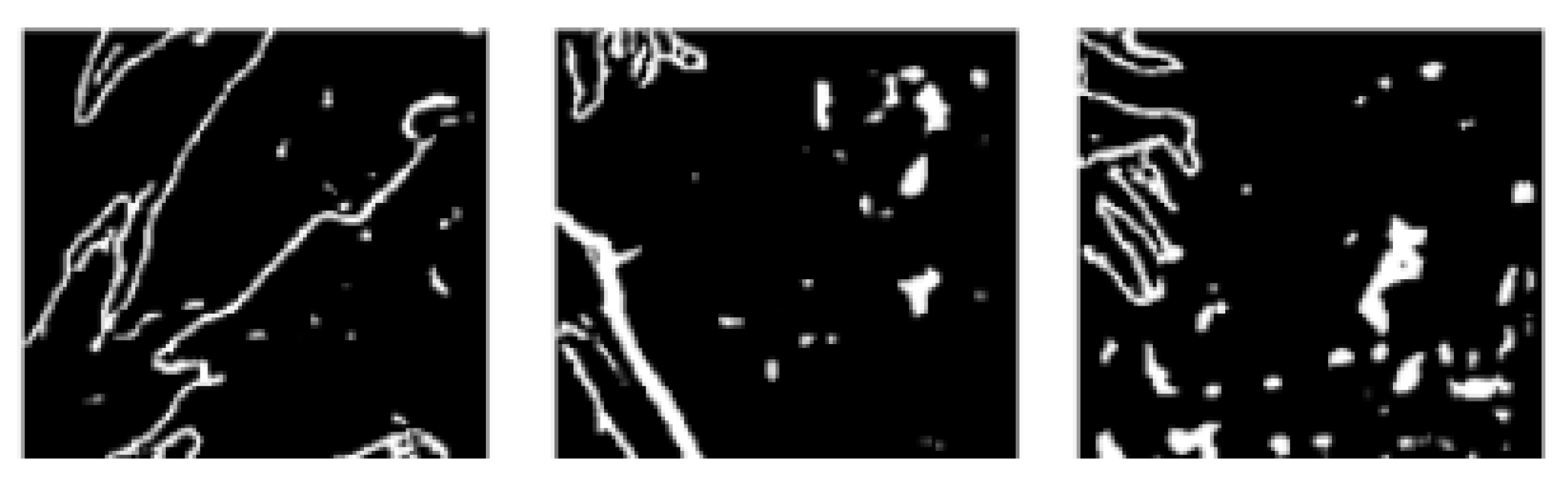
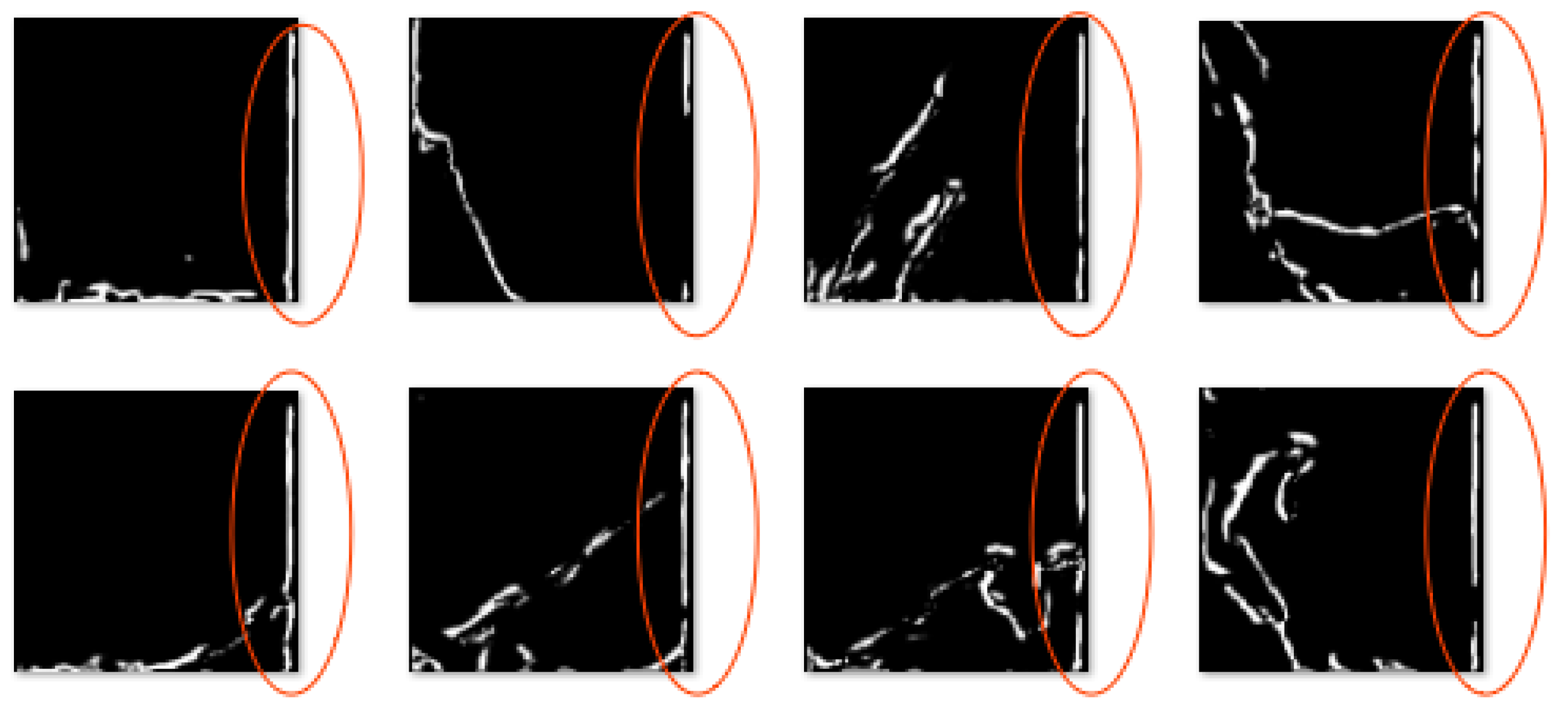
4. Results and Evaluation
4.1. Implementation
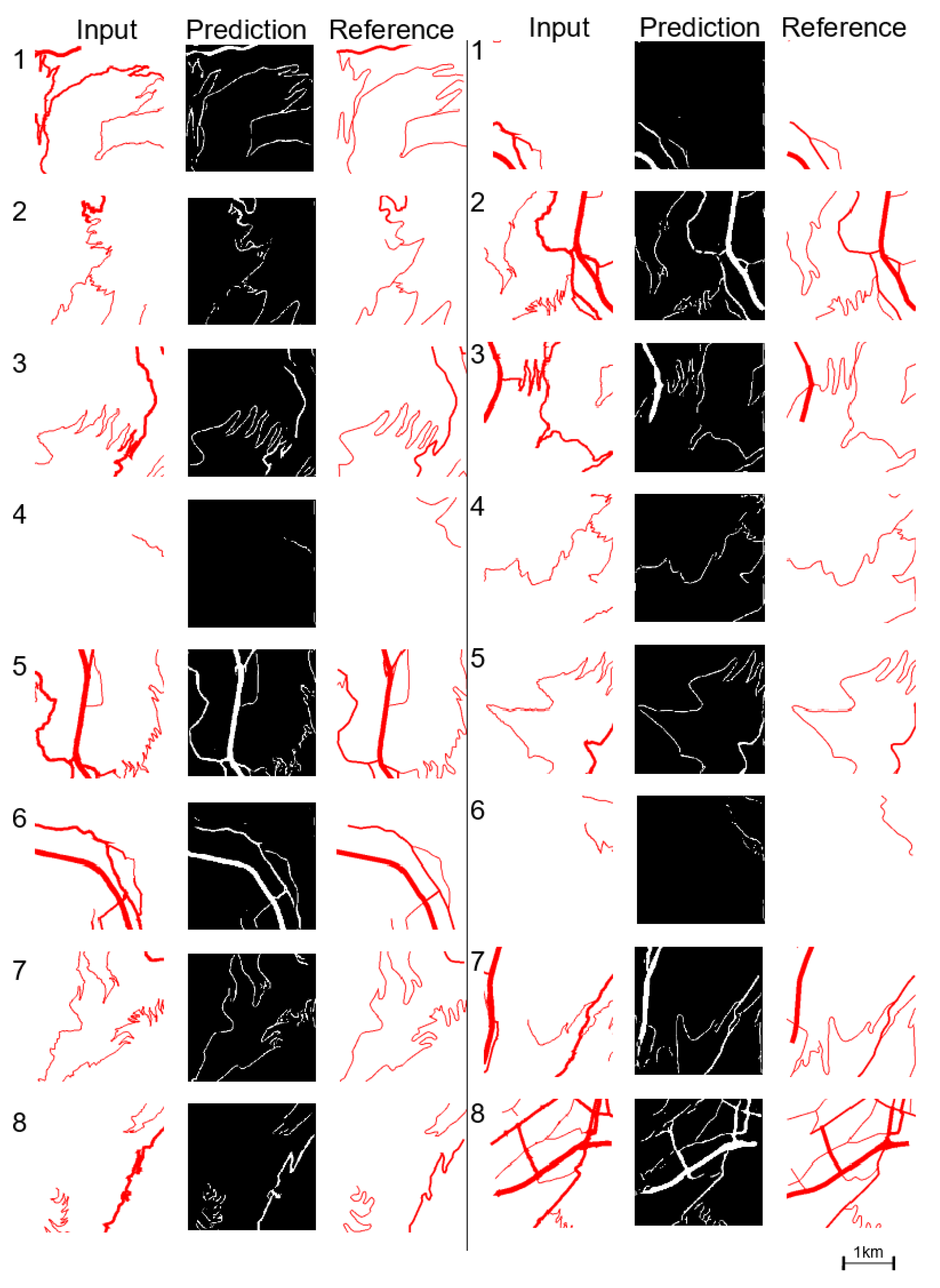
4.2. Results
- tile size is 2.5 km and a pixel represent 10 m;
- overlapping rate between tiles is 60 percent;
- road width represents importance level;
- the included roads are only the roads that matched during the pre-process matching.
4.3. Training Dataset Parameters
4.3.1. Is Data Matching Pre-Process Useful?
4.3.2. Comparison of Tiling Methods
4.3.3. Calibration of the Fixed-Scale Tiling Approach
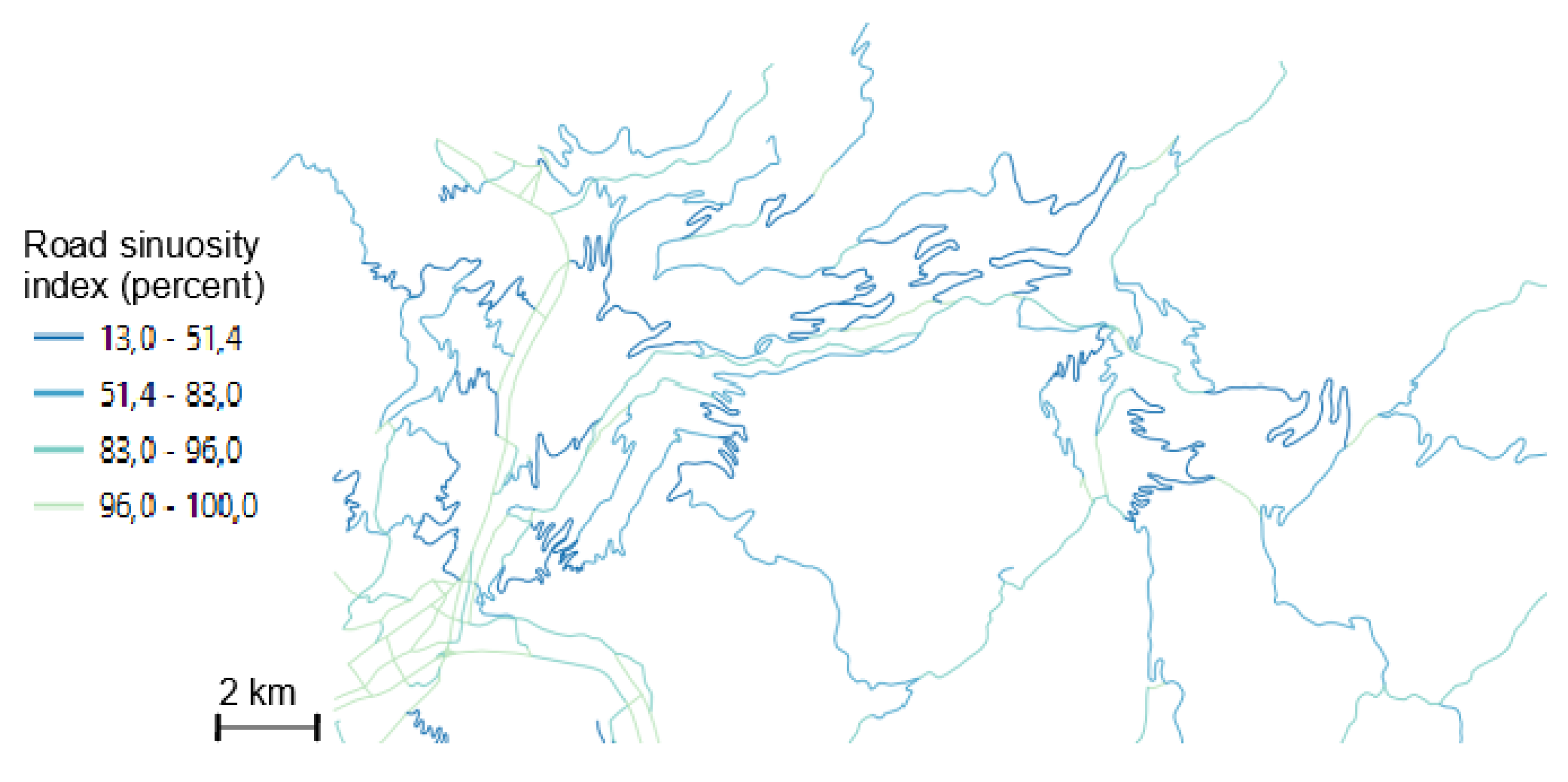
4.3.4. Importance of Road Sinuosity
4.3.5. Summary
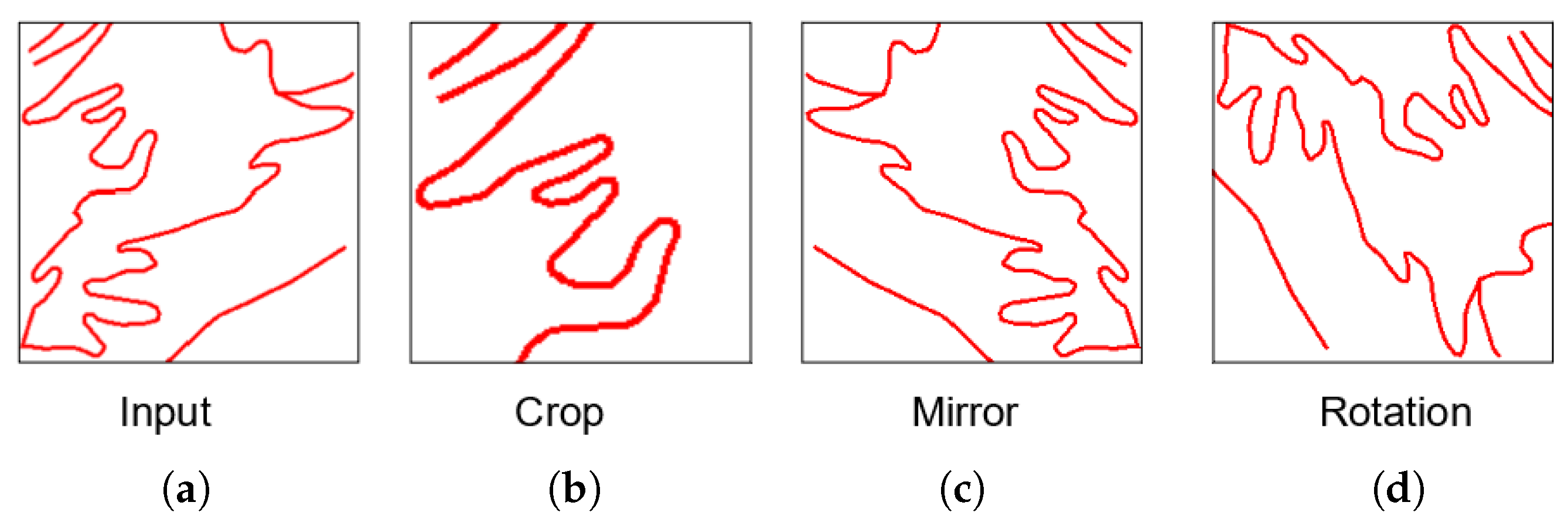
4.4. Usefulness of Data Enrichment and Filtering
- Randomly horizontally and vertically cropping 10% for all images;
- Randomly horizontally and vertically cropping 20% for all images;
- Rotate half of the images in a random way (90, 180, or 270 degrees);
- Rotate all the images in a random way (90, 180, or 270 degrees);
- Rotate all images with the three angles (90, 180, and 270 degrees).
5. Discussion
- the evaluation measure, and associated loss function should be improved;
- our dataset has a limited size and it does not contain enough examples of very narrow and sinuous bend series;
- we also faced computation time and memory limitations.
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Stanislawski, L.V.; Buttenfield, B.P.; Bereuter, P.; Savino, S.; Brewer, C.A. Generalisation Operators. In Abstracting Geographic Information in a Data Rich World; Burghardt, D., Duchêne, C., Mackaness, W., Eds.; Lecture Notes in Geoinformation and Cartography; Springer International Publishing: Cham, Switzerland, 2014; pp. 157–195. [Google Scholar] [CrossRef]
- Duchêne, C.; Baella, B.; Brewer, C.A.; Burghardt, D.; Buttenfield, B.P.; Gaffuri, J.; Käuferle, D.; Lecordix, F.; Maugeais, E.; Nijhuis, R.; et al. Generalisation in Practice Within National Mapping Agencies. In Abstracting Geographic Information in a Data Rich World; Burghardt, D., Duchêne, C., Mackaness, W., Eds.; Lecture Notes in Geoinformation and Cartography; Springer International Publishing: Cham, Switzerland, 2014; pp. 329–391. [Google Scholar] [CrossRef]
- Regnauld, N.; Touya, G.; Gould, N.; Foerster, T. Process Modelling, Web Services and Geoprocessing. In Abstracting Geographic Information in a Data Rich World; Burghardt, D., Duchêne, C., Mackaness, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 198–225. [Google Scholar]
- Weibel, R.; Keller, S.; Reichenbacher, T. Overcoming the knowledge acquisition bottleneck in map generalization: The role of interactive systems and computational intelligence. In Spatial Information Theory A Theoretical Basis for GIS; Frank, A.U., Kuhn, W., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germny, 1995; Volume 988, pp. 139–156. [Google Scholar] [CrossRef]
- Sester, M. Kwoledge acquisition for automatic interpretation of spatial data. Int. J. Geograph. Inf. Sci. 2000, 14, 1–24. [Google Scholar] [CrossRef]
- Kilpelainen, T. Knowledge Acquisition for Generalization Rules. Cartogr. Geogr. Inf. Sci. 2000, 27, 41–50. [Google Scholar] [CrossRef]
- Mustière, S.; Zucker, J.D.; Saitta, L. Abstraction-Based Machine Learning Approach To Cartographic Generalisation. In Proceedings of the 9th International Symposium on Spatial Data Handling; IGU: Beijing, China, 2000; Volume 1a, pp. 50–63. [Google Scholar]
- Touya, G.; Zhang, X.; Lokhat, I. Is deep learning the new agent for map generalization? Int. J. Cartogr. 2019, 5, 142–157. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Volume abs/1505.04597, pp. 234–241. [Google Scholar]
- Feng, Y.; Thiemann, F.; Sester, M. Learning cartographic building generalization with deep convolutional neural networks. ISPRS J. Geo-Inf. 2019, 8, 258. [Google Scholar] [CrossRef]
- Robert, C.T.; Dianne, E.R. The ‘Good Continuation’ Principle of Perceptual Organization applied to the Generalization of Road Networks. In Proceedings of the ICA Proceedings, Ottawa, ON, Canada, 14–21 August 1999. [Google Scholar]
- Touya, G. A Road Network Selection Process Based on Data Enrichment and Structure Detection. Trans. GIS 2010, 14, 595–614. [Google Scholar] [CrossRef]
- Benz, S.; Weibel, R. Road network selection using an extended stroke-mesh combination algorithm. In Proceedings of the 16th ICA Workshop on Generalisation and Multiple Representation, Dresden, Germany, 23–24 August 2013. [Google Scholar]
- Visvalingam, M.; Williamon, P.J. Simplification and Generalization of Large Scale Data for Roads: A Comparison of Two Filtring Algorithms. Cartogr. Geogr. Inf. Syst. 1995, 22, 264–275. [Google Scholar] [CrossRef]
- Lecordix, F.; Plazanet, C.; Lagrange, J.P. A Platform for Research in Generalization: Application to Caricature. GeoInformatica 1997, 1, 161–182. [Google Scholar] [CrossRef]
- Duchêne, C. Individual Road Generalisation in the 1997–2000 AGENT European Project; Technical Report; IGN, COGIT Lab: Saint-Mandé, France, 2014. [Google Scholar]
- Bader, M.; Barrault, M. Cartographic Displacement in Generalization: Introducing Elastic Beams. In Proceedings of the 4th ICA Workshop on Progress in Automated Map Generalisation, Beijing, China, 2–4 August 2001. [Google Scholar]
- Sester, M. Optimization approaches for generalization and data abstraction. Int. J. Geogr. Inf. Sci. 2005, 19, 871–897. [Google Scholar] [CrossRef]
- Mustiere, S. GALBE: Adaptative generalization. The need for an adaptative process for automated generalisation an exemple on roads. In Proceedings of the 1st GIS PlaNet Conference, Lisbon, Portugal, 7–11 September 1998. [Google Scholar]
- Zhou, Q.; Li, Z. A comparative study of various strategies to concatenate road segments into strokes for map generalization. Int. J. Geogr. Inf. Sci. 2012, 26, 691–715. [Google Scholar] [CrossRef]
- García-Balboa, J.L.; Ariza-López, F.J. Generalization-oriented road line classification by means of an artificial neural network. Geoinformatica 2008, 12, 289–312. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, Z. A comparative study of various supervised learning approaches to selective omission in a road network. Cartogr. J. 2016, 54, 254–264. [Google Scholar] [CrossRef]
- Kang, Y.; Gao, S.; Roth, R. Transferring Multiscale Map Style Using Generative Adversarial Network. Int. J. Cartogr. 2019, 5, 115–141. [Google Scholar] [CrossRef]
- Mackaness, W.A.; Ruas, A. Chapter 5—Evaluation in the Map Generalisation Process. In Generalisation of Geographic Information; Mackaness, W.A., Ruas, A., Sarjakoski, L.T., Eds.; International Cartographic Association, Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; pp. 89–111. [Google Scholar] [CrossRef]
- Stoter, J.; Zhang, X.; Stigmar, H.; Harrie, L. Evaluation in Generalisation. In Abstracting Geographic Information in a Data Rich World; Burghardt, D., Duchêne, C., Mackaness, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 259–297. [Google Scholar]
- Touya, G. Social Welfare to Assess the Global Legibility of a Generalized Map. In International Conference on Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mustiere, S.; Devogele, T. Matching networks with different levels of detail. Geoinformatica 2008, 12, 435–453. [Google Scholar] [CrossRef]
- Olteanu-Raimond, A.M.; Mustière, S.; Ruas, A. Knowledge Formalization for Vector Data Matching Using Belief Theory. J. Spat. Inf. Sci. 2015, 10, 21–46. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Shunbao, L.; Zhongqiang, B.; Yan, B. Errors Prediction for Vector-to-Raster Conversion Based on Map Load and Cell Size. Chin. Geogr. Sci. 2012, 22, 695–704. [Google Scholar]
- Touya, G.; Lokhat, I. Deep Learning for Enrichment of Vector Spatial Databases: Application to Highway Interchange. ACM Trans. Spat. Algorithms Syst. 2020, 6, 1–21. [Google Scholar] [CrossRef]
- Peter, B.; Weibel, R. Using vector and raster-based techniques in categorical map generalization. In Proceedings of the Third ICA Workshop on Progress in Automated Map Generalization, Ottawa, ON, Canada, 12–14 August 1999. [Google Scholar]
- Touya, G.; Berli, J.; Lokhat, I.; Regnauld, N. Experiments to Distribute and Parallelize Map Generalization Processes. Cartogr. J. 2017, 54, 322–332. [Google Scholar] [CrossRef]
- Ruas, A. Modèle de Généralisation de Données Gégraphiques à Base de Contraintes et d’Autonomie. Ph.D. Thesis, Université de Marne la Vallée, Champs-sur-Marne, France, 1999. [Google Scholar]
- Shorten, C.; Khoshgoftaa, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Simo-Serra, E.; Iizuka, S.; Sasaki, K.; Ishikawa, H. Learning to Simplify: Fully Convolutional Networks for Rough Sketch Cleanup. ACM Trans. Graph. 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Olaf, R.; Philipp, F.; Thomas, B. U-Net: Convolutional Networks for BiomedicalImage Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Gabriela, C.; Diane, L.; Florent, P. What is a good evaluation measure for semantic segmentation? In Proceedings of the BMVC, Bristol, UK, 9–13 September 2013. [Google Scholar]
- Chollet, F. Deep Learning with Python; Apress: Berkeley, CA, USA, 2018. [Google Scholar]
- Touya, G.; Lokhat, I.; Duchêne, C. CartAGen: An Open Source Research Platform for Map Generalization. In Proceedings of the ICA, Tokyo, Japan, 15–20 July 2019; Volume 2, pp. 1–9. [Google Scholar] [CrossRef]
- Touya, G.; Hoarau, C.; Christophe, S. Clutter and Map Legibility in Automated Cartography: A Research Agenda. Cartogr. Int. J. Geogr. Inf. Geovis. 2016, 51, 198–207. [Google Scholar] [CrossRef]
- Dumont, M.; Touya, G.; Duchêne, C. Assessing the Variation of Visual Complexity in Multi-Scale Maps with Clutter Measures. In Proceedings of the ICA Workshop on Generalisation and Multiple Representation, lsinki, Finland, 14 June 2016. [Google Scholar]
- Gatys, L.A.; Ecker, A.; Bethge, M. Image Style Transfer Using Convolutional Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2414–2423. [Google Scholar] [CrossRef]


| Width in Pixel | Symbolization at 1:25,000 | Attribute Values Translation at 1:250,000 |
|---|---|---|
| 1 | 5 | Irrelevant, forbidden, local narrow roads, lane |
| 2 | 4 | Regional roads and narrow regional roads |
| 3 | 3 | Regional roads with bike path |
| 4 | Ø | Major roads |
| 5 | 2 | Highway |
| Method | Test | Training Size | IOU | Dice | Visual Rank |
|---|---|---|---|---|---|
| object-based | reference | 688 | 0.05 | 0.1 | REF |
| object-based | special bias correction | 688 | 0.05 | 0.1 | − |
| object-based | no bias correction | 688 | 0.05 | 0.1 | − |
| object-based | training only on sinuous tiles | 262 | 0.2 | 0.3 | − |
| object-based | training only on not sinuous tiles | 426 | 0.2 | 0.3 | − |
| fixed-size | reference | 560 | 0.2 | 0.3 | REF |
| fixed-size | initial tile with all roads | 560 | 0.1 | 0.2 | − |
| fixed-size | no bias correction | 560 | 0 | 0 | − |
| fixed-size | tiles with 50% overlap | 790 | 0.4 | 0.5 | + |
| fixed-size | tiles with 60% overlap | 1255 | 0.5 | 0.6 | + |
| fixed-size | tiles size 3 × 3 km | 411 | 0.2 | 0.3 | = |
| fixed-size | tiles size 5 × 5 km | 182 | 0.3 | 0.4 | − |
| fixed-size | training only on sinuous tiles | 284 | 0.1 | 0.2 | − |
| fixed-size | training only on not sinuous tiles | 324 | 0.2 | 0.3 | − |
| Test | Training Size | IOU | Dice | Visual Rank |
|---|---|---|---|---|
| reference | 688 | 0.05 | 0,1 | REF |
| augmentation with crop of 10% | 1376 | 0.1 | 0.2 | + |
| augmentation with crop of 20% | 1376 | 0.1 | 0.2 | = |
| augmentation with rotation for half of the images | 1049 | 0.05 | 0.1 | − |
| augmentation with rotation for all images | 1376 | 0.1 | 0.2 | − |
| augmentation with rotation in 3 angles for all images | 2752 | 0.1 | 0.2 | − |
| Test | Training Size | IOU | Dice | Visual Rank |
|---|---|---|---|---|
| reference | 560 | 0.2 | 0.3 | REF |
| augmentation with crop of 10% | 1120 | 0.3 | 0.4 | − |
| augmentation with crop of 20% | 1120 | 0.3 | 0.4 | − |
| augmentation with rotation for half of the images | 826 | 0.2 | 0.4 | = |
| augmentation with rotation for all images | 1120 | 0.2 | 0.4 | = |
| augmentation with rotation in 3 angles for all images | 2240 | 0.2 | 0.4 | = |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Courtial, A.; El Ayedi, A.; Touya, G.; Zhang, X. Exploring the Potential of Deep Learning Segmentation for Mountain Roads Generalisation. ISPRS Int. J. Geo-Inf. 2020, 9, 338. https://doi.org/10.3390/ijgi9050338
Courtial A, El Ayedi A, Touya G, Zhang X. Exploring the Potential of Deep Learning Segmentation for Mountain Roads Generalisation. ISPRS International Journal of Geo-Information. 2020; 9(5):338. https://doi.org/10.3390/ijgi9050338
Chicago/Turabian StyleCourtial, Azelle, Achraf El Ayedi, Guillaume Touya, and Xiang Zhang. 2020. "Exploring the Potential of Deep Learning Segmentation for Mountain Roads Generalisation" ISPRS International Journal of Geo-Information 9, no. 5: 338. https://doi.org/10.3390/ijgi9050338
APA StyleCourtial, A., El Ayedi, A., Touya, G., & Zhang, X. (2020). Exploring the Potential of Deep Learning Segmentation for Mountain Roads Generalisation. ISPRS International Journal of Geo-Information, 9(5), 338. https://doi.org/10.3390/ijgi9050338






