Subjective or Objective? How Objective Measures Relate to Subjective Life Satisfaction in Europe
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Subjective Data
2.1.2. Objective Data
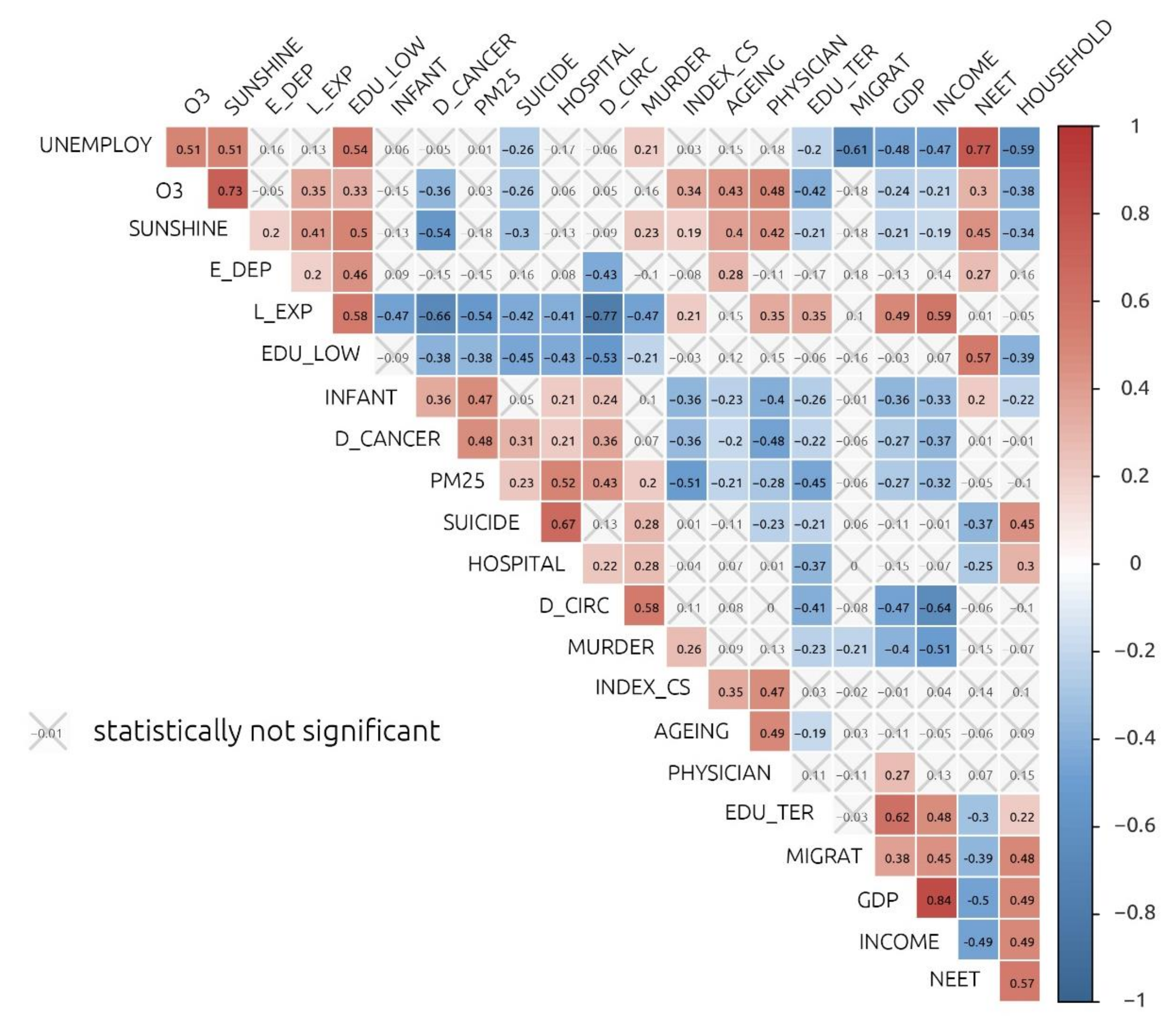
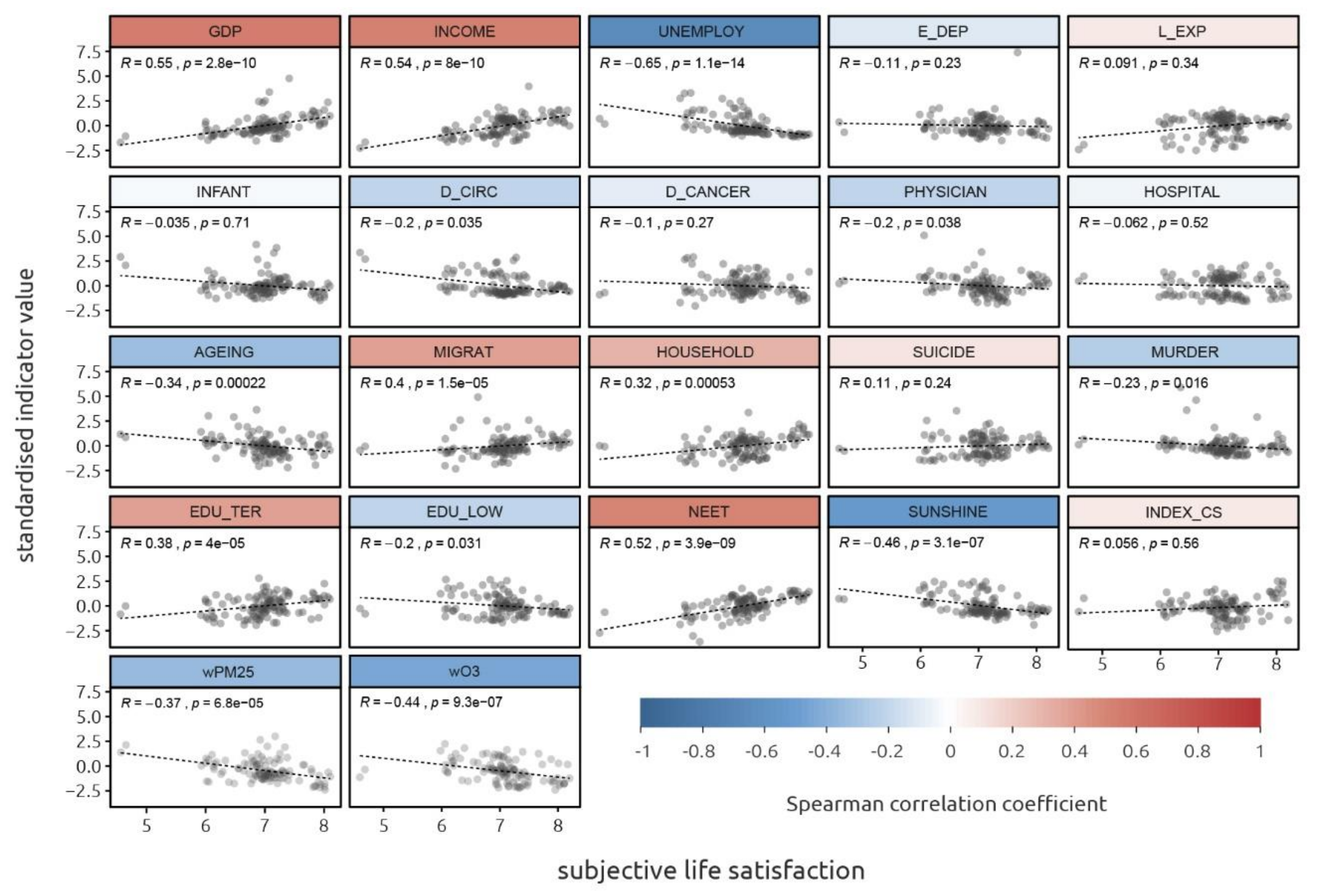
2.2. Data analysis
3. Results
| Indicator | aL | aC | aU | aC − aL | aU − aC |
|---|---|---|---|---|---|
| intercept | 9.731 | 9.731 | 9.731 | 0 | 0 |
| INCOME ** | −17,766 | −17,766 | −17,766 | 0 | 0 |
| E_DEP | −0.0023 | −0.0023 | −0.0023 | 0 | 0 |
| INFANT ** | −0.0497 | 0.0708 | 0.0708 | 0.1206 | 0 |
| D_CANCER | 0.0001 | 0.0001 | 0.0022 | 0 | 0.0020 |
| PHYSICIAN * | −0.1392 | −0.0895 | −0.0895 | 0.0497 | 0 |
| HOSPITAL ** | −0.0069 | −0.0069 | −0.0069 | 0 | 0 |
| AGEING ** | −0.0055 | -0.0055 | −0.0055 | 0 | 0 |
| MIGRAT | −0.0058 | −0.0058 | −0.0058 | 0 | 0 |
| HOUSEHOLD | 0.0104 | 0.0104 | 0.0104 | 0 | 0 |
| SUICIDE | 0.0007 | 0.0007 | 0.0014 | 0 | 0.0135 |
| MURDER | −0.2509 | 0.0443 | 0.0443 | 0.295 | 0 |
| EDU_TER ** | −0.0146 | −0.0146 | −0.0146 | 0 | 0 |
| NEET ** | −0.0427 | −0.0427 | −0.0423 | 0 | 0.0004 |
| INDEX_CS ** | 0.0923 | 0.0923 | 0.0923 | 0 | 0 |
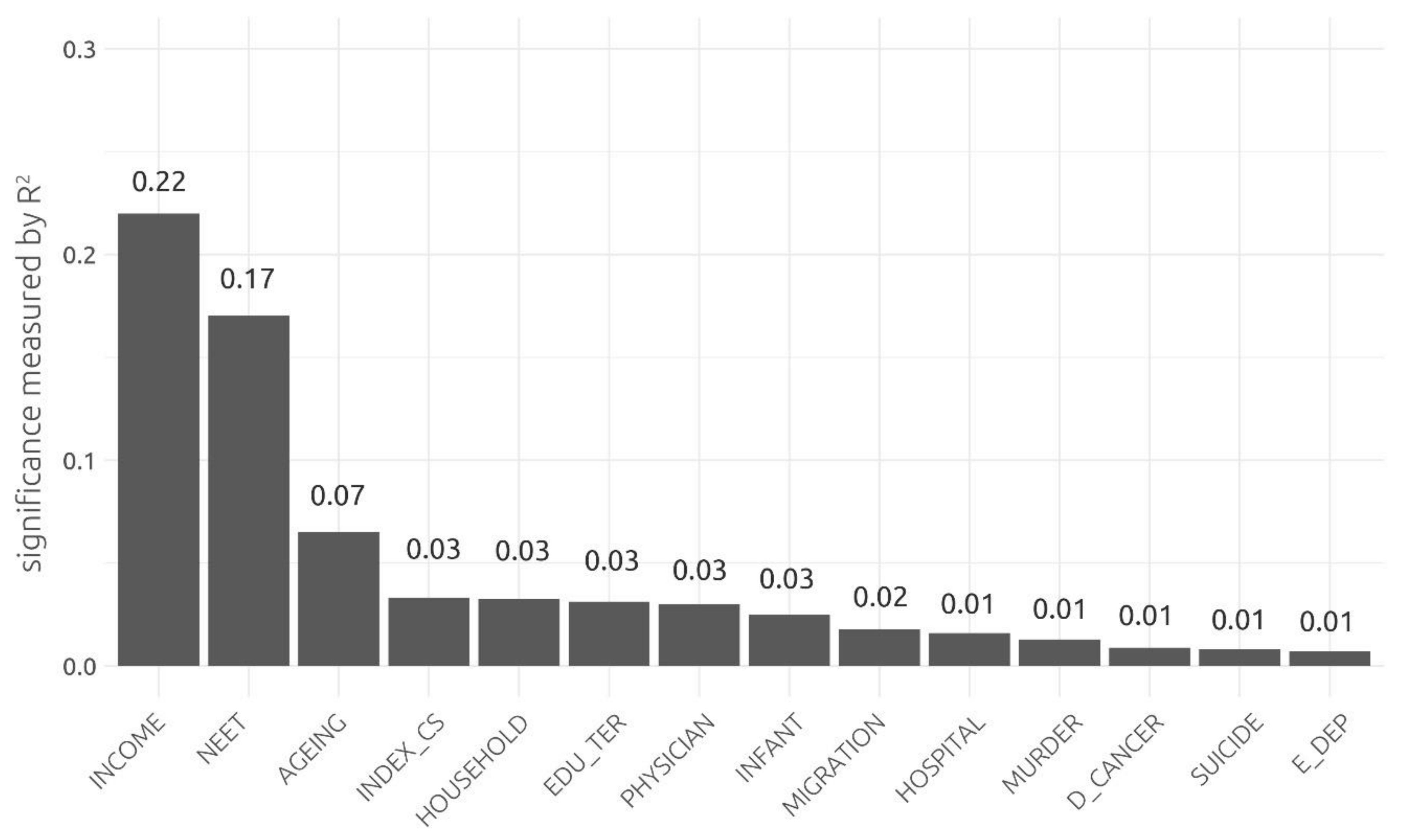
- Easy to interpret (INCOME, INDEX_CS, NEET): the relationship of these indicators with life satisfaction is not surprising and can be easily explained. The INCOME indicator (the negative coefficient value caused by the transformation of the input data) proved to be the most significant. It can be agreed that with a better financial situation of the household, the satisfaction of the household members increases. Based on the model, hypothetically, life satisfaction measured with the Cantril Ladder would increase by one point if the household income was increased by approximately 17,800 EUR PPS. Similarly, in the case of INDEX_CS, the quality of the landscape can also be easily perceived and valued. The results suggest that respondents perceive the quality of landscape expressed by the INDEX_CS indicator in a similar way and mostly positively. To implicitly express how a change in the quality of landscape influences subjective satisfaction is not that straightforward, since the quality of the landscape is a complex unitless index. Finally, the NEET indicator, as a measure of the labour market (eventually a measure of the transfer of education to the labour market), can be also perceived in life satisfaction. The concerned group of young people can be affected by growing up under the unfavourable conditions, which might lead to long-term life dissatisfaction. Moreover, this indicator is correlated with overall long-term unemployment (correlation coefficient, 0.77), which leads to material insecurity and has a negative impact in the context of life satisfaction.
- Difficult to interpret (AGEING): the signum of the coefficients of this indicator is the same as the expected meaning in the context of quality of life, but its perception for life satisfaction can be biased. In this case, people living in an old society may perceive this fact negatively, as the ageing of the population can cause social and economic dependencies but also disagreements on a personal level (intergenerational incomprehension).
- “Contra-indicators” (EDU_TER, HOSPITAL, PHYSICIAN, INFANT): this group was expected to increase subjective life satisfaction with higher indicative values, since higher levels of these measures are considered positive quality of life indicators. However, regression coefficients were negative against the assumptions of expected meaning in the context of quality of life. These indicators might have some hidden or indirect relationships with life satisfaction, which are not straightforward to explain.
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Indicator | Unit | Indicator Description |
|---|---|---|
| GDP per capita | euro PPS per capita | Gross domestic product. |
| Net disposable household income per capita | euro PPS per capita | The total income of a household, after tax and other deductions, that is available for spending or saving, divided by the number of household members converted into equalized adults; household members are equalized or made equivalent by weighting each according to their age. |
| Long-term unemployment | % | Expresses the number of long-term unemployed (12 months and more) aged 15–74 as a percentage of the active population of the same age. |
| Economic dependency index | ratio | The ratio of population aged 0–15 and older than 65 years to the size of the economically active population. |
| Life expectancy at birth | year | The mean number of years that a person can expect to live at birth if subjected to current mortality conditions throughout the rest of their life. |
| Infant mortality rate | ‰ | The infant mortality rate is defined as the number of deaths of children under one year of age during the year to the number of live births in that year. The value is expressed per 1000 live births. |
| Death rate—diseases of the circulatory system | ratio | Standardised death rate (weighted average of age-specific mortality rates) caused by diseases of the circulatory system according to the International Statistical Classification of Diseases and Related Health Problems (categories I00–I99). Expressed as a rate per 100,000 inhabitants. |
| Death rate—diseases of the circulatory system | ratio | Standardised death rate (weighted average of age-specific mortality rates) caused by malignant neoplasms according to the International Statistical Classification of Diseases and Related Health Problems (categories C00–C97). Expressed as a rate per 100,000 inhabitants. |
| Physician rate | ratio | The number of physicians per 10,000 inhabitants. |
| Hospital capacity rate | ratio | The number of hospital beds per 10,000 inhabitants. |
| Ageing index | ratio | The ratio of the population older than 65 years to the population aged 0–15. |
| Migration | ratio | Crude rate of net migration (including statistical adjustment during the year to the average population in that year). Three-year average was applied; data expressed as a rate per 10,000 inhabitants. |
| Household size | % | Ratio of one person households to the total number of households. |
| Suicide rate | ratio | Derived from the death rate caused by an intentional self-harm according to the International Statistical Classification of Diseases and Related Health Problems (categories X60–X84). Expressed as a rate per 100,000 inhabitants. |
| Criminality (murder rate) | ratio | Derived from the death rate caused by an assault according to the International Statistical Classification of Diseases and Related Health Problems (categories X85–Y09). Expressed as a rate per 100,000 inhabitants. |
| Ratio of tertiary educated | % | Defined as the percentage of the population aged 25–64 who successfully completed tertiary studies. This education level refers to ISCED (International Standard Classification of Education) 2011 level 5–8. |
| Ratio of low educated | % | Defined as the percentage of the population aged 25–64 who successfully completed less than primary or primary and lower secondary education. This education level refers to ISCED (International Standard Classification of Education) 2011 level 0–2. |
| NEET | % | Young people aged between 15 and 24, Neither in Employment nor Education or Training. |
| Sunshine duration | hour | Annual sum of sunshine duration. |
| Quality of landscape | index | Cultural function of the landscape based on the study by Burkhard et al. [59]. Index calculated from the Corine Land Cover 2012 as the average area-weighted score. |
| Ozone concentration (SOMO35) | μg·m−3·day | The annual average of the sum of the amounts by which maximum daily 8-h concentrations (in μg·m−3) exceed 70 μg·m−3 on each day in a calendar year. |
| Air pollution (PM2.5 particles) | μg·m−3 | The annual mean PM2.5 concentrations based on interpolation of observed values in control stations. |
Appendix B
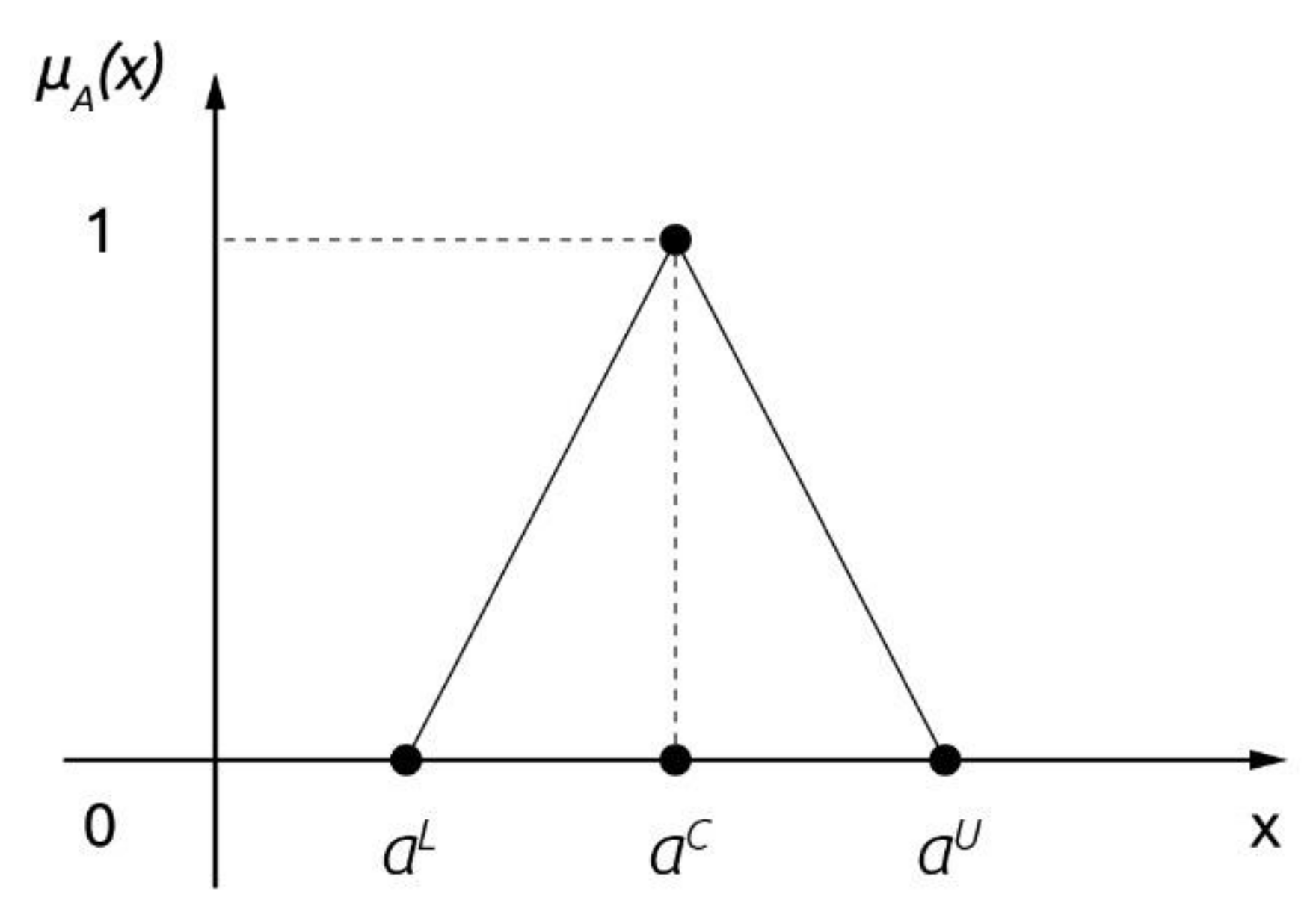
Appendix C
| Author | Domains Used |
|---|---|
| Greyling and Tregenna (2017) [21] | housing, social relationships, economic dimension, health, governance, civic engagement, safety, life satisfaction, environmental satisfaction |
| Dasgupta and Weale (1992) [60] | income, life expectancy, infant mortality, adult literacy, political rights, civil rights |
| González, Cárcaba and Ventura (2011) [61] | health, education, personal activities, housing, political voice, social connections, environmental conditions, personal/economic insecurity |
| Martín and Mendoza (2013) [20] | health, education, personal activities, political voice and government, social connections, environmental conditions, personal/economic insecurity |
| Rao et al. (2012) [62] | environmental conditions, material welfare, population |
| Morais and Camanho (2011) [5] | demography, social aspects, economic aspects, training and education, environment, transport and travel, information society, culture and recreation |
| Felce and Perry (1995) [63] | physical wellbeing, material wellbeing, social wellbeing, development and activities, emotional wellbeing |
| Murgaš and Klobučník (2016) [64] | family, health, education, job, natural environment |
| Lo and Faber (1997) [65] | land cover, NDVI, population density, income, home value, college graduates |
| Li and Weng (2007) [66] | population density, housing density, green vegetation, surface temperature, family income, per capita income, poverty level, college graduates, unemployment, house value, number of rooms |
| Bérenger and Verdier-Chouchane (2007) [17] | standard of health, standard of education, material wellbeing |
| Lagas et al. (2015) [40] | public services, purchasing power and employment, housing, social environment, natural environment, recreation, health, education, governance |
| Baliamoune-Lutz and McGillivray (2006) [67] | health, education, income |
| Hancock (2000) [68] | social aspect, health, economic aspect, environmental aspect |
| Puskorius (2015) [69] | health, employment and occupancy rate, environment, lifetime, income, consumption, consumption, environment, accommodation education, spiritual, moral-ethical and cultural values, gender equality, safety, law, order, corruption |
| Morris (1978) [70] | health, education |
| Hardeman and Dijkstra (2014) [71] | health, knowledge, income |
| Eurostat (2015) [35] | material living conditions, employment, education, health, leisure and social interactions, economic and physical safety, governance and basic rights, natural and living environment, overall life satisfaction |
| Annoni, Weziak-Bialowolska, and Dijkstra (2012) [39] | earnings and income, absolute poverty, relative poverty, objective health, subjective health |
| United Nations Development Programme (1990) [72] | long and healthy life, knowledge, a decent standard of living |
| OECD (2011) [23] | income, job, housing, health, education, environment, safety, civil engagement, accessibility of services, community, life satisfaction |
| UK Deprivation index (2007) | income, employment, education, skills and training, health, crime, barriers to housing and services, access to services, housing, physical environment |
| Smith (1972) [73] | income, wealth and employment, environment, health, social disorganisation, alienation and participation, education |
| Veenhoven (1996) [74] | life expectancy, life satisfaction |
| Diener (1995) [75] | physicians per capita, subjective wellbeing, university attendance, income equality, major environmental treaties, monetary savings rate, income per capita |
| Pena and Somarriba (2008) [37] | employment, accommodation, education, leisure, income, health, social relations, satisfaction |
| Glatzer (2007) [1] | health, wealth, knowledge, freedom & governance, equity |
| Rahman et al. (2005) [22] | social relations, emotional wellbeing, health, job, material wellbeing, community participation, safety, quality of environment |
| Veneri and Murtin (2018) [76] | income, health, job |
| Canadian Wellbeing Index (2011) | community vitality, democratic engagement, education, environment, healthy population, leisure and culture, living standards, time use |
| European Index of Social Progress (2016) | nutrition and basic medical care, shelter, personal safety, access to basic knowledge, access to information and communication technology, environmental quality, personal rights, tolerance and inclusion |
References
- Glatzer, W. Quality of Life in the European Union and the United States of America: Evidence from Comprehensive Indices. Appl. Res. Qual. Life 2007, 1, 169–188. [Google Scholar] [CrossRef]
- Smith, D.M. The Geography of Social Well-Being in the United States: An Introduction to Territorial Social Indicators. Soc. Indic. Res. 1973, 1, 257–259. [Google Scholar]
- Campbell, A.; Converse, P.E.; Rodgers, W.L. The Quality of American Life: Perceptions, Evaluations and Satisfactions; Russell Sage Foundation: New York NY, USA, 1976; ISBN 9780871541949. [Google Scholar]
- Andrews, F.M. Research on the Quality of Life; Survey Research Center—Instiute of Social Research: Ann Arbor, MI, USA, 1986; ISBN 9780879443085. [Google Scholar]
- Morais, P.; Camanho, A.S. Evaluation of performance of European cities with the aim to promote quality of life improvements. Omega 2011, 39, 398–409. [Google Scholar] [CrossRef]
- Liu, B.C. Quality of Life Indicators in U.S. Metropolitan Areas: A Statistical Analysis. In Praeger Special Studies in U.S. Economic, Social, and Political Issues; Praeger: New York NY, USA, 1976. [Google Scholar]
- Emerson, E. Evaluating the impact of deinstitutionalization on the lives of mentally retarded people. Am. J. Ment. Defic. 1985, 90, 277–288. [Google Scholar]
- Meeberg, G.A. Quality of life: A concept analysis. J. Adv. Nurs. 1993, 18, 32–38. [Google Scholar] [CrossRef]
- Cummins, R.A. The Comprehensive Quality of Life Scale—Intellectual/Cognitive Disability; School of Psychology: Melbourne, Australia, 1997; ISBN 07300-27252. [Google Scholar]
- Somarriba, N.; Pena, B. Synthetic indicators of quality of life in Europe. Soc. Indic. Res. 2009, 94, 115–133. [Google Scholar] [CrossRef]
- Andráško, I. Quality of Life: An Introduction to the Concept; Masarykova Univerzita: Brno, Czech Republic, 2013; ISBN 978-80-210-6669-4. [Google Scholar]
- Cantril, H. The Pattern of Human Concerns; Rutgers University Press: New Jersey NJ, USA, 1965. [Google Scholar]
- Diener, E.; Suh, E. Measuring quality of life: Economic, social, and subjective indicators. Soc. Indic. Res. 1997, 40, 189–216. [Google Scholar] [CrossRef]
- Kahneman, D.; Krueger, A.B. Developments in the Measurement of Subjective Well-Being. J. Econ. Perspect. 2006, 20, 3–24. [Google Scholar] [CrossRef]
- Dodge, R.; Daly, A.; Huyton, J.; Sanders, L. The challenge of defining wellbeing. Int. J. Wellbeing 2012, 2, 222–235. [Google Scholar] [CrossRef]
- Cambridge University Press Well-being. Available online: https://dictionary.cambridge.org/dictionary/english/well-being (accessed on 18 June 2019).
- Bérenger, V.; Verdier-Chouchane, A. Multidimensional Measures of Well-Being: Standard of Living and Quality of Life Across Countries. World Dev. 2007, 35, 1259–1276. [Google Scholar] [CrossRef]
- Easterlin, R.A. Does Economic Growth Improve the Human Lot? Some Empirical Evidence. In Nations and Households in Economic Growth; David, P.A., Reder, M.W., Eds.; Elsevier: New York, NY, USA, 1974; Volume 8, pp. 89–125. [Google Scholar]
- Mederly, P.; Novacek, P.; Topercer, J. Sustainable development assessment: Quality and sustainability of life indicators at global, national and regional level. Foresight 2003, 5, 42–49. [Google Scholar] [CrossRef]
- Martín, J.C.; Mendoza, C. A DEA Approach to Measure the Quality-of-Life in the Municipalities of the Canary Islands. Soc. Indic. Res. 2013, 113, 335–353. [Google Scholar] [CrossRef]
- Greyling, T.; Tregenna, F. Construction and Analysis of a Composite Quality of Life Index for a Region of South Africa. Soc. Indic. Res. 2017, 131, 887–930. [Google Scholar] [CrossRef]
- Rahman, T.; Mittelhammer, R.C.; Wandschneider, P. Measuring the Quality of Life across Countries A Sensitivity Analysis of Well-being Indices; World Institute for Development Economic Research: Helsinki, Finland, 2005; Volume 5, ISBN 9291906735. [Google Scholar]
- OECD OECD Well Being Indicators Compendium; OECD Publishinig: Paris, France, 2011.
- Oswald, A.J.; Wu, S. Objective Confirmation of Subjective Measures of Human Well-Being: Evidence from the U.S.A. Science 2010, 327, 576–579. [Google Scholar] [CrossRef]
- Boarinii, R.; Comolai, M.; Smith, C.; Machin, R.; de Keulenaerii, F. What Makes for a Better Life. In The Determinants of Subjective Well-Being in OECD Countries—Evidence from the Gallup World Poll; OECD Publishing: Paris, France, 2012. [Google Scholar]
- Hoskins, P.; May, D. The Determinants of Life Satisfaction. In Proceedings of the International Association for Research in Income and Wealth General Conference, Dresden, Germany, 21–27 May 2016. [Google Scholar]
- Dolan, P.; Peasgood, T.; White, M. Do we really know what makes us happy? A review of the economic literature on the factors associated with subjective well-being. J. Econ. Psychol. 2008, 29, 94–122. [Google Scholar] [CrossRef]
- Clark, A.E.; Oswald, A.J. Satisfaction and comparison income. J. Public Econ. 1996, 61, 359–381. [Google Scholar] [CrossRef]
- Layard, R. Happiness: Lessons from a New Science, 2nd ed.; Allen Lane: London, UK, 2005; ISBN 9780713997699. [Google Scholar]
- Poláčková, J.; Jindrová, A. Measurement of Life Satisfaction across the Czech Republic. Statistika 2011, 48, 35–45. [Google Scholar]
- Kämpfer, S.; Mutz, M. On the Sunny Side of Life: Sunshine Effects on Life Satisfaction. Soc. Indic. Res. 2011, 110, 579–595. [Google Scholar] [CrossRef]
- Haslauer, E.; Delmelle, E.C.; Keul, A.; Blaschke, T.; Prinz, T. Comparing Subjective and Objective Quality of Life Criteria: A Case Study of Green Space and Public Transport in Vienna, Austria. Soc. Indic. Res. 2014, 124, 911–927. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Tanaka, H.; Satoru, U.; Asai, K. Linear Regression Analysis with Fuzzy Model. IEEE Trans. Syst. Man. Cybern. 1982, 12, 903–907. [Google Scholar]
- Rogge, N.; Van Nijverseel, I. Quality of Life in the European Union: A Multidimensional Analysis. Soc. Indic. Res. 2019, 141, 765–789. [Google Scholar] [CrossRef]
- Ivaldi, E.; Bonatti, G.; Soliani, R. The Construction of a Synthetic Index Comparing Multidimensional Well-Being in the European Union. Soc. Indic. Res. 2016, 125, 397–430. [Google Scholar] [CrossRef]
- Pena, B.; Somarriba, N. Quality of life and subjective welfare in Europe: An econometric analysis. Appl. Econom. Int. Dev. 2008, 8, 55–66. [Google Scholar]
- Eurostat Quality of Life—Facts and Views; Publications Office of the European Union: Luxembourg, 2015; ISBN 978-92-79-43616-1.
- Annoni, P.; Weziak-Bialowolska, D.; Dijkstra, L. Quality of Life at the Sub-National Level: An Operational Example for the EU.; Publications Office of the European Union: Luxembourg, 2012; Volume EUR 25630, ISBN 9789279277436. [Google Scholar]
- Lagas, P.; Kuiper, R.; Van Dongen, F.; Van Rijn, F.; Amsterdam, H. Van Regional quality of living in Europe. J. ERSA 2015, 2, 1–26. [Google Scholar]
- Petrucci, A.; D’Andrea, S.S. Quality of Life in Europe: Objective and Subjective Indicators. In Advances in Quality of Life Research 2001; Zumbo, B.D., Ed.; Springe: Berlin/Heidelberg, Germany, 2002; pp. 55–88. ISBN 978-90-481-6209-3. [Google Scholar]
- European Commission Communication from the Commission to the Council and the European Parliament on the GDP and Beyond: Measuring Progress in a Changing World; European Union: European Commision: Brussels, Belgium, 2009.
- European Commission Commission Staff Working Document: Progress on “GDP and Beyond” Actions; European Union: Brussels, Belgium, 2013; Volume 1.
- Di Meglio, E. Living Conditions in Europe, 2018th ed.; Meglio, E., Di Kaczmarek-Firth, A., Litwinska, A., Rusu, C., Eds.; Publications Office of the European Union: Luxembourg, 2018; ISBN 978-92-79-86498-8. [Google Scholar]
- Sponsorship Group on Measuring Progress, Well-being and Sustainable Development. Final Report adopted by the European Statistical System Committee; European Statistical System: Luxembourg, 2011; Available online: https://ec.europa.eu/eurostat/documents/7330775/7339383/SpG-Final-report-Progress-wellbeing-and-sustainable-deve/428899a4-9b8d-450c-a511-ae7ae35587cb (accessed on 11 May 2020).
- Ishibuchi, H.; Nii, M. Fuzzy regression using asymmetric fuzzy coefficients and fuzzified neural networks. Fuzzy Sets Syst. 2001, 119, 273–290. [Google Scholar] [CrossRef]
- Nahmias, S. Fuzzy variables. Fuzzy Sets Syst. 1978, 1, 97–110. [Google Scholar] [CrossRef]
- Anile, A.M.; Deodato, S.; Privitera, G. Implementing fuzzy arithmetic. Fuzzy Sets Syst. 1995, 72, 239–250. [Google Scholar] [CrossRef]
- Hanss, M. Applied Fuzzy Arithmetic; Springer Heidelberg: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-24201-7. [Google Scholar]
- Makhorin, A. GLPK (GNU Linear Programming Kit); Department for Applied Informatics, Moscow Aviation Institute: Moscow, Russia, 2012. [Google Scholar]
- Kalogirou, S. Testing local versions of correlation coefficients. Jahrb. für Reg. 2012, 32, 45–61. [Google Scholar] [CrossRef]
- De Vaus, D. Analyzing Social Science Data; SAGE Publications Ltd: London, UK, 2002; ISBN 978-0761959380. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning. In Springer Texts in Statistics; Springer New York: New York, NY, USA, 2014; ISBN 978-1-4614-7137-0. [Google Scholar]
- Azen, R.; Budescu, D.V. The dominance analysis approach for comparing predictors in multiple regression. Psychol. Methods 2003, 8, 129–148. [Google Scholar] [CrossRef]
- Caha, J.; Marek, L.; Dvorský, J. Predicting PM 10 Concentrations Using Fuzzy Kriging. In Hybrid Artificial Intelligent Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 371–381. ISBN 978-3-319-19643-5. [Google Scholar]
- Caha, J.; Nevtípilová, V.; Dvorský, J. Constraint and Preference Modelling for Spatial Decision Making with Use of Possibility Theory. In Hybrid Artificial Intelligence Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 145–155. ISBN 978-3-319-07616-4. [Google Scholar]
- Lucas, R.E.; Donnellan, M.B. How stable is happiness? Using the STARTS model to estimate the stability of life satisfaction. J. Res. Pers. 2007, 41, 1091–1098. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, N.; Clore, G.L. Mood, misattribution, and judgments of well-being: Informative and directive functions of affective states. J. Pers. Soc. Psychol. 1983, 45, 513–523. [Google Scholar] [CrossRef]
- Burkhard, B.; Kroll, F.; Müller, F.; Windhorst, W. Landscapes’ capacities to provide ecosystem services—A concept for land-cover based assessments. Landsc. Online 2009, 15, 1–22. [Google Scholar] [CrossRef]
- Dasgupta, P.; Weale, M. On measuring the quality of life. World Dev. 1992, 20, 119–131. [Google Scholar] [CrossRef]
- González, E.; Cárcaba, A.; Ventura, J. Quality of life ranking of spanish municipalities. Rev. Econ. Apl. 2011, 29, 123–148. [Google Scholar]
- Rao, K.R.M.; Kant, Y.; Gahlaut, N.; Roy, P.S. Assessment of Quality of Life in Uttarakhand, India using geospatial techniques. Geocarto Int. 2012, 27, 315–328. [Google Scholar] [CrossRef]
- Felce, D.; Perry, J. Quality of life: Its definition and measurement. Res. Dev. Disabil. 1995, 16, 51–74. [Google Scholar] [CrossRef]
- Murgaš, F.; Klobučník, M. Municipalities and Regions as Good Places to Live: Index of Quality of Life in the Czech Republic. Appl. Res. Qual. Life 2016, 11, 553–570. [Google Scholar] [CrossRef]
- Lo, C.P.; Faber, B.J. Integration of landsat thematic mapper and census data for quality of life assessment. Remote Sens. Environ. 1997, 62, 143–157. [Google Scholar] [CrossRef]
- Li, G.; Weng, Q. Measuring the quality of life in city of Indianapolis by integration of remote sensing and census data. Int. J. Remote Sens. 2007, 28, 249–267. [Google Scholar] [CrossRef]
- Baliamoune-Lutz, M.; McGillivray, M. Fuzzy well-being achievement in Pacific Asia. J. Asia Pacific Econ. 2006, 11, 168–177. [Google Scholar] [CrossRef]
- Hancock, T. Quality of life indicators and the DHC. South-eastern Ontario 2000. [Google Scholar]
- Puskorius, S. The Methodology of Calculation the Quality of Life Index. Int. J. Inf. Educ. Technol. 2015, 5, 156–159. [Google Scholar] [CrossRef]
- Morris, M.D. A physical quality of life index. Urban Ecol. 1978, 3, 225–240. [Google Scholar] [CrossRef]
- Hardeman, S.; Dijkstra, L. The EU Regional Human Development Index; Publication Office of the European Union: Luxembourg, 2014; ISBN 9789279398612. [Google Scholar]
- United Nations Development Programme Human Development Report 1990; Oxford University Press: New York, NY, USA, 1990.
- Smith, D.M. Geography and social indicators. South African Geogr. J. 1972, 54, 43–57. [Google Scholar] [CrossRef]
- Veenhoven, R. Happy life-expectancy. Soc. Indic. Res. 1996, 39, 1–58. [Google Scholar] [CrossRef]
- Diener, E. A Value Based Index for Measuring National Quality of Life. Soc. Indic. Res. 1995, 36, 107–127. [Google Scholar] [CrossRef]
- Veneri, P.; Murtin, F. Where are the highest living standards? Measuring well-being and inclusiveness in OECD regions. Reg. Stud. 2018, 53, 657–666. [Google Scholar] [CrossRef]
| Domain | Aspect | Unit | Abbreviation |
|---|---|---|---|
| Economic and material welfare | GDP per capita | PPS euro per capita | GDP |
| Net disposable household income per capita | PPS euro per capita | INCOME | |
| Long-term unemployment | % | UNEMPLOY | |
| Economic dependency index | ratio | E_DEP | |
| Health | Life expectancy at birth | year | L_EXP |
| Infant mortality rate | ‰ | INFANT | |
| Death rate—diseases of the circulatory system | rate per 100,000 inhabitants | D_CIRC | |
| Death rate—malignant neoplasms | rate per 100,000 inhabitants | D_CANCER | |
| Social environment | Physician rate | rate per 10,000 inhabitants | PHYSICIAN |
| Hospital capacity rate | rate per 10,000 inhabitants | HOSPITAL | |
| Ageing index | ratio | AGEING | |
| Migration | rate per 10,000 inhabitants | MIGRAT | |
| Household size | % | HOUSEHOLD | |
| Suicide rate | rate per 100,000 inhabitants | SUICIDE | |
| Criminality (murder rate) | rate per 100,000 inhabitants | MURDER | |
| Education | Ratio of tertiary educated | % | EDU_TER |
| Ratio of low educated | % | EDU_LOW | |
| NEET | % | NEET | |
| Natural environment | Sunshine duration | hour | SUNSHINE |
| Quality of landscape | index | INDEX_CS | |
| Air pollution (PM2.5) | μg·m−3 | PM25 | |
| Ozone concentration (SOMO35) | μg·m−3·day | O3 |
| MODEL1 | MODEL2 | |
|---|---|---|
| GDP | 9.25 | x |
| INCOME | 9.73 | 3.76 |
| UNEMPLOY | 6.89 | x |
| E_DEP | 2.56 | 1.53 |
| L_EXP | 36.12 | x |
| INFANT | 3.35 | 1.83 |
| D_CIRC | 27.41 | x |
| D_CANCER | 4.22 | 1.78 |
| PHYSICIAN | 2.91 | 1.81 |
| HOSPITAL | 4.68 | 3.02 |
| AGEING | 2.43 | 1.61 |
| MIGRAT | 2.58 | 2.05 |
| HOUSEHOLD | 3.67 | 2.16 |
| SUICIDE | 3.57 | 3.02 |
| MURDER | 2.95 | 1.80 |
| EDU_TER | 5.44 | 2.64 |
| EDU_LOW | 7.75 | x |
| NEET | 4.86 | 2.26 |
| SUNSHINE | 7.51 | x |
| INDEX_CS | 3.37 | 1.57 |
| PM25 | 5.02 | x |
| O3 | 7.51 | x |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macků, K.; Caha, J.; Pászto, V.; Tuček, P. Subjective or Objective? How Objective Measures Relate to Subjective Life Satisfaction in Europe. ISPRS Int. J. Geo-Inf. 2020, 9, 320. https://doi.org/10.3390/ijgi9050320
Macků K, Caha J, Pászto V, Tuček P. Subjective or Objective? How Objective Measures Relate to Subjective Life Satisfaction in Europe. ISPRS International Journal of Geo-Information. 2020; 9(5):320. https://doi.org/10.3390/ijgi9050320
Chicago/Turabian StyleMacků, Karel, Jan Caha, Vít Pászto, and Pavel Tuček. 2020. "Subjective or Objective? How Objective Measures Relate to Subjective Life Satisfaction in Europe" ISPRS International Journal of Geo-Information 9, no. 5: 320. https://doi.org/10.3390/ijgi9050320
APA StyleMacků, K., Caha, J., Pászto, V., & Tuček, P. (2020). Subjective or Objective? How Objective Measures Relate to Subjective Life Satisfaction in Europe. ISPRS International Journal of Geo-Information, 9(5), 320. https://doi.org/10.3390/ijgi9050320





