When Traditional Selection Fails: How to Improve Settlement Selection for Small-Scale Maps Using Machine Learning
Abstract
1. Introduction
- Which variables are essential in settlement selection for small-scale maps?
- Is there a correlation between the proposed variables?
1.1. Variables Considered in Settlement Selection
1.2. Machine Learning in Cartographic Generalization
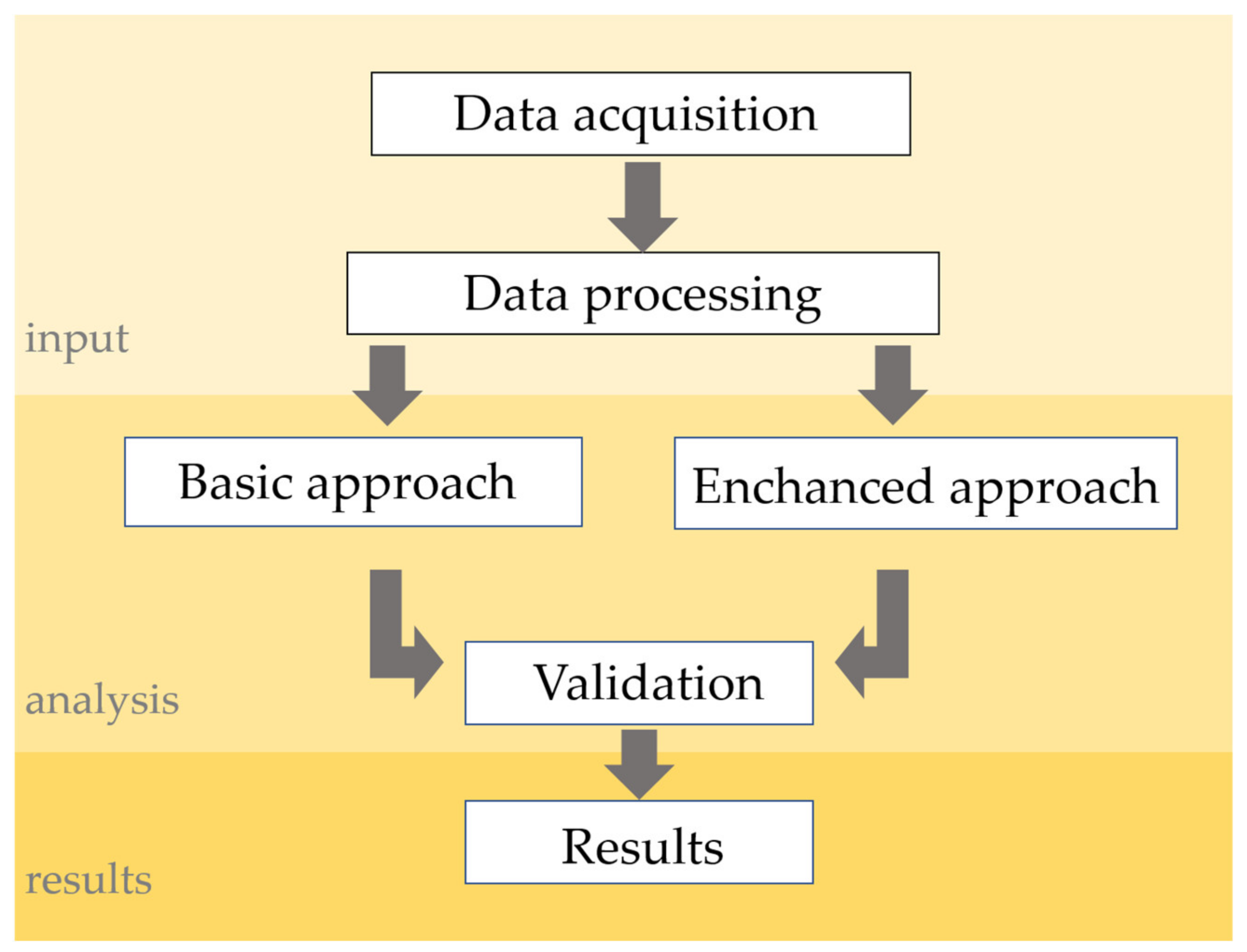
2. Materials and Methods
- Population (number of inhabitants);
- Administrative status (seat of administrative office);
- Settlement type (“city”, “village”, “hamlet”, etc.);
- Population density (calculated per district).
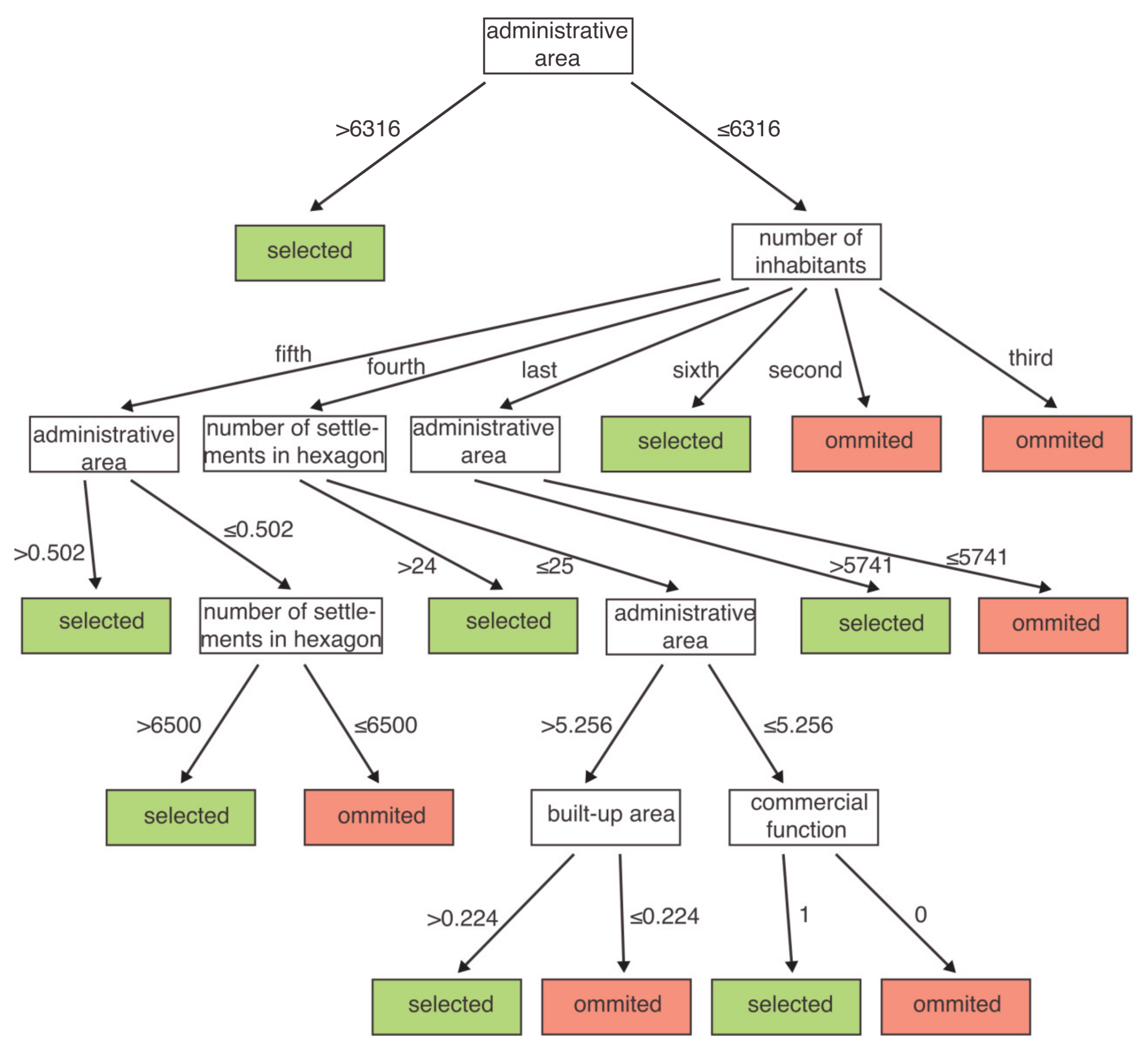
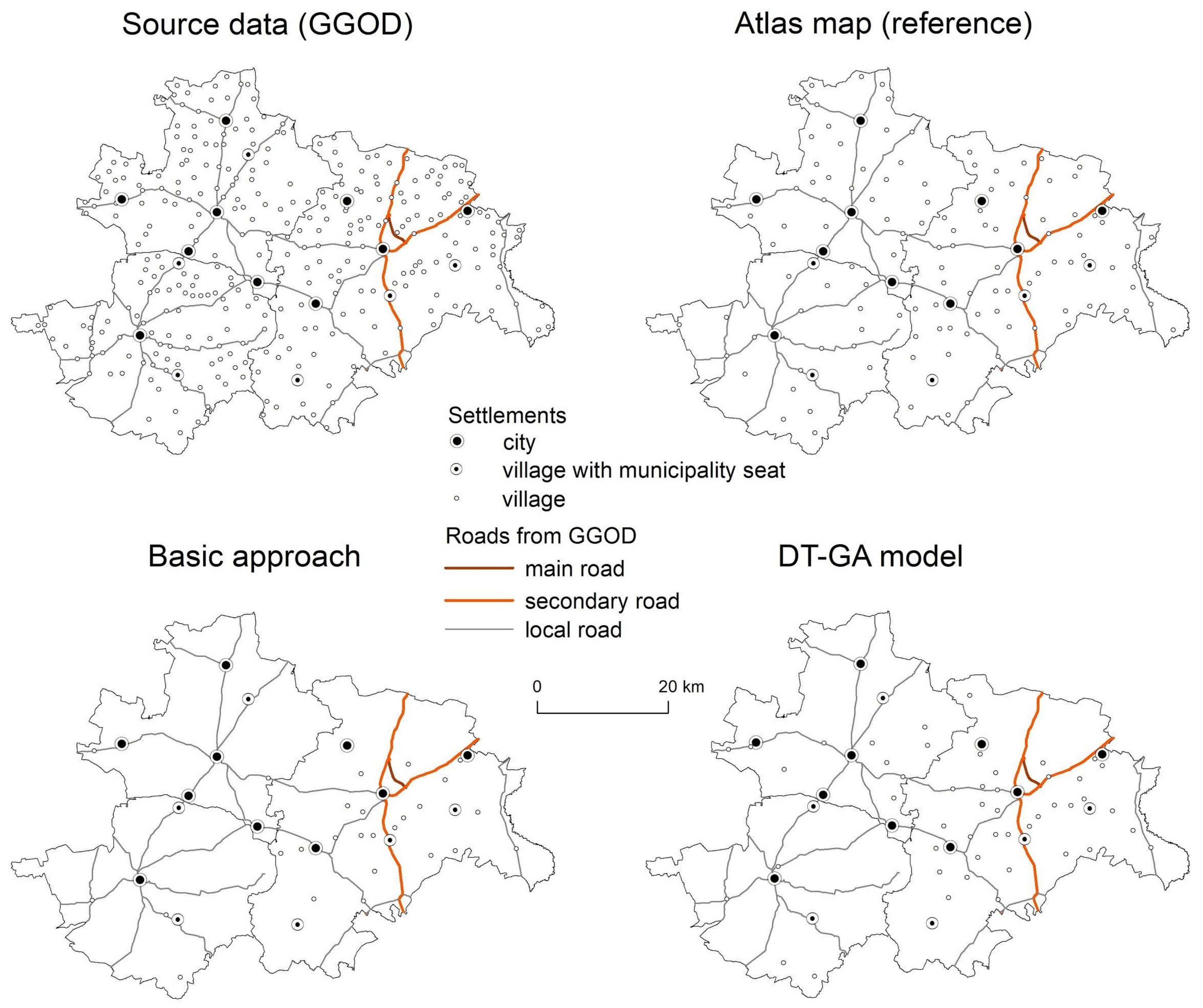
3. Results
4. Discussion
4.1. Which Variables Are Essential in Settlement Selection for Small-Scale Maps?
4.2. Is There a Correlation between Proposed Variables?
- How many settlement variables will be optimal for efficient machine learning?
- Which variables are essential in the settlement selection process?
- Will extending the data sample influence machine learning results?
- − Population;
- − Sacral function;
- − Distance to the nearest neighborhood;
- − Built-up area;
- − Density of settlement calculated in a grid.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ICA, International Cartographic Association. Multilingual Dictionary of Technical Terms in Cartography; Franz Steiner Verlag: Wiesbaden, Germany, 1973. [Google Scholar]
- Stanislawski, L.V.; Buttenfield, B.P.; Bereuter, P.; Savino, S.; Brewer, C.A. Generalisation operators. In Abstracting Geographic Information in a Data Rich World; Burghardt, D., Duchêne, C., Mackaness, W., Eds.; Springer: Cham, Switzerland, 2014; pp. 157–195. [Google Scholar]
- Richardson, D.E.; Muller, J.-C. Rule selection for small-scale map generalization. In Map Generalization: Making Rules for Knowledge Representation; Buttenfield, B.P., McMaster, R.B., Eds.; Longman: London, UK, 1991; pp. 136–149. [Google Scholar]
- Stoter, J.; van Altena, V.; Post, M.; Burghardt, D.; Duchêne, C. Automated generalisation within NMAs in 2016. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XLI-B4, XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Stoter, J.; Van Smaalen, J.; Bakker, N.; Hardy, P. Specifying map requirements for automated generalization of topographic data. Cartogr. J. 2009, 46, 214–227. [Google Scholar] [CrossRef]
- Stoter, J.; Post, M.; van Altena, V.; Nijhuis, R.; Bruns, B. Fully automated generalization of a 1:50k map from 1:10k data. Cartogr. Geogr. Inf. Sci. 2014, 41, 1–13. [Google Scholar] [CrossRef]
- Regnauld, N.G. Data Quality. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XL-3/W3, La Grande Motte, France, 28 September–3 October 2015; pp. 91–94. [Google Scholar]
- Burghardt, D.; Schmid, S.; Duchêne, C.; Stoter, J.; Baella, B.; Regnauld, N.; Touya, G. Methodologies for evaluation of generalised data derived with commercial available generalisation systems. In Proceedings of the ICA Workshop on Generalization and Multiple Representation, Montpellier, France, 20–21 June 2008. [Google Scholar]
- Chaundhry, O.Z.; Mackaness, W.A. Automatic identification of urban settlement boundaries for multiple representation databases. Comput. Environ. Urban Syst. 2008, 32, 95–109. [Google Scholar] [CrossRef]
- Karsznia, I.; Sielicka, K. Exploring essential variables in the settlement selection for small-scale maps using machine learning. Abstr. Int. Cartogr. Assoc. 2019, 1, 162. [Google Scholar] [CrossRef]
- Topfer, F.; Pillewizer, W. The Principles of Selection. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Kadmon, N. Automated selection of settlements in map generation. Cartogr. J. 1972, 9, 93–98. [Google Scholar] [CrossRef]
- Sirko, M. Teoretyczne i metodyczne aspekty obiektywizacji doboru osiedli na mapach [Theoretical and methodical aspects of objectifying the selection of settlements on the maps]. In Rozprawy Wydziału Biologii i Nauk o Ziemi Uniwersytetu Marii Curie-Skłodowskiej, Rozprawy Habilitacyjne; Wydawnictwo Uniwersytetu Marii Curie-Skłodowskiej: Lublin, Poland, 1988. [Google Scholar]
- Van Kreveld, M.; van Oostrum, R.; Snoeyink, J. Efficient settlement selection for interactive display. In Proceedings of the ACSM/ASPRS Annual Convention & Exposition, Seattle, WA, USA, 7–10 April 1997; Volume 5, pp. 287–296. [Google Scholar]
- Pietkiewicz, F. La carte de la Pologne au millionieme de L’Institut Geographique Militare; Comptes Rondus du Congres, Travaux de la Section I; Institut Geographique Militare: Warszawa, Poland, 1935; pp. 286–289. [Google Scholar]
- Rado, S. Az 1:2 500 000 meretaranyu vilag terkep. Geodezia es Kartografia 1965, 17, 166–173. [Google Scholar]
- Ostrowski, J. Analiza doboru osiedli na Mapie Świata 1:2 500 000. Polski Przegląd Kartograficzny 1970, 2, 1–14. [Google Scholar]
- Baranowski, M.; Grygorenko, W. Próba obiektywnego doboru osiedli na mapie z zastosowaniem maszyny cyfrowej. Polski Przegląd Kartograficzny 1974, 6, 149–155. [Google Scholar]
- Ratajski, L. Commission V of the ICA: The Tasks It Faces. Int. Yearb. Cartogr. 1974, 14, 140–144. [Google Scholar]
- Flewelling, D.M.; Egenhofer, M.J. Formalizing importance: Parameters for settlement selection in a geographic database. Proceedings Auto-Carto XI. 1993, pp. 167–175. Available online: https://cartogis.org/docs/proceedings/archive/auto-carto-11/pdf/formalizing-importance-parameters-for-settlement-selection-from-a-geographic-database.pdf (accessed on 2 March 2020).
- Batty, M. Hierarchy in cities and city systems. In Hierarchy in Natural and Social Sciences; Pumain, D., Ed.; Springer: Amsterdam, The Netherlands, 2006; pp. 143–168. [Google Scholar]
- Carol, H. The hierarchy of central functions within the city. Ann. Assoc. Am. Geogr. 1960, 50, 419–438. [Google Scholar] [CrossRef]
- Smith, R.H.T. Method and purpose in functional town classification. Ann. Assoc. Am. Geogr. 1965, 55, 539–548. [Google Scholar] [CrossRef]
- Christaller, W. Central Places in Southern Germany; Prentice-Hall: New York, NY, USA, 1933. [Google Scholar]
- Dixon, O.M. The selection of towns and other features on Atlas maps of Nigeria. Cartogr. J. 1967, 4, 16–23. [Google Scholar] [CrossRef]
- Weibel, R.; Keller, S.; Reichenbacher, T. Overcoming the knowledge acquisition bottleneck in map generalization: The role of interactive systems and computational intelligence. In Lecture Notes in Computer Science; Proceedings COSIT; Springer: Berlin, Germany, 1995; Volume 988, pp. 139–156. [Google Scholar]
- Mustière, S. GALBE: Adaptive Generalisation. The need for an Adaptive Process for Automated Generalisation, an Example on Roads. In Proceedings of the 1st GIS’PlaNet Conference, Lisbonne, Portugal, 22 July 1998. [Google Scholar]
- Sester, M. Knowledge acquisition for the automatic interpretation of spatial data. Int. J. Geogr. Inf. Sci. 2000, 14, 1–24. [Google Scholar] [CrossRef]
- Lagrange, F.; Landras, B.; Mustiere, S. Machine learning techniques for determining parameters of cartographic generalisation algorithms. Int. Arch. Photogramm. Remote Sens. 2000, 33, 718–725. [Google Scholar]
- Balboa, G.J.L.; López, A.F.J. Generalization-oriented Road Line Classification by Means of an Artificial Neural Network. Geoinformatica 2008, 12, 289–312. [Google Scholar] [CrossRef]
- Sester, M.; Feng, Y.; Thiemann, F. Building generalization using deep learning. International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2018, XLII-4, 565–572. [Google Scholar]
- Feng, Y.; Thiemann, F.; Sester, M. Learning Cartographic Building Generalization with Deep Convolutional Neural Network. Int. J. Geo-Inf. 2019, 8, 258. [Google Scholar] [CrossRef]
- Karsznia, I.; Weibel, R. Improving Settlement Selection for Small-scale Maps Using Data Enrichment and Machine Learning. Cartogr. Geogr. Inf. Sci. 2018, 45, 111–127. [Google Scholar] [CrossRef]
- Polskie Przedsiębiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera S.A. In Atlas Rzeczypospolitej Polskiej [Atlas of Republic of Poland]; Główny Geodeta Kraju: Warsaw, Poland, 1993; pp. 1993–1997.
- Regulation of the Minister of Interior and Administration of 17 November 2011 on the topographical objects database, the general geographical objects database and standard cartographic elaborations. 2011. Available online: http://prawo.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20112791642 (accessed on 4 March 2020).
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; The MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Murphy, K.P. Machine Learning. A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Rapid Miner Reference Manual. Available online: https://docs.rapidminer.com/latest/studio/operators/rapidminer-studio-operator-reference.pdf (accessed on 19 January 2020).

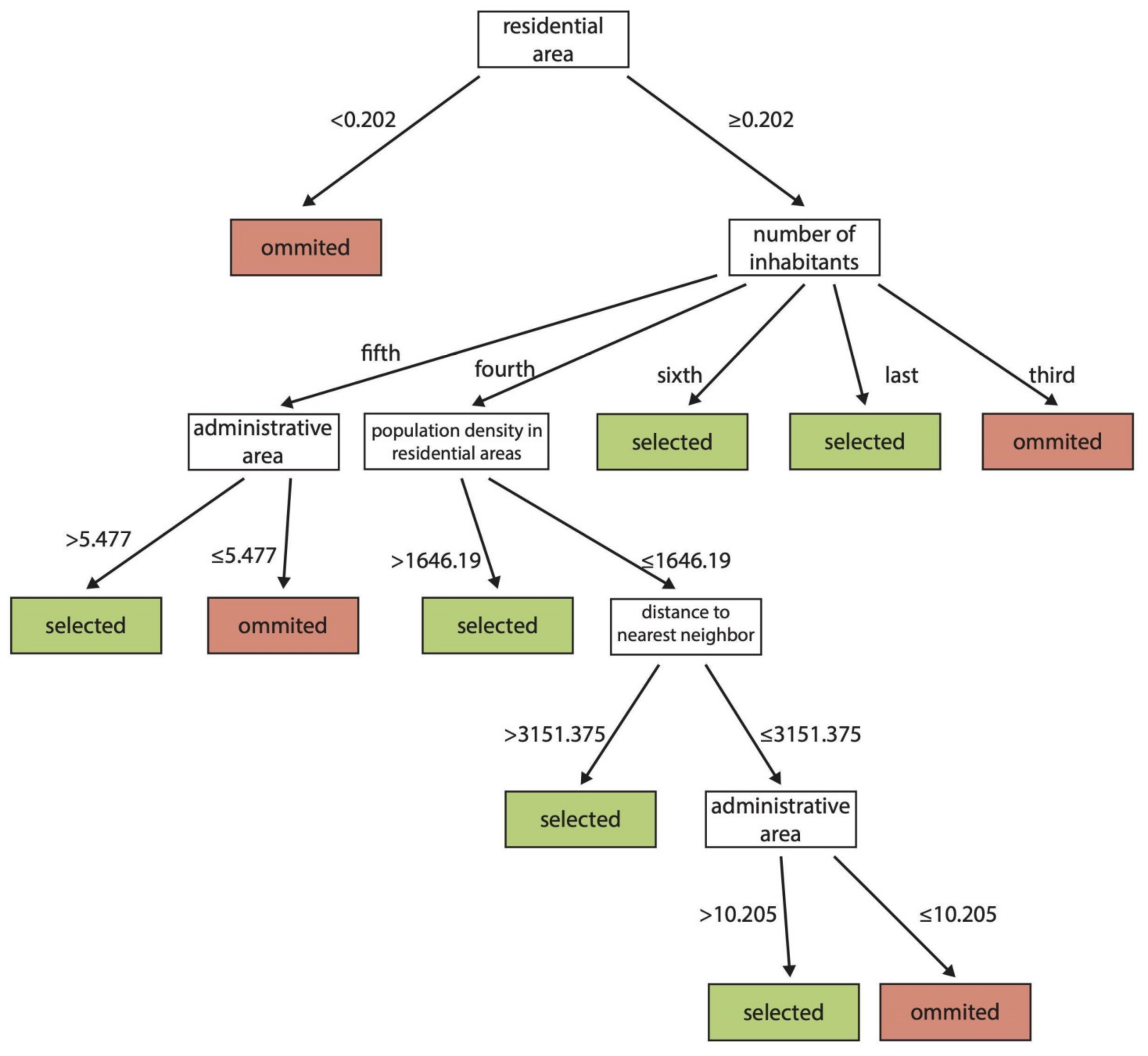

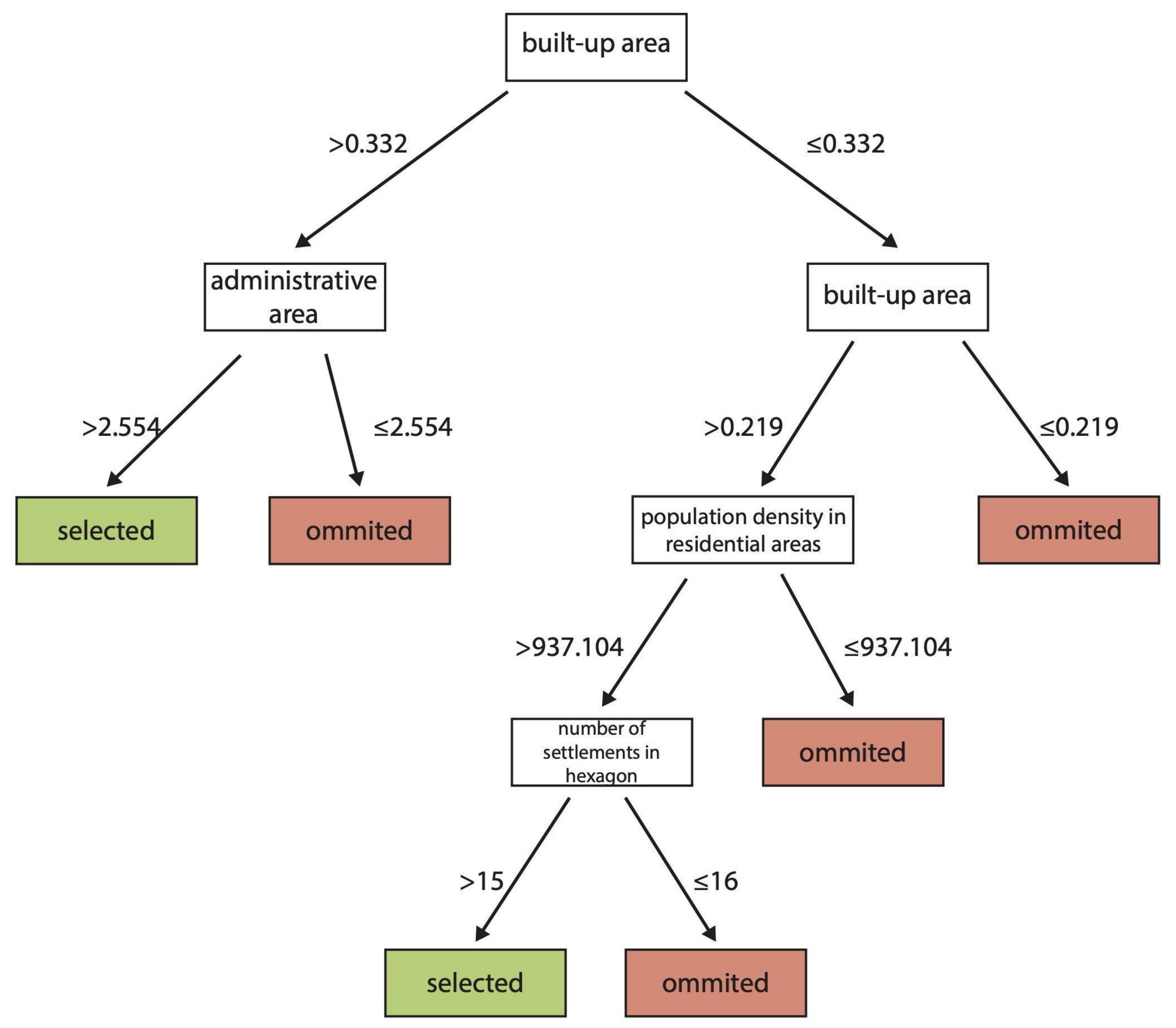
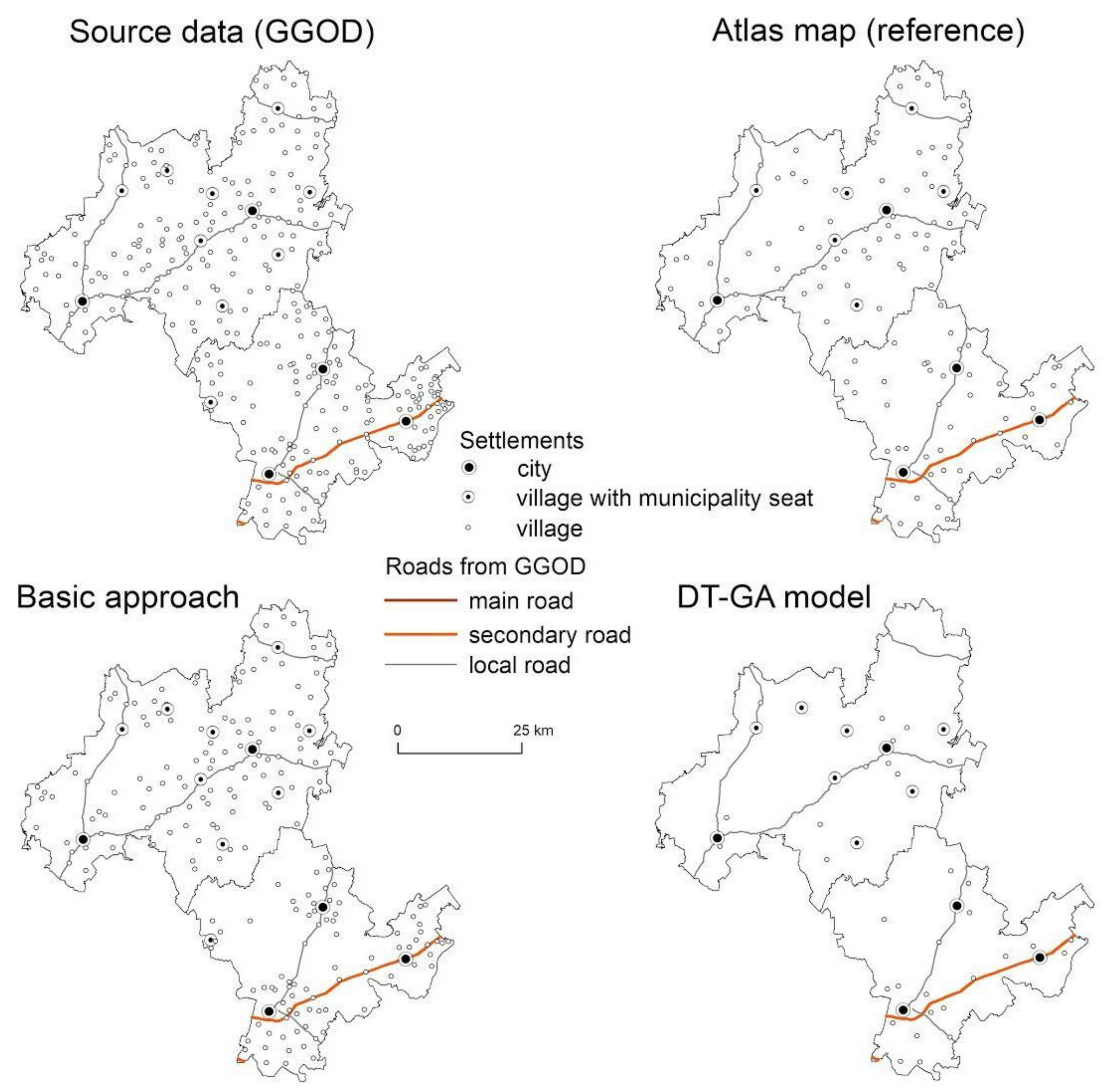
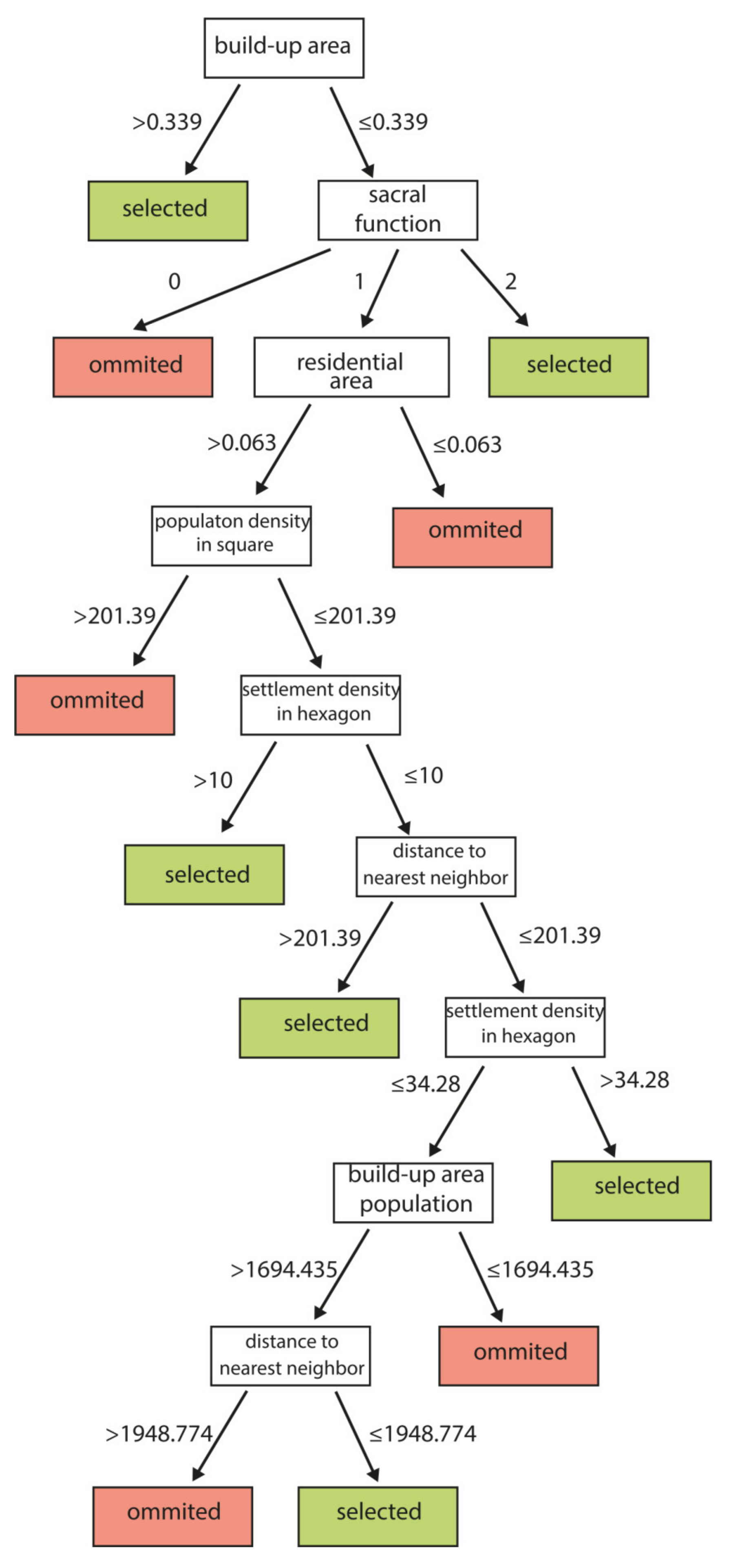
| Group no. | Characteristic | Districts |
|---|---|---|
| 1. | High population density area—151.84 people per km2 | Brzeski, Dębicki, Rzeszowski, Tarnowski |
| 2. | Medium population density area—101.36 people per km2 | Krotoszyński, Ostrowski, Milicki, Złotoryjski |
| 3. | Low population density area—85.04 people per km2 | Łowicki, Skierniewicki, Żyrardowski |
| 4. | Very low population density area—41.98 people per km2 | Bytowski, Chojnicki, Gołdapski, Olecki, Suwalski |
| Variable | Variable Description |
|---|---|
| Administrative area of the settlement | In square kilometers |
| Built-up area of the settlement | In square kilometers |
| Residential area of the settlement | In square kilometers |
| Service and commercial area of the settlement | In square kilometers |
| Industrial and storage area of the settlement | In square kilometers |
| Population density in residential areas | People per square kilometer |
| Number of railway stops within settlement area | Calculated using the basic ArcGIS and Python functionality |
| Number of airports within settlement area | Calculated using the basic ArcGIS and Python functionality |
| Number of ports within settlement area | Calculated using the basic ArcGIS and Python functionality |
| Number of at least district rank roads crossing the settlement border | Number of roads (national, voivodeship and district) crossing the administrative borders of the settlement |
| Total number of communication nodes within settlement area | Calculated using the basic ArcGIS and Python functionality |
| Number of crossings of higher category roads within the settlement area | Number of national, voivodeship and district intersections |
| Density of settlement in the district | Number of settlements per square kilometer |
| Density of settlement calculated in a rectangular grid | Number of settlements per 5 km × 5 km grid |
| Density of settlement calculated in a hexagonal grid | Number of settlements per 25 km2 grid |
| Population density calculated in a rectangular grid | Population density per grid 5 km × 5 km |
| Population density calculated in a hexagonal grid | Population density per 25 km2 grid |
| Population density in districts * | People per square kilometer in districts |
| Population * | Number of inhabitants |
| Administrative status * | Information concerning the seat of administrative office |
| Settlement type * | Information concerning settlement type, for instance: city, village, colony, etc. |
| Cultural function * | Number of buildings fulfilling cultural function within the settlement administrative area |
| Educational function * | Number of buildings fulfilling educational function within the settlement administrative area |
| Trading function * | Number of buildings fulfilling trading function within the settlement administrative area |
| Industrial function * | Number of buildings fulfilling industrial function within the settlement administrative area |
| Monumental function * | Number of buildings fulfilling monumental function within the settlement administrative area |
| Sacral function * | Number of buildings fulfilling sacral function within the settlement administrative area |
| Accommodation function * | Number of buildings fulfilling accommodation function the within settlement administrative area |
| Communication and finance * | Number of buildings fulfilling communication and finance function within the settlement administrative area |
| Health function * | Number of buildings fulfilling health function within the settlement administrative area |
| Other functions * | Number of buildings fulfilling functions not assigned to any other group, which might however be important for the selection process |
| Voronoi area * | Area of the Voronoi diagram |
| Distance to nearest neighbor * | Distance to the nearest settlement |
| Basic Approach | Enhanced Approach | Difference * | ||
|---|---|---|---|---|
| DT | DT-GA | |||
| Group 1 | 71.62% | 76.4% | 78.02% | +6.40 |
| Group 2 | 71.02% | 77.26% | 80.90% | +9.88 |
| Group 3 | 84.39% | 84.57% | 85.87% | +1.48 |
| Group 4 | 68.39% | 80.23% | 81.98% | +13.59 |
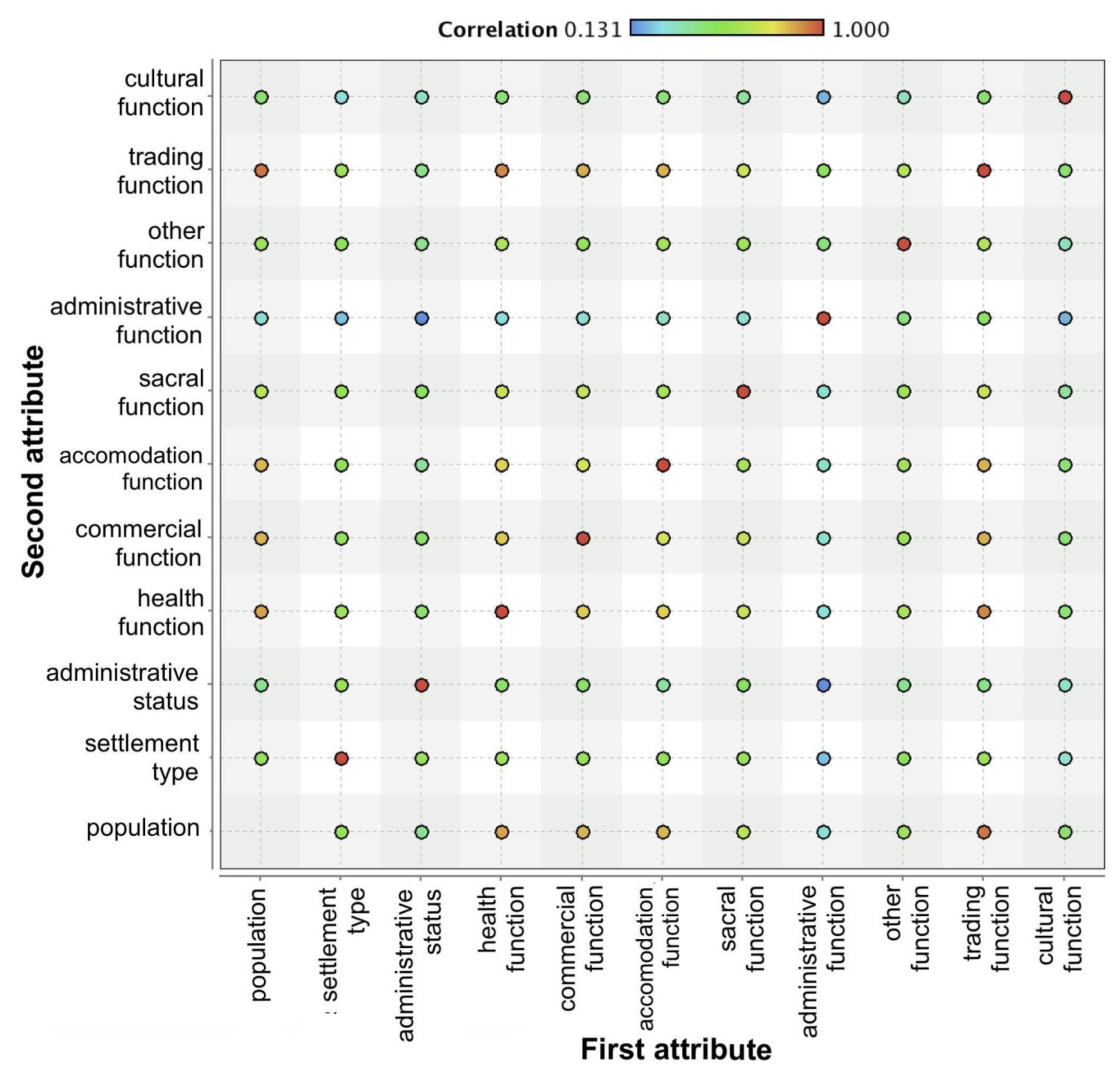
| First Attribute | Second Attribute | Correlation |
|---|---|---|
| Population | Trade function | 0.934 |
| Health function | Trade function | 0.907 |
| Population | Health function | 0.867 |
| Commercial function | Trade function | 0.849 |
| Population | Commercial function | 0.844 |
| Accommodation function | Trade function | 0.844 |
| Population | Accommodation function | 0.837 |
| Health function | Commercial function | 0.811 |
| Health function | Accommodation function | 0.799 |
| Commercial function | Accommodation function | 0.743 |
| Health function | Sacral function | 0.707 |
| Sacral function | Trade function | 0.707 |
| Commercial function | Sacral function | 0.703 |
| Attribute | Weight |
|---|---|
| Area of Voronoi diagram | 1.0 |
| Population | 0.952 |
| Population density per district | 0.858 |
| Population density in hexagons (100 km2) | 0.807 |
| Population density in squares 10 km × 10 km | 0.756 |
| Population density in squares 5 km × 5 km | 0.713 |
| Population density in hexagons (25 km2) | 0.649 |
| Administrative area | 0.593 |
| Distance to the nearest neighbor | 0.498 |
| Commercial area | 0.372 |
| Number of settlements in hexagons (25 km2) | 0.29 |
| Number of settlements in hexagons (100 km2) | 0.257 |
| Number of settlements in squares 5 km × 5 km | 0.244 |
| Industrial area | 0.227 |
| Number of settlements in squares 10 km × 10 km | 0.217 |
| Residential area | 0.033 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karsznia, I.; Sielicka, K. When Traditional Selection Fails: How to Improve Settlement Selection for Small-Scale Maps Using Machine Learning. ISPRS Int. J. Geo-Inf. 2020, 9, 230. https://doi.org/10.3390/ijgi9040230
Karsznia I, Sielicka K. When Traditional Selection Fails: How to Improve Settlement Selection for Small-Scale Maps Using Machine Learning. ISPRS International Journal of Geo-Information. 2020; 9(4):230. https://doi.org/10.3390/ijgi9040230
Chicago/Turabian StyleKarsznia, Izabela, and Karolina Sielicka. 2020. "When Traditional Selection Fails: How to Improve Settlement Selection for Small-Scale Maps Using Machine Learning" ISPRS International Journal of Geo-Information 9, no. 4: 230. https://doi.org/10.3390/ijgi9040230
APA StyleKarsznia, I., & Sielicka, K. (2020). When Traditional Selection Fails: How to Improve Settlement Selection for Small-Scale Maps Using Machine Learning. ISPRS International Journal of Geo-Information, 9(4), 230. https://doi.org/10.3390/ijgi9040230






