Numerical Simulation of Donghu Lake Hydrodynamics and Water Quality Based on Remote Sensing and MIKE 21
Abstract
1. Introduction
2. Study Area
3. Research Methodology
3.1. MIKE21 Model
3.1.1. Hydrodynamic Module
3.1.2. Water Quality Module
3.2. Remote Sensing Inversion Model
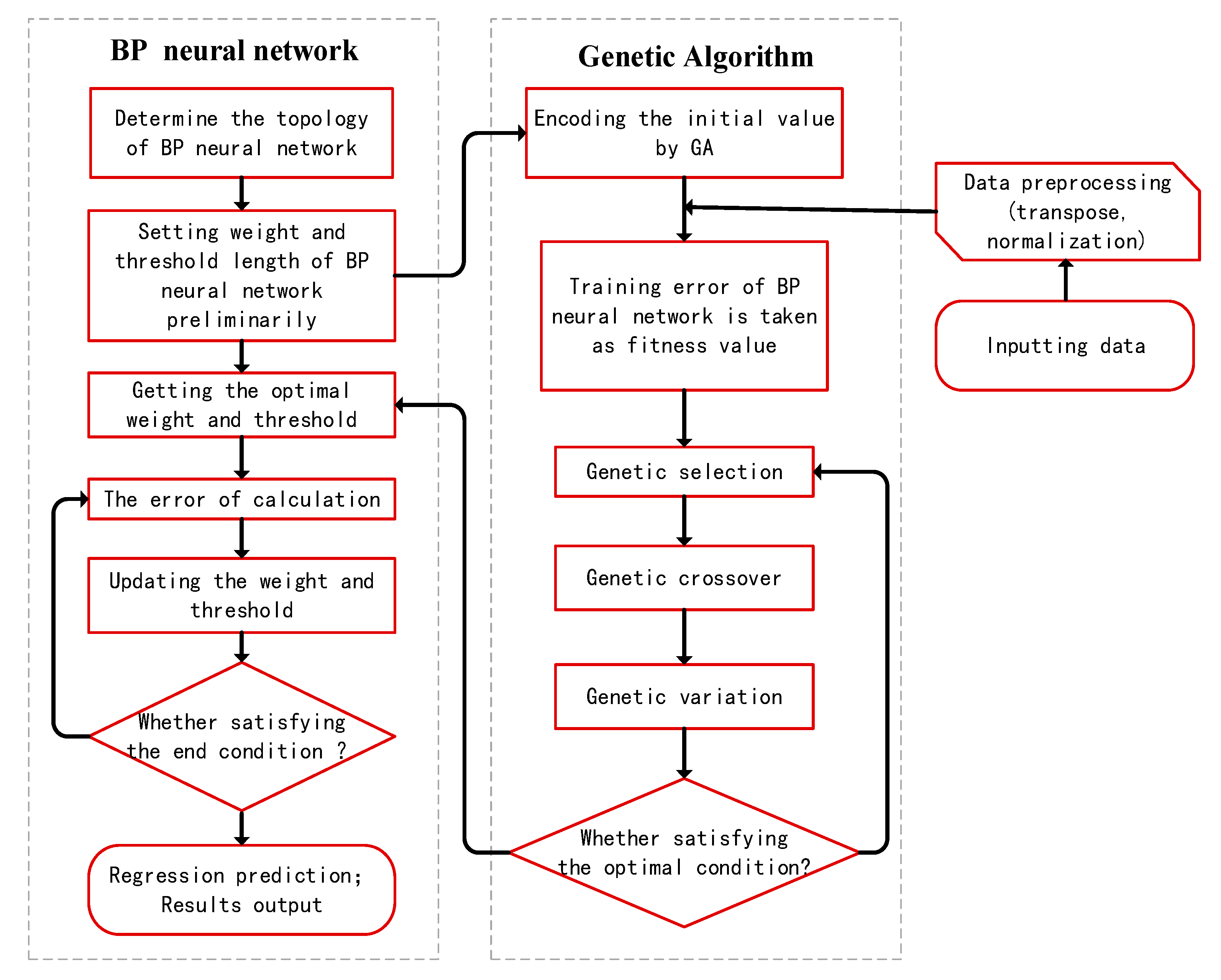
3.2.1. BP Neural Network Optimized by GA
3.2.2. Model Implementation
4. Hydrodynamic and Water Quality Numerical Simulation of Donghu Lake
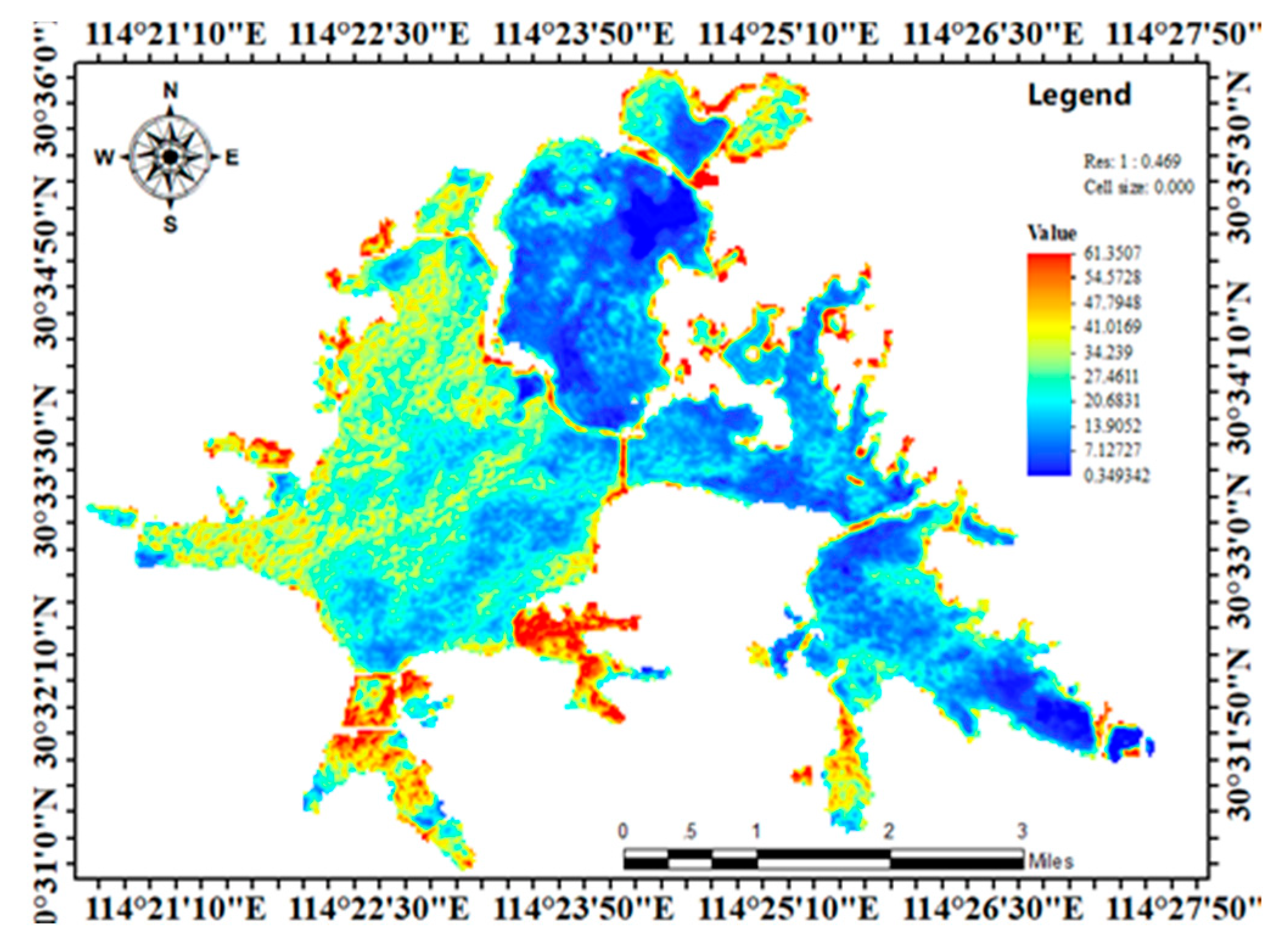
4.1. Remote Sensing Inversion of Water Quality in Donghu Lake
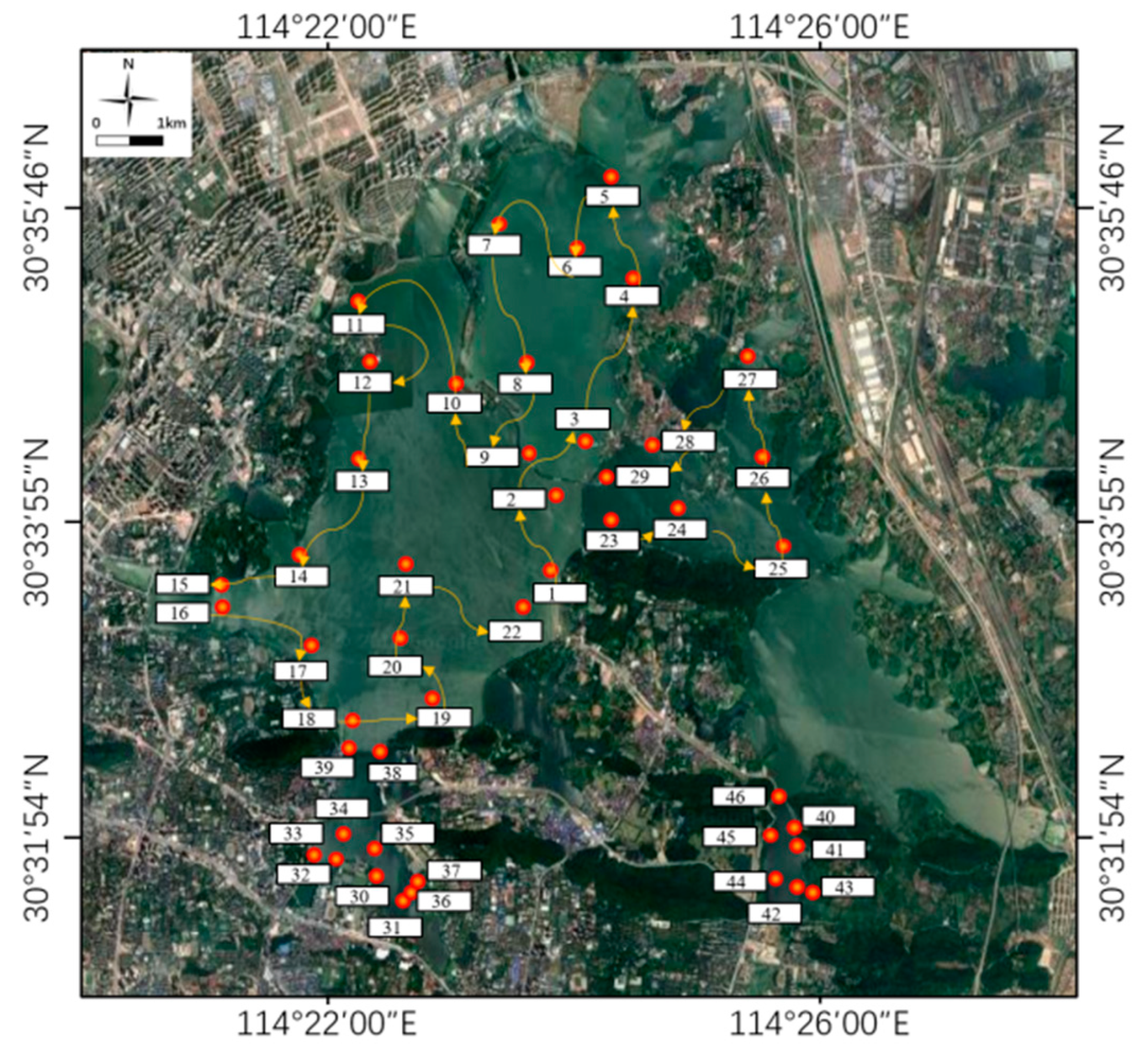
4.1.1. Data Sources and Data Processing
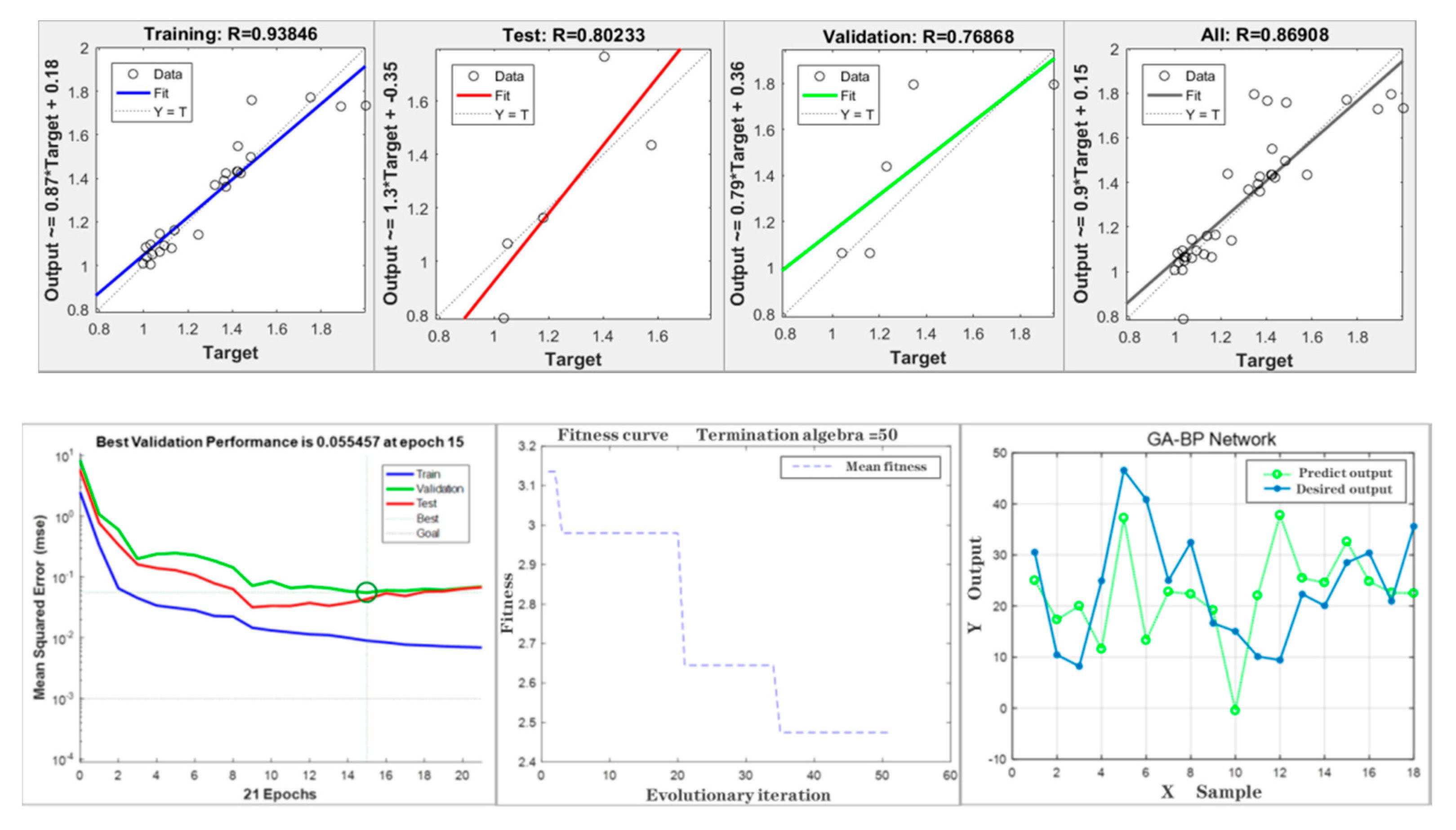
4.1.2. GA-BP Model Training
4.1.3. GA-BP Model Validation
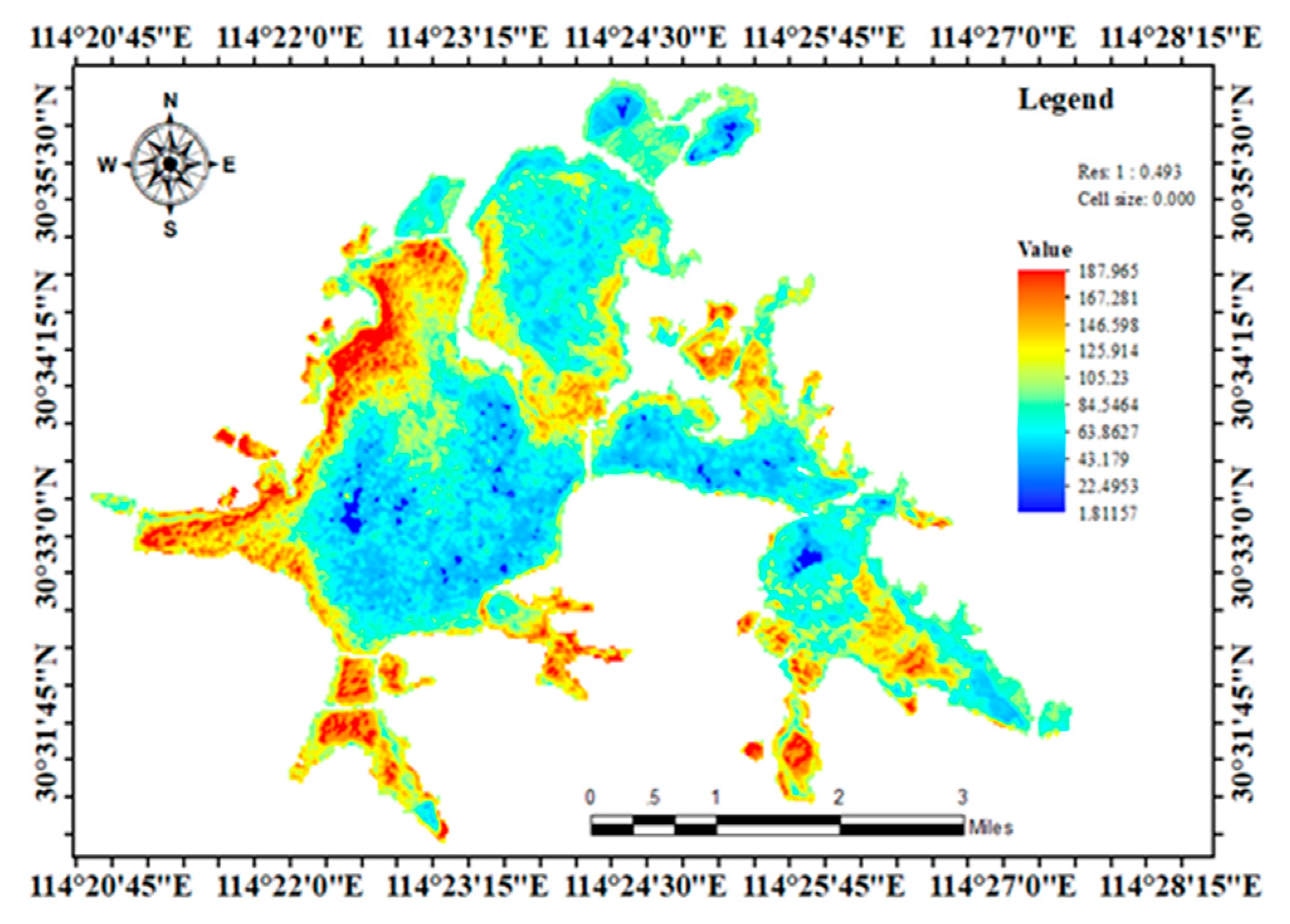
4.1.4. GA-BP Model Application
4.2. Hydrodynamics Numerical Simulation of Donghu Lake
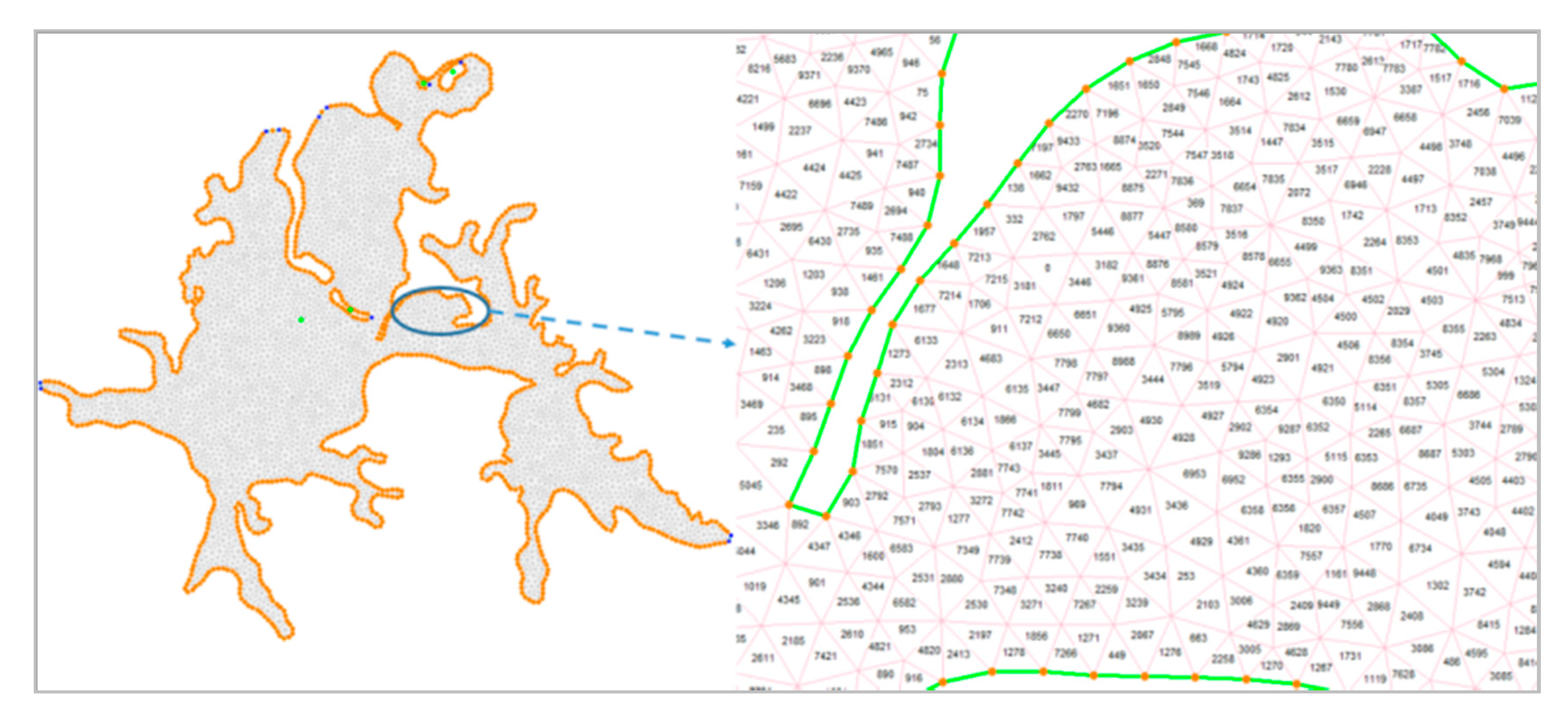
4.2.1. Grid Division of Study Area
4.2.2. Initial Boundary Condition
4.2.3. Parameter Setting
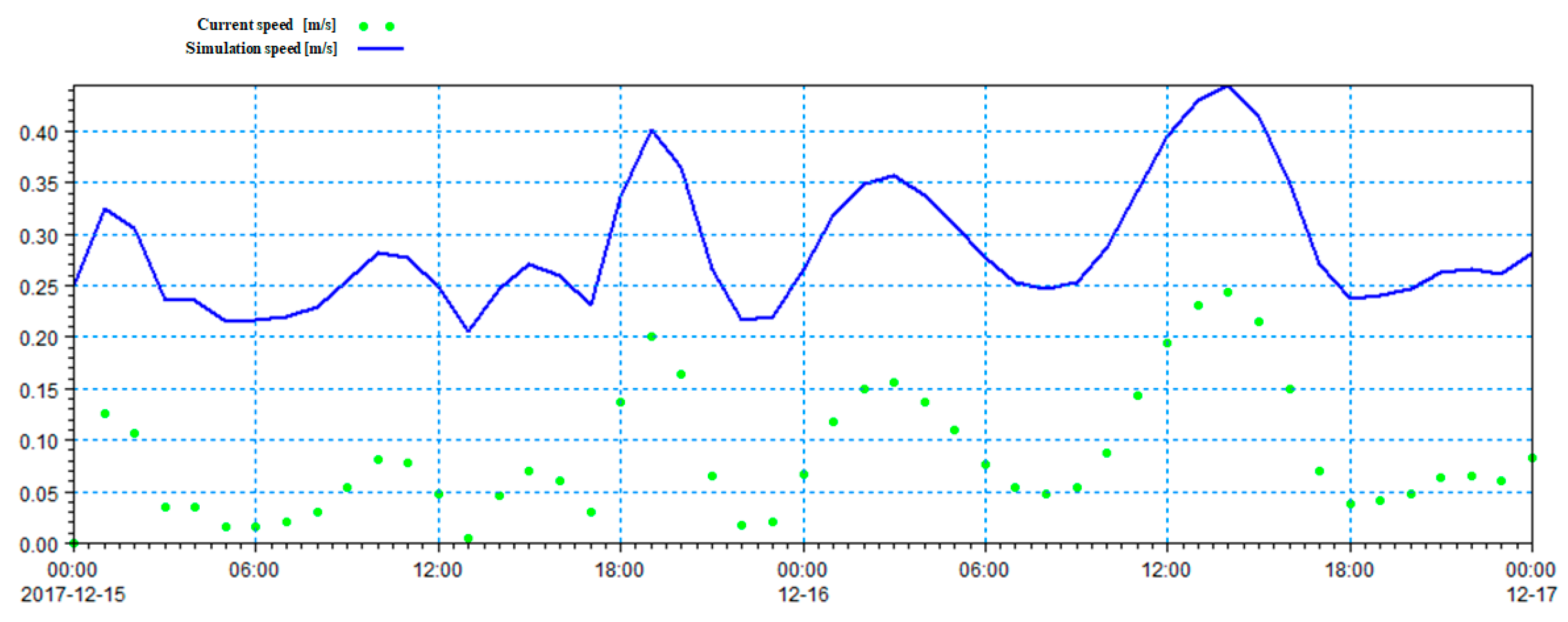
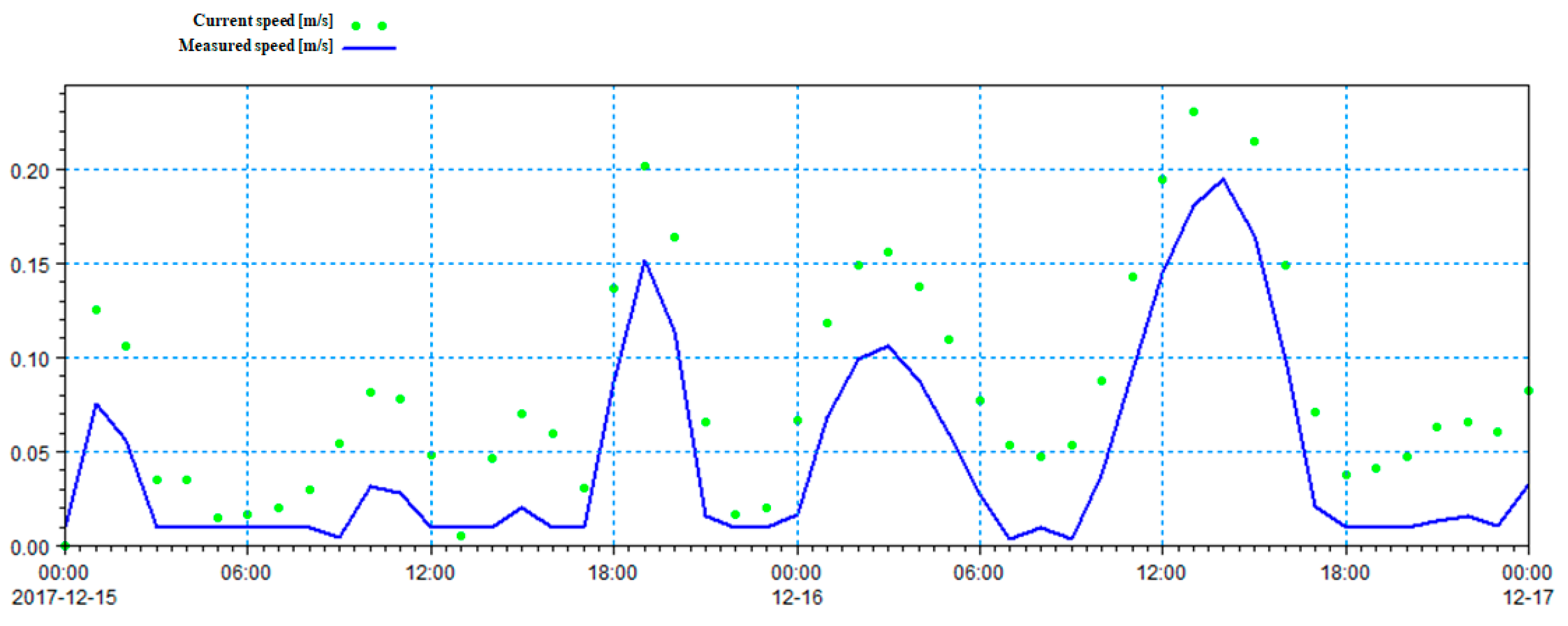
4.2.4. Calibration and Validation of Model Parameters
4.3. Water Quality Numerical Simulation of Donghu Lake by Remote Sensing Inversion
4.3.1. Basic Setting
4.3.2. Settings Optimization Based Remote Sensing
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Song, N.; Bai, L.; Xu, H.; Jiang, H. The composition difference of macrophyte litter-derived dissolved organic matter by photodegradation and biodegradation: Role of reactive oxygen species on refractory component. Chemosphere 2020, 242, 125155. [Google Scholar] [CrossRef] [PubMed]
- Qin, B.; Gao, G.; Zhu, G.; Zhang, Y.; Song, Y.; Tang, X.; Xu, H.; Deng, J. Lake eutrophication and its ecosystem response. Chin. Sci. Bull. 2013, 58, 961–970. [Google Scholar] [CrossRef]
- Weichun, M.A.; Zhang, C. The Numerical Simulation of Water Quality of Suzhou Creek Based on Gis. Acta Geographica Sinica 1998, 53 (Suppl. 6), 66–75. [Google Scholar]
- Xiao, C.; Liang, X.; Du, C.; Xie, S.; Fang, Z.; Ma, Z.; Feng, B.; Tian, Z. Numerical Simulation and Improvement Measures of Water Quality in Yangshapao Lake. In Proceedings of the 2009 3rd International Conference on Bioinformatics and Biomedical Engineering, Beijing, China, 11 June 2009; pp. 1–4. [Google Scholar]
- Mano, A.; Malve, O.; Koponen, S.; Kallio, K.; Taskinen, A.; Ropponen, J.; Juntunen, J.; Liukko, N. Assimilation of satellite data to 3D hydrodynamic model of Lake Säkylän Pyhäjärvi. Water Sci. Technol. 2015, 71, 1033–1039. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Fu, G.; Zhao, X.; Moore, B.C. Integration of environmental fluid dynamics code (EFDC) model with geographical information system (GIS) platform and its applications. J. Environ. Inform. 2011, 17, 75–82. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, Y.; Guo, Y. The development of a multi-species algal ecodynamic model for urban surface water systems and its application. Ecol. Model. 2010, 221, 1831–1838. [Google Scholar] [CrossRef]
- Wu, G.; Xu, Z. Prediction of algal blooming using EFDC model:Case study in the Daoxiang Lake. Ecol. Model. 2011, 222, 1245–1252. [Google Scholar] [CrossRef]
- Huang, M.; Tian, Y. An Integrated Graphic Modeling System for Three-Dimensional Hydrodynamic and Water Quality Simulation in Lakes. ISPRS Int. J. Geo-Inf. 2019, 8, 18. [Google Scholar] [CrossRef]
- Safaa, H.; Esam, I. Detection and Evaluation of Groundwater in Siwa Oasis, Egypt Using Hydrogeochemical and Remote Sensing Data Analysis. Water Environ. Res. 2018, 90, 465–478. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Tian, L.; Wai, O.W.; Li, J.; Sun, Z.; Li, W. High-Frequency Monitoring of Suspended Sediment Variations for Water Quality Evaluation at Deep Bay, Pearl River Estuary, China: Influence Factors and Implications for Sampling Strategy. Water 2018, 10, 323. [Google Scholar] [CrossRef]
- Koponen, S.; Pulliainen, J.; Kallio, K.; Hallikainen, M. Lake water quality classification with airbrone hyperspectral specyrometer and simulated MERIS data. Remote Sens. Environ. 2002, 79, 51–59. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, L.; Li, J.; Chen, Y.; Zhang, Y.; Hou, H.; Ju, X.; Zhang, Y. The study of inversion of chlorophyll a in Taihu based on GF-1 WFV image and BP neural network. Acta Scientiae Circumstantiae 2017, 37, 130–137. [Google Scholar]
- Shi, R.; Zhang, H.; Yue, R.; Zhang, X.; Wang, M.; Shi, W. A wavelet theory based remote sensing inversion of chlorophyll a concentrations for inland Lakes in arid areas using TM image data. Acta Ecol. Sin. 2017, 37, 1043–1053. [Google Scholar]
- Cao, Y.; Ye, Y.; Zhao, H.; Jiang, Y.; Wang, H.; Wang, J. Ensemble modeling methods for remote sensing retrieval of water quality parameters in inland water. China Environ. Sci. 2017, 37, 3940–3951. (In Chinese) [Google Scholar]
- Wang, J.; Cheng, S.; Jia, H.; Wang, Z.; Tang, U. An Artificial Neural Network Model for Lake Color Inversion Using TM Imagery. Environ. Sci. 2003, 24, 73–76. (In Chinese) [Google Scholar]
- Chang, N.B.; Xuan, Z.; Yang, Y.J. Exploring spatiotemporal patterns of phosphorus concentrations in a coastal bay with MODIS images and machine learning models. Remote Sens. Environ. 2013, 134, 100–110. [Google Scholar] [CrossRef]
- Hajigholizadeh, M.; Melesse, A.M.; Fuentes, H.R. Erosion and Sediment Transport Modeling in Shallow Waters: A Review on Approaches, Models and Applications. Int. J. Environ. Res. Public Health. 2018, 15, 518. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Huang, M.; Tang, X. Eutrophication assessment of seasonal urban Lakes in China Yangtze River Basin using Landsat 8-derived Forel-Ule index: A six-year (2013–2018) observation. Available online: https://www.sciencedirect.com/science/article/pii/S0048969719353859 (accessed on 22 April 2019).
- Luo, Y.X. Research progress on environmental quality of water resources in Donghu Lake of Wuhan. J. Green Sci. Technol. 2018, 58–60. (In Chinese) [Google Scholar]
- Hubei Water Resources and Hydropower Survey and Design Institute. Feasibility study report on construction of water network connection project of dadong Lake ecological water network in wuhan, hubei province. M Environ. Study Monit. 2010. (In Chinese) [Google Scholar]
- Wuhan Bureau of Ecology and Environment. Environmental Quality of Surface Water in Wuhan in December 2017. Available online: http://hbj.wuhan.gov.cn/hbDbsjcbg/28411.jhtml73107479-1/2018-00058 (accessed on 17 April 2019).
- Guo, X.R. Water Quality Simulation of East Lake in Wuhan City Based on Hydrodynamics. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2018. (In Chinese). [Google Scholar]
- Jing, Z. Numerical Simulations of the Lake Water Environment and Parallel Computations of the Non-hydrostatic Flows. Available online: http://gb.oversea.cnki.net/KCMS/detail/detail.aspx?filename=1017145957.nh&dbcode=CDFD&dbname=CDFDREF (accessed on 12 April 2019).
- Li, X. The Mechanism of Nitrogen Migration and Transformation in Shallow Lake Sediments. Ph.D. Thesis, Tianjin University, Tianjin, China, 2012. (In Chinese). [Google Scholar]
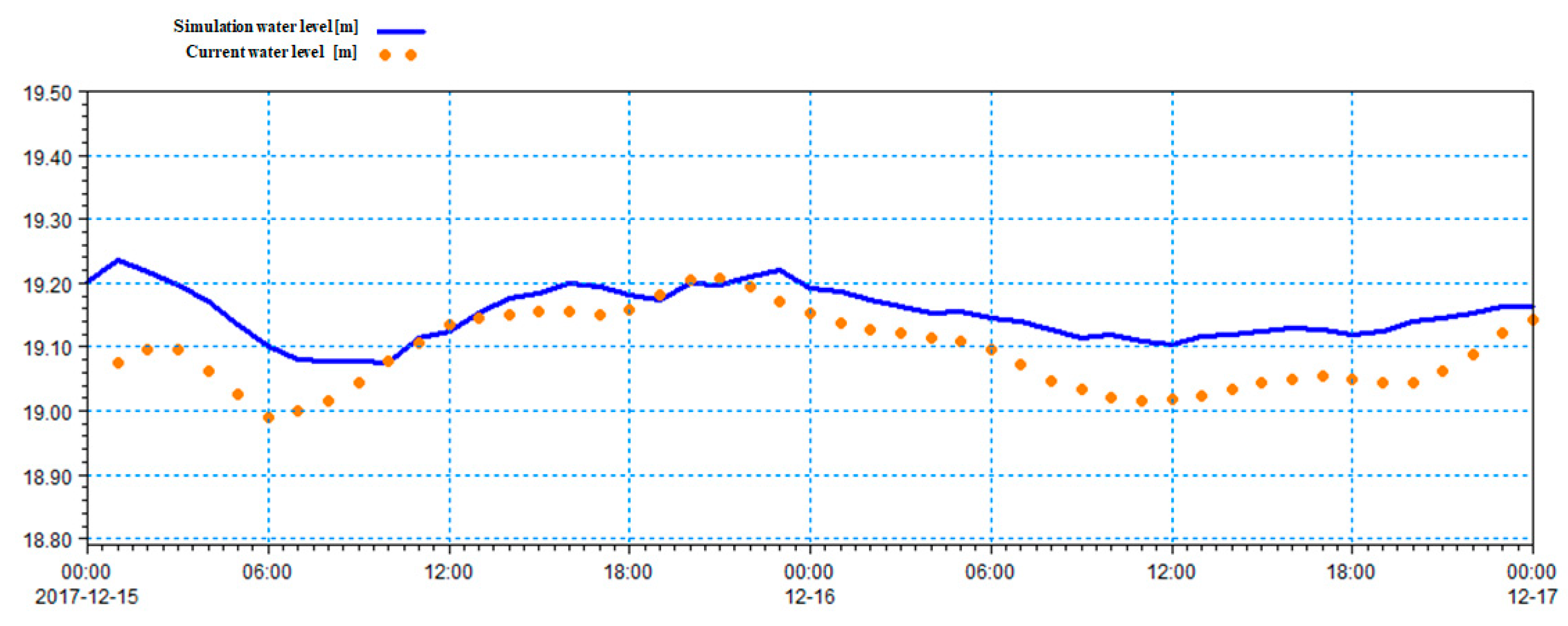
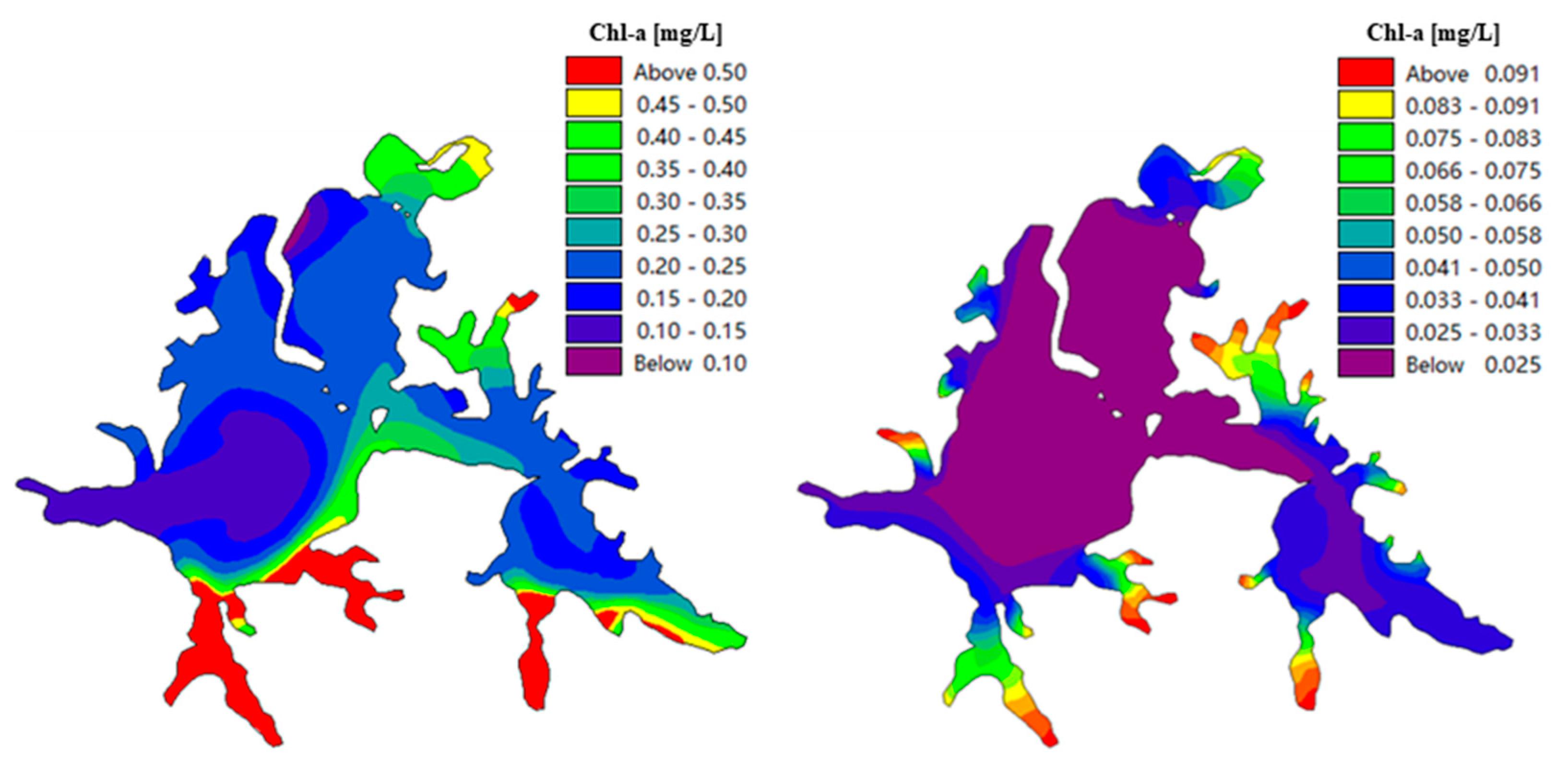
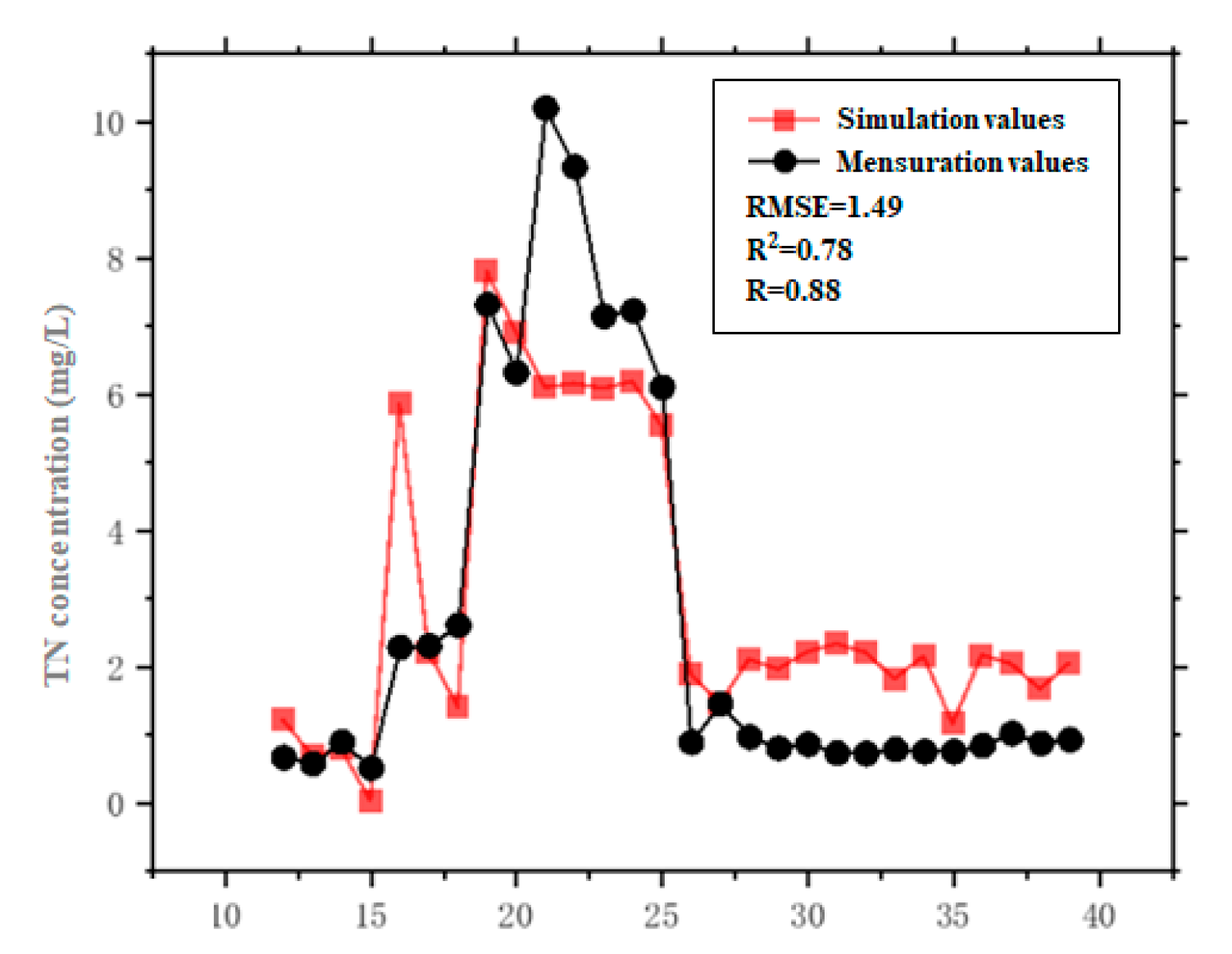

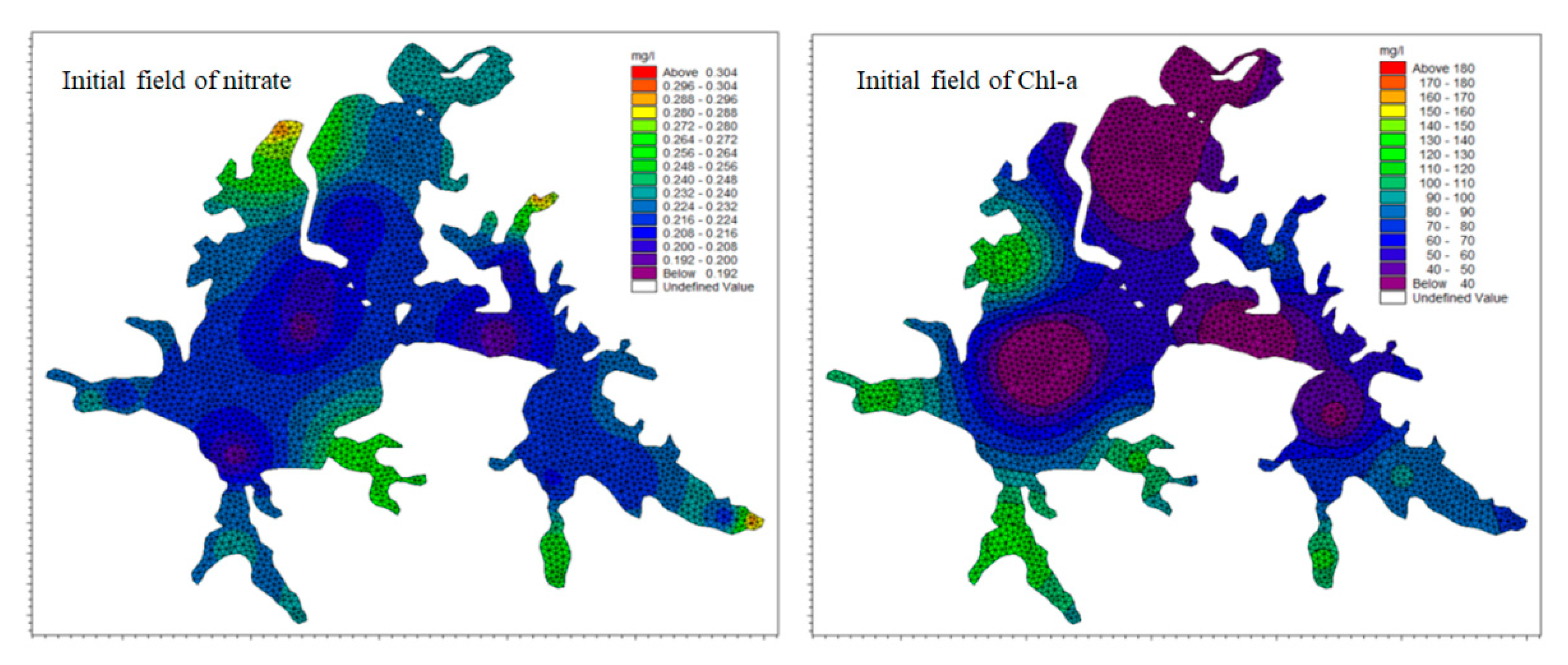
| Point | Northern Latitude | East Longitude | PH | Turbidity (NTU) | TP (mg/L) | TN (mg/L) | DO | Chlorophyll a (mg/m3) | CODcr (mg/L) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 30.553 | 114.397 | 6.850 | 19.980 | 0.126 | 0.538 | 10.22 | 22.201 | 10.566 |
| 2 | 30.560 | 114.398 | 7.470 | 22.600 | 0.095 | 2.782 | 10.45 | 15.690 | 15.094 |
| 3 | 30.565 | 114.402 | 7.600 | 12.160 | 0.097 | 1.134 | 10.36 | 5.814 | 18.113 |
| 4 | 30.581 | 114.407 | 7.660 | 56.700 | 0.190 | 1.005 | 10.35 | 5.978 | 13.585 |
| 5 | 30.590 | 114.405 | 7.810 | 31.400 | 0.166 | 1.658 | 10.31 | 5.246 | 15.094 |
| 6 | 30.584 | 114.401 | 7.620 | 11.180 | 0.094 | 1.372 | 10.22 | 6.695 | 10.566 |
| 7 | 30.586 | 114.391 | 7.760 | 24.500 | 0.128 | 1.980 | 10.27 | 6.771 | 18.113 |
| 8 | 30.573 | 114.394 | 7.790 | 12.980 | 0.111 | 1.933 | 10.47 | 10.996 | 27.170 |
| 9 | 30.564 | 114.395 | 7.890 | 48.500 | 0.174 | 0.745 | 10.52 | 6.971 | 34.717 |
| GA | BP | ||
|---|---|---|---|
| Name of Parameter | Set Value | Name of Parameter | Set Value |
| Population size (20~100) | 8 | Number of nodes in input layer | 7 |
| Generation number of training (100~1000) | 50 | Number of nodes in hidden layer | 4 |
| Crossover probability (0.4~0.9) | 0.3 | Number of nodes in output layer | 1 |
| Mutation probability (0.0001~0.1) | 0.1 | Maximum iterations | 1000 |
| Objectives of training | 0.001 | ||
| Output function in hidden layer | Tansig | ||
| Output function in output layer | Purelin | ||
| Training function | Trainlm | ||
| Parameter | Value |
|---|---|
| Solution Technique | Low order, fast algorithm |
| Depth | No depth correction |
| Flood and Dry | Standard flood and dry |
| Density | Barotropic |
| Eddy Viscosity | Smagorinsky constant value (0.32) |
| Bed Resistance | Manning constant (35 m1/3/s) |
| Coriolis Forcing | Varying in Domain |
| Wind Forcing | Time varying spatial constant |
| Initial Condition | The mean water level (19.05 m), Flow velocity (0 m/s) |
| Boundary Condition | Water level boundary (import DFS1 file) |
| Parameter Name | Set Point |
|---|---|
| Degradation rate at 20 °C of BOD | 0.5 (/d) |
| Temperature coefficient of BOD | 1.07 dimensionless |
| Consumes oxygen half-saturation constant in process of BOD degradation | 2 mg/L |
| Oxygen rate of aquatic plants | 0 (/d) |
| The temperature coefficient in the process of oxygen consumption | 1.08 dimensionless |
| Half-saturation constant in the process of oxygen consumption | 2 mg/L |
| Oxygen consumption per square meter of mud | 0.5 (/d) |
| Half-saturation constant—The ammonia nitrogen in photosynthesis | 0.066 gNH4/g BOD |
| Half-saturation constant—The absorbed orthophosphates in photosynthesis | 0.015 gP/g BOD |
| Chlorophyll a decay rate | 0.01 (/d) |
| Nitrification rate | 0.05 (/d) |
| Nitrification oxygen demand (NH4-NO2) | 3.42 gO2/g NH4-N |
| Nitrification oxygen demand (NO2 ~ NO3) | 1.14 gO2/g NO2-N |
| Attenuating release phosphorus content of BOD | g P/g BOD |
| Temperature | 11.04 degrees C |
| Salinity | 95 psu |
| Transverse and longitudinal diffusion coefficients | 6.2 m2/s |
| Parameter Name | Parameter Values |
|---|---|
| Smagorinsky Eddy viscosity coefficient | 0.29 |
| Manning constant | 42 m1/3/s |
| Coriolis force | It is automatically calculated with the latitude information of the surface area |
| Transverse and longitudinal diffusion coefficients | average 9.2 m2/s |
| Ammonia nitrogen degradation coefficient (20 °C standard) | 0.045 (/d) |
| Orthophosphate Phosphorus degradation coefficient (20 °C standard) | 0.035 (/d) |
| BOD attenuation coefficient (20 °C standard) | 0.025 (/d) |
| Chlorophyll a attenuation coefficient (20 °C standard) | 0.015 (/d) |
| Nitrification rate (20 °C standard) | 0.035 (/d) |
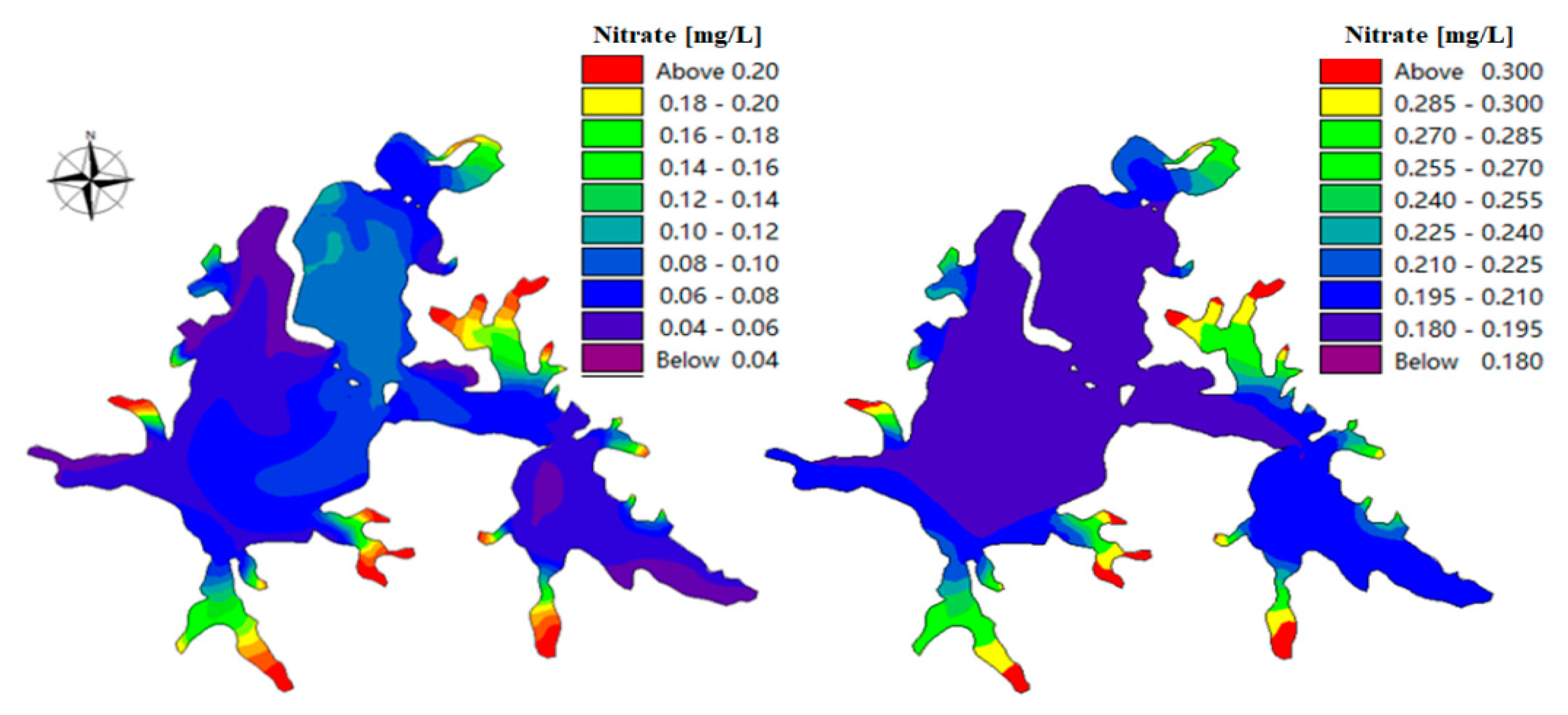
| Pollution Parameter | Simulated Result Not Based on Remote Sensing Optimization | Simulated Result Based on Remote Sensing Optimization |
|---|---|---|
| Chlorophyll a | 19.60 | 17.8093 |
| Nitrate nitrogen | 31.02 | 24.9610283 |
| Name of Lake | Chlorophyll a Measured Value (Mg/L) | Chlorophyll a Value of Simulation (Mg/L) | RE (%) | NO3-N Measured Value (Mg/L) | NO3-N Value of Simulation (Mg/L) | RE (%) |
|---|---|---|---|---|---|---|
| Tangling Lake | 0.01551 | 0.0240 | 54.6396 | 0.3150 | 0.1901 | 39.6489 |
| Shaoji Lake | 0.02532 | 0.0240 | 5.0569 | 0.1400 | 0.1902 | 35.8321 |
| Tuan Lake | 0.02625 | 0.0239 | 8.8301 | 0.1700 | 0.1900 | 11.7518 |
| Lingjiao Lake | 0.02525 | 0.0303 | 20.1192 | 0.2020 | 0.2245 | 11.1158 |
| Xiaotan Lake 2 | 0.01821 | 0.0243 | 33.5124 | 0.2920 | 0.1948 | 33.2877 |
| Fruit Lake | 0.02742 | 0.0255 | 6.9325 | 0.1780 | 0.1986 | 11.5781 |
| Guozhen Lake 1 | 0.02566 | 0.0239 | 6.6933 | 0.1200 | 0.1898 | 58.1617 |
| Yujia Lake | 0.05096 | 0.0516 | 1.2223 | 1.0600 | 1.1818 | 11.4925 |
| Xiaotan Lake 1 | 0.02816 | 0.0248 | 11.8487 | 0.1620 | 0.2014 | 24.3290 |
| Tiane Lake | 0.02241 | 0.0243 | 8.6158 | 0.1500 | 0.1919 | 27.9527 |
| Guozhen Lake 2 | 0.02176 | 0.0239 | 9.9508 | 0.1420 | 0.1897 | 33.6204 |
| Hou Lake | 0.04015 | 0.0247 | 38.5599 | 0.2140 | 0.2103 | 1.7107 |
| Miao Lake | 0.06256 | 0.0466 | 25.5400 | 0.4250 | 0.3229 | 24.0120 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Huang, M.; Wang, R. Numerical Simulation of Donghu Lake Hydrodynamics and Water Quality Based on Remote Sensing and MIKE 21. ISPRS Int. J. Geo-Inf. 2020, 9, 94. https://doi.org/10.3390/ijgi9020094
Li X, Huang M, Wang R. Numerical Simulation of Donghu Lake Hydrodynamics and Water Quality Based on Remote Sensing and MIKE 21. ISPRS International Journal of Geo-Information. 2020; 9(2):94. https://doi.org/10.3390/ijgi9020094
Chicago/Turabian StyleLi, Xiaojuan, Mutao Huang, and Ronghui Wang. 2020. "Numerical Simulation of Donghu Lake Hydrodynamics and Water Quality Based on Remote Sensing and MIKE 21" ISPRS International Journal of Geo-Information 9, no. 2: 94. https://doi.org/10.3390/ijgi9020094
APA StyleLi, X., Huang, M., & Wang, R. (2020). Numerical Simulation of Donghu Lake Hydrodynamics and Water Quality Based on Remote Sensing and MIKE 21. ISPRS International Journal of Geo-Information, 9(2), 94. https://doi.org/10.3390/ijgi9020094




