From Massive Trajectory Data to Traffic Modeling for Better Behavior Prediction in a Usage-Based Insurance Context
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Additional Information about the Data
3.2. Model Description
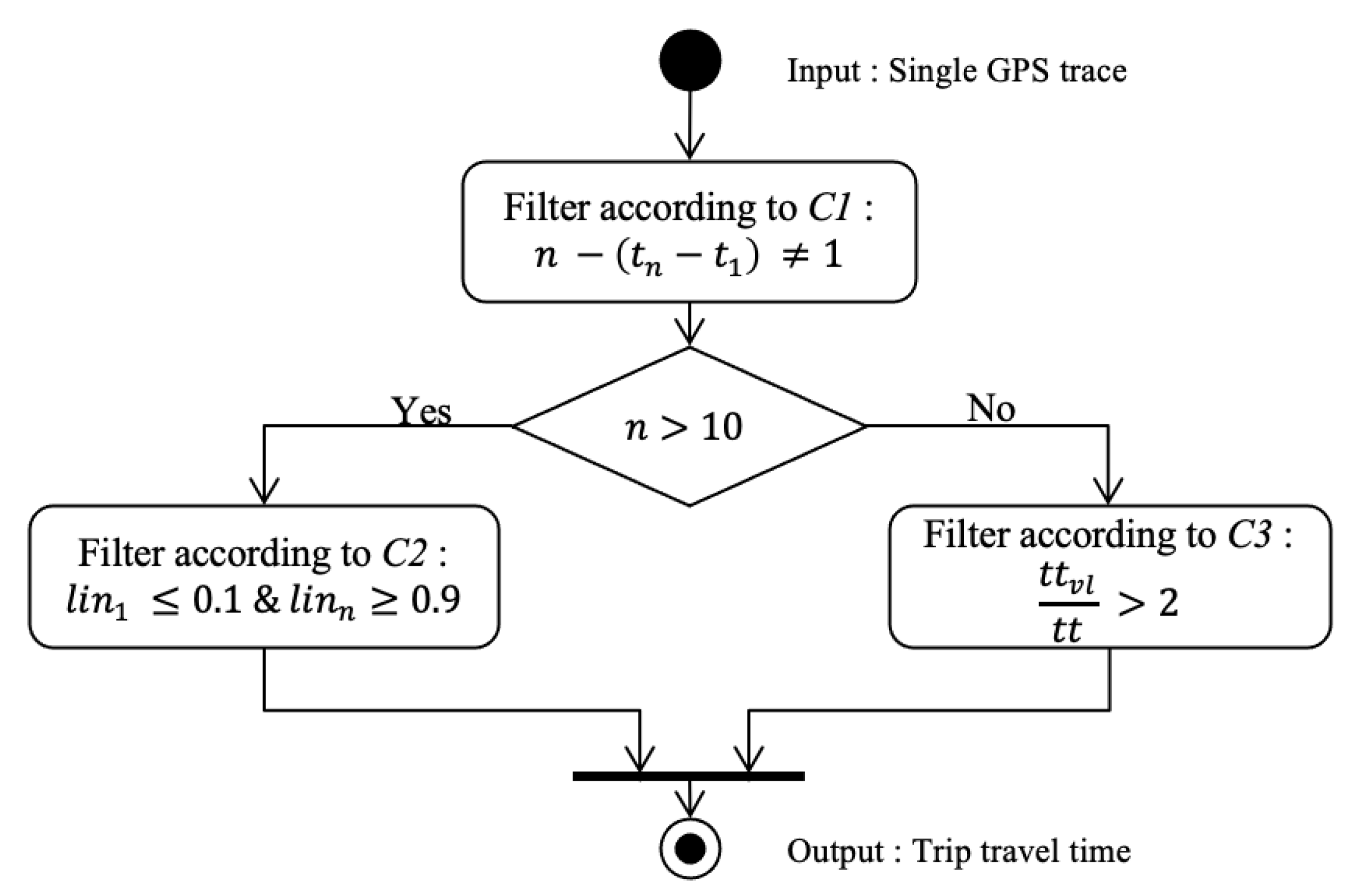
3.2.1. Link Travel Time Calculation and Filtering
3.2.2. Travel Time Index
3.2.3. Scaling at the Road Network Level
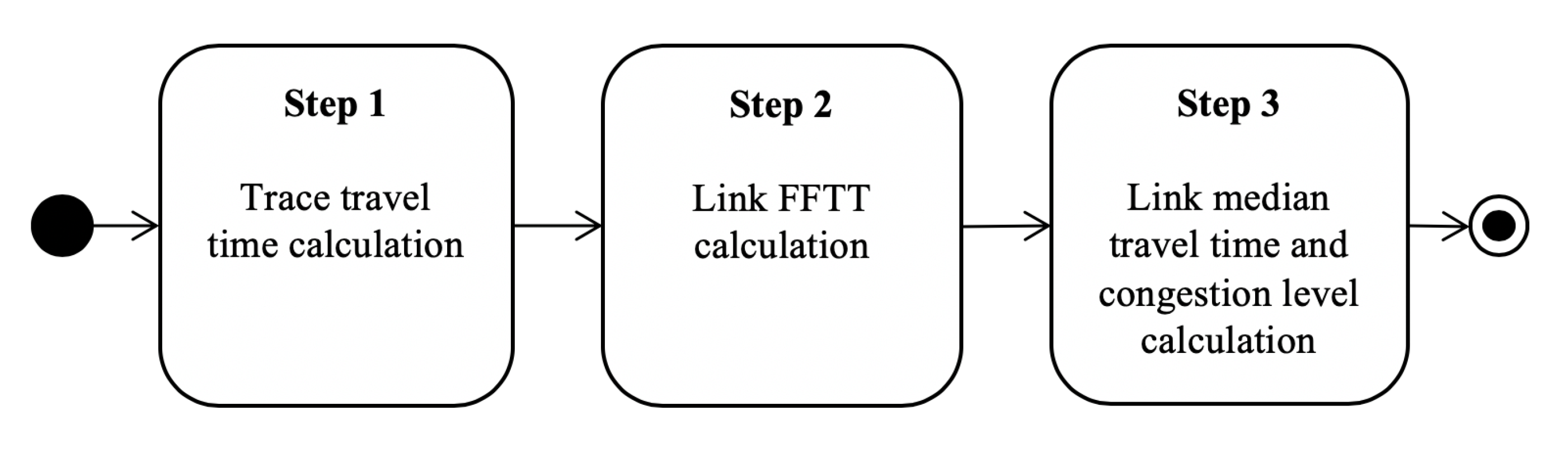
| Algorithm 1 Trace travel times’ calculation. |
 |
| Algorithm 2 Free flow travel time calculation. |
 |
| Algorithm 3 Median travel time and congestion level calculation. |
 |
3.3. Data Used
3.4. Validation Methodology
3.4.1. TTI Classes’ Validation
3.4.2. Travel Time Validation
4. Results
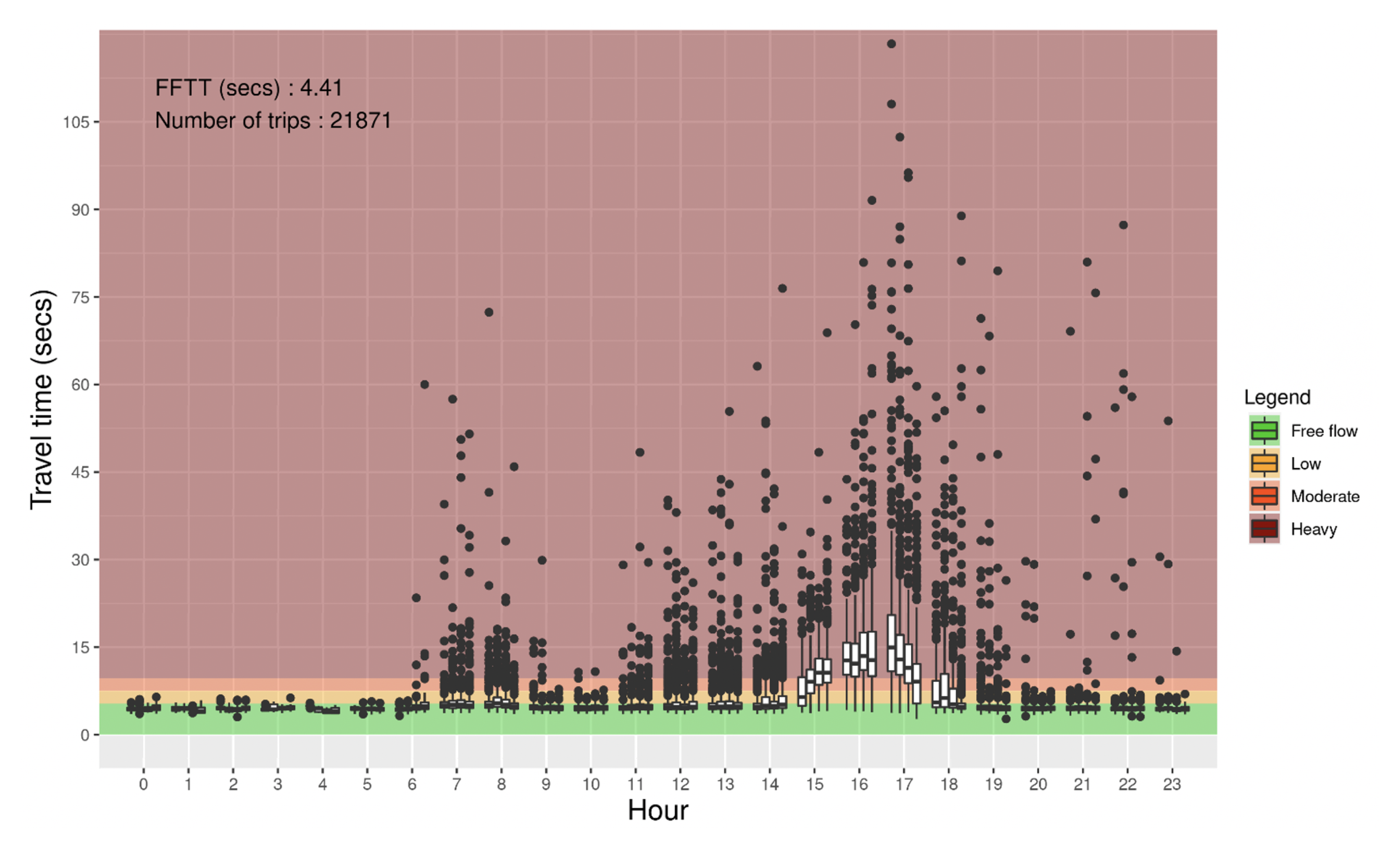
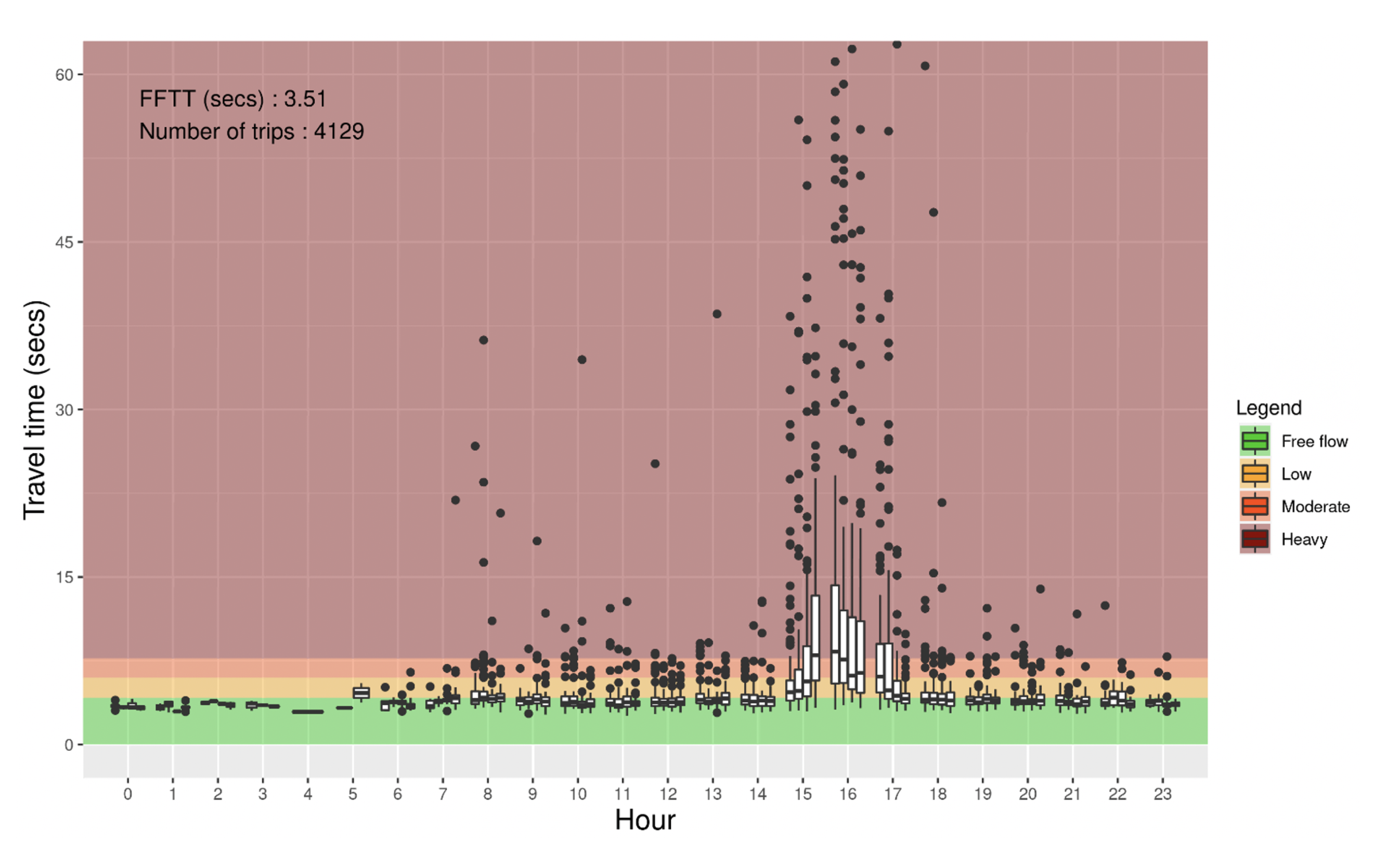
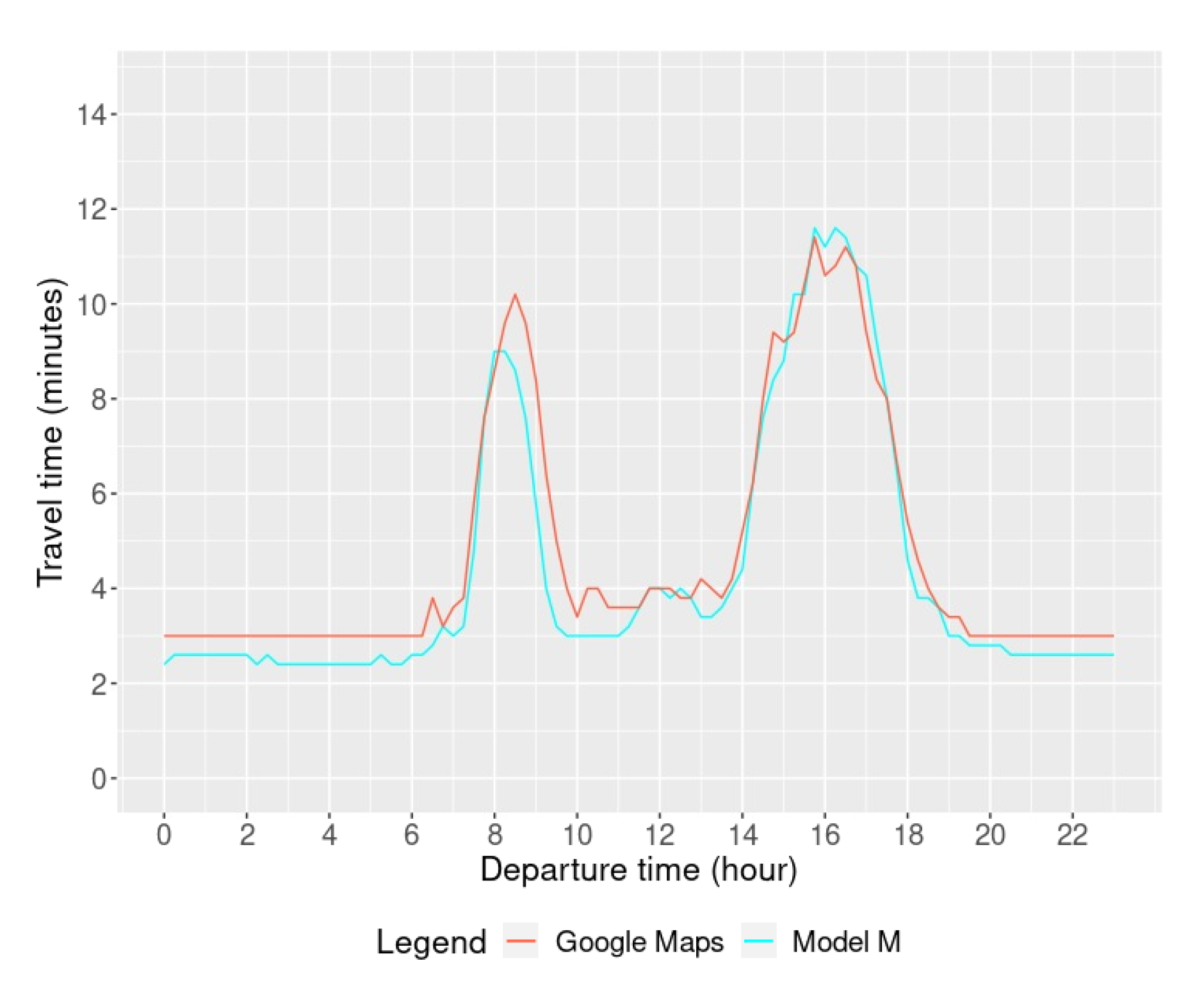
4.1. Travel Time
4.2. Validation Results
4.2.1. TTI Classes
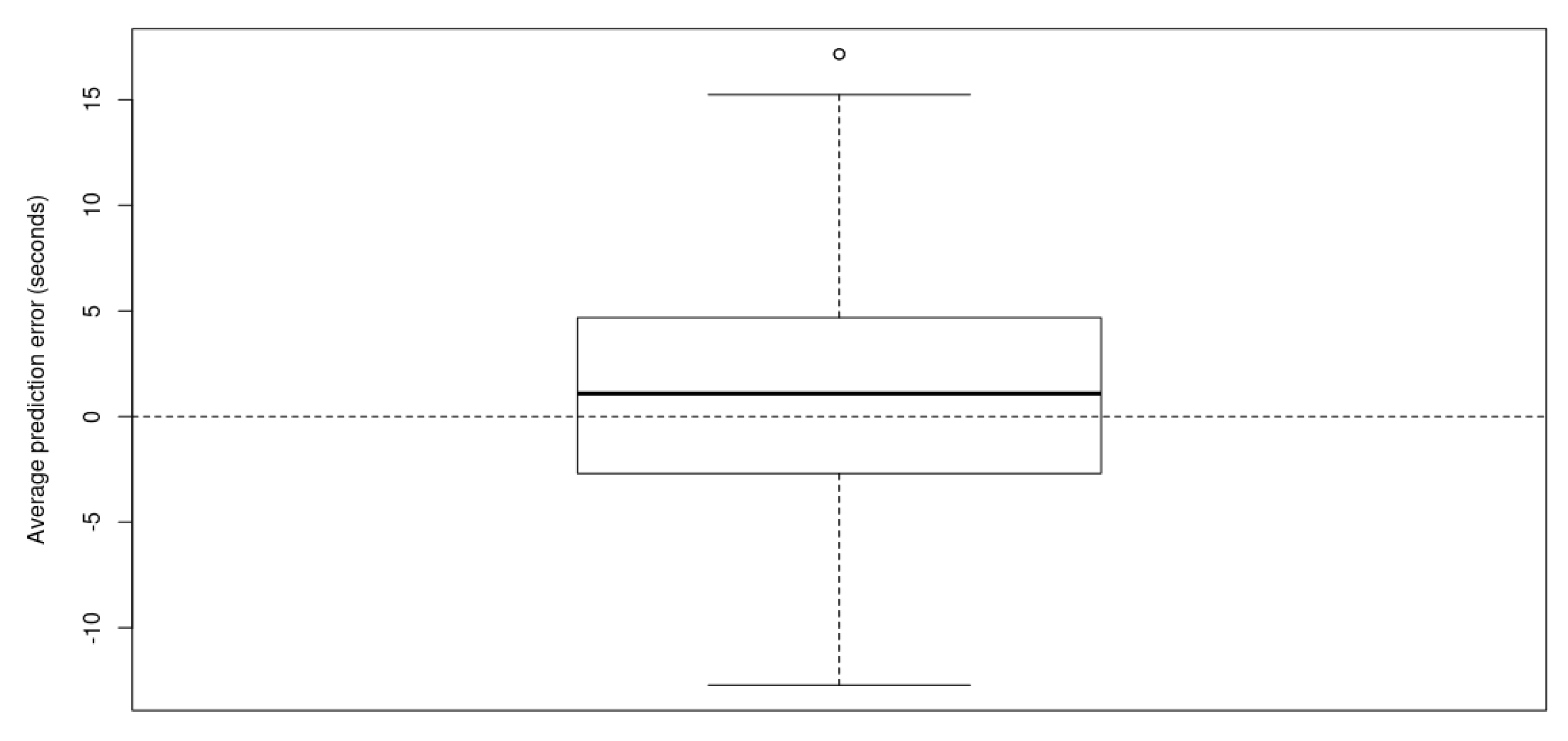
4.2.2. Travel Time
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, Y.; Meng, S. Automobile insurance classification ratemaking based on telematics driving data. Decis. Support Syst. 2019, 127, 113156. [Google Scholar] [CrossRef]
- Baecke, P.; Bocca, L. The value of vehicle telematics data in insurance risk selection processes. Decis. Support Syst. 2017, 98, 69–79. [Google Scholar] [CrossRef]
- Verbelen, R.; Antonio, K. Unravelling the predictive power of telematics data in car insurance pricing. Appl. Stat. 2018, 1275–1304. [Google Scholar] [CrossRef]
- Ma, Y.L.; Zhu, X.; Hu, X.; Chiu, Y.C. The use of context-sensitive insurance telematics data in auto insurance rate making. Transp. Res. Part A Policy Pract. 2018, 113, 243–258. [Google Scholar] [CrossRef]
- Jie, L.; Zuylen, H.V.; Chunhua, L.; Shoufeng, L. Social and Monitoring travel times in an urban network using video, GPS and Bluetooth. Procedia-Soc. Behav. Sci. 2011, 20, 630–637. [Google Scholar] [CrossRef][Green Version]
- Phan, A.; Ferrie, F. Obtaining Dense Road Speed Estimates from Sparse GPS Measurements. In Proceedings of the 2008 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; pp. 157–162. [Google Scholar] [CrossRef]
- Kong, X.; Yang, J.; Yang, Z. Measuring Traffic Congestion with Taxi GPS Data and Travel Time Index. In Proceedings of the 15th COTA International Conference of Transportation Professionals, Beijing, China, 24–27 July 2015; pp. 1016–1027. [Google Scholar] [CrossRef]
- Stipancic, J.; Miranda-Moreno, L.; Labbe, A.; Saunier, N. Measuring and visualizing space–time congestion patterns in an urban road network using large-scale smartphone-collected GPS data. Transp. Lett. 2019, 11, 391–401. [Google Scholar] [CrossRef]
- Castro, P.S.; Zhang, D.; Li, S. Urban Traffic Modelling and Prediction Using Large Scale Taxi GPS Traces. In International Conference on Pervasive Computing; Springer: Berlin/Heidelberg, Germany, 2012; pp. 57–72. [Google Scholar]
- Suhas, S.; V, V.K.; Katti, M.; V, A.P.B.; Naveena, C. A Comprehensive Review on Traffic Prediction for Intelligent Transport System. In Proceedings of the 2017 International Conference on Recent Advances in Electronics and Communication Technology, Bangalore, India, 16–17 March 2017. [Google Scholar] [CrossRef]
- Olszewski, P.; Dybicz, T.; Jamroz, K.; Kustra, W.; Romanowska, A. Assessing highway travel time reliability using probe vehicle data. Transp. Res. Rec. 2018, 2672, 118–130. [Google Scholar] [CrossRef]
- Puangprakhon, P.; Narupiti, S. Allocating Travel Times Recorded from Sparse GPS Probe Vehicles into Individual Road Segments. Transp. Res. Procedia 2017, 25, 2208–2221. [Google Scholar] [CrossRef]
- Fusco, G.; Colombaroni, C.; Comelli, L.; Isaenko, N. Short-term traffic predictions on large urban traffic networks: Applications of network-based machine learning models and dynamic traffic assignment models. In Proceedings of the 2015 International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Budapest, Hungary, 3–5 June 2015; pp. 93–101. [Google Scholar] [CrossRef]
- Sisiopiku, V.P.; Rostami-Hosuri, S. Congestion quantification using the national performance management research data set. Data 2017, 2, 39. [Google Scholar] [CrossRef]
- Xu, F.; Huang, Z.; Zhu, X. A New Design of Real-Time Traffic Index Model for Freeway. In Proceedings of the 5th International Conference on Advanced Cloud and Big Data, CBD 2017, Shanghai, China, 13–16 August 2017; pp. 302–307. [Google Scholar] [CrossRef]
- OpenStreetMap Contributors. Planet Dump. 2018. Available online: https://www.openstreetmap.org (accessed on 1 December 2020).
- Open Source Routing Machine. Available online: http://project-osrm.org/ (accessed on 27 April 2012).
- Xu, M.; Guo, K. Utilizing Artificial Neural Network in GPS-Equipped Probe Vehicles Data-Based Travel Time Estimation. IEEE Access 2019, 7, 89412–89426. [Google Scholar] [CrossRef]
- Chepuri, A.; Kumar, C.; Bhanegaonkar, P.; Arkatkar, S.S.; Joshi, G. Travel Time Reliability Analysis on Selected Bus Route of Mysore Using GPS Data. Transp. Dev. Econ. 2019, 5, 1–15. [Google Scholar] [CrossRef]
- Google Maps. Available online: https://www.google.com/maps (accessed on 2 June 2012).
- Herring, R. Estimating arterial traffic conditions using sparse probe data. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 929–936. [Google Scholar] [CrossRef]
- Luraschi, J.; Kuo, K.; Ushey, K.; Allaire, J.; Falaki, H.; Wang, L.; Zhang, A.; Li, Y.; The Apache Software Foundation. Sparklyr: R Interface to Apache Spark, R Package Version 1.2.0; Available online: http://spark.rstudio.com (accessed on 1 December 2020).
- Mo, A.; Pokonieczny, K.; Wilbik, A.; Wabi, J. Transport Accessibility of Warsaw: A Case Study. Sustainability 2019, 11, 5536. [Google Scholar]



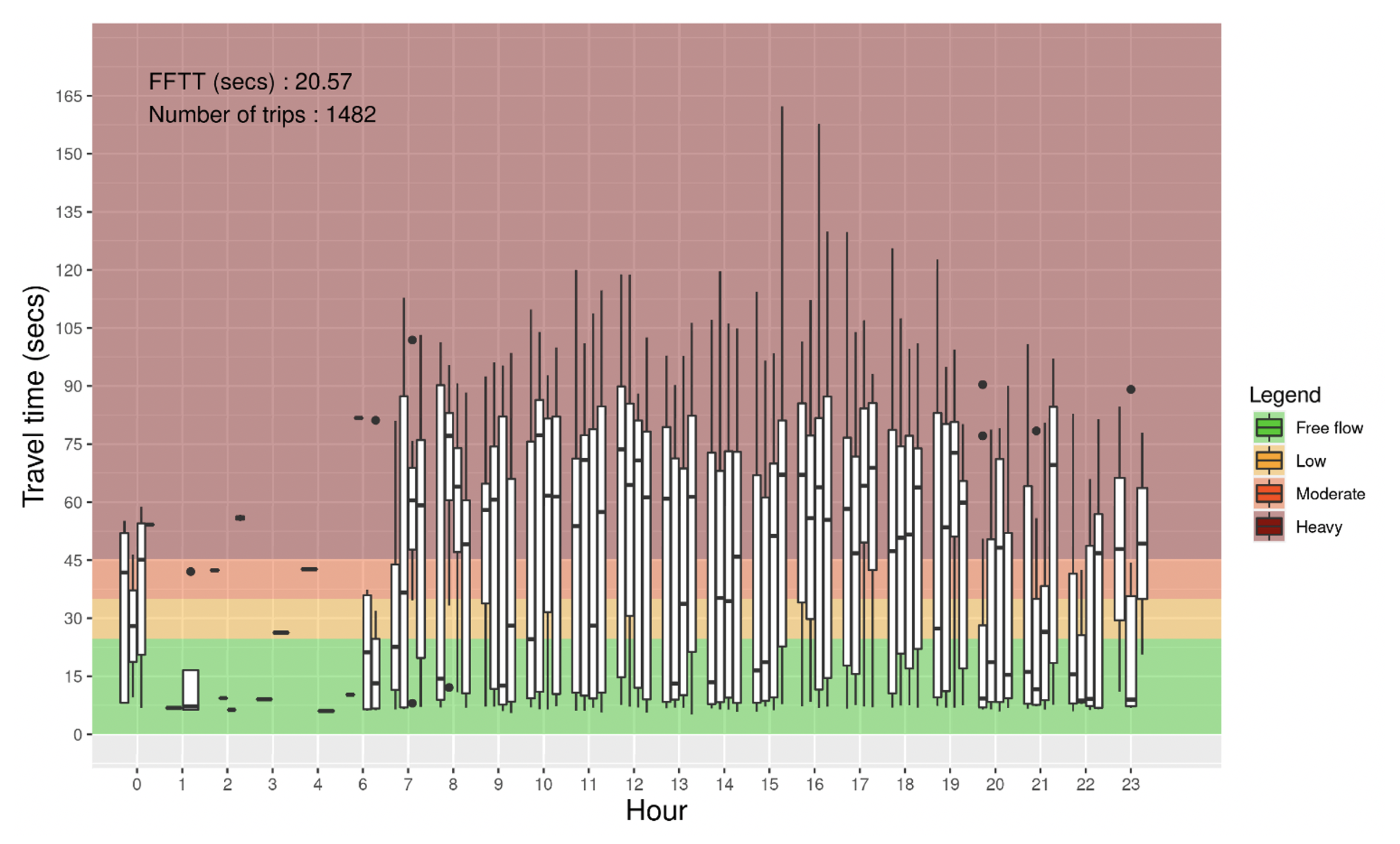
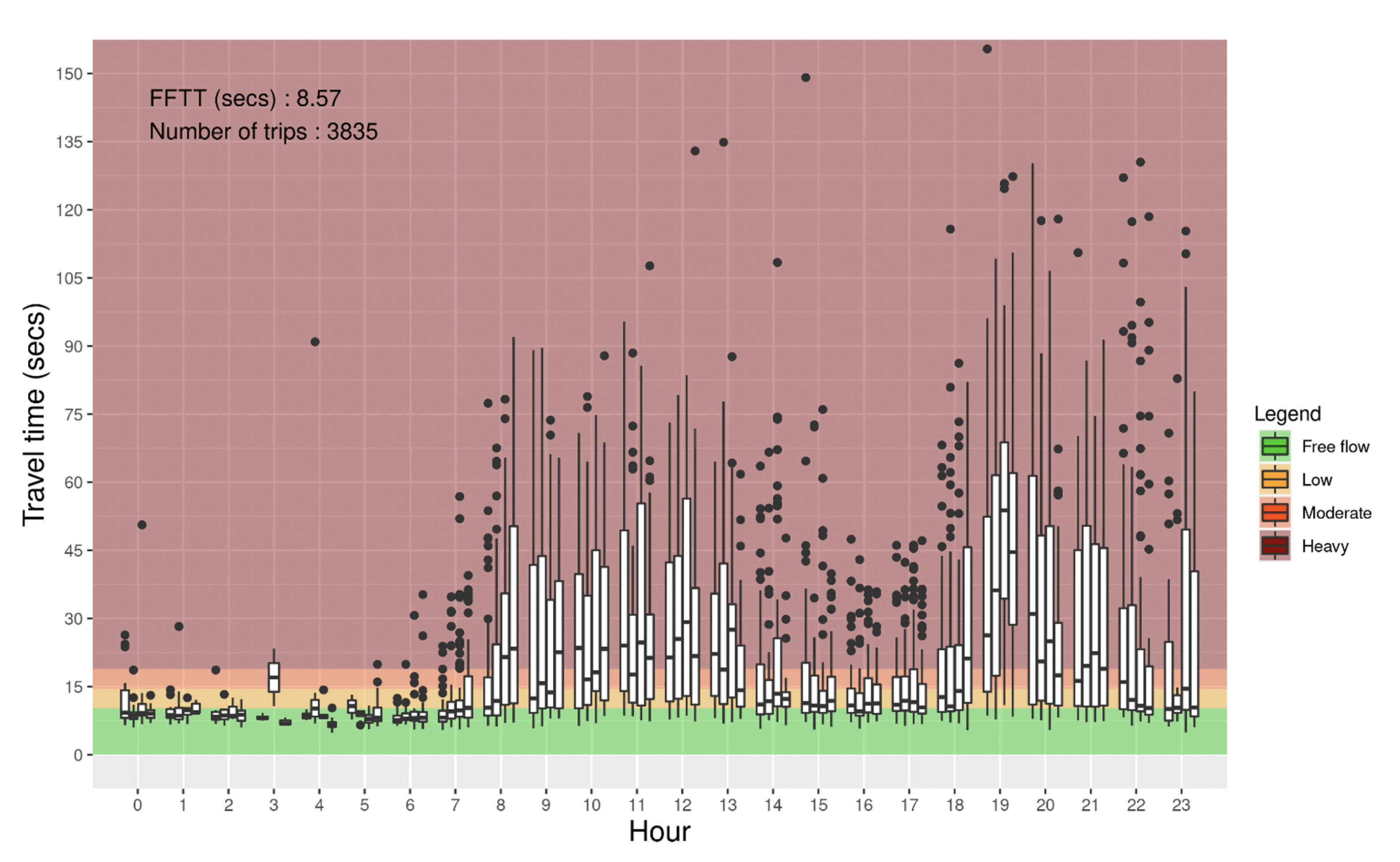
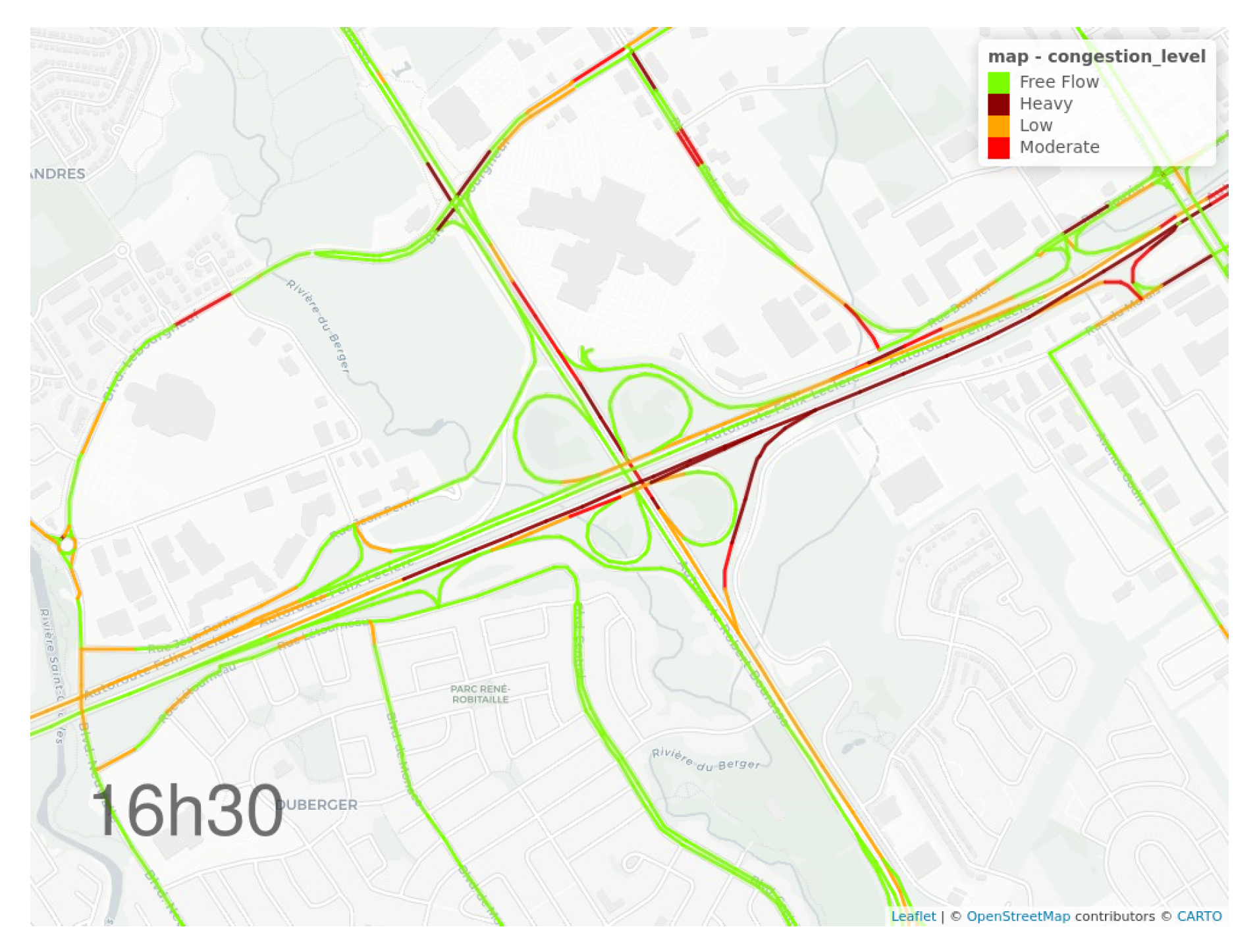

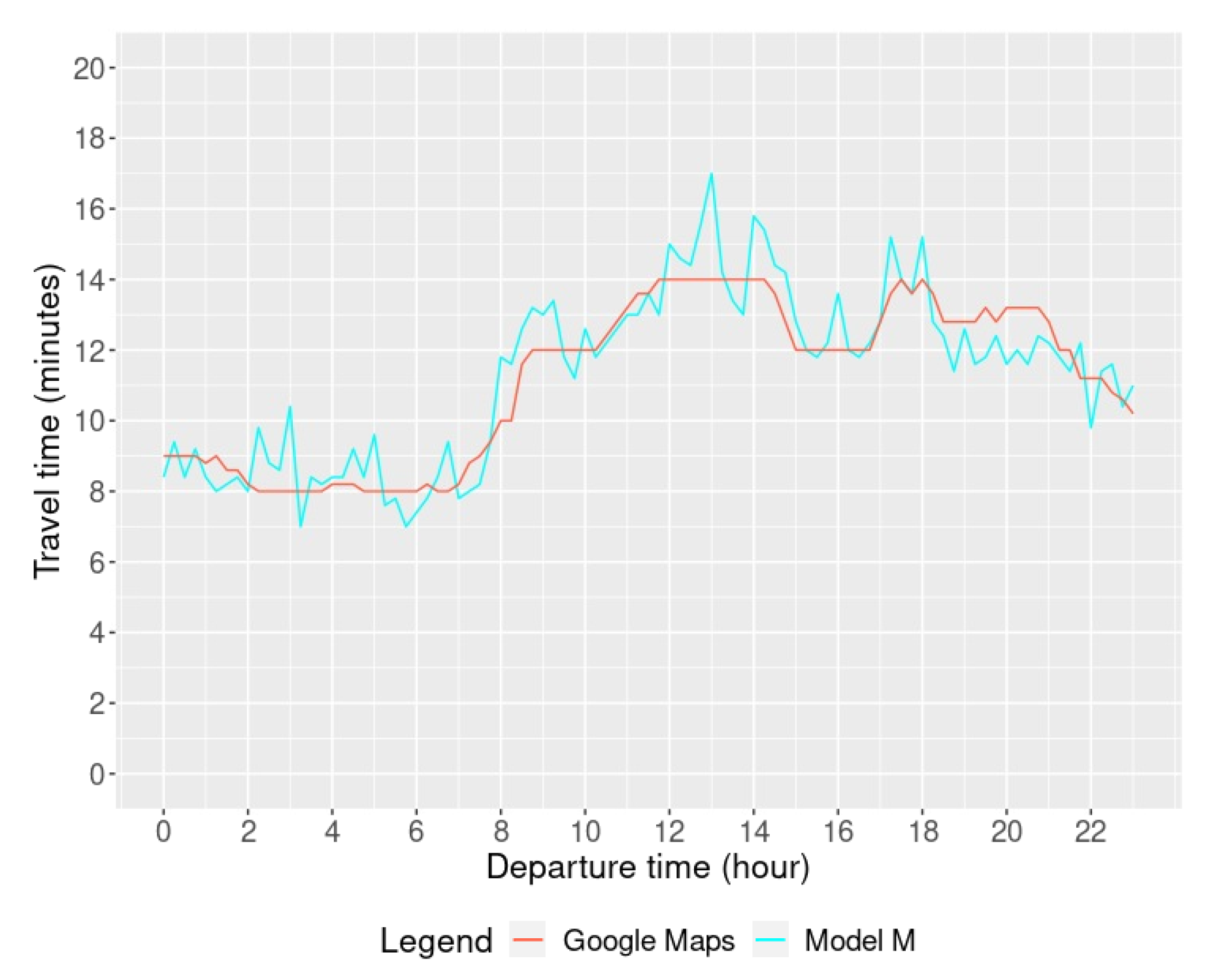
| Google Maps [20] | Xu et al [15] | Proposed Model | |||
|---|---|---|---|---|---|
| Unknown < TTI < Unknown | Fast | 0.0 < TTI ≤ 1.3 | smooth | 0.0 < TTI ≤ 1.2 | free flow |
| Unknown < TTI < Unknown | Unknown | 1.3 < TTI ≤ 1.6 | relatively smooth | 1.2 < TTI ≤ 1.7 | low congestion |
| Unknown < TTI < Unknown | Unknown | 1.6 < TTI ≤ 1.9 | mild congestion | 1.7 < TTI ≤ 2.2 | moderate congestion |
| TTI > Unknown | Slow | 1.9 < TTI ≤ 2.2 | moderate congestion | TTI > 2.2 | heavy congestion |
| TTI > 2.2 | severe congestion | ||||
| Sherbrooke | Quebec City | Montreal | Toronto | |
|---|---|---|---|---|
| Number of GPS observations | 229,589,252 | 702,197,751 | 3,437,191,916 | 4,047,701,407 |
| Number of trips | 275,676 | 695,417 | 2,781,157 | 3,433,869 |
| Number of drivers | 3554 | 8321 | 28,033 | 39,047 |
| City | Number of Routes | Highway Types Used | Average Length of Routes (km) | Maximum Length (km) | Minimum Length (km) |
|---|---|---|---|---|---|
| Sherbrooke | 8 | Motorway, Primary, Secondary, Tertiary | 5.1 | 6.8 | 3.0 |
| Quebec City | 12 | Motorway, Primary, Secondary, Tertiary, mixed | 6.2 | 11.5 | 3.2 |
| Montreal | 8 | Motorway, Primary, Secondary, Tertiary | 3.9 | 4.3 | 3.3 |
| Toronto | 10 | Motorway, Secondary, Tertiary | 4.2 | 7.0 | 2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blais, P.; Badard, T.; Duchesne, T.; Côté, M.-P. From Massive Trajectory Data to Traffic Modeling for Better Behavior Prediction in a Usage-Based Insurance Context. ISPRS Int. J. Geo-Inf. 2020, 9, 722. https://doi.org/10.3390/ijgi9120722
Blais P, Badard T, Duchesne T, Côté M-P. From Massive Trajectory Data to Traffic Modeling for Better Behavior Prediction in a Usage-Based Insurance Context. ISPRS International Journal of Geo-Information. 2020; 9(12):722. https://doi.org/10.3390/ijgi9120722
Chicago/Turabian StyleBlais, Philippe, Thierry Badard, Thierry Duchesne, and Marie-Pier Côté. 2020. "From Massive Trajectory Data to Traffic Modeling for Better Behavior Prediction in a Usage-Based Insurance Context" ISPRS International Journal of Geo-Information 9, no. 12: 722. https://doi.org/10.3390/ijgi9120722
APA StyleBlais, P., Badard, T., Duchesne, T., & Côté, M.-P. (2020). From Massive Trajectory Data to Traffic Modeling for Better Behavior Prediction in a Usage-Based Insurance Context. ISPRS International Journal of Geo-Information, 9(12), 722. https://doi.org/10.3390/ijgi9120722






