A Comparative Study of Several Metaheuristic Algorithms to Optimize Monetary Incentive in Ridesharing Systems
Abstract
1. Introduction
1.1. Motivation
1.2. Research Question, Goals and Objectives
2. Problem Formulation
3. Fitness Function and Constraint Handling Method
- , where
4. Implementation of Discrete Metaheuristic Algorithms
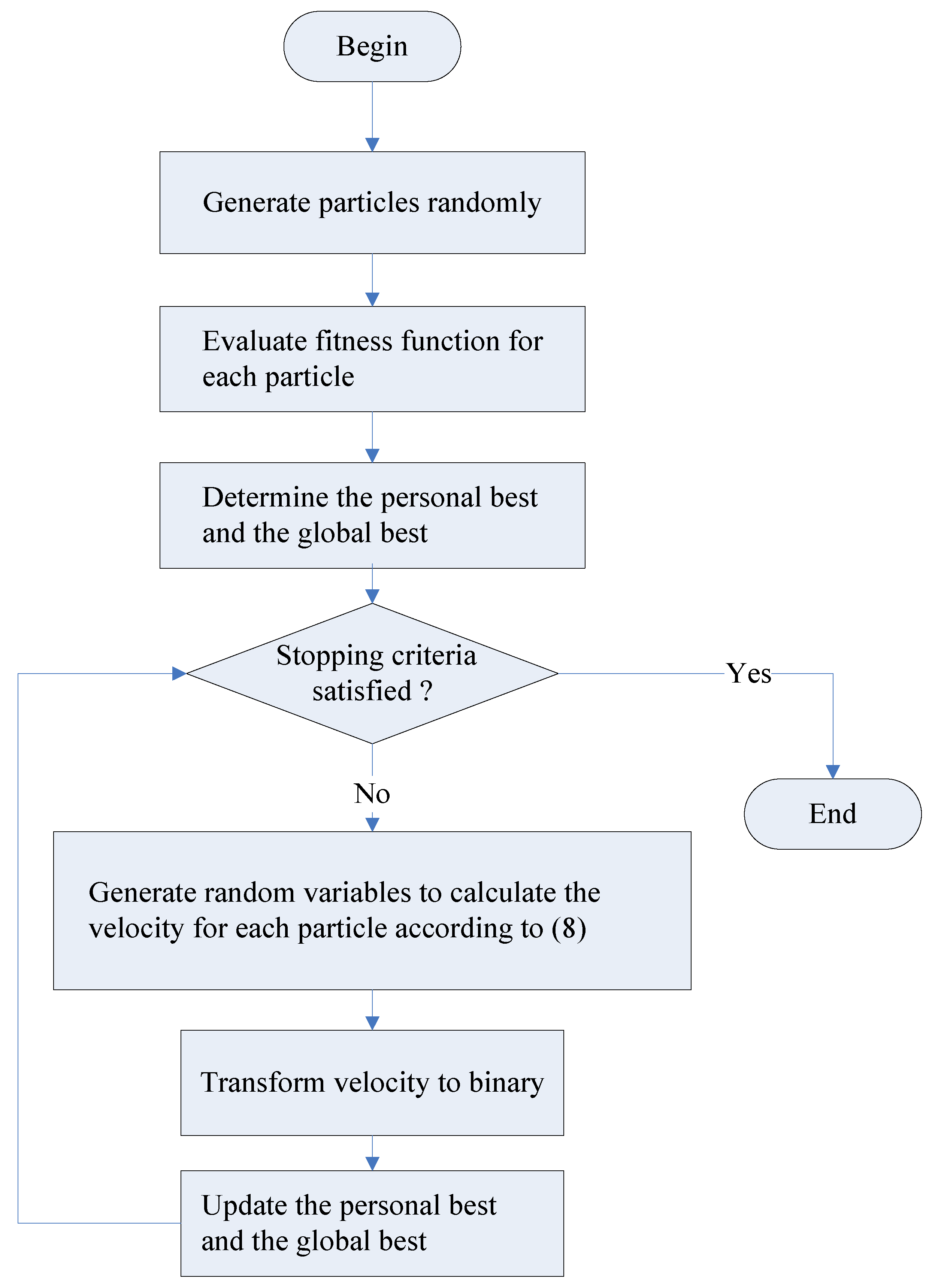
4.1. Discrete PSO Algorithm
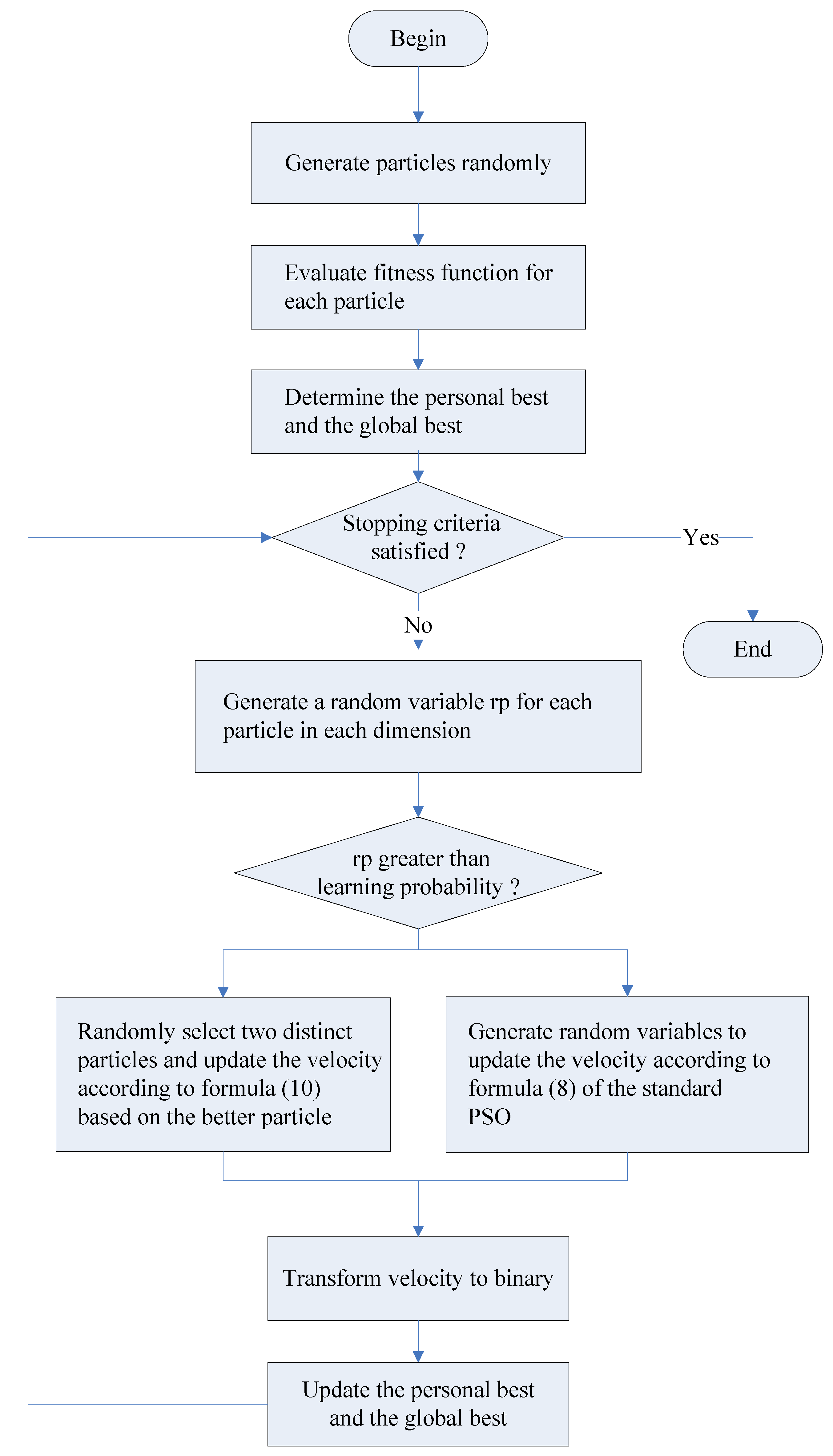
4.2. Discrete CLPSO Algorithm
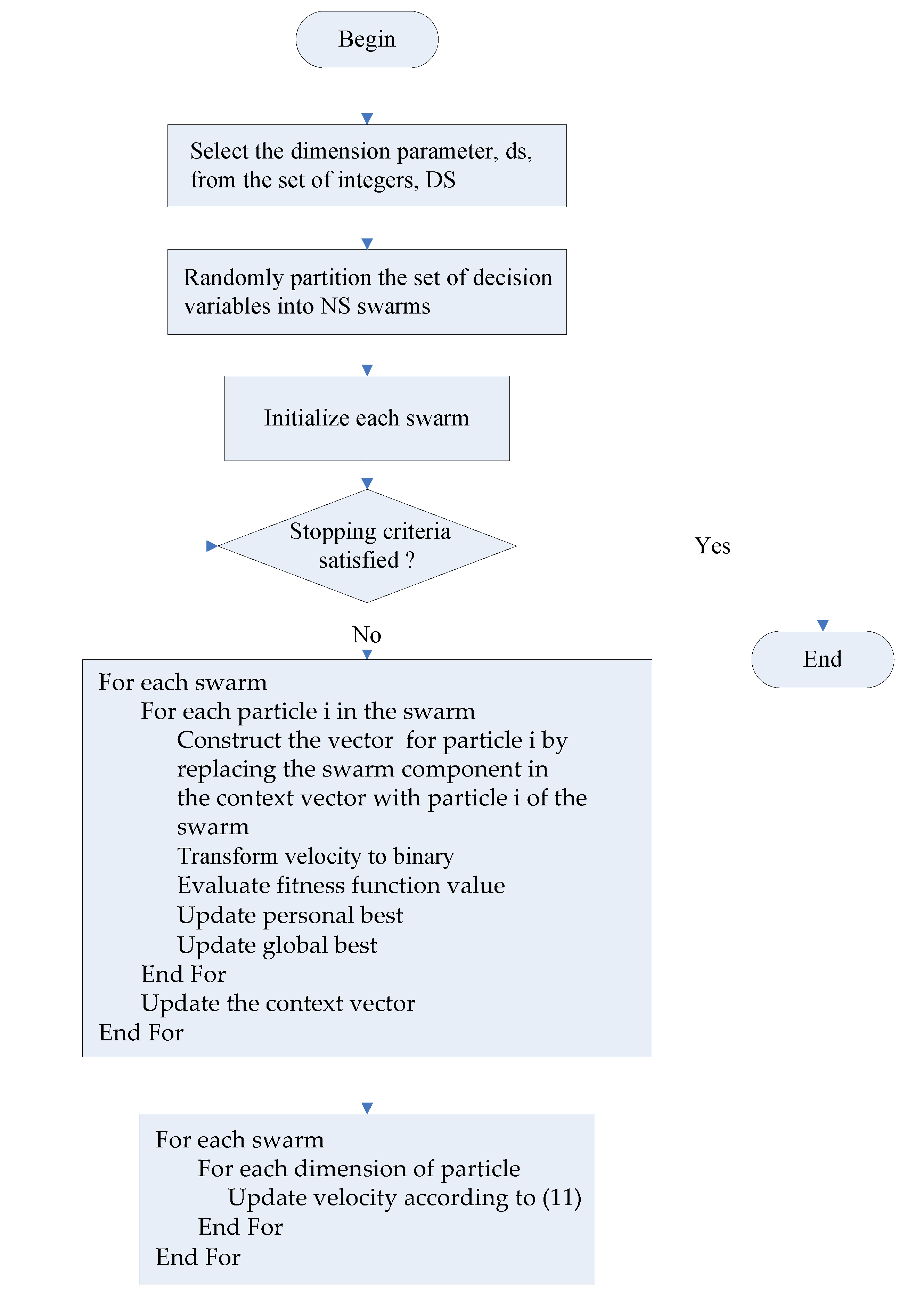
4.3. Discrete CCPSO Algorithm
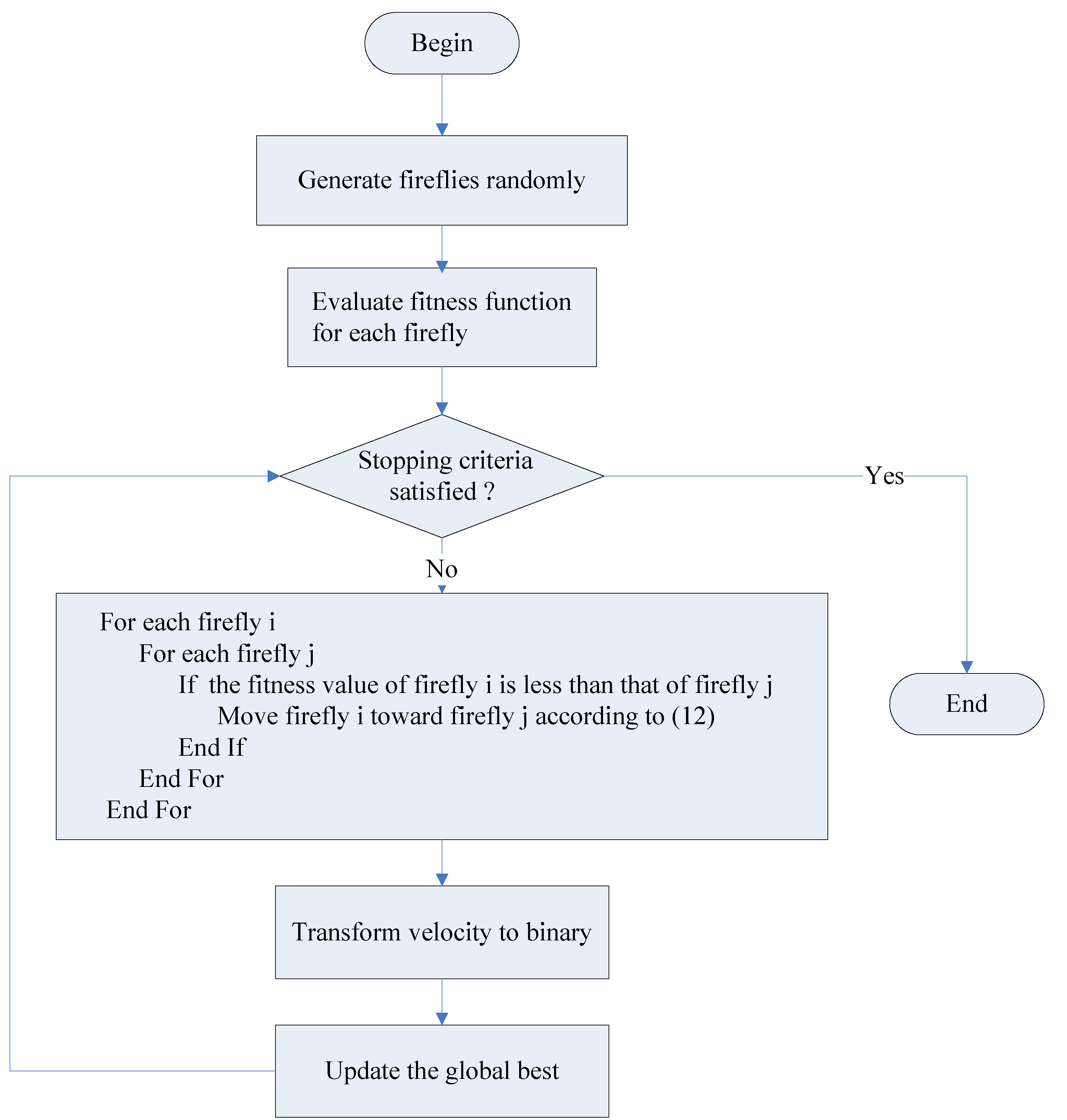
4.4. Discrete Firefly Algorithm
4.5. Discrete Differential Evolution Algorithm
5. Results
5.1. Data and Parameters
- = {2, 5, 10}
- = 0.5
- = 0.5
- = 1.0
- = 4
- = 10,000
- = 0.4
- = 0.4
- = 0.6
- = 4
- = 10,000
- = 1.0
- = 0.2
- = 0.2
- = 4
- = 10,000
- = 0.4
- = 0.4
- = 0.6
- = 0.5
- = 4
- = 10,000
- = 0.5
- : Gaussian random variable with zero mean and standard deviation set to 1.0
- = 4
- = 10,000
- Population size = 10
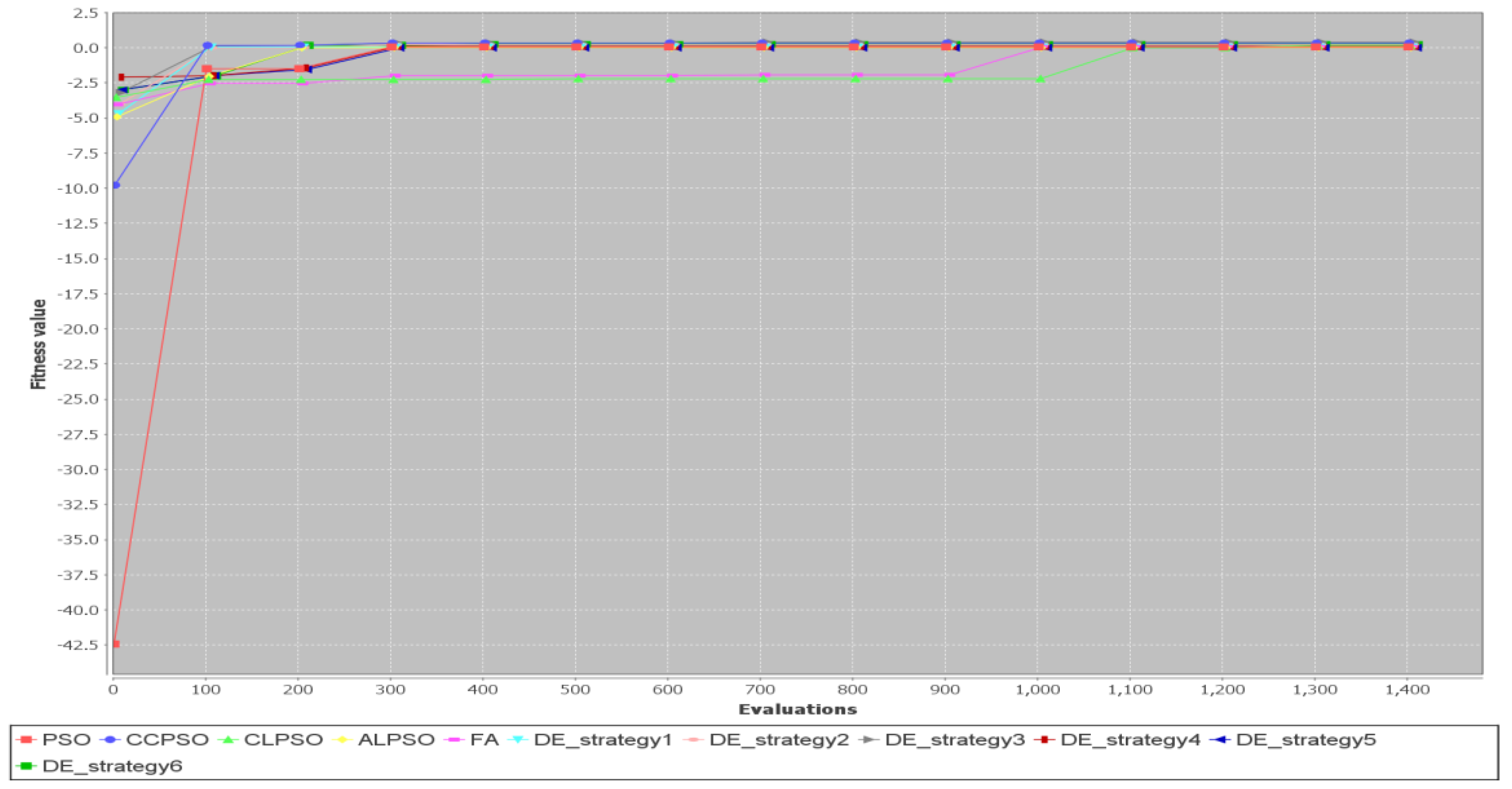
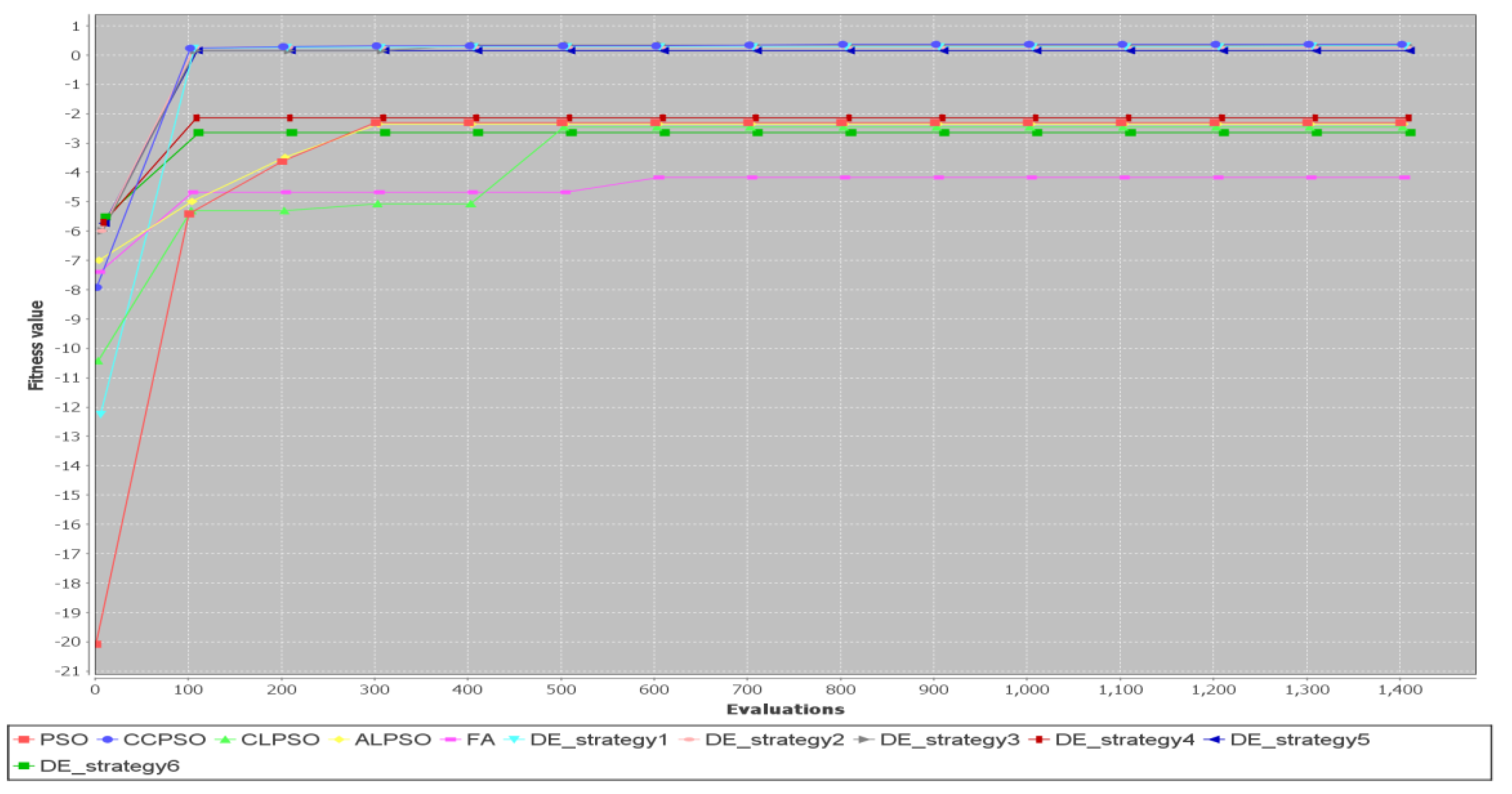
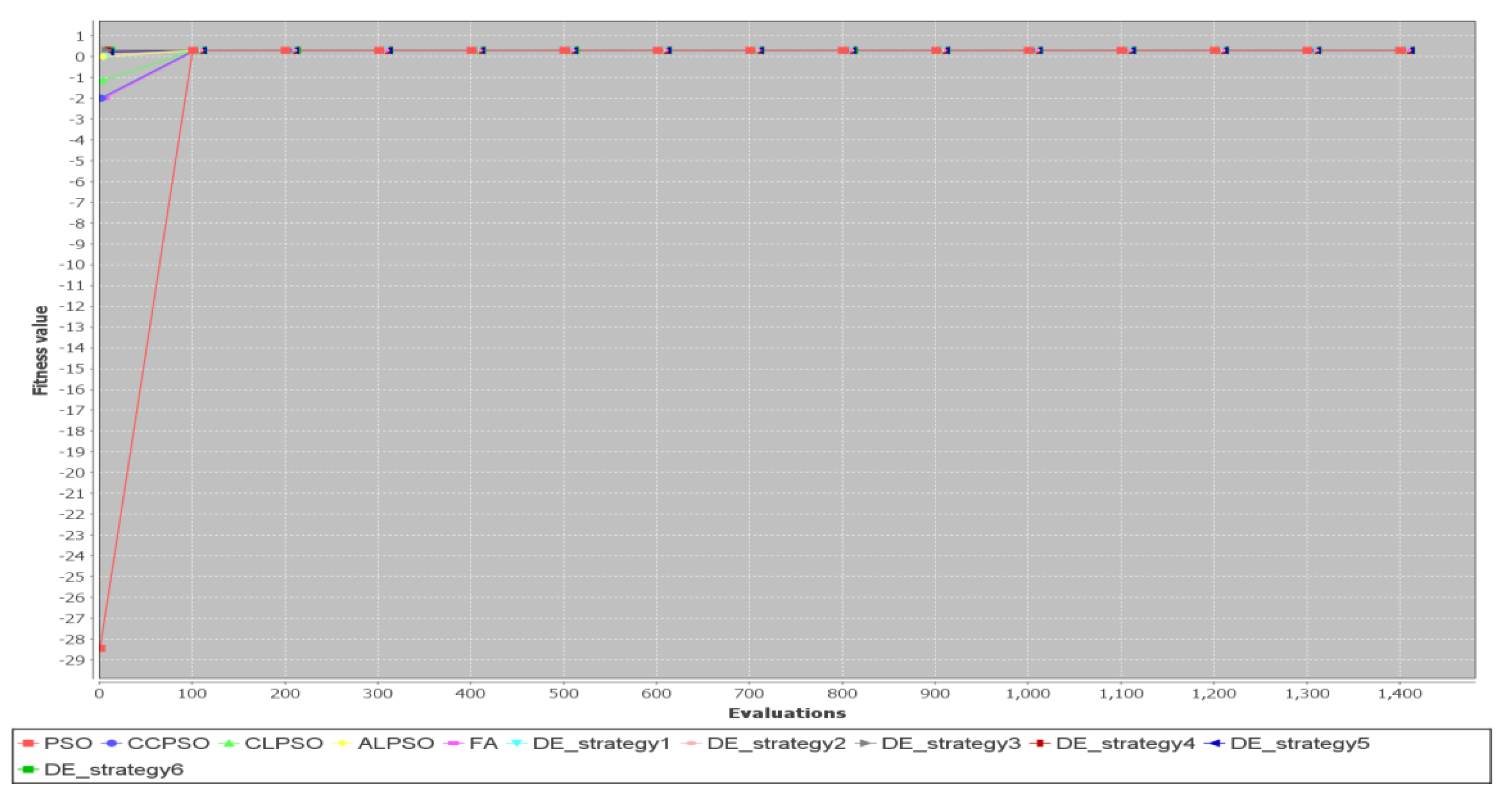
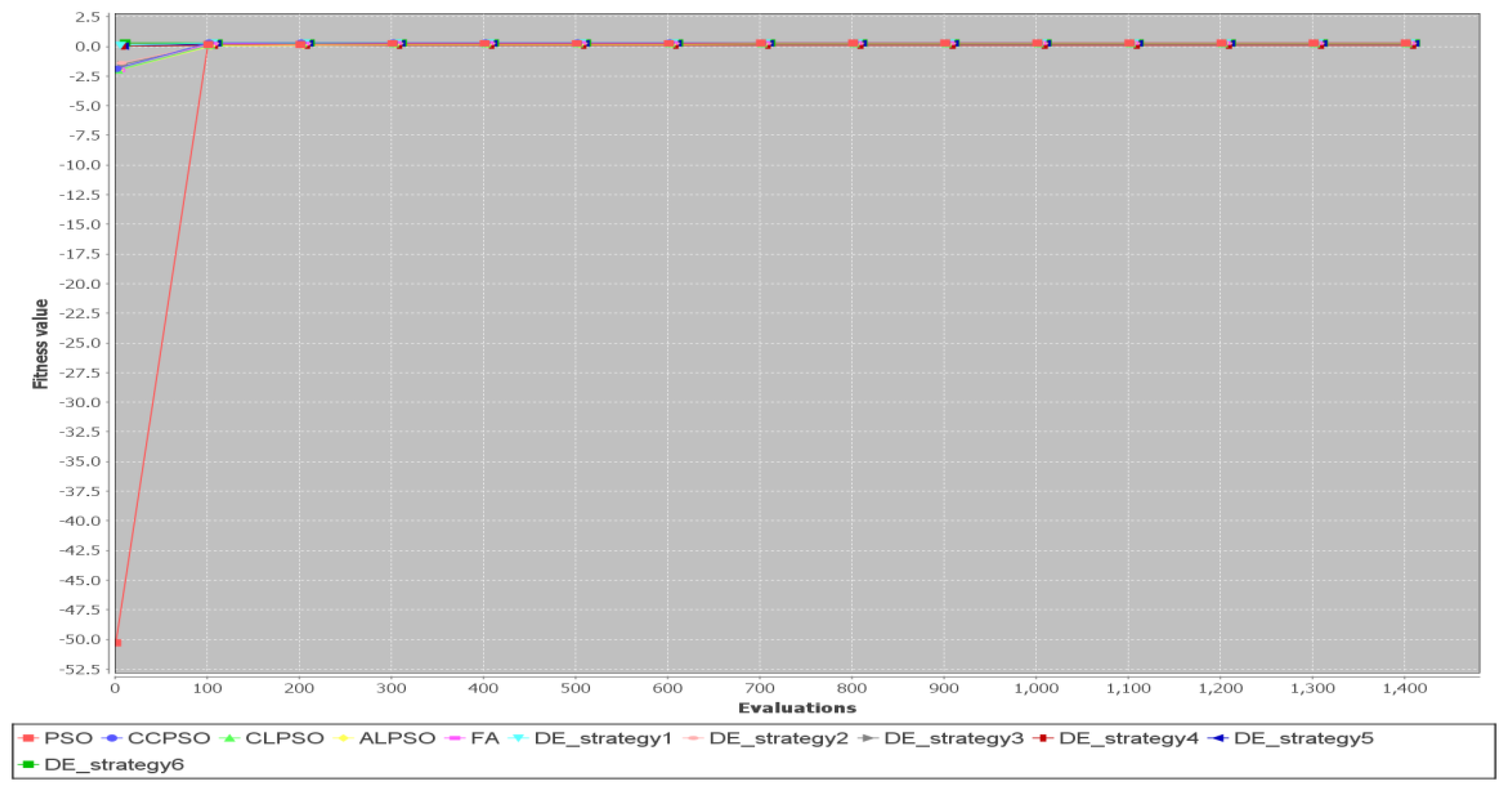
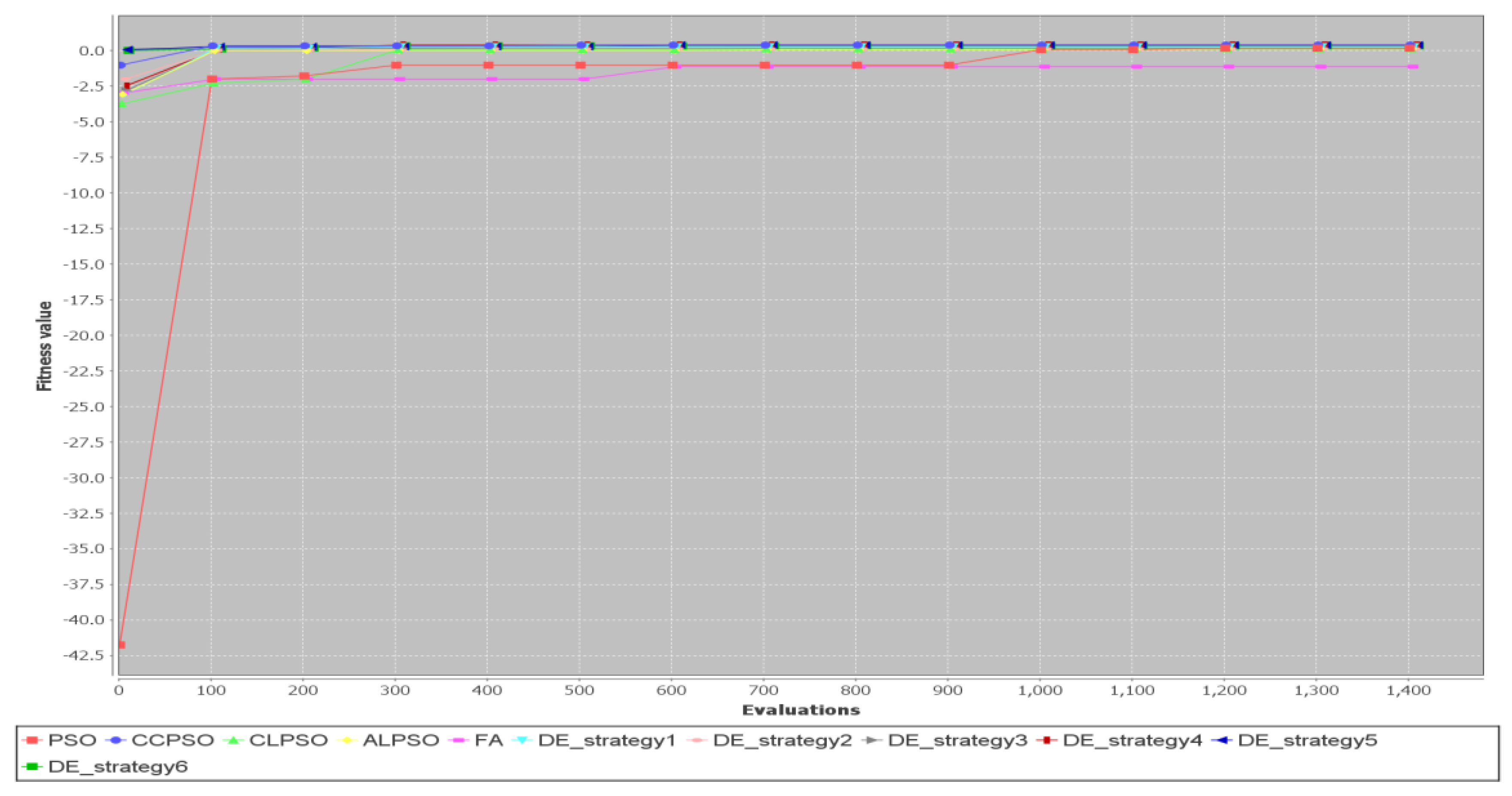
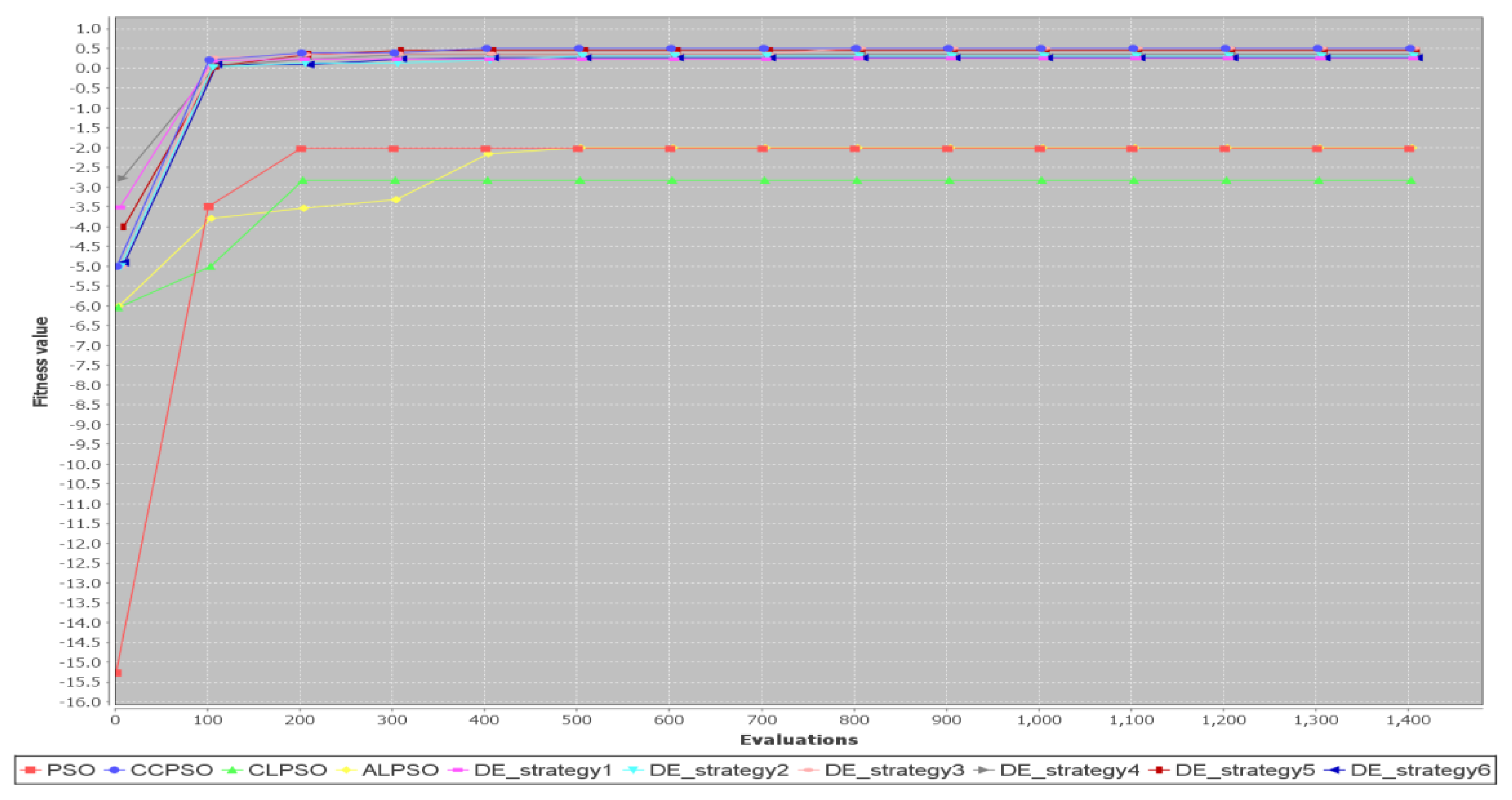
5.2. Comparison of Different Metaheuristic Algorithms
6. Conclusions
Funding
Conflicts of Interest
References
- Furuhata, M.; Dessouky, M.; Ordóñez, F.; Brunet, M.; Wang, X.; Koenig, S. Ridesharing: The state-of-the-art and future directions. Transp. Res. Pt. B-Methodol. 2013, 57, 28–46. [Google Scholar] [CrossRef]
- Agatz, N.; Erera, A.; Savelsbergh, M.; Wang, X. Optimization for dynamic ride-sharing: A review. Eur. J. Oper. Res. 2012, 223, 295–303. [Google Scholar] [CrossRef]
- Genikomsakis, K.N.; Ioakimidis, C.S.; Bocquier, B.; Savvidis, D.; Simic, D. Electromobility and carsharing/carpooling services at the University of Deusto: A preliminary exploratory survey. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 1935–1940. [Google Scholar]
- Bruglieri, M.; Ciccarelli, D.; Colorni, A.; Luè, A. PoliUniPool: A carpooling system for universities. Procedia Soc. Behav. Sci. 2011, 20, 558–567. [Google Scholar] [CrossRef]
- Baldacci, R.; Maniezzo, V.; Mingozzi, A. An Exact Method for the Car Pooling Problem Based on Lagrangean Column Generation. Oper. Res. 2004, 52, 422–439. [Google Scholar] [CrossRef]
- Maniezzo, V.; Carbonaro, A.; Hildmann, H. An ants heuristic for the long-term car pooling problem. In New Optimization Techniques in Engineering; Onwubolu, G., Babu, B.V., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 141, pp. 411–430. [Google Scholar]
- Agatz, N.A.H.; Erera, A.L.; Savelsbergh, M.W.P.; Wang, X. Dynamic ride-sharing: A simulation study in metro Atlanta. Transp. Res. Pt. B-Methodol. 2011, 45, 1450–1464. [Google Scholar] [CrossRef]
- Bicocchi, N.; Mamei, M. Investigating ride sharing opportunities through mobility data analysis. Pervasive Mob. Comput. 2014, 14, 83–94. [Google Scholar] [CrossRef]
- Toader, B.; Sprumont, F.; Faye, S.; Popescu, M.; Viti, F. Usage of Smartphone Data to Derive an Indicator for Collaborative Mobility between Individuals. ISPRS Int. J. Geo-Inf. 2017, 6, 62. [Google Scholar] [CrossRef]
- Hsieh, F.S. Car Pooling Based on Trajectories of Drivers and Requirements of Passengers. In Proceedings of the 2017 IEEE 31st International Conference on Advanced Information Networking and Applications (AINA 2017), Taipei, Taiwan, 27–29 March 2017; pp. 972–978. [Google Scholar]
- Bian, Z.; Liu, X.; Bai, Y. Mechanism design for on-demand first-mile ridesharing. Transp. Res. Pt. B-Methodol. 2020, 138, 77–117. [Google Scholar] [CrossRef]
- Delhomme, P.; Gheorghiu, A. Comparing French carpoolers and non-carpoolers: Which factors contribute the most to carpooling? Transport. Res. Part D-Transport. Environ. 2016, 42, 1–115. [Google Scholar] [CrossRef]
- Waerden, P.; Lem, A.; Schaefer, W. Investigation of Factors that Stimulate Car Drivers to Change from Car to Carpooling in City Center Oriented Work Trips. Transp. Res. Procedia 2015, 10, 335–344. [Google Scholar] [CrossRef]
- Shaheen, S.A.; Chan, N.D.; Gaynor, T. Casual carpooling in the San Francisco Bay Area: Understanding user characteristics, behaviors, and motivations. Transp. Policy 2016, 51, 165–173. [Google Scholar] [CrossRef]
- Santos, D.O.; Xavier, E.C. Taxi and Ride Sharing: A Dynamic Dial-a-Ride Problem with Money as an Incentive. Expert Syst. Appl. 2015, 42, 6728–6737. [Google Scholar] [CrossRef]
- Watel, D.; Faye, A. Taxi-sharing: Parameterized complexity and approximability of the dial-a-ride problem with money as an incentive. Theor. Comput. Sci. 2018, 745, 202–8223. [Google Scholar] [CrossRef]
- Hsieh, F.S. Optimization of Monetary Incentive in Ridesharing Systems. In Advances and Trends in Artificial Intelligence, From Theory to Practice; Lecture Notes in Computer Science; Wotawa, F., Friedrich, G., Pill, I., Koitz-Hristov, R., Ali, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 11606, pp. 835–840. [Google Scholar]
- Ting, T.O.; Yang, X.S.; Cheng, S.; Huang, K. Hybrid Metaheuristic Algorithms: Past, Present, and Future. In Recent Advances in Swarm Intelligence and Evolutionary Computation. Studies in Computational Intelligence; Yang, X.S., Ed.; Springer: Cham, Switzerland, 2015; Volume 585, pp. 71–83. [Google Scholar] [CrossRef]
- de Rosa, G.H.; Papa, J.P.; Yang, X. Handling dropout probability estimation in convolution neural networks using meta-heuristics. Soft Comput. 2018, 22, 6147–6156. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Su, J.; Wang, J. Research and application based on the swarm intelligence algorithm and artificial intelligence for wind farm decision system. Renew. Energy 2019, 134, 681–697. [Google Scholar] [CrossRef]
- Slowik, A.; Kwasnicka, H. Nature inspired methods and their industry applications—Swarm intelligence algorithms. IEEE Trans. Ind. Inform. 2018, 14, 1004–1015. [Google Scholar] [CrossRef]
- Anandakumar, H.; Umamaheswari, K. A bio-inspired swarm intelligence technique for social aware cognitive radio handovers. Comput. Electr. Eng. 2018, 71, 925–937. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5792, pp. 169–178. [Google Scholar]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Monarch Butterfly Optimization Based Convolutional Neural Network Design. Mathematics 2020, 8, 936. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparison between genetic algorithms and particle swarm optimization. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1447, pp. 169–178. [Google Scholar]
- Hassan, R.; Cohanim, B.; Weck, O.D. A Comparison of Particle Swarm Optimization and the Genetic Algorithm. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005. [Google Scholar]
- Dulebenets, M.A.; Moses, R.; Ozguven, E.E.; Vanli, A. Minimizing carbon dioxide emissions due to container handling at marine container terminals via hybrid evolutionary algorithms. IEEE Access 2017, 5, 8131–8147. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics: Computational Cybernetics and Simulation, Orlando, FL, USA,, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Hsieh, F.S.; Zhan, F.; Guo, Y. A solution methodology for carpooling systems based on double auctions and cooperative coevolutionary particle swarms. Appl. Intell. 2019, 49, 741–763. [Google Scholar] [CrossRef]
- Hsieh, F.S.; Zhan, F. A Discrete Differential Evolution Algorithm for Carpooling. In Proceedings of the 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), Tokyo, Japan, 23–27 July 2018; pp. 577–582. [Google Scholar]
- Bergh, F.; Engelbrecht, A.P. A Cooperative approach to particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar]
- Potter, M.A.; De Jong, K.A. A cooperative coevolutionary approach to function optimization. In Parallel Problem Solving from Nature—PPSN III; Lecture Notes in Computer Science; Davidor, Y., Schwefel, H.P., Männer, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; Volume 866, pp. 741–763. [Google Scholar]
- Yang, Z.; Tang, K.; Yao, X. Large scale evolutionary optimization using cooperative coevolution. Inf. Sci. 2008, 178, 2985–2999. [Google Scholar] [CrossRef]
- Ravindran, A.; Ragsdell, K.M.; Reklaitis, G.V. Engineering Optimization: Methods and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Deb, K. Optimization for Engineering Design: Algorithms and Examples; Prentice-Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Li, K.; Lin, Z.; Yang, J.; Shen, X.L. A hybrid particle swarm optimization algorithm using adaptive learning strategy. Inf. Sci. 2018, 436–437, 162–177. [Google Scholar] [CrossRef]




| Variable/Symbol | Meaning |
|---|---|
| total number of passengers | |
| the ID of a passenger, where | |
| total number of drivers | |
| the ID of a driver, where | |
| total number of locations of passengers, | |
| the location ID, | |
| the number of seats requested by passenger for location , where | |
| the number of bids placed by driver | |
| the bid submitted by driver , where | |
| the routing cost for transporting the passengers in the bid submitted by driver | |
| the original travel cost of driver (without transporting any passenger) | |
| the number of seats available at location in the bid submitted by driver | |
| , the bid submitted by driver | |
| the original price of passenger (without ridesharing) | |
| : the bid submitted by passenger . The bid is an offer to pay the price for transporting passengers for each | |
| a binary decision variable: it indicates whether the bid placed by driver is a winning bid ( = 1) or not ( = 0) | |
| a binary decision variable: it indicates whether the bid placed by passenger is a winning bid ( = 1) or not ( = 0) |
| Variable/Symbol | Meaning |
|---|---|
| the maximum number of generations | |
| the iteration/generation variable | |
| population size. | |
| the problem dimension, where | |
| the position of particle , where , and = (, ), is the position vector associated with the decision variable and yi is the position vector associated with the decision variable | |
| the velocity of particle ; denotes the element of the vector | |
| the personal best of particle , where , and is the element of the vector , | |
| the global best, and is the element of the vector , where | |
| a non-negative real parameter less than 1 | |
| a non-negative real parameter less than 1 | |
| a random variable with uniform distribution | |
| a random variable with uniform distribution | |
| the maximum value of velocity | |
| the probability of the bit | |
| the learning probability, where is greater than 0 and less than 1 | |
| a random variable with uniform distribution | |
| total number of swarms | |
| a swarm, where | |
| and | weighting factors for updating velocity; ; |
| a scaling factor for updating velocity; | |
| a set of integers | |
| an integer is selected from | |
| t he context vector obtained by concatenating the global best particles from all swarms | |
| the particle in the swarm | |
| the personal best of the particle in swarm | |
| the global best of the component of the swarm | |
| the distance between firefly and firefly | |
| the light absorption coefficient | |
| the attractiveness when the distance between firefly and firefly is zero | |
| the attractiveness when the distance between firefly i and firefly j | |
| a random number generated from a uniform distribution in [0, 1] | |
| a constant parameter in [0, 1] | |
| = a function to transform a real value into a value in | |
| the crossover rate | |
| the scale factor | |
| the scale factor for individual i | |
| a mutant vector for individual i |
| Procedure |
| If End If If End If Generate a random variable with uniform distribution Return |
| Discrete PSO Algorithm |
|---|
Generate particle for each in the population Evaluate the fitness function for particle , where Determine the personal best for each Determine the global best of swarm While (stopping criteria not satisfied) For each For each Generate a random variable with uniform distribution Generate a random variable with uniform distribution Calculate the velocity of particle Transform each element of into one or zero End For Update personal best and global best If = End If If = End If End While |
| Discrete CLPSO Algorithm |
|---|
| t ← 0 Generate particle for each in the population Evaluate the fitness function for each Determine the personal best of each particle Determine the global best of the swarm While (stopping criteria not satisfied) t ← t + 1 For each For each Generate a random variable with uniform distribution If > Generate , a random variable with uniform distribution Generate , a random variable with uniform distribution Calculate the velocity of particle as follows else Randomly select two distinct integers and from If Calculate the velocity of particle as follows Else Calculate the velocity of particle i as follows End If End If Transform each element of into one or zero End For Update personal best and global best If = End If If = End If End While |
| Discrete CCPSO Algorithm |
|---|
While (stopping criteria not satisfied) t ← t + 1 Step 1: Select from and randomly partition the set of decision variables into subsets, each with decision variables Initialize swarm for each Step 2: For each For each particle Construct the vector consisting of with its component being replaced by Calculate Evaluate fitness function value of Update personal best if is better than Update swarm best if is better than End For Update the context vector () End For For each For each particle For each Update velocity with a Gaussian random variable End For End For End For End While |
| Discrete Firefly Algorithm |
|---|
Generate fireflies in the initial population of swarm While (stopping criteria not satisfied) t ← t + 1 Evaluate the fitness function for each firefly For each For each If Move firefly toward in -dimensional space according to the following formula: Update firefly as follows: Generate , a random variable with uniform distribution Evaluate End For End For Find the global best End While |
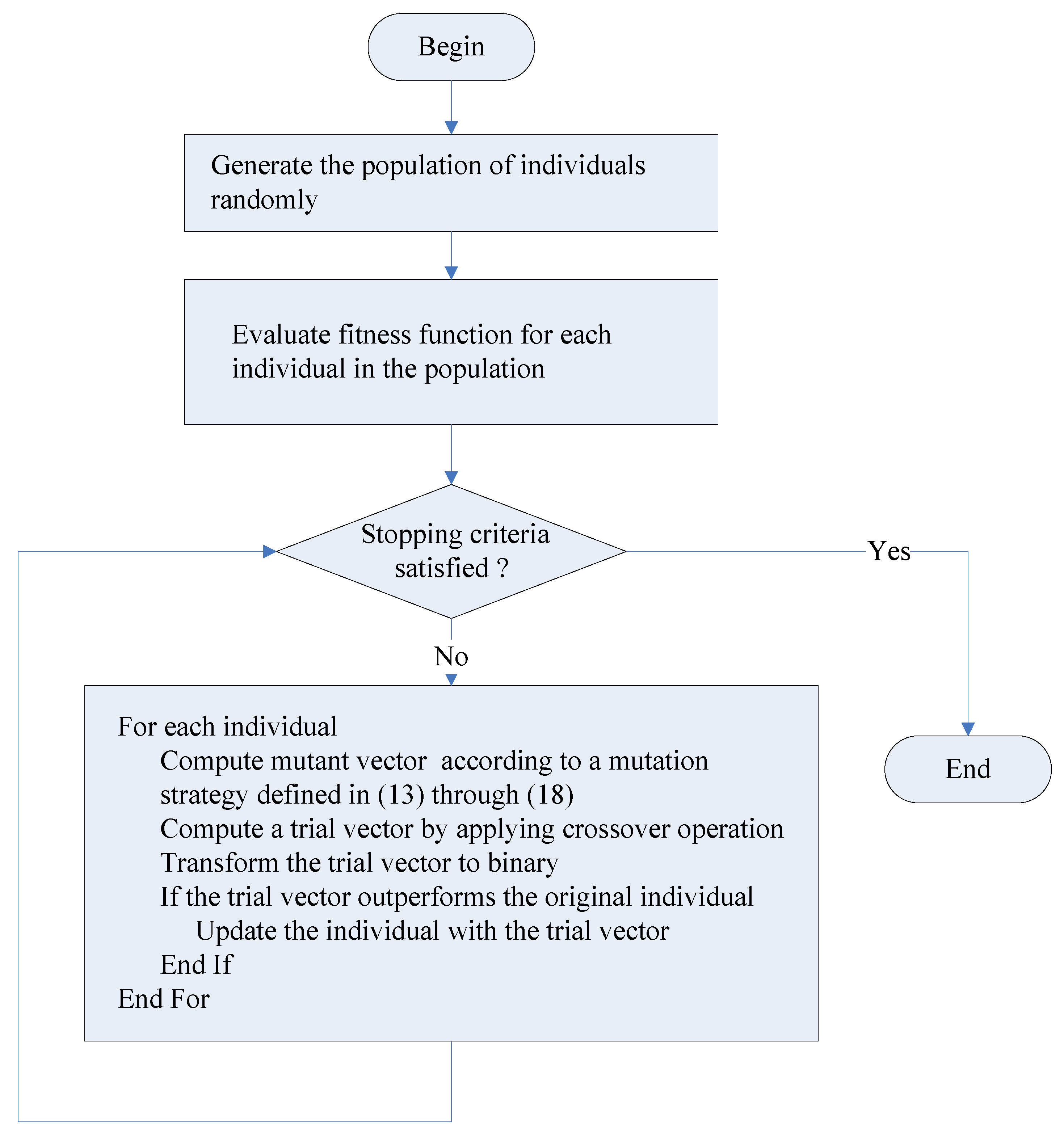
| Discrete DE Algorithm |
|---|
Set parameters , where is a Gaussian random variable with mean 0 and standard deviation 1.0 For End For : A mutation strategy defined in (13) through (18) Generate an initial population randomly While (stopping criteria not satisfied) t ← t + 1 For Compute mutant vector Compute according to mutation strategy Compute trial vector by crossover operation For End For Transform each element of into one or zero Update individual If = End If End For End While |
| Participant | Origin | Destination |
|---|---|---|
| Driver 1 | 24.13046 120.7047 | 24.2493791 120.6989202 |
| Passenger 1 | 24.13745 120.68354 | 24.15294 120.65751 |
| Passenger 2 | 24.17119 120.65015 | 24.13423 120.65639 |
| Passenger 3 | 24.2033643 120.7047477 | 24.1344881 120.6674565 |
| Passenger 4 | 24.2057 120.67951 | 24.2261 120.65644 |
| 1 | 1 | 0 | 0 | 0 | 55.4325 | 58.815 |
| 1 | 1 | 0 | 0 | 0 | 11.8775 |
| 2 | 0 | 1 | 0 | 0 | 13.01 |
| 3 | 0 | 0 | 1 | 0 | 24.33 |
| 4 | 0 | 0 | 0 | 1 | 10.155 |
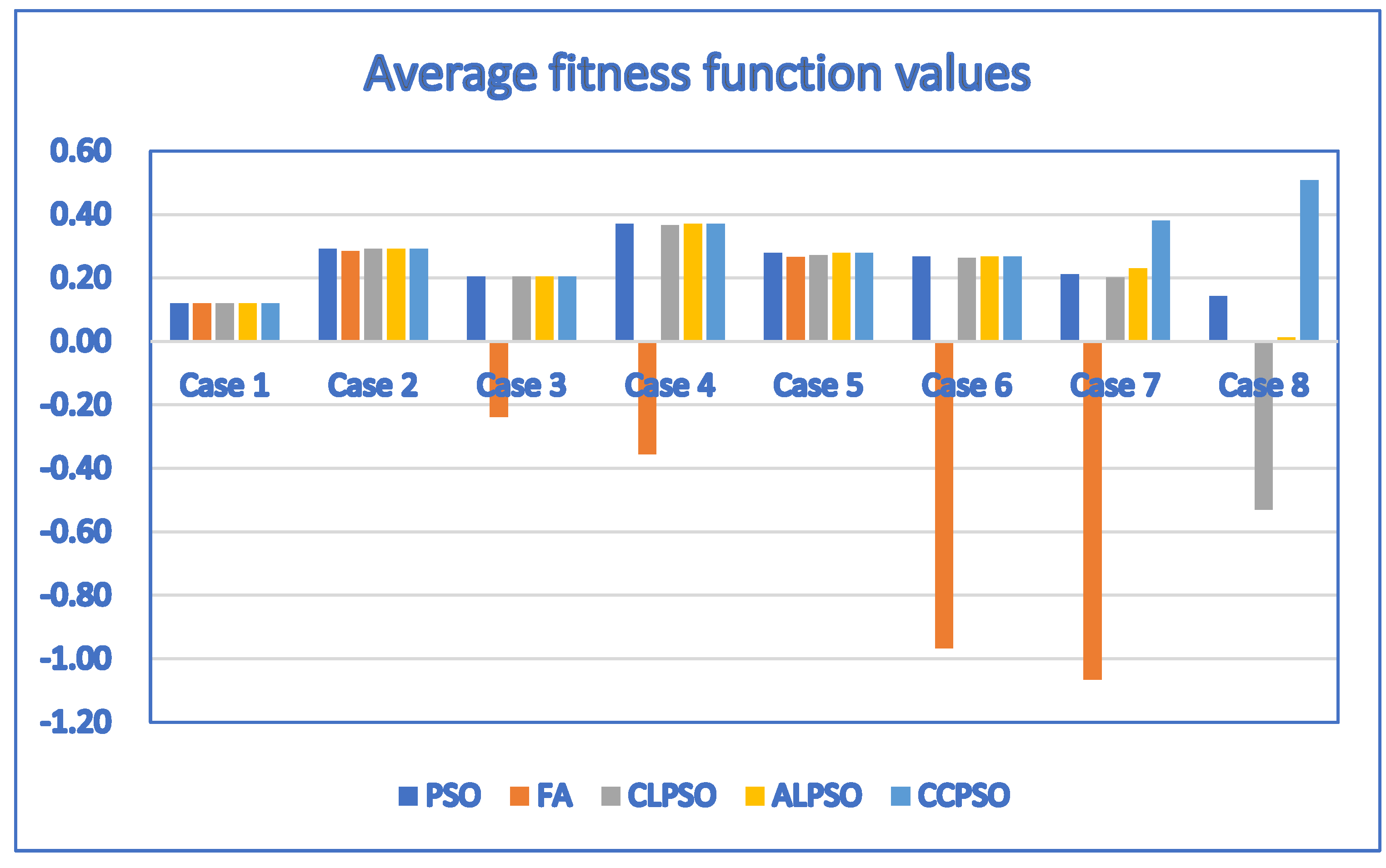
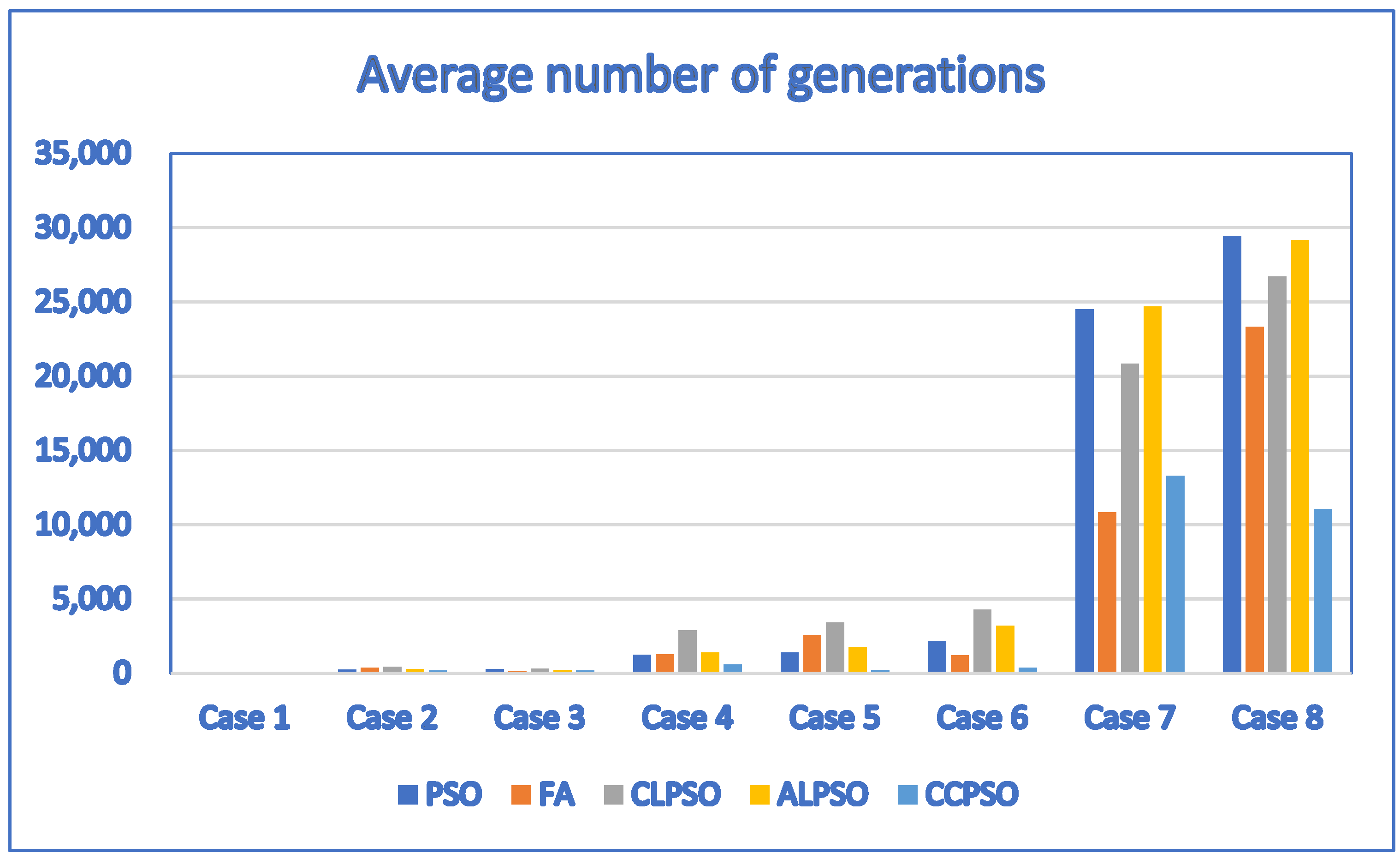
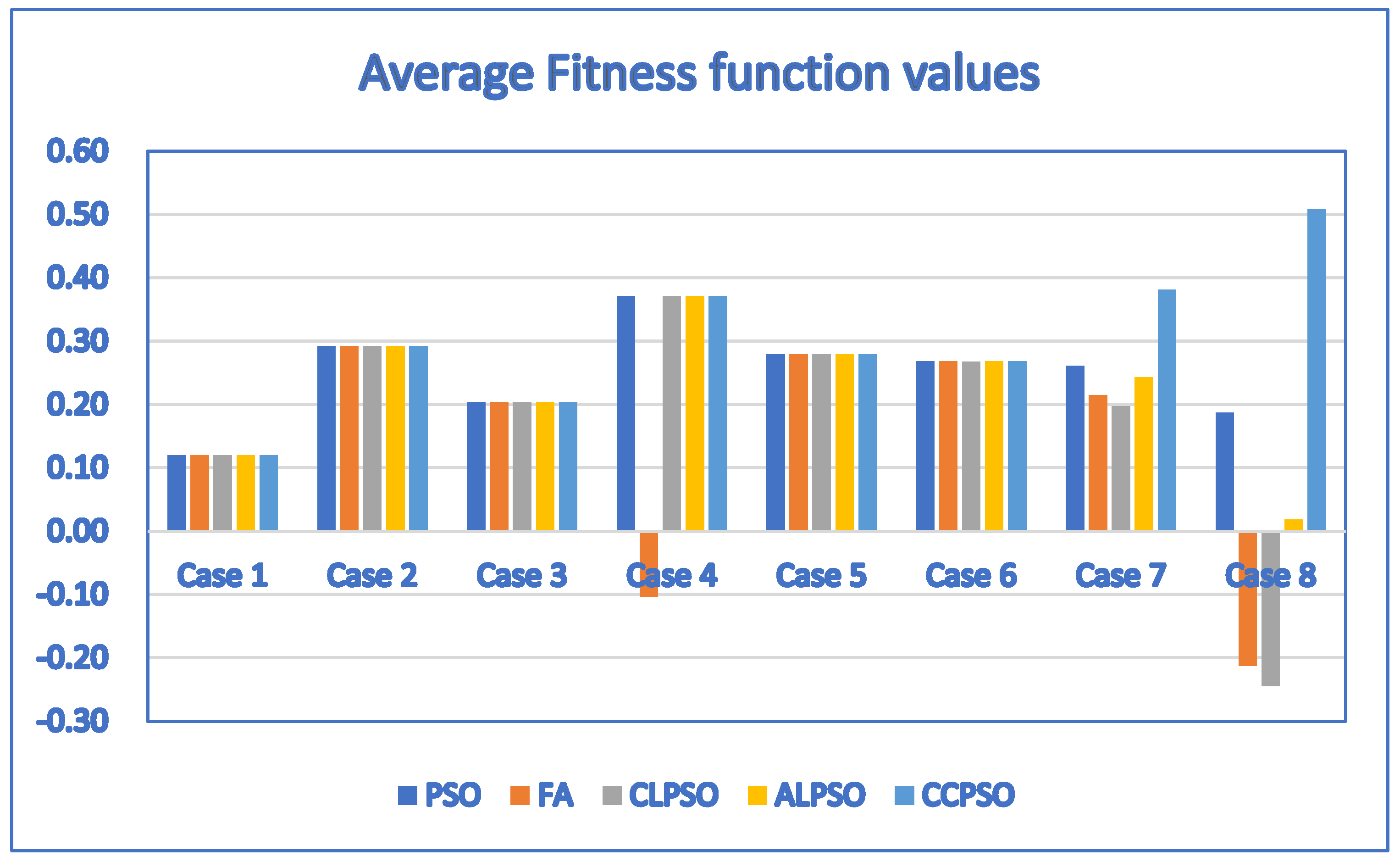
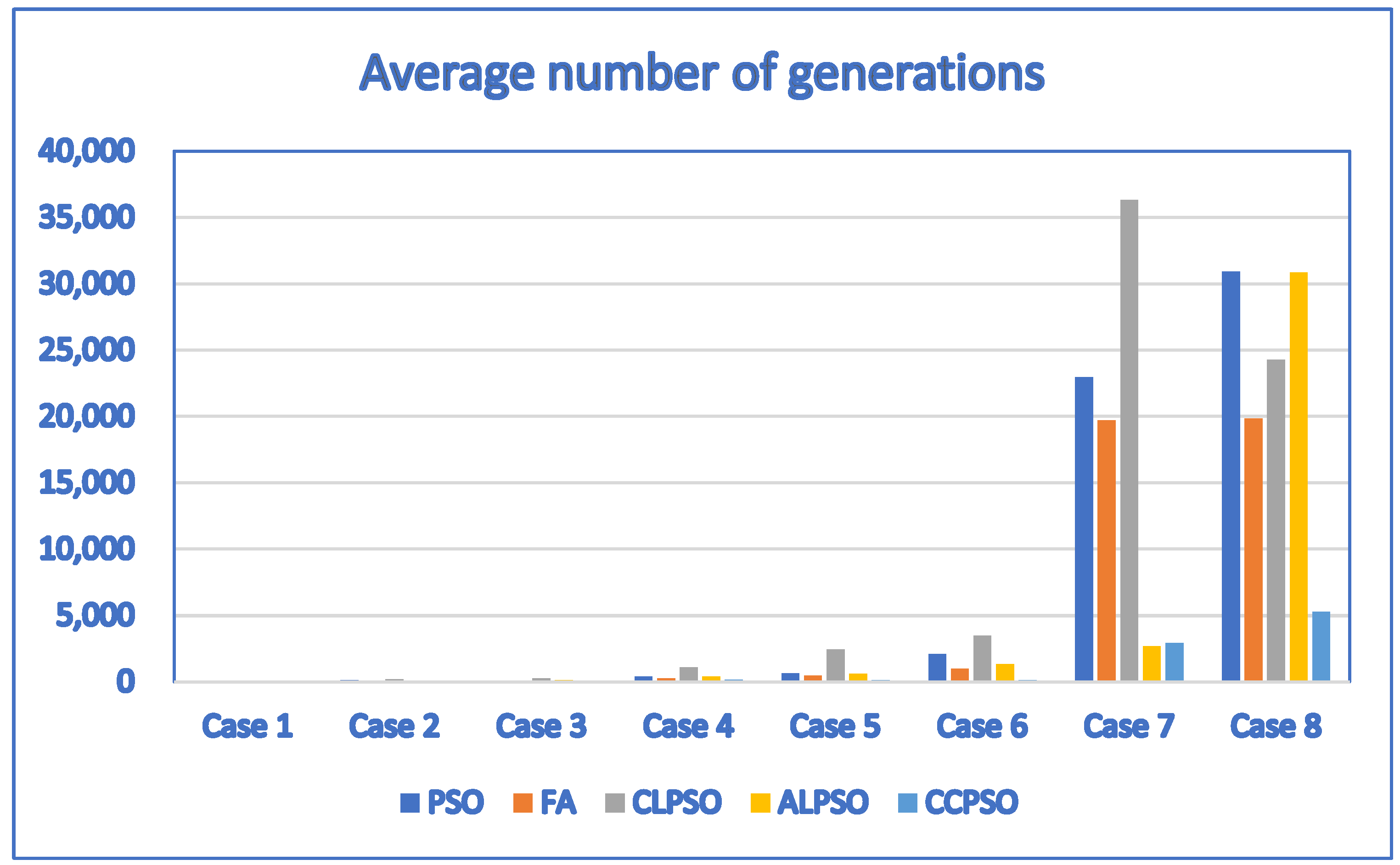
| Case | D | P | PSO | FA | CLPSO | ALPSO | CCPSO |
|---|---|---|---|---|---|---|---|
| Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | |||
| 1 | 1 | 4 | 0.12/3.2 | 0.12/4.6 | 0.12/3.1 | 0.12/3.3 | 0.12/3.9 |
| 2 | 3 | 10 | 0.292/216.4 | 0.2849/344 | 0.292/410.4 | 0.292/263.3 | 0.292/156.9 |
| 3 | 3 | 10 | 0.204/267.9 | −0.2373/95.1 | 0.204/297.6 | 0.204/205.3 | 0.204/177.2 |
| 4 | 5 | 11 | 0.371/1222.1 | −0.3558/1252.6 | 0.3667/2855.7 | 0.371/1365.6 | 0.371/568.7 |
| 5 | 5 | 12 | 0.279/1381.2 | 0.2663/2513.6 | 0.2721/3388.9 | 0.279/1756.5 | 0.279/184.4 |
| 6 | 6 | 12 | 0.268/2147.6 | −0.9662/1195.2 | 0.2638/4282.2 | 0.2679/3187.1 | 0.268/364.5 |
| 7 | 20 | 20 | 0.2111/24,501 | −1.0659/10,817.5 | 0.2023/20,843.7 | 0.2298/24,681 | 0.381/13,288.5 |
| 8 | 30 | 30 | 0.1423/29,449.2 | −1.6923/23,324.6 | −0.5304/26,707.3 | 0.0125/29,172 | 0.508/11,036.7 |
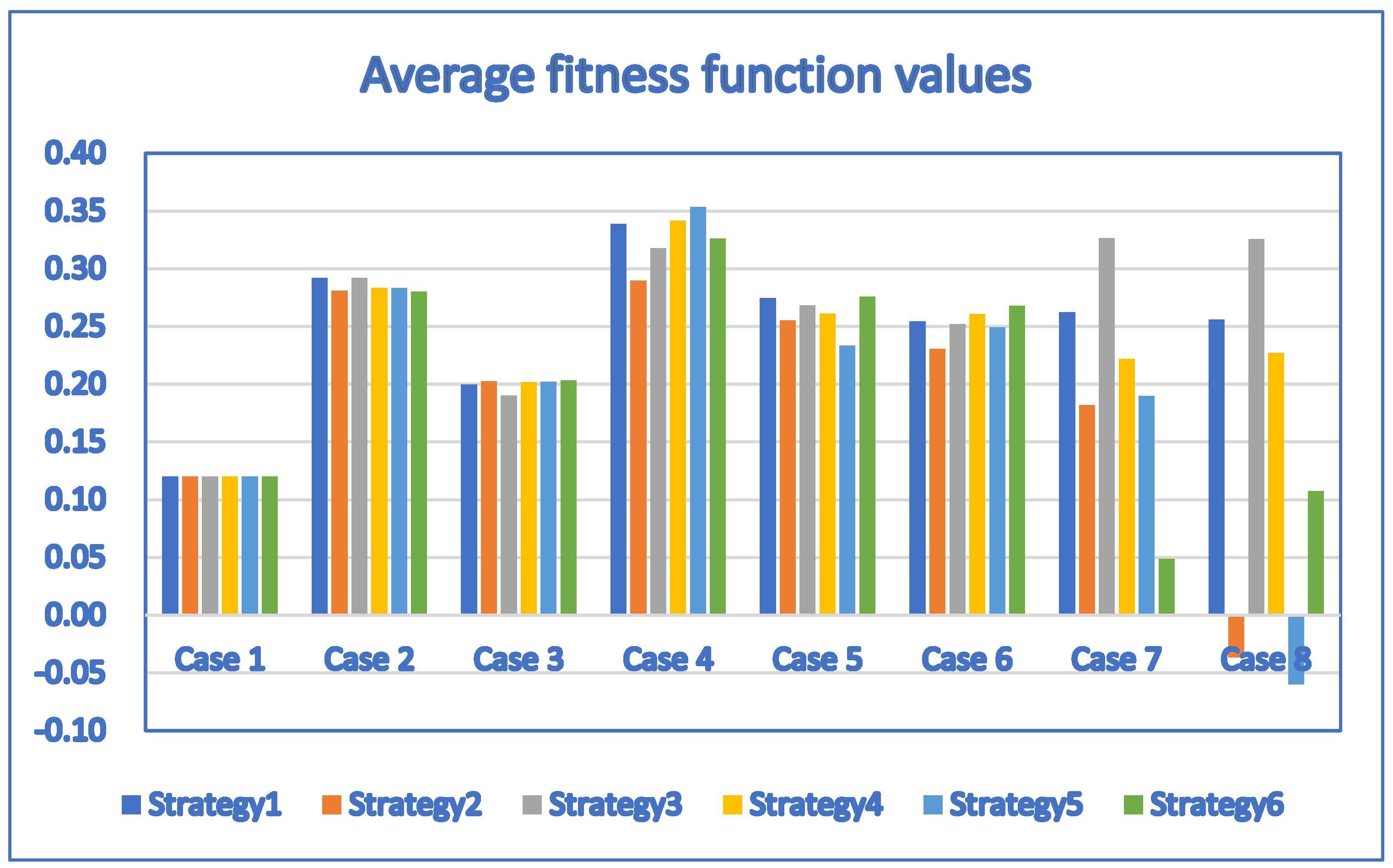
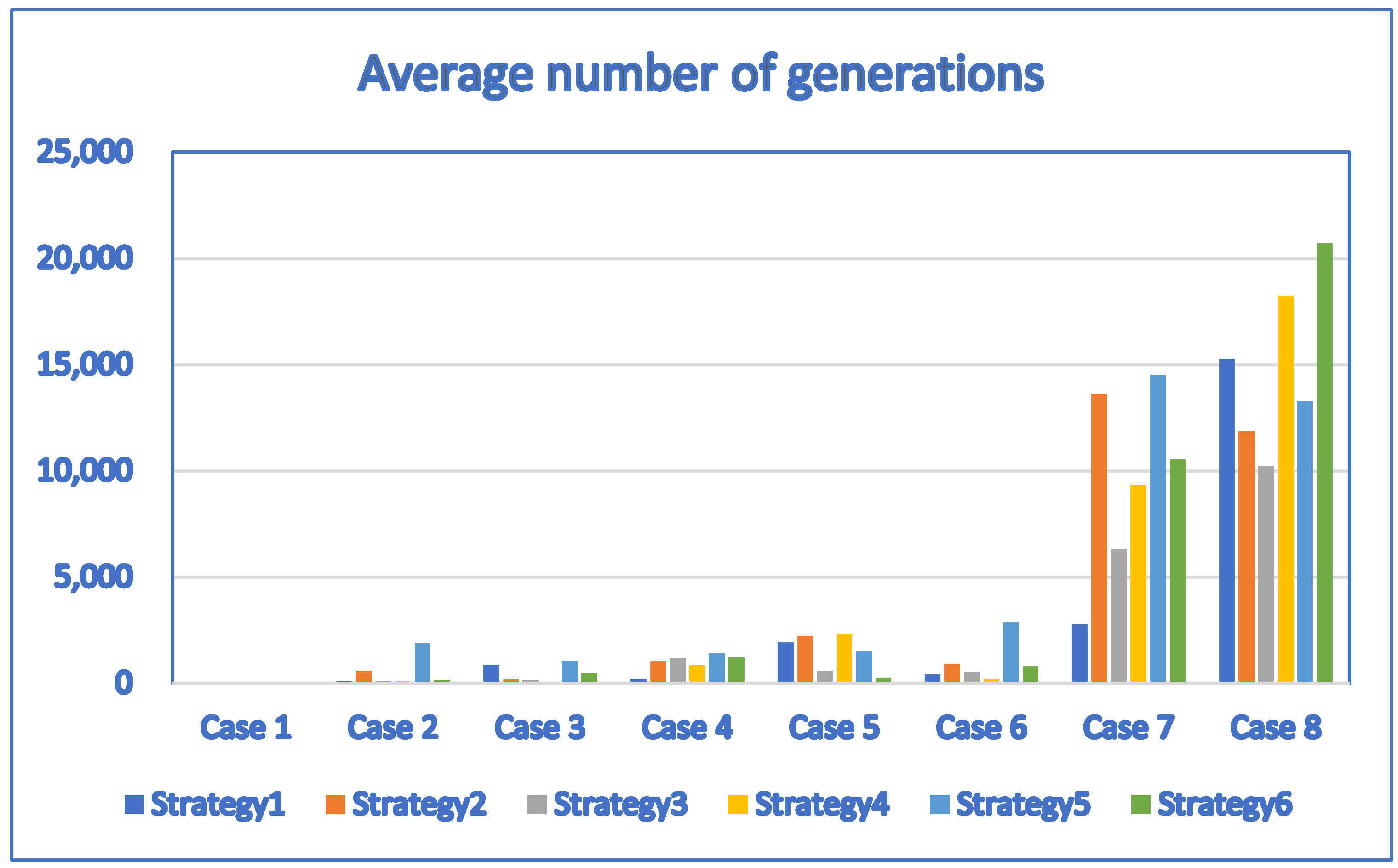
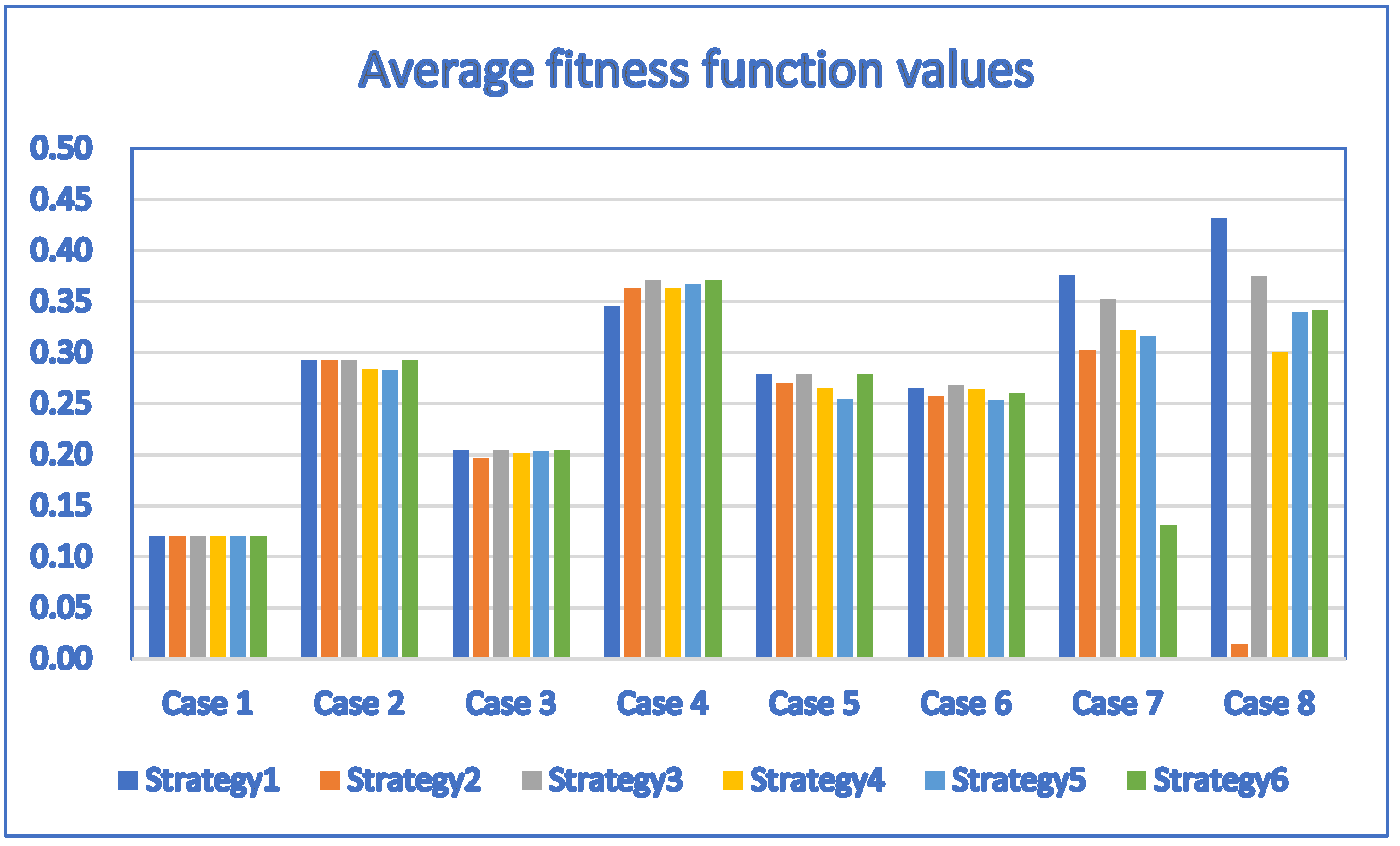
| Case | D | P | DE_Strategy 1 | DE_Strategy 2 | DE_Strategy 3 |
|---|---|---|---|---|---|
| Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | |||
| 1 | 1 | 4 | 0.12/3.1 | 0.12/4.4 | 0.12/2.3 |
| 2 | 3 | 10 | 0.292/86.7 | 0.281/574.8 | 0.292/102.7 |
| 3 | 3 | 10 | 0.1995/867 | 0.2023/180.2 | 0.1903/146.4 |
| 4 | 5 | 11 | 0.3389/220.5 | 0.2896/1027.4 | 0.3177/1179.6 |
| 5 | 5 | 12 | 0.2745/1914.2 | 0.2553/2233.4 | 0.2681/574 |
| 6 | 6 | 12 | 0.2542/417 | 0.2307/894.2 | 0.2521/541.3 |
| 7 | 20 | 20 | 0.2622/2764.4 | 0.1819/13,610.3 | 0.3266/6310.3 |
| 8 | 30 | 30 | 0.256/15,267.8 | −0.0367/11,861.2 | 0.3258/10,241.7 |
| Case | D | P | DE_Strategy 4 | DE_Strategy 5 | DE_Strategy 6 |
|---|---|---|---|---|---|
| Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | |||
| 1 | 1 | 4 | 0.12/2.3 | 0.12/2.8 | 0.12/2.4 |
| 2 | 3 | 10 | 0.2834/79.9 | 0.2834/1867.6 | 0.2801/170.2 |
| 3 | 3 | 10 | 0.2017/63.3 | 0.202/1065.3 | 0.2031/475.8 |
| 4 | 5 | 11 | 0.3416/835.4 | 0.3536/1393.3 | 0.3263/1201.9 |
| 5 | 5 | 12 | 0.261/2318.2 | 0.2332/1491.5 | 0.2758/256.1 |
| 6 | 6 | 12 | 0.2606/219.1 | 0.2491/2854.4 | 0.2677/796.9 |
| 7 | 20 | 20 | 0.2219/9339.7 | 0.1898/14,519.7 | 0.0485/10,533.6 |
| 8 | 30 | 30 | 0.227/18,229.7 | −0.0598/13,292.6 | 0.1072/20,699.7 |
| Case | D | P | PSO | FA | CLPSO | ALPSO | CCPSO |
|---|---|---|---|---|---|---|---|
| Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | |||
| 1 | 1 | 4 | 0.12/2.1 | 0.12/2 | 0.12/2.3 | 0.12/2.1 | 0.12/2.4 |
| 2 | 3 | 10 | 0.292/114.7 | 0.292/34.7 | 0.292/176.3 | 0.292/65.3 | 0.292/40.1 |
| 3 | 3 | 10 | 0.204/69.6 | 0.204/29 | 0.204/241.1 | 0.204/118.4 | 0.204/84.2 |
| 4 | 5 | 11 | 0.371/371.7 | −0.1032/236.4 | 0.371/1074.1 | 0.371/383.4 | 0.371/141.8 |
| 5 | 5 | 12 | 0.279/619.8 | 0.279/450.5 | 0.279/2424.8 | 0.279/586.9 | 0.279/93.8 |
| 6 | 6 | 12 | 0.268/2090.9 | 0.268/958.8 | 0.2678/3479.7 | 0.268/1325.2 | 0.268/116.8 |
| 7 | 20 | 20 | 0.2609/22,957.7 | 0.2149/19,716.8 | 0.1971/36,331.3 | 0.2432/2663.7 | 0.381/2909.8 |
| 8 | 30 | 30 | 0.1875/30,923.7 | −0.213/19,855.3 | −0.2449/24,290.3 | 0.1811/30,853.2 | 0.508/5266.9 |
| Case | D | P | DE_Strategy1 | DE_Strategy2 | DE_Strategy3 |
|---|---|---|---|---|---|
| Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | |||
| 1 | 1 | 4 | 0.12/1.2 | 0.12/1.5 | 0.12/1.6 |
| 2 | 3 | 10 | 0.292/22.5 | 0.292/25.875 | 0.292/25.625 |
| 3 | 3 | 10 | 0.204/22.3 | 0.1966/478.3 | 0.204/30.7 |
| 4 | 5 | 11 | 0.3458/756.7 | 0.3624/94.8 | 0.371/79.9 |
| 5 | 5 | 12 | 0.279/66.4 | 0.27/216.2 | 0.279/88.5 |
| 6 | 6 | 12 | 0.2646/97.2 | 0.2571/548.8 | 0.268/76.9 |
| 7 | 20 | 20 | 0.3758/10,239 | 0.3027/6492.6 | 0.3528/6385.7 |
| 8 | 30 | 30 | 0.4316/15,061.3 | 0.0142/11,460 | 0.3754/18,206.9 |
| Case | D | P | DE_Strategy4 | DE_Strategy5 | DE_Strategy6 |
|---|---|---|---|---|---|
| Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | Avg. Fitness Value/Avg. Generation | |||
| 1 | 1 | 4 | 0.12/1.5 | 0.12/1.1 | 0.12/1.5 |
| 2 | 3 | 10 | 0.28425/577.375 | 0.283/88.75 | 0.292/16.123 |
| 3 | 3 | 10 | 0.2011/1162.5 | 0.2035/160 | 0.204/30.9 |
| 4 | 5 | 11 | 0.3624/1290.4 | 0.3667/1063 | 0.371/395.9 |
| 5 | 5 | 12 | 0.2647/310.9 | 0.2546/667.8 | 0.279/38.7 |
| 6 | 6 | 12 | 0.2637/1179.8 | 0.2538/922.4 | 0.2607/160.4 |
| 7 | 20 | 20 | 0.3218/8211.2 | 0.3157/6530.8 | 0.1311/5601.5 |
| 8 | 30 | 30 | 0.3003/17,476.7 | 0.3393/11,709.7 | 0.3413/13,503.9 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, F.-S. A Comparative Study of Several Metaheuristic Algorithms to Optimize Monetary Incentive in Ridesharing Systems. ISPRS Int. J. Geo-Inf. 2020, 9, 590. https://doi.org/10.3390/ijgi9100590
Hsieh F-S. A Comparative Study of Several Metaheuristic Algorithms to Optimize Monetary Incentive in Ridesharing Systems. ISPRS International Journal of Geo-Information. 2020; 9(10):590. https://doi.org/10.3390/ijgi9100590
Chicago/Turabian StyleHsieh, Fu-Shiung. 2020. "A Comparative Study of Several Metaheuristic Algorithms to Optimize Monetary Incentive in Ridesharing Systems" ISPRS International Journal of Geo-Information 9, no. 10: 590. https://doi.org/10.3390/ijgi9100590
APA StyleHsieh, F.-S. (2020). A Comparative Study of Several Metaheuristic Algorithms to Optimize Monetary Incentive in Ridesharing Systems. ISPRS International Journal of Geo-Information, 9(10), 590. https://doi.org/10.3390/ijgi9100590





