Abstract
This paper examines the relationship between pedestrian density and space syntax measures in a university campus using ordinal logistic regression analysis. The pedestrian density assumed as the dependent variable of regression analysis was categorised in low, medium, and high classes by using Jenks natural break classification. The data elements of groups were derived from pedestrian counts performed in 22 gates 132 times. The counting period grouped in nominal categories was assumed as an independent variable. Another independent was one of the 15 derived measures of axial analysis and visual graphic analysis. The statistically significant model results indicated that the integration of axial analysis was the most reasonable measure that explained the pedestrian density. Then, the changes in integration values of current and master plan datasets were analysed using paired sample t-test. The calculated p-value of t-test proved that the master plan would change the campus morphology for pedestrians.
1. Introduction
A geographic area with buildings to visit and streets where pedestrians can easily walk encourages people to travel on foot [1,2,3,4,5,6,7,8]. Pedestrians generally prefer to move along linear lines characterised by a minimum number of turns, with movement guided by the perception of visual spaces. These spaces, defined by Hillier [9] as walkable physical environments for pedestrians in city centres where buildings’ density is high, physically coincide with the street network [10]. Space syntax (SS) techniques are often used to analyse pedestrian walking behaviour in an urban environment consisting of street and building configurations. Axial analysis (AA) and visual graph analysis (VGA) are two of them [11].
The last decade has seen a remarkable increase in studies that examine walking behaviours via AA measures. Lerman and Omer [12], for example, analysed the relationship between pedestrian movement in two neighbouring regions located in Tel-Aviv based on integration, choice, and connectivity measures. Monokrousou and Giannopoulou [13] incorporated integration and choice into a correlation analysis to explain pedestrian movement and predict the future condition of Athens. Ahmed et al. [14] inquired into the morphological changes that occurred from 1947 to 2007 in Dhaka City, Bangladesh, using the integration, connectivity, and control measures. Hajrasouliha and Li [15] explained pedestrian movement in the centre of Buffalo City in New York through the connectivity measure. Liu et al. [16] used control and integration as the basis in determining the walking behaviours of tourists in scenic Mt. Sanqingshan, one of China’s major tourism regions. Jabbari et al. [17] investigated the association between connectivity and pedestrian movement by conducting multi-criteria analyses in the city centre of Oporto, Portugal. In addition, some recent studies examine the relationships between measures obtained from VGA and pedestrian movements and evaluate them together with AA measures. Dessylas and Duxburry [18] and Hölscher et al. [19] compared some measures obtained from VGA and AA to determine the correlation of data with pedestrian movement. Heitor et al. [20] evaluated a campus of the Technical Institute of Lisbon in Portugal with the connectivity measures derived via the integration of VGA and AA. Bendjedidi et al. [21] used the connectivity and integration measures of VGA to look into the intensity of pedestrian movement in the city squares of Biskra in Algeria. Koutsolampros et al. [22] employed VGA measures to analyse indoor walking. Pagkratidou et al. [23] explored the behaviours of individuals unfamiliar with the Temple University campus using the integration, choice, and connectivity measures of both VGA and AA.
All of these studies mentioned above showed that the researchers had a significant effort to explain pedestrian movements using the measures obtained from AA and VGA. However, it was striking that these researchers did not choose a general measure valid in their study areas to explain the pedestrian movement. The number of measures they used was usually more than one. This confusing situation points to a need to determine a proper measure that explains the pedestrian movement for each study area. The appropriate measure should be a specific measure that reflects the walkability character of the concerned area, except that it is a general measure valid for all study areas. This paper aims to determine the most appropriate measure defining the intensity of pedestrian movements in a specified test area to overcome this deficiency mentioned above. For this purpose, the relationships between pedestrian movements and measures are evaluated using regression analysis. In addition, the study aims to reveal how future changes in accordance with the master plan will affect pedestrian density. The general assessment of the effects of these changes is made based on the results of the paired sample t-test, which is commonly used to compare the differences between two samples.
The remainder of the paper is organised as follows. Section 2 briefly describes the study area and the datasets used in this study. Section 3 introduces the use of SS techniques and statistical methods to determine the most proper measure related to pedestrian density, and Section 4 presents the results. Section 5 concludes the paper with final remarks.
2. Study Area
University campuses with a high student population are substantial settlements with characteristics that are similar to those of urban areas. Several university campuses can be found in most of the densely populated metropolitan cities in Europe. One of these cities is Istanbul, which has a population of more than 15 million and is home to the leading higher education institutions of Turkey. Among these institutions, Yildiz Technical University is the fourth oldest, founded in 1911. It offers most of its educational services in Davutpasa Campus, which occupies an area of approximately 124 ha and is the largest educational expanse in Istanbul. The campus had eight faculties, two institutes, and various administrative units at the end of 2019. The total area of the buildings and length of the road network is about 13 ha and 14.5 km, respectively (grey areas in Figure 1).
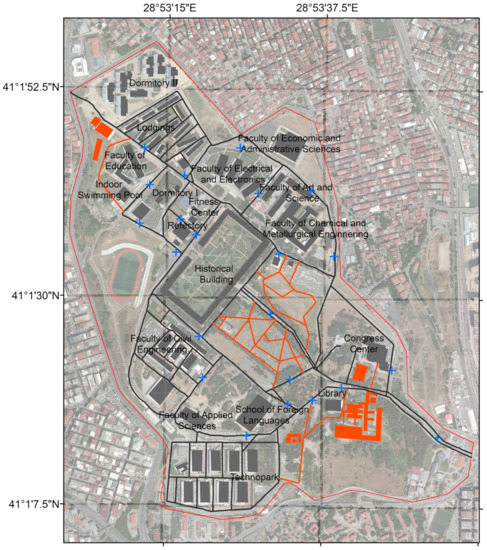
Figure 1.
Buildings and roads of Davutpasa Campus digitised from orthophotos.
The historical building in the centre of the campus was built in 1832. According to inventory records, the rest of the buildings were constructed after 2001. The master plan that the university administration intends to implement after 2019 will expand the total building area and road network length by approximately 1 ha and 4.2 km, respectively (orange areas in Figure 1). The new buildings will be built on open spaces in the northwestern and southeastern sides of the campus, and the planned roads will provide access to these buildings. Some walking paths leading to the open spaces in the campus centre will also be built. The morphological changes occurring from 2001 to 2019, together with the data in the master plan, reflect the dynamic structure of the study area.
3. Materials and Methods
The datasets needed to derive AA and VGA measures in the study area were obtained by digitizing from the existing orthophotos of the region. The axial map and building footprints are the baseline data used in the AA and VGA, respectively. The axial map used for AA consists of a minimum number of axial lines. Each axial line in this map shows the direction between the two points where the pedestrian movement starts and ends [24,25]. All of them must be compatible with the street network configurations [24,26,27]. VGA is implemented depending on the building configuration of the space [28,29,30]. This technique entails dividing geographic areas into grid cells and subsequently calculating measures through an examination of empty cells, together with nearby neighbours where pedestrians can move. In this study, a total of 15 measures, described below, were obtained using both analyses.
3.1. AA and VGA Measures
Open source tools were used to calculate the measures derived from the AA and VGA. One of these was the SS toolkit, the Geographic Information System (GIS) software Quantum GIS (QGIS) plug-in used to obtain AA measures from an axial map. It is a multi-platform spatial network analysis tool that integrates SS techniques with GIS data analysis and visualisation features [31]. Another open-source tool used in this study was DepthMap, which was developed as a platform for visibility analysis of urban and architectural designs [30]. Both SS toolkit and DepthMap allow researchers to use several measures (Figure 2).
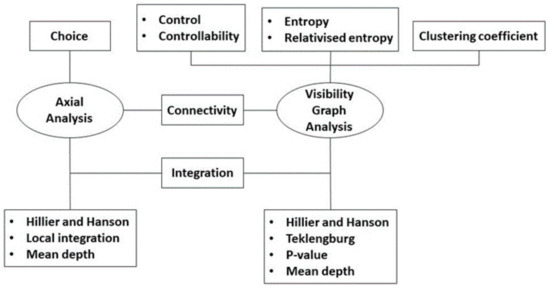
Figure 2.
Measures obtained from the space syntax (SS) analyses.
Integration describes accessibility from a location to all other locations [32]. Accessibility is one of the most important factors that increase or decrease the movement of pedestrians [33,34,35]. Both analyses can determine integration based on source data. Hillier and Hanson’s [24] integration () is a global measure obtained from AA [11]; it also shows the topological proximity of an axial line to other lines in an axial map. When integration is calculated for axial lines delimited by a radius value, it is called local integration . Mean depth () is an inverse of global integration and provides the mean of the total depth of an axial line connected to other axial lines. VGA integration () developed by Hillier and Hanson [24] yields the ratio of the visibility of any grid cell in the space to the visibility of other cells. Teklenburg [36] suggested normalising VGA integration () to secure an opportunity to compare the integration obtained from analyses performed in different areas. Similarly, Campos and Fong [37] normalised integration using a p-value (). The mean depth of VGA () is the mean of the depth value calculated from one cell to other grid cells. Connectivity is another measure that can be obtained from AA and VGA. AA connectivity () is the total number of axial lines connected to an axial line, whereas VGA connectivity () refers to the total number of adjacent grids connected to a grid cell in the space. AA can be used to derive another measure called choice (), which reflects the total distance of an axial line to other axial lines. It provides the number of shortest paths that connect an axial line to other axial lines. The distance between two axial lines is the shortest route calculated topologically [38].
The other measures evaluated in this study were obtained through VGA. Hillier and Hanson’s [24] control measure () and Turner’s [30] controllability () are two measures. Control involves visually selecting dominant areas, whereas controllability determines easily monitored regions during a walk. Visual entropy () is adopted in the examination of the depth values of a grid cell and other adjacent cells. If the depth value of neighbouring cells is approximately equal to that of an investigated cell, entropy is high. If the depth values between adjacent cells differ from one another, then entropy is low. Relativized entropy () is a calculation of the expected distribution of mean depth value. The clustering coefficient () is employed to ascertain how a pedestrian’s space perception changes in case of moving away from a current location. The loss of visual information due to pedestrian movement reduces the value of the clustering coefficient [30].
3.2. Determining the Most Proper Measure
In this study, regression analysis was used to explain the relationships between abovementioned measures and pedestrian density. It was decided the most appropriate measure by evaluating the results of its analysis models. Regression analysis is a statistical approach implemented to analyse the relationship between a dependent variable and one or more independent variables. In this study, the pedestrian density data calculated according to the number of people counted at 22 gates in the campus area (blue marks in Figure 1) was accepted as the dependent variable. People counting, also known as the gate-count method [39], is the most straightforward approach to sensitively determining pedestrian movement in a location where an automated data collection method cannot be used [40]. The appropriate selection of places from where people will be counted is critical in effectively reflecting pedestrian mobility. Enough points with different characteristics that reveal the frequency of use in a region by pedestrians are also needed [41]. The counts at 22 gates continued on weekdays for two weeks. Each gate was tried to count for 15 min at least once in four different periods (08.30–10:30, 10.30–12:30, 12:30–14:30, 14:30–16:30). Besides, it was counted two more times over random periods. The 15-min count for totally 22 gates was 132 times. Then, the authors categorised all data elements into three classes that represent ordered density groups (low, medium, and high). Three groups were sufficient for 132 gate-count data in this study. On the other hand, if researchers achieve more repetitive counts at more gates for a more extensive study area, they can also increase the number of density groups.
Before the classification, a pre-check process was applied to determine whether there were potential outliers among the gate-count data. One of the essential methods to reveal the potential outliers in statistics is to choose a criterion value known as z-score. Data elements with a value greater or less than the z-score are investigated as the outliers. In this study, the z-score of each data element in the dataset is calculated using Equation (1) [42].
where x indicates the value of data element, and are the mean and the standard deviation values of the dataset, respectively. The default threshold values in this study were selected as ±2.5. The identified potential outliers were not considered as insignificant data elements that need to be deleted; it was investigated whether they distorted the limit values of the classes.
In this study, the Jenks natural break (JNB) algorithm, which identifies the best groups that have similar values, was used to categorize the data into ordinal three classes. JNB is an optimization technique that maximises the differences among classes. It addresses the problem of how to split a range of numbers into contiguous classes to minimise the squared deviation within each class [43]. This algorithm iteratively processes the data and assigns it into classes whose names are specified by the user. It then returns the sum of squares of deviations (SSD) of data elements from the sample mean (Equation (2)) within each class and calculates the total value for all classes. The classification that gives the minimum total value among iterative processes is optimum [44].
The goodness of variance fit (GVF) for the specified class elements gives the strength of the classification process (Equation (3)). GVF takes a value between 0 and 1. The closer GVF to 1, the better the fit is.
where is the minimum total value of SDD for optimum classification, and is the squared deviation of all elements in the dataset.
The first independent variable used to create a regression model is the measures whose relationship with pedestrian densities are investigated. They take continuous values calculated with the software. Since the measures obtained from AA and VGA are typically inter-correlated, a multi-colinearity problem occurs when all measures are given as input data in the regression model. Therefore, a separate model was established for each measure, and they were evaluated separately. The second independent variable for the regression model was the periods of pedestrian counts. Since the measures are collected in four different periods, this independent variable takes categorical values ranging from nominal 1 to 4.
An analyst has to use a proper regression model depending on the data types of dependent and independent variables entering the model. The dependent variable used in this study includes numerical data grouped in three ordered classes. When the ordered data that constitutes the dependent variable has at least three groups in a natural order, it is modelled using ordinal logistic regression [45]. The ordinal logistic regression model is based on the existence of a continuous and unobserved random Y* latent variable under the categorically dependent Y variable. The categories in this variable are predicted as sequential intervals in a continuous plane called a threshold value [46,47]. Four separate tests check the robustness of the ordinal logistic regression model. These tests are (1) model fitting, (2) goodness of fit, (3) pseudo R2, and (4) parallel lines. Model fitting examines −2 log-likelihood. A significant (p < 0.05) change in the −2 log-likelihood statistics between the baseline model and the final model indicates that the predictors were significant based on these tests [48]. Two types of the goodness of fit tests called Pearson chi-square, and deviance statistics evaluate the discrepancy between the current model and the full model. However, these tests are sensitive to empty cells. If there are many empty cells in the model, −2 log-likelihood is considered a more robust indicator than Pearson chi-square and deviance statistics [49,50]. Pseudo R2 values are used to estimate the variance explained by the independent variable. When these values are closer zero, model fitting diminishes. Lower R2 values do not prevent interpreting parameters. One of the assumptions underlying ordinal logistic regression is based on that the relationship between each pair of outcomes is the same. In other words, ordinal logistic regression assumes that the coefficients defining a relationship between the lowest and all higher categories of the response variable are the same as those that describe the relationship between the next lowest category and all higher categories. This is called the parallel lines assumption, and the chi-square test is used to test the validity of the assumption of parallelism. At the end of the regression analysis process, the test sensitivities of each ordinal logistic regression model created in this study were checked. The most suitable model reflecting the pedestrian density was determined according to the results of parameter estimation tables.
3.3. Analysing the Effect of Master Plan
At this stage, it was aimed to determine how the new walkways to be added in the future, according to the master plan could affect the pedestrian density in the study area. Pedestrian density was examined according to the reference measure determined by regression analysis in the previous stage. The evaluations were made analysing measure values of the same features both in the current situation and master plan.
The number of features in the master plan dataset is higher than the current dataset due to newly added walking paths. The reference measure values of features in both datasets were normalised to make a reasonable comparison between the newly added and current walking paths. In this study, the normalisation process was performed using the interval between zero and one (Equation (4)).
where represents the measure values, and and pertain to the maximum and minimum values in the datasets, respectively.
The differences between the current and master plan datasets were compared using a paired sample t-test, which is a parametric inferential procedure designed to evaluate two means calculated from two related samples. The three assumptions espoused in the paired sample t-test are the same as those adopted in an independent sample t-test. The first assumption indicates that the dependent variable contains a scale or ratio scale and is distributed normally. The second assumption holds that the variances in raw scores are equivalent to populations estimated by . The third assumption posits that represented populations exhibit homogeneous variances. The number of samples in the two groups for before and after situations must be equal to generate score pairs from the relevant samples. The paired samples are based on H0 and Ha. The t-value is used in the statistical evaluation of the test. The calculated t-value is compared with the corresponding value from the t distribution table for a selected confidence level. If the calculated t-value is higher than the critical value, H0 is rejected. Rejection shows that means statistically differ from one another [42].
4. Results
4.1. Calculated Values for Measures
In this study, AA and VGA values calculated for 22 gates are given in Table 1 and Table 2, respectively. Since the local integrations of AA were calculated for two different radii (r = 3 and r = 6), the total number of measures in the two tables was 16. Besides, the grid spacing was used as 10 m while calculating the VGA measures.

Table 1.
Axial analysis (AA) values calculated for each observation gate.

Table 2.
Visual graph analysis (VGA) values calculated for each observation gate.
4.2. Ordinal Logistic Regression Analysis
The dependent variable of the ordinal logistic regression process is based on gate-count data in this study. The mean and the standard deviation values of totally 132 data elements were calculated as 189.16 and 228.97, respectively. Depending on these values, z-scores were generated using Eq.1 for each element, and those that could be outliers were determined. Figure 3 shows the distribution range of the gate-count data. In this graph, three data elements with z-score values outside the ±2.5 default threshold can be considered as potential outliers (shown with the blue rings). Attention should be paid to these elements in a classification process using the JNB algorithm.
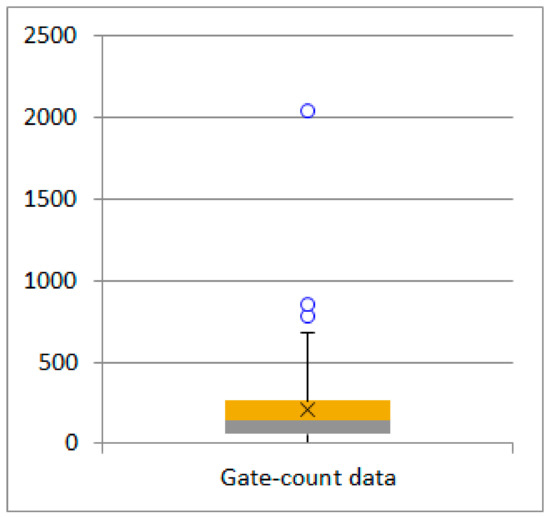
Figure 3.
Box plot graphic for gate-count data.
According to the first JNB classification with 132 data elements, 106 data were assigned to the low, 25 data to the medium, and only one data to the high classes (Table 3). The GVF value for this classification is calculated as 0.823. Assigning only one element to the high class and the GVF value lower than 0.850 led the authors to exclude the outliers in the first JNB classification. According to the second classification with 129 data elements, 75 data were assigned to low, 44 data to medium, and 10 data to high classes (Table 3). The GVF value for this classification is 0.870. The more successful distribution of the data to the classes and the GVF value higher than 0.850 showed that this procedure was applicable. Besides, the three outliers were added to the high class and the number of data of this class was 13.

Table 3.
Jenks natural break (JNB) classification results with the class limits.
Descriptive information about the dependent and independent variables used in this study is presented in Table 4. A total of 16 different models were created. The dependent variable pedestrian density and the independent variable periods were used in each model. The independent variable measures were included in each model one by one.

Table 4.
Descriptive statistics for all variables.
The significance of the models created in this study was examined by the model fitting and parallel lines tests (Table 5). The goodness of fit and pseudo R2 tests were not evaluated because the data contained a large number of empty cells and sorting the models was unnecessary. All of the 16 models provided the assumption of parallel lines because of p > 0.05. When the fit values explaining the significance of the model were evaluated, the four models highlighted in gray in Table 5 were found statistically significant because of p < 0.05.

Table 5.
Results of model fitting and parallel lines tests.
The effects of independent variables (periods and measures) on the dependent variable (pedestrian density) were analysed with parameter estimation statistics for the four significant models identified above. Parameter estimation uses a table of statistics to explain the direction, strength, and statistical significance of the relationships between variables.
Table 6 gives the model results of the integration measure obtained from AA. Since the authors demanded to analyze the variables that increased the pedestrian density, they selected the high pedestrian density group as a reference in this study. This preference causes ß-value of the independent variables that increase the pedestrian density to be positive. The p-value lower than 0.05 for notifies that integration has a significant effect on the established model. According to periods variable, T2 was statistically significant (p < 0.05); T1 and T3 were not significant (p > 0.05), when T4 was selected as a reference. The non-significant effects for T1 and T3 explain that the pedestrian density in these periods was not significantly different from T4. ß is a coefficient that expresses how the effect of variables on the dependent variable proportionally. A variable with a high ß-value has more effect in the model than others. In this study, since has greater ß-value than the others, integration was accepted as the most significant variable in explaining the pedestrian density. On the other hand, the ß-values of the periods are not statistically as effective as the integration in explaining the pedestrian density. eβ and w-values are used to interpret the effects of variables like ß-values. eβ-value takes values less than one when ß-value is negative and greater than one when it is positive. A high ß coefficient for a variable indicates that its effect on the dependent variable is considerable. Briefly, AA integration in this model was more effective than the periods in explaining the pedestrian density.

Table 6.
Parameter estimation for .
Table 7 gives the model results of the mean depth measure obtained from AA. The p-value lower than 0.05 for notifies that mean depth has a significant effect. The results for periods variable are similar to the model established with . Because is an inverse of , its ß-value is negative, and therefore its eβ-value is lower than one. The ß-value, eβ-value, and w-value for were lower than the values of has. These statistical results show that does not reflect pedestrian density as successful as does.

Table 7.
Parameter estimation for .
Table 8 gives the model results of the choice measure obtained from AA. The p-value higher than 0.05 for notifies that choice does not have a significant effect on pedestrian density. Therefore the authors could not evaluate ß-value, eβ-value, and w-value for choice. The results for periods variable are similar to the models established with and .

Table 8.
Parameter estimation for
Table 9 gives the model results of the control measure obtained from VGA. The p-value higher than 0.05 for notifies that control does not have a significant effect on pedestrian density. Therefore the authors could not evaluate ß-value, eβ-value, and w-value for control. The results for periods variable are similar to the models established with , and .

Table 9.
Parameter estimation for
The four tables prepared for parameter estimations of ordinal logistic regression analyses verify that integration was the most effective measure to predict the pedestrian density in this study area. Since the p-values of T1 and T3 groups, which were among the periods used in all models, were higher than 0.05, the counts made in these periods were not significantly different from the reference T4 in determining the pedestrian density. The effect of the T2 group, which was statistically significant in each model, was negative compared to the reference T4 group. The significant effect for T2 implies that the pedestrian volume at T2 was significantly lower than at the reference T4. If it were aimed to determine the low pedestrian density of the study area, it would be appropriate to make the counts in the period corresponding to the T2 group.
4.3. Evaluation of Current and Master Plan Datasets
Figure 4a,b show the axial maps of Davutpaşa Campus created according to normalized AA integration values, respectively. Classes (low: green, medium: blue, and high: pink) representing integration values with colours were designed using the JNB classification algorithm. Standard class limits were used in both maps to facilitate visual comparison.
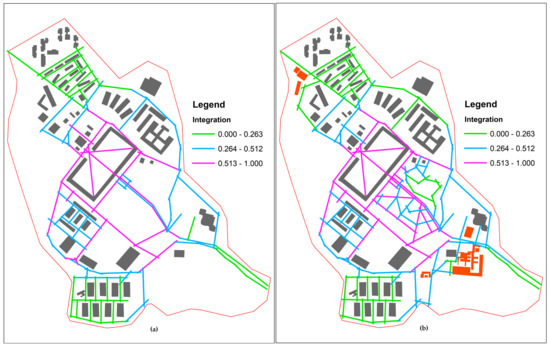
Figure 4.
AA Integration values for (a) current and (b) master plan dataset.
The new axial lines that were planned to be connected to the axes categorized in high class in the current axial map were generally grouped in high class. These axial lines often appeared in the central part of the campus in the master plan. However, other new axes planned to be added around the campus boundaries were in the medium and low classes. They increased overall accessibility by helping spread the centrality to the edges as well.
Table 10 shows the paired sample t-test results for the current and master plan datasets. There are 96 axial lines in the current dataset, and their mean integration value is 0.388. According to the master plan, when 41 new walkways were added to the campus area, the mean integration value decreased to 0.356. Paired sample t-test was performed for 96 common walkways in both datasets. The mean integration value of these 96 paths in the master plan was calculated as 0.370. These differences between the mean values showed that new paths to be added would reduce the mean value of the current ones. Besides, the mean values of the new paths were lower than the current ones. The p-value of 0.002 indicated that the changes in the means mentioned above were statistically significant. The value proved that the master plan would change the campus morphology for pedestrians.

Table 10.
Results of paired sample t-test for AA.
5. Conclusions
This study investigated the relationship between pedestrian density and measures obtained from AA and VGA. These two analysis methods enabled the derivation of 15 different measures. The relationship of each measure to pedestrian density was analysed using ordinal logistic regression. The integration and mean depth of AA yielded statistically significant results to explain the pedestrian density. However, the coefficient values of the regression analysis revealed that integration was more effective than mean depth. For this reason, integration was accepted as the most effective tool to explain the pedestrian movement in the study area.
According to the regression analysis results in the Davutpaşa Campus case, AA integration value of an axial line reflects usage intensity of walking path that physically coincides with this line. This axial line with high integration value enables to identify the walking path with high pedestrian density. Moreover, the analysis results prove that AA, as a SS technique, explain pedestrian density better than VGA. This assessment emphasises the importance of AA integration obtained from a two-dimensional axial map. However, some environmental characteristics such as the topography of the region and land use characteristics are other factors affecting the walkability and pedestrian density on the walkways. Since Davutpaşa Campus has much less street connection than a large urban area, the environmental characteristics of the walking paths can be easily observed. Considering the environmental features, walking paths, which have high pedestrian density according to the integration measure, are also suitable for walking in the campus area. However, their effects have not been investigated statistically in this study. In the future, the authors intend to examine these relationships between the walkways with high integration values and the environmental factors on a broader study area that has many street connections.
Increasing accessibility and pedestrian mobility to a maximum by adding minimum number of new walkways is the most optimal solution for planners. Statistical analysis of the effects of new walkways on the existing ones, depending on the alternative plans, helps to decide on the most appropriate solution. In the second part of this study, changes in integration values of axial lines in the current and master plan datasets were analysed by using paired sample t-test. This comparison only determines whether the master plan significantly affects existing walkways. In the case of more than one alternative plan, the significance of the changes created by each plan on existing walkways should be examined in order to compare the plans.
Author Contributions
Conceptualization, F.G. and S.B.; methodology, Ö.Ö.H.; F.G. and S.B.; software, Ö.Ö.H.; validation, F.G., S.B. and Ö.Ö.H.; formal analysis, F.G. and S.B.; investigation, Ö.Ö.H.; resources, Ö.Ö.H.; data curation, Ö.Ö.H.; writing-original draft preparation, Ö.Ö.H.; writing-review & editing, F.G.; visualization, Ö.Ö.H.; F.G. and S.B.; supervision, F.G. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. It was prepared from a part of the first author master thesis.
Acknowledgments
The authors acknowledge the contribution of all the anonymous reviewers that improved the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seneviratne, P.N.; Morrall, J.F. Analysis of factors affecting the choice of route of pedestrians. Trans. Plan. Technol. 1985, 10, 147–159. [Google Scholar] [CrossRef]
- Hillier, B.; Penn, A.; Hanson, J.; Grajewski, T.; Xu, J. Natural movement: Or, configuration and attraction in urban pedestrian movement. Environ. Plan. B Plan. Des. 1993, 20, 29–66. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.J.; Molnar, P.; Vicsek, T. Simulation of pedestrian crowds in normal and evacuation situations. In Pedestrian Evacuation Dynamics, 1st ed.; Schreckenberg, M., Sharma, S.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 21, pp. 21–58. ISBN 978-3-642-07658-9. [Google Scholar]
- Kim, S.; Choi, J.; Kim, Y. Determining the sidewalk pavement width by using pedestrian discomfort levels and movement characteristics. KSCE J. Civ. Eng. 2011, 15, 883. [Google Scholar] [CrossRef]
- Asadi-Shekari, Z.; Moeinaddini, M.; Shah, M.Z. A pedestrian level of service method for evaluating and promoting walking facilities on campus streets. Land Use Policy 2014, 38, 175–193. [Google Scholar] [CrossRef]
- Larrañaga, A.M.; Rizzi, L.I.; Arellana, J.; Strambi, O.; Cybis, H.B.B. The influence of built environment and travel attitudes on walking: A case study of Porto Alegre, Brazil. Int. J. Sustain. Trans. 2016, 10, 332–342. [Google Scholar] [CrossRef]
- Dovey, K.; Pafka, E. What is walkability? The urban DMA. Urban Stud. 2019, 57, 93–108. [Google Scholar] [CrossRef]
- Ericson, J.D.; Chrastil, E.R.; Warren, W.H. Space syntax visibility graph analysis is not robust to changes in spatial and temporal resolution. Environ. Plan. B Urban Anal. City Sci. 2020, in press. [Google Scholar] [CrossRef]
- Hillier, B. The art of place and the science of space. World Arch. 2005, 11, 96–102. [Google Scholar]
- Jacoby, K. What is space syntax? Does the Urban Form of the City Affect the Level of Burglary and Crime. Master’s Thesis, Architectures et Villes Face Ala Mondialisation, Royal Institute of Architecture, Stockholm, Sweden, June 2006. [Google Scholar]
- Turner, A.; Doxa, M.; O’sullivan, D.; Penn, A. From isovists to visibility graphs: A methodology for the analysis of architectural space. Environ. Plann. B Plan Urban Anal. City Sci. 2001, 28, 103–121. [Google Scholar] [CrossRef]
- Lerman, Y.; Omer, I. The effects of configurational and functional factors on the spatial distribution of pedestrians. In Geographic Information Science at the Heart of Europe, 1st ed.; Vandenbroucke, D., Bucher, B., Crompvoets, J., Eds.; Springer International Publishing: Cham, Switzerland, 2013; pp. 383–398. ISBN 978-3-319-03280-1. [Google Scholar]
- Monokrousou, K.; Giannopoulou, M. Interpreting and predicting pedestrian movement in public space through space syntax analysis. Procedia Soc. Behav. Sci. 2016, 223, 509–514. [Google Scholar] [CrossRef]
- Ahmed, B.; Hasan, R.; Maniruzzaman, K.M. Urban morphological change analysis of Dhaka city, Bangladesh, using space syntax. ISPRS Int. J. Geoinf. 2014, 3, 1412–1444. [Google Scholar] [CrossRef]
- Hajrasouliha, A.; Yin, L. The impact of street network connectivity on pedestrian volume. Urban Stud. 2015, 52, 2483–2497. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, X.; Zhang, J.; Wu, R.; Zhang, H. Spatial configuration and online attention: A space syntax perspective. Sustainability 2018, 10, 221. [Google Scholar] [CrossRef]
- Jabbari, M.; Fonseca, F.; Ramos, R. Combining multi-criteria and space syntax analysis to assess a pedestrian network: The case of Oporto. J. Urban Des. 2018, 23, 23–41. [Google Scholar] [CrossRef]
- Desyllas, J.; Duxbury, E. Axial maps and visibility graph analysis. In Proceedings of the 3rd International Space Syntax Symposium, Atlanta, GA, USA, 7–11 May 2001; Volume 27, p. 27.1-27.13. [Google Scholar]
- Hölscher, C.; Brösamle, M.; Vrachliotis, G. Challenges in multilevel wayfinding: A case study with the space syntax technique. Environ. Plan. B Plan. Des. 2012, 39, 63–82. [Google Scholar] [CrossRef]
- Heitor, T.; Nascimento, R.; Tomé, A.; Medeiros, V. Accessible Campus: Space syntax for universal design. In Proceedings of the 9th International Space Syntax Symposium, Seoul, Korea, 31 October–3 November 2013. [Google Scholar]
- Bendjedidi, S.; Bada, Y.; Meziani, R. Urban plaza design process using space syntax analysis. Int Rev. Spat. Plan. Sustain. Dev. 2019, 7, 125–142. [Google Scholar] [CrossRef]
- Koutsolampros, P.; Sailer, K.; Varoudis, T.; Haslem, R. Dissecting Visibility Graph Analysis: The metrics and their role in understanding workplace human behaviour. In Proceedings of the 12th International Space Syntax Symposium, Beijing, China, 8–13 July 2019; Volume 12. [Google Scholar]
- Pagkratidou, M.; Galati, A.; Avraamides, M. Do environmental characteristics predict spatial memory about unfamiliar environments? Spat. Cogn. Comput. 2020, 20, 1–32. [Google Scholar] [CrossRef]
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: Cambridge, UK, 1984; ISBN 978-0-521-23365-1. [Google Scholar]
- Turner, A.; Penn, A.; Hillier, B. An algorithmic definition of the axial map. Environ. Plan. B Plan. Des. 2005, 32, 425–444. [Google Scholar] [CrossRef]
- Bafna, S. Space syntax: A brief introduction to its logic and analytical techniques. Environ. Behav. 2003, 35, 17–29. [Google Scholar] [CrossRef]
- Portugali, J.; Meyer, H.; Stolk, E.; Tan, E. Complexity Theories of Cities Have Come of Age: An Overview with Implications to Urban Planning and Design; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Turner, A.; Penn, A. Making isovists syntactic: Isovist integration analysis. In Proceedings of the 2nd International Symposium on Space Syntax, Brasilia, Brazil, 29 March–2 April 1999. [Google Scholar]
- Turner, A. Angular analysis. In Proceedings of the 3rd International Symposium on Space Syntax, Atlanta, GA, USA, 7–11 May 2001; pp. 1–30. [Google Scholar]
- Turner, A. Depthmap: A program to perform visibility graph analysis. In Proceedings of the 3rd International Symposium on Space Syntax, Atlanta, GA, USA, 7–11 May 2001; pp. 12–31. [Google Scholar]
- Gil, J.; Varoudis, T.; Karimi, K.; Penn, A. The space syntax toolkit: Integrating depthmapX and exploratory spatial analysis workflows in QGIS. In Proceedings of the SSS 2015-10th International Space Syntax Symposium, Space Syntax Laboratory, The Bartlett School of Architecture, University College London, London, UK, 3–7 July 2015; Volume 10. [Google Scholar]
- Hillier, B. Space Is the Machine: A Configurational Theory of Architecture; Space Syntax: London, UK, 2007. [Google Scholar]
- Goldsberry, K.; Duvall, C.S.; Howard, P.H.; Stevens, J.E. Visualizing nutritional terrain: A geospatial analysis of pedestrian produce accessibility in Lansing, Michigan, USA. Geocarto Int. 2010, 25, 485–499. [Google Scholar] [CrossRef]
- Cao, K.; Liu, M.; Wang, S.; Liu, M.; Zhang, W.; Meng, Q.; Huang, B. Spatial Multi-Objective Land Use Optimization toward Livability Based on Boundary-Based Genetic Algorithm: A Case Study in Singapore. ISPRS Int. J. Geo-Inf. 2020, 9, 40. [Google Scholar] [CrossRef]
- Yenisetty, P.T.; Bahadure, P. Measuring Accessibility to Various ASFs from Public Transit using Spatial Distance Measures in Indian Cities. ISPRS Int. J. Geo-Inf 2020, 9, 446. [Google Scholar] [CrossRef]
- Teklenburg, J.A.F.; Timmermans, H.J.P.; Van Wagenberg, A.F. Space syntax: Standardised integration measures and some simulations. Environ. Plan. B Plan. Des. 1993, 20, 347–357. [Google Scholar] [CrossRef]
- De Arruda Campos, M.B.; Fong, P.S. A proposed methodology to normalise total depth values when applying the visibility graph analysis. In Proceedings of the 4th International Space Syntax Symposium, London, UK, 17–19 June 2003. [Google Scholar]
- Hillier, B.; Burdett, R.; Peponis, J.; Penn, A. Creating life: Or, does architecture determine anything? Arch. Behav. 1987, 3, 233–250. [Google Scholar]
- Vaughan, L.; Grajewski, T. Space Syntax Observation Manual; University College London: London, UK, 2001. [Google Scholar]
- Petrasova, A.; Hipp, J.A.; Mitasova, H. Visualization of Pedestrian Density Dynamics Using Data Extracted from Public Webcams. ISPRS Int. J. Geo-Inf. 2019, 8, 559. [Google Scholar] [CrossRef]
- Cambra, P.; Moura, F.; Gonçalves, A. On the correlation of pedestrian flows to urban environment measures: A Space Syntax and Walkability Analysis comparison case. In Proceedings of the 11th Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017; pp. 1–21. [Google Scholar]
- Heiman, G. Basic Statistics for the Behavioral Sciences; Cengage Learning: Boston, MA, USA, 2000. [Google Scholar]
- De Smith, M.J.; Goodchild, M.F.; Longley, P. Geospatial Analysis: A Comprehensive Guide to Principles, Techniques and Software Tools; Troubador Publishing Ltd.: Kibworth Harcourt, UK, 2007. [Google Scholar]
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Agresti, A. Categorical Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 482. [Google Scholar]
- Anderson, J.A. Regression and ordered categorical variables. J. R. Stat. Soc. Ser. B (Methodol.) 1984, 46, 1–22. [Google Scholar] [CrossRef]
- Liao, T.F. Interpreting Probability Models: Logit, Probit, and Other Generalized Linear Models (No. 101); Sage: Thousand Oaks, CA, USA, 1994. [Google Scholar]
- Norris, C.M.; Ghali, W.A.; Saunders, L.D.; Brant, R.; Galbraith, D.; Faris, P. Ordinal regression model and the linear regression model were superior to the logistic regression models. J. Clin. Epid. 2006, 59, 448–456. [Google Scholar] [CrossRef]
- Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. Multivariate Analysemethoden; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Schendera, C.F. Regressionsanalyse Mit SPSS; Walter de Gruyter: Berlin, Germany, 2011. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).