1. Introduction
Geospatial processing and analysis of large amounts of geospatial data in the Geographic Information System (GIS) represents an application domain that obtains significant benefits from parallel and high-performance computing [
1]. Digital Terrain Analysis (DTA) is one of the fundamental features of contemporary GISs used in hydrological modeling, soil erosion, flood simulations, landslide hazard assessment, visibility analysis, telecommunication, and military applications, etc. DTA includes implementation of various algorithms performed by the digital model of the earth surface and terrain, most often Digital Elevation Model (DEM), such as watershed analysis, viewshed analysis, terrain visualization, etc.
Watershed analysis refers to the process of using DEM and iterative operations through raster (gridded) data to delineate watersheds and to detect watershed features such as streams, stream network, drainage divides, basin, outlets, etc. The watershed analysis is used in flood control, erosion detection, and landslide monitoring to provide decision support capabilities.
Watershed analysis consists of several computationally and data intensive tasks (phases) performed over massive DEM data in an iterative manner. As such, it is suitable for accelerating these tasks leveraging parallel and high-performance computing (HPC) methods and techniques.
There are several HPC approaches that can be applied to improve the performance of advanced computationally and data intensive applications, such as the watershed analysis. Such approaches are based on a parallel computing paradigm applied through multi/many-core computer systems, or through distributed computing infrastructure, such as a cluster or cloud infrastructure. While multi-core CPUs are suitable for general-purpose tasks, many-core special purpose processors (Intel Xeon Phi or GPU), comprising of a larger number of lower frequency cores, have been used in general-purpose solutions, performing equally well, or even better in scalable applications. The development of a parallel application and HPC application for such parallel/distributed architectures could be based on various parallel programming frameworks, including OpenACC, OpenCL (Open Computing Language), OpenMP (Open Multi-Processing), and NVIDIA CUDA (Compute Unified Device Architecture). OpenMP is a set of compiler directives, library routines, and environment variables for programming shared-memory parallel computing systems. Furthermore, OpenMP has been extended to support programming of heterogeneous systems that contain CPUs and accelerators. General-purpose computing on a Graphics Processing Unit (GPGPU) represents a new paradigm based on tightly coupled, massively parallel computing units [
2]. It represents a method and a technique for performing general purpose computations on a GPU by using an appropriate framework, an API, and a programming model, such as OpenCL, Microsoft’s DirectCompute, and NVIDIA CUDA. OpenCL supports portable programming for computer architectures provided by various vendors, while CUDA runs only on NVIDIA Graphics Processing Units (GPU). CUDA combines C/C++ on the host side with C-like kernels that enable general purpose applications to access massively parallel GPUs for non-graphical computing. CUDA C/C++ compiler, libraries, and run-time software enable programmers to develop and accelerate data-intensive applications on GPU. Writing CUDA applications and kernels is a task that is time-consuming and prone to errors requiring detailed knowledge of the target NVIDIA GPU architecture and design of kernel maximally tailored for a particular architecture. In order to provide a parallel programming framework for a large audience and a wide spectrum of multi-core and many-core architectures, an OpenACC standard and parallel programming model has been developed.
OpenACC is a specification of compiler directives and API routines for writing a parallel code in C, C++, and FORTRAN. That code can be compiled into different parallel architectures, such as multi-core CPUs, or many-core parallel accelerators, such as GPUs. In contrast to CUDA where the programmer is required to explicitly decompose the computation into parallel kernels, when using OpenACC, the programmer annotates the existing loops and data structures in the code, so that the OpenACC compiler can target the code to different devices. For NVIDIA GPU devices, the OpenACC compiler generates the kernels, creates the register and shared memory variables, and applies performance optimization.
In this paper, the focus is on accelerating a sequential watershed analysis algorithm using different parallel implementations, a native NVIDIA GPU implementation using CUDA, and OpenACC implementations mapped to both GPU and multi-core CPU. The proposed solutions have been evaluated with respect to the execution time, energy consumption, and programming effort for program parallelization for a different size of input DEM data. Experimental evaluation proves expected improvements in performance of watershed analysis with respect to a single-core CPU-based solution. It shows feasibility in using CUDA and OpenACC programming frameworks on GPUs and multi-core CPUs, for digital terrain analysis and similar GIS algorithms. Furthermore, our evaluation shows better performance of the OpenACC watershed analysis implementation with respect to the CUDA one, with gains in lower energy consumption and less programming efforts.
The main contributions of this paper are shown below.
We have developed parallel implementation of all phases and steps of the watershed analysis using CUDA and OpenACC for NVIDIA GPUs and OpenACC for multi-core CPU.
We have tested and evaluated OpenACC parallel implementation through several large DEM datasets both for multi-core CPUs and many-core GPUs, over commodity PC NVIDIA GPU, as well as high end NVIDIA Tesla K80 available through NVIDIA Docker plugin (nvidia-docker) through scientific cloud infrastructure.
We have shown that the parallel implementation of OpenACC watershed analysis outperforms corresponding CUDA implementation for different DEM sizes, while consuming less energy and requiring less programming efforts.
The rest of the paper is organized as follows.
Section 2 provides an overview of the related work in parallel and HPC implementation in DTA in general and watershed analysis in particular.
Section 3 describes algorithms for watershed analysis, requirements, and motivation for their acceleration.
Section 4 describes the parallel implementation of watershed algorithm, using CUDA and OpenACC programming frameworks and APIs (Application Programming Interfaces).
Section 5 presents the experimental evaluation over multi-core CPU and many-core GPUs for large DEM datasets. Lastly,
Section 6 concludes the paper and gives major directions for future research.
2. Related Work
Many GIS algorithms may benefit from parallel processing of geospatial data, such as: map-matching, viewshed analysis, watershed analysis, spatial overlay, trajectory analysis, and more [
1]. The recent proliferation of distributed and cloud computing infrastructures and platforms, both public clouds (e.g., Amazon EC2) and private and hybrid computer clouds and clusters, has provided a rise in processing and analysis of geospatial data. The parallel GIS algorithms implemented on clusters of multi-core shared-memory computers, based on frameworks such as MPI (Message Passing Interface), MapReduce/Hadoop, and Apache Spark, have set this paradigm as an emerging research and development topic [
3].
Zhang [
4], Xia et al. [
5], and Stojanovic and Stojanovic [
6] have considered parallel processing of geospatial data in a personal computing environment. They argued that modern personal computers, equipped with multi-core CPUs and many-core GPUs, provide excellent support for parallel and high-performance processing of spatial data, which is comparable in efficiency and even in performance to cluster and cloud computing solutions using MPI or a MapReduce framework.
2.1. Remote Sensing and DTA Algorithms Implementation on a GPU
Many interesting and computationally and data-intensive algorithms in remote sensing and digital terrain analysis, such as flood modeling and simulations, LiDAR (Light Detection and Ranging) data processing, and watershed analysis have recently become the focus of research community oriented to parallel computing on many-core GPU architectures [
7,
8].
Li et al. [
9] presented a parallel GPU implementation of map reprojection algorithms for raster datasets using CUDA. They demonstrated performance improvements over a serial version on a CPU through a series of tests, and achieved speedup from 10 to 100. Wang et al. [
10] proposed a hybrid parallel spatial interpolation algorithm executed on both the CPU and GPU to increase the performance of massive LiDAR point clouds processing. Their experimental results have shown that their hybrid CPU-GPU solution outperforms the CPU-only and GPU-only implementations. Kang et al. [
11] proposed a parallel algorithm implemented with OpenACC to use a GPU to parallelize the reservoir simulations. The experimental results show that the proposed approach outperform the CPU-based one while preserving the small programming effort for porting the algorithm to a parallel execution on a GPU. García-Feal et al. [
12] presented a new parallel code in NVIDIA CUDA for two-dimensional (2D) flood inundation modelling using GPU. The experiments show a significant improvement in computational efficiency that opens up the possibility of using their solution for real-time forecasting of flood events as well. Liu et al. [
13] proposed parallel OpenACC implementation of the two-dimensional shallow water model for flood simulation. The results of their experiments demonstrated achievements of up to one order of magnitude in speedup in comparison with the serial solution. Wu et al. [
14] presented a parallel algorithm for DEM generalization implemented using CUDA applied in multi-scale terrain analysis. They proposed a parallel-multi-point algorithm for DEM generalization that outperforms other methods, such as ANUDEM (
https://fennerschool.anu.edu.au/research/products/anudem), compound, and maximum z-tolerance method, while reducing the response time by up to 96%. Although not in focus in this research, OpenCL framework have been used in acceleration of several remote sensing and digital terrain analysis algorithms on GPU architectures as well [
15,
16]. OpenCL enables cross-platform parallel programming on heterogeneous platforms such as GPU, CPU, FPGA (Field-Programmable Gate Array), and DSP (Digital Signal Processing). Zhu et al. [
15] have implemented a Non-Local means (NLM) denoising algorithm for image processing using OpenMP and OpenCL and conducted the experiment on CPU, GPU, and MIC (Many Integrated Core) Intel Xeon Phi Coprocessor. They show that OpenCL-based implementation has better performance on Xeon Phi 7120 than on NVIDIA Kepler K20M GPU, and slightly better performance than OpenMP-based implementation on Intel Xeon Phi 7120. Huang et al. [
16] proposed implementation of a parallel compressive sampling matching pursuit (CoSaMP) for compressed sensing signal reconstruction using the OpenCL framework. Based on experiments using remote sensing images, they demonstrated that the proposed parallel OpenCL-based implementation can achieve significant speedup on heterogeneous platforms (AMD HD7350 and NVIDIA K20Xm), without modifying the application code. Since OpenCL and CUDA have similar parallel computing capabilities and expected performance improvements, we have not considered OpenCL in our implementation and experiments.
2.2. Watershed Analysis Implementation Using CUDA, OpenACC, and OpenCL
Different parallelization techniques and corresponding computer architectures have been particularly used for accelerating watershed analysis algorithms. Due to the recursive nature of the watershed algorithms, their parallelization is not a trivial task and it has been the focus of research for its acceleration through execution on parallel architectures with distributed memory [
17,
18,
19], shared memory [
20,
21,
22], and many-core GPUs [
23,
24,
25,
26,
27,
28]. Kauffmann and Piche [
23] described a cellular automation to perform the watershed transformation in N-D images. Due to the local nature of cellular automation algorithms, these algorithms have been designed to execute on massively parallel processors and, therefore, be efficiently implemented on low cost consumer GPUs. Quesada-Barriuso et al. [
24] showed that an algorithm for watershed analysis based on a cellular automaton is a good choice for implementing on the most recent GPU architectures, especially when the synchronization rules are relaxed. They compared the synchronous and asynchronous implementation of the algorithm. Their results showed high speedups for both implementations, especially for the asynchronous one.
Hučko and Šramek [
25] presented a new algorithm for watershed analysis supporting data larger than the available memory. They modified one of the previous CPU intended algorithms for execution on a GPU architecture using OpenCL API. Two variants of the algorithm were designed and implemented. The tests showed no difference in the running time, which indicates that the storage of intermediate results in multi-pass algorithms consumes the main part of the running time and can be shortened using the RAID technology. It was shown that it was possible to reduce computational time of the watershed analysis approximately three times with respect to the original CPU version.
Ortega and Rueda were among the first to propose a GPU implementation of a classic watershed analysis algorithm [
26]. They used CUDA for parallelizing the single-flow direction algorithm. They used a structure called the flow-transfer matrix to parallelize the D8 algorithm on a GPU. They achieved up to eight times speedup increase of CUDA-based drainage network computation with respect to the corresponding single-core implementation. Quin and Yhan [
27] used CUDA to parallelize and accelerate both iterative DEM preprocessing step and a multiple-flow accumulation step of the watershed algorithm. Eranen et al. [
28] implemented all the steps of the drainage network extraction algorithm on a GPU, for single flow directions, considering the uncertainty in the input digital elevation model.
Rueda et al. [
29] implemented the flow accumulation step of the D8 algorithm in CPU, using OpenACC and two different CUDA versions, and compared the length and complexity of the programming code and its performance on different datasets. They concluded that, although OpenACC cannot match the performance of CUDA optimized implementation (3.5× slower in average), it provides a significant performance improvement against the CPU implementation (2–6×) with a much simpler parallel code and less implementation effort.
3. Algorithms for Watershed Analysis
Watersheds are catchment areas or drainage basins representing an extent from the land surface where water from different sources like rain, melting snow, and others, converges to the same point, called the outlet. Watersheds can be modeled considering a DEM as a grid model, where the cells represent the elevation of a square surface. Extracting a digital representation of the flow network is an essential step in the study of watershed delineation, erosion sites, mineral or pollution distribution, the cost estimation, the design of constructing new roads, the simulation of flood plains in paddy fields, and more.
The watershed analysis consists of two steps (phases): (1) DEM preprocessing concerning flow directions over flat areas and depressions in DEMs, and (2) Computation of flow distribution of each cell to its neighboring cells.
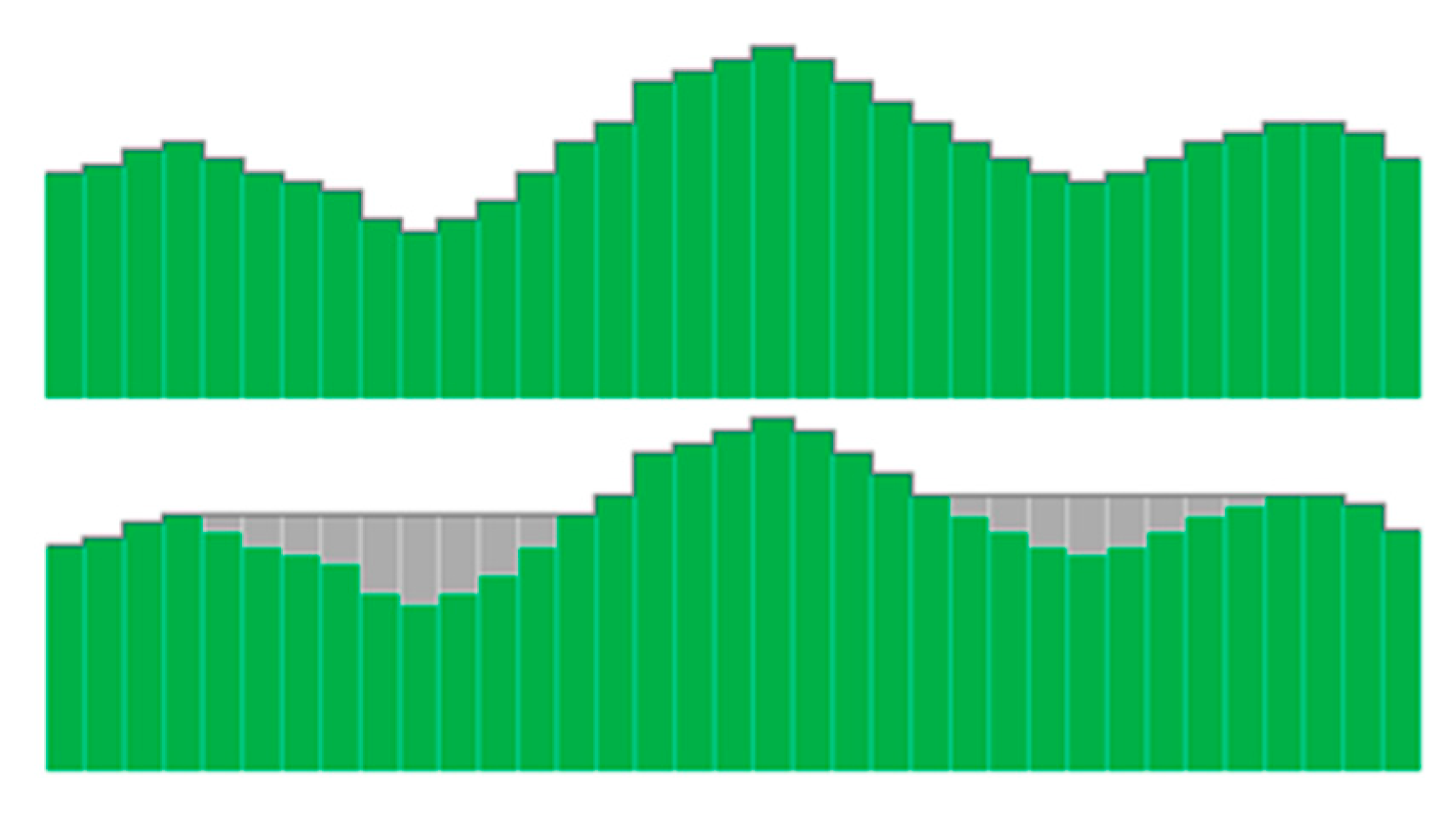
The DEM preprocessing algorithm is used to fill in depressions and remove flat areas existing in real DEMs. The result of depression filling in the DEM preprocessing phase is illustrated in
Figure 1. The most proposed preprocessing algorithms are based on increasing the elevation of the cells located in a depression until the sink is filled (
Figure 1) and the flow is routed over a flat area to the next lower cell. In this paper, the DEM preprocessing algorithm proposed in [
30] is used.
The DEM preprocessing algorithm gets elevation raster zDEM as an input, and generates elevation raster wDEM as an output, by performing the following.
Adding a thick layer of water to each cell of elevation raster zDEM, except for the boundary cells.
Removing excess water since, for each cell, there is a non-increasing path to the boundary with two operations.
where c represents a current cell on the position (i, j), n represents a boundary cell on the position (k, l), and ε is a slope of filled depression.
As long as the removal of the excess water (added in the first step) is possible, processing of the whole DEM is repeating iteratively in the while loop.
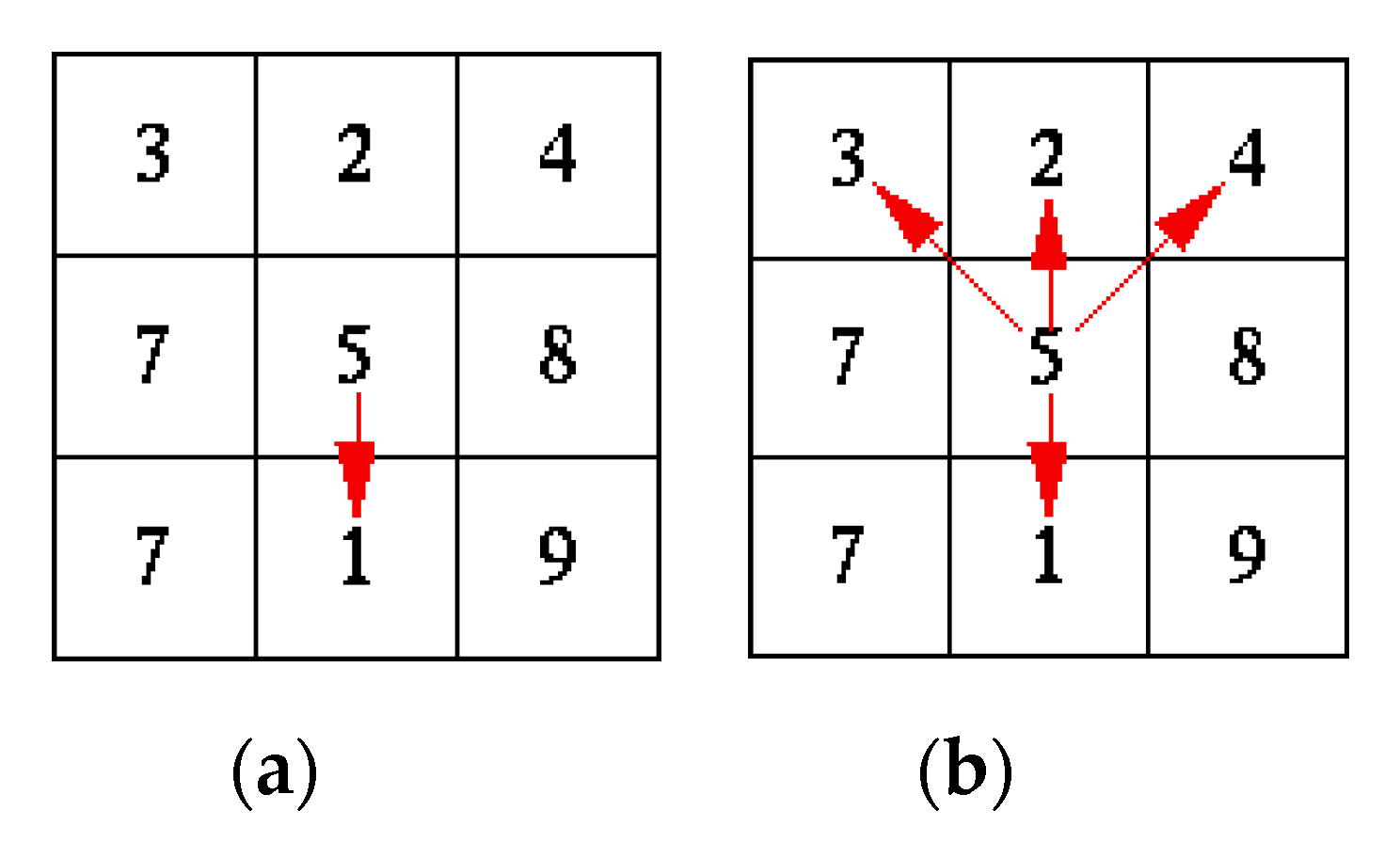
The second step in the watershed analysis represents computation of flow distribution from each cell to its neighboring cells. Two approaches can be used in this step: (i) Single Flow Direction (SFD) algorithms, where the flow is always passed to one of the eight neighboring cells, and (ii) Multiple Flow Direction (MFD) algorithms, where the flow is distributed to multiple neighbors, according to the predefined rule (
Figure 2). In this paper, the MFD algorithm was used, which is better than SFD from the perspective of the algorithm error.
In the MFD algorithm fraction of water
di from the current cell to the i-th neighboring cell is calculated by the following expression.
where
represents the slope between the current cell and the
i-th cell. The value of
Li depends on the position of the neighboring cell and it is calculated only for a cell whose elevation is less than the current cell elevation. Its value is 0.354 for diagonal cells and 0.5 for cardinal cells. In most MFD algorithms, the value of exponent p is equal to 1. There is a slight modification of the MFD algorithm, named MFD-md, where the value of
p depends on terrain conditions, and it is calculated using Equation (3). Experimental results have shown that MFD-md gives more accurate results compared to classic MFD and SFD. Therefore, MFD-md was implemented. The MFD-md algorithm consists of two steps: (i) calculation of flow directions and (ii) calculation of flow accumulations. Calculation of flow directions is performed according to Equation (3), as shown in
Figure 3.
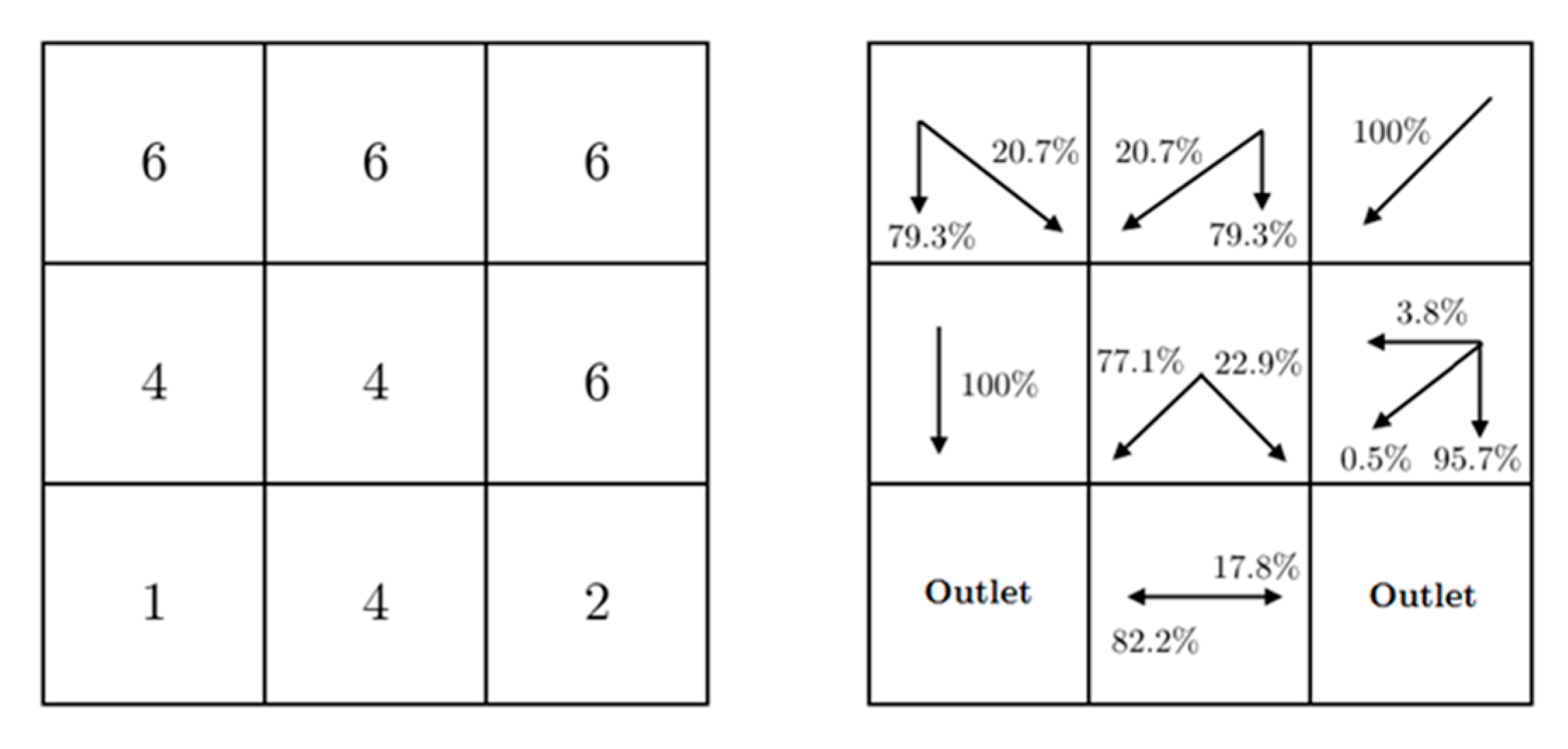
When flow directions are determined in DEM, in the second phase, the flow accumulations are calculated. In this paper, the Flow-Transfer Matrix (FTM)-based algorithm is used for parallelization of calculating the flow accumulation, as proposed in [
26,
27]. This is because its iterative version enables parallelization in each round of the iterative process. The FTM algorithm represents iterative process where, in each iteration (round), the flow accumulation for every cell, originated from its neighboring cells, is calculated. These values are recorded in a flow-transfer matrix,
FlowTransfer(i). The iterative process finishes when the zero flow-transfer matrix is obtained. The final
FlowAccumulation matrix is obtained as the sum of
FlowTransfer(i) matrices.
4. Parallelization of Watershed Analysis
In order to accelerate sequential execution of the watershed algorithm, we have implemented parallel applications using CUDA and OpenACC frameworks. Watershed analysis algorithm consists of two phases that can be executed either sequentially, or in parallel: (i) DEM preprocessing and (ii) computation of flow distribution of each cell to its neighboring cells. In this research, both steps in achieving a maximum increase in performance are parallelized. Both a CUDA solution for execution on a GPU and an OpenACC solution for execution on a GPU and a multi-core CPU have been implemented. The source code and executables for Watershed analysis implementation, as well as experimental DEM datasets, are available at public GitHub repository listed in
Supplementary Materials section at the end of the paper.
As mentioned in
Section 3, the DEM preprocessing algorithm in the first phase consists of two steps: the water covering step and the water removal step, and parallelization of both steps has been implemented. wDEM[i][j] > zDEM[i][j] is denoted as U(0). The conditions defined in Equations (1) and (2) are denoted as U(1) and U(2), respectively. The pseudo code for DEM preprocessing implementation is given in
Figure 4.
Regarding DEM preprocessing algorithm parallelization, we have used the fact that computation for the current cell is based on values of the neighboring cells that have been updated during the current iteration. As a consequence, computations in all cells can be performed in parallel during current iteration. This fact is exploited in both CUDA and OpenACC solutions.
As the pseudo-code inside double outer
for loops (statements 13–22 in
Figure 4) can be executed by single CUDA thread, its implementation can be placed into the appropriate kernel function. In this case, a double
for loop is replaced with a kernel function. When the kernel function is called, a two-dimensional grid containing as many threads as the number of cells in the DEM is launched on the GPU. The kernel function is called from the host part of the algorithm (executed on a CPU) iteratively until none of the cells in DEM change their value during the current iteration of DEM preprocessing. Part of the host code is shown in
Figure 5.
In the case of OpenACC implementation, the independence of operations in the DEM processing algorithm is also taken into account. However, the parallelization is done in a different way in order to optimize execution of an OpenACC implementation. First of all, MFD algorithm is divided into functions: DEMpreprocessing, GenerateFlowDirections, GenerateFlowFractions, and FlowAccumulation. Each function contains OpenACC directives for parallel loop processing because there is no dependence of operations between loop iterations. In addition, it must be ensured that required data is stored in a GPU memory at the start of each parallel region. Data transfer has to be performed in an optimal way with respect to time consumption. For example, the input data for DEM preprocessing is zDEM and it must be transferred from the host to the device memory (GPU memory) beforehand. Since the DEM preprocessing function generates wDEM, it is not necessary to copy its values into the device memory. It is sufficient to allocate GPU memory for it. zDEM values are needed only during preprocessing, while wDEM is needed in other model processing functions. Thus, we need to assure that its values remain in the device memory during further execution of the successive functions.
One solution to the data transfer problem is to perform it once at the beginning of the parallel region in each of the four functions. In that case, the data transfer will be performed in each function, which is a time-consuming solution.
A better approach that was applied in this paper is to completely separate the OpenACC data transfer region and the parallel region. The necessary allocation of the device memory can be made and the necessary data can be copied from/to the host memory, using one OpenACC region (
Figure 6).
When calling any function involved in processing of the DEM model, the necessary data (wDEM) is available in the device memory. However, since each parallel region is out of the “scope” of the region that controls the parallel processing of data, the compiler cannot conclude that the data processed in each function has already been stored in the device memory. As a result, the compiler generates a generic data transfer region in each parallel region. To prevent this, we used additional OpenACC directives to notify the compiler that the data processed in a parallel region already exists in the device memory. Therefore, inside the DEM preprocessing function, before parallelization of both the water covering step and the water removal step, we added the following directive:
to determine compiler data processed in parallel regions that already exist in the device memory. The same directive has to be used before the parallel region in the
GenerateFlowDirections function with wDEM [:size], RMFD [:height] [:width] as parameters, before the parallel region in
GenerateFlowFractions function with wDEM[:size], RMFD[:height][:width], flowFractions [:size1] as parameters, and before the parallel region in
FlowAccumulation function with wDEM [:length], flowFractions [:size1], RMFD [:height] [:width], flowAccumulation[:length] as parameters.
5. Experimental Evaluation
5.1. Experimental Settings
The proposed implementations have been tested on DEMs of different dimensions to evaluate efficiency and performance depending on the size of input data. Efficiency has been measured with respect to execution time, energy consumption, and programming efforts for algorithm parallelization. The experiment was carried out on the following parallel architectures.
Intel(R) Core i5-4670K processor running at 3.40GHz, 8GB RAM (Random Access Memory), and NVIDIA GTX 770 graphic card.
Tesla K80 GPU available on Hasso Plattner Institute (HPI) Future SOC (Service-Oriented Computing) Lab infrastructure (
https://hpi.de/en/research/future-soc-lab-service-oriented-computing). NVIDIA Tesla K80 Accelerator contains 4992 cores, 24 GB of GDDR5 memory, and 480 GB/s memory bandwidth, according to the specification. We implemented the Docker image for our Watershed algorithm implementation and ran a container on Tesla K80 using NVIDIA Docker plugin (
nvidia-docker) and its options.
Intel® Xeon® Processor E5-2620 v4, with eight physical and 16 logical cores, 128 GB RAM, which is also available at HPI Future SOC Lab infrastructure.
We have applied the Watershed analysis over DEMs of several dimensions: 1691 × 2877, 2414 × 2912, 2433 × 4152, 3278 × 4277, and 3308 × 5967 to evaluate the scalability of implementation with the data size increasing. These DEMs represent the models of digital terrain in Alaska displayed in
Figure 7 in the original form, using isohypses and
hill shade relief
, respectively, downloaded from the
EarthExplorer USGS (United States Geological Survey) service (
http://earthexplorer.usgs.gov).
To measure the execution time and the energy consumption for both GPU and CPU, we used the MeterPU library (
https://www.ida.liu.se/labs/pelab/meterpu/). The execution times were measured in seconds and energy consumption in Joules. We also calculated programming productivity, i.e., programming effort for program parallelization
defined as:
where
(
Lines of Code total) represents total lines of code and
(
Lines of Code parallel) number of code lines, which are used for code parallelization.
5.2. Experimental Results
For the implemented MFD algorithm, we have compared results for sequential (single-core) program execution, parallel multi-core CPU program execution (parallelized using OpenACC library), parallel many-core GPU execution (parallelized using OpenACC library), and parallel many-core GPU execution (parallelized using native CUDA code). The experimental results are shown in
Table 1,
Table 2,
Table 3 and
Table 4.
According to these experiments, CPU and GPU execution times increases with DEM size, as expected. In the first dataset, CUDA and OpenACC GPU implementations outperform single-core CPU implementation by 11.2× and 25.7×, respectively, and multi-core CPU implementation by 5.4× and 12.5×, respectively. In the largest DEM dataset, CUDA and OpenACC GPU implementations outperform multi-core CPU implementation by 6.2× and 17.2×, respectively, and single-core CPU implementation by 12.3× and 34.2×, respectively.
For better performance evaluation, we calculated the Speedup (S) to compare the execution time of parallel implementations of the MFD algorithm (
Tparallel) to the execution time of sequential MFD implementation on a single core CPU processor (
Tsequential):
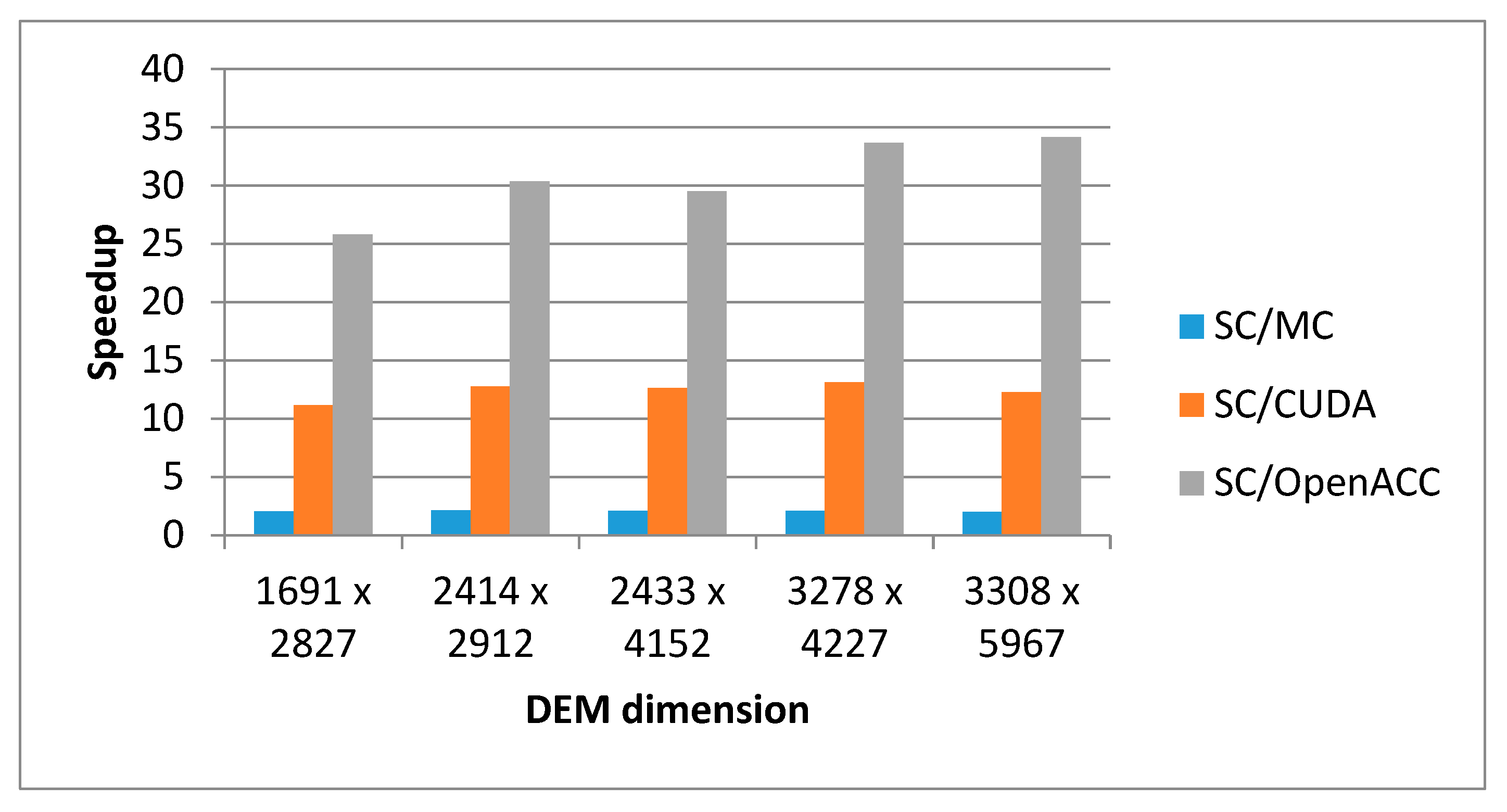
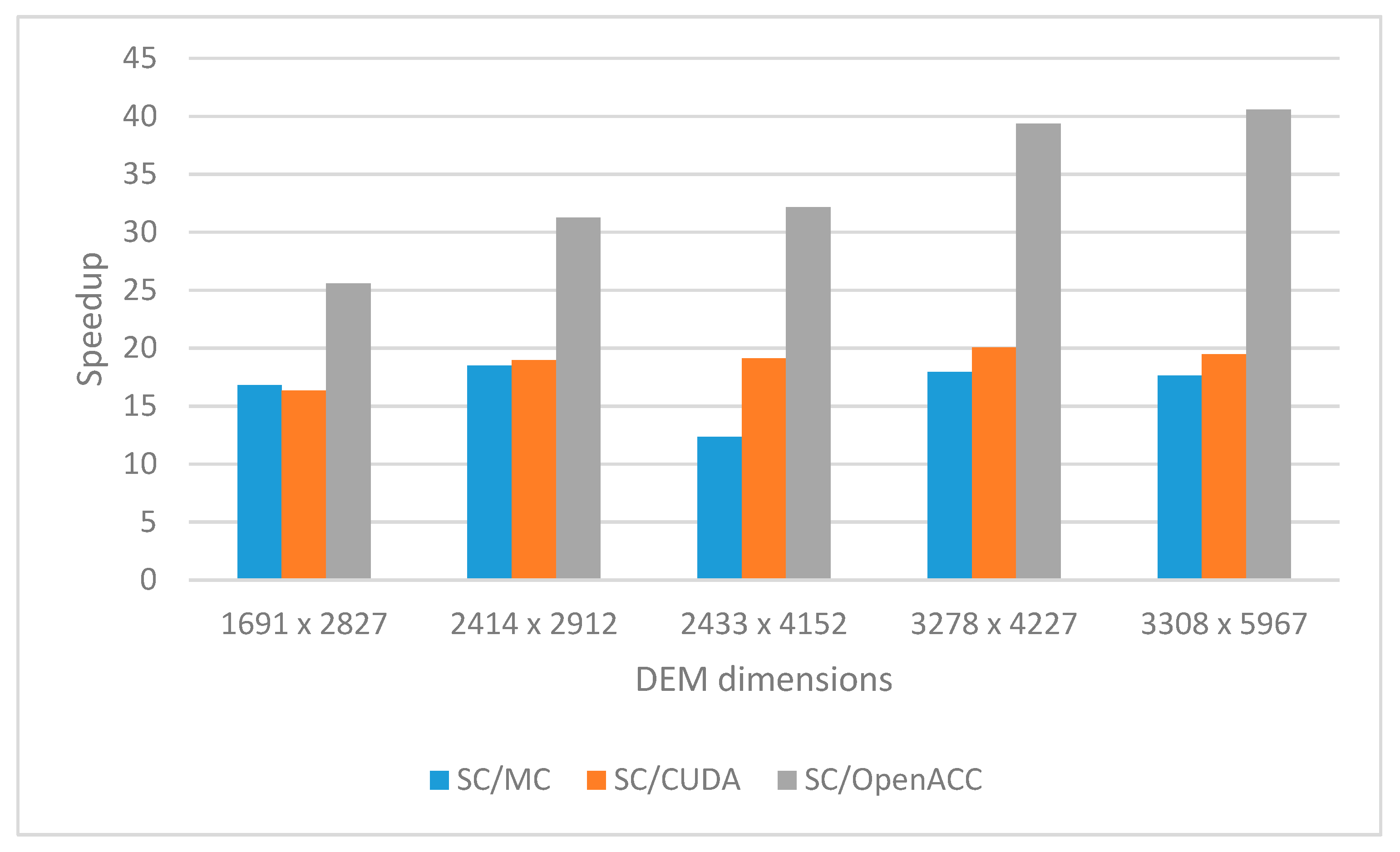
Figure 8 shows experimental results for the speedup of the corresponding parallel solution with respect to the sequential solution for different sizes of input DEM.
It can be concluded that all parallel implementations have speedup greater than 1 with respect to the sequential solution (marked as SC in
Figure 8). Thus, OpenACC multi-core implementation (marked as MC in
Figure 8) shows the speedup is, on average, 2.1, CUDA many-core implementation (marked as CUDA in
Figure 8) shows the speedup, on average, is 12.4, and OpenACC many-core implementation (marked as OpenACC in
Figure 8) shows the speedup, on average, is 30.1. The results in
Figure 8 illustrate that OpenACC many-core GPU implementation achieves higher speedup than counterpart CUDA implementations. The reason is found in the fact that, in the OpenACC implementation, all phases of DEM processing through to the final result are parallelized: preprocessing, generating auxiliary matrices (a matrix that stores the direction of the water flow and a matrix that memorizes the percentage of water swelling in each direction), while, in the CUDA implementation, only the preprocessing and processing of DEM data are parallelized. In addition, the OpenACC implementation eliminates unnecessary data transfers between the host and GPU at the beginning of the execution of each phase, which are performed in the CUDA version. This has a significant impact on the overall execution time of OpenACC implementation.
Since there are no parallel constructions in the serial implementation, the programming effort for the serial implementation is zero. There are no instructions for parallel processing (
Table 1). Since the same code was extended with the OpenACC parallel processing directives used to generate multi-core programs and many-core GPU programs, the value of the programming effort is the same for both, which is 0.03 (
Table 2 and
Table 4). This value is less than 1%, or less than 1% of the instruction of the entire code referring to the parallelization of the program. On the other hand, the programming effort for the original CUDA application is 0.3012 (
Table 3), or almost one third of the instructions in the code are instructions for parallel processing. As is shown, the optimal solution is based on OpenACC applied on a GPU because it is easy to parallelize to obtain satisfactory results.
In order to measure the execution time and the energy consumption of Watershed analysis, the MeterPU library is provided for advanced architectures, such as NVIDIA Tesla K80 and Intel
® Xeon
® Processor E5-2620 v4 CPU that we used at a Future SOC Lab. The experimental results of the sequential and parallel CUDA and OpenACC implementations on these architectures are presented in
Table 5,
Table 6,
Table 7 and
Table 8. The Speedup achieved for different parallel implementations with respect to the sequential ones is presented in
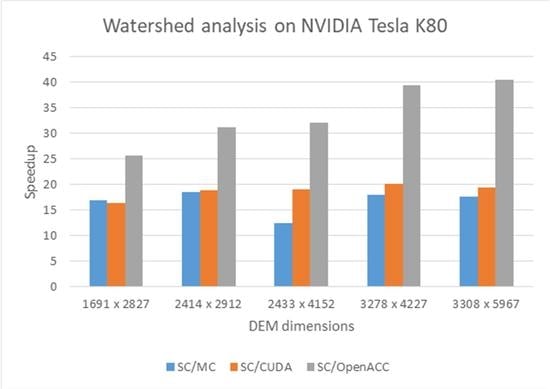
Table 9 and displayed in
Figure 9.
Based on
Table 5,
Table 6,
Table 7,
Table 8 and
Table 9 and
Figure 9, it can be concluded that OpenACC multi-core CPU implementation (marked as MC in
Figure 9) shows speedup on average 16.6 (maximum 18.5), CUDA many-core GPU implementation (marked as CUDA in
Figure 9) shows speedup on average 18.7 (maximum 20), and OpenACC many-core GPU implementation shows speedup on average 33.7 (maximum 40.6). These results show similar behavior to the previous results shown in
Figure 8, and they confirm previously presented conclusions. The obtained results are better with respect to the results shown in
Figure 8 because, this time, we used more powerful hardware. The significant difference in Speedup is especially visible in the case of OpenACC multi-core CPU solution since the Intel Xeon processor is used.
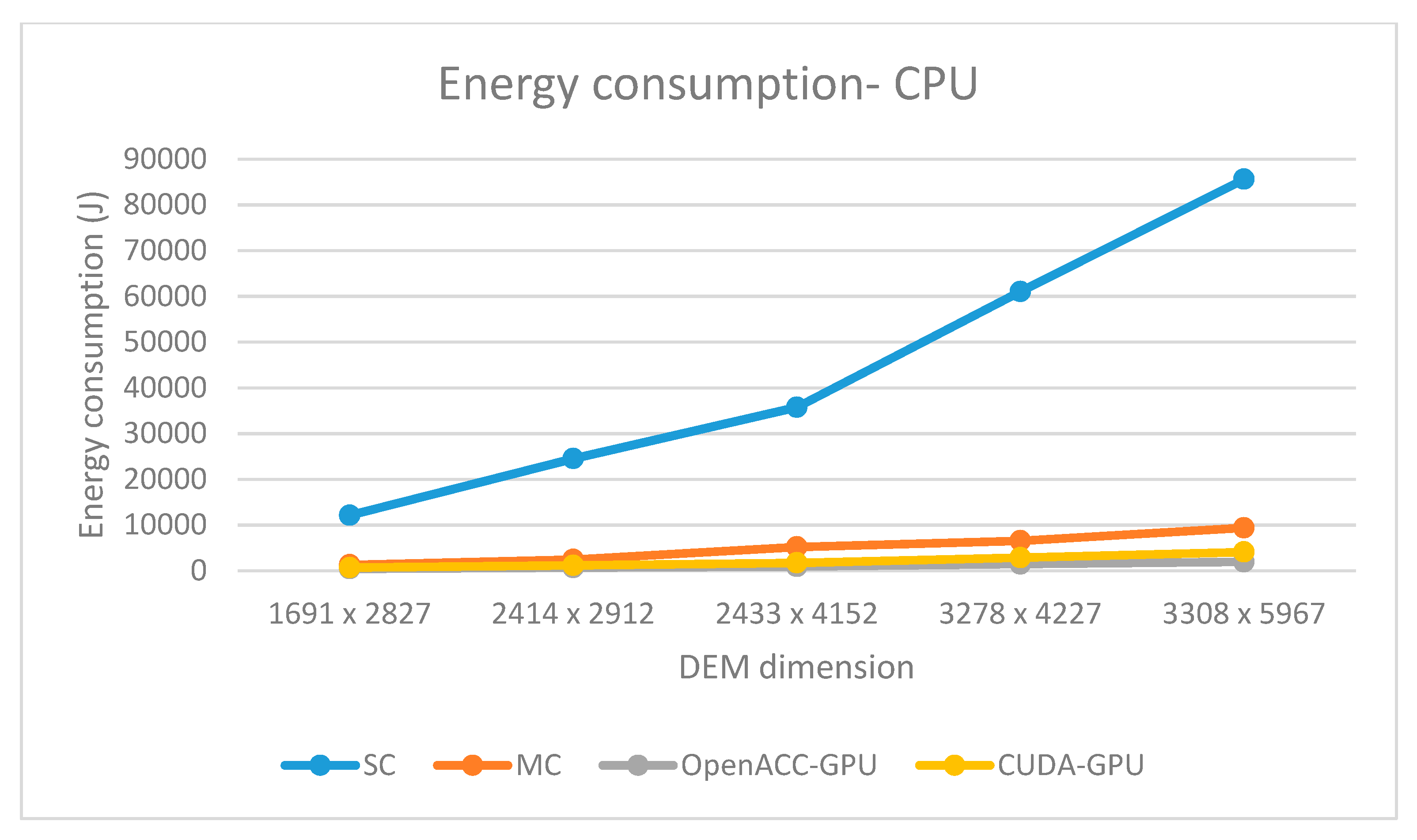
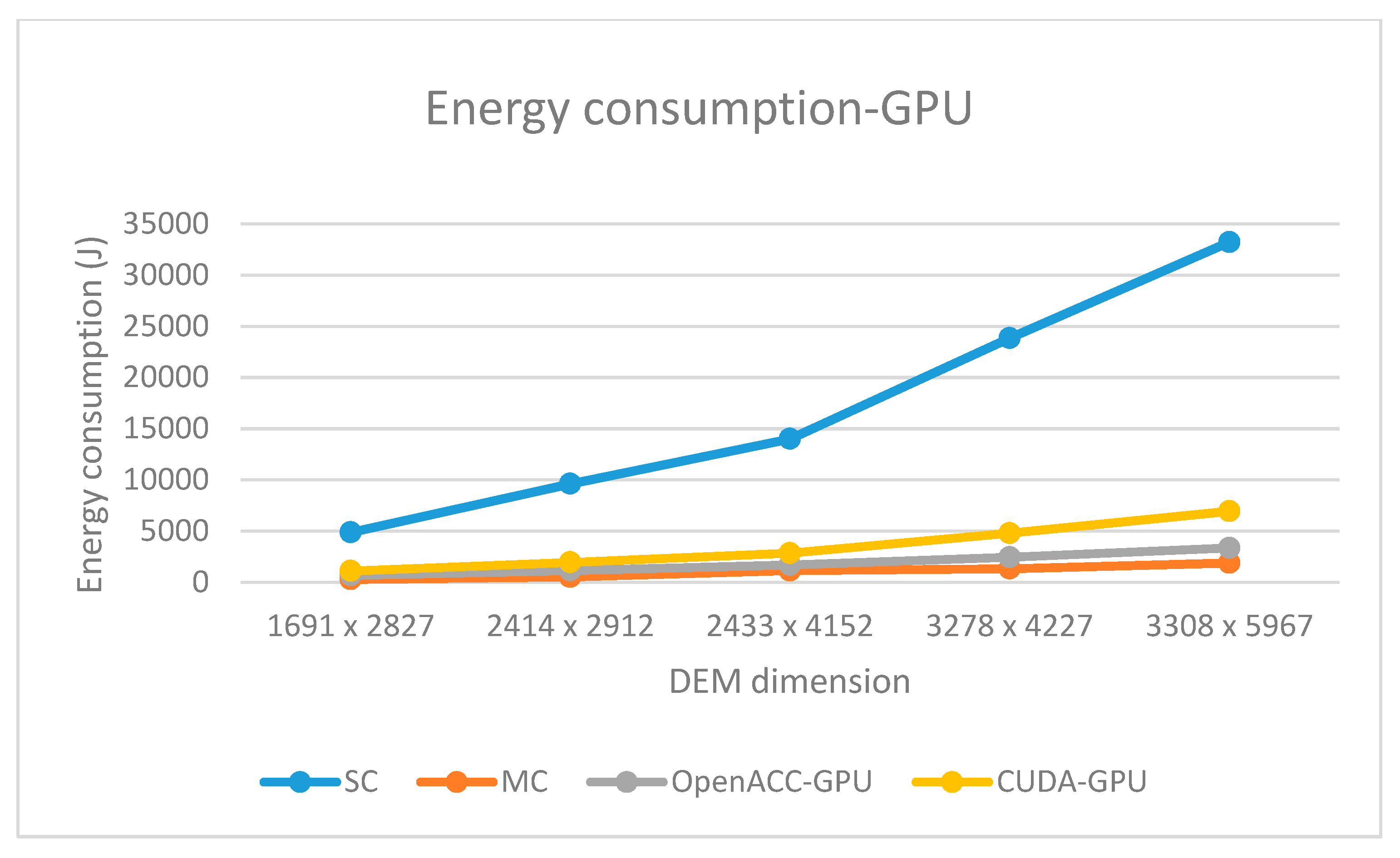
Regarding energy consumption, all parallel solutions consume less total energy (CPU+GPU) than the corresponding sequential solution. The total energy consumption of multi-core OpenACC solution is comparable to the CUDA GPU solution. The first one consumes more CPU energy while the second one consumes more GPU energy (
Figure 10 and
Figure 11). When comparing GPU-based solutions, OpenACC implementation consumes almost two times less energy than its CUDA counterpart (
Figure 11).
6. Conclusions
Advances in remote sensing, geo-sensor networks, and mobile positioning in recent years, have provided a generation of massive geospatial data of various formats. This has caused great interest in processing, analysis, and visualization of Big geospatial and spatio-temporal data, both offline and as fast data streams in recent years. GPGPU represents a new parallel computing paradigm that provides significant gains in term of performance improvements in various data intensive applications. This paper shows that using OpenACC and CUDA parallel programming paradigms can significantly improve the performance in executing various computation and data intensive GIS algorithms and that using parallelization and high-performance computing in GIS represents a promising direction for research and development.
The benefits of parallel processing of geospatial data is confirmed in parallelization of watershed analysis algorithms and they are evaluated on multi-core CPU and many-core GPU using CUDA and OpenACC frameworks.
Adaptation of sequential watershed algorithm implementation to many-core GPU requires significant code transformations and optimizations for CUDA parallel implementation, and that is why we considered OpenACC for parallel implementation for many-core GPU, but also for multi-core CPU. OpenACC requires less development effort, lower risk of errors, and better code readability with respect to the CUDA GPU solution. We have implemented the watershed analysis algorithm that consists of two computationally intensive and time-consuming phases: (1) iterative DEM preprocessing and (2) iterative MFD algorithm, which are both suitable for parallelization. Experimental evaluation indicates improvement in performance with respect to a single-core CPU-based solution and shows feasibility of using GPU and multicore CPU for watershed analysis. The evaluation of proposed solutions is performed with respect to execution time, energy consumption, and programming effort for program parallelization for a different size of input data. The experimental results show benefits of using the OpenACC framework over CUDA for parallelization of watershed analysis using the MFD algorithm and, thus, its feasibility for GIS analytic algorithms over Big raster and vector geospatial data.