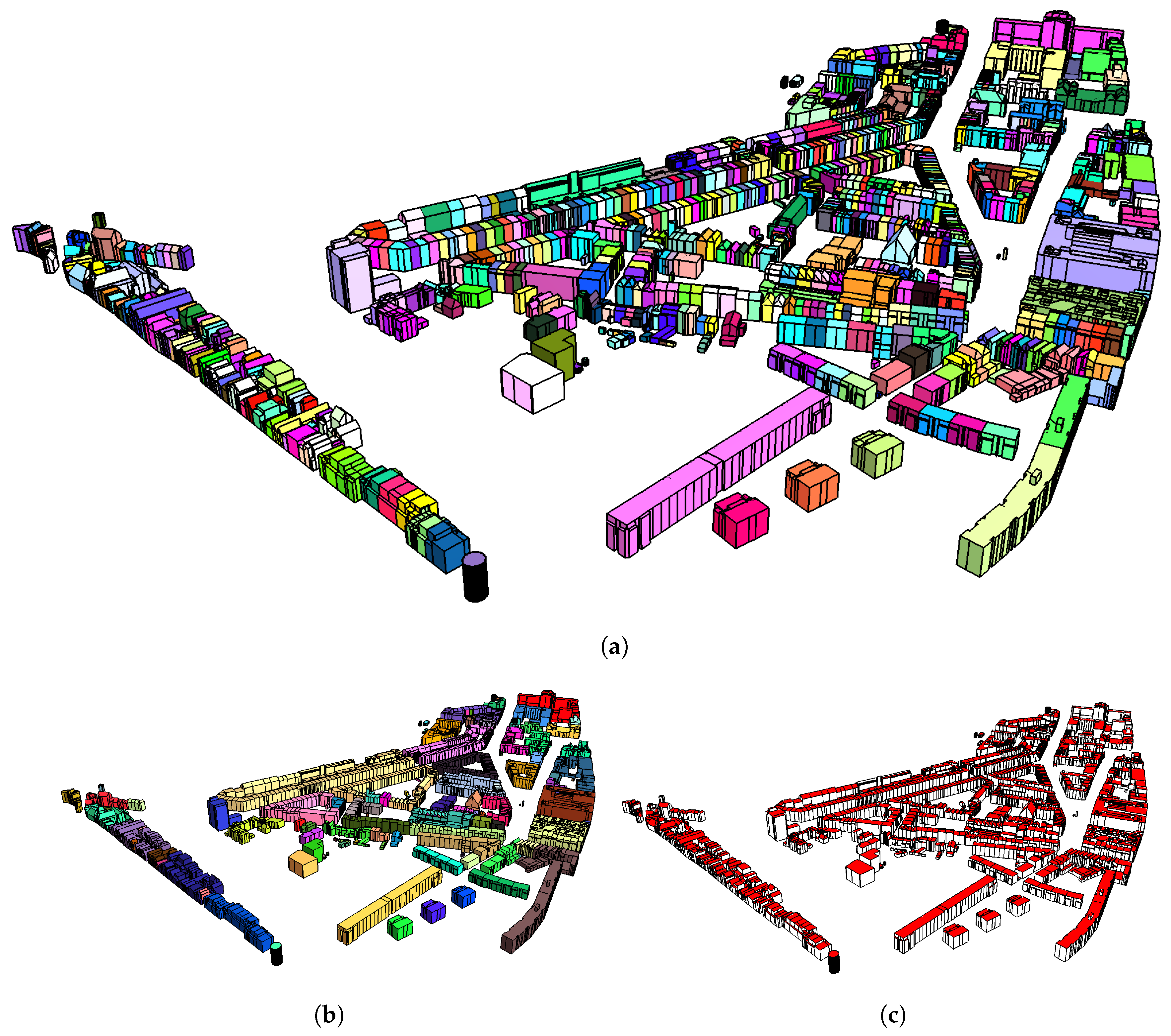
4.1. Algorithm
To validate our proposed extension, we developed an algorithm that parses a CityJSON model and appends the LCC information to the model. In [
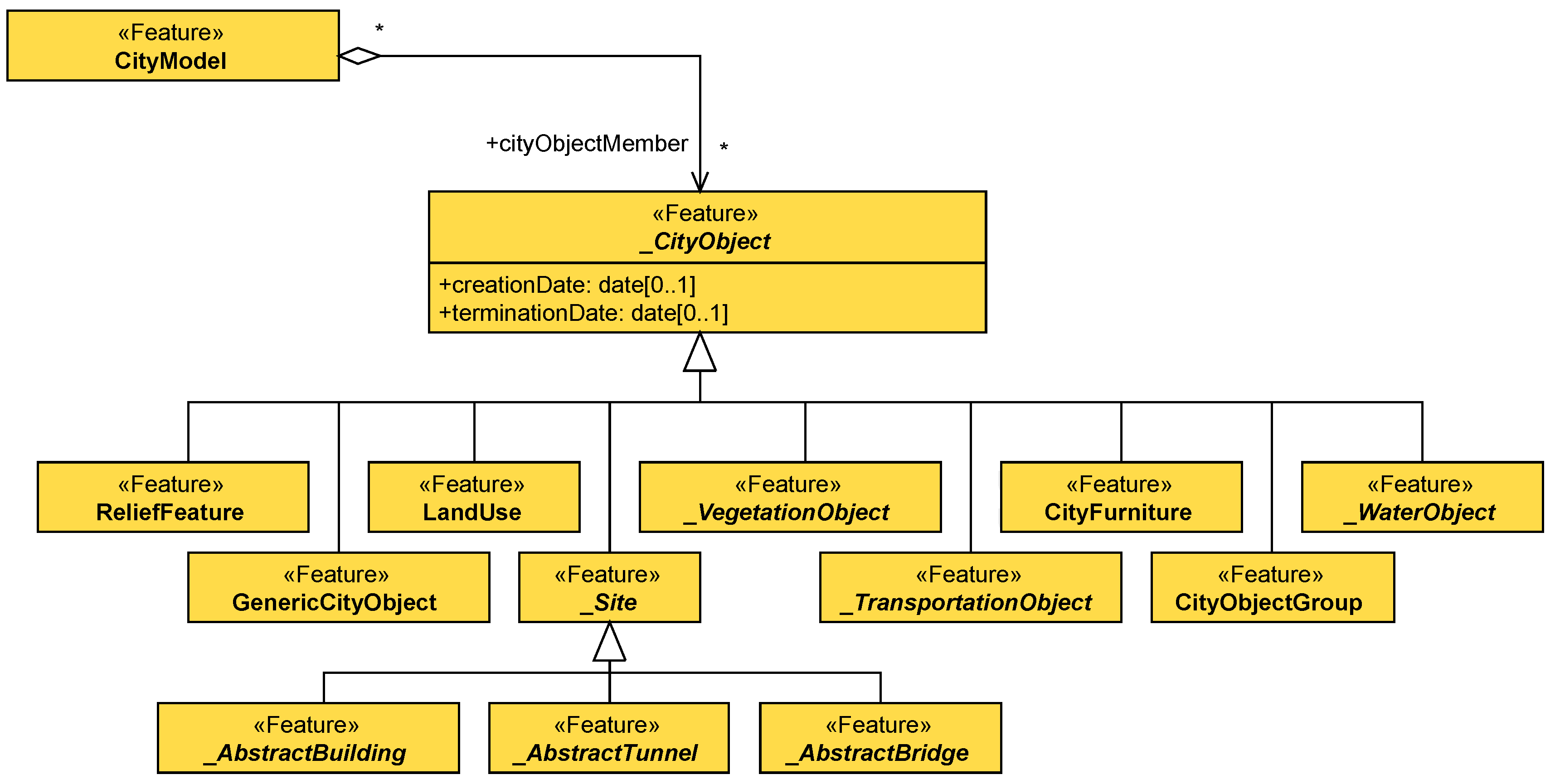
12], we proposed two variations of an algorithm that topologically reconstructs a CityGML model. For the purposes of the research presented in this article, we worked on the basis of the “geometric-oriented” algorithm. We chose this variation because it results in a true topological representation of the model. In addition, our proposed extension does not lose semantic information as it associates two-cells of the resulting LCC with the city model. Therefore, even when multiple city objects are represented under the same three-cell, the semantic association is retained.
We introduced a number of modifications to the original algorithm in order to adjust it towards the requirements of our research. First, the algorithm had to conform with a flat representation of city objects and geometries, as described by the CityJSON specification. Therefore, the recursive call in Algorithm 2 has been removed. Second, we only have to define the essential information that ensures a complete association between city objects and cells, as described in
Section 3.2. The resulting methodology is described by Algorithms 1–5.
We have to clarify that the purpose of the reconstruction is to describe the topological relationships between the geometries as described by the original dataset. No modification of the geometry is conducted during the reconstruction in order to ensure the topological validity of the resulting LCC.
Initially, the reconstruction is conducted by the main body (Algorithm 1). This function iterates through the city objects listed in the city model and calls ReadCityObject for every city object.
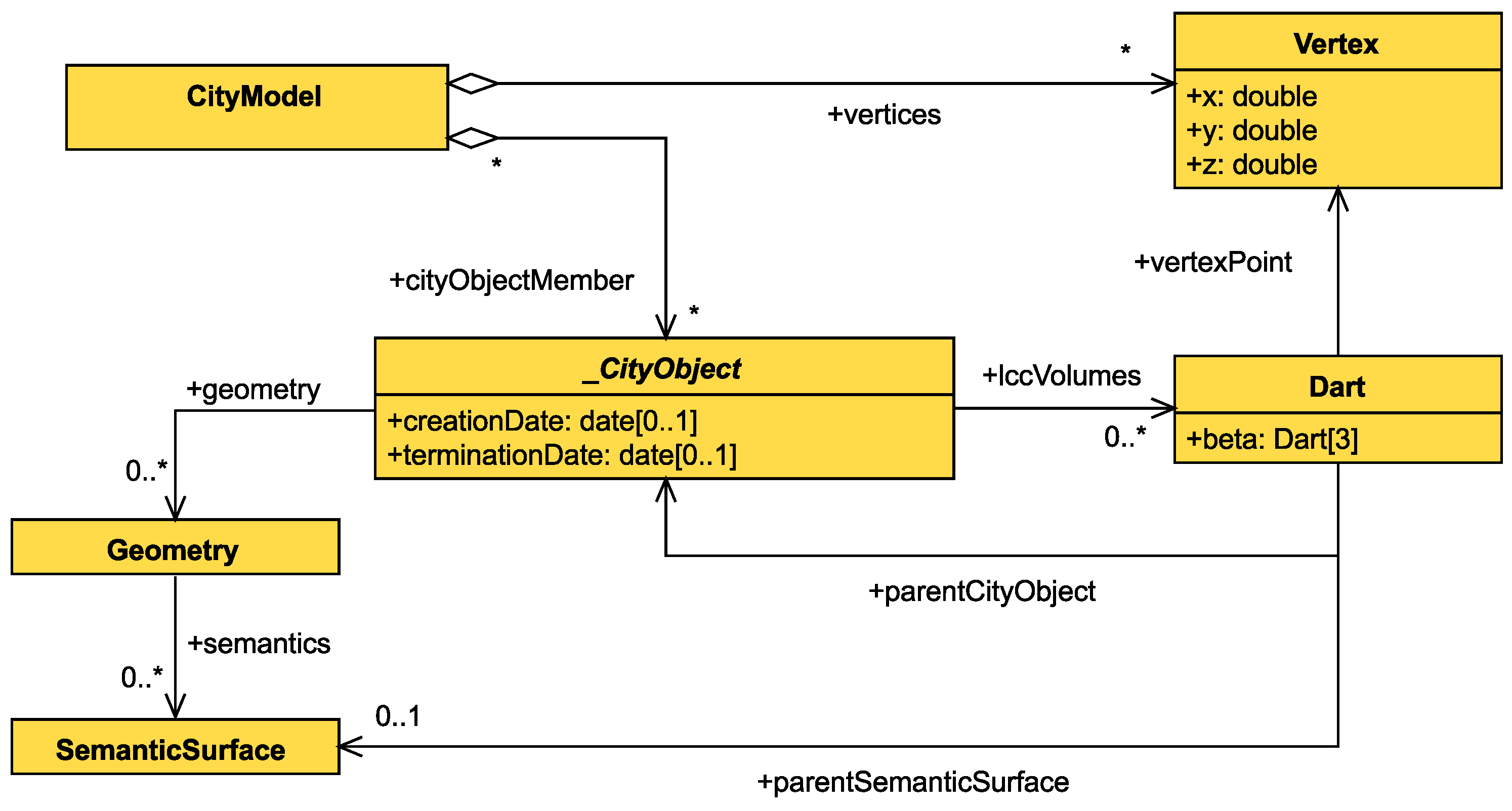
Function ReadCityObject (Algorithm 2) iterates through the geometries of the city object. For every geometry, function ReadGeometry is called and, then, the created darts’ two-attributes are associated to the object’s id and geometry’s id.
The ReadGeometry function (Algorithm 3) parses the geometry by getting all polygons that bound the object. For every polygon, the algorithm iterates through the edges and creates a dart that represents this edge, by calling GetEdge. The newly created dart that represents the edge is, then, associated with the semantic surface of the polygon by assigning the respective two-attribute value. Finally, the algorithm accesses the items of index in order to find adjacent three-free two-cells, in which case the two two-cells must be three-sewed. This ensures that volumes sharing a common surface are going to have their adjacency relationship represented in the resulting LCC.
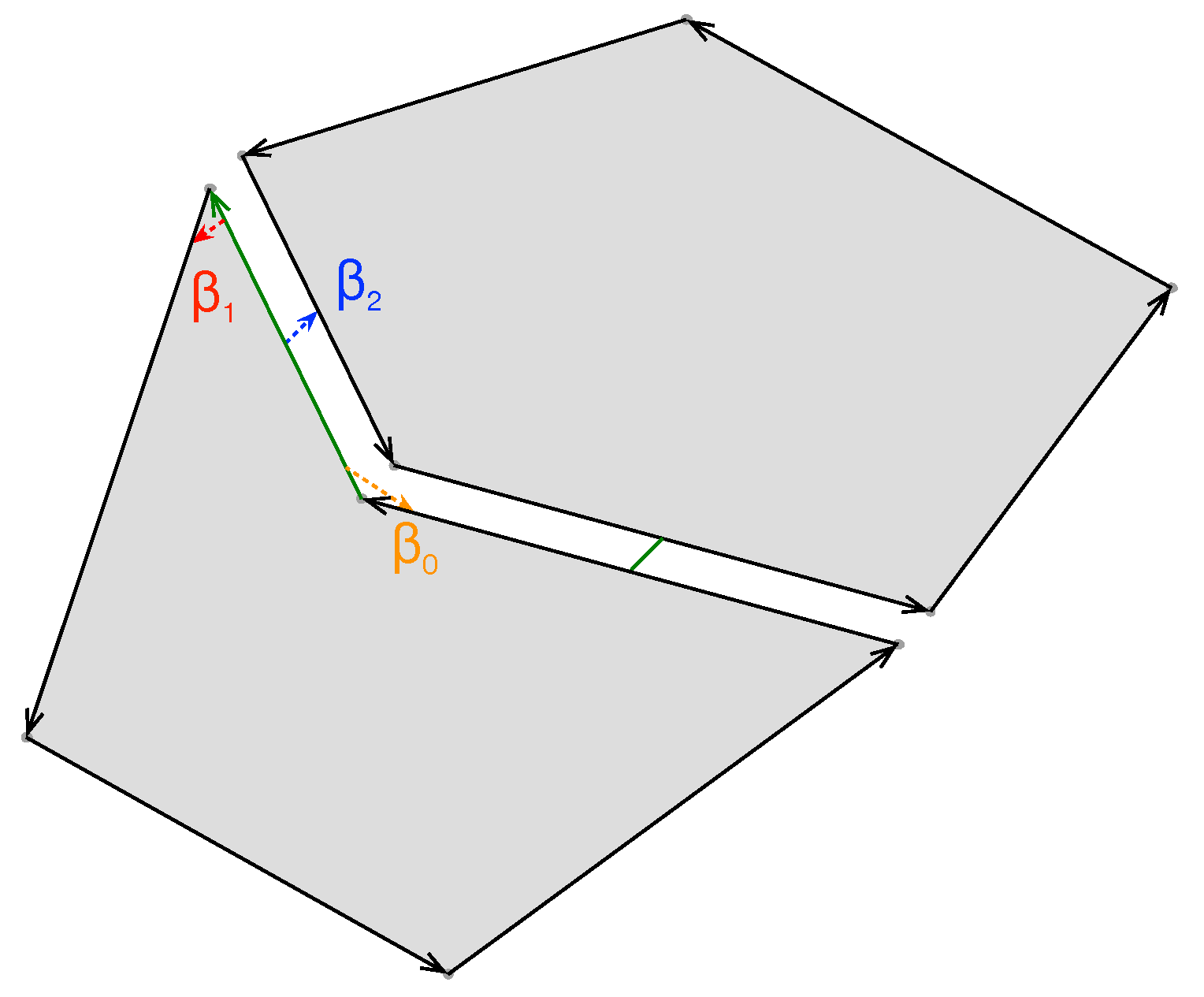
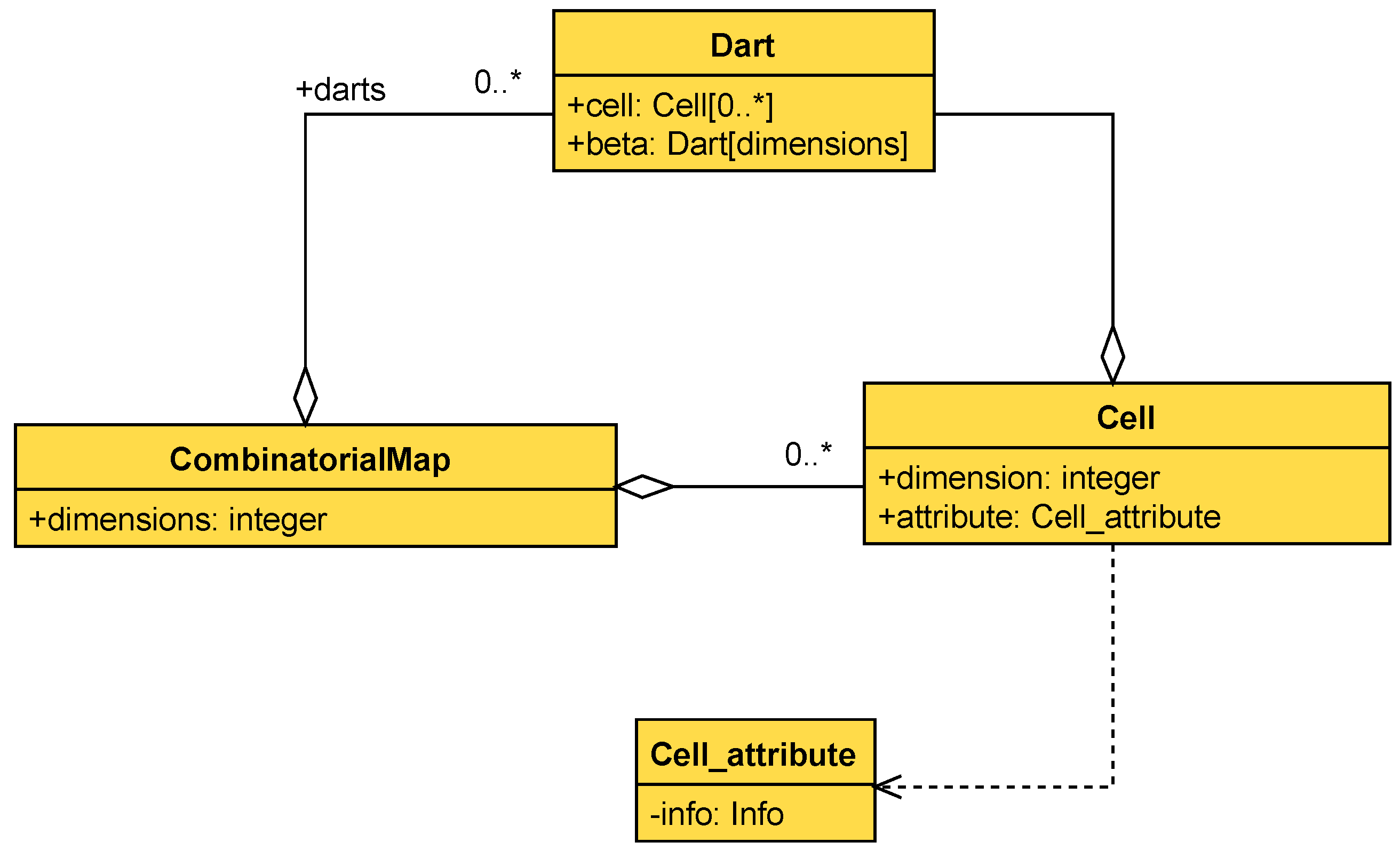
Function GetEdge (Algorithm 4) creates a dart that represents an edge, given the two end points of the edge. It gets one dart per point by calling the GetVertex function and then conducts a one-sew operation between them. Finally, it iterates through index in order to find adjacent two-free one-cells so that they can be two-sewed.
Finally, function GetVertex (Algorithm 5) is responsible for creating darts that represent a vertex in the LCC. The function iterates through the LCC in order to find existing one-free darts with the same coordinates as the point provided; if such a dart is found, it is returned. If no dart is found, the algorithm creates a new dart, associates the coordinates to its zero-attribute, and returns it.
| Algorithm 1: Main body of reconstruction. |
![Ijgi 08 00347 i005]() |
| Algorithm 2:ReadCityObject |
![Ijgi 08 00347 i006]() |
| Algorithm 3:ReadGeometry. |
![Ijgi 08 00347 i007]() |
| Algorithm 4:GetEdge. |
![Ijgi 08 00347 i008]() |
| Algorithm 5:GetVertex |
![Ijgi 08 00347 i009]() |
Algorithms 1–5 call each other in reverse order, meaning that GetEdge calls GetVertex, ReadGeometry calls GetEdge, etc. This means that the overall complexity is given by Algorithm 1. Individually, the complexity of the algorithms is as follows:
The runtime of GetVertex depends on the number of darts in the LCC (), i.e. its time complexity is of order .
GetEdge calls GetVertex twice, which means that the complexity of the first part of the algorithm is as well. In a reasonable implementation, the sewing operation should be constant time, while the insertion and deletion should be logarithmic, and thus would not change the overall complexity. Because of this, the time complexity is again of order .
ReadGeometry iterates through all vertices of the given geometry () and calls GetEdge, therefore the first iteration’s time complexity is of order . As the second iteration depends on , which does not change the order of complexity, the final time complexity of ReadGeometry is that of the first iteration: . This assumes the same logarithmic access to the index and constant time iteration from one dart to another (for sewing and setting attributes).
ReadCityObject iterates through all geometries of a city object and calls ReadGeometry for every one, which means that the previous calls to GetEdge are applied to every vertex of the city object (as opposed to those of a single two-cell). Therefore, the algorithm depends on the size of all vertices of all geometries () and in accordance with ReadGeometry complexity it is of order ).
Finally, the main iteration repeats ReadCityObject for every city object. Following the same logic as before, GetEdge ends up being called for every vertex of the city model (). Therefore, the time complexity of the algorithm is of order ).