Modeling the Vagueness of Areal Geographic Objects: A Categorization System
Abstract
1. Introduction
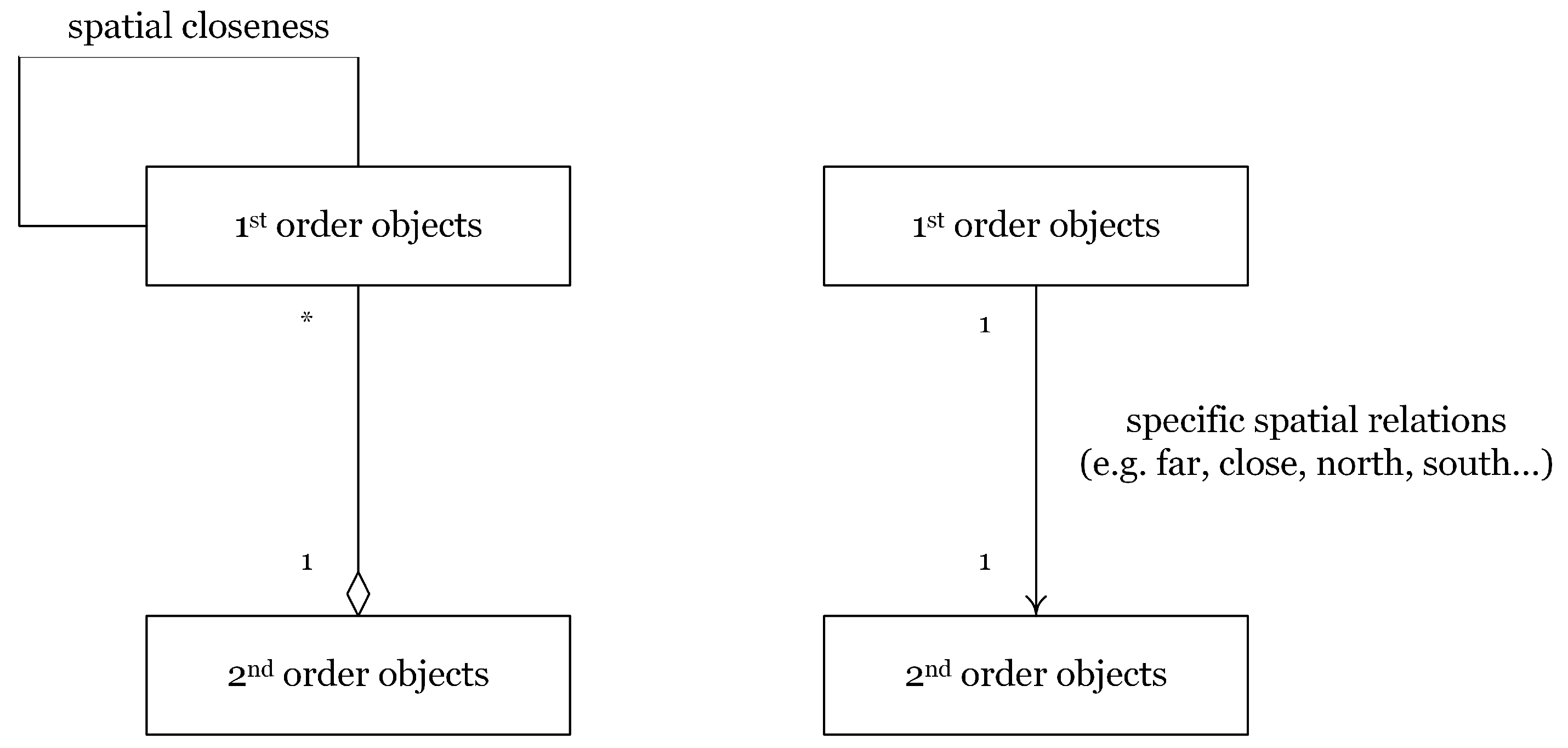
2. Modeling Vague Regions from an Ontological Perspective
3. A Categorization System for Vague Regions
3.1. Five Categories of Vague Regions
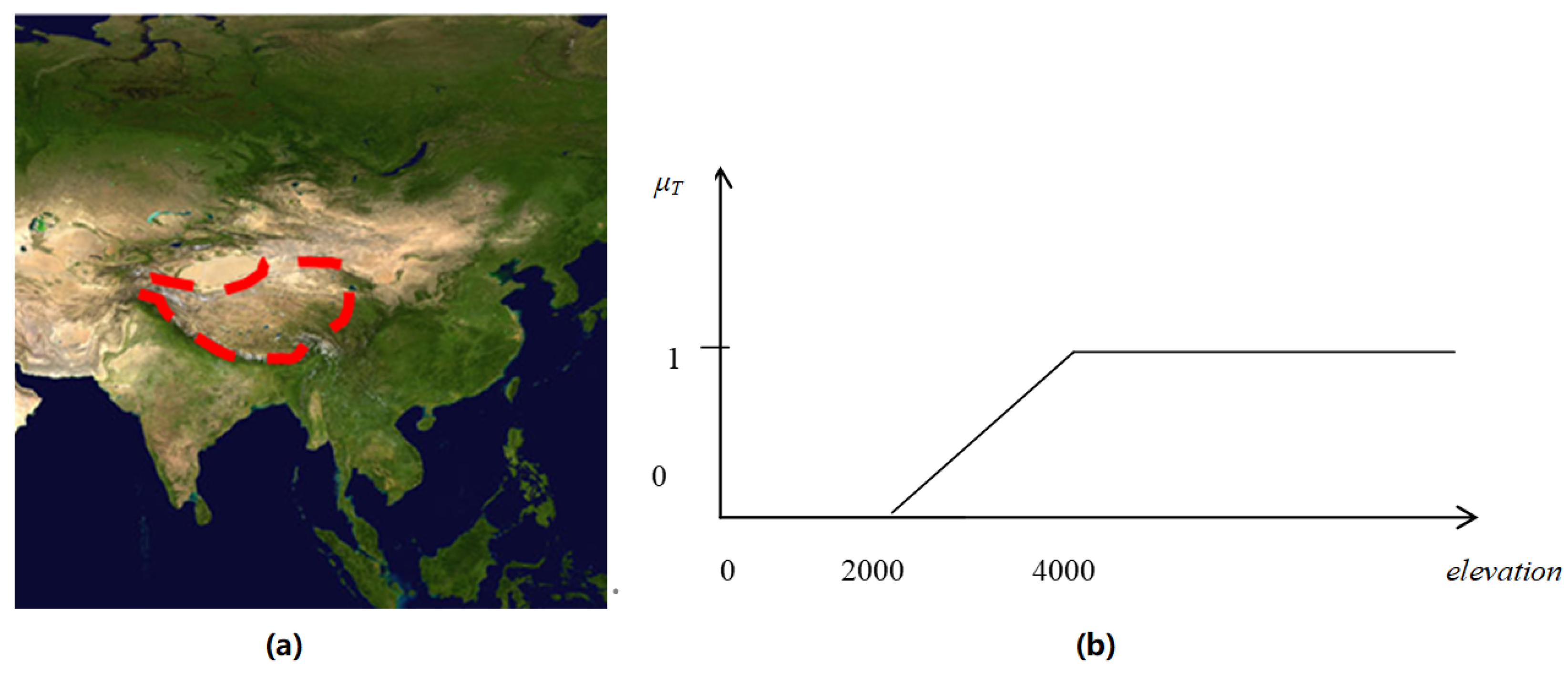
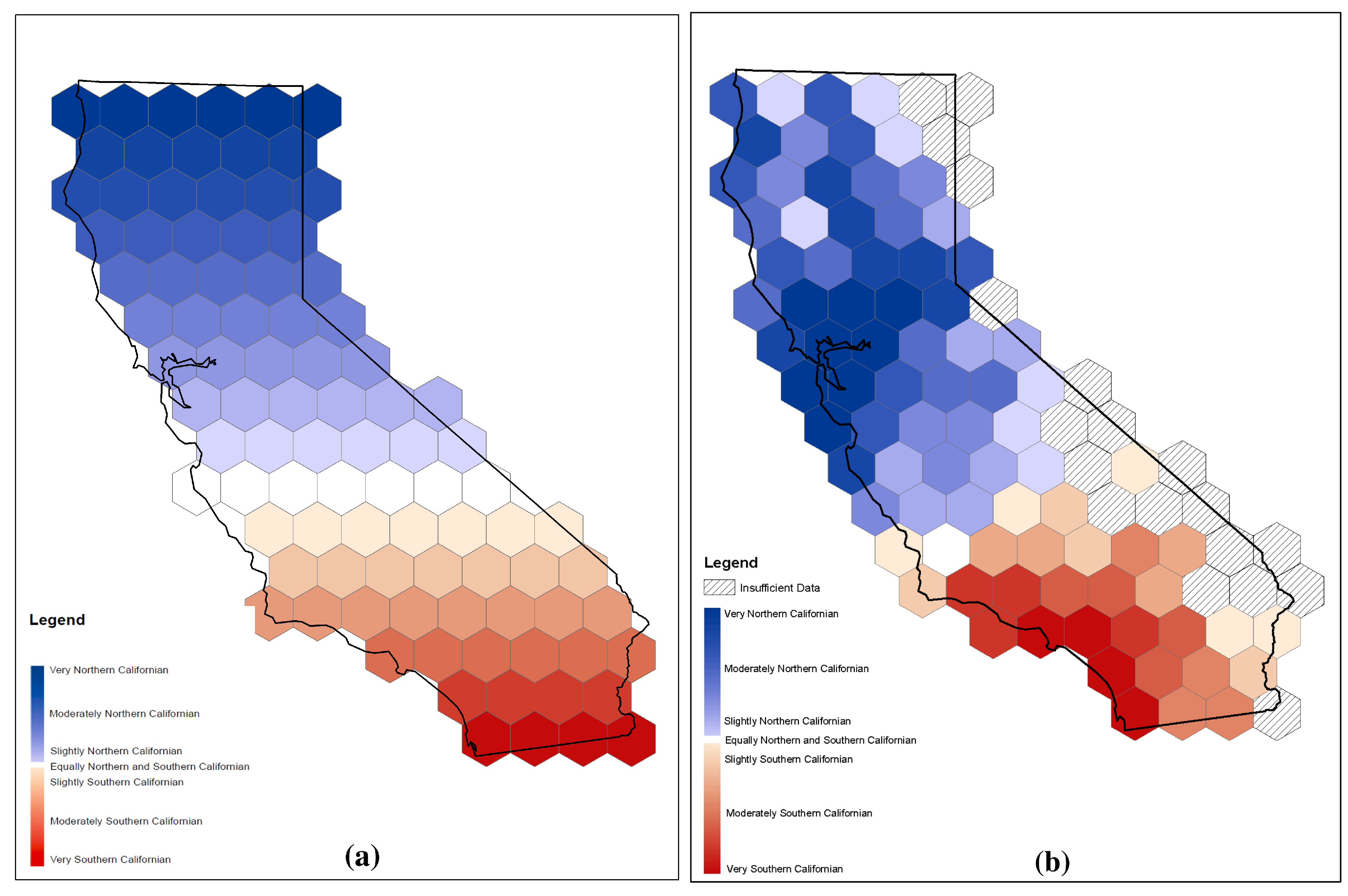
3.1.1. Direct Field-Cutting Objects
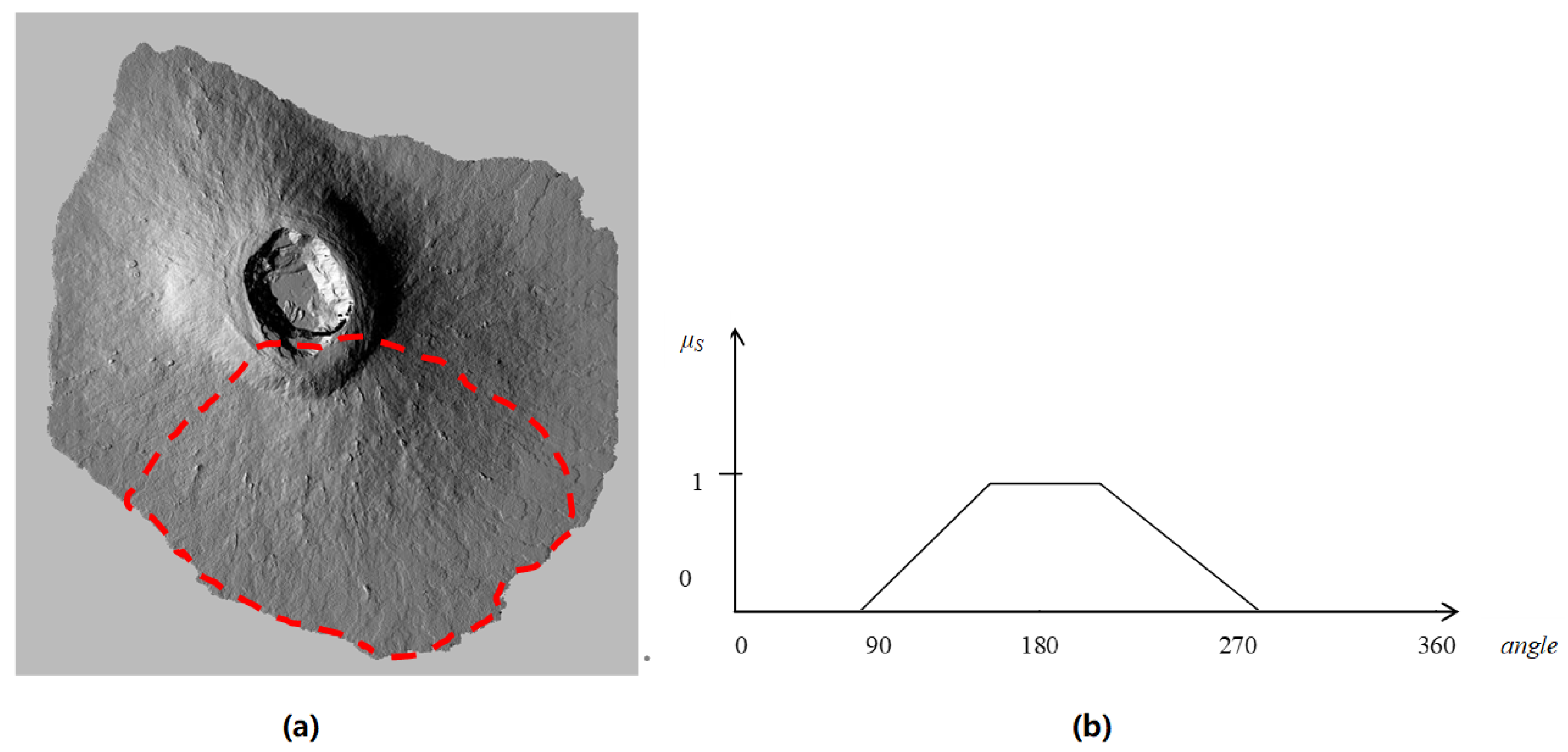
3.1.2. Focal Operation-Based Field-Cutting Objects
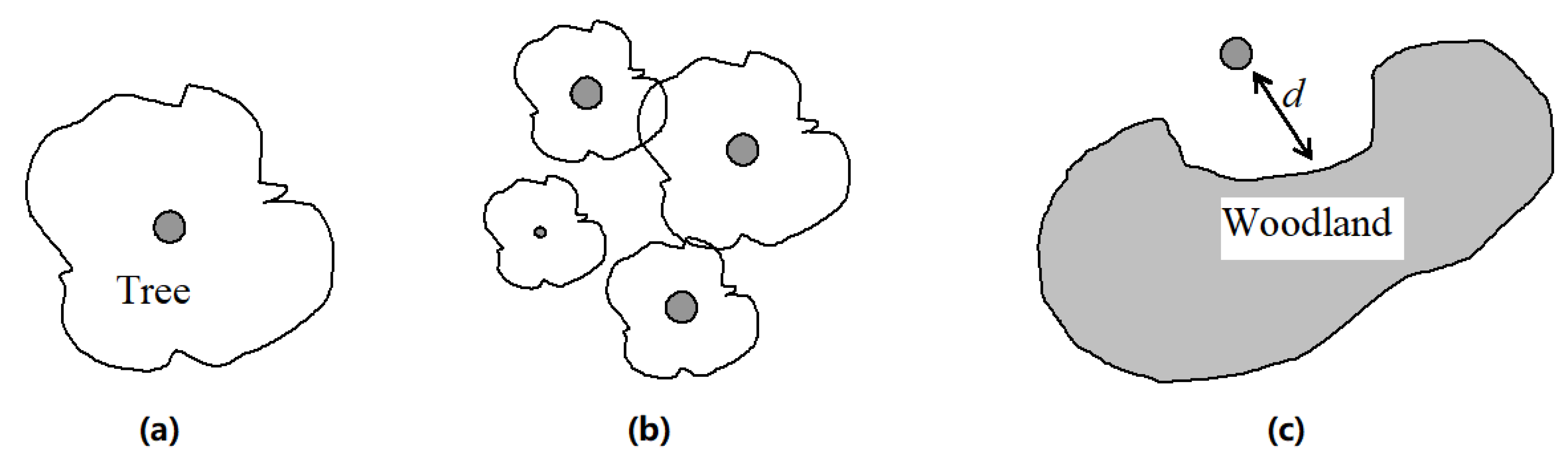
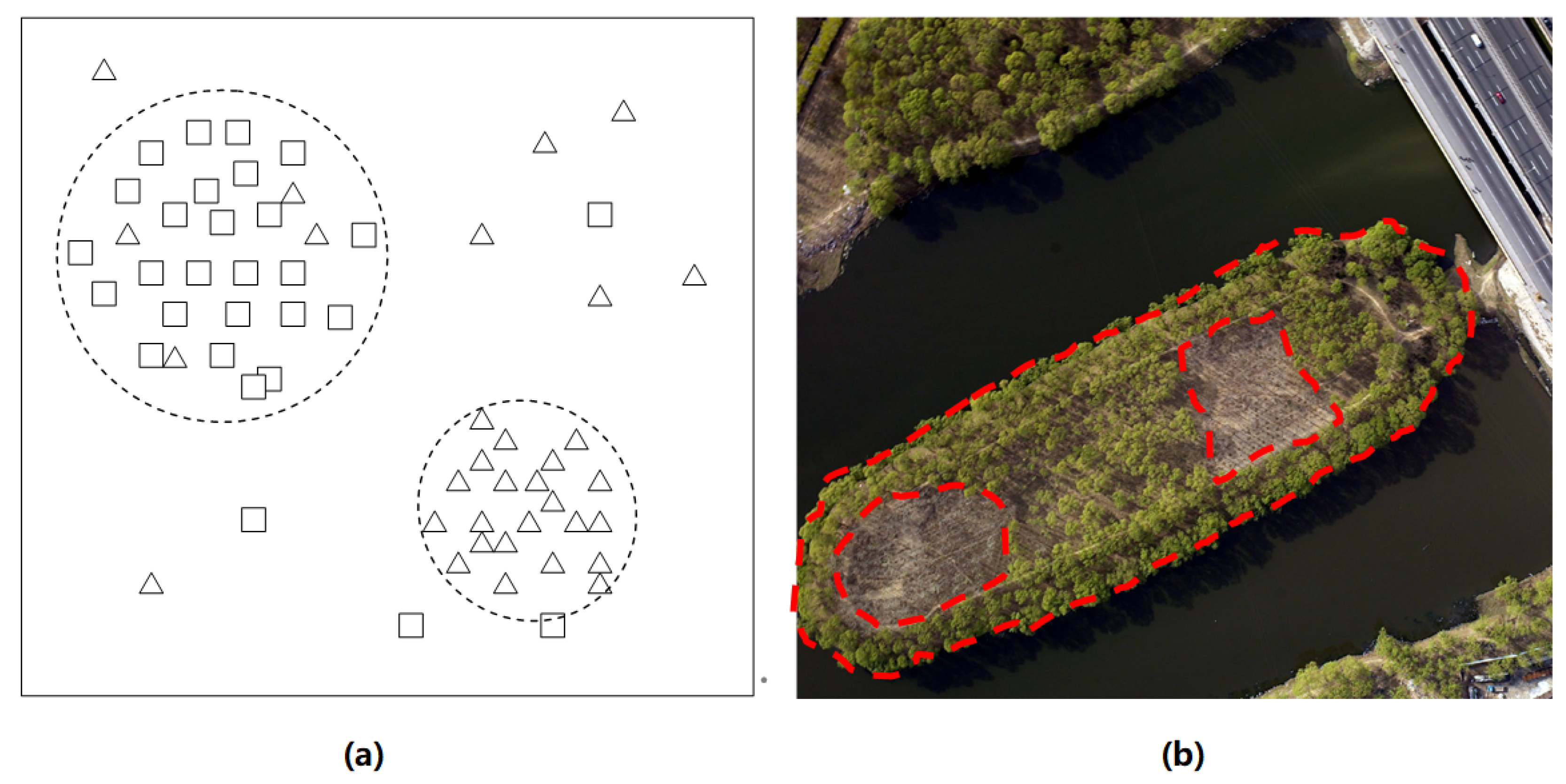
3.1.3. Element-Clustering Objects
3.1.4. Object-Referenced Objects
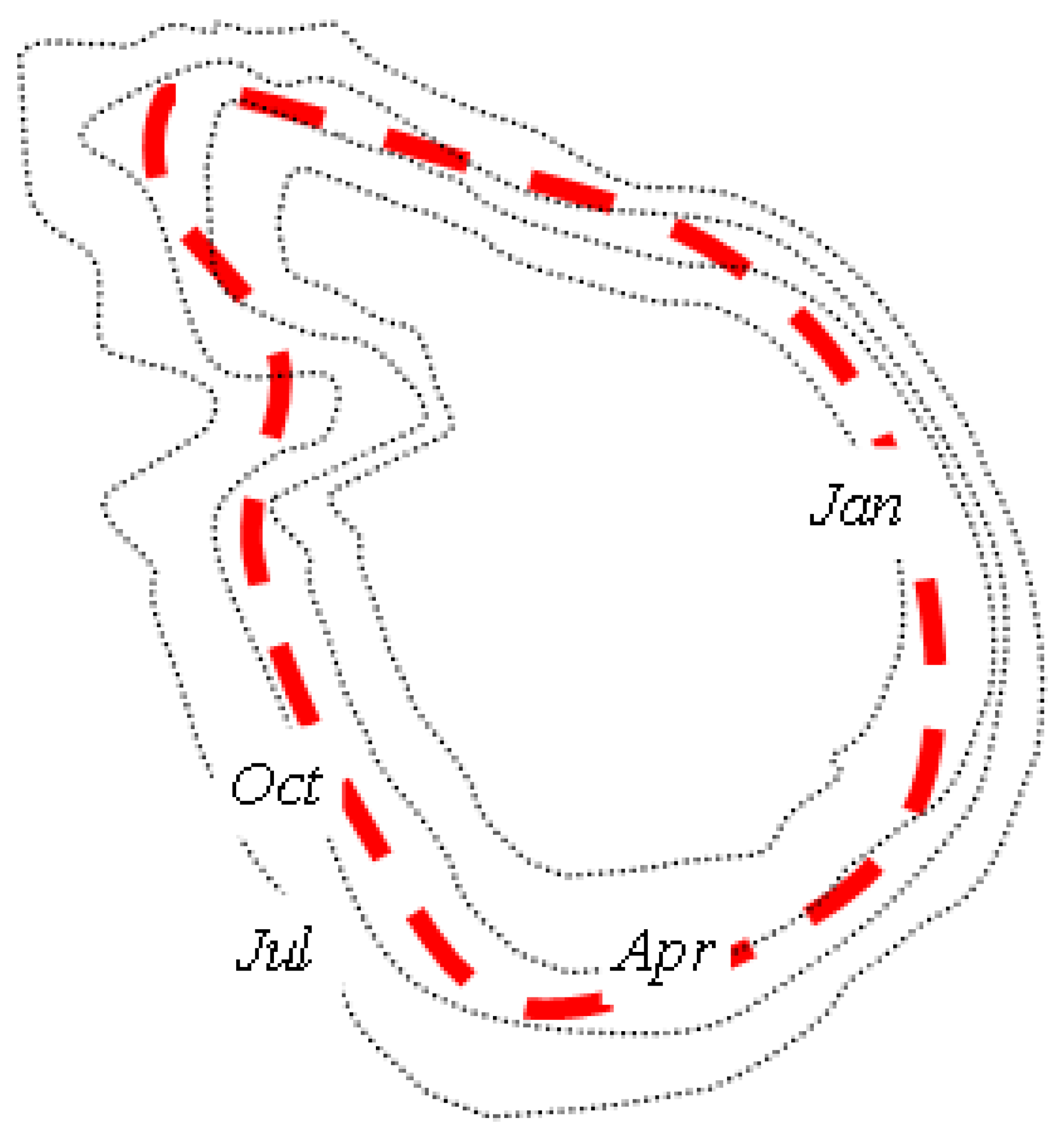
3.1.5. Dynamic Boundary Objects
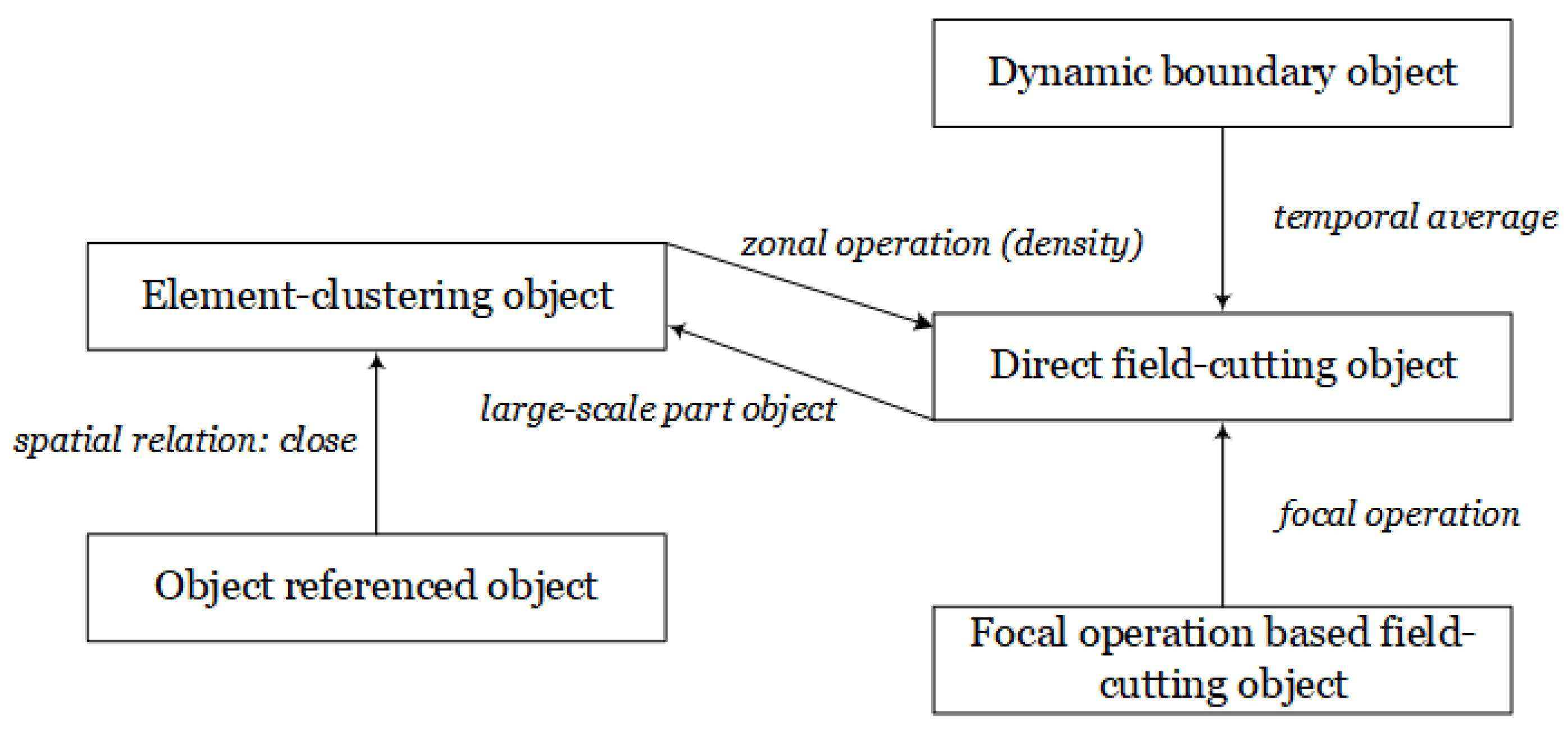
3.2. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MF | Membership function |
| DFCO | Direct field-cutting object |
| FoFCO | Focal operation based field-cutting object |
| ECO | Element-clustering object |
| ORO | Object-referenced object |
| DBO | Dynamic boundary object |
References
- Couclelis, H. Towards an operational typology of geographic entities with ill-defined boundaries. In Geographic Objects with Indeterminate Boundaries; Burrough, P.A., Frank, A.U., Eds.; Taylor & Francis: London, UK, 1996; pp. 45–55. [Google Scholar]
- Varzi, A.C. Vagueness in geography. Philos. Geogr. 2001, 4, 49–65. [Google Scholar] [CrossRef]
- Burrough, P.A. Natural objects with indeterminate boundaries. In Geographic Objects with Indeterminate Boundaries; Burrough, P.A., Frank, A.U., Eds.; Taylor & Francis: London, UK, 1996; pp. 3–28. [Google Scholar]
- Smith, B.; Mark, D.M. Do mountains exist? Towards an ontology of landforms. Environ. Plan. B 2007, 30, 411–427. [Google Scholar] [CrossRef]
- Fisher, P.; Cheng, T.; Wood, J. Higher order vagueness in geographical information: Empirical geographical population of type n fuzzy sets. Geoinformatica 2007, 11, 311–330. [Google Scholar] [CrossRef]
- Cheng, T.; Molenaar, M.; Lin, H. Formalizing fuzzy objects from uncertain classification results. Int. J. Geogr. Inf. Sci. 2001, 15, 27–42. [Google Scholar] [CrossRef]
- Montello, D.R.; Goodchild, M.F.; Gottsegen, J.; Fohl, P. Where’s downtown? Behavioral methods for determining referents of vague spatial queries. Spat. Cognit. Comput. 2003, 3, 185–204. [Google Scholar]
- Fisher, P.; Arnot, C.; Wadsworth, R.; Wellens, J. Detecting change in vague interpretations of landscapes. Ecol. Inform. 2006, 1, 163–178. [Google Scholar] [CrossRef]
- Foody, G.M. A fuzzy set approach to the representation of vegetation continua from remote-sensed data: An example from lowland heath. Photogeom. Eng. Remote Sens. 1992, 58, 221–225. [Google Scholar]
- Brown, D.G. Mapping historical forest types in Baraga County Michigan, USA as fuzzy sets. Plant Ecol. 1998, 134, 97–111. [Google Scholar] [CrossRef]
- Bennett, B. What is a forest? On the vagueness of certain geographic concepts. Topoi 2001, 20, 189–201. [Google Scholar] [CrossRef]
- Kronenfeld, B.J. Gradation and map analysis in area-class maps. In Proceedings of the COSIT 2005; Cohn, A.G., Mark, D.M., Eds.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 2005; Volume 3693, pp. 330–351. [Google Scholar]
- Worboys, M.F. Clementini, E. Integration of imperfect spatial information. J. Vis. Lang. Comput. 2001, 12, 61–80. [Google Scholar] [CrossRef]
- Gao, S.; Janowicz, K.; Montello, D.R.; Hu, Y.; Yang, J.-A.; McKenzie, G.; Ju, Y.; Gong, L.; Adams, B.; Yan, B. A data-synthesis-driven method for detecting and extracting vague cognitive regions. Int. J. Geogr. Inf. Sci. 2017, 31, 1245–1271. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Schneider, M. Uncertainty management for spatial data in databases: Fuzzy spatial data types. In Proceedings of the SSD’99; Guting, R.H., Papadias, D., Lochovsky, F., Eds.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 1999; Volume 1651, pp. 330–351. [Google Scholar]
- Fonte, C.C.; Lodwick, W.A. Areas of fuzzy geographical entities. Int. J. Geogr. Inf. Sci. 2004, 18, 127–150. [Google Scholar] [CrossRef]
- Cohn, A.G.; Gotts, N.M. The ‘egg-yolk’ representation of regions with indeterminate boundaries. In Geographic Objects with Indeterminate Boundaries; Burrough, P.A., Frank, A.U., Eds.; Taylor & Francis: London, UK, 1996; pp. 171–188. [Google Scholar]
- Shi, W.; Liu, K. Modeling fuzzy topological relations between uncertain objects in a GIS. Photogramm. Eng. Remote Sens. 2004, 70, 921–929. [Google Scholar] [CrossRef]
- Zhan, F.B.; Lin, H. Overlay of two simple polygons with indeterminate boundaries. Trans. GIS 2003, 7, 67–81. [Google Scholar] [CrossRef]
- Dilo, A.; de By, R.A.; Stein, A. A system of types and operators for handling vague spatial objects. Int. J. Geogr. Inf. Sci. 2007, 21, 397–426. [Google Scholar] [CrossRef]
- Jones, C.B.; Purves, R.S.; Clough, P.D.; Joho, H. Modeling vague places with knowledge from the Web. Int. J. Geogr. Inf. Sci. 2008, 22, 1045–1065. [Google Scholar] [CrossRef]
- Wang, D.; Laffan, S.W.; Liu, Y.; Wu, L. Morphometric characterisation of landform from DEMs. Int. J. Geogr. Inf. Sci. 2010, 24, 305–326. [Google Scholar] [CrossRef]
- Couclelis, H. People manipulate objects (but cultivate fields): Beyond the raster-vector debate in GIS. In Theories and Methods of Spatio-Temporal Reasoning in Geographic Space; Frank, A.U., Campari, I., Eds.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 1992; Volume 639, pp. 65–77. [Google Scholar]
- Goodchild, M.F. Geographical data modeling. Comput. Geosci. 1992, 18, 401–408. [Google Scholar] [CrossRef]
- Bian, L. Object-oriented representation of environmental phenomena: Is everything best represented as an object? Ann. Assoc. Am. Geogr. 2007, 97, 267–281. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Yuan, M.; Cova, T.J. Towards a general theory of geographic representation in GIS. Int. J. Geogr. Inf. Sci. 2007, 21, 239–260. [Google Scholar] [CrossRef]
- Liu, Y.; Goodchild, M.F.; Guo, Q.; Tian, Y.; Wu, L. Towards a General Field model and its order in GIS. Int. J. Geogr. Inf. Sci. 2008, 22, 623–643. [Google Scholar] [CrossRef]
- Goodchild, M.F. Modeling error in objects and field. In Accuracy of Spatial Databases; Goodchild, M.F., Gopal, S., Eds.; Taylor & Francis: London, UK, 1989; pp. 107–114. [Google Scholar]
- Liu, Y.; Yuan, Y.; Xiao, D.; Zhang, Y.; Hu, J. A point-set-based approximation for areal objects: A case study of representing localities. Comput. Environ. Urb. Syst. 2010, 34, 28–39. [Google Scholar] [CrossRef]
- Longley, P.A.; Goodchild, M.F.; Maguire, D.J.; Rhind, D.W. Geographic Information Science and Systems, 4th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Cova, T.J.; Goodchild, M.F. Extending geographical representation to include fields of spatial objects. Int. J. Geogr. Inf. Sci. 2002, 16, 509–532. [Google Scholar] [CrossRef]
- Freksa, C.; Barkowsky, T. On the relations between spatial concept and geographic objects. In Geographic Objects with Indeterminate Boundaries; Burrough, P.A., Frank, A.U., Eds.; Taylor & Francis: London, UK, 1996; pp. 109–121. [Google Scholar]
- Mark, D.M.; Smith, B.; Tversky, B. Ontology and geographic objects: An empirical study of cognitive categorization. In Proceedings of the COSIT 1999; Freksa, C., Mark, D.M., Eds.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 1999; Volume 1661, pp. 283–298. [Google Scholar]
- Mark, D.M.; Skupin, A.; Smith, B. Features, objects, and other things: Ontological distinctions in the geographic domain. In Proceedings of the COSIT 2001; Montello, D.R., Ed.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 2001; Volume 2205, pp. 489–502. [Google Scholar]
- Smith, B. On drawing lines on a map. In Proceedings of the COSIT 1995; Frank, A.U., Kuhn, W., Eds.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 1995; Volume 988, pp. 475–484. [Google Scholar]
- Yan, Y.; Feng, C.-C.; Wang, Y.-C. Utilizing fuzzy set theory to assure the quality of volunteered geographic information. GeoJournal 2017, 82, 517–532. [Google Scholar] [CrossRef]
- Jamil, M.; Ahmed, R.; Sajjad, H. Land suitability assessment for sugarcane cultivation in Bijnor district, India using geographic information system and fuzzy analytical hierarchy process. GeoJournal 2018, 83, 596–611. [Google Scholar] [CrossRef]
- Bovkir, R.; Aydinoglu, A.C. Providing land value information from geographic data infrastructure by using fuzzy logic analysis approach. Land Use Policy 2018, 78, 46–60. [Google Scholar] [CrossRef]
- Tomlin, D. Geographic Information Systems and Cartographic Modeling; Prentice-Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Burrough, P.A.; McDonell, R.A. Principles of Geographical Information Systems; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- McKenzie, G.; Adams, B. Juxtaposing thematic regions derived from spatial and platial user-generated content. In Proceedings of the COSIT 2017; Clementini, E., Donnelly, M., Yuan, M., Kray, C., Fogliaroni, P., Ballatore, A., Eds.; Leibniz International Proceedings in Informatics (LIPIcs); Dagstuhl Publishing: Dagstuhl, Germany, 2017; Volume 86, pp. 20:1–20:14. [Google Scholar]
- Goodchild, M.F. A geographer looks at spatial information theory. In Proceedings of the COSIT 2001; Montello, D.R., Ed.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 2001; Volume 2205, pp. 1–13. [Google Scholar]
- Papadimitriou, F. The Algorithmic Complexity of Landscapes. Landsc. Res. 2012, 37, 599–611. [Google Scholar] [CrossRef]
- Frank, A.U. Qualitative spatial reasoning about distances and directions in geographic space. J. Vis. Lang. Comput. 1992, 3, 343–371. [Google Scholar] [CrossRef]
- Cohn, A.G.; Hazarika, S.M. Qualitative spatial representation and reasoning: An overview. Fundam. Inform. 2001, 46, 1–29. [Google Scholar]
- Liu, Y.; Wang, X.; Jin, X.; Wu, L. On internal cardinal direction relations. In Proceedings of the COSIT 2005; Cohn, A.G., Mark, D.M., Eds.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 2005; Volume 3693, pp. 283–299. [Google Scholar]
- Papadias, D.; Karacapilidis, N.; Arkoumanis, D. Processing fuzzy spatial queries: A configuration similarity approach. Int. J. Geogr. Inf. Sci. 1999, 13, 93–118. [Google Scholar] [CrossRef]
- Dutta, S. Qualitative spatial reasoning: A semi-quantitative approach using fuzzy logic. In Proceedings of the First Symposium on Design and Implementation of Large Spatial Databases; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 1990; Volume 409, pp. 345–364. [Google Scholar]
- Yao, X.; Thill, J.-C. Spatial queries with qualitative locations in spatial information systems. Comput. Environ. Urban Syst. 2006, 30, 485–502. [Google Scholar] [CrossRef]
- Montello, D.R. Regions in geography: Process and content. In Foundations of Geographic Information Science; Goodchild, M.F., Worboys, M.F., Eds.; Taylor & Francis: London, UK, 2003; pp. 173–189. [Google Scholar]
- Galton, A. Fields and objects in space, time, and space-time. Spat. Cognit. Comput. 2004, 4, 1–29. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit Region. Econom. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yuan, Y.; Gao, S. Modeling the Vagueness of Areal Geographic Objects: A Categorization System. ISPRS Int. J. Geo-Inf. 2019, 8, 306. https://doi.org/10.3390/ijgi8070306
Liu Y, Yuan Y, Gao S. Modeling the Vagueness of Areal Geographic Objects: A Categorization System. ISPRS International Journal of Geo-Information. 2019; 8(7):306. https://doi.org/10.3390/ijgi8070306
Chicago/Turabian StyleLiu, Yu, Yihong Yuan, and Song Gao. 2019. "Modeling the Vagueness of Areal Geographic Objects: A Categorization System" ISPRS International Journal of Geo-Information 8, no. 7: 306. https://doi.org/10.3390/ijgi8070306
APA StyleLiu, Y., Yuan, Y., & Gao, S. (2019). Modeling the Vagueness of Areal Geographic Objects: A Categorization System. ISPRS International Journal of Geo-Information, 8(7), 306. https://doi.org/10.3390/ijgi8070306




